Parçalı Fonksiyonların İntegrali
Konu tekrarı için: Parçalı Fonksiyonlar
Tanım kümesinin farklı aralıklarında farklı tanımlara sahip olan fonksiyonlara parçalı fonksiyon denir. Bir parçalı fonksiyonun farklı tanıma sahip olduğu alt aralıklara fonksiyonun dalları ya da parçaları, fonksiyon tanımının değiştiği noktalara fonksiyonun geçiş noktaları denir.
Bir parçalı fonksiyonun bir ya da birden fazla geçiş noktasını içeren bir aralıkta belirli integralini tek bir integral işlemiyle alamayız. Buna göre bir parçalı fonksiyonun belirli integralini alırken izlememiz gereken yöntem aşağıdaki gibidir.
- Eğer fonksiyonun bir geçiş noktasını içeren bir aralıkta integrali alınıyorsa integral işlemi her biri parçalı fonksiyonun tek bir tanımına karşılık gelecek şekilde birden fazla integral işleminin toplamı şeklinde yazılır.
- Eğer integral işleminin sınır değerleri parçalı fonksiyonun tek bir tanımına karşılık geliyorsa bu tanım kullanılarak integral tek işlemde alınır.
Bir parçalı fonksiyonun bir geçiş noktasını içeren bir aralıkta integralinin alınabilmesi için fonksiyonun bu noktada limitli, sürekli ya da türevlenebilir olma zorunluluğu yoktur.
Bir parçalı fonksiyonun belirli integralini nasıl hesaplayabileceğimizi bir örnek üzerinden gösterelim.
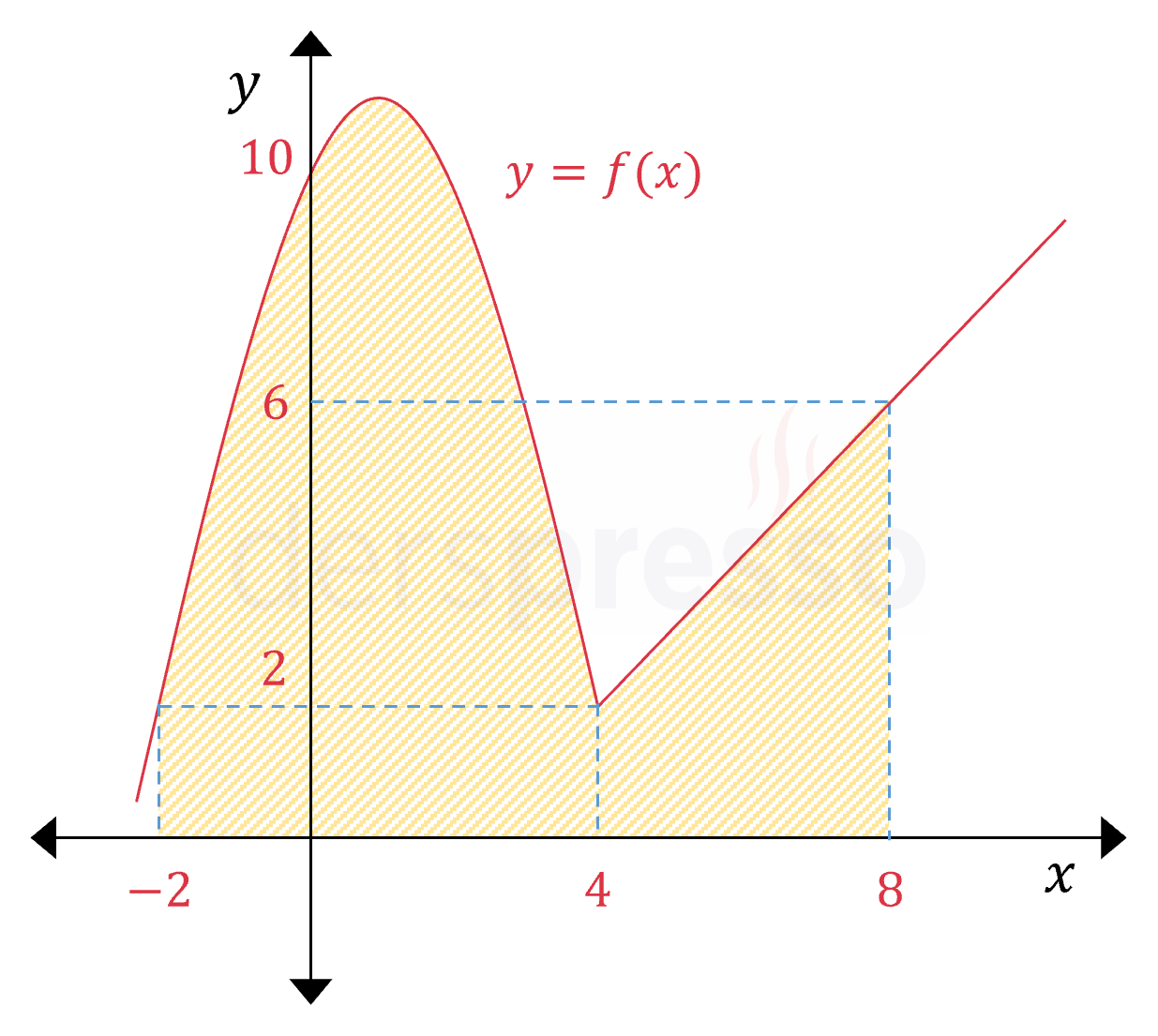
\( f(x) = \begin{cases} -x^2 + 2x + 10 & x \lt 4 \\ x - 2 & x \ge 4 \end{cases} \) olduğuna göre,
\( \displaystyle\int_{-2}^8 f(x)\ dx \) integralinin sonucu kaçtır?
Verilen parçalı fonksiyonun geçiş noktası \( x = 4 \) noktasıdır.
Bu geçiş noktası integral sınır değerleri arasında kaldığı için integral işlemini her biri parçalı fonksiyonun tek bir tanımına karşılık gelecek şekilde birden fazla integral işleminin toplamı şeklinde yazalım.
\( \displaystyle\int_{-2}^8 f(x)\ dx = \displaystyle\int_{-2}^4 f(x)\ dx + \displaystyle\int_4^8 f(x)\ dx \)
\( f(x) \) yerine her aralıkta geçerli olan fonksiyon tanımını yazalım.
\( = \displaystyle\int_{-2}^4 (-x^2 + 2x + 10)\ dx + \displaystyle\int_4^8 (x - 2)\ dx \)
İfadenin integralini alalım.
\( = (-\dfrac{x^3}{3} + x^2 + 10x)|_{-2}^4 + (\dfrac{x^2}{2} - 2x)|_4^8 \)
Sınır değerlerini yerine koyarak belirli integral değerini bulalım.
\( = [(-\dfrac{4^3}{3} + 4^2 + 10(4)) - (-\dfrac{(-2)^3}{3} + (-2)^2 + 10(-2))] + [(\dfrac{8^2}{2} - 2(8)) - (\dfrac{4^2}{2} - 2(4))] \)
\( = [(\dfrac{104}{3} + \dfrac{40}{3}) - (16 - 0) \)
\( = 48 - 16 = 32 \) bulunur.
Parçalı fonksiyonun grafiği ve her aralıkta belirli integralin karşılık geldiği alanlar aşağıdaki şekilde gösterilmiştir.
İkiden fazla aralıktan oluşan parçalı fonksiyonların belirli integralini de benzer bir yöntemle hesaplayabiliriz.
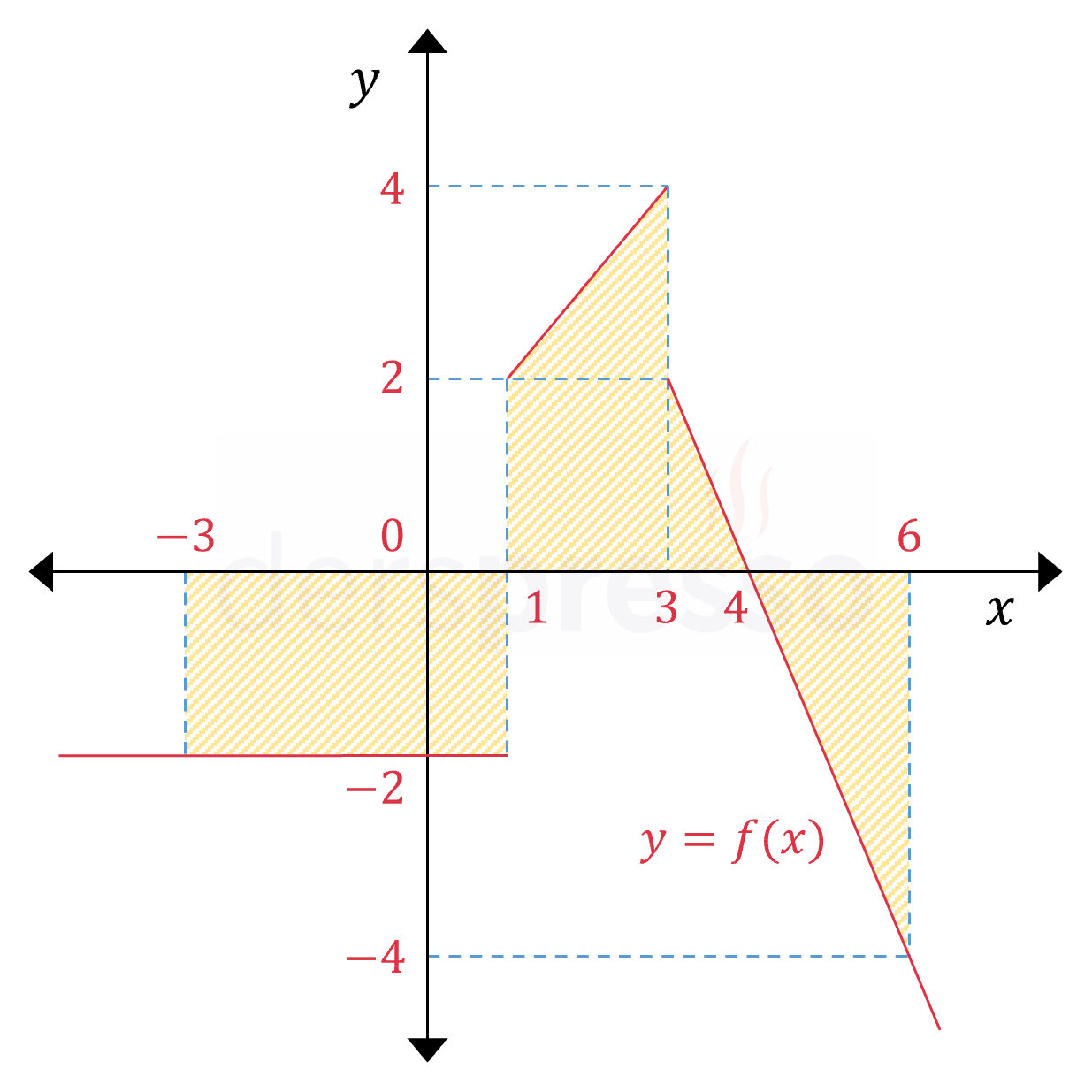
\( f(x) = \begin{cases} -2 & x \lt 1 \\ x + 1 & 1 \le x \lt 3 \\ 8 - 2x & x \ge 3 \end{cases} \) olduğuna göre,
\( \displaystyle\int_{-3}^6 f(x)\ dx \) integralinin sonucu kaçtır?
Verilen parçalı fonksiyonun geçiş noktaları \( x = 1 \) ve \( x = 3 \) noktalarıdır.
Bu geçiş noktası integral sınır değerleri arasında kaldığı için integral işlemini her biri parçalı fonksiyonun tek bir tanımına karşılık gelecek şekilde birden fazla integral işleminin toplamı şeklinde yazalım.
\( \displaystyle\int_{-3}^6 f(x)\ dx = \displaystyle\int_{-3}^1 f(x)\ dx + \displaystyle\int_1^3 f(x)\ dx + \displaystyle\int_3^6 f(x)\ dx \)
\( f(x) \) yerine her aralıkta geçerli olan fonksiyon tanımını yazalım.
\( = \displaystyle\int_{-3}^1 -2\ dx + \displaystyle\int_1^3 (x + 1)\ dx + \displaystyle\int_3^6 (8 - 2x)\ dx \)
İfadenin integralini alalım.
\( = (-2x)|_{-3}^1 + (\dfrac{x^2}{2} + x)|_1^3 + (8x - x^2)_3^6 \)
Sınır değerlerini yerine koyarak belirli integral değerini bulalım.
\( = (-2(1) + 2(-3)) + ((\dfrac{3^2}{2} + 3) - (\dfrac{1^2}{2} + 1)) + ((8(6) - 6^2) - (8(3) - 3^2)) \)
\( = -8 + 6 + (-3) \)
\( = -5 \) bulunur.
Parçalı fonksiyonun grafiği ve her aralıkta belirli integralin karşılık geldiği alanlar aşağıdaki şekilde gösterilmiştir.