Parabolün Kökleri
\( f(x) \) bir parabol olmak üzere, \( f(x) = 0 \) denklemini sağlayan \( x \) değerleri parabolün kökleridir. Bu \( x \) değerleri aynı zamanda parabolün \( x \) eksenini kestiği noktaların apsis değerlerini verir.
İkinci dereceden denklemler konusunda incelediğimiz üzere, bir parabolün kökleri üç şekilde bulunabilir.
- Grafiği verilen bir parabolün \( x \) eksenini kestiği noktaların apsis değerleri parabolün reel kökleridir.
- Parabol denklemi çarpanlarına ayrıldığında her çarpanı sıfır yapan \( x \) değerleri parabolün kökleridir.
- Diskriminant formülü parabolün reel olan ve olmayan kökleri bulunabilir.
Bir parabolün \( x \) eksenine göre durumu ve reel kökleri üç şekilde olabilir.
- İki reel kök: Parabol \( x \) eksenini iki farklı noktada keser.
- Bir reel kök: Parabol \( x \) eksenini tek bir noktada (teğet) keser.
- Reel kök yok: Parabol \( x \) eksenini kesmez.
Bir parabolün bu üç durumdan hangisinde olduğu denklemin deltası (diskriminantı) hesaplanarak aşağıdaki şekilde bulunabilir.
\( y = ax^2 + bx + c \) parabolün denklemi,
\( \Delta = b^2 - 4ac \) denklemin deltası olmak üzere,
Parabol \( x \) eksenini;
- \( \Delta \gt 0 \) ise iki noktada keser,
- \( \Delta = 0 \) ise tek bir noktada (teğet) keser,
- \( \Delta \lt 0 \) ise kesmez.
\( y = 3x^2 - 4x + 2 \)
\( \Delta = (-4)^2 - 4\cdot 3 \cdot 2 = -8\)
\( \Delta \lt 0 \) olduğu için parabol \( x \) eksenini kesmez.
Şimdi bu üç durumu daha detaylı inceleyelim.
Parabol x Eksenini İki Noktada Keser
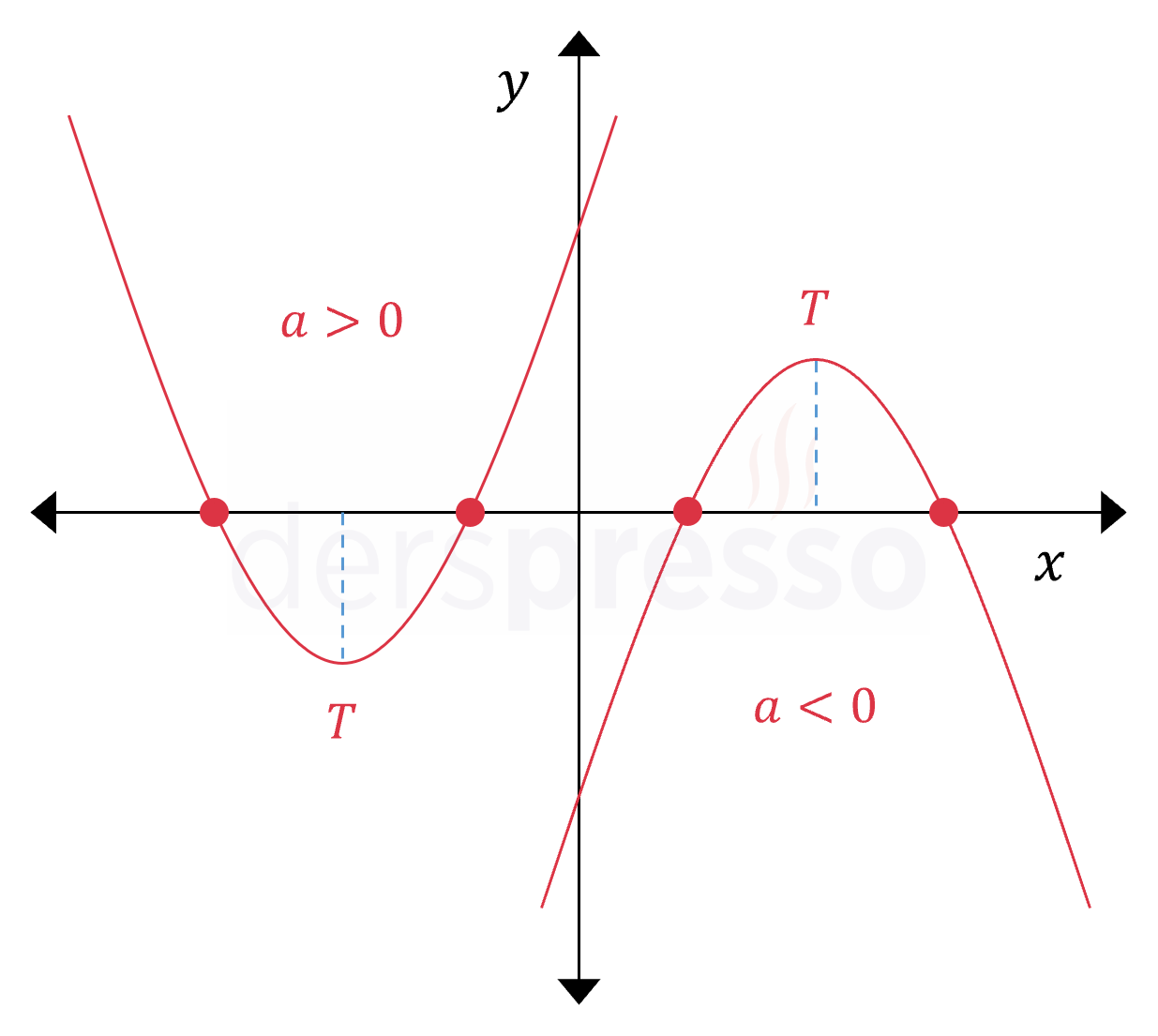
Bir parabol \( x \) eksenini \( x = x_1 \) ve \( x = x_2 \) şeklinde iki farklı noktada kesiyorsa aşağıdaki çıkarımlar yapılabilir.
- Parabolün deltası sıfırdan büyüktür.
- \( f(x) = 0 \) denkleminin birbirinden farklı iki reel kökü vardır.
- Parabol denklemi \( f(x) = a(x - x_1)(x - x_2) \) şeklinde çarpanlarına ayrılabilir.
- Parabolün bir kısmı \( x \) ekseninin üstünde, bir kısmı altında kalır, yani \( y \) hem pozitif hem negatif değer alır.
- Parabolün tepe noktasının apsis değeri parabolün \( x \) eksenini kestiği iki noktanın orta noktasının apsis değerine eşittir.
Parabol x Eksenini Tek Bir Noktada (Teğet) Keser
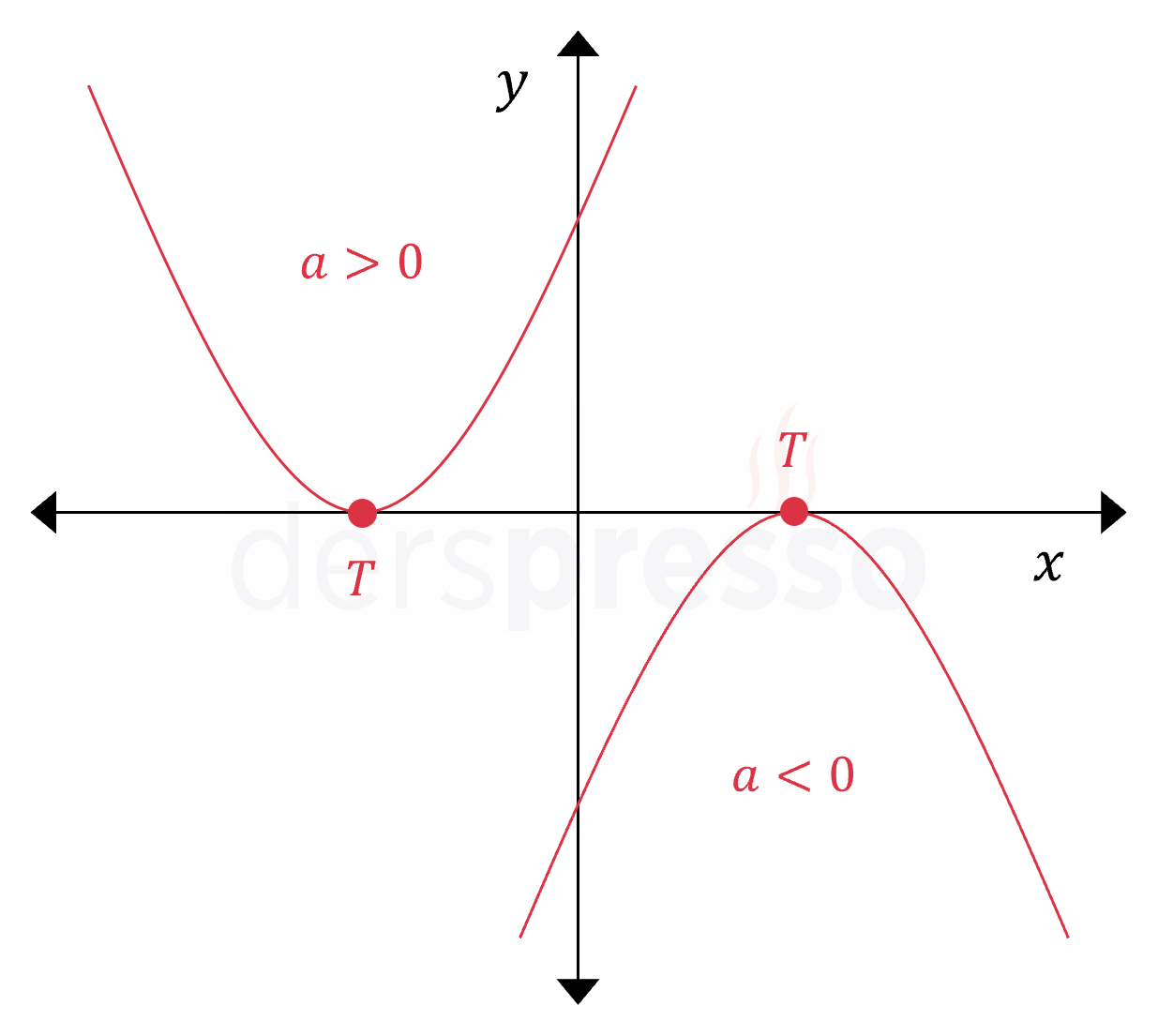
Bir parabol \( x \) eksenini \( x = x_1 \) şeklinde tek bir noktada kesiyorsa aşağıdaki çıkarımlar yapılabilir.
- Parabolün deltası sıfıra eşittir.
- \( f(x) = 0 \) denkleminin tek bir (iki katlı, çakışık) reel kökü vardır.
- Parabol denklemi \( f(x) = a(x - x_1)^2 \) şeklinde çarpanlarına ayrılabilir.
- \( a \gt 0 \) ise parabolün değeri her zaman sıfır ya da pozitiftir (\( f(x) \ge 0 \)), yani parabol negatif değer almaz.
- \( a \lt 0 \) ise parabolün değeri her zaman sıfır ya da negatiftir (\( f(x) \le 0 \)), yani parabol pozitif değer almaz.
- Parabolün tepe noktası parabolün \( x \) eksenini kestiği noktadır.
Parabol x Eksenini Kesmez
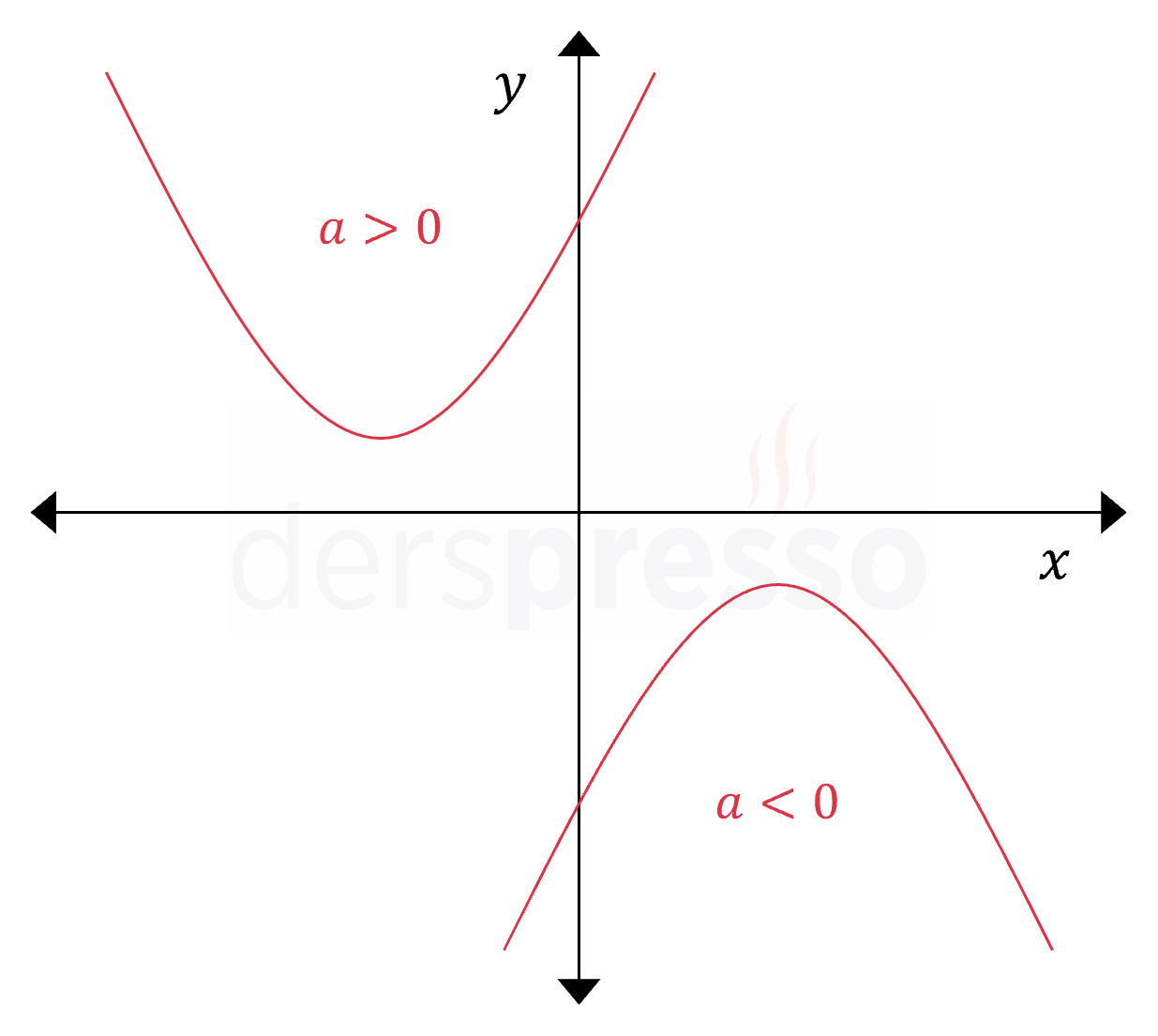
Bir parabol \( x \) eksenini kesmiyorsa aşağıdaki çıkarımlar yapılabilir.
- Parabolün deltası sıfırdan küçüktür.
- \( f(x) = 0 \) denkleminin reel kökü yoktur, birbirinin eşleniği iki karmaşık sayı kökü vardır.
- Parabol denklemi kökleri reel sayı olacak şekilde çarpanlarına ayrılamaz.
- \( a \gt 0 \) ise parabolün değeri her zaman pozitiftir (\( f(x) \gt 0 \)).
- \( a \lt 0 \) ise parabolün değeri her zaman negatiftir (\( f(x) \lt 0 \)).
Reel katsayılı ikinci dereceden bir denklemin tek bir karmaşık sayı kökü olamaz, denklemin karmaşık sayı kökü varsa bu kökler iki tane ve birbirinin eşleniği şeklinde olur.
Parabolün Kökleri ve Katsayıları
Bir parabolün kökleri ile denkleminin katsayıları arasında aşağıdaki ilişkiler vardır. Bu formüllerin nasıl türetildiği ile ilgili detaylı bilgi için ikinci dereceden denklemlerde kök katsayı ilişkisi sayfasını inceleyebilirsiniz.
| İfade | Formül |
|---|---|
| Kökler toplamı | \( x_1 + x_2 = -\dfrac{b}{a} \) |
| Kökler çarpımı | \( x_1 \cdot x_2 = \dfrac{c}{a} \) |
| Köklerin çarpmaya göre terslerinin toplamı | \( \dfrac{1}{x_1} + \dfrac{1}{x_2} = -\dfrac{b}{c} \) |
| Kökler farkının mutlak değeri | \( \abs{x_1 - x_2} = \dfrac{\sqrt{\Delta}}{\abs{a}} \) |
| Simetrik köklerde kökler toplamı | \( x_1 + x_2 = 0 \) |
Bunlara ek olarak, özdeşlikler kullanılarak bir parabol denkleminin kökleri arasında aşağıdaki ilişkiler de kurulabilir.
\( x_1^2 + x_2^2 = (x_1 + x_2)^2 - 2x_1x_2 \)
\( x_1^3 + x_2^3 = (x_1 + x_2)(x_1^2 - x_1x_2 + x_2^2) \)
\( f(x) = 3x^2 - 4x + 2m + 1 \) fonksiyonunun grafiği \( x \) eksenine teğet olduğuna göre, \( m \) kaçtır?
Çözümü GösterParabolün grafiği \( x \) eksenine teğet olduğuna göre, denklemin çakışık (çift katlı) iki reel kökü vardır ve deltası sıfırdır.
\( \Delta = b^2 - 4ac = 0 \)
Parabolün katsayılarını yazalım.
\( a = 3, \quad b = -4, \quad c = 2m + 1 \)
\( (-4)^2 - 4(3)(2m + 1) = 0 \)
\( 16 - 24m - 12 = 0 \)
\( m = \dfrac{1}{6} \) bulunur.
\( f(x) = x^2 - 4x + m - 2 \) fonksiyonunun grafiği \( x \) eksenini iki noktada kestiğine göre, \( m \) değer aralığı nedir?
Çözümü GösterParabolün grafiği \( x \) eksenini iki noktada kestiğine göre, denklemin deltası sıfırdan büyüktür.
\( \Delta = b^2 - 4ac \gt 0 \)
Parabolün katsayılarını yazalım.
\( a = 1, \quad b = -4, \quad c = m - 2 \)
\( (-4)^2 - 4(1)(m - 2) \gt 0 \)
\( 16 - 4m + 8 \gt 0 \)
\( m \lt 6 \) bulunur.
\( f(x) = x^2 - mx + 3m \) fonksiyonunun grafiği \( x \) eksenini kesmediğine göre, \( m \) değer aralığı nedir?
Çözümü GösterParabolün grafiği \( x \) eksenini kesmediğine göre, denklemin deltası sıfırdan küçüktür.
\( \Delta = b^2 - 4ac \lt 0 \)
Parabolün katsayılarını yazalım.
\( a = 1, \quad b = -m, \quad c = 3m \)
\( (-m)^2 - 4(1)(3m) \lt 0 \)
\( m^2 - 12m \lt 0 \)
\( m(m - 12) \lt 0 \)
\( 0 \lt m \lt 12 \) bulunur.
\( y = x^2 - (4m + 3)x + 16 \) parabolünün tepe noktasının \( x \) ekseni üzerinde olmasını sağlayan \( m \) değerlerinin toplamı kaçtır?
Çözümü GösterParabolün tepe noktasının \( x \) ekseni üzerinde olması için parabolün grafiği \( x \) eksenine teğet olmalıdır, yani deltası sıfır olmalıdır.
\( \Delta = b^2 - 4ac = 0 \)
Parabolün katsayılarını yazalım.
\( a = 1, \quad b = -(4m + 3), \quad c = 16 \)
\( [-(4m + 3)]^2 - 4(1)(16) = 0 \)
\( (4m + 3)^2 - 8^2 = 0 \)
Kare farkı özdeşliğini uygulayalım.
\( (4m + 3 - 8)(4m + 3 + 8) = 0 \)
\( (4m - 5)(4m + 11) = 0 \)
Geçerli \( m \) değerleri her bir çarpanı sıfır yapan değerlerden oluşur.
\( m \in \{-\frac{11}{4}, \frac{5}{4}\} \)
\( -\dfrac{11}{4} + \dfrac{5}{4} = -\dfrac{3}{2} \) bulunur.
\( y = x^2 - (m - 4)x - 2m - 1 \) parabolünün tepe noktası \( y \) ekseni üzerinde olduğuna göre, parabolün \( x \) eksenini kestiği noktalar arasındaki uzaklık nedir?
Çözümü GösterParabolün katsayılarını yazalım.
\( a = 1, \quad b = -(m - 4), \quad c = -2m - 1 \)
Parabolün tepe noktasının \( y \) ekseni üzerinde olması için tepe noktasının apsis değeri, dolayısıyla \( b \) katsayısı 0 olmalıdır.
Parabolün tepe noktasına \( T(r, k) \) diyelim.
\( r = -\dfrac{b}{2a} \)
\( r = 0 \Longrightarrow b = 0 \)
\( -(m - 4) = 0 \Longrightarrow m = 4 \)
Parabolün denklemi aşağıdaki gibi olur.
\( y = x^2 - 9 \)
Parabolün \( x \) eksenini kestiği noktaları bulmak için denklemde \( y = 0 \) yazalım.
\( y = x^2 - 9 = 0 \)
\( (x - 3)(x + 3) = 0 \)
Buna göre parabol \( x \) eksenini \( x = -3 \) ve \( x = 3 \) noktalarında keser.
Bu iki nokta arasındaki uzaklık \( \abs{x_2 - x_1} = \abs{3 - (-3)} = 6 \) olarak bulunur.
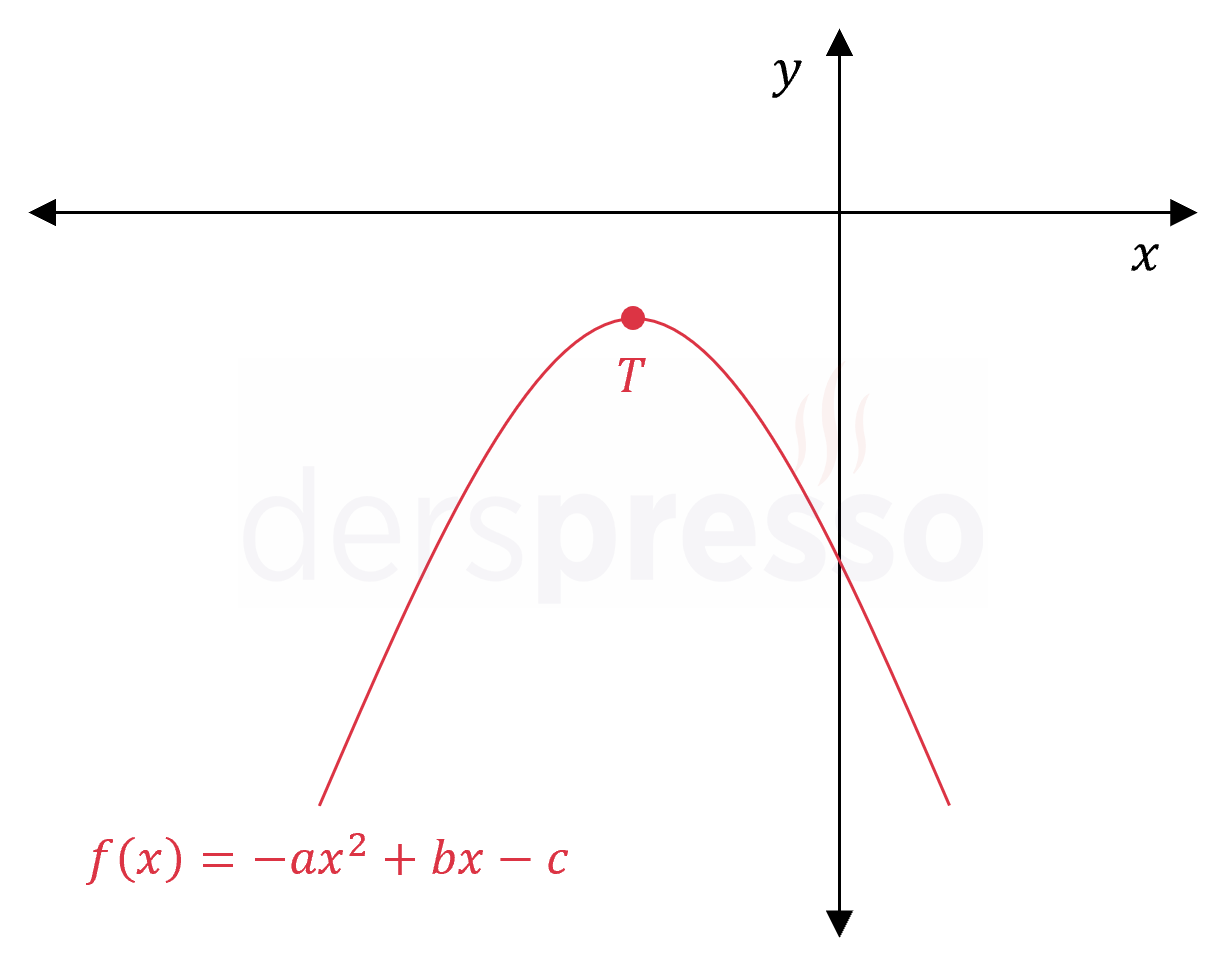
Şekildeki \( f(x) = -ax^2 + bx - c \) parabolü için aşağıdaki ifadelerden hangileri doğrudur?
I. \( abc \lt 0 \)
II. \( \dfrac{b^2}{4} - ac \lt 0 \)
III. \( \dfrac{a}{c} \gt 0 \)
Çözümü GösterParabolün kolları aşağı yönlü olduğu için başkatsayısı negatiftir.
\( -a \lt 0 \)
\( a \gt 0 \)
Tepe noktası III. bölgede yer aldığı için apsisi negatiftir.
\( -\dfrac{b}{2(-a)} \lt 0 \)
\( a \) pozitif olduğu için eşitsizliğin sağlanması için \( b \) negatif olmalıdır.
\( b \lt 0 \)
Parabolün \( y \) eksenini kestiği noktanın ordinatı negatif olduğu için denklemin sabit terimi de negatiftir.
\( -c \lt 0 \)
\( c \gt 0 \)
Parabol \( x \) eksenini kesmediği için deltası negatiftir.
\( \Delta \lt 0 \)
Bu bilgileri kullanarak verilen öncülleri inceleyelim.
I. öncül:
\( abc \lt 0 \)
\( a \) ve \( c \) pozitif, \( b \) negatif olduğu için \( abc \) çarpımı negatif olur.
I. öncül doğrudur.
II. öncül:
\( \dfrac{b^2}{4} - ac \lt 0 \)
\( b^2 - 4ac \lt 0 \)
Eşitsizliğin sol tarafı parabolün deltasına eşittir.
\( \Delta \lt 0 \)
II. öncül doğrudur.
III. öncül:
\( \dfrac{a}{c} \gt 0 \)
\( a \) ve \( c \) pozitif olduğu için \( \frac{a}{c} \) oranı da pozitif olur.
III. öncül doğrudur.
Buna göre öncüllerin tümü doğrudur.
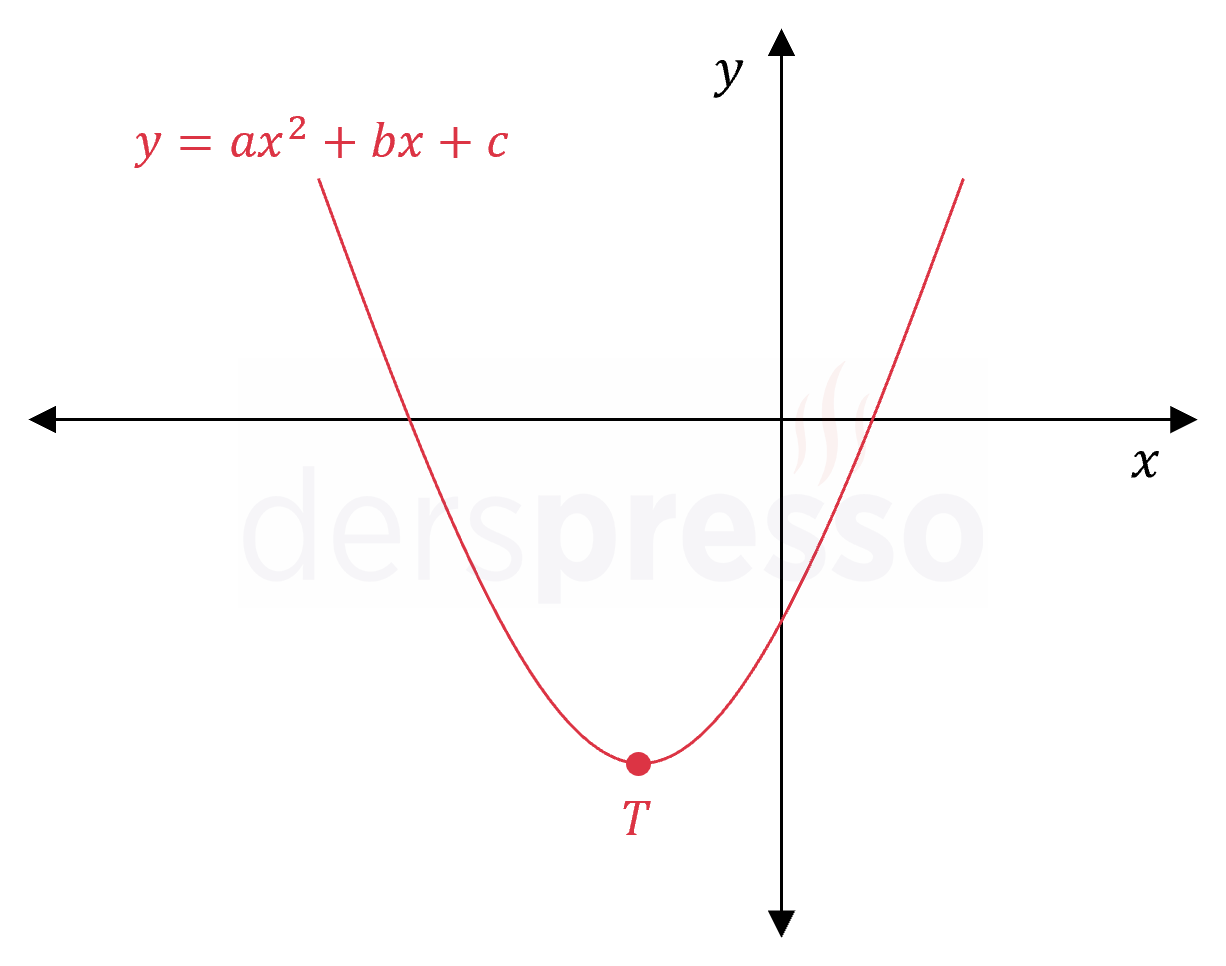
Şekildeki \( y = ax^2 + bx + c \) parabolü için aşağıdakilerden hangileri doğrudur?
I. \( a + b - c \gt 0 \)
II. \( abc \gt 0 \)
III. \( b^2 \gt 4a(c - b) \)
Çözümü GösterParabolün kolları yukarı yönlü olduğu için başkatsayısı pozitiftir.
\( a \gt 0 \)
Parabolün \( y \) eksenini kestiği noktanın ordinatı negatif olduğu için denklemin sabit terimi negatiftir.
\( c \lt 0 \)
Parabolün tepe noktası III. bölgede yer aldığından tepe noktasının apsisi negatiftir.
\( r = -\dfrac{b}{2a} \lt 0 \)
\( a \) pozitif olduğu için eşitsizliğin sağlanması için \( b \) de pozitif olmalıdır.
\( b \gt 0 \)
Bu bilgileri kullanarak verilen öncülleri inceleyelim.
I. öncül:
\( a + b - c \gt 0 \)
\( a \) ve \( b \) pozitif, \( c \) negatif olduğundan \( a + b - c \) ifadesi pozitif olur.
I. öncül doğrudur.
II. öncül:
\( abc \gt 0 \)
\( a \) ve \( b \) pozitif, \( c \) negatif olduğundan \( abc \) çarpımı negatif olur.
II. öncül yanlıştır.
III. öncül:
\( b^2 \gt 4a(c - b) \)
\( b^2 \gt 4ac - 4ab \)
\( b^2 - 4ac \gt -4ab \)
Eşitsizliğin sol tarafı parabolün deltasına eşittir.
\( \Delta \gt -4ab \)
\( a \) ve \( b \) pozitif olduğu için eşitsizliğin sağ tarafı negatiftir.
Parabol \( x \) eksenini iki farklı noktada kestiğinden deltası pozitiftir, dolayısıyla negatif bir sayıdan büyüktür.
III. öncül doğrudur.
Buna göre I. ve III. öncüller doğrudur.

Şekildeki \( f(x) = ax^2 + bx + c \) parabolü için aşağıdaki ifadelerden hangileri doğrudur?
I. \( f(-\dfrac{b}{2a}) \lt 0 \)
II. \( bc \lt 0 \)
III. \( \dfrac{ab}{c} \gt 0 \)
IV. \( -a - b \lt 0 \)
V. \( \dfrac{b^2 - 4ac}{b} \lt 0 \)
Çözümü GösterParabolün kolları aşağı yönlü olduğu için başkatsayısı negatiftir.
\( a \lt 0 \)
Parabolün tepe noktasına \( T(r, k) \) diyelim.
Parabolün tepe noktası II. bölgede yer aldığına göre apsisi negatif, ordinatı pozitiftir.
\( r = -\dfrac{b}{2a} \lt 0 \)
\( a \) negatif olduğu için eşitsizliğin sağlanması için \( b \) de negatif olmalıdır.
\( b \lt 0 \)
Parabolün \( y \) eksenini kestiği noktanın ordinatı negatif olduğu için denklemin sabit terimi de negatiftir.
\( c \lt 0 \)
Parabol \( x \) eksenini iki farklı noktada kestiği için deltası pozitiftir.
\( \Delta = b^2 - 4ac \gt 0 \)
Bu bilgileri kullanarak verilen öncülleri inceleyelim.
I. öncül:
\( f(-\dfrac{b}{2a}) \lt 0 \)
\( -\frac{b}{2a} \) değeri tepe noktasının apsis değerine eşittir.
\( f(-\dfrac{b}{2a}) = f(r) = k \)
Parabolün tepe noktası II. bölgede yer aldığına göre bu noktada ordinatı pozitiftir.
I. öncül yanlıştır.
II. öncül:
\( bc \lt 0 \)
\( b \) ve \( c \) negatif olduğu için çarpımları pozitif olur.
II. öncül yanlıştır.
III. öncül:
\( \dfrac{ab}{c} \gt 0 \)
\( a \), \( b \) ve \( c \) negatif olduğundan bu ifade negatif olur.
III. öncül yanlıştır.
IV. öncül:
\( -a - b \lt 0 \)
\( -(a + b) \lt 0 \)
\( a + b \gt 0 \)
\( a \) ve \( b \) negatif olduğu için toplamları da negatiftir.
IV. öncül yanlıştır.
V. öncül:
\( \dfrac{b^2 - 4ac}{b} \lt 0 \)
\( \dfrac{\Delta}{b} \lt 0 \)
Parabolün deltası pozitif, \( b \) negatif olduğundan bu ifade negatif olur.
V. öncül doğrudur.
Buna göre sadece V. öncül doğrudur.
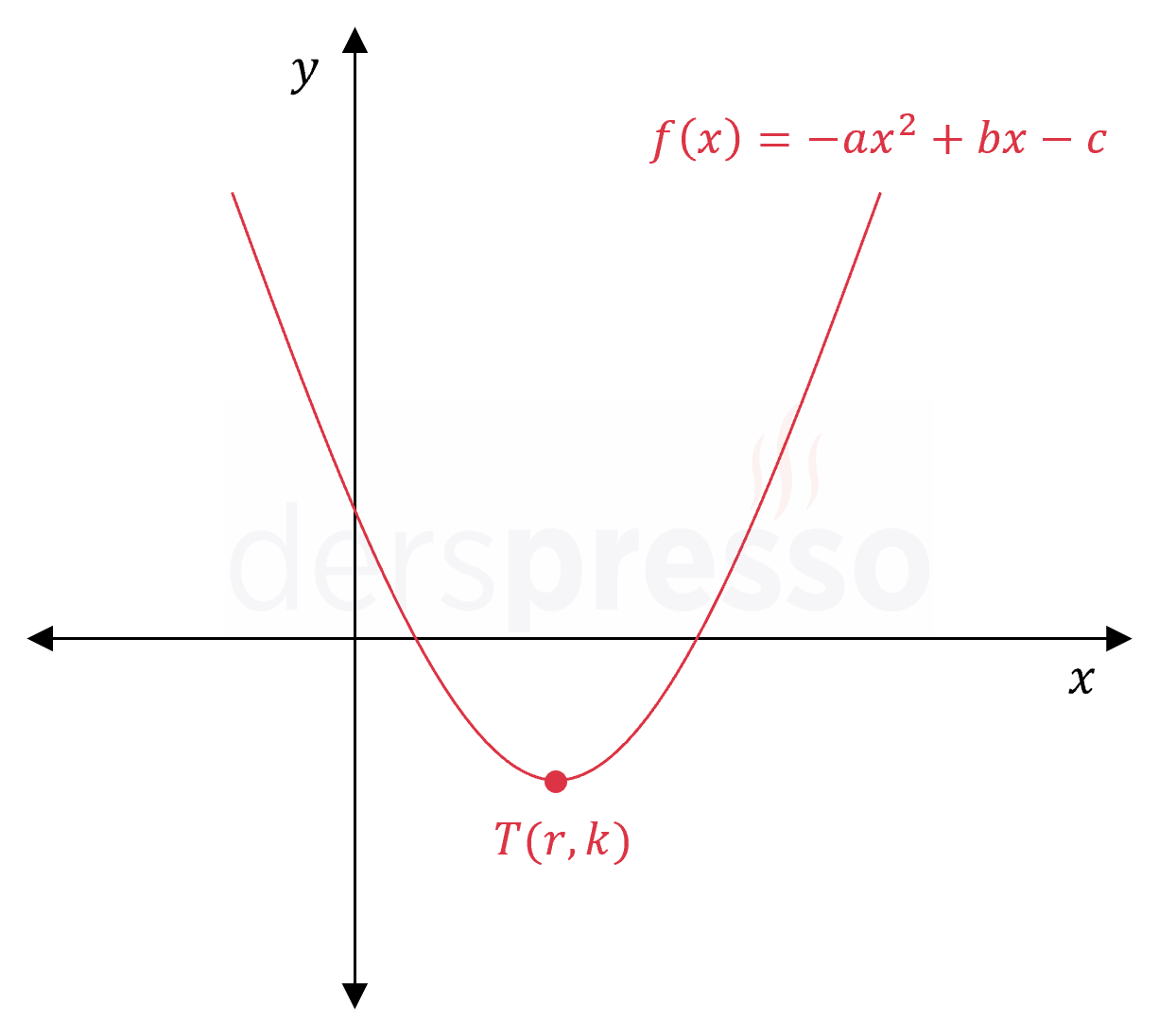
Şekildeki \( f(x) = -ax^2 + bx - c \) parabolü için aşağıdaki ifadelerden hangileri doğrudur?
I. \( a + b + c \gt 0 \)
II. \( \dfrac{abc}{\Delta} \lt 0 \)
III. \( b \lt -2\sqrt{ac} \)
Çözümü GösterParabolün kolları yukarı yönlü olduğu için başkatsayısı pozitiftir.
\( -a \gt 0 \)
\( a \lt 0 \)
Grafiğin tepe noktası IV. bölgede yer aldığından apsisi pozitiftir.
\( r = -\dfrac{b}{2(-a)} \gt 0 \)
\( a \) negatif olduğu için eşitsizliğin sağlanması için \( b \) de negatif olur.
\( b \lt 0 \)
Parabolün \( y \) eksenini kestiği noktanın ordinatı pozitif olduğu için denklemin sabit terimi de pozitiftir.
\( -c \gt 0 \)
\( c \lt 0 \)
Parabol \( x \) eksenini iki farklı noktada kestiği için deltası pozitiftir.
\( \Delta = b^2 - 4(-a)(-c) \)
\( = b^2 - 4ac \gt 0 \)
Bu bilgileri kullanarak verilen öncülleri inceleyelim.
I. öncül:
\( a + b + c \gt 0 \)
\( a, b, c \) negatif olduğu için toplamları da negatif olur.
I. öncül yanlıştır.
II. öncül:
\( \dfrac{abc}{\Delta} \lt 0 \)
\( a, b, c \) negatif olduğu için \( abc \) çarpımı da negatif olur. Delta pozitif olduğu için bu ifade negatif olur.
II. öncül doğrudur.
III. öncül:
\( b \lt -2\sqrt{ac} \)
Parabolün deltası pozitiftir.
\( \Delta = b^2 - 4ac \gt 0 \)
\( b^2 \gt 4ac \)
İki tarafın karekökünü alalım.
\( \sqrt{b^2} \gt \sqrt{4ac} \)
\( \abs{b} \gt 2\sqrt{ac} \)
\( b \) negatiftir.
\( -b \gt 2\sqrt{ac} \)
\( b \lt -2\sqrt{ac} \)
III. öncül doğrudur.
Buna göre II. ve III. öncüller doğrudur.
\( f: \mathbb{R} \to \mathbb{R} \) olmak üzere,
\( f(x) = (k + 2)x^2 - 2kx + k - 3 \) parabolünün grafiği daima \( x \) ekseninin altında kaldığına göre, \( k \) değer aralığını bulunuz.
Çözümü GösterParabolün katsayılarını yazalım.
\( a = k + 2, \quad b = -2k, \quad c = k - 3 \)
Parabolün grafiği daima \( x \) ekseninin altında kalıyorsa iki koşul sağlanmalıdır.
Koşul 1:
Parabolün kolları aşağı yönlüdür (başkatsayısı negatiftir).
\( k + 2 \lt 0 \)
\( k \lt -2 \)
Koşul 2:
Parabol \( x \) eksenini hiçbir noktada kesmez (deltası sıfırdan küçüktür).
\( \Delta = b^2 - 4ac \lt 0 \)
\( (-2k)^2 - 4(k + 2)(k - 3) \lt 0 \)
\( 4k^2 - 4(k^2 - k - 6) \lt 0 \)
\( 4k^2 - 4k^2 + 4k + 24 \lt 0 \)
\( k \lt -6 \)
Bulduğumuz iki aralığın kesişim kümesi \( k \) değer aralığını verir.
\( k \lt -6 \) bulunur.
\( f: \mathbb{R} \to \mathbb{R} \) olmak üzere,
\( f(x) = (2n + 2)x^2 - 4nx + 2n + 1 \) parabolünün grafiği daima \( x \) ekseninin üstünde kaldığına göre, \( n \) değer aralığı nedir?
Çözümü GösterParabolün katsayılarını yazalım.
\( a = 2n + 2, \quad b = -4n, \quad c = 2n + 1 \)
Parabol \( x \) ekseninin daima üstünde kalıyorsa iki koşul sağlanmalıdır.
Koşul 1:
Parabolün kolları yukarı yönlü, yani başkatsayısı pozitif olmalıdır.
\( 2n + 2 \gt 0 \)
\( n \gt -1 \)
Koşul 2:
Parabol \( x \) eksenini hiçbir noktada kesmemelidir, yani deltası sıfırdan küçük olmalıdır.
\( \Delta = b^2 - 4ac \lt 0 \)
\( (-4n)^2 - 4(2n + 2)(2n + 1) \lt 0 \)
\( 16n^2 - 4(4n^2 + 6n + 2) \lt 0 \)
\( 16n^2 - 16n^2 - 24n - 8 \lt 0 \)
\( n \gt -\dfrac{1}{3} \)
Bulunan iki aralığın kesişim kümesi \( n \) değer aralığını verir.
\( n \in (-\dfrac{1}{3}, \infty) \) bulunur.
\( f(x) = x^2 + 4x - 4 \) fonksiyonunun \( x \) eksenini kestiği noktalar arasındaki uzaklık kaç birimdir?
Çözümü Göster1. yöntem:
Parabolün \( x \) eksenini kestiği noktaları bulmak için diskriminant formülünü kullanalım.
\( f(x) = x^2 + 4x - 4 \)
\( \Delta = b^2 - 4ac \)
\( = 4^2 - 4(1)(-4) = 32 \)
\( x_{1, 2} = \dfrac{-b \pm \sqrt{\Delta}}{2a} \)
\( = \dfrac{-4 \pm \sqrt{32}}{2(1)} \)
\( = -2 \pm 2\sqrt{2} \)
Buna göre parabol \( x \) eksenini \( x_1 = -2 - 2\sqrt{2} \) ve \( x_2 = -2 + 2\sqrt{2} \) noktalarında keser.
Bu iki nokta arasındaki uzaklığı bulalım.
\( \abs{x_2 - x_1} = \abs{-2 + 2\sqrt{2} - (-2 - 2\sqrt{2})} \)
\( = 4\sqrt{2} \)
2. yöntem:
İkinci dereceden bir denklemin kökler farkının mutlak değeri bu iki nokta arasındaki uzaklığı verir.
Kökler farkının mutlak değeri formülünü kullanalım.
\( \abs{x_2 - x_1} = \dfrac{\sqrt{\Delta}}{\abs{a}} \)
\( = \dfrac{\sqrt{32}}{\abs{1}} = 4\sqrt{2} \)
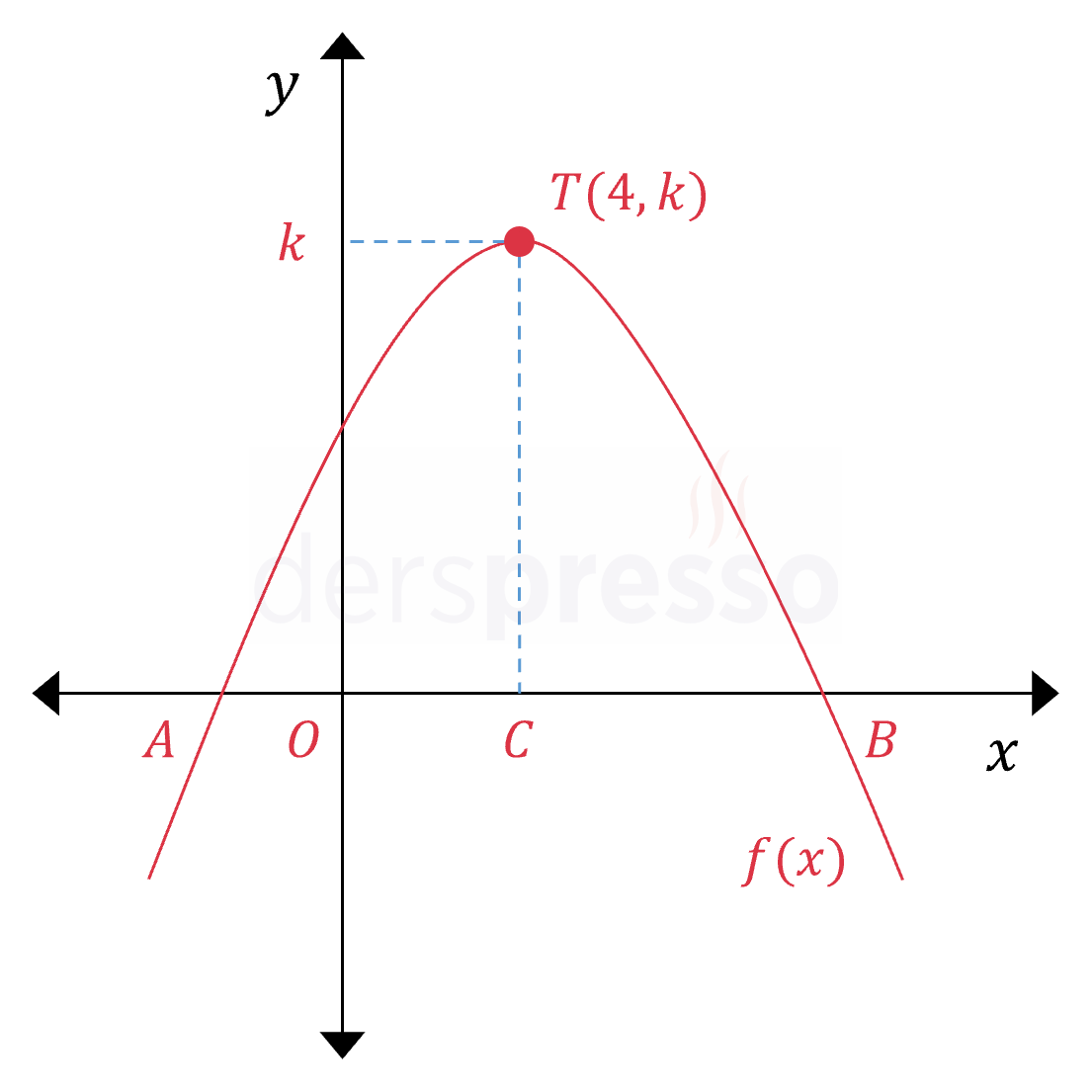
Yukarıda grafiği verilen parabolün tepe noktası \( T(4, k) \) noktasıdır.
\( \abs{OB} = 5\abs{OA} \) olduğuna göre, \( A \) ve \( B \) noktalarının apsislerinin çarpımı kaçtır?
Çözümü Göster\( \abs{AO} = m \) diyelim.
\( \abs{OB} = 5\abs{AO} = 5m \)
\( \abs{AB} = m + 5m = 6m \)
Parabolün simetri ekseninin parabol üzerinde ordinatı aynı olan noktalara yatay uzaklığı eşittir.
\( \abs{AC} = \abs{CB} = \dfrac{6m}{2} = 3m \)
\( \abs{OC} = 3m - m = 2m = 4 \)
\( m = 2 \) bulunur.
Buradan \( A \) ve \( B \) noktalarının apsis değerlerini aşağıdaki gibi buluruz.
\( A(-m, 0) = A(-2, 0) \)
\( B(5m, 0) = B(10, 0) \)
\( A \) ve \( B \) noktalarının apsislerinin çarpımı \( -2 \cdot 10 = -20 \) olarak bulunur.
\( f \) parabolünün katsayılar toplamı, kökler toplamı ve kökler çarpımı birbirine eşittir.
\( f(2) = 4 \) olduğuna göre, \( f(1) \) kaçtır?
Çözümü GösterParabolün denklemini aşağıdaki şekilde yazalım.
\( a, b, c \in \mathbb{R} - \{0\} \)
\( f(x) = ax^2 + bx + c \)
Parabolün katsayılar toplamı, kökler toplamı ve kökler çarpımı birbirine eşittir.
\( a + b + c = -\dfrac{b}{a} = \dfrac{c}{a} \)
İlk önce kökler toplamı ve çarpımını birbiriyle karşılaştıralım.
\( -\dfrac{b}{a} = \dfrac{c}{a} \)
\( -b = c \)
Şimdi katsayılar toplamı ile kökler çarpımını karşılaştıralım.
\( a + b + c = \dfrac{c}{a} \)
\( a + b - b = \dfrac{c}{a} \)
\( a^2 = c \)
\( -b = c \) eşitliğini kullanalım.
\( -a^2 = b \)
Fonksiyon tanımındaki katsayıları \( a \) cinsinden yazalım.
\( f(x) = ax^2 - a^2x + a^2 \)
\( f(2) \) değerini kullanarak \( a \) değerini bulalım.
\( f(2) = a(2)^2 - a^2(2) + a^2 = 4 \)
\( a^2 - 4a + 4 = 0 \)
\( (a - 2)^2 = 0 \)
\( a = 2 \)
Parabol denklemi aşağıdaki gibi olur.
\( f(x) = 2x^2 - 4x + 4 \)
\( f(1) \) değerini bulalım.
\( f(1) = 2(1)^2 - 4(1) + 4 = 2 \) bulunur.
Yukarıdaki şekilde \( f(x) = x^2 + 5x + c \) parabolünün grafiği verilmiştir.
Parabolün \( x \) eksenini kestiği noktalar \( A \) ve \( B \) ve \( \abs{AB} = 1 \) birim olduğuna göre, parabolün \( y \) eksenini kestiği noktanın ordinatı kaçtır?
Çözümü GösterParabolün kökler toplamını bulalım.
\( x_1 + x_2 = -\dfrac{b}{a} = -\dfrac{5}{1} = -5 \)
\( A \) ve \( B \) noktaları arasındaki uzaklığı aşağıdaki şekilde ifade edebiliriz.
\( \abs{AB} = \abs{x_1 - x_2} = 1 \)
\( x_1 \)'i büyük kök olarak kabul edelim.
\( x_1 - x_2 = 1 \)
İki bilinmeyenli iki denklemi çözersek aşağıdaki kök değerlerini buluruz.
\( x_1 = -2, \quad x_2 = -3 \)
Parabolün \( y \) eksenini kestiği noktanın ordinatı parabolün sabit terimi olan \( c \)'ye eşittir.
Kökler çarpımı formülünü kullanarak \( c \) değerini bulalım.
\( x_1 \cdot x_2 = \dfrac{c}{a} \)
\( -3 \cdot (-2) = c \)
\( c = 6 \) bulunur.
\( f \) bir parabol olup tüm reel sayılarda \( f(x) \le 0 \) bilgisi veriliyor.
\( f(3) = 0 \) ve \( f(8) = -20 \) olduğuna göre, \( f(-7) \) kaçtır?
Çözümü GösterTüm reel sayılarda \( f(x) \le 0 \) olduğuna göre, parabolün kolları aşağı yönlüdür ve başkatsayısı negatiftir.
\( f(3) = 0 \) olduğuna göre parabol \( x \) eksenini kesmektedir. \( f(x) \le 0 \) olduğu için parabol pozitif değer almaz, yani \( x \) eksenini teğet keser, dolayısıyla \( x = 3 \) noktasında çift katlı bir kökü vardır.
Buna göre fonksiyonun denklemi aşağıdaki formda olur.
\( f(x) = a(x - 3)^2 \)
\( a \) değerini bulmak için \( x = 8 \) yazalım.
\( f(8) = a(8 - 3)^2 = -20 \)
\( a = \dfrac{-20}{25} = -\dfrac{4}{5} \)
Parabolün denklemi aşağıdaki gibi olur.
\( f(x) = -\dfrac{4}{5}(x - 3)^2 \)
\( f(-7) \) değerini bulmak için \( x = -7 \) yazalım.
\( f(-7) = -\dfrac{4}{5}(-7 - 3)^2 \)
\( = -80 \) bulunur.
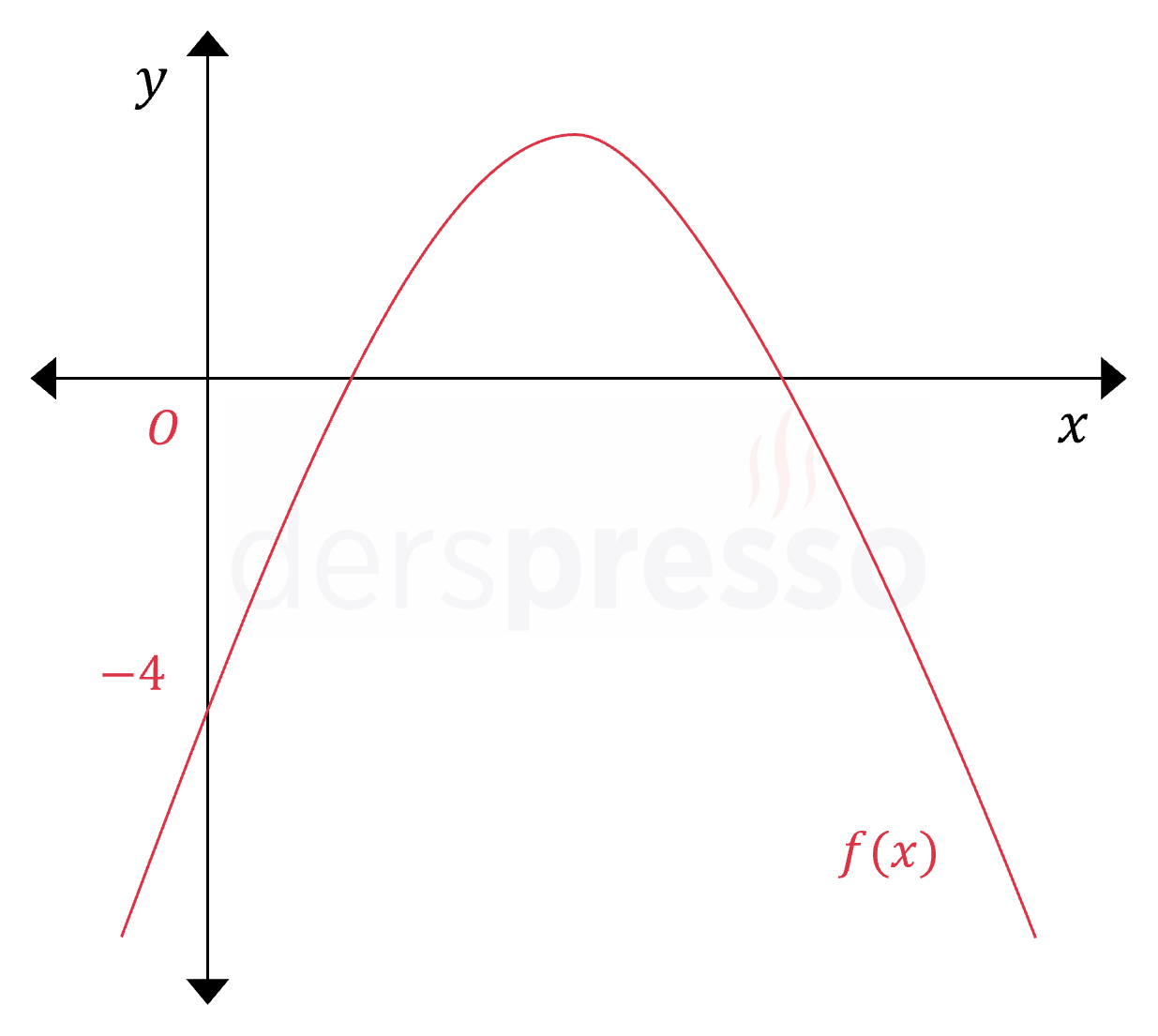
Yukarıdaki şekilde \( f(x) = -x^2 - mx - n \) parabolü verilmiştir.
\( x_1 + x_2 = 4x_1 \cdot x_2 \) olduğuna göre, fonksiyonun alabileceği en büyük değer kaçtır?
Çözümü GösterParabolün katsayılarını yazalım.
\( a = -1, \quad b = -m, \quad c = -n \)
Kökler toplamı formülünü yazalım.
\( x_1 + x_2 = -\dfrac{b}{a} = -m \)
Kökler çarpımı formülünü yazalım.
\( x_1 \cdot x_2 = \dfrac{c}{a} = n \)
\( x_1 + x_2 = 4x_1 \cdot x_2 \) olarak veriliyor.
\( -m = 4n \)
Parabolün \( y \) eksenini kestiği noktanın ordinatı aynı zamanda parabolün sabit terimine eşittir.
\( -n = -6 \)
\( n = 6 \)
\( m = -4n = -24 \)
Buna göre parabolün denklemi aşağıdaki gibi olur.
\( f(x) = -x^2 + 24x - 6 \)
Negatif başkatsayılı parabol en büyük değerini tepe noktasında alır.
Parabolün tepe noktasına \( T(r, k) \) diyelim.
\( r = -\dfrac{b}{2a} = -\dfrac{24}{2(-1)} = 12 \)
\( k = f(12) = -12^2 + 24(12) - 6 \)
\( = 138 \) bulunur.
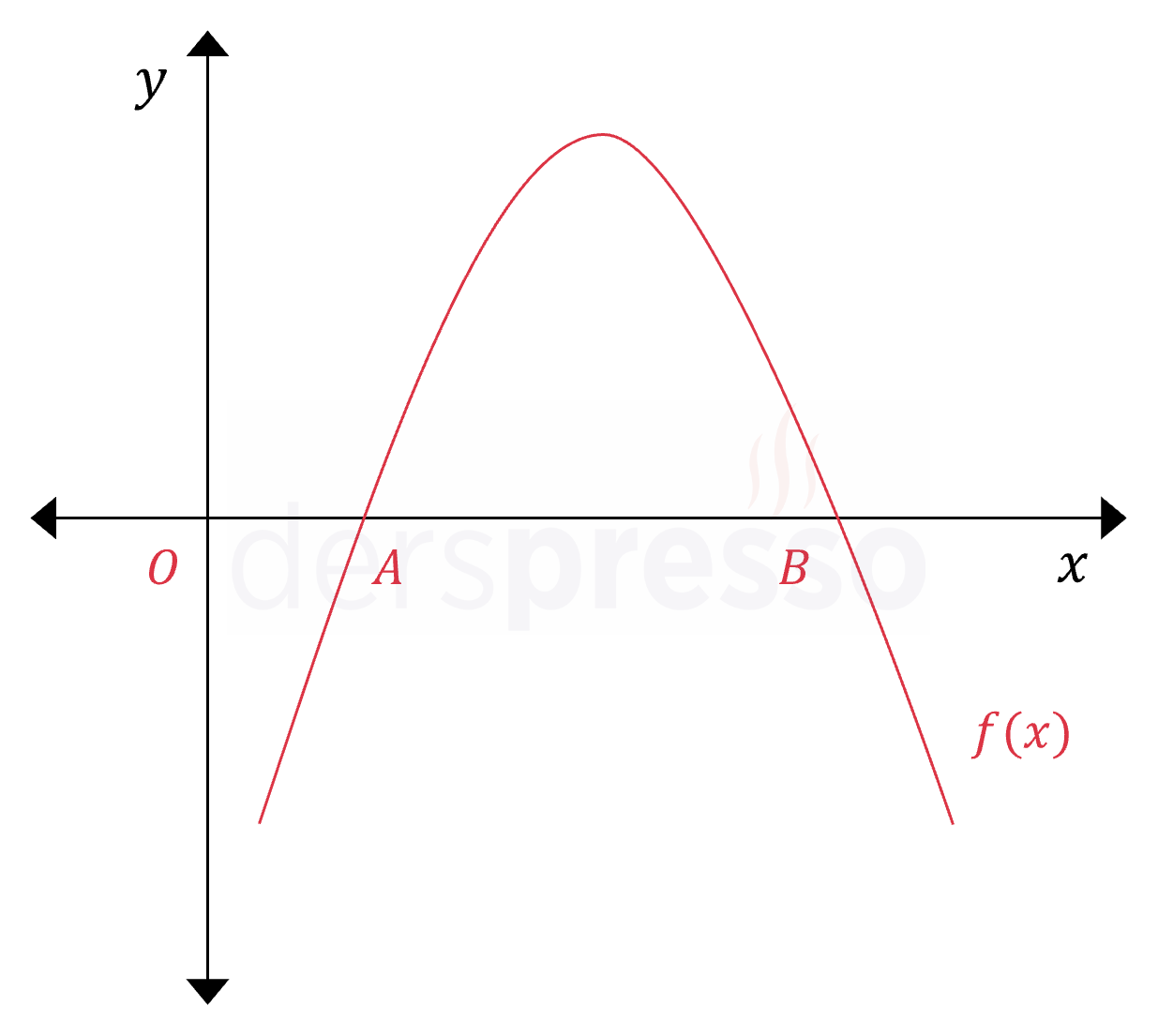
Yukarıdaki şekilde \( f(x) = -x^2 + 30x + 5 - 2m \) parabolünün grafiği verilmiştir.
\( 7a = 3b \) olduğuna göre, \( m \) kaçtır?
Çözümü GösterParabolün katsayılarını yazalım.
\( a = -1, \quad b = 30, \quad c = 5 - 2m \)
Parabolün tepe noktasına \( T(r, k) \) diyelim.
\( r = -\dfrac{b}{2a} = -\dfrac{30}{2(-1)} = 15 \)
Parabolün \( x \) eksenini kestiği noktalara \( A(a, 0) \) ve \( B(b, 0) \) diyelim.
\( 7a = 3b \) olduğuna göre, \( a = 3k \) ve \( b = 7k \) diyelim.
Bu iki noktanın apsis değerlerinin ortalaması tepe noktasının apsis değerini verir.
\( \dfrac{3k + 7k}{2} = 15 \)
\( k = 3 \)
\( A(3k, 0) = A(9, 0) \)
\( A \) noktasının koordinatlarını parabol denkleminde yerine koyalım.
\( f(9) = -9^2 + 30(9) + 5 - 2m = 0 \)
\( 194 - 2m = 0 \)
\( m = 97 \) bulunur.
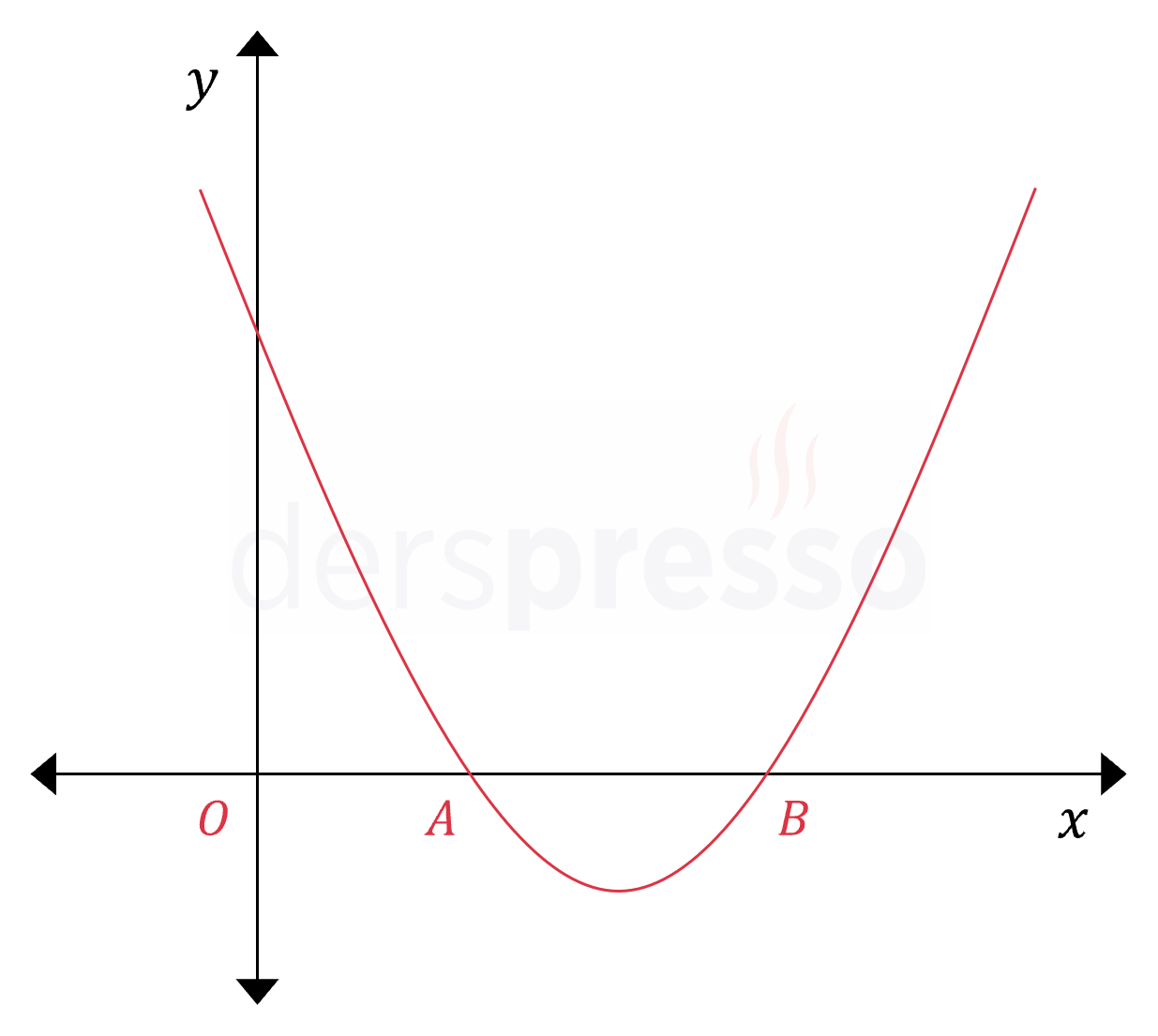
Yukarıdaki şekilde \( f(x) = x^2 + 2mx + 12 \) parabolünün grafiği verilmiştir.
\( \abs{AB} = 4 \) olduğuna göre, \( f(-3) \) kaçtır?
Çözümü GösterParabolün katsayılarını yazalım.
\( a = 1, \quad b = 2m, \quad c = 12 \)
Parabolün köklerine \( x_1 \) ve \( x_2 \) diyelim ve \( x_2 \)'yi büyük kök olarak kabul edelim.
Kökler toplamı formülünü yazalım.
\( x_1 + x_2 = -\dfrac{b}{a} = -2m \)
\( \abs{AB} = 4 \) olarak veriliyor.
\( x_2 = x_1 + 4 \)
\( x_1 + x_1 + 4 = -2m \)
\( 2x_1 + 4 = -2m \)
Kökler çarpımı formülünü yazalım.
\( x_1 \cdot x_2 = \dfrac{c}{a} = 12 \)
\( x_1 \cdot (x_1 + 4) = 12 \)
\( x_1^2 + 4x_1 - 12 = 0 \)
\( (x_1 + 6)(x_1 - 2) = 0 \)
Kökler \( x \) ekseninin pozitif tarafında olduğu için işaretleri pozitiftir, dolayısıyla \( x_1 = 2 \) olur.
\( x_2 = x_1 + 4 = 6 \)
\( -2m = x_1 + x_2 = 8 \)
\( m = -4 \)
Buna göre parabolün denklemi aşağıdaki gibi olur.
\( f(x) = x^2 - 8x + 12 \)
\( f(-3) \) değerini bulalım.
\( f(-3) = (-3)^2 - 8(-3) + 12 = 45 \) bulunur.
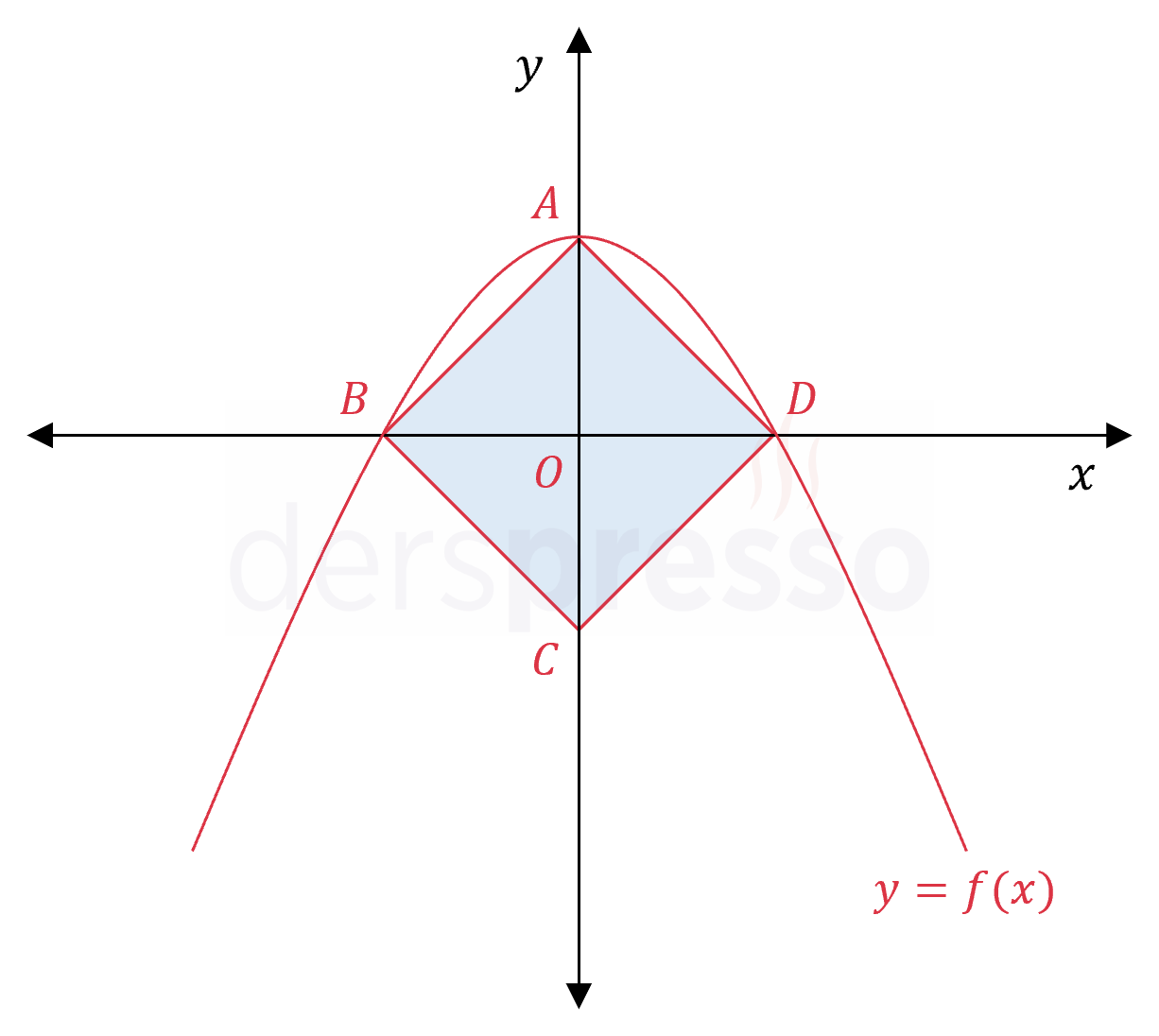
Merkezi orijinde olan \( ABCD \) karesinin üç köşesi \( y = f(x) \) parabolünün eksenleri kestiği noktalar, diğer köşesi \( y \) ekseni üzerindedir.
Karenin alanı 16 olduğuna göre, \( y = f(x) \) parabolünün denklemi nedir?
Çözümü GösterMerkezi orijinde olan \( ABCD \) karesinin köşegen uzunluğuna \( 2k \) diyelim.
Karenin alanı bir köşegen uzunluğunun karesinin yarısına eşittir.
\( A = \dfrac{(2k)^2}{2} = 16 \)
\( k = \pm 2\sqrt{2} \)
Buna göre karenin \( x \) ekseni üzerindeki iki köşesinin (dolayısıyla parabolün köklerinin) koordinatları aşağıdaki gibi olur.
\( B(-2\sqrt{2}, 0), \quad D(2\sqrt{2}, 0) \)
\( x \) eksenini \( (x_1, 0) \) ve \( (x_2, 0) \) noktalarında kesen parabolün denklemini aşağıdaki formda yazabiliriz.
\( f(x) = a(x - x_1)(x - x_2) \)
\( f(x) = a(x - 2\sqrt{2})(x + 2\sqrt{2}) \)
\( O \) noktası karenin köşegenlerinin kesişim noktasıdır, dolayısıyla karenin köşelerinin orijine uzaklıkları birbirine eşittir.
\( A(0, 2\sqrt{2}) \)
\( A \) noktası parabolün üzerinde olduğu için koordinatları parabol denklemini sağlar.
\( f(0) = a(0 - 2\sqrt{2})(0 + 2\sqrt{2}) = 2\sqrt{2} \)
\( a(-2\sqrt{2})(2\sqrt{2}) = 2\sqrt{2} \)
\( a = -\dfrac{1}{2\sqrt{2}} = -\dfrac{\sqrt{2}}{4} \)
Parabol denklemi aşağıdaki gibi bulunur.
\( f(x) = -\dfrac{\sqrt{2}}{4}(x - 2\sqrt{2})(x + 2\sqrt{2}) \)
\( f \) fonksiyonu bir parabol olup her \( x \) için \( f(x) \ge 0 \) veriliyor.
\( f(1) = 8 \) ve \( f(2) = 2 \) olduğuna göre, \( f \) fonksiyonunun başkatsayısı hangi aralıktadır?
Çözümü GösterFonksiyon tanımını aşağıdaki şekilde yazalım.
\( f(x) = ax^2 + bx + c \)
Fonksiyonda \( x = 1 \) yazalım.
\( f(1) = a + b + c = 8 \)
Fonksiyonda \( x = 2 \) yazalım.
\( f(2) = 4a + 2b + c = 2 \)
\( b \) ifadesini \( a \) cinsinden ifade etmek için birinci denklemi ikinci denklemden taraf tarafa çıkaralım.
\( 3a + b = -6 \)
\( b = -(3a + 6) \)
\( c \) ifadesini \( a \) cinsinden ifade etmek için birinci denklemin taraflarını 2 ile çarpıp ikinci denklemden taraf tarafa çıkaralım.
\( 2a - c = -14 \)
\( c = 2a + 14 \)
\( b \) ve \( c \) ifadelerini fonksiyon tanımında yerine koyalım.
\( f(x) = ax^2 - (3a + 6)x + 2a + 14 \)
Her \( x \) için \( f(x) \ge 0 \) olduğuna göre iki koşul sağlanmalıdır.
Koşul 1:
Parabolün kolları yukarı yönlüdür (başkatsayısı pozitiftir).
\( a \gt 0 \)
Koşul 2:
Parabol \( x \) eksenini ya tek noktada keser ya da kesmez (deltası sıfıra eşit ya da sıfırdan küçüktür).
\( \Delta = b^2 - 4ac \le 0 \)
\( [-(3a + 6)]^2 - 4a(2a + 14) \le 0 \)
\( 9a^2 + 36a + 36 - 8a^2 - 56a \le 0 \)
\( a^2 - 20a + 36 \le 0 \)
\( (a - 2)(a - 18) \le 0 \)
Bu eşitsizlik \( a \in [2, 18] \) aralığında sağlanır.
Bulduğumuz iki aralığın kesişim kümesi \( a \) değer aralığını verir.
\( a \in [2, 18] \) bulunur.
\( f(x) = -x^2 - 8x - 7 \) parabolünün tepe noktasının ve eksenleri kestiği noktaların birleştirilmesiyle oluşan dörtgenin alanı kaçtır?
Çözümü Göster\( f(x) \) parabolünün \( x \) eksenini hangi noktalarda kestiğini bulmak için köklerini bulalım.
\( -x^2 - 8x - 7 = 0 \)
\( -(x + 7)(x + 1) = 0 \)
Buna göre parabol \( x \) eksenini \( x = -7 \) ve \( x = -1 \) noktalarında keser.
Parabolün \( y \) eksenini kestiği noktayı bulmak için denklemde \( x = 0 \) yazalım.
\( f(0) = -0^2 - 8(0) - 7 = -7 \)
Buna göre parabol \( y \) eksenini \( (0, -7) \) noktasında keser.
Parabolün tepe noktasına \( T(r, k) \) diyelim.
Parabolün katsayılarını yazalım.
\( a = -1, \quad b = -8, \quad c = -7 \)
\( r = -\dfrac{b}{2a} = -\dfrac{-8}{2(-1)} = -4 \)
\( k = f(r) \)
\( = -(-4)^2 - 8(-4) - 7 = 9 \)
\( T(r, k) = T(-4, 9) \)
Parabolün tepe noktasını ve eksenleri kestiği üç noktayı analitik düzlemde çizelim.
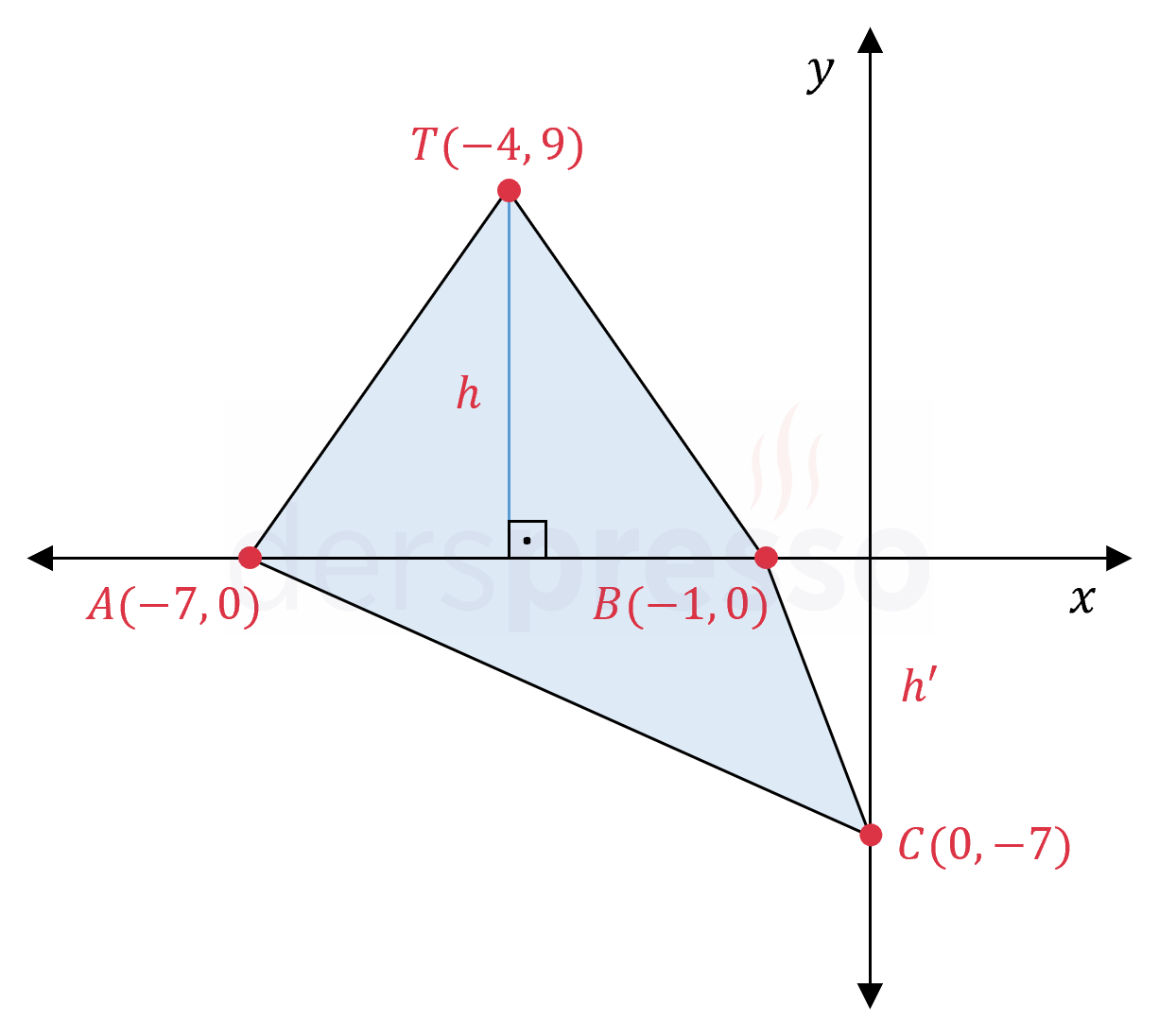
Parabolün \( x \) eksenini kestiği noktalara \( A \) ve \( B \), \( y \) eksenini kestiği noktaya \( C \) diyelim.
Bu noktaların oluşturduğu dörtgenin alanı \( ABT \) ve \( ABC \) üçgenlerinin alanları toplamına eşittir.
\( A(TACB) = A(TAB) + A(ACB) \)
\( A(TAB) = \dfrac{\abs{AB} \cdot h}{2} \)
\( = \dfrac{6 \cdot 9}{2} = 27 \)
\( A(ACB) = \dfrac{\abs{AB} \cdot h'}{2} \)
\( = \dfrac{6 \cdot 7}{2} = 21 \)
\( A(TACB) = A(TAB) + A(ACB) \)
\( = 27 + 21 = 48 \) bulunur.

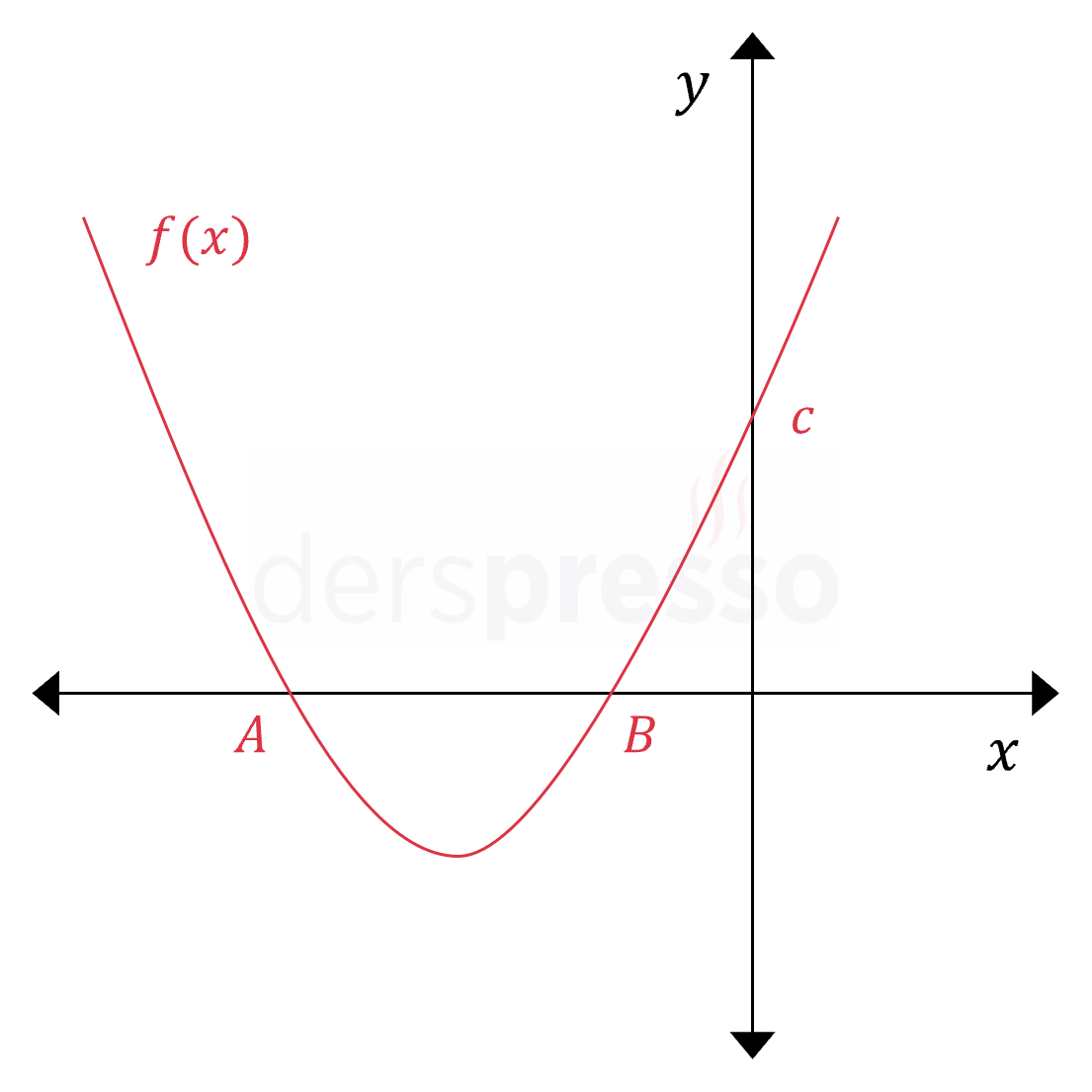
Şekildeki parabollerin denklemleri aşağıdaki gibidir.
\( f(x) = x^2 + (b - 2)x + c + 1 \)
\( g(x) = -2x^2 - (2b - 6)x + c - 2 \)
Buna göre \( \abs{BC} \) kaçtır?
Çözümü Göster\( f \) parabolünün \( A \) noktasındaki köküne \( x_1 \), \( B \) noktasındaki köküne \( x_2 \), \( g \) parabolünün \( C \) noktasındaki köküne \( x_3 \) diyelim.
\( f \) ve \( g \) parabolleri \( A \) noktasında kesişmektedir. Bu durumda \( x_1 \) kökleri iki parabol için ortaktır.
\( \abs{BC} \) uzunluğunu kökler cinsinden ifade edelim.
\( \abs{BC} = x_3 - x_2 \)
\( x_3 - x_2 \) değerini iki parabolün kökler toplamı cinsinden yazalım.
\( x_3 - x_2 = (x_1 + x_3) - (x_1 + x_2) \)
\( x_1 + x_3 \) ifadesi \( g \) parabolünün, \( x_1 + x_2 \) ifadesi \( f \) parabolünün kökler toplamına eşittir.
Parabollerin denklemlerinde kökler toplamı formülünü kullanarak bu değerleri bulalım.
\( f \) parabolünün kökler toplamını bulalım.
\( x_1 + x_2 = -\dfrac{b - 2}{1} \)
\( = 2 - b \)
\( g \) parabolünün kökler toplamını bulalım.
\( x_1 + x_3 = -\dfrac{-(2b - 6)}{-2} \)
\( = 3 - b \)
Bulduğumuz değerleri yerine yazalım.
\( \abs{BC} = (x_1 + x_3) - (x_1 + x_2) \)
\( = 3 - b - (2 - b) = 1 \) bulunur.