Parabolün Analitik Uygulamaları
Parabolün Parabole Göre Durumu
İki parabolün birbirine göre durumu da (parabolün doğruya göre durumuna benzer şekilde) üç farklı şekilde olabilir: Paraboller \( f(x) \) parabolünde olduğu gibi iki noktada kesişebilir, \( g(x) \) parabolünde olduğu gibi tek bir noktada (teğet) kesişebilir ya da \( h(x) \) parabolünde olduğu gibi kesişmeyebilir.
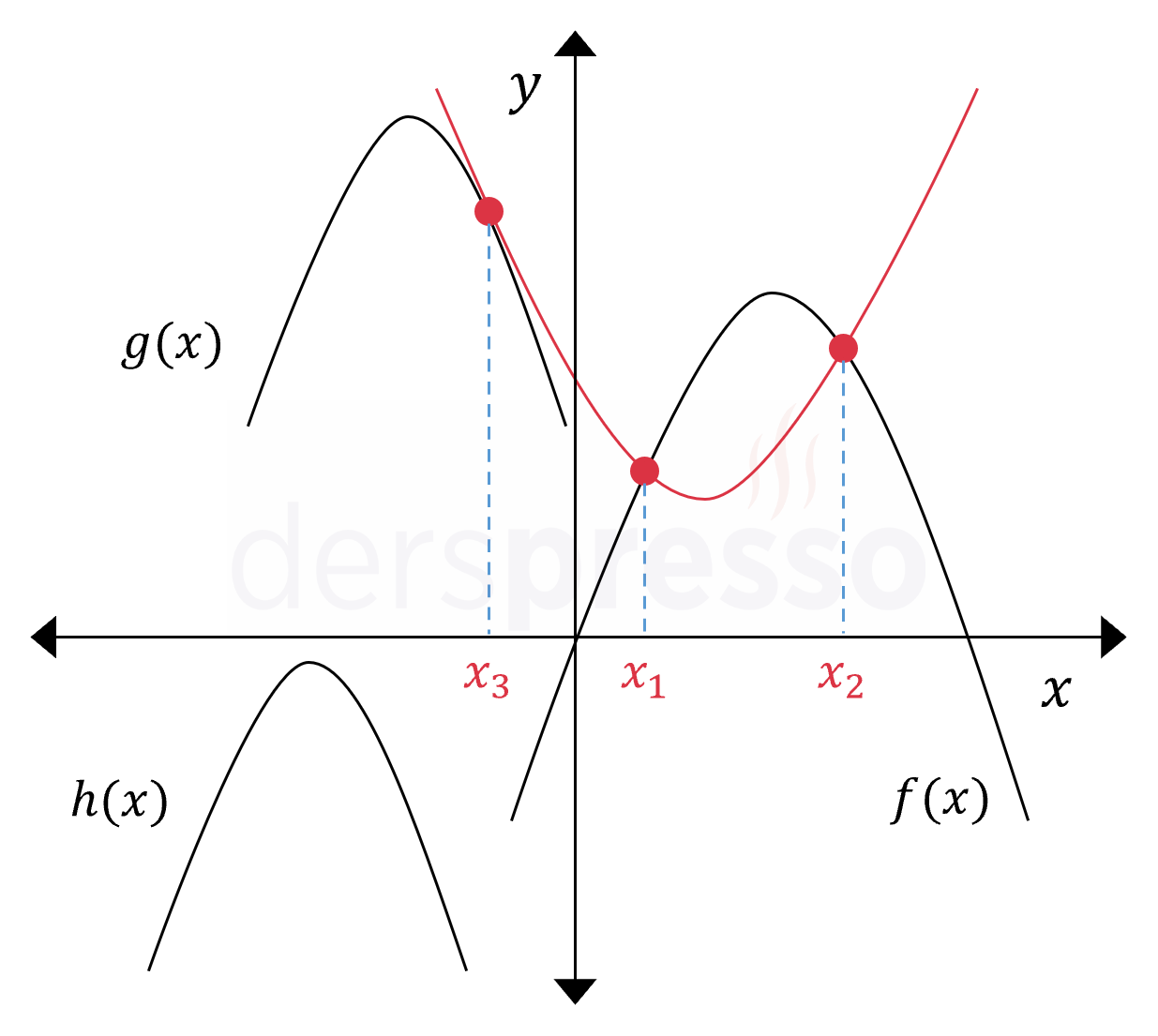
Parabollerin birbirine göre durumunu anlayabilmek için iki parabol denklemi ortak çözülür ve elde edilen ikinci dereceden denklemin deltası incelenir.
\( \Delta = b^2 - 4ac \) denklemin deltası olmak üzere,
Paraboller;
- \( \Delta \gt 0 \) ise iki noktada kesişir,
- \( \Delta = 0 \) ise tek bir noktada (teğet) kesişir,
- \( \Delta \lt 0 \) ise kesişmez.
Aşağıda denklemleri verilen parabollerin birbirine göre durumlarını inceleyelim.
\( f(x) = x^2 + 3x + 1 \)
\( g(x) = -3x^2 + 15x - 8 \)
İki denklemi ortak çözelim.
\( f(x) = g(x) \)
\( x^2 + 3x + 1 = -3x^2 + 15x - 8 \)
Tüm terimleri tek tarafta toplayıp ifadeyi sıfıra eşitleyelim.
\( 4x^2 - 12x + 9 = 0 \)
İkinci dereceden denklemin deltasını bulalım.
\( \Delta = b^2 - 4ac \)
\( = 12^2 - 4(4)(9) = 0 \)
\( \Delta = 0 \) olduğuna göre iki parabol tek bir noktada kesişir.
Bulduğumuz denklemi \( x \) için çözdüğümüzde parabollerin kesişim noktasının apsis değerini buluruz.
\( (2x - 3)^2 = 0 \)
\( x = \dfrac{3}{2} \)
Bu değeri parabollerden birinin denkleminde yerine yazdığımızda kesişim noktasının ordinat değerini buluruz.
\( f(\frac{3}{2}) = (\frac{3}{2})^2 + 3(\frac{3}{2}) + 1 \)
\( = \dfrac{31}{4} \)
Buna göre iki parabol \( (\frac{3}{2}, \frac{31}{4}) \) noktasında kesişir.
Parabollerin grafikleri aşağıda verilmiştir.
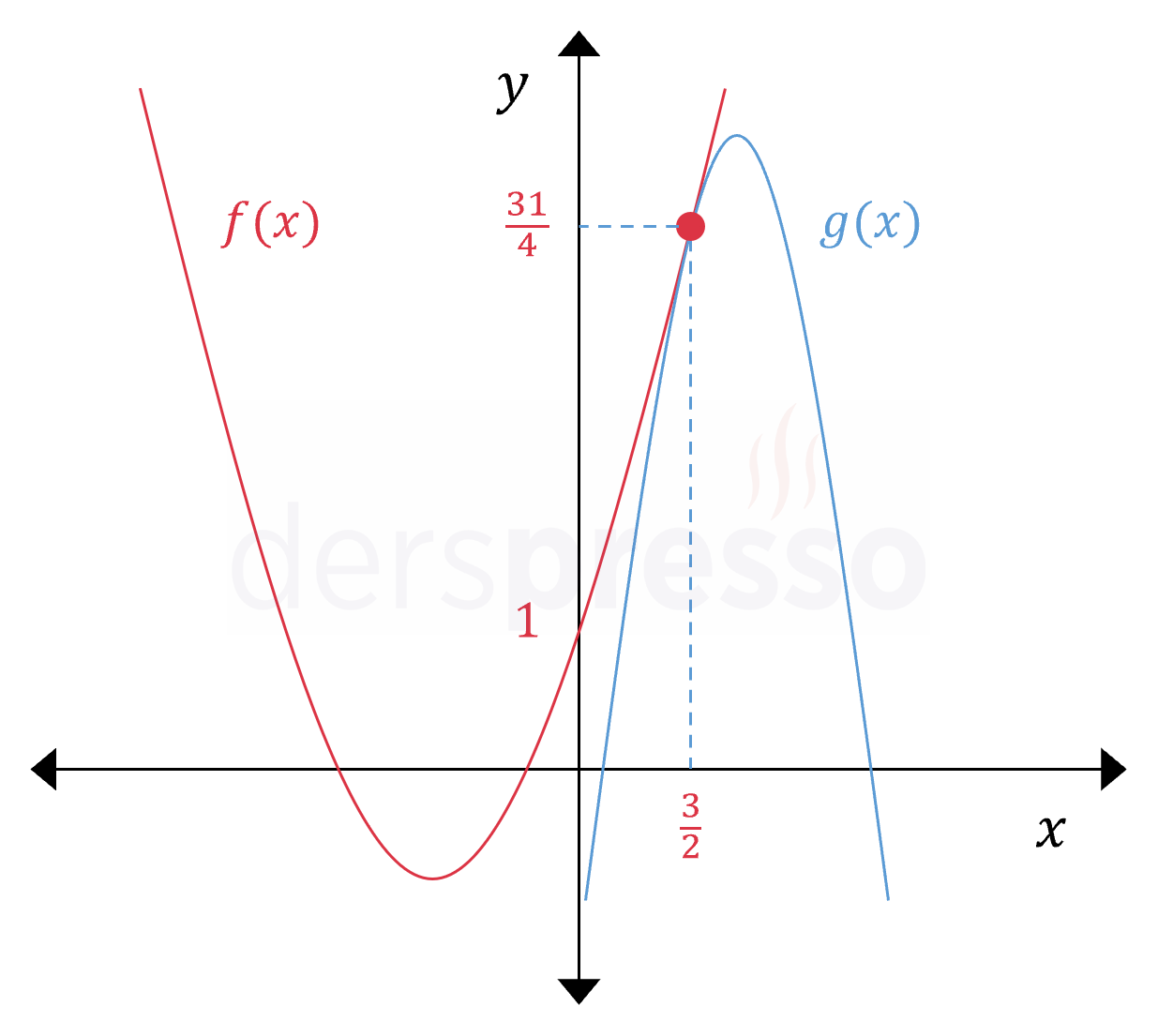
Eğer parabollerin başkatsayıları birbirine eşitse denklemlerin ortak çözümünde ikinci dereceden terimler birbirini götürür ve birinci dereceden bir denklem elde edilir. Bu denklemin \( x \) için bir çözümü varsa iki parabol tek bir noktada kesişir, aksi takdirde (\( x \)'li terimler de birbirini götürüyorsa) iki parabol kesişmez.
Aşağıda denklemleri verilen parabollerin birbirine göre durumlarını inceleyelim.
\( f(x) = x^2 - 3x + 7 \)
\( g(x) = x^2 + 2x - 8 \)
İki denklemi ortak çözelim.
\( f(x) = g(x) \)
\( x^2 - 3x + 7 = x^2 + 2x - 8 \)
İkinci dereceden terimler birbirini götürür.
\( 5x - 15 = 0 \)
\( x = 3 \)
Bu değeri parabollerden birinin denkleminde yerine yazdığımızda kesişim noktasının ordinat değerini buluruz.
\( f(3) = 3^2 - 3(3) + 7 = 7 \)
Buna göre iki parabol \( (3, 7) \) noktasında kesişir.
Parabollerin grafikleri aşağıda verilmiştir.
Bir Parabole Orijinden Çizilen Teğetler
Bir parabole orijinden çizilen teğet doğruların eğimlerinin çarpımı parabolün deltasına eşittir.
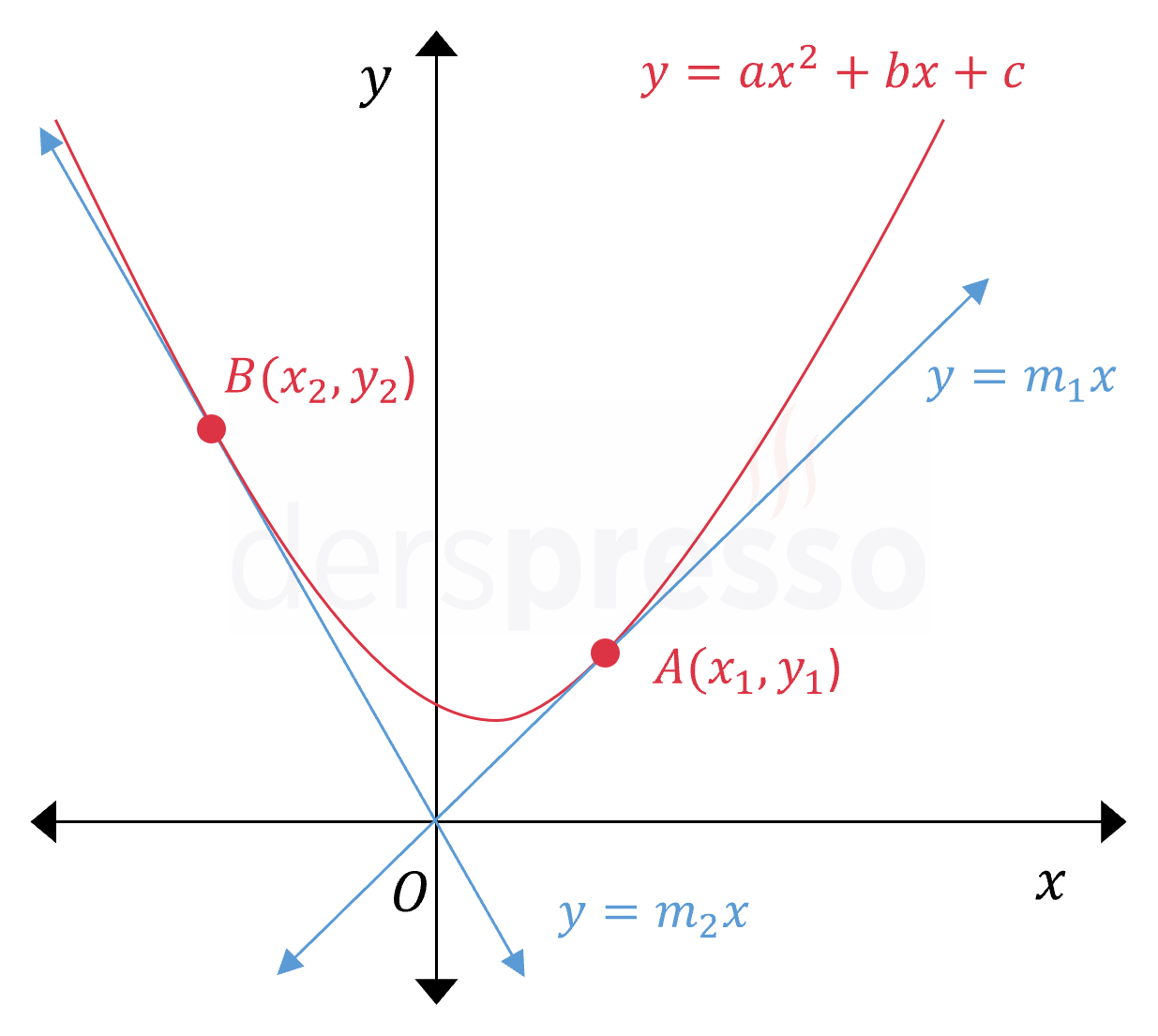
Parabol: \( y = ax^2 + bx + c \)
Teğet doğru 1: \( y = m_1x \)
Teğet doğru 2: \( y = m_2x \)
\( m_1 \cdot m_2 = \Delta = b^2 - 4ac \)
İSPATI GÖSTER
Bir parabole orijinden kaç teğet doğru çizilebileceğini bilmeden eğimi \( m \) olan genel bir teğet doğru denklemi yazalım.
Parabol: \( y = ax^2 + bx + c \)
Teğet doğru: \( y = mx \)
Doğrular parabole teğet olduğu için parabolü tek bir noktada keserler, dolayısıyla bu iki denklemin ortak çözümünün deltası sıfır olmalıdır.
\( ax^2 + bx + c = mx \)
\( ax^2 + (b - m)x + c = 0 \)
\( \Delta = (b - m)^2 - 4ac = 0 \)
\( b^2 - 2bm + m^2 - 4ac = 0 \)
İfadeyi \( m \)'ye göre düzenleyelim.
\( m^2 - 2bm + b^2 - 4ac = 0 \)
Ortak çözüm sonucunda ikinci dereceden bir denklem elde etmemiz denklemin kökleri olarak iki \( m \) değeri elde edeceğimizi, dolayısıyla orijinden bir parabole teğet iki farklı doğru çizilebileceğini gösterir (tüm ikinci derece denklemlerde olduğu gibi bazı durumlarda tek bir kök ve sıfır kök de olabilir). Verilen herhangi bir parabol denkleminin \( a \), \( b \), \( c \) katsayılarını bu eşitlikte yerine koyduğumuzda, bu denklemin kökleri teğet doğruların \( m_1 \) ve \( m_2 \) eğimlerini verecektir.
Dikkat edilirse, elde ettiğimiz \( m \) cinsinden denklemin kökler çarpımına karşılık gelen \( b^2 - 4ac \) ifadesi aynı zamanda orijinal parabol denkleminin deltasına eşittir. Dolayısıyla bir parabole orijinden çizilen teğet doğruların eğimlerinin çarpımının parabol denkleminin deltasına eşit olduğu sonucuna varabiliriz.
\( m_1 \cdot m_2 = \Delta = b^2 - 4ac \)
Bunun bir sonucu olarak, bir parabole orijinden çizilen teğet doğruların birbirine dik olması istenirse dik doğruların eğimlerinin çarpımı \( -1 \) olduğu için parabolün deltası da \( -1 \)'e eşit olmalıdır.
Orijinden bir parabole çizilen teğetlerin dik olma koşulu:
\( \Delta = b^2 - 4ac = m_1 \cdot m_2 = -1 \)
Yukarıdaki ispatta ortak çözüm sonucunda elde edilen denklemde kökler toplamına karşılık gelen \( 2b \) ifadesi de parabole çizilen teğet doğruların eğimleri toplamını verir. Bu teğet doğruların eğimleri toplamının sıfır olması istenirse \( 2b \) ifadesi, dolayısıyla parabolün \( b \) katsayısı sıfır olmalıdır.
Bir Parabole x Eksenini Kestiği Noktalardan Çizilen Teğetler
Bir parabole \( x \) eksenini kestiği noktalardan çizilen teğet doğruların eğimlerinin çarpımı parabolün deltasının ters işaretlisine eşittir.
Parabol: \( y = ax^2 + bx + c \)
Teğet doğru 1: \( y = m_1x + c_1 \)
Teğet doğru 2: \( y = m_2x + c_2 \)
\( m_1 \cdot m_2 = -\Delta = -(b^2 - 4ac) \)
İSPATI GÖSTER
Bir parabole \( x \) eksenini kestiği noktalardan çizilen teğetlerin eğimlerini parabolün kökleri cinsinden aşağıdaki şekilde yazabiliriz (bu eğim değerlerini nasıl bulduğumuzu türev konusuna bırakıyoruz).
Parabol: \( y = ax^2 + bx + c \)
Parabolün kökleri: \( x_1, x_2 \)
1. teğet doğrunun eğimi: \( m_1 = 2ax_1 + b \)
2. teğet doğrunun eğimi: \( m_2 = 2ax_2 + b \)
Bu teğet doğruların eğimlerinin çarpımını alalım.
\( m_1 \cdot m_2 = (2ax_1 + b)(2ax_2 + b) \)
\( = 4a^2x_1x_2 + 2abx_1 + 2abx_2 + b^2 \)
\( = 4a^2x_1x_2 + 2ab(x_1 + x_2) + b^2 \)
Parabol kökler toplamı: \( x_1 + x_2 = -\dfrac{b}{a} \)
Parabol kökler çarpımı: \( x_1 \cdot x_2 = \dfrac{c}{a} \)
Yukarıdaki iki ifadeyi denklemde yerine koyalım.
\( = 4a^2 \dfrac{c}{a} - 2ab\dfrac{b}{a} + b^2 \)
\( = 4ac - 2b^2 + b^2 \)
\( = 4ac - b^2 \)
\( = -(b^2 - 4ac) \)
Parantez içindeki ifadenin parabol denkleminin deltası olduğunu hatırlarsak, parabole \( x \) eksenini kestiği noktalardan çizdiğimiz teğet doğruların eğimleri çarpımının parabolün deltasının ters işaretlisi olduğunu görürüz.
\( m_1 \cdot m_2 = -\Delta = -(b^2 - 4ac) \)
Bunun bir sonucu olarak, bu teğet doğruların birbirine dik olması istenirse dik doğruların eğimlerinin çarpımı \( -1 \) olduğu için parabolün deltası \( +1 \)'e eşit olmalıdır.
\( x \) eksenini kestiği noktalardan bir parabole çizilen teğetlerin dik olma koşulu:
\( \Delta = b^2 - 4ac = -m_1 \cdot m_2 = 1 \)
\( y = x^2 + mx + 5 \) ve \( y = -x^2 + (2m + 1)x + 3 \)
parabolleri birbirine teğet olduğuna göre, \( m \)'nin pozitif değeri nedir?
Çözümü Gösterİki parabol birbirine teğet ise tek noktada kesişirler, dolayısıyla ortak çözüldüklerinde elde edeceğimiz ikinci dereceden denklemin deltası sıfır olur.
\( y \) değerlerini eşitleyerek iki denklemi ortak çözelim.
\( x^2 + mx + 5 = -x^2 + (2m + 1)x + 3 \)
\( 2x^2 + mx - 2mx - x + 2 = 0 \)
\( 2x^2 - (m + 1)x + 2 = 0 \)
Ortak çözümle elde ettiğimiz parabolün katsayılarını yazalım.
\( a = 2, \quad b = -(m + 1), \quad c = 2 \)
\( \Delta = b^2 - 4ac = 0 \)
\( [-(m + 1)]^2 - 4(2)(2) = 0 \)
\( (m + 1)^2 = 16 \)
Bu eşitlik iki durumda sağlanır.
Durum 1:
\( m + 1 = 4 \)
\( m = 3 \)
Durum 2:
\( m + 1 = -4 \)
\( m = -5 \)
\( m \)'nin pozitif değeri \( m = 3 \) olarak bulunur.
\( y = x^2 - 3x + m \)
parabolünün \( x \) eksenini kestiği noktalardan parabole çizilen teğetler birbirine dik olduğuna göre, \( m \) kaçtır?
Çözümü GösterParabolün katsayılarını yazalım.
\( a = 1, \quad b = -3, \quad c = m \)
Parabolün \( x \) eksenini kestiği noktalardan parabole çizilen teğetler birbirine dik ise parabolün deltası 1'e eşit olmalıdır.
\( \Delta = b^2 - 4ac = 1 \)
\( (-3)^2 - 4(1)(m) = 1 \)
\( 4m = 8 \)
\( m = 2 \) bulunur.
\( y = x^2 + 2x - n \) ve \( y = -2x^2 - 4x + m \) parabollerinin kesişim noktalarını birleştiren doğru parçasının orta noktasının apsisi kaçtır?
Çözümü Gösterİki parabolün denklemini ortak çözdüğümüzde kesişim noktalarının apsis değerlerini buluruz.
\( x^2 + 2x - n = -2x^2 - 4x + m \)
\( 3x^2 + 6x - n - m = 0 \)
Ortak çözümle elde ettiğimiz bu parabol denkleminin kökler toplamı aynı zamanda iki parabolün kesişim noktalarının apsis değerlerinin toplamını verir, parabolün tepe noktasının apsisi de iki kesişim noktasının orta noktasının apsis değerine eşit olur.
Ortak çözümle elde ettiğimiz parabolün katsayılarını yazalım.
\( a = 3, \quad b = 6, \quad c = -n - m \)
Parabolün tepe noktasına \( T(r, k) \) diyelim.
\( r = -\dfrac{b}{2a} = -\dfrac{6}{2(3)} = -1 \) bulunur.
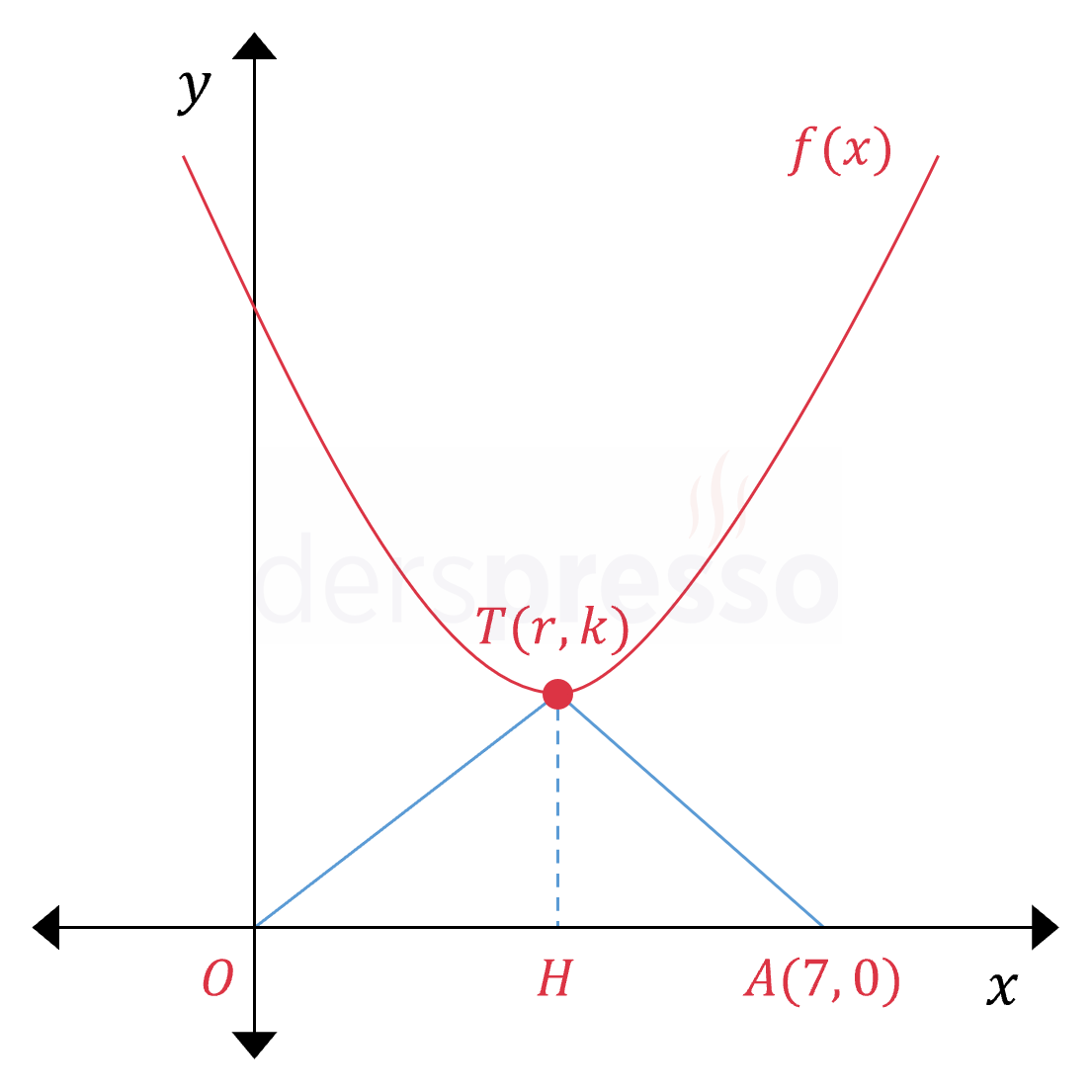
Yukarıda \( y = x^2 - 4x + m \) parabolünün grafiği verilmiştir.
\( T \) parabolün tepe noktası ve \( OTA \) üçgeninin alanı 14 birimkare olduğuna göre, \( m \) kaçtır?
Çözümü Göster\( OTA \) üçgeni için alan formülünü yazalım. Üçgenin yüksekliği parabolün tepe noktasının ordinatına eşittir.
\( A(OTA) = \dfrac{\abs{OA} \cdot \abs{TH}}{2} \)
\( 14 = \dfrac{7k}{2} \)
\( k = 4 \)
Parabolün tepe noktasının apsis değeri aşağıdaki formülle bulunur.
\( r = -\dfrac{b}{2a} = -\dfrac{-4}{2(1)} = 2 \)
Buna göre parabolün tepe noktası \( T(2, 4) \) olur.
Bu noktayı parabol denkleminde yerine koyalım.
\( f(2) = 2^2 - 4(2) + m = 4 \)
\( 4 - 8 + m = 4 \)
\( m = 8 \) bulunur.
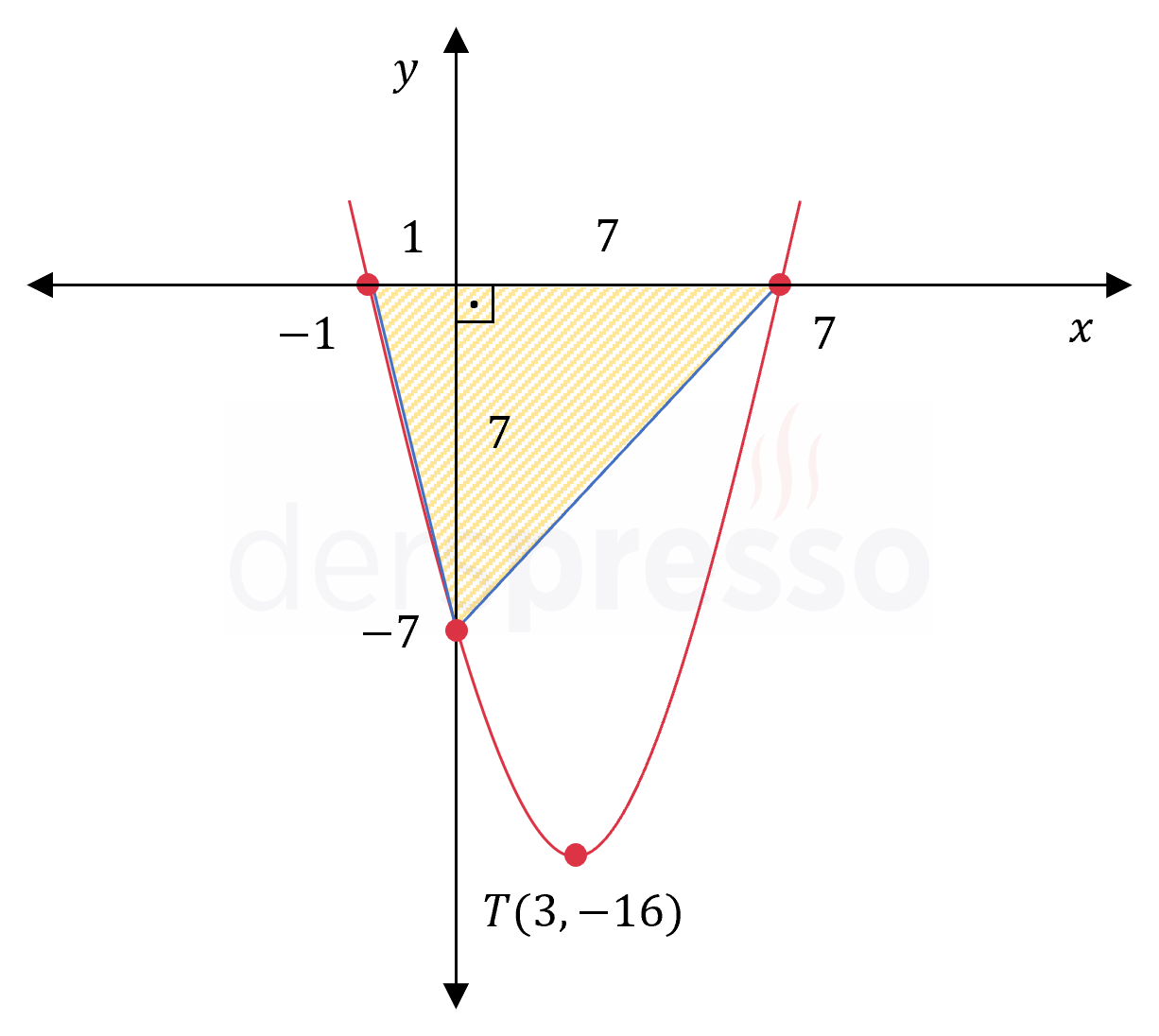
\( f(x) = x^2 - 6x + 2m - 3 \) parabolünün tepe noktasının ordinatı \( -16 \)'dır.
Buna göre parabolün eksenleri kestiği üç noktayı köşe kabul eden üçgenin alanı kaçtır?
Çözümü GösterParabolün katsayılarını yazalım.
\( a = 1, \quad b = -6, \quad c = 2m - 3 \)
Parabolün tepe noktasına \( T(r, k) \) diyelim.
\( r = -\dfrac{b}{2a} = -\dfrac{-6}{2(1)} = 3 \)
Buna göre parabolün tepe noktası \( T(3, -16) \) noktasıdır.
Bu noktanın koordinatlarını parabol denkleminde yerine koyalım.
\( f(3) = 3^2 - 6(3) + 2m - 3 = -16 \)
\( m = -2 \)
Buna göre parabolün denklemi aşağıdaki gibi olur.
\( f(x) = x^2 - 6x - 7 \)
\( = (x + 1)(x - 7) \)
Parabol \( x \) eksenini \( x = -1 \) ve \( x = 7 \) noktalarında, \( y \) eksenini de fonksiyonun sabit terimi olan \( y = -7 \) noktasında keser.
Taban uzunluğu \( 7 - (-1) = 8 \) birim ve yüksekliği \( \abs{-7} = 7 \) birim olan üçgenin alanını bulalım.
Alan \( = \dfrac{8 \cdot 7}{2} = 28 \) bulunur.
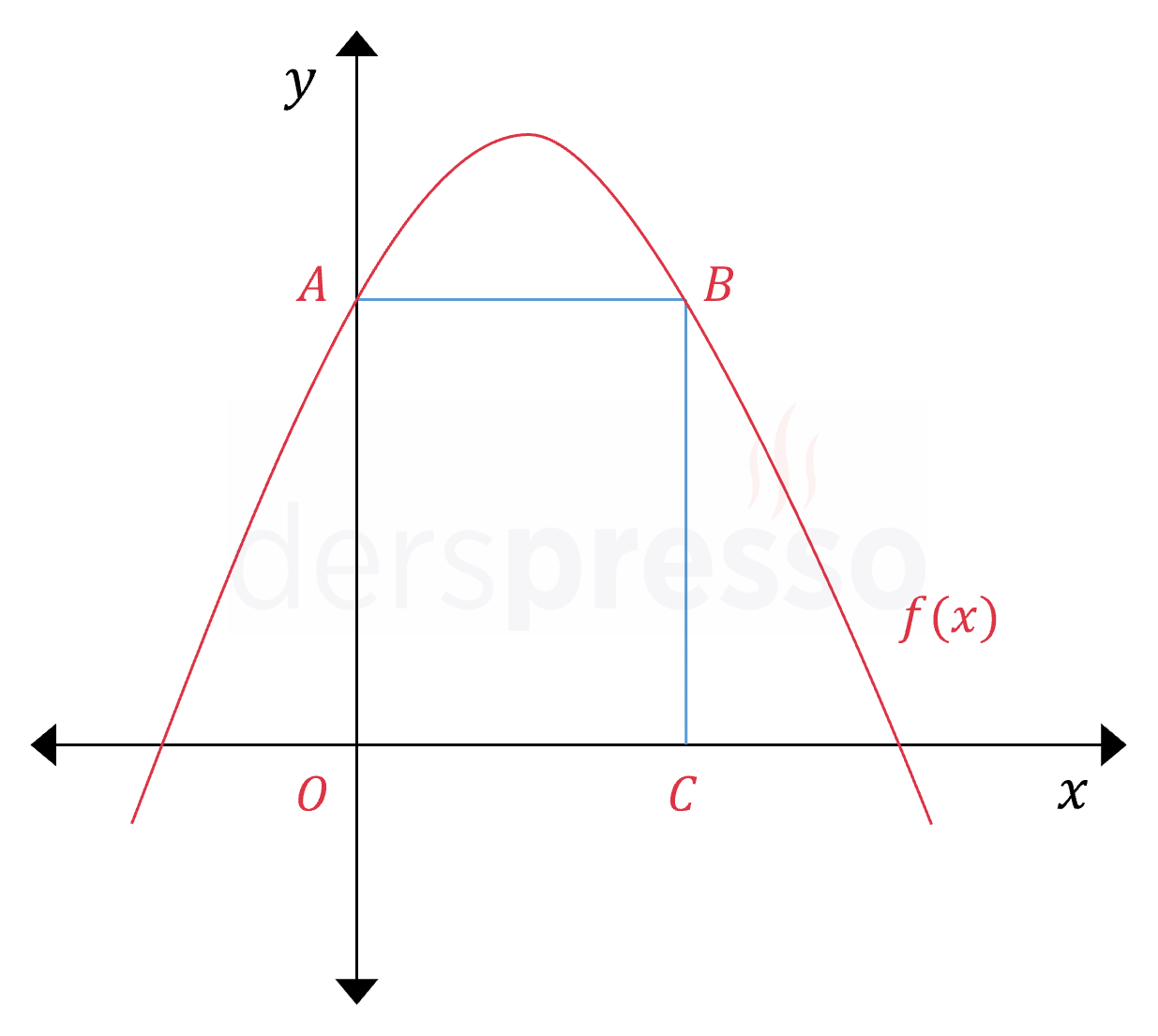
Yukarıdaki şekilde \( y = -x^2 + 3x + 8 \) parabolü verilmiştir.
Parabolün \( y \) eksenini kestiği nokta \( A \) olduğuna göre, \( OABC \) dikdörtgeninin alanı kaç birimkaredir?
Çözümü GösterParabolün \( y \) eksenini kestiği noktanın ordinatı parabol denkleminin sabit terimidir.
\( A(0, 8) \)
\( B \) noktasının koordinatlarına \( B(b, 8) \) diyelim ve koordinatlarını parabol denkleminde yerine koyalım.
\( 8 = -b^2 + 3b + 8 \)
\( b^2 - 3b = 0 \)
\( b(b - 3) = 0 \)
\( B \) noktasının ordinatı sıfırdan büyük olduğu için \( b = 3 \) olur.
\( B(b, 8) = B(3, 8) \)
Buna göre \( OABC \) dikdörtgeninin tabanı 3 birim, yüksekliği 8 birimdir.
\( A(OABC) = 3 \cdot 8 = 24 \) birimkare bulunur.
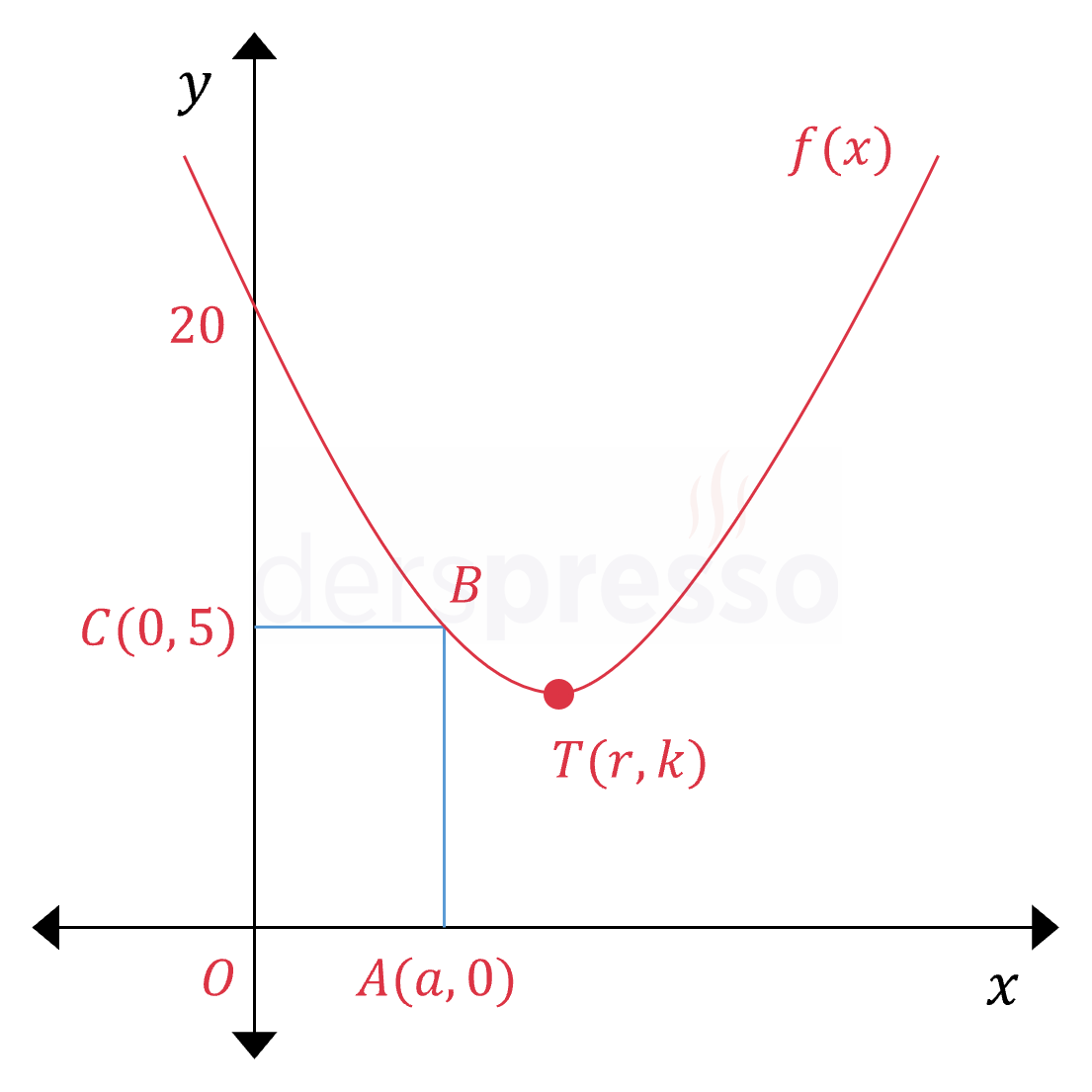
\( OABC \) dikdörtgeninin \( B \) köşesi \( f(x) = x^2 - 8x + m \) parabolü üzerindedir. Parabol \( y \) eksenini \( (0, 20) \) noktasında kestiğine göre, \( OABC \) dikdörtgeninin alanı kaç birimkaredir?
Çözümü GösterParabolün \( y \) eksenini kestiği noktayı bulmak için denklemde \( x = 0 \) koyalım.
\( f(0) = m = 20 \)
Parabolün denklemi aşağıdaki gibi olur.
\( f(x) = x^2 - 8x + 20 \)
\( A(a, 0) \) ve \( C(0, 5) \) olduğuna göre, \( B(a, 5) \) olur.
\( B \) noktasının koordinatlarını parabol denkleminde yerine koyarak \( a \) değerini bulalım.
\( f(a) = a^2 - 8a + 20 = 5 \)
\( a^2 - 8a + 15 = 0 \)
\( (a - 3)(a - 5) = 0 \)
\( a = 3 \) veya \( a = 5 \)
Tepe noktasının apsisi 4 olduğuna göre \( A \) noktasının apsisi 4'ten küçük olmalıdır, buna göre \( a = 3 \) olur.
\( A(OABC) = 3 \cdot 5 = 15 \) birimkare bulunur.
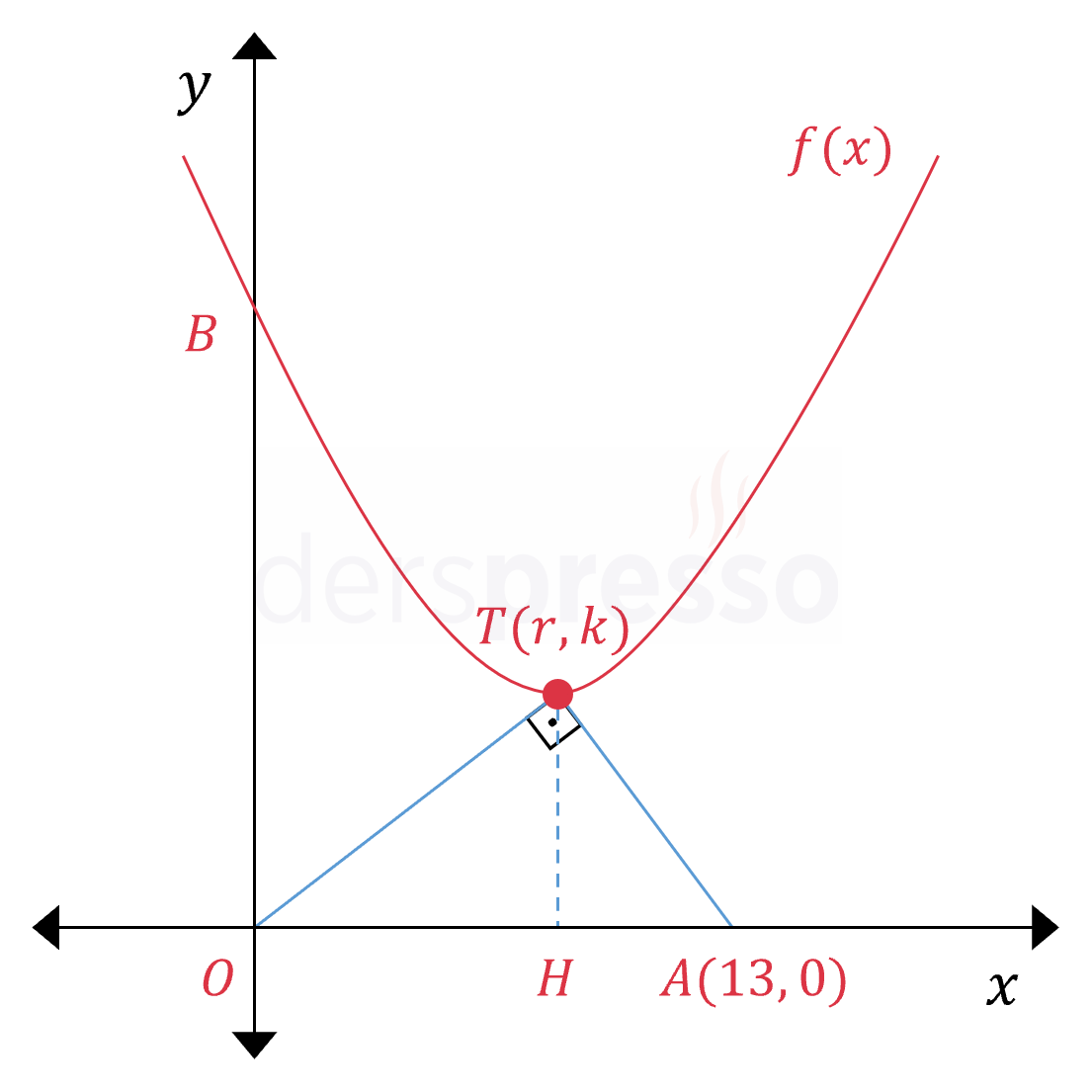
Yukarıdaki şekilde \( f(x) = x^2 - 8x + c \) parabolünün tepe noktası \( T \) olarak veriliyor.
\( OTA \) dik üçgeninde \( A(13, 0) \) olduğuna göre, \( B \) noktasının ordinatı kaçtır?
Çözümü GösterTepe noktasından \( x \) eksenine bir dikme çizelim ve ekseni kestiği noktaya \( H \) diyelim.
Parabolün tepe noktasının apsis değeri aşağıdaki formülle bulunur.
\( r = -\dfrac{b}{2a} = -\dfrac{-8}{2(1)} = 4 \)
\( OTA \) üçgeninde Öklid bağıntısını uygulayalım.
\( \abs{HT}^2 = \abs{OH} \cdot \abs{HA} \)
\( k^2 = 4(13 - 4) \)
\( k = 6 \)
\( T(4, 6) \)
Tepe noktasının koordinatlarını parabol denkleminde yerine koyarak \( c \) değerini bulalım.
\( 6 = 4^2 - 8(4) + c \)
\( c = 22 \)
\( B \) noktasının ordinatı parabolün sabit terimine eşit olduğu için \( c = 22 \) bulunur.
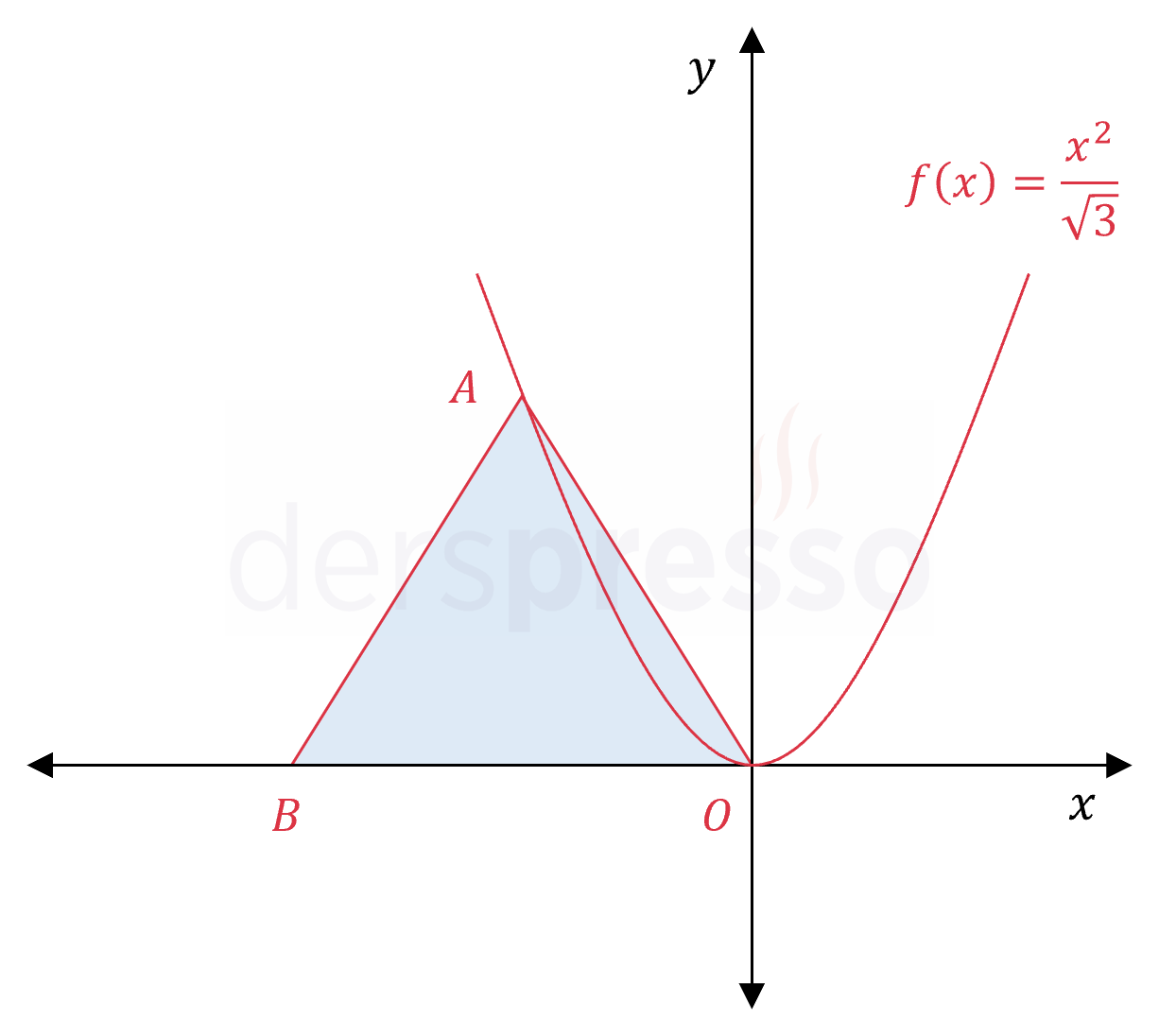
Şekildeki \( ABO \) üçgeninin \( [BO] \) kenarı \( x \) ekseni, \( A \) köşesi \( f(x) = \frac{\sqrt{3}x^2}{3} \) parabolü üzerindedir.
\( ABO \) eşkenar üçgen olduğuna göre, \( A(ABO) \) kaçtır?
Çözümü Göster\( A \) noktasından \( x \) eksenine bir dikme çizelim ve ekseni kestiği noktaya \( D \) diyelim.
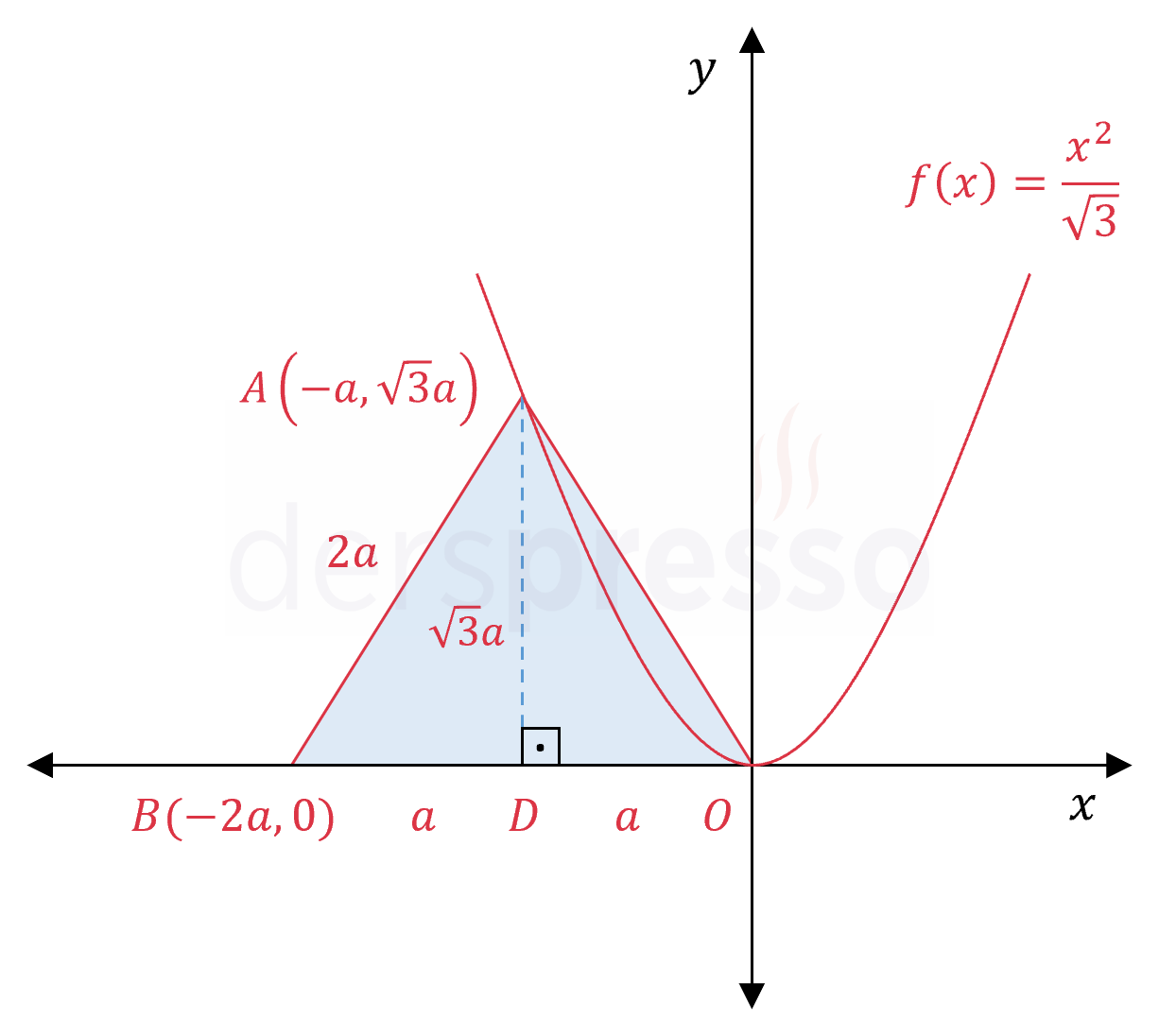
Eşkenar üçgende bir köşeden indirilen dikme hem açıortay hem kenarortay hem de orta dikmedir.
Eşkenar üçgenin bir kenarına \( 2a \) diyelim.
\( \abs{AB} = \abs{AO} = \abs{BO} = 2a \)
\( \abs{BD} = \abs{OD} = a \)
Bir kenar uzunluğu \( x \) olan eşkenar üçgenin yüksekliği \( \frac{\sqrt{3}x}{2} \) olur.
\( \abs{AD} = \frac{\sqrt{3}(2a)}{2} = \sqrt{3}a \)
\( A(-a, \sqrt{3}a) \)
\( A \) noktası parabol üzerinde olduğu için koordinatları parabol denklemini sağlar.
\( f(-a) = \sqrt{3}a \)
\( \dfrac{\sqrt{3}(-a)^2}{3} = \sqrt{3}a \)
\( a = 3 \)
\( \abs{AB} = \abs{AO} = \abs{BO} = 2a = 6 \)
Bir kenar uzunluğu \( x \) olan eşkenar üçgenin alanı \( \frac{\sqrt{3}x^2}{4} \) formülü ile bulunur.
\( A(ABO) = \dfrac{\sqrt{3}(6)^2}{4} \)
\( = 9\sqrt{3} \) bulunur.
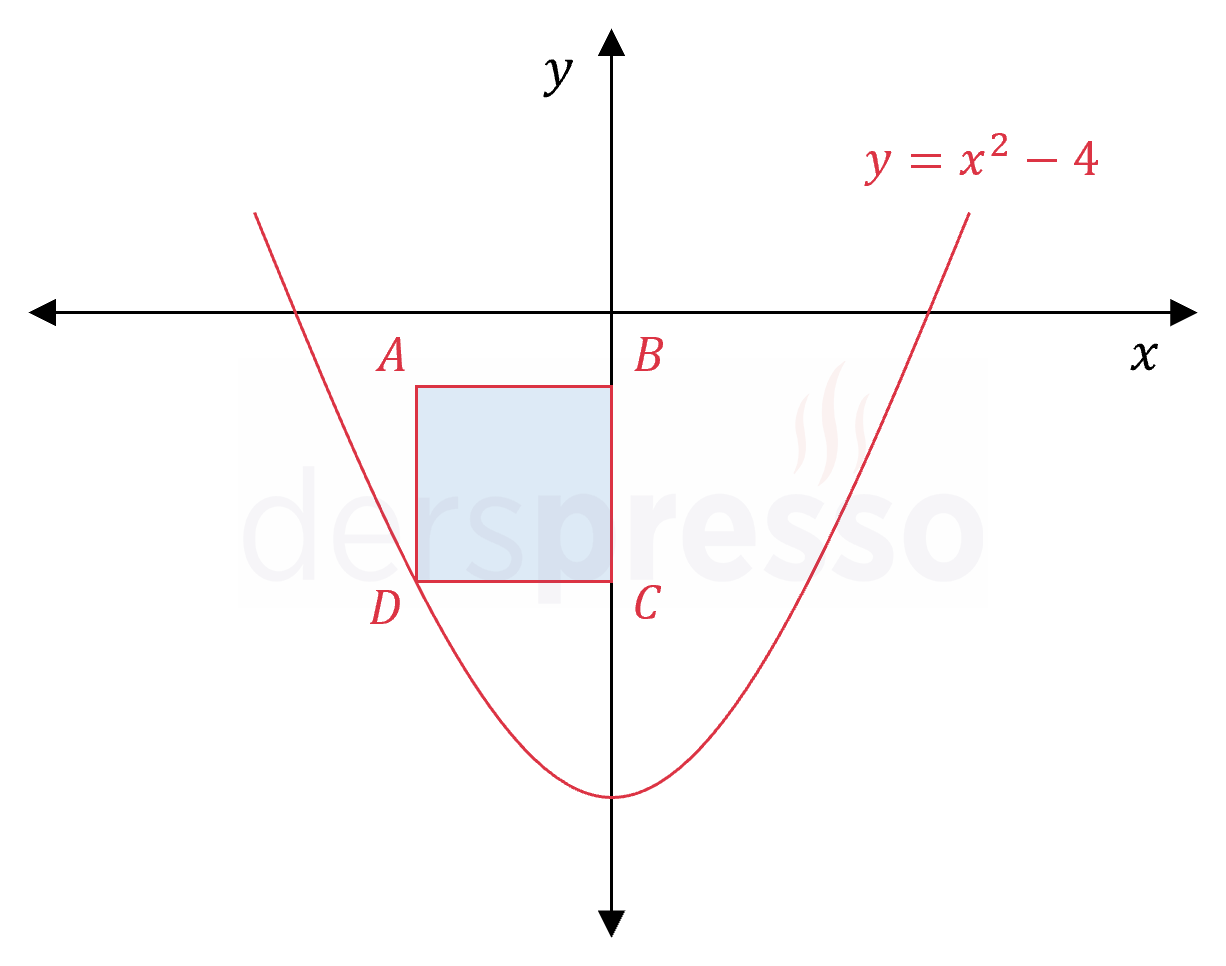
Şekilde \( y = x^2 - 4 \) parabolü ve bir kenarı \( y \) ekseni üzerinde olan \( ABCD \) karesi verilmiştir.
\( A \) noktasının koordinatları toplamı \( -3 \) olduğuna göre, karenin çevresi kaçtır?
Çözümü GösterKarenin bir kenar uzunluğuna \( a \) diyelim.
Karenin \( D \) köşesinin apsisi \( -a \) olur.
\( D \) köşesi \( y = x^2 - 4 \) parabolü üzerinde olduğundan ordinatı \( (-a)^2 - 4 = a^2 - 4 \) olur.
\( D(-a, a^2 - 4) \)
\( A \) noktasının apsisi \( D \) noktası ile aynıdır, ordinatı \( D \) noktasının ordinatından \( a \) kadar fazladır.
\( A(-a, a^2 - 4 + a) \)
\( A \) noktasının koordinatları toplamı \( -3 \)'e eşittir.
\( -a + (a^2 - 4 + a) = -3 \)
\( a^2 = 1 \)
\( a = \pm 1 \)
\( a \) karenin bir kenar uzunluğu olduğu için değeri pozitiftir.
\( a = 1 \)
Karenin çevresi \( 4 \cdot 1 = 4 \) olarak bulunur.
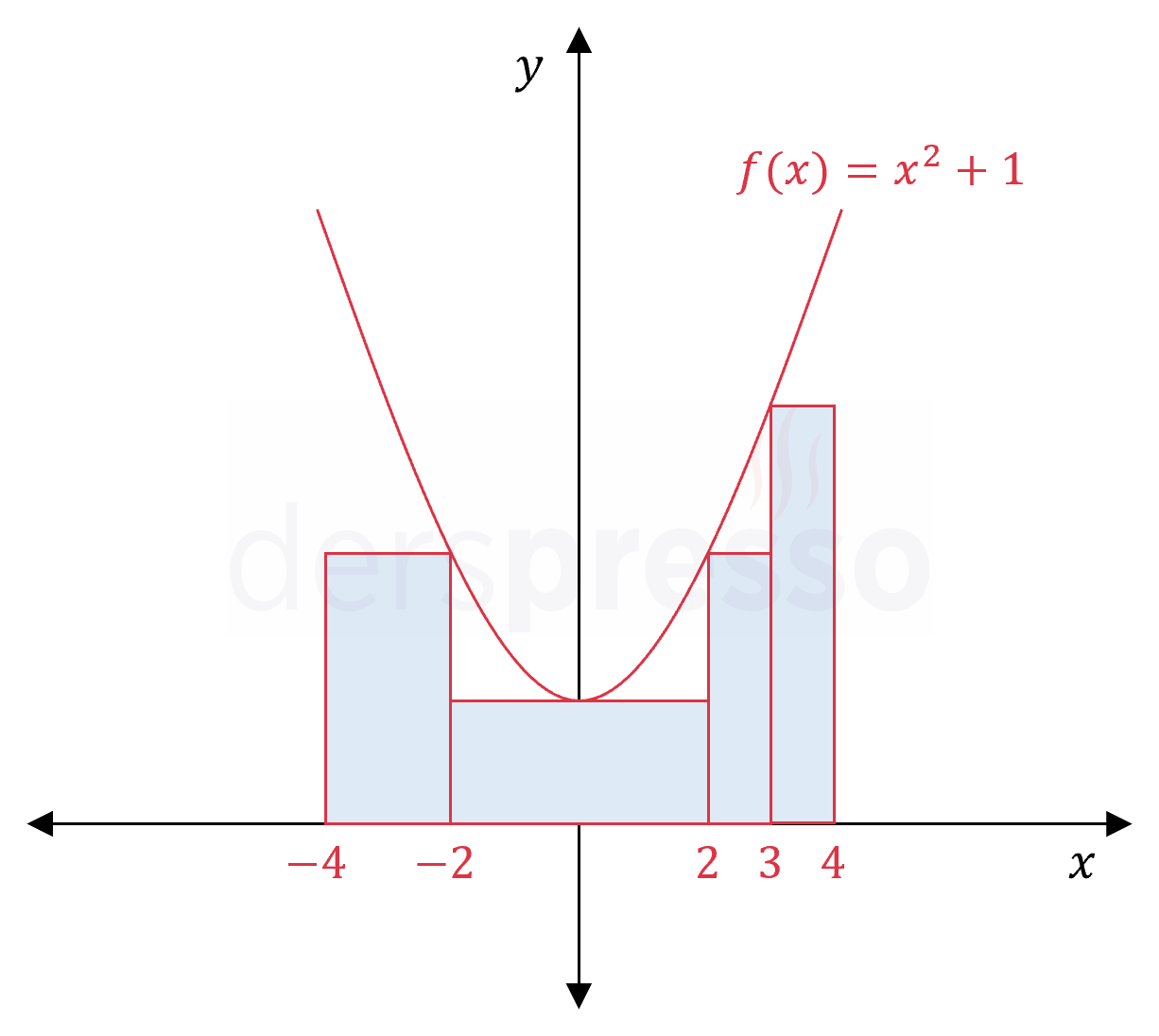
Yukarıdaki şekilde \( f(x) = x^2 + 1 \) parabolü ve dört adet dikdörtgen verilmiştir.
Buna göre şekildeki dikdörtgenlerin alanları toplamı kaç birimkaredir?
Çözümü Göster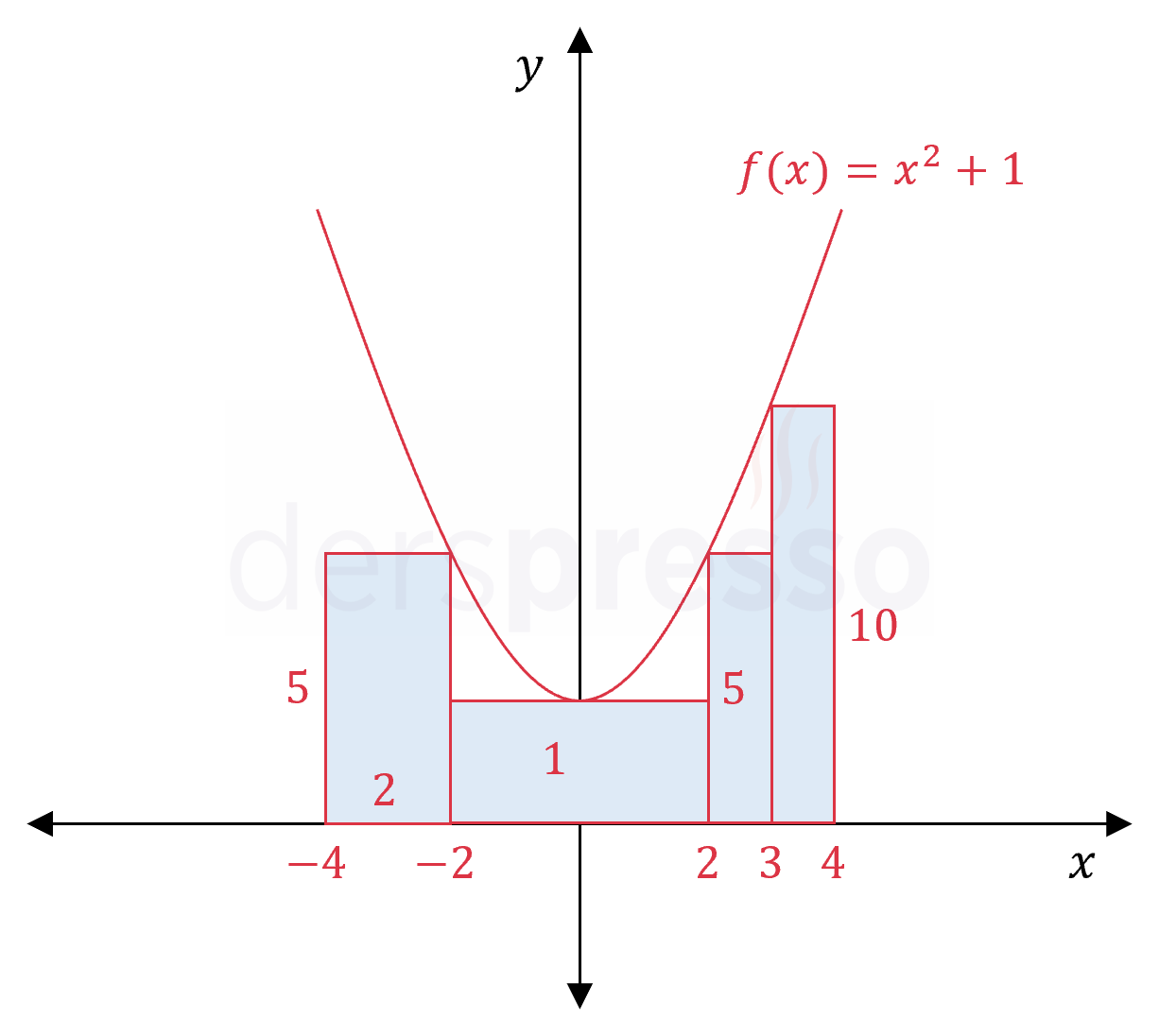
Dikdörtgenleri soldan sağa doğru 1, 2, 3, 4 şeklinde numaralandıralım.
Birinci dikdörtgenin yüksekliği \( x = -2 \) için fonksiyon değerine eşittir.
\( f(-2) = (-2)^2 + 1 = 5 \)
Birinci dikdörtgenin genişliğini bulalım.
\( \abs{-4 - (-2)} = 2 \)
Birinci dikdörtgenin alanını bulalım.
\( A_1 = 5 \cdot 2 = 10 \)
İkinci dikdörtgenin yüksekliği \( x = 0 \) için fonksiyon değerine eşittir.
\( f(0) = 0^2 + 1 = 1 \)
İkinci dikdörtgenin genişliğini bulalım.
\( \abs{2 - (-2)} = 4 \)
İkinci dikdörtgenin alanını bulalım.
\( A_2 = 1 \cdot 4 = 4 \)
Üçüncü dikdörtgenin yüksekliği \( x = 2 \) için fonksiyon değerine eşittir.
\( f(2) = 2^2 + 1 = 5 \)
Üçüncü dikdörtgenin genişliğini bulalım.
\( \abs{3 - 2} = 1 \)
Üçüncü dikdörtgenin alanını bulalım.
\( A_3 = 5 \cdot 1 = 5 \)
Dördüncü dikdörtgenin yüksekliği \( x = 3 \) için fonksiyon değerine eşittir.
\( f(3) = 3^2 + 1 = 10 \)
Dördüncü dikdörtgenin genişliğini bulalım.
\( \abs{4 - 3} = 1 \)
Dördüncü dikdörtgenin alanını bulalım.
\( A_4 = 10 \cdot 1 = 10 \)
Dört dikdörtgenin alanlarının toplamını bulalım.
\( A_1 + A_2 + A_3 + A_4 = 10 + 4 + 5 + 10 \)
\( = 29 \) birimkare bulunur.
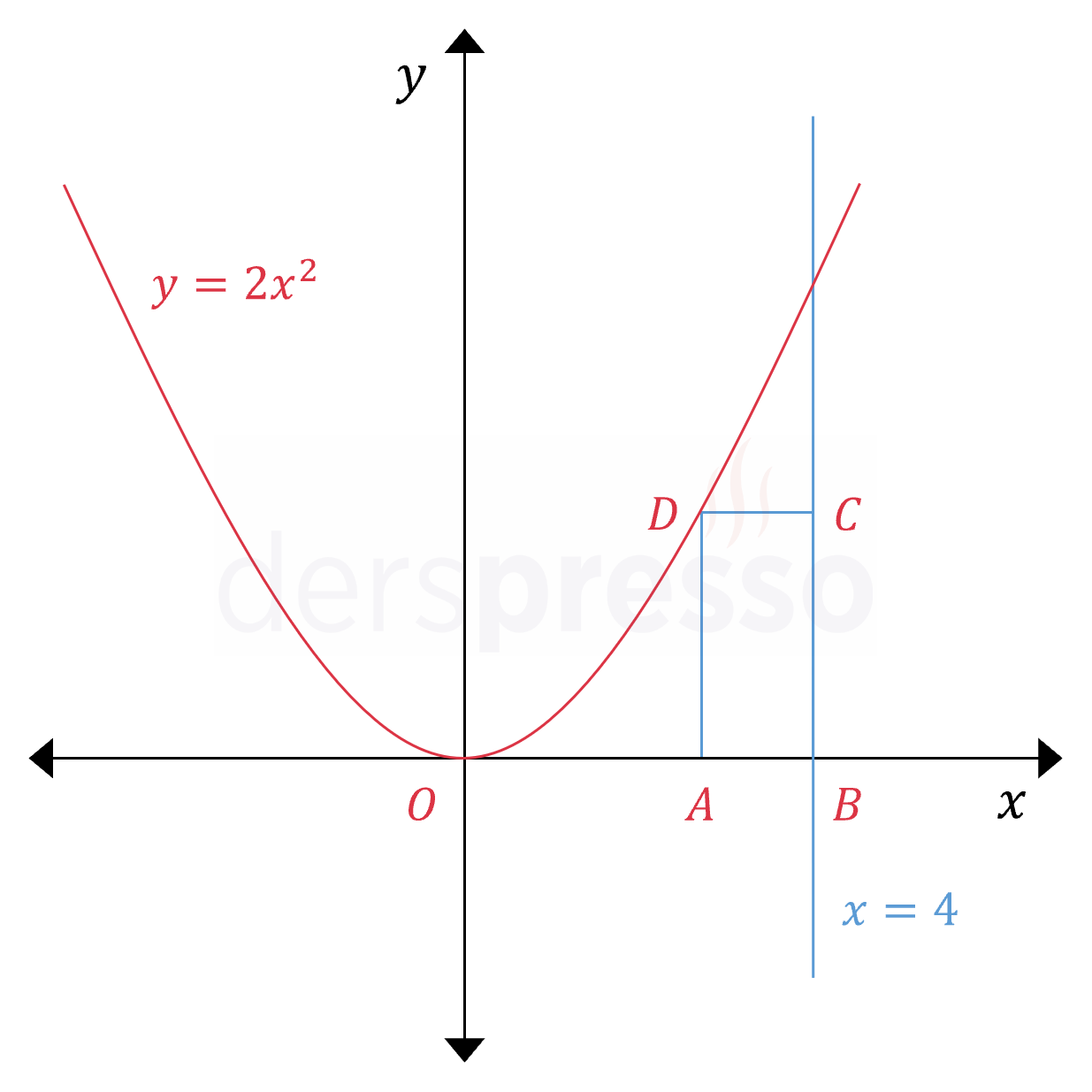
Yukarıdaki şekilde \( y = 2x^2 \) parabolü ve bu parabol ile \( x = 4 \) doğrusu arasında kalan \( ABCD \) dikdörtgeni verilmiştir.
\( \abs{BC} = 4\abs{DC} \) olduğuna göre, \( ABCD \) dikdörtgeninin alanı kaç birimkaredir?
Çözümü Göster\( \abs{AB} = \abs{DC} = a \) diyelim.
\( \abs{AD} = \abs{BC} = 4\abs{DC} = 4a \)
\( C \) noktasının apsis değeri 4 olduğu için \( D \) noktasının koordinatları \( D(4 - a, 4a) \) olur.
\( D \) noktasının koordinatlarını parabol denkleminde yerine koyalım.
\( y = 2x^2 \)
\( 4a = 2(4 - a)^2 \)
\( 4a = 2(16 - 8a + a^2) \)
\( a^2 - 10a + 16 = 0 \)
\( (a - 2)(a - 8) = 0 \)
\( A \) noktası \( x = 4 \) doğrusunun solunda kaldığı için \( a = 8 \) olamaz, dolayısıyla \( a = 2 \) olur.
\( \abs{AB} = \abs{DC} = 2 \)
\( \abs{AD} = \abs{BC} = 4a = 8 \)
Buna göre \( A(ABCD) = 2 \cdot 8 = 16 \) birimkare bulunur.
Yukarıdaki şekildeki \( y = x^2 + x + 8 \) parabolü \( y = -x^2 - 7x \) parabolüne \( K \) noktasında teğettir.
Buna göre \( AKO \) üçgeninin alanını bulunuz.
Çözümü GösterKolları aşağı yönlü olan parabolün \( x \) eksenini kestiği noktaları bulmak için denklemini sıfıra eşitleyelim.
\( -x^2 - 7x = 0 \)
\( -x(x + 7) = 0 \)
Buna göre parabol \( x \) eksenini \( x = -7 \) ve \( x = 0 \) noktalarında keser.
\( A(-7, 0) \)
İki parabolün denklemini ortak çözerek \( K \) noktasının apsis değerini bulalım.
\( x^2 + x + 8 = -x^2 - 7x \)
\( 2x^2 + 8x + 8 = 0 \)
\( x^2 + 4x + 4 = 0 \)
İki parabol tek bir noktada kesiştikleri için denklemlerinin ortak çözümünün çift katlı bir kökü vardır.
\( (x + 2)^2 = 0 \)
\( x = -2 \)
Bu apsis değerini iki parabol denkleminden birinde yerine koyarak \( K \) noktasının ordinat değerini bulalım.
\( y = (-2)^2 + (-2) + 8 = 10 \)
\( K(-2, 10) \)
\( AKO \) üçgeni taban uzunluğu 7 birim, yüksekliği 10 birim olan bir üçgendir.
\( A(AKO) = \dfrac{7 \cdot 10}{2} = 35 \) birimkare bulunur.
\( m \in \mathbb{R^+} \) olmak üzere,
\( y = x^2 - 4mx + 3 \) parabolünün tepe noktası orijine hangi \( m \) değerinde en yakın olur?
Çözümü GösterParabolün tepe noktasına \( T(r, k) \) diyelim.
\( r = -\dfrac{b}{2a} = -\dfrac{-4m}{2(1)} = 2m \)
\( r \) değerini parabol denkleminde yerine koyarak \( k \) değerini bulalım.
\( k = (2m)^2 - 4m(2m) + 3 \)
\( = -4m^2 + 3 \)
\( T(r, k) = T(2m, 3 - 4m^2) \)
\( T \) noktasının orijine olan uzaklığına \( d \) diyelim.
Bir noktanın orijine olan uzaklık formülünü kullanalım.
\( d^2 = (2m)^2 + (3 - 4m^2)^2 \)
\( = 4m^2 + 9 - 24m^2 + 16m^4 \)
\( = 16m^4 - 20m^2 + 9 \)
İfadeyi tam kareye tamamlayalım.
\( ax^2 + bx + c \) ifadesini tam kareye tamamlamak için ifadeye \( \frac{b^2}{4a} \) terimi eklenir ve çıkarılır.
\( \dfrac{b^2}{4a} = \dfrac{(-20)^2}{4(16)} = \dfrac{25}{4} \)
\( = 16m^4 - 20m^2 + \dfrac{25}{4} - \dfrac{25}{4} + 9 \)
İlk üç terimi gruplayarak tam kare formuna getirelim.
\( = \left( 16m^4 - 20m^2 + \dfrac{25}{4} \right) + \dfrac{11}{4} \)
\( = 16\left( m^4 - \dfrac{5}{4}m^2 + \dfrac{25}{64} \right) + \dfrac{11}{4} \)
\( = 16\left( m^2 - \dfrac{5}{8} \right) + \dfrac{11}{4} \)
\( d \) en küçük değerini parantez içi sıfır olduğunda alır.
\( m^2 - \dfrac{5}{8} = 0 \)
\( m^2 = \dfrac{5}{8} \)
\( m \) pozitif olarak veriliyor.
\( m = \dfrac{\sqrt{5}}{\sqrt{8}} = \dfrac{\sqrt{10}}{4} \) bulunur.
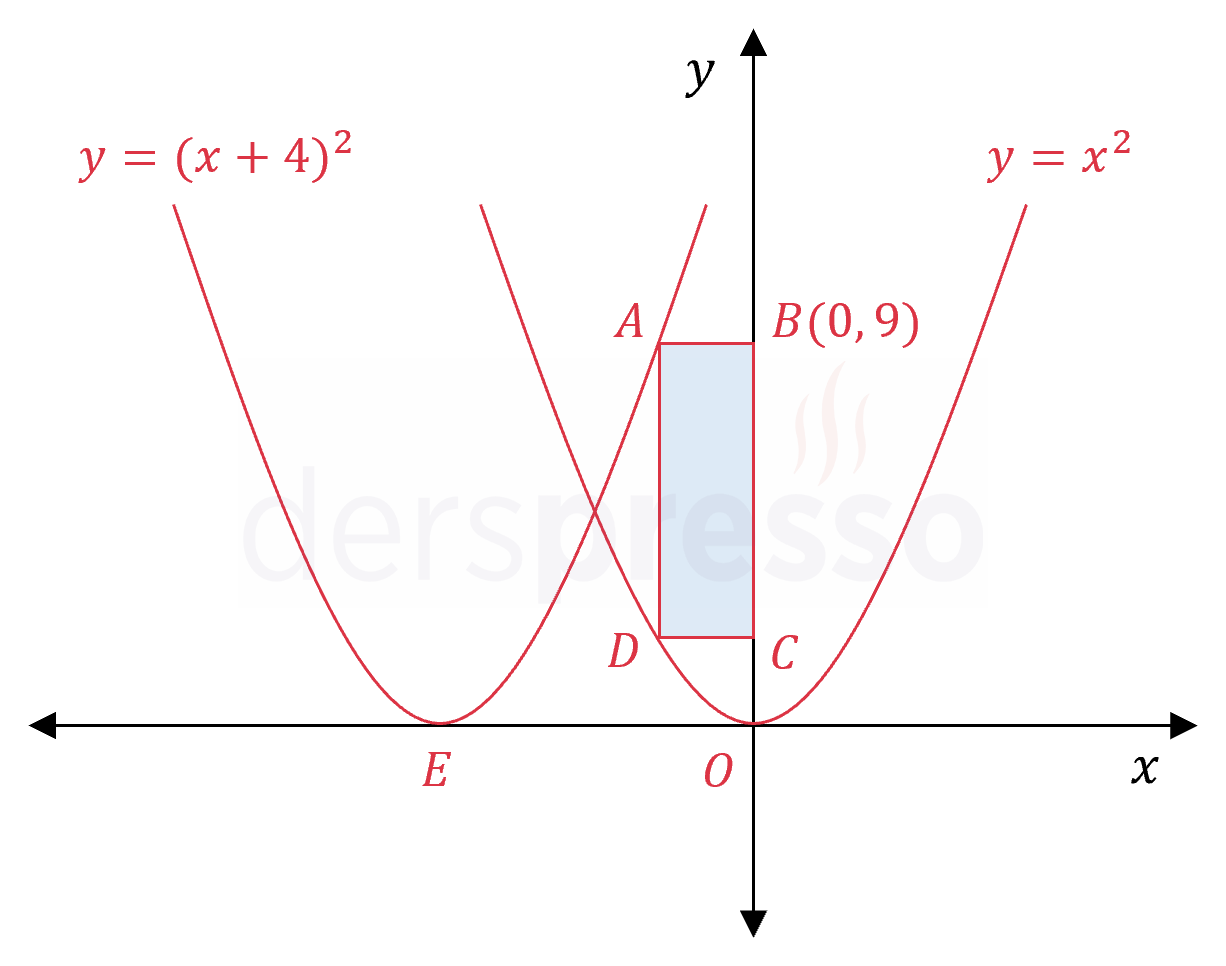
Şekilde \( y = x^2 \) ve \( y = (x + 4)^2 \) parabolleri verilmiştir.
\( B \) noktasının koordinatları \( (0, 9) \) olduğuna göre, \( ABCD \) dikdörtgeninin alanı kaçtır?
Çözümü Göster\( B \) noktasının ordinatı 9 olduğuna göre \( A \) noktasının ordinatı da 9 olur.
\( A \) noktası \( y = (x + 4)^2 \) parabolü üzerinde olduğu için koordinatları parabol denklemini sağlar.
\( (x + 4)^2 = 9 \)
\( x + 4 = \pm 3 \)
\( x = -1 \) ya da \( x = -7 \)
\( A \) noktası parabolün 9 değerini aldığı iki noktadan daha büyük apsis değerli nokta olduğu için \( x = -1 \) olur.
\( A(-1, 9) \)
\( D \) noktası \( y = x^2 \) parabolü üzerinde olup apsisi \( A \) noktası ile aynıdır.
\( D \) noktasının ordinatına \( a \) diyelim.
\( D(-1, a) \)
\( D \) noktası \( y = x^2 \) parabolü üzerinde olduğu için koordinatları parabol denklemini sağlar.
\( a = (-1)^2 = 1 \)
\( D(-1, 1) \)
\( y \) ekseni üzerindeki \( C \) noktasının ordinatı \( D \) noktası ile aynıdır.
\( C(0, 1) \)
\( ABCD \) dikdörtgeninin kısa kenar uzunluğu 1 birim, uzun kenar uzunluğu \( 9 - 1 = 8 \) birimdir.
\( A(ABCD) = 1 \cdot 8 = 8 \) bulunur.
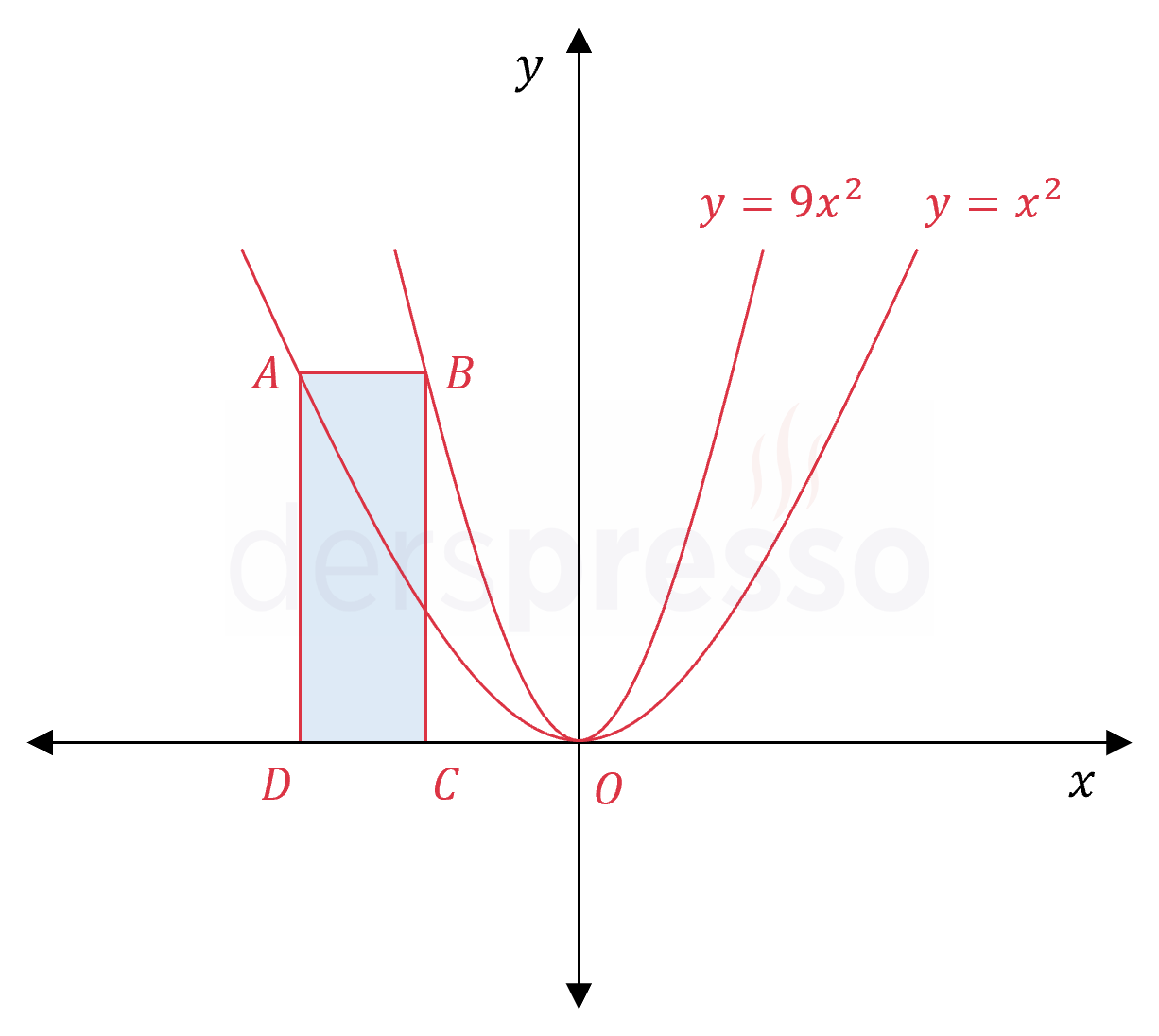
\( A \) ve \( B \) köşeleri \( y = x^2 \) ve \( y = 9x^2 \) parabolleri üzerinde olan \( ABCD \) dikdörtgeni şekilde verilmiştir.
\( ABCD \) dikdörtgeninin alanı 144 birimkare olduğuna göre, çevresi kaç birimdir?
Çözümü Göster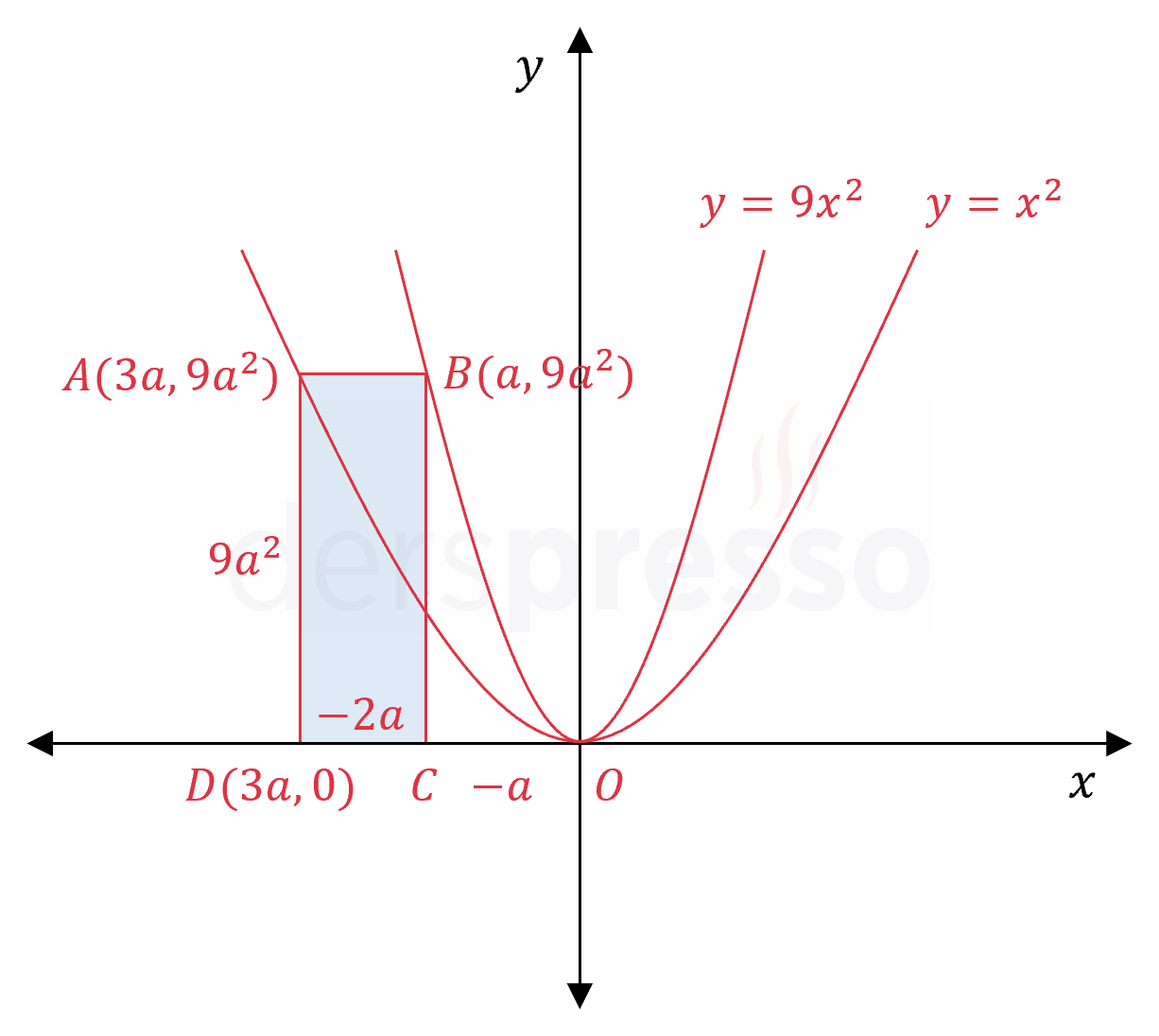
\( B \) noktasının apsisine \( a \) diyelim.
\( \abs{CO} = \abs{a} = -a \)
\( B \) noktası \( y = 9x^2 \) parabolü üzerinde olduğuna göre koordinatları parabol denklemini sağlar.
\( B(a, 9a^2) \)
\( \abs{BC} = 9a^2 \)
\( A \) ve \( B \) noktalarının ordinatları eşittir.
\( A \) noktası \( y = x^2 \) parabolü üzerinde olduğuna göre koordinatları parabol denklemini sağlar.
\( A(3a, 9a^2) \)
\( ABCD \) dikdörtgeninin kısa ve uzun kenar uzunluklarını bulalım.
\( \abs{AB} = \abs{DC} = \abs{DO} - \abs{CO} \)
\( = -3a - (-a) = -2a \)
\( \abs{AD} = \abs{BC} = 9a^2 \)
\( A(ABCD) = \abs{AB} \cdot \abs{AD} \)
\( 144 = -2a \cdot 9a^2 \)
\( 144 = -18a^3 \)
\( a = -2 \)
\( ABCD \) dikdörtgeninin çevresini hesaplayalım.
\( \text{Ç}(ABCD) = 2(9a^2 + (-2a)) \)
\( = 2(9(-2)^2 - 2(-2)) \)
\( = 80 \) birim bulunur.
Yukarıdaki şekilde \( d_1 \perp d_2 \) olduğuna göre, \( f(-3) \) kaçtır?
Çözümü GösterParabol \( x \) eksenini -2 ve 6 noktalarında kestiği için denklemini aşağıdaki şekilde yazabiliriz.
\( f(x) = a(x + 2)(x - 6) \)
\( A \) noktasının koordinatlarına \( A(0, c) \) diyelim.
\( d_1 \) doğrusunun eğimini bulalım.
\( m_1 = \dfrac{c - 0}{0 - (-2)} = \dfrac{c}{2} \)
\( d_2 \) doğrusunun eğimini bulalım.
\( m_2 = \dfrac{c - 0}{0 - 6} = -\dfrac{c}{6} \)
İki doğru birbirine dik oldukları için eğimlerinin çarpımı -1 olur.
\( \dfrac{c}{2} \cdot (-\dfrac{c}{6}) = -1 \)
\( c^2 = 12 \)
\( c = \pm 2\sqrt{3} \)
\( A \) noktası \( y \) ekseninin pozitif tarafında olduğu için \( c \) pozitif olur.
\( A(0, 2\sqrt{3}) \)
Parabolün başkatsayısını bulmak için \( A \) noktasının koordinatlarını denklemde yerine koyalım.
\( f(0) = a(0 + 2)(0 - 6) = 2\sqrt{3} \)
\( a = -\dfrac{\sqrt{3}}{6} \)
Buna göre parabolün denklemi aşağıdaki gibi olur.
\( f(x) = -\dfrac{\sqrt{3}}{6}(x + 2)(x - 6) \)
\( f(-3) \) değerini bulalım.
\( f(-3) = -\dfrac{\sqrt{3}}{6}(-3 + 2)(-3 - 6) \)
\( = -\dfrac{3\sqrt{3}}{2} \) bulunur.
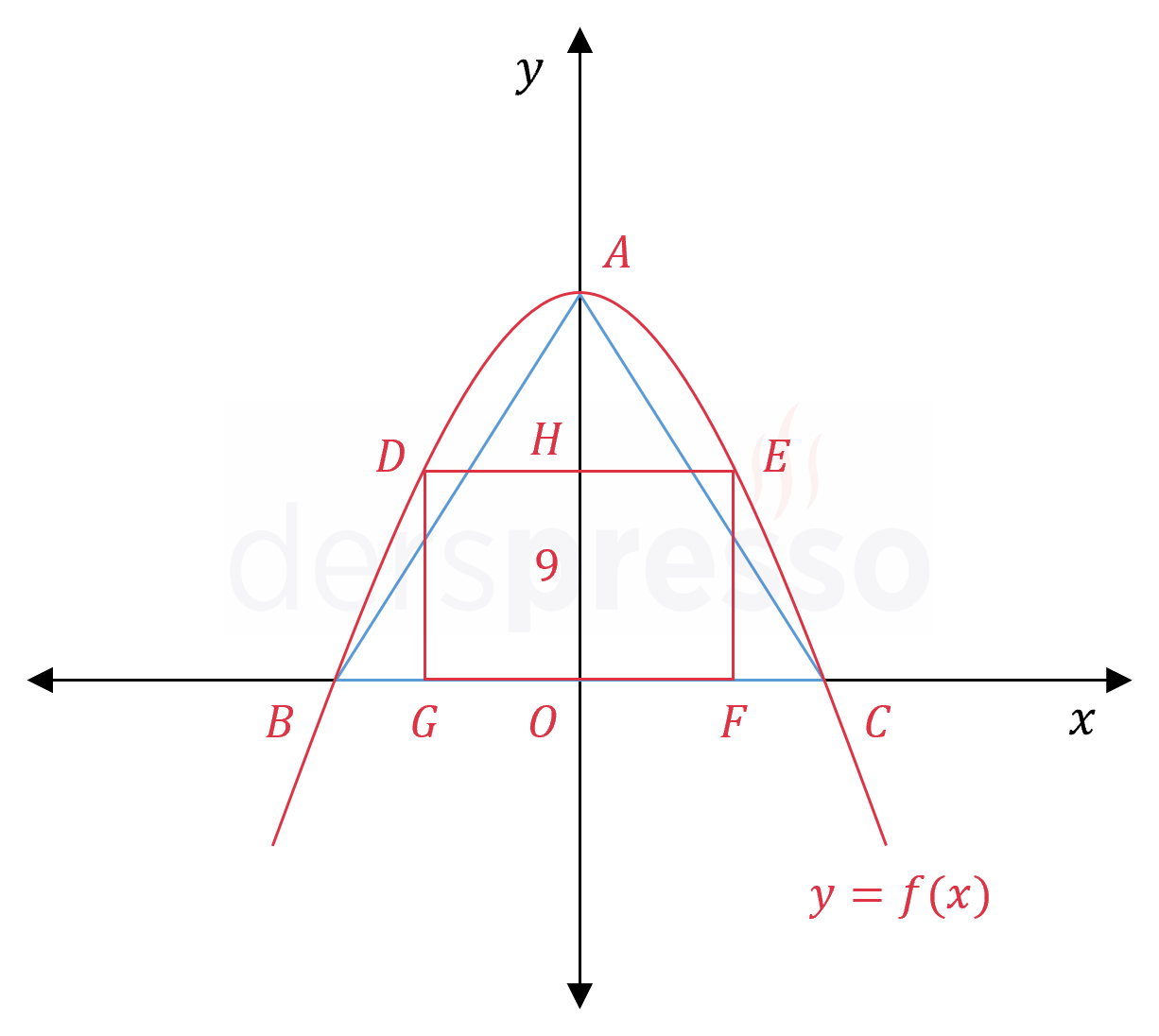
Yukarıdaki şekilde \( f(x) = kx^2 - (k^2 - 9)x + 12 \) parabolü, \( ABC \) üçgeni ve \( DEFG \) dikdörtgeni verilmiştir.
Parabolün tepe noktası \( y \) ekseni üzerinde ve \( \abs{OH} = 9 \) olduğuna göre, üçgenin alanı dikdörtgenin alanından kaç birimkare fazladır?
Çözümü GösterParabolün katsayılarını yazalım.
\( a = k, \quad b = -(k^2 - 9), \quad c = 12 \)
Parabolün tepe noktası \( y \) ekseni üzerinde olduğuna göre apsisi sıfırdır.
\( r = -\dfrac{b}{2a} = 0 \)
\( -\dfrac{-(k^2 - 9)}{2k} = 0 \)
\( k^2 - 9 = 0 \)
\( k = \pm 3 \)
\( f \) parabolünün kolları aşağı yönlü olduğu için başkatsayısı negatif olmalıdır.
\( k = -3 \)
Parabolün denklemini yazalım.
\( f(x) = -3x^2 + 12 \)
\( B \) ve \( C \) noktaları parabolün \( x \) eksenini kestiği noktalar olup parabolün kökleridir.
Parabolün köklerini bulalım.
\( f(x) = -3x^2 + 12 = 0 \)
\( x = \pm 2 \)
\( B(-2, 0), \quad C(2, 0) \)
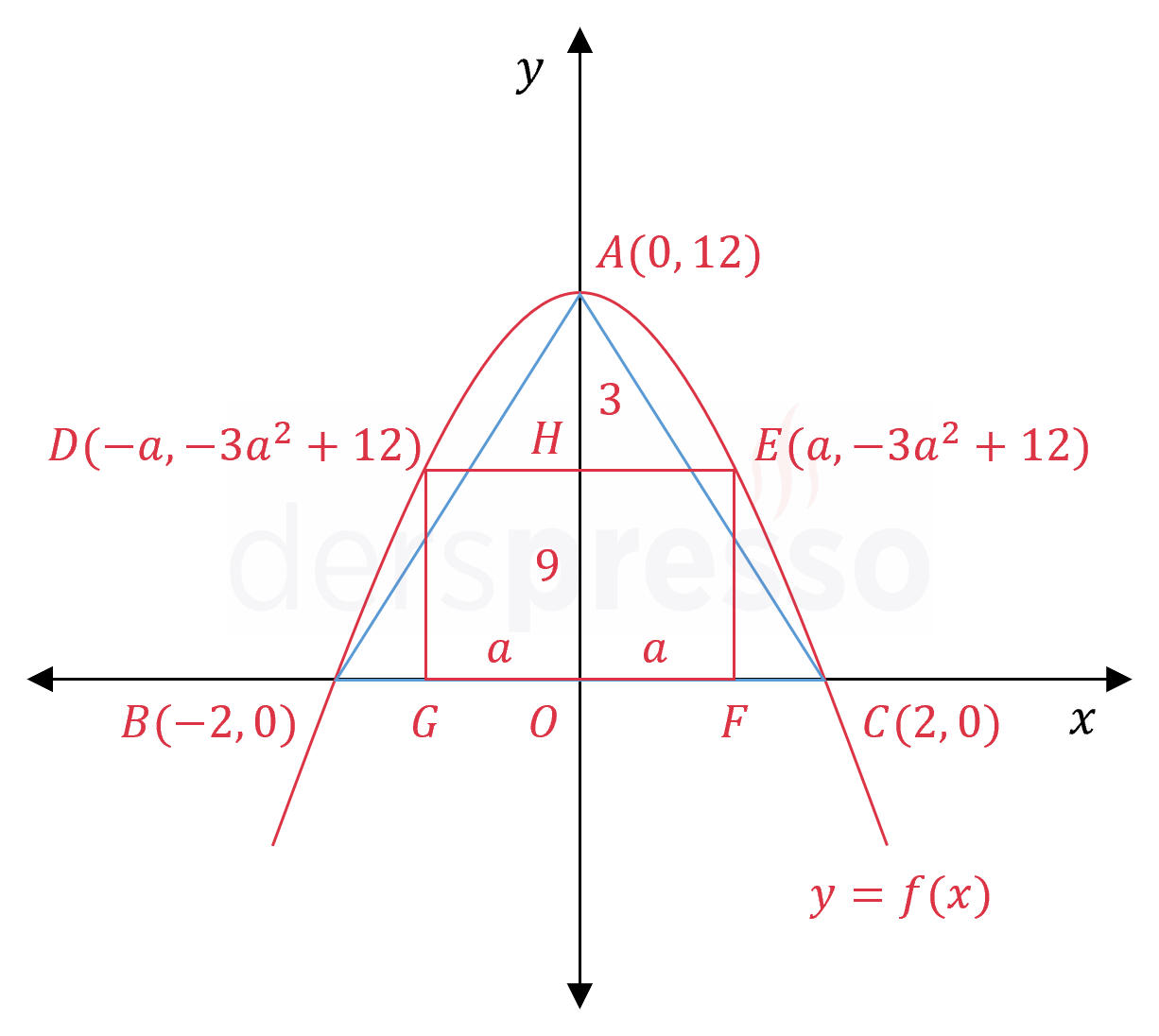
\( E \) noktası parabol üzerinde olduğuna göre koordinatları parabol denklemini sağlar.
\( E \) noktasının apsisine \( a \) diyelim. Denklemde yerine yazarak ordinatını bulalım.
\( f(a) = -3a^2 + 12 \)
\( E(a, -3a^2 + 12) \)
\( \abs{OH} \) uzunluğunu kullanarak \( a \) değerini bulalım.
\( \abs{OH} = \abs{GD} = \abs{FE} = 9 \)
\( -3a^2 + 12 = 9 \)
\( a = \pm 1 \)
\( E \) noktası I. bölgede yer aldığına göre, apsisi pozitif olmalıdır.
\( a = 1 \)
Tepe noktası \( y \) ekseni üzerinde olduğuna göre, \( y \) ekseni parabolün simetri eksenidir.
\( \abs{OF} = \abs{OG} = a = 1 \)
\( E(1, 9), \quad D(-1, 9) \)
Parabolün \( y \) eksenini kestiği noktayı bulmak için parabol denkleminde \( x = 0 \) yazalım.
\( f(0) = -3(0)^2 + 12 = 12 \)
\( A(0, 12) \)
Üçgenin alanını hesaplayalım.
\( A(ABC) = \dfrac{\abs{BC} \cdot \abs{AO}}{2} \)
\( = \dfrac{4 \cdot 12}{2} = 24 \)
Dikdörtgenin alanını hesaplayalım.
\( A(DEFG) = \abs{GF} \cdot \abs{EF} \)
\( = 2 \cdot 9 = 18 \)
Üçgenin alanı dikdörtgenin alanından \( 24 - 18 = 6 \) birimkare fazladır.