Parabol Tanımı
Analitik düzlemde bir doğruya ve bu doğru üzerinde olmayan bir noktaya eşit uzaklıktaki noktalar kümesine parabol denir.
Aşağıdaki grafikte \( d \) doğrusuna ve \( V \) noktasına eşit uzaklıktaki noktaların oluşturduğu parabol gösterilmiştir.
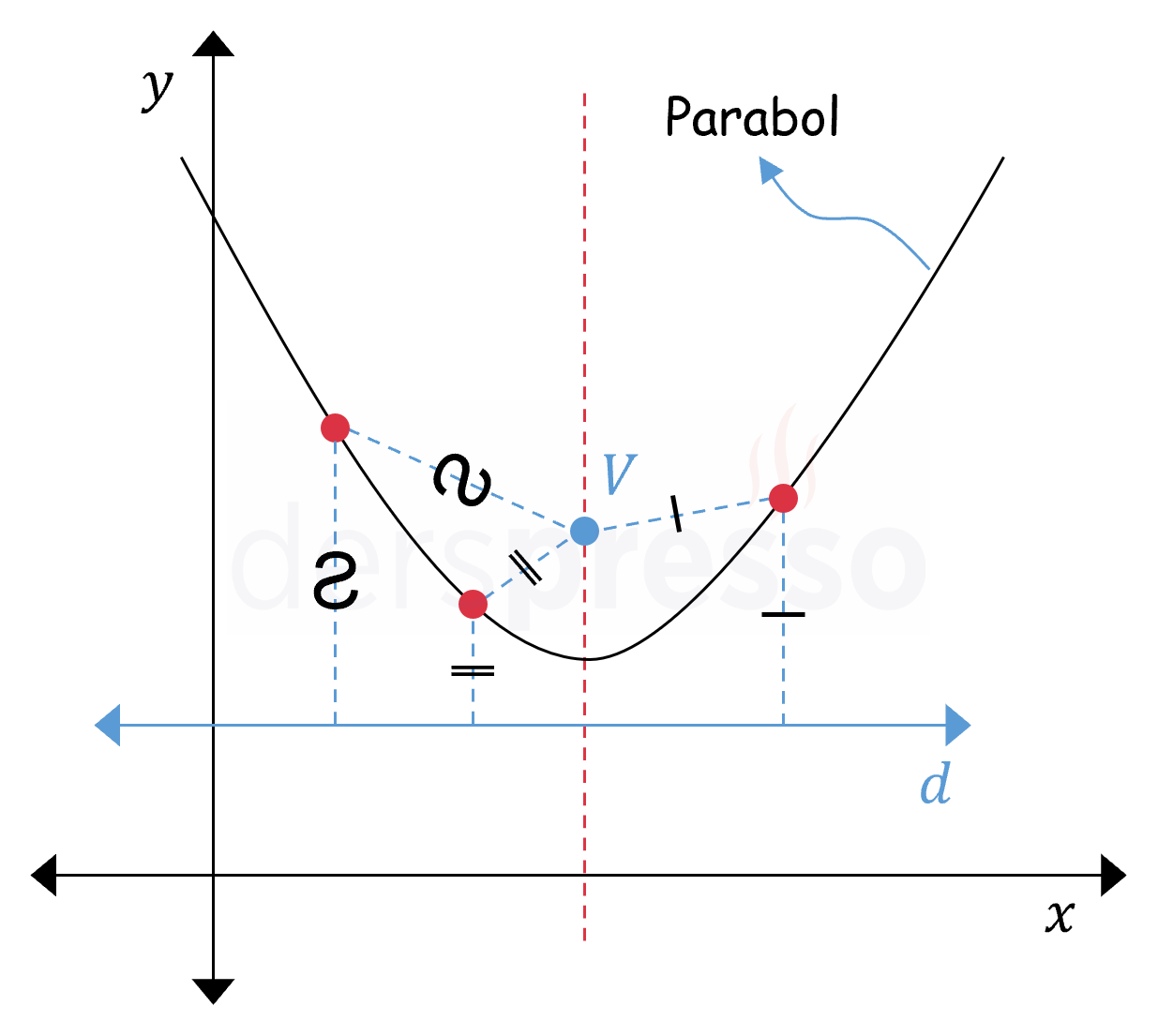
Bir parabol grafiğinin iki önemli özelliği şunlardır.
- Kollarının yönü değişebilse de, U harfine benzer bir şekle sahiptir.
- Simetri ekseni adı verilen bir doğru etrafında simetriktir (grafikteki gri kesikli doğru).
Yukarıdaki şekildeki parabolün simetri ekseni \( y \) eksenine paraleldir, ancak bir parabol yukarıdaki tanımı sağladığı sürece farklı doğrultularda simetri eksenine sahip olabilir. Buna göre aşağıdaki eğrilerin tümü birer paraboldür.
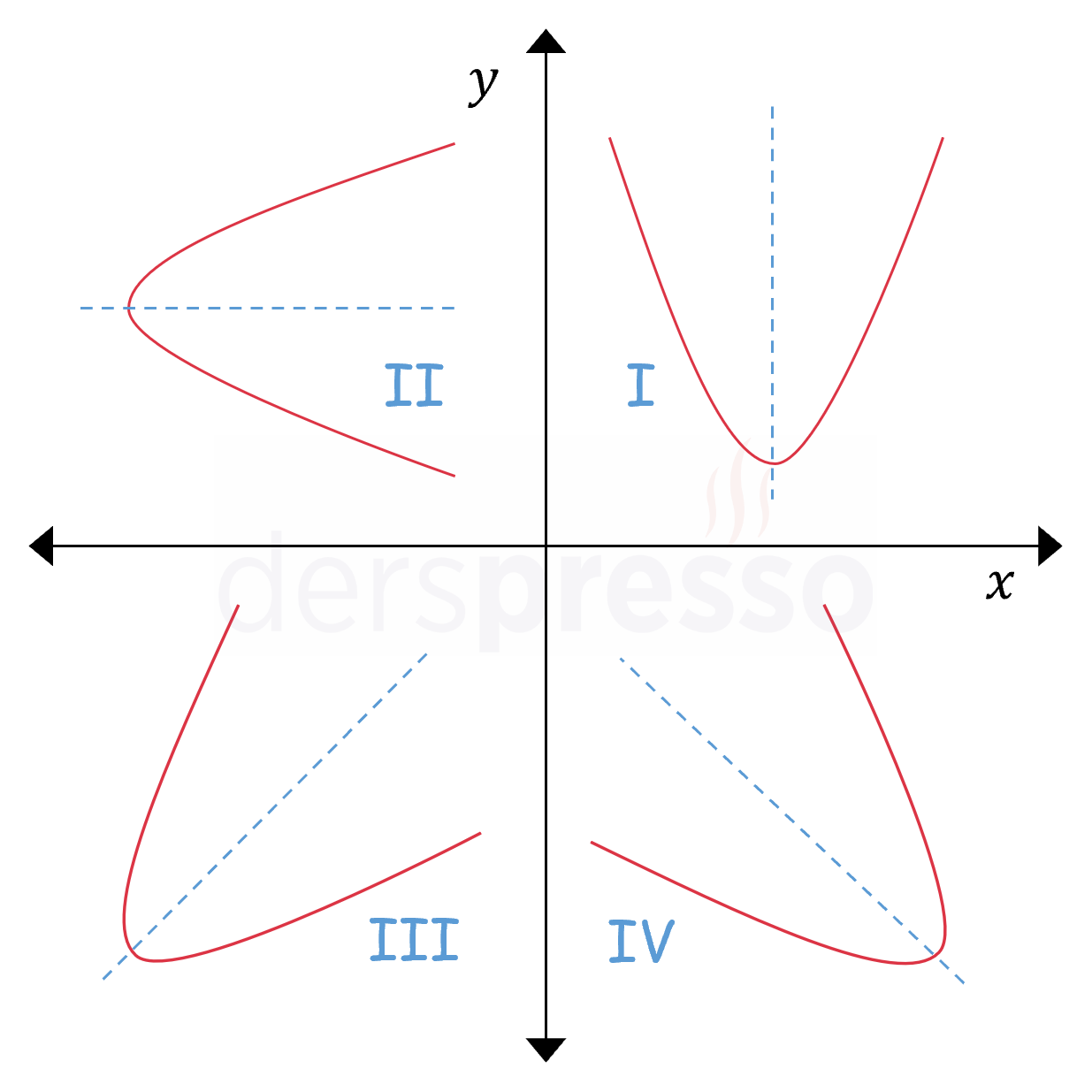
Bu parabollerle ilgili bazı ek bilgiler aşağıdaki gibidir.
| Parabol | Özellikler | Denklem |
|---|---|---|
| I | Simetri ekseni \( y \) eksenine paraleldir. Kollar simetri ekseni doğrultusunda yukarı (\( a \gt 0 \)) ya da aşağı (\( a \lt 0 \)) bakar. | \( y = ax^2 + bx + c \) |
| II | Simetri ekseni \( x \) eksenine paraleldir. Kollar simetri ekseni doğrultusunda sağa (\( a \gt 0 \)) ya da sola (\( a \lt 0 \)) bakar. | \( x = ay^2 + by + c \) |
| III ve IV | Simetri ekseni yatay ve dikey olmayan herhangi bir doğrudur. Kollar simetri ekseni doğrultusunda iki yönden birine bakar. | Bu parabollerin denklemlerine burada değinmeyeceğiz. |
Yukarıdaki parabol tiplerinden sadece birincisi fonksiyon tanımına uymaktadır, diğer grafiklerin birer fonksiyon olmaması parabol olmalarına engel değildir.
Bu parabol konusunda sadece birinci tipteki, yani simetri ekseni \( y \) eksenine paralel ve kolları yukarı ya da aşağı yönlü olan parabolleri inceleyeceğiz ve parabol terimini bu kapsamda kullanıyor olacağız.
Parabolün Denklemi
Simetri ekseni \( y \) eksenine paralel olan parabollerin genel denklemi aşağıdaki gibidir. Eşitliğin sağındaki ifade ikinci dereceden bir polinomdur.
\( a, b, c \in \mathbb{R}, \quad a \ne 0 \) olmak üzere,
\( y = ax^2 + bx + c \)
\( y = x^2 + 2x - 3 \)
\( y = 2x^2 - 6 \)
\( y = -x^2 \)
Bu denklemde \( x \) ve \( y \) parabolün değişkenleri, \( a \), \( b \) ve \( c \) de katsayılarıdır. \( x^2 \)'li terimin katsayısı parabolün başkatsayısı, \( x \) değişkeni olmayan sondaki terim de parabolün sabit terimidir.
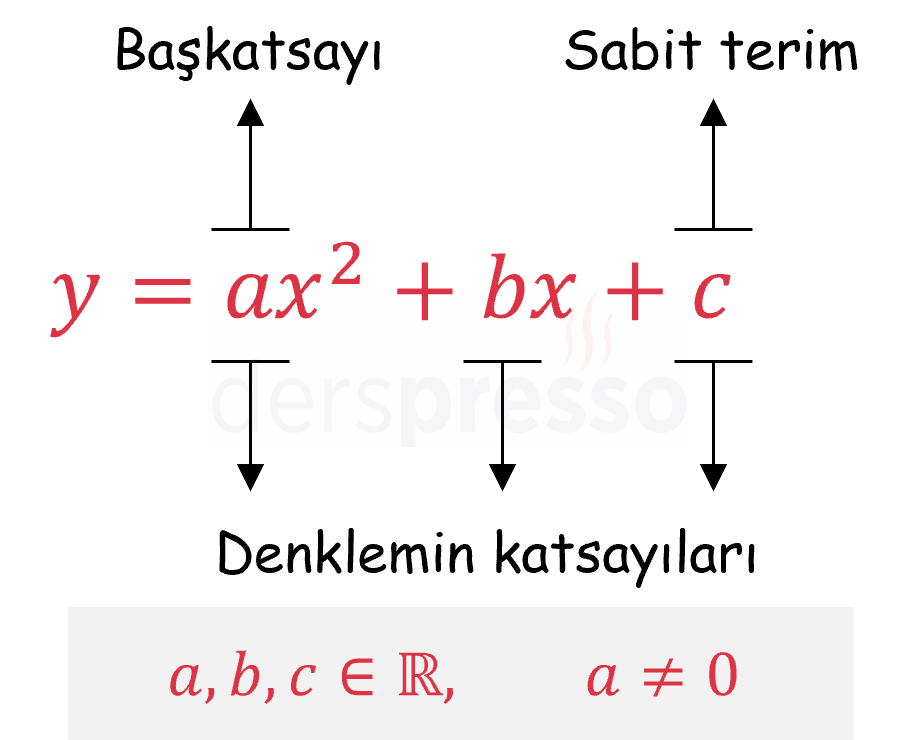
Örnek Bir Parabol
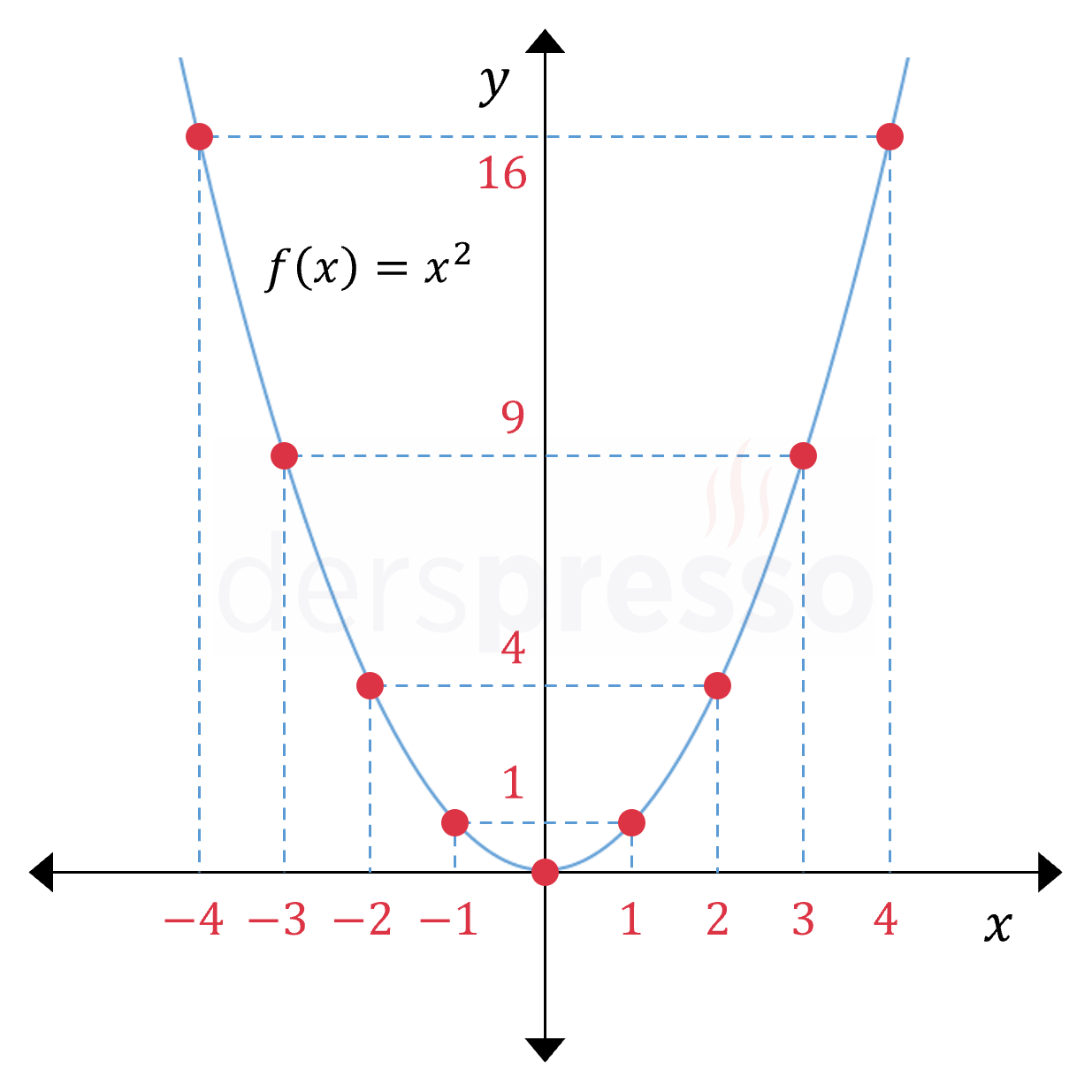
\( f(x) = x^2 \) parabolünün bazı \( x \) değerleri için değer tablosu aşağıdaki gibidir.
| \( x \) | \( f(x) = x^2 \) | Nokta \( (x, y) \) |
|---|---|---|
| \( -4 \) | \( f(-4) = (-4)^2 = 16 \) | \( (-4, 16) \) |
| \( -3 \) | \( f(-3) = (-3)^2 = 9 \) | \( (-3, 9) \) |
| \( -2 \) | \( f(-2) = (-2)^2 = 4 \) | \( (-2, 4) \) |
| \( -1 \) | \( f(-1) = (-1)^2 = 1 \) | \( (-1, 1) \) |
| \( 0 \) | \( f(0) = 0^2 = 0 \) | \( (0, 0) \) |
| \( 1 \) | \( f(1) = 1^2 = 1 \) | \( (1, 1) \) |
| \( 2 \) | \( f(2) = 2^2 = 4 \) | \( (2, 4) \) |
| \( 3 \) | \( f(3) = 3^2 = 9 \) | \( (3, 9) \) |
| \( 4 \) | \( f(4) = 4^2 = 16 \) | \( (4, 16) \) |
Bu noktalar analitik düzlemde işaretlendiğinde aşağıdaki grafik elde edilir.
Parabol İçin Gerekli Nokta Sayısı
Noktalardan biri parabolün simetri ekseninin geçtiği nokta (tepe noktası) olmadığı durumda, analitik düzlemde iki farklı noktadan geçen sonsuz sayıda parabol çizilebilir.
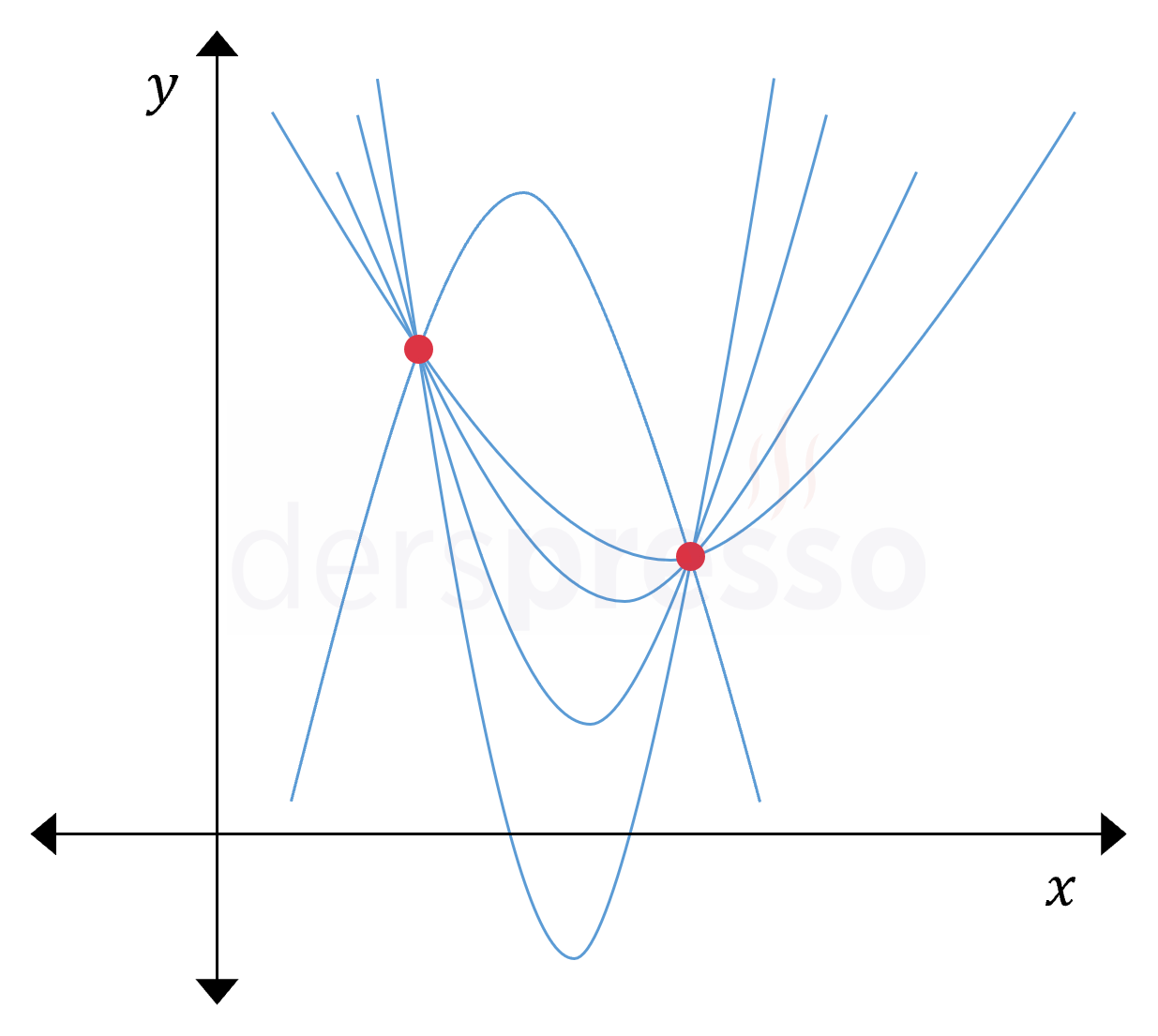
Noktalardan belirli biri parabolün tepe noktası olduğu durumda, iki farklı noktadan geçen tek bir parabol çizilebilir.
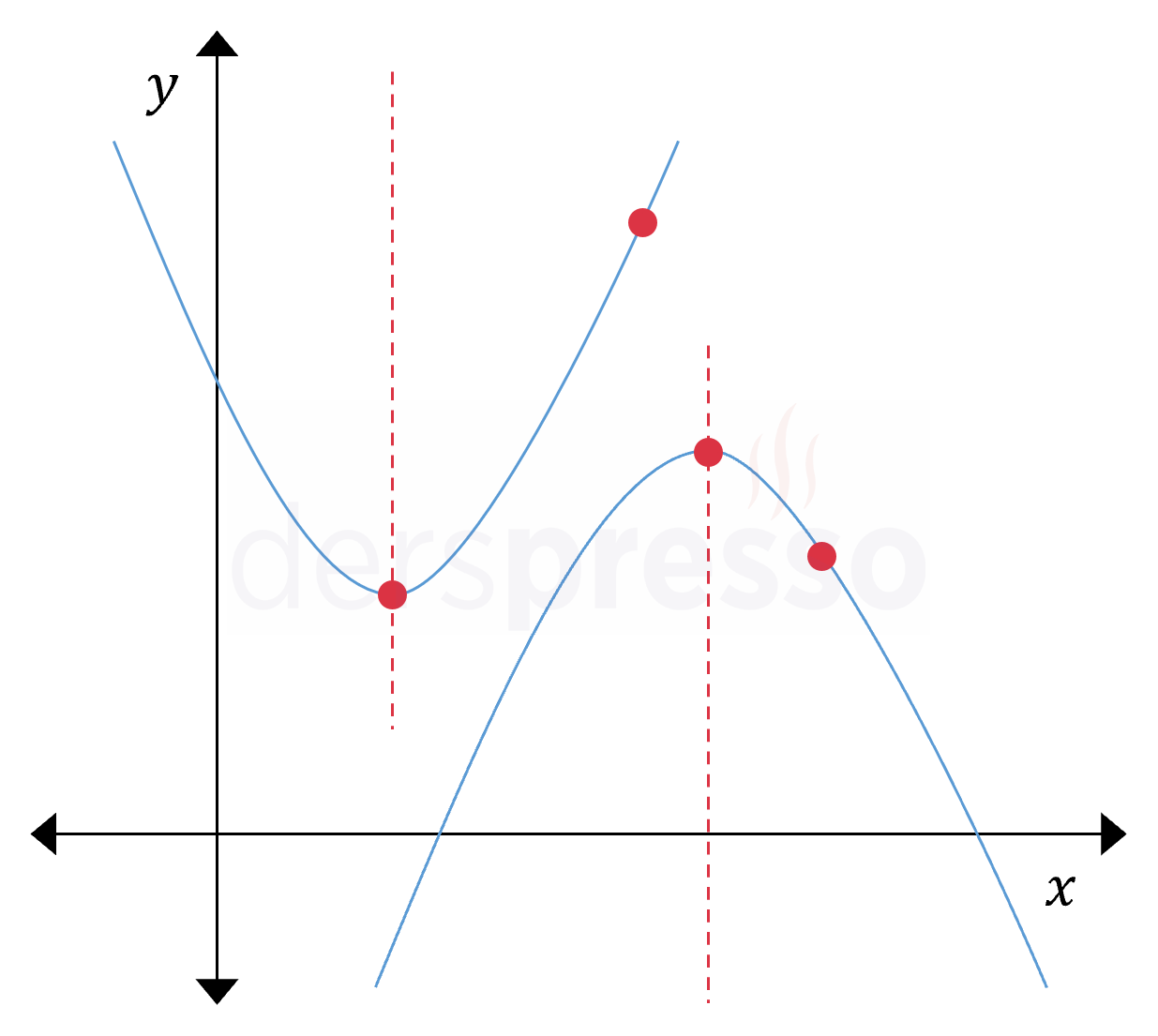
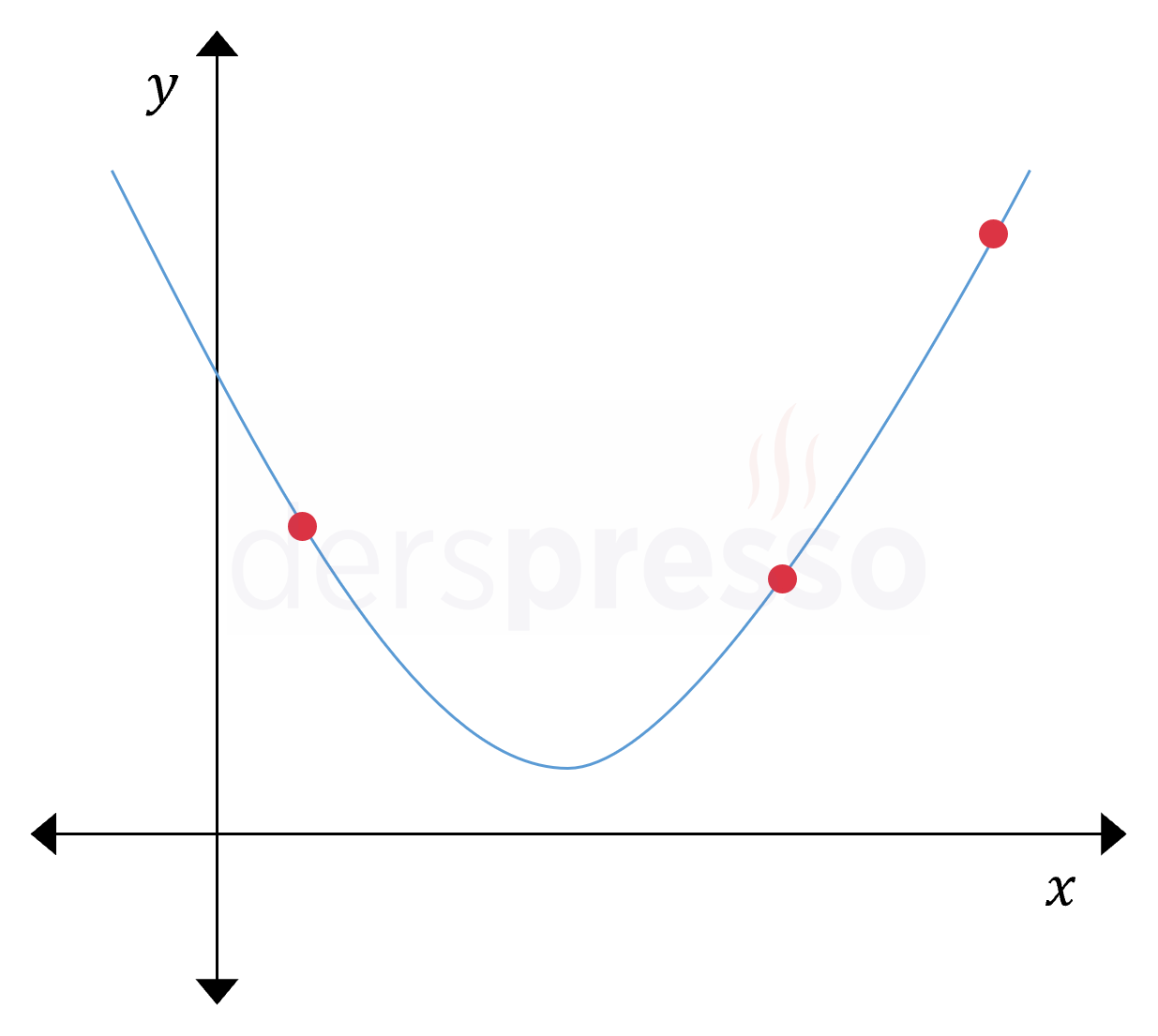
Doğrusal olmayan ve biri parabolün tepe noktası olmayan üç farklı noktadan geçen tek bir parabol çizilebilir.
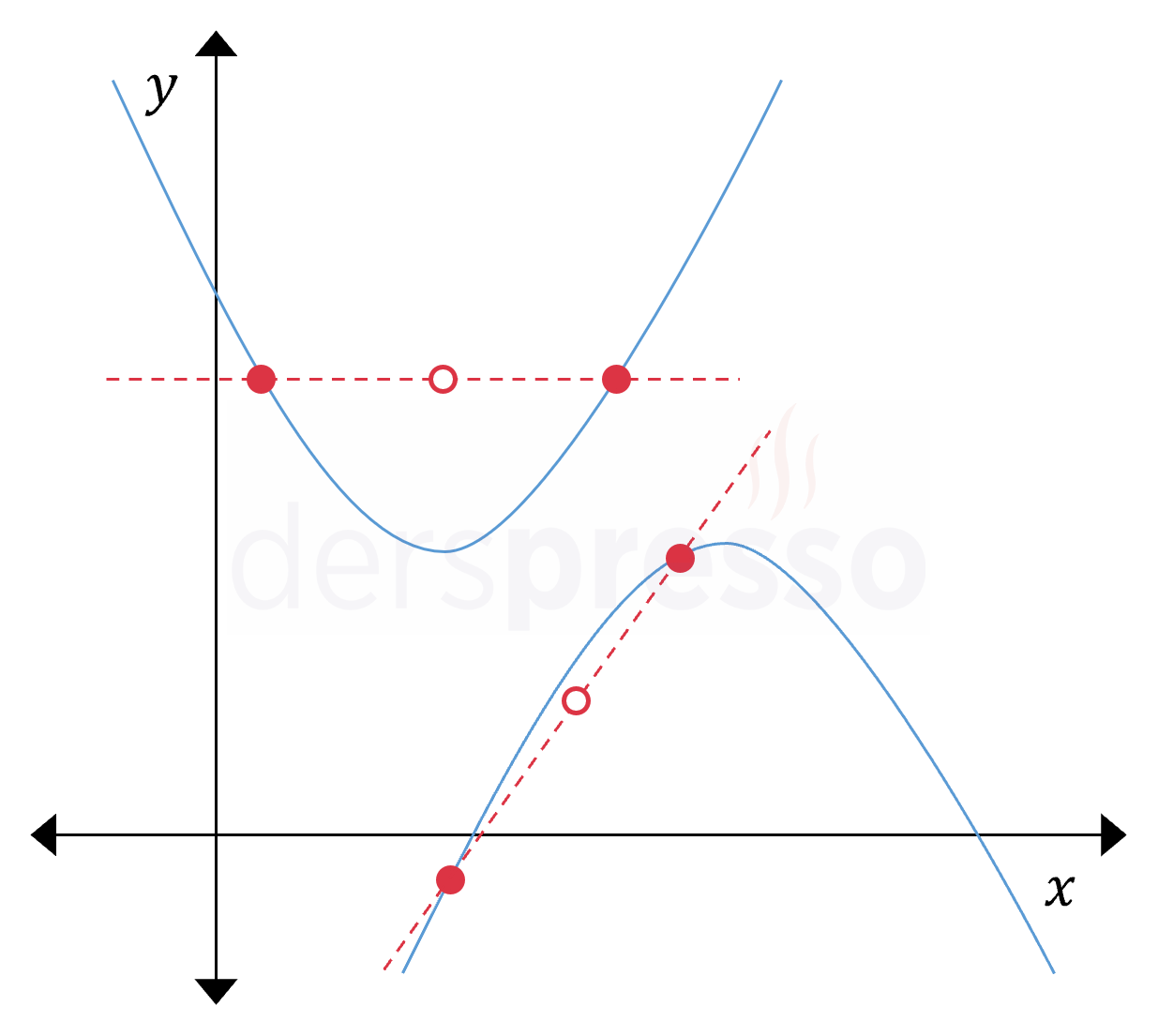
Doğrusal üç farklı noktadan geçen bir parabol çizilemez.
\( m, n \in \mathbb{R} \) olmak üzere,
\( f(x) = (m + 3)x^4 - 2x^{n + 4} + mx - n \)
fonksiyonu bir parabol olduğuna göre, \( f(2) \) kaçtır?
Çözümü GösterFonksiyon bir parabol olduğuna göre denklemi ikinci dereceden bir polinom olmalıdır.
Buna göre birinci terimin katsayısı sıfır, ikinci terimin üssü 2 olmalıdır.
\( m + 3 = 0 \Longrightarrow m = -3 \)
\( n + 4 = 2 \Longrightarrow n = -2 \)
Buna göre fonksiyonun tanımı aşağıdaki şekilde olur.
\( f(x) = (-3 + 3)x^4 - 2x^{-2 + 4} + (-3)x - (-2) \)
\( = -2x^2 - 3x + 2 \)
\( f(2) \) değerini bulmak için \( x = 2 \) yazalım.
\( f(2) = -2(2)^2 - 3(2) + 2 = -12 \) bulunur.
\( A(-4, 7) \) noktası \( y = x^2 + mx + m - 3 \) parabolünün üzerinde olduğuna göre, \( m \) kaçtır?
Çözümü Göster\( A \) noktası verilen parabolün üzerinde olduğuna göre, koordinatları parabol denklemini sağlar.
\( 7 = (-4)^2 + m(-4) + m - 3 \)
\( 7 = 16 - 4m + m - 3 \)
\( m = 2 \) bulunur.
\( f(x) = (m + 1)x^2 - 4mx + 2m - 1 \) parabolü \( A(2, 3m) \) noktasından geçtiğine göre, \( m \) kaçtır?
Çözümü GösterVerilen parabol \( A \) noktasından geçtiğine göre, bu noktanın koordinatları parabol denklemini sağlar.
\( f(2) = 3m \)
\( (m + 1)2^2 - 4m(2) + 2m - 1 = 3m \)
\( 4m + 4 - 8m + 2m - 1 = 3m \)
\( m = \dfrac{3}{5} \) bulunur.
\( f(x) = ax^2 - bx - 5 \) fonksiyonunun grafiği \( A(2, 9) \) ve \( B(-1, 3) \) noktalarından geçtiğine göre, \( a - b \) kaçtır?
Çözümü GösterBir nokta bir parabolün üzerinde ise koordinatları parabol denklemini sağlar.
\( A(2, 9) \) noktasının koordinatlarını denklemde yerine yazalım.
\( f(2) = 9 \)
\( a(2)^2 - b(2) - 5 = 9 \)
\( 2a - b = 7 \)
\( B(-1, 3) \) noktasının koordinatlarını denklemde yerine yazalım.
\( f(-1) = 3 \)
\( a(-1)^2 - b(-1) - 5 = 3 \)
\( a + b = 8 \)
Bulduğumuz iki bilinmeyenli iki denklemi ortak çözelim.
Denklemleri taraf tarafa toplayalım.
\( 2a - b + a + b = 7 + 8 \)
\( 3a = 15 \)
\( a = 5 \)
Bu değeri kullanarak \( b \) değerini bulalım.
\( a + b = 8 \)
\( b = 3 \)
\( a - b = 5 - 3 = 2 \) bulunur.
\( f(x) = x^2 - 5x + 10 \) parabolü üzerinde ordinatı apsisinin iki katı olan noktaları bulunuz.
Çözümü GösterOrdinatı apsisinin iki katı olan noktaların kümesi \( y = 2x \) doğrusunu oluşturur ve koordinatları \( (a, 2a) \) şeklindedir.
Bu noktalardan \( f \) parabolü üzerinde de olanlar parabol denklemini sağlar.
\( f(a) = 2a \)
\( a^2 - 5a + 10 = 2a \)
\( a^2 - 7a + 10 = 0 \)
\( (a - 2)(a - 5) = 0 \)
\( a \in \{2, 5\} \)
Bu \( a \) değerleri aşağıdaki iki noktayı oluşturur.
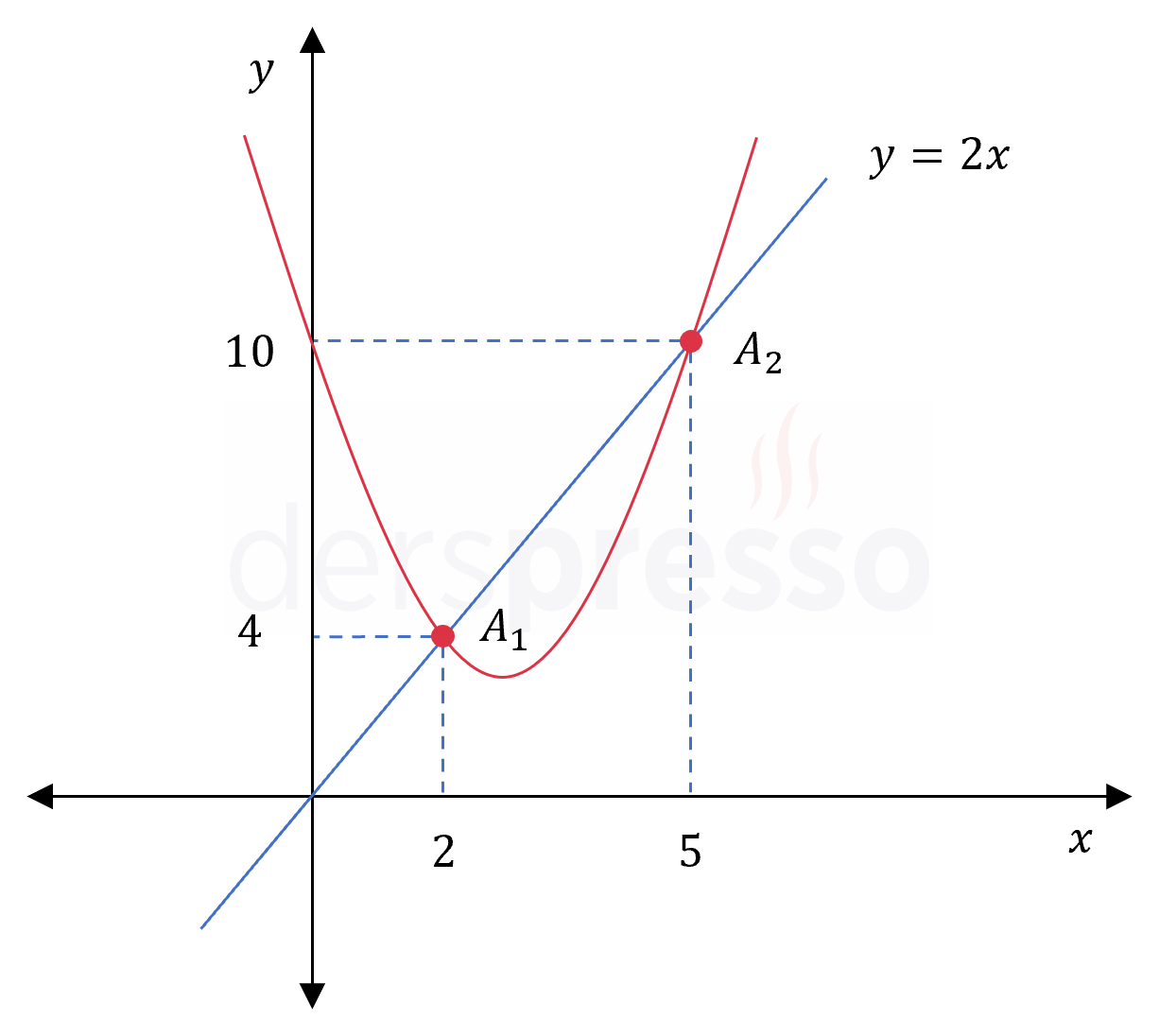
\( A_1(2, 2(2)) = A_1(2, 4) \)
\( A_2(5, 2(5)) = A_2(5, 10) \)
\( f \) parabolü ve bu iki nokta aşağıdaki şekilde gösterilmiştir.
\( f(x) = x^2 - 2x - 16 \) parabolü \( A(a, -5) \) noktasından geçtiğine göre, \( (a - 7)(a + 5) \) çarpımı kaçtır?
Çözümü Göster\( A(a, -5) \) noktası parabolün üzerinde olduğuna göre, koordinatları parabol denklemini sağlar.
\( f(a) = -5 \)
\( a^2 - 2a - 16 = -5 \)
\( a^2 - 2a = 11 \)
Değeri sorulan ifadenin açılımını yazalım.
\( (a - 7)(a + 5) = a^2 - 2a - 35 \)
\( = 11 - 35 = -24 \) bulunur.
\( A \) ve \( B \) noktaları \( y = x^2 + 2x - 4 \) parabolünün üzerinde iki noktadır.
\( [AB] \) doğru parçasının orta noktası orijin olduğuna göre, \( \abs{AB} \) uzunluğu kaç birimdir?
Çözümü Göster\( A \) noktasının koordinatlarına \( (a, b) \) diyelim.
\( A \) noktası parabol üzerinde olduğuna göre, koordinatları parabol denklemini sağlar.
\( b = a^2 + 2a - 4 \)
\( [AB] \) doğru parçasının orta noktası orijin olduğuna göre, iki nokta orijine göre simetriktir.
Buna göre, \( B \) noktasının koordinatları \( (-a, -b) \) olur.
\( B \) noktası da parabol üzerinde olduğuna göre, koordinatları parabol denklemini sağlar.
\( -b = (-a)^2 + 2(-a) - 4 \)
\( -b = a^2 - 2a - 4 \)
Eşitliğin taraflarını -1 ile çarpalım.
\( b = -a^2 + 2a + 4 \)
\( A \) ve \( B \) noktaları için bulduğumuz iki eşitliği birbirine eşitleyelim.
\( a^2 + 2a - 4 = -a^2 + 2a + 4 \)
\( 2a^2 = 8 \)
\( a = \pm 2 \)
İki nokta birbirinin simetriği olduğu için apsis değerleri mutlak değerce eşit olacaktır, dolayısıyla \( a \)'nın pozitif ya da negatif değerini almamız sonucu değiştirmeyecektir.
\( a = 2 \)
\( a \) değerini kullanarak \( b \) değerini bulalım.
\( b = 2^2 + 2(2) - 4 = 4 \)
Buna göre iki noktanın koordinatları \( A(2, 4) \) ve \( B(-2, -4) \) olarak bulunur.
İki nokta arasındaki uzaklığı bulalım.
\( \abs{AB} = \sqrt{((2 - (-2))^2 + (4 - (-4))^2} \)
\( = \sqrt{16 + 64} \)
\( = 4\sqrt{5} \) bulunur.
\( f(x) = -x^2 + 6x + 16 \) parabolünün koordinatları pozitif tam sayılar olan kaç noktası vardır?
Çözümü GösterParabol denkleminde \( x \) değeri parabol üzerindeki bir noktanın apsis değerine, \( -x^2 + 6x + 16 \) ifadesi de bu noktanın ordinat değerine karşılık gelir.
Koordinatları pozitif tam sayılar olan noktaları bulmak için önce ordinatı pozitif olan noktaları bulalım.
\( y = f(x) \gt 0 \)
\( -x^2 + 6x + 16 \gt 0 \)
Eşitsizliğin taraflarını \( -1 \) ile çarpalım. Bir eşitsizliğin tarafları negatif bir sayı ile ile çarpıldığında eşitsizlik yön değiştirir.
\( x^2 - 6x - 16 \lt 0 \)
\( (x + 2)(x - 8) \lt 0 \)
Bu eşitsizlik her bir çarpanı sıfır yapan \( x = -2 \) ve \( x = 8 \) değerlerinin arasındaki aralıkta sağlanır.
\( -2 \lt x \lt 8 \)
Buna göre bu aralıktaki \( x \) değerlerinde parabolün ordinatı pozitif olur.
\( x \)'in bu aralıktaki pozitif tam sayı değerlerini bulalım.
\( x \in \{ 1, 2, 3, 4, 5, 6, 7 \} \)
Parabolün katsayıları tam sayı olduğu için, \( x \)'in tam sayı değerlerinde \( y \) de tam sayı olur.
Buna göre verilen parabolün koordinatları pozitif tam sayı olan 7 noktası vardır.