Köklü Eşitsizlikler
Köklü ifade içinde değişken içeren eşitsizliklere köklü eşitsizlik denir. Önceki bölümlerde bahsettiğimiz eşitsizlik özellikleri köklü eşitsizlikler için de geçerlidir.
Çift dereceli köklü ifadelerde kök içi negatif olamaz, dolayısıyla eşitsizliklerdeki her çift dereceli köklü ifade için kök içinin sıfır ya da pozitif olma durumu çözüme ek bir koşul olarak eklenmelidir.
\( \sqrt{x} \gt c \) Formundaki Eşitsizlikler
Karekök içindeki bir ifade ve sabit bir sayı arasındaki eşitsizliklerin çözüm kümesi her iki tarafın karesi alınarak bulunabilir. Karekök içindeki ifadenin içi negatif olamayacağı için bu ifadenin sıfır ya da pozitif olma durumu çözüme ek bir koşul olarak eklenmelidir. Eşitsizliğin çözüm kümesi, ana eşitsizlik ve kök içinin sıfır/pozitif olma durumu için bulunan aralıkların kesişimi olur.
\( \sqrt{x - 5} \lt 3 \) eşitsizliğinin çözüm kümesini bulalım.
Ana eşitsizliğin çözüm kümesini bulmak için iki tarafın karesini alalım.
\( (\sqrt{x - 5})^2 \lt 3^2 \)
\( x - 5 \lt 9 \Longrightarrow \textcolor{red}{x \lt 14} \)
Köklü ifadenin içi negatif olamaz.
\( x - 5 \ge 0 \Longrightarrow \textcolor{red}{x \ge 5} \)
Eşitsizliğin çözüm kümesi, bulduğumuz iki aralığın kesişimidir.
Çözüm kümesi: \( x \in [5, 14) \)
Karekök içindeki bir ifadenin sonucu her zaman sıfır ya da pozitif olacağı için, köklü bir ifadenin negatif bir sayıdan küçük olduğu eşitsizliklerin çözüm kümesi boş küme olur.
\( \sqrt{x} \le -2 \)
Çözüm kümesi: \( x = \{ \} \)
Aynı sebeple köklü ifadenin negatif bir sayıdan büyük olduğu eşitsizliklerde sadece kök içinin sıfır ya da pozitif olma durumunun kontrol edilmesi yeterlidir.
\( \sqrt{x - 1} \ge -2 \)
Köklü ifadenin içi negatif olamaz.
\( x - 1 \ge 0 \Longrightarrow \textcolor{red}{x \ge 1} \)
Çözüm kümesi: \( x \ge 1 \)
Yukarıdaki yöntem tüm çift dereceli köklü ifadelere uygulanabilir.
\( \sqrt[4]{2x - 6} \le 2 \) eşitsizliğinin çözüm kümesini bulalım.
Ana eşitsizliğin çözüm kümesini bulmak için iki tarafın 4. kuvvetini alalım.
\( (\sqrt[4]{2x - 6})^4 \le 2^4 \)
\( 2x - 6 \le 16 \Longrightarrow \textcolor{red}{x \le 11} \)
Köklü ifadenin içi negatif olamaz.
\( 2x - 6 \ge 0 \Longrightarrow \textcolor{red}{x \ge 3} \)
Eşitsizliğin çözüm kümesi, bulduğumuz iki aralığın kesişimidir.
Çözüm kümesi: \( x \in [3, 11] \)
Tek dereceli köklü ifadelerde de köklü ifadeyi kökten kurtaracak şekilde tarafların kuvveti alınır, ancak tek dereceli ifadelerde kök içi negatif olabileceği için kök içindeki ifadenin sıfır ya da pozitif olma durumunun kontrol edilmesine gerek yoktur.
\( \sqrt[3]{x - 7} \gt 4 \) eşitsizliğinin çözüm kümesini bulalım.
Köklü ifadeden kurtulmak için iki tarafın küpünü alalım.
\( (\sqrt[3]{x - 7})^3 \gt 4^3 \)
\( x - 7 \gt 64 \Longrightarrow \textcolor{red}{x \gt 71} \)
Köklü ifadenin içi için ek bir koşul eklememize gerek yoktur.
Çözüm kümesi: \( x \gt 71 \)
\( 4\sqrt{x - 1} \le 12 \) eşitsizliğinin çözüm kümesini bulunuz.
Çözümü GösterEşitsizliğin çözüm kümesini önce cebirsel sonra grafiksel olarak bulalım.
Yöntem 1:
Eşitsizliğin taraflarını 4'e bölelim.
\( \sqrt{x - 1} \le 3 \)
Kök işaretinden kurtulmak için eşitsizliğin taraflarının karesini alalım.
\( (\sqrt{x - 1})^2 \le 3^2 \)
\( x - 1 \le 9 \)
\( x \le 10 \)
Çift dereceli köklü ifadelerin içi negatif olamaz, dolayısıyla her çift dereceli köklü ifade için kök içinin sıfır ya da pozitif olma durumunu çözüme ek bir koşul olarak eklememiz gerekir.
\( x - 1 \ge 0 \)
\( x \ge 1 \)
Yukarıda bulduğumuz iki aralığın kesişimi eşitsizliğin çözüm kümesidir.
Çözüm kümesi: \( 1 \le x \le 10 \)
Yöntem 2:
Eşitsizliğin her iki tarafını birer fonksiyon gibi düşünürek ayrı ayrı grafiklerini çizelim.
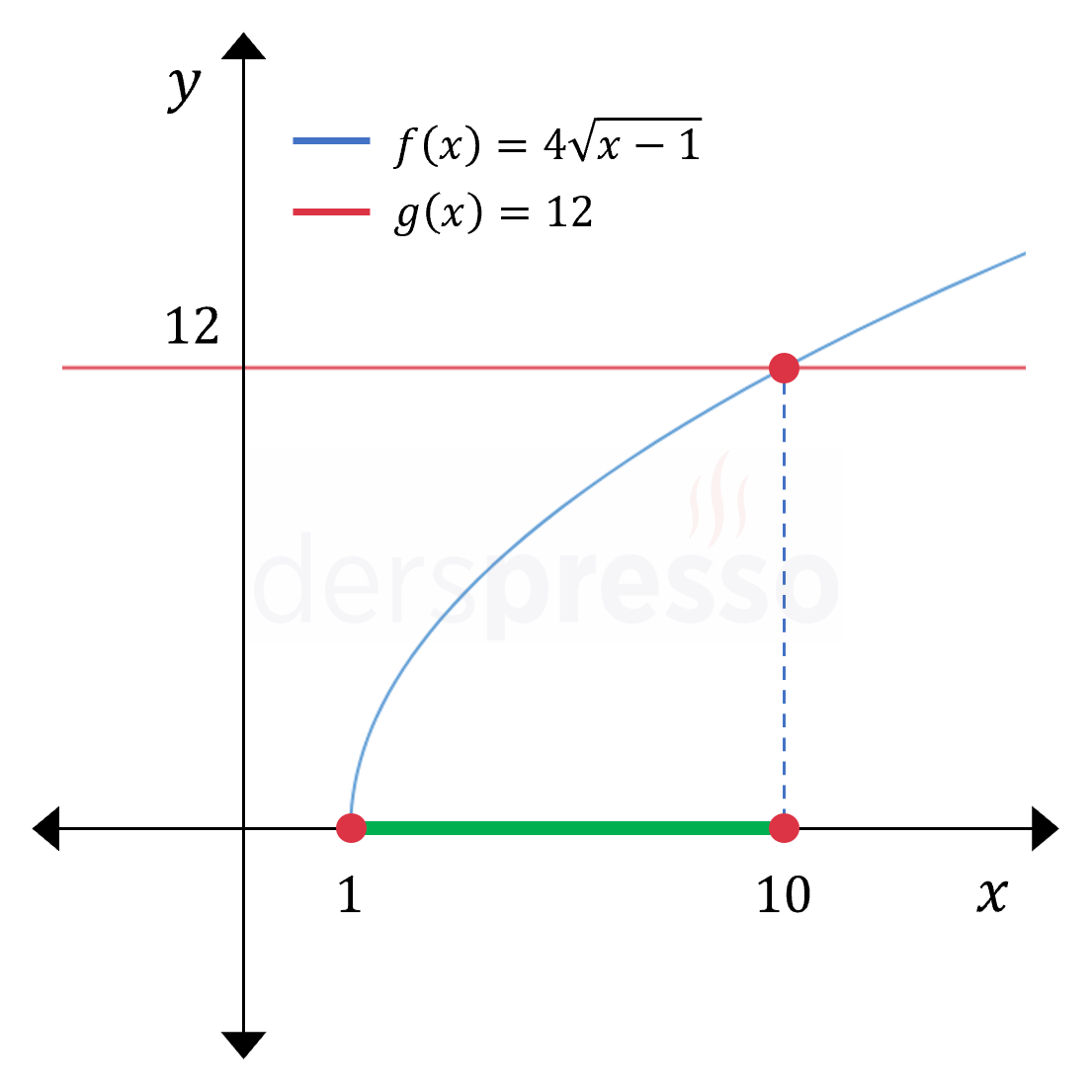
\( f(x) = 4\sqrt{x - 1} \) fonksiyonunun grafiğini \( \sqrt{x} \) grafiğine \( af(x + c) \) dönüşümlerini uygulayarak çizebiliriz (fonksiyon grafiklerinin dönüşümleri için: Fonksiyonların Dönüşümü).
\( g(x) = 12 \) fonksiyonunun grafiği yatay bir doğrudur.
Bu iki fonksiyonun grafiklerinde eşitsizliğin sağlandığı aralık \( g(x) \) grafiğinin \( f(x) \) grafiğinin üzerinde kaldığı ya da ona eşit olduğu aralıktır, bu aralık da grafikte \( x \) ekseni üzerinde yeşil çizgi ile gösterilen \( [1, 10] \) aralığıdır.
\( \sqrt{x + 2} \ge -1 \) eşitsizliğinin çözüm kümesini bulunuz.
Çözümü GösterVerilen eşitsizlikte kareköklü ifade negatif bir sayıdan büyüktür. Çift dereceli köklü bir ifadenin sonucu sadece sıfır ya da pozitif olabileceği için karekök içi sıfır ya da pozitif olduğu sürece bu eşitsizlik her zaman sağlanacaktır. Dolayısıyla sadece kök içinin sıfır ya da pozitif olma durumunu kontrol etmemiz yeterlidir.
\( x + 2 \ge 0 \)
\( x \ge -2 \)
Çözüm kümesi: \( x \ge -2 \)
Önemli bir not:
Verilen eşitsizlikte kareköklü ifadenin negatif bir sayıdan büyük olma detayını dikkate almayıp her iki tarafın karesini aldığımızı varsayalım.
\( (\sqrt{x + 2})^2 \ge (-1)^2 \)
\( x + 2 \ge 1 \)
\( x \ge -1 \)
Bu durumda eşitsizliğin gerçek çözüm kümesini değil, onun bir alt kümesi olan \( x \ge -1 \) aralığını bulmuş olduk.
Bu yüzden çift dereceli bir köklü ifadenin negatif bir sayıdan büyük olduğu eşitsizliklerde, sadece kök içinin sıfır ya da pozitif olma durumunu dikkate alarak eşitsizliği çözmemiz önem taşımaktadır.
\( \sqrt{x} \gt \sqrt{y} \) Formundaki Eşitsizlikler
Karekök içindeki iki ifade arasındaki eşitsizlikler her iki tarafın karesi alınarak çözülebilir. Karekök içindeki ifadelerin içi negatif olamayacağı için bu iki ifadenin sıfır ya da pozitif olma durumları da çözüme ek birer koşul olarak eklenmelidir. Çözüm kümesi, bu üç eşitsizlik (ana eşitsizlik ve iki kök içinin sıfır/pozitif olma durumları) için bulunan aralıkların kesişimi olur.
\( \sqrt{x - 1} \gt \sqrt{2x - 6} \) eşitsizliğinin çözüm kümesini bulalım.
Ana eşitsizliğin çözüm kümesini bulmak için iki tarafın karesini alalım.
\( (\sqrt{x - 1})^2 \gt (\sqrt{2x - 6})^2 \)
\( x - 1 \gt 2x - 6 \Longrightarrow \textcolor{red}{x \lt 5} \)
1. köklü ifadenin içi negatif olamaz.
\( x - 1 \ge 0 \Longrightarrow \textcolor{red}{x \ge 1} \)
2. köklü ifadenin içi negatif olamaz.
\( 2x - 6 \ge 0 \Longrightarrow \textcolor{red}{x \ge 3} \)
Eşitsizliğin çözüm kümesi, bulduğumuz üç aralığın kesişimidir.
Çözüm kümesi: \( x \in [3, 5) \)
Aynı yöntemi derecesi ikiden büyük tüm çift dereceli köklü ifadelere uygulanabilir.
Tek dereceli köklü ifadelerde yine köklü ifade kökten kurtulacak şekilde tarafların kuvveti alınır, ancak tek dereceli ifadelerde kök içi negatif olabileceği için kök içindeki ifadenin sıfır ya da pozitif olma durumunun kontrol edilmesine gerek yoktur.
Eşitsizliğin tarafları farklı derecelerde köklü ifadelerden oluşuyorsa her iki ifadeyi de kökten kurtaracak derecede (derecelerin EKOK'u) tarafların kuvveti alınır. Çift dereceli köklü ifadelerin içi negatif olamayacağı için bu ifadelerin sıfır ya da pozitif olma durumları da çözüme ek birer koşul olarak eklemelidir.
\( \sqrt[4]{2x} \le \sqrt[3]{x} \) eşitsizliğinin çözüm kümesini bulalım.
Köklü ifadelerin derecelerinin EKOK'u 12 olduğu için her iki taraftaki kök işaretinden kurtulmak için tarafların 12. kuvvetini alalım.
\( (\sqrt[4]{2x})^{12} \le (\sqrt[3]{x})^{12} \)
\( (2x)^{\frac{12}{4}} \le x^{\frac{12}{3}} \)
\( (2x)^3 \le x^4 \)
\( 8x^3 \le x^4 \)
İfadeleri eşitsizliğin aynı tarafında toplayalım.
\( x^4 - 8x^3 \ge 0 \)
\( x^3(x - 8) \ge 0 \)
Bu eşitsizliğin çözüm kümesi \( x = 0 \) ve \( x = 8 \) noktalarının dışında kalan aralıktır.
\( \textcolor{red}{x \in (-\infty, 0] \cup [8, \infty)} \)
Çift dereceli köklü ifadelerin içi negatif olamaz.
\( \sqrt[4]{2x} \) ifadesi için:
\( 2x \ge 0\Longrightarrow \textcolor{red}{x \ge 0} \)
Eşitsizliğin çözüm kümesi, bulduğumuz iki aralığın kesişimidir.
Çözüm kümesi: \( \{ 0 \} \cup x \ge 8 \)
\( \sqrt{3x - 6} \lt \sqrt{2x + 4} \) eşitsizliğinin çözüm kümesini bulunuz.
Çözümü GösterEşitsizliğin çözüm kümesini önce cebirsel sonra grafiksel olarak bulalım.
Yöntem 1:
Kök işaretlerinden kurtulmak için eşitsizliğin taraflarının karesini alalım.
\( (\sqrt{3x - 6})^2 \lt (\sqrt{2x + 4})^2 \)
\( 3x - 6 \lt 2x + 4 \)
\( x \lt 10 \)
Çift dereceli köklü ifadelerin içi negatif olamaz, dolayısıyla eşitsizlikteki her iki köklü ifade için kök içinin sıfır ya da pozitif olma durumunu çözüme ek birer koşul olarak eklememiz gerekir.
\( 3x - 6 \ge 0 \)
\( x \ge 2 \)
\( 2x + 4 \ge 0 \)
\( x \ge -2 \)
Eşitsizliğin çözüm kümesi her durum için bulduğumuz çözümlerin kesişiminden oluşur.
Çözüm kümesi: \( 2 \le x \lt 10 \)
Yöntem 2:
Eşitsizliğin her iki tarafını birer fonksiyon gibi düşünürek ayrı ayrı grafiklerini çizelim.
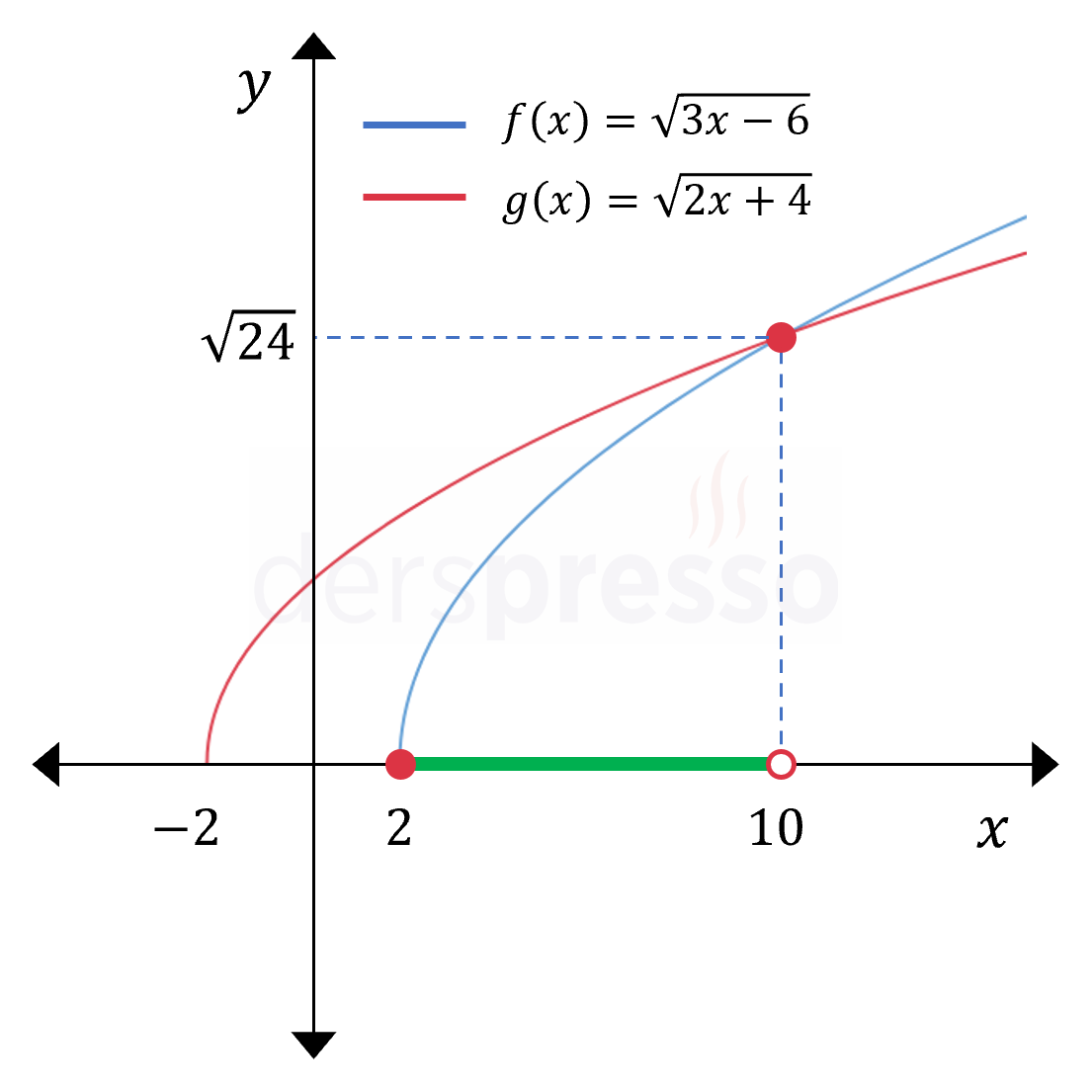
\( f(x) = \sqrt{3x - 6} \) ve \( g(x) = \sqrt{2x + 4} \) fonksiyonlarının grafiklerini \( \sqrt{x} \) grafiğine \( f(ax + c) \) dönüşümlerini uygulayarak çizebiliriz (fonksiyon grafiklerinin dönüşümleri için: Fonksiyonların Dönüşümü).
Bu iki fonksiyonun grafiklerinde eşitsizliğin sağlandığı aralık \( g(x) \) grafiğinin \( f(x) \) grafiğinin üzerinde kaldığı aralıktır, bu aralık da grafikte \( x \) ekseni üzerinde yeşil çizgi ile gösterilen \( [2, 10) \) aralığıdır.
\( \sqrt{x} \gt y \) Formundaki Eşitsizlikler
Köklü eşitsizliklerde tarafların karesi alınırken her iki tarafın da işaretinin pozitif olduğundan emin olunmalıdır, aksi takdirde aşağıdaki örnekte olduğu gibi yanlış sonuç elde edilebilir.
\( \sqrt{x} \ge -2 \) eşitsizliğinin çözüm kümesini bulalım.
\( (\sqrt{x})^2 \ge (-2)^2 \)
\( x \ge 4 \)
Çözüm kümesi olarak \( x \ge 4 \) bulmuş olsak da köklü ifade hiçbir zaman negatif olamayacağı ve verilen eşitsizlik her zaman sağlanacağı için gerçek çözüm kümesi \( x \ge 0 \) olmalıdır.
Buna göre yukarıda "\( \sqrt{x} \gt c \) Formundaki Eşitsizlikler" bölümünde belirttiğimiz gibi, bu tip eşitsizlikler \( \sqrt{x} \ge 0 \) formuna getirilerek çözülmelidir.
Bu sebeple \( \sqrt{x} \gt y \) formundaki eşitsizliklerde kök içinde olmayan taraf pozitif ve negatif değer alabileceği için problem ikiye bölünerek ayrı ayrı çözülmelidir.
\( \sqrt{x} \gt y \) formundaki bir eşitsizliğin çözüm kümesini bulmak için,
Köklü ifadenin tanımlı olma koşulu: Çift dereceli köklü ifadelerin içi negatif olamaz.
\( x \ge 0 \)
Durum 1: Eşitsizliğin sağ tarafı sıfır ya da pozitif
\( \sqrt{x} \gt y \) eşitsizliği \( y \ge 0 \) koşulu ile birlikte çözülür.
Durum 2: Eşitsizliğin sağ tarafı negatif
\( \sqrt{x} \gt 0 \) eşitsizliği \( y \lt 0 \) koşulu ile birlikte çözülür.
Eşitsizliğin çözüm kümesi, bu iki durumdan elde edilen aralıkların birleşim kümesi ile köklü ifadenin tanımlı olma koşulundan gelen aralığın (\( x \ge 0 \)) kesişimi olur.
\( \sqrt{x - 2} \ge x - 4 \) eşitsizliğinin çözüm kümesini bulalım.
Köklü ifadenin tanımlı olma koşulu: Çift dereceli köklü ifadelerin içi negatif olamaz.
\( x - 2 \ge 0 \Longrightarrow \textcolor{red}{x \ge 2} \)
Durum 1: Eşitsizliğin sağ tarafı sıfır ya da pozitif
\( x - 4 \ge 0 \Longrightarrow \textcolor{red}{x \ge 4} \)
Kökten kurtulmak için her iki tarafın karesini alalım.
\( (\sqrt{x - 2})^2 \ge (x - 4)^2 \)
\( x - 2 \ge x^2 - 8x + 16 \)
\( x^2 - 9x + 18 \le 0 \)
\( (x - 3)(x - 6) \le 0 \)
\( 3 \le x \le 6 \)
Bu durumun ana koşulu \( x \ge 4 \) olduğu için çözüm aralığı aşağıdaki gibi olur.
Durum 1 için çözüm aralığı: \( \textcolor{red}{4 \le x \le 6} \)
Durum 2: Eşitsizliğin sağ tarafı negatif
\( x - 4 \lt 0 \Longrightarrow \textcolor{red}{x \lt 4} \)
Bu durumda yukarıda hatalı örnekte belirttiğimiz sebeple çözmemiz gereken eşitsizlik aşağıdaki gibi olur.
\( \sqrt{x - 2} \ge 0 \)
\( x - 2 \ge 0 \)
\( x \ge 2 \)
Bu durumun ana koşulu \( x \lt 4 \) olduğu için çözüm aralığı aşağıdaki gibi olur.
Durum 2 için çözüm aralığı: \( \textcolor{red}{2 \le x \lt 4} \)
Eşitsizliğin çözüm kümesi, bu iki durumdan elde edilen aralıkların birleşim kümesi ile köklü ifadenin tanımlı olma koşulundan gelen aralığın (\( x \ge 2 \)) kesişimi olur.
Çözüm kümesi: \( 2 \le x \le 6 \)
Aynı eşitsizliğin çözüm kümesini grafiksel olarak bulalım.
Eşitsizliğin her iki tarafını birer fonksiyon olarak düşünürek ayrı ayrı grafiklerini çizelim.
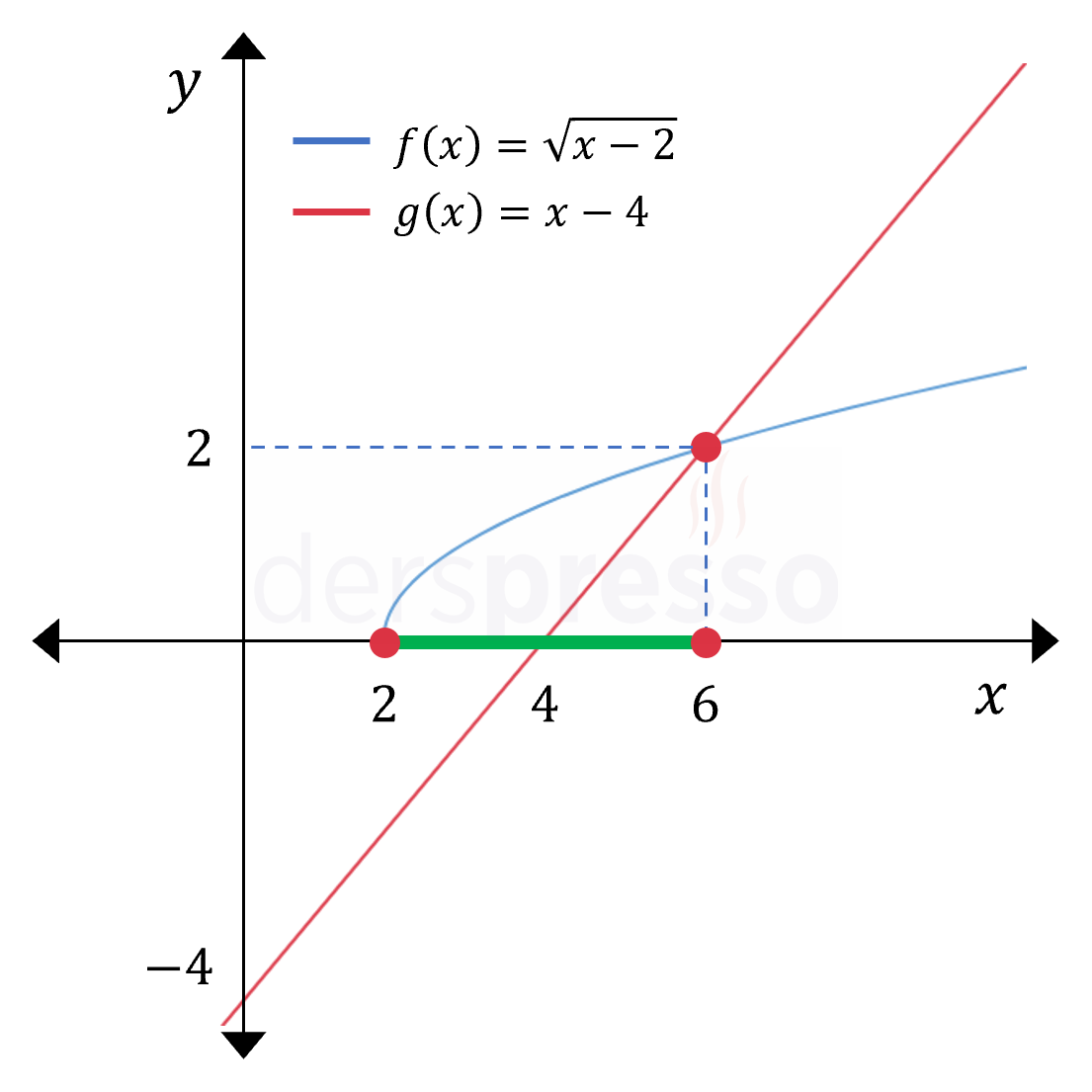
\( f(x) = \sqrt{x - 2} \) fonksiyonunun grafiğini \( \sqrt{x} \) grafiğine \( f(x + c) \) dönüşümü uygulayarak çizebiliriz (fonksiyon grafiklerinin dönüşümleri için: Fonksiyonların Dönüşümü).
\( g(x) = x - 4 \) fonksiyonunun grafiği bir doğrudur.
Bu iki fonksiyonun grafiklerinde eşitsizliğin sağlandığı aralık \( f(x) \) grafiğinin \( g(x) \) grafiğinin üzerinde kaldığı ya da ona eşit olduğu aralıktır, bu da grafikte \( x \) ekseni üzerinde yeşil çizgi ile gösterilen \( [2, 6] \) aralığıdır.