Tek ve Çift Fonksiyonlar
Fonksiyonlar gösterdikleri bazı simetri özelliklerine göre tek ya da çift fonksiyon olarak adlandırılırlar.
Çift Fonksiyonlar
Tanım Olarak Çift Fonksiyon
Bir \( f \) fonksiyonunun tüm tanım aralığında \( f(-x) = f(x) \) ise bu fonksiyon bir çift fonksiyondur.
\( f: A \to B \) olmak üzere, her \( x \in A \) için,
\( f(-x) = f(x) \) ise,
\( f \) bir çift fonksiyondur.
\( f(x) = x^4 - 2x^2 + 2 \)
\( f(-x) = (-x)^4 - 2(-x)^2 + 2 = x^4 - 2x^2 + 2 \)
\( f(-x) = f(x) \) olduğu için \( f \) bir çift fonksiyondur.
\( g(x) = \abs{x} - 2 \)
\( g(-x) = \abs{-x} - 2 = \abs{x} - 2 \)
\( g(-x) = g(x) \) olduğu için \( g \) bir çift fonksiyondur.
Çift fonksiyonlar için yukarıdaki eşitlik aşağıdaki şekilde de yazılabilir.
\( f(x) - f(-x) = 0 \)
Grafik Olarak Çift Fonksiyon
Yukarıdaki tanıma göre, bir çift fonksiyonun tanım aralığında \( y \) eksenine göre simetrik her nokta ikilisi için fonksiyon değerleri birbirine eşittir, bu da çift fonksiyonların grafiklerinin \( y \) eksenine göre simetrik olması anlamına gelir. Buna göre, bir çift fonksiyonun grafiği üzerindeki her \( (a, b) \) noktası için \( (-a, b) \) noktası da grafiğin üzerindedir.
Yukarıdaki tanıma göre, bir çift fonksiyonun tanım aralığında \( y \) eksenine göre simetrik her nokta ikilisi için fonksiyon değerleri birbirine eşittir, bu da çift fonksiyonların grafiklerinin \( y \) eksenine göre simetrik olması anlamına gelir. Buna göre, bir çift fonksiyonun grafiği üzerindeki her \( (a, b) \) noktası için \( (-a, b) \) noktası da grafiğin üzerindedir.
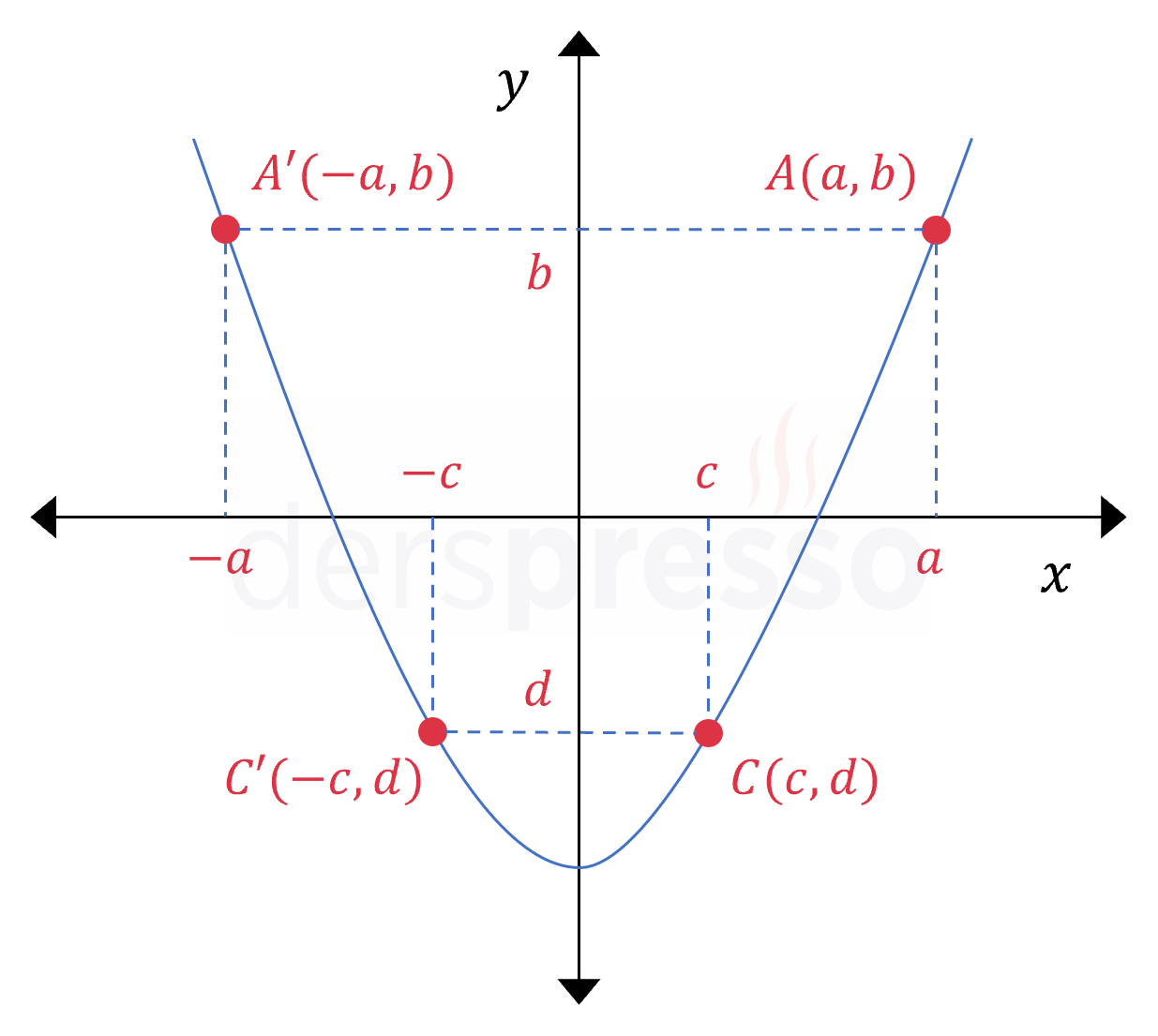
Aşağıdaki fonksiyonlar birer çift fonksiyondur, dolayısıyla hem yukarıdaki çift fonksiyon tanım kriterini sağlarlar hem de grafikleri \( y \) eksenine göre simetriktir.
| Fonksiyon | Örnek |
|---|---|
| Sabit fonksiyonlar | \( f(x) = 3 \) |
| Çift dereceli kuvvet fonksiyonları | \( f(x) = 3x^4 \) |
| Tek ve çift fonksiyonların mutlak değeri | \( f(x) = \abs{x} \) |
| Kosinüs fonksiyonu | \( f(x) = \cos{x} \) |
| Sekant fonksiyonu | \( f(x) = \sec{x} \) |
| Sadece çift dereceli terimlerden oluşan polinom fonksiyonları (sabit terim dahil) | \( f(x) = 2x^8 - x^4 + 3x^2 - 1 \) |
| Sonlu sayıda çift fonksiyonun toplamı/farkı | \( f(x) = x^6 + 3x^2 - 2\cos{x} - 4\abs{x^3} + 5 \) |
Tek Fonksiyonlar
Tanım Olarak Tek Fonksiyon
Bir \( f \) fonksiyonunun tüm tanım aralığında \( f(-x) = -f(x) \) ise bu fonksiyon bir tek fonksiyondur.
\( f: A \to B \) olmak üzere, her \( x \in A \) için,
\( f(-x) = -f(x) \) ise,
\( f \) bir tek fonksiyondur.
\( f(x) = 3x^3 + x \)
\( f(-x) = 3(-x)^3 + (-x) = -3x^3 - x = -(3x^3 + x) \)
\( f(-x) = -f(x) \) olduğu için \( f \) bir tek fonksiyondur.
\( g(x) = x + \sin{x} \)
\( g(-x) = (-x) + \sin(-x) = -x - \sin{x} = -(x + \sin{x}) \)
\( g(-x) = -g(x) \) olduğu için \( g \) bir tek fonksiyondur.
Tek fonksiyonlar için yukarıdaki eşitlik aşağıdaki şekilde de yazılabilir.
\( f(x) + f(-x) = 0 \)
Grafik Olarak Tek Fonksiyon
Yukarıdaki tanıma göre, bir tek fonksiyonun \( y \) eksenine göre simetrik her nokta ikilisi için fonksiyon değerleri birbirinin ters işaretlisidir, bu da tek fonksiyonların grafiklerinin orijine göre simetrik olması anlamına gelir. Buna göre, bir tek fonksiyonun grafiği üzerindeki her \( (a, b) \) noktası için \( (-a, -b) \) noktası da grafiğin üzerindedir.
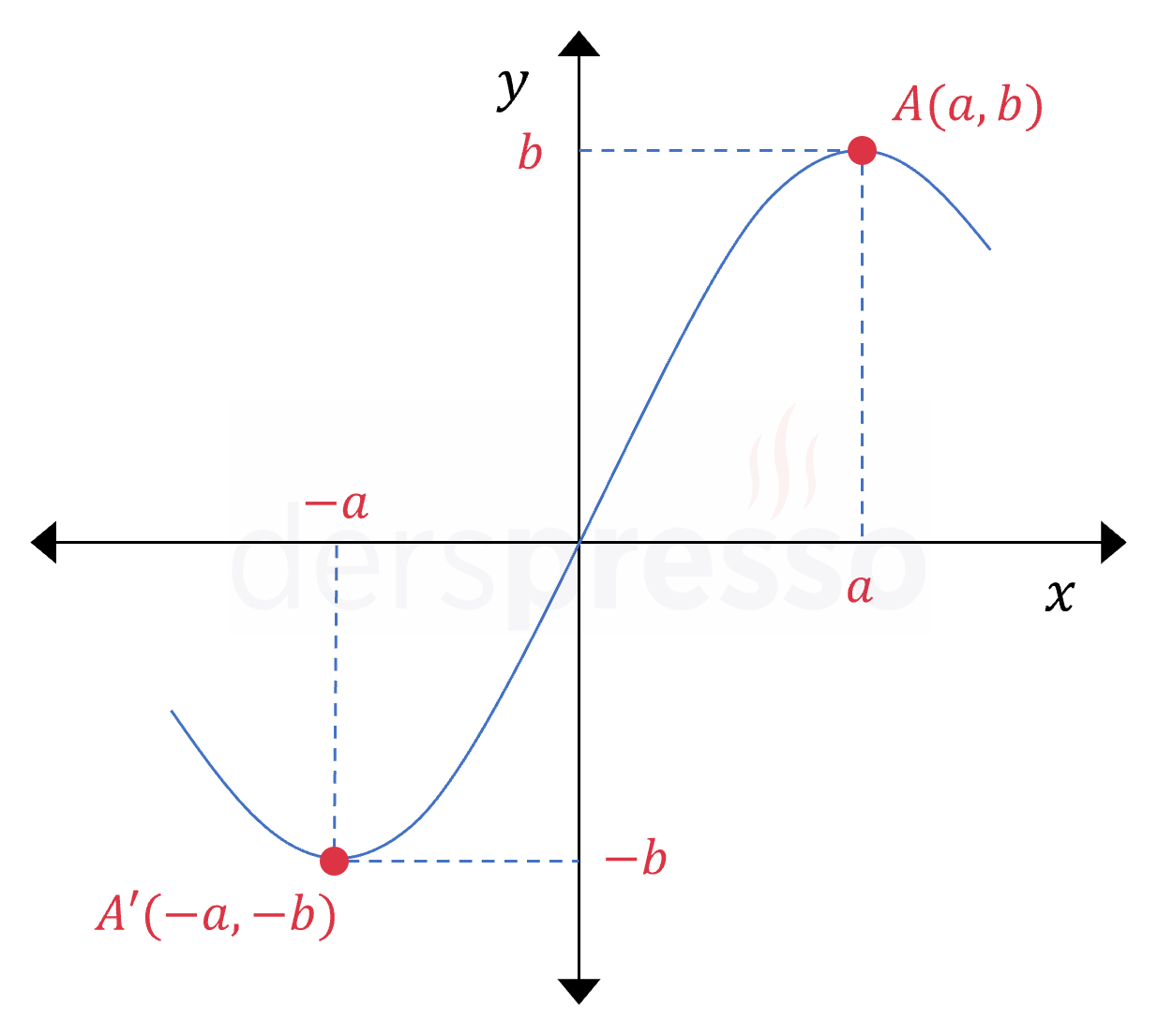
Bir fonksiyonun \( x = 0 \) noktasında tek fonksiyon olma koşulunu sağlaması için \( f(0) \) sıfır ya da tanımsız olmalıdır. Buna göre bir tek fonksiyonun grafiği ya orijinden geçer ya da \( x = 0 \) için tanımsızdır.
Aşağıdaki fonksiyonlar birer tek fonksiyondur, dolayısıyla hem yukarıdaki tek fonksiyon tanım kriterini sağlarlar hem de grafikleri orijine göre simetriktir.
| Fonksiyon | Örnek |
|---|---|
| Tek dereceli kuvvet fonksiyonları | \( f(x) = 2x^3 \) |
| Sinüs fonksiyonu | \( f(x) = \sin{x} \) |
| Tanjant fonksiyonu | \( f(x) = \tan{x} \) |
| Kotanjant fonksiyonu | \( f(x) = \cot{x} \) |
| Kosekant fonksiyonu | \( f(x) = \csc{x} \) |
| Sadece tek dereceli terimlerden oluşan polinom fonksiyonları | \( f(x) = 2x^7 + 3x^5 - 7x^3 - x \) |
| Sonlu sayıda tek fonksiyonun toplamı/farkı | \( f(x) = x^5 + 3x - 2\sin{x} \) |
Fonksiyonların Tek/Çift Olma Durumu
Bir fonksiyon yukarıda paylaştığımız koşulları sağlama durumuna göre tek fonksiyon olabilir, çift fonksiyon olabilir ya da ikisi de olmayabilir. Sadece sınırlı sayıda özel bazı fonksiyonlar tek ya da çifttir, bu fonksiyonlar dışında kalan çoğu fonksiyon her ikisi de değildir.
Hem tek hem de çift fonksiyon koşullarını sağlayan fonksiyon sadece \( f(x) = 0 \) fonksiyonudur.
Fonksiyonlarla İşlemlerin Tek/Çift Olma Durumu
Bu bölümde tek ya da çift olduğunu bildiğimiz fonksiyonlar arasındaki işlemlerin sonucunun tek ya da çift olma durumunu inceleyeceğiz.
Toplama ve Çıkarma
Tek/çift fonksiyonların toplama/çıkarma işlem sonuçlarının tek/çift fonksiyon olma durumları aşağıdaki gibidir.
| \( f \) | \( g \) | \( f + g \) \( f - g \) |
Örnek |
|---|---|---|---|
| Çift | Çift | Çift | \( x^6 + x^2 \) |
| Çift | Tek | İkisi de değil | \( x^4 + x^3 \) |
| Tek | Çift | İkisi de değil | \( \sin{x} + x^2 \) |
| Tek | Tek | Tek | \( x^3 + \sqrt[3]{x} \) |
Çarpma ve Bölme
Tek/çift fonksiyonların çarpma/bölme işlem sonuçlarının tek/çift fonksiyon olma durumları aşağıdaki gibidir.
| \( f \) | \( g \) | \( f \cdot g \) \( f \div g \) |
Örnek |
|---|---|---|---|
| Çift | Çift | Çift | \( x^6 \cdot x^2 = x^8 \) |
| Çift | Tek | Tek | \( \abs{x} \cdot x^3 \) |
| Tek | Çift | Tek | \( \cot{x} \cdot \cos{x} \) |
| Tek | Tek | Çift | \( x \cdot \sqrt[3]{x} \) |
Tek/çift fonksiyonların parantez içi ya da dışı sabit bir sayı ile çarpıldığında (\( f(bx) \) ya da \( af(x) \)) fonksiyonların tek/çift olma durumları değişmez. Bu işlemler fonksiyon grafiği üzerindeki tüm noktaların sırasıyla \( y \) ve \( x \) eksenlerinden bu katsayı oranında uzaklaşmasına ya da bu eksenlere yakınlaşmasına yol açtığı için grafiklerin \( y \) ekseni ya da orijine göre simetrisinde bir değişiklik olmaz.
\( f(x) = x^2 + 5 \) çift fonksiyon olduğu için aşağıdaki iki fonksiyon da birer çift fonksiyondur.
\( f(2x) = (2x)^2 + 5 \)
\( 2f(x) = 2(x^2 + 5) \)
Tek/Çift Sayı Kuvvet
Tek/çift fonksiyonların tek/çift sayı kuvvetlerinin tek/çift fonksiyon olma durumları aşağıdaki gibidir (\( n \in \mathbb{Z}^+\)).
| \( f \) | \( n \) | \( f^{n} \) | Örnek |
|---|---|---|---|
| Çift Fonksiyon | Çift Sayı | Çift Fonksiyon | \( (x^2)^4 = x^8 \) |
| Çift Fonksiyon | Tek Sayı | Çift Fonksiyon | \( \abs{x}^3 \) |
| Tek Fonksiyon | Çift Sayı | Çift Fonksiyon | \( (x^3)^4 = x^{12} \) |
| Tek Fonksiyon | Tek Sayı | Tek Fonksiyon | \( (x^3)^5 = x^{15} \) |
Bileşke Fonksiyon
Tek/çift fonksiyonların bileşke fonksiyonlarının tek/çift fonksiyon olma durumu aşağıdaki tablodaki gibidir.
| \( f \) | \( g \) | \( f \circ g \) | Örnek |
|---|---|---|---|
| Çift | Çift | Çift | \( f[g(x)] = \abs{x^4 - 2x^2 - 5} \) |
| Çift | Tek | Çift | \( f[g(x)] = \cos(\sin{x}) \) |
| Tek | Çift | Çift | \( f[g(x)] = \sin(x^2) \) |
| Tek | Tek | Tek | \( f[g(x)] = \sqrt[3]{x^5 - x^3 + 2x} \) |
Bir Fonksiyonun Tek/Çift Fonksiyon Bileşenleri
Her fonksiyon bir çift ve bir tek fonksiyonun toplamı şeklinde yazılabilir. Toplamları \( f \) fonksiyonunu veren çift \( g \) ve tek \( h \) fonksiyonları aşağıdaki formülle bulunabilir.
\( f \) reel sayılarda tanımlı olmak üzere,
\( f(x) = g(x) + h(x) \)
\( g(x) = \dfrac{f(x) + f(-x)}{2} \)
\( h(x) = \dfrac{f(x) - f(-x)}{2} \)
\( f(x) = 3x^4 - 2x^3 + 4x^2 - x + 7 \)
\( f(-x) = 3x^4 + 2x^3 + 4x^2 + x + 7 \)
\( g(x) = \dfrac{6x^4 + 8x^2 + 14}{2} \)
\( = 3x^4 + 4x^2 + 7 \)
\( h(x) = \dfrac{-4x^3 - 2x}{2} \)
\( = -2x^3 - x \)
\( g \) çift, \( h \) tek fonksiyondur ve toplamları \( f \) fonksiyonuna eşittir.
İSPATI GÖSTER
Önce \( g \) ve \( h \) fonksiyonlarının toplamının \( f \) fonksiyonuna eşit olduğunu gösterelim.
\( g(x) = \dfrac{f(x) + f(-x)}{2} \)
\( h(x) = \dfrac{f(x) - f(-x)}{2} \)
\( g(x) + h(x) = \dfrac{f(x) + f(-x)}{2} + \dfrac{f(x) - f(-x)}{2} \)
\( = \dfrac{f(x) + f(-x) + f(x) - f(-x)}{2} \)
\( = \dfrac{2f(x)}{2} = f(x) \)
Şimdi her \( f \) fonksiyonu için \( g \) fonksiyonunun bir çift fonksiyon olduğunu gösterelim.
\( g(-x) = \dfrac{f(-x) + f(-(-x))}{2} \)
\( = \dfrac{f(-x) + f(x)}{2} \)
\( = \dfrac{f(x) + f(-x)}{2} \)
\( = g(x) \)
Buna göre \( g \) fonksiyonu bir çift fonksiyondur.
Şimdi her \( f \) fonksiyonu için \( h \) fonksiyonunun bir tek fonksiyon olduğunu gösterelim.
\( h(-x) = \dfrac{f(-x) - f(-(-x))}{2} \)
\( = \dfrac{f(-x) - f(x)}{2} \)
\( = -\dfrac{f(x) - f(-x)}{2} \)
\( = -h(x) \)
Buna göre \( h \) fonksiyonu bir tek fonksiyondur.
Her \( f \) fonksiyonu için bu koşulları sağlayan yalnız bir \( g \) ve \( h \) fonksiyon ikilisi vardır.
\( f \) fonksiyonu çift ise \( h \) fonksiyonu, tek ise \( g \) fonksiyonu sıfır fonksiyonu olarak bulunur.
\( f(x) = e^x \) fonksiyonunu tek ve çift bileşenlerine ayıralım.
\( f(x) = e^x \)
\( f(-x) = e^{-x} \)
\( g(x) = \dfrac{e^x + e^{-x}}{2} \)
\( h(x) = \dfrac{e^x - e^{-x}}{2} \)
\( g \) fonksiyonunun çift, \( h \) fonksiyonunun tek oldukları \( x \) yerine \( -x \) yazılarak gösterilebilir.
\( f(x) = (a - 3)x^4 + a^2x^3 + (b + 2)x^2 - b^2x \) fonksiyonu tek fonksiyon olduğuna göre, \( f(a + b) \) kaçtır?
Çözümü GösterTek polinom fonksiyonları sadece tek dereceli terimler içerebilir.
Buna göre \( x^4 \) ve \( x^2 \)'li terimlerin katsayıları sıfır olmalıdır.
\( a - 3 = 0 \Longrightarrow a = 3 \)
\( b + 2 = 0 \Longrightarrow b = -2 \)
Fonksiyon tanımı aşağıdaki gibi olur.
\( f(x) = 9x^3 - 4x \)
\( f(a + b) = f(3 + (-2)) = f(1) \)
\( = 9(1)^3 - 4(1) = 5 \) bulunur.
\( f(x) = ax^4 + (b - 4)x^3 + 2x^2 - (a + b)x + 4 \) fonksiyonu çift fonksiyon olduğuna göre, \( ab \) çarpımı kaçtır?
Çözümü GösterÇift polinom fonksiyonları sadece çift dereceli terimler (ve yine çift dereceli bir terim olan sabit terim) içerebilir.
Buna göre \( x^3 \) ve \( x \)'li terimlerin katsayıları sıfır olmalıdır.
\( b - 4 = 0 \Longrightarrow b = 4 \)
\( a + b = 0 \Longrightarrow a = -4 \)
\( ab = -4 \cdot 4 = -16 \) bulunur.
\( f \) tek, \( g \) çift fonksiyondur.
\( f(-1) = 4, \quad g(-1) = -3 \)
\( h(x) = \dfrac{3f(x) + 2g(x)}{4f(x)} \) olduğuna göre, \( h(1) \) kaçtır?
Çözümü Göster\( h \) fonksiyonunda \( x = 1 \) yazalım.
\( h(1) = \dfrac{3f(1) + 2g(1)}{4f(1)} \)
\( f \) tek fonksiyon olduğu için \( f(1) = -f(-1) = -4 \) olur.
\( g \) çift fonksiyon olduğu için \( g(1) = g(-1) = -3 \) olur.
\( h(1) = \dfrac{3(-4) + 2(-3)}{4(-4)} \)
\( = \dfrac{-12 - 6}{-16} = \dfrac{9}{8}\) bulunur.
Tüm reel sayılarda tanımlı aşağıdaki fonksiyonlardan hangileri çift fonksiyondur?
I. \( f(x) = x^4 - 2x \)
II. \( g(x) = -2x^3 + 3 \)
III. \( h(x) = -9 \)
IV. \( k(x) = (x - 4)^2 \)
Çözümü GösterSadece tek dereceli terimler içeren bir polinom fonksiyonu tektir, sadece çift dereceli terimler içeren bir polinom fonksiyonu çifttir, hem tek hem çift dereceli terimler içeren bir polinom fonksiyonu ne tektir ne çifttir.
Sabit terim, \( x \) değişkeninin üssü sıfır olarak kabul edilebileceği için çift dereceli bir terimdir.
I. öncül:
\( f(x) = x^4 - 2x \)
Yukarıdaki tanıma göre \( f \) ne tektir ne çifttir.
II. öncül:
\( g(x) = -2x^3 + 3 \)
Yukarıdaki tanıma göre \( g \) ne tektir ne çifttir.
III. öncül:
\( h(x) = -9 \)
Yukarıdaki tanıma göre \( h \) çifttir.
IV. öncül:
\( k(x) = (x - 4)^2 \)
İfadenin açılımını yazalım.
\( = x^2 - 8x + 16 \)
Yukarıdaki tanıma göre \( k \) ne tektir ne çifttir.
Buna göre sadece III. öncüldeki fonksiyon çift fonksiyondur.
\( f \) fonksiyonu orijine göre simetriktir.
\( 2f(x) + 6x = 3x^3 + f(-x) \) olduğuna göre, \( f(2) \) kaçtır?
Çözümü Göster\( f \) fonksiyonu orijine göre simetrik ise tek fonksiyondur.
\( f(-x) = -f(x) \)
Verilen eşitlikte \( f(-x) \) yerine \( -f(x) \) yazalım.
\( 2f(x) + 6x = 3x^3 - f(x) \)
\( 3f(x) = 3x^3 - 6x \)
\( f \) fonksiyon tanımı aşağıdaki gibidir.
\( f(x) = x^3 - 2x \)
\( f(2) = 2^3 - 2(2) = 4 \) bulunur.
\( f(x) = 2g(x) + x \)
\( g(-6) = 56 \) olmak üzere,
\( f(x) \) bir çift fonksiyon olduğuna göre, \( g(6) \) kaçtır?
Çözümü Göster\( f \) çift fonksiyon olduğu için \( f(-x) = f(x) \) olur.
\( f(-x) = 2g(-x) + (-x) = f(x) \)
\( 2g(-x) - x = 2g(x) + x \)
\( 2g(-x) = 2g(x) + 2x \)
\( g(-x) = g(x) + x \)
\( x = 6 \) yazalım.
\( g(-6) = g(6) + 6 \)
\( g(-6) \) değeri soruda veriliyor.
\( 56 = g(6) + 6 \)
\( g(6) = 50 \) bulunur.
\( f(x) = 2x^2 - 4x + 5 \)
\( g(x) = f(x + k) \) olmak üzere,
\( g(x) \) bir çift fonksiyon olduğuna göre, \( g(k) \) kaçtır?
Çözümü GösterBu soruyu iki yöntemle çözebiliriz.
1. yöntem:
\( g(x) = f(x + k) \)
\( = 2(x + k)^2 - 4(x + k) + 5 \)
\( = 2x^2 + 4kx + 2k^2 - 4x - 4k + 5 \)
\( = 2x^2 + (4k - 4)x + 2k^2 - 4k + 5 \)
Çift polinom fonksiyonları sadece çift dereceli terimler ve sabit terim içerebilir.
Buna göre \( x \)'li terimin katsayısı sıfır olmalıdır.
\( 4k - 4 = 0 \Longrightarrow k = 1 \)
\( g(x) = 2x^2 + 3 \)
\( g(k) = g(1) = 2(1)^2 + 3 = 5 \) bulunur.
2. yöntem:
Çift fonksiyonların grafikleri \( y \) eksenine göre simetriktir, dolayısıyla bir parabolün ötelenmiş hali olduğu için yine bir parabol olan \( g \) fonksiyonunun tepe noktası \( y \) ekseni üzerinde olmalıdır.
\( f \) fonksiyonunun tepe noktasına \( T(r, k) \) diyelim.
\( r = -\dfrac{b}{2a} = -\dfrac{-4}{2(2)} = 1 \)
\( g \) fonksiyonunun tepe noktasının \( y \) ekseni üzerinde olması için \( f \) fonksiyonu 1 birim sola ötelenmelidir, bu da \( f(x + 1) \) fonksiyonudur.
\( k = 1 \)
Fonksiyonlarda \( x = 1 \) yazalım.
\( g(1) = f(2) = 2(2)^2 - 4(2) + 5 = 5 \) bulunur.
\( f \) ve \( g \) fonksiyonlarının grafikleri sırasıyla orijin ve \( y \) eksenine göre simetriktir.
\( f(-6) = 4, \quad g(2) = 6 \)
olduğuna göre, \( (f \circ g)(-2) \) değeri kaçtır?
Çözümü Göster\( f \) fonksiyonu orijine göre simetrik olduğuna göre tek fonksiyondur.
\( f(-x) = -f(x) \)
\( f(6) = -f(-6) = -(4) = -4 \)
\( g \) fonksiyonu \( y \) eksenine göre simetrik olduğuna göre çift fonksiyondur.
\( g(-x) = g(x) \)
\( g(-2) = g(2) = 6 \)
Buna göre verilen işlemin sonucunu bulalım.
\( (f \circ g)(-2) = f(g(-2)) \)
\( = f(6) = -4 \) bulunur.
\( f(x) \ne 0 \) olmak üzere,
\( f \) çift fonksiyon olduğuna göre, aşağıdakilerden hangileri tek fonksiyondur?
I. \( 2x + f(x) \)
II. \( 3x^2 - 2f(x) \)
III. \( 4xf(x) \)
IV. \( f(x^5) \)
Çözümü GösterI. öncül:
\( 2x + f(x) \)
\( 2x \) tek fonksiyondur. Bir tek fonksiyon ile çift fonksiyonun toplamı/farkı ne tek ne çift olur.
II. öncül:
\( 3x^2 - 2f(x) \)
\( 3x^2 \) çift fonksiyondur. İki çift fonksiyonun toplamı/farkı çift olur.
III. öncül:
\( 4xf(x) \)
\( x \) tek fonksiyondur. Bir tek fonksiyon ile çift fonksiyonun çarpımı tek olur.
IV. öncül:
\( f(x^5) \)
\( x^5 \) tek fonksiyondur. Çift fonksiyonun tek fonksiyon ile bileşkesi çift olur.
Buna göre sadece III. öncüldeki fonksiyon tektir.
Aşağıdaki fonksiyonlardan hangileri çift fonksiyondur?
(a) \( f(x) = \abs{x} - 3 \)
(b) \( g(x) = \abs{x - 3} \)
(c) \( h(x) = x^2 - \abs{x} \)
Çözümü Göster\( \abs{x} \) fonksiyonunun grafiği \( y \) eksenine göre simetrik olduğu için bir çift fonksiyondur.
I. öncül:
\( f(x) = \abs{x} - 3 \)
\( f \) fonksiyonu bir çift fonksiyonun 3 birim aşağıya ötelenmiş halidir, dolayısıyla fonksiyonun \( y \) eksenine göre simetrisi bozulmaz.
Buna göre \( f \) fonksiyonu çifttir.
II. öncül:
\( g(x) = \abs{x - 3} \)
\( g \) fonksiyonu bir çift fonksiyonun 3 birim sağa ötelenmiş halidir, dolayısıyla fonksiyonun \( y \) eksenine göre simetrisi bozulur.
Buna göre \( g \) fonksiyonu ne tek ne çifttir.
III. öncül:
\( h(x) = x^2 - \abs{x} \)
İki çift fonksiyonun toplamı/farkı çifttir.
Buna göre \( h \) fonksiyonu çifttir.
Buna göre I. ve III. öncüllerdeki fonksiyonlar çifttir.
\( f(x) \ne 0 \) ve \( g(x) \ne 0 \) olmak üzere,
\( f \) çift ve \( g \) tek fonksiyon olduğuna göre, aşağıdakilerden hangileri çift fonksiyondur?
I. \( f(x^2)g(x^5) \)
II. \( f(x) + g(x^4) \)
III. \( x^{99}f(x)g(x^3) \)
IV. \( f(x^3) + g^2(x) \)
Çözümü GösterI. öncül:
\( f(x^2)g(x^5) \)
\( f(x^2) \): Çift fonksiyonun çift fonksiyonla bileşkesi çift fonksiyondur.
\( g(x^5) \): Tek fonksiyonun tek fonksiyonla bileşkesi tek fonksiyondur.
Çift ve tek iki fonksiyonun çarpımı tek fonksiyondur.
II. öncül:
\( f(x) + g(x^4) \)
\( g(x^4) \): Tek fonksiyonun çift fonksiyonla bileşkesi çift fonksiyondur.
İki çift fonksiyonun toplamı çift fonksiyondur.
III. öncül:
\( x^{99}f(x)g(x^3) \)
\( g(x^3) \): Tek fonksiyonun tek fonksiyonla bileşkesi tek fonksiyondur.
Buna göre 1. çarpan tek, 2. çarpan çift, 3. çarpan tek fonksiyondur.
Tek, çift ve tek üç fonksiyonun çarpımı çift fonksiyondur.
IV. öncül:
\( f(x^3) + g^2(x) \)
\( f(x^3) \): Çift fonksiyonun tek fonksiyonla bileşkesi çift fonksiyondur.
\( g^2(x) \): Tek fonksiyonun çift sayı kuvveti çift fonksiyondur.
İki çift fonksiyonun toplamı çift fonksiyondur.
Buna göre II., III. ve IV. öncüllerdeki fonksiyonlar çifttir.
\( f(x) = \ln{\dfrac{e - x}{e + x}} \) fonksiyonunun tek/çift olma durumunu inceleyin.
Çözümü Göster\( f(-x) \) fonksiyonunu bulalım.
\( f(-x) = \ln{\dfrac{e - (-x)}{e + (-x)}} \)
\( = \ln{\dfrac{e + x}{e - x}} \)
\( = \ln \left( \dfrac{e - x}{e + x} \right)^{-1} \)
\( = -\ln{\dfrac{e - x}{e + x}} = -f(x) \)
\( f(-x) = -f(x) \) olduğu için \( f \) tek fonksiyondur.
\( f \) reel sayılarda tanımlı bir fonksiyondur.
\( g(x) = \dfrac{1}{4}f(x) + \dfrac{1}{4}f(-x) \)
\( h(x) = \dfrac{1}{4}f(x) - \dfrac{1}{4}f(-x) \)
olduğuna göre, \( g(x) \) ve \( h(x) \) fonksiyonlarının tek/çift olma durumlarını inceleyin.
Çözümü Göster\( g(-x) \) fonksiyonunu bulalım.
\( g(-x) = \dfrac{1}{4}f(-x) + \dfrac{1}{4}f(-(-x)) \)
\( = \dfrac{1}{4}f(-x) + \dfrac{1}{4}f(x) = g(x) \)
\( g(-x) = g(x) \) olduğu için \( g \) çift fonksiyondur.
\( h(-x) \) fonksiyonunu bulalım.
\( h(-x) = \dfrac{1}{4}f(-x) - \dfrac{1}{4}f(-(-x)) \)
\( = \dfrac{1}{4}f(-x) - \dfrac{1}{4}f(x) = -h(x) \)
\( h(-x) = -h(x) \) olduğu için \( h \) tek fonksiyondur.
\( f(x) = \sqrt{2x^2 - x + 7} - \sqrt{2x^2 + x + 7} \) fonksiyonunun tek/çift fonksiyon olma durumunu inceleyin.
Çözümü Göster\( f(-x) \) fonksiyonunu bulalım.
\( f(-x) = \sqrt{2(-x)^2 - (-x) + 7} - \sqrt{2(-x)^2 + (-x) + 7} \)
\( = \sqrt{2x^2 + x + 7} - \sqrt{2x^2 - x + 7} \)
\( = -(\sqrt{2x^2 - x + 7} - \sqrt{2x^2 + x + 7}) \)
\( = -f(x) \)
\( f(-x) = -f(x) \) olduğu için \( f \) tek fonksiyondur.
\( f(x) = x^{11} - ax^5 + bx - 2 \) fonksiyonu veriliyor.
\( f(8) = 21 \) olduğuna göre, \( f(-8) \) kaçtır?
Çözümü Göster\( f \) fonksiyonunun sabit terim dışındaki terimlerinin derecesi tektir.
Bu sabit terimi içermeyen aşağıdaki şekilde bir \( g \) fonksiyonu tanımlayalım.
\( g(x) = f(x) + 2 = x^{11} - ax^5 + bx \)
\( g \) fonksiyonu sadece tek dereceli terimlerden oluştuğu için tek fonksiyondur.
\( g(8) = f(8) + 2 = 21 + 2 = 23 \)
\( g \) tek fonksiyon olduğu için \( g(-8) = -g(8) = -23 \) olur.
\( g(-8) = f(-8) + 2 = -23 \)
\( f(-8) = -25 \) bulunur.
Aşağıdaki fonksiyonlardan hangileri çift fonksiyondur?
I. \( f(x) = \sin{x} + \tan{x} \)
II. \( g(x) = \cot^2(-x) + \sec{x} \)
III. \( h(x) = \sin^3{x} + \cos^2(-x) \)
IV. \( k(x) = \cos^3{x} + \csc^4{x} + 3 \)
Çözümü GösterTrigonometrik fonksiyonlardan kosinüs ve sekant çift fonksiyon, diğerleri tek fonksiyondur.
Herhangi bir \( f(x) \) fonksiyonu için, \( f(-x) \) fonksiyonu \( f(x) \) fonksiyonunun \( y \) eksenine göre simetriğidir ve tek/çift olma/olmama durumu \( f(x) \) fonksiyonu ile aynıdır.
Öncülleri sırayla inceleyelim.
I. öncül:
\( f(x) = \sin{x} + \tan{x} \)
Sinüs ve tanjant fonksiyonları tek fonksiyonlardır.
İki tek fonksiyonun toplamı tek fonksiyondur.
II. öncül:
\( g(x) = \cot^2(-x) + \sec{x} \)
Kotanjant fonksiyonu tek fonksiyondur, iki tek fonksiyonun çarpımı çift fonksiyon olduğu için karesi çift fonksiyondur.
Sekant fonksiyonu çift fonksiyondur.
İki çift fonksiyonun toplamı çift fonksiyondur.
III. öncül:
\( h(x) = \sin^3{x} + \cos^2(-x) \)
Sinüs fonksiyonu tek fonksiyondur, tek fonksiyonun üçüncü kuvveti de tek fonksiyondur.
Kosinüs fonksiyonu çift fonksiyondur, iki çift fonksiyonun çarpımı çift fonksiyon olduğu için karesi de çift fonksiyondur.
Bir tek fonksiyon ile çift fonksiyonun toplamı ne tek ne de çift fonksiyondur.
IV. öncül:
\( k(x) = \cos^3{x} + \csc^4{x} + 3 \)
Kosinüs fonksiyonu çift fonksiyondur, çift fonksiyonun üçüncü kuvveti de çift fonksiyondur.
Kosekant fonksiyonu tek fonksiyondur, tek fonksiyonun dördüncü kuvveti çift fonksiyondur.
Sabit terim çift fonksiyondur.
Çift fonksiyonların toplamı çift fonksiyondur.
Buna göre II. ve IV. öncüllerdeki fonksiyonlar çift fonksiyondur.
\( f(x) \) sabit ve periyodik olmayan bir çift fonksiyondur.
Buna göre, aşağıdakilerden hangileri çift fonksiyondur?
I. \( 2f(x) \)
II. \( -f(x) \)
III. \( f(x) + 2 \)
IV. \( f(2x) \)
V. \( f(-x) \)
VI. \( f(x + 2) \)
VII. \( f^2(x) \)
Çözümü GösterÇift fonksiyonlar \( y \) eksenine göre simetriktir.
I. öncül:
\( 2f(x) \) fonksiyonunda tüm noktaların \( x \) eksenine uzaklığı \( \times 2 \) olur. Bu dönüşüm sonucunda \( y \) eksenine göre simetrik noktaların fonksiyon değerleri yine eşit olur ve grafiğin \( y \) eksenine göre simetrisi bozulmaz.
I. öncül çift fonksiyondur.
II. öncül:
\( -f(x) \) fonksiyonu \( f(x) \) fonksiyonunun \( x \) eksenine göre simetriğidir. Bu dönüşüm sonucunda grafiğin \( y \) eksenine göre simetrisi bozulmaz.
II. öncül çift fonksiyondur.
III. öncül:
\( f(x) + 2 \) fonksiyonunda tüm noktalar 2 birim yukarı ötelenir. Bu dönüşüm sonucunda grafiğin \( y \) eksenine göre simetrisi bozulmaz.
III. öncül çift fonksiyondur.
IV. öncül:
\( f(2x) \) fonksiyonunda tüm noktaların \( y \) eksenine uzaklığı \( \times \frac{1}{2} \) olur. Bu dönüşüm sonucunda grafiğin \( y \) eksenine göre simetrisi bozulmaz.
IV. öncül çift fonksiyondur.
V. öncül:
\( f(-x) \) fonksiyonu \( f(x) \) fonksiyonunun \( y \) eksenine göre simetriğidir. Bu dönüşüm sonucunda grafiğin \( y \) eksenine göre simetrisi bozulmaz.
V. öncül çift fonksiyondur.
VI. öncül:
\( f(x + 2) \) fonksiyonunda tüm noktalar 2 birim sola ötelenir. Bu dönüşüm sonucunda grafiğin \( y \) eksenine göre simetrisi bozulur.
VI. öncül çift fonksiyon değildir.
VII. öncül:
\( f^2(x) \) fonksiyonunda tüm \( y \) değerlerinin karesi alınır, ancak \( y \) eksenine göre simetrik noktaların fonksiyon değerleri yine eşit olur ve grafiğin \( y \) eksenine göre simetrisi bozulmaz.
VII. öncül çift fonksiyondur.
Buna göre VI. öncül dışındaki öncüller çift fonksiyondur.
\( f \) reel sayılarda tanımlı bir fonksiyondur.
\( f(x) = \ln(\sqrt{x^2 + 1} + x) \) fonksiyonunun tek/çift olma durumunu inceleyin.
Çözümü Göster\( f(-x) \) fonksiyonunu bulalım.
\( f(-x) = \ln(\sqrt{(-x)^2 + 1} + (-x)) \)
\( = \ln(\sqrt{x^2 + 1} - x) \)
Logaritma içindeki ifadeyi eşleniği ile çarpıp bölelim.
\( = \ln{\dfrac{(\sqrt{x^2 + 1} - x)(\sqrt{x^2 + 1} + x)}{\sqrt{x^2 + 1} + x}} \)
\( = \ln{\dfrac{(\sqrt{x^2 + 1})^2 - x^2}{\sqrt{x^2 + 1} + x}} \)
\( = \ln{\dfrac{x^2 + 1 - x^2}{\sqrt{x^2 + 1} + x}} \)
\( = \ln{\dfrac{1}{\sqrt{x^2 + 1} + x}} \)
\( = \ln(\sqrt{x^2 + 1} + x)^{-1} \)
\( = -\ln(\sqrt{x^2 + 1} + x) = -f(x) \)
\( f(-x) = -f(x) \) olduğu için \( f \) tek fonksiyondur.
\( f \) reel sayılarda tanımlı bir fonksiyondur.
\( f(x) = \dfrac{e^{\sin{x}} + 1}{e^{\sin{x}} - 1} \) fonksiyonunun tek/çift olma durumunu inceleyin.
Çözümü Göster\( f(-x) \) fonksiyonunu bulalım.
\( f(-x) = \dfrac{e^{\sin(-x)} + 1}{e^{\sin(-x)} - 1} \)
\( \sin(-x) = -\sin{x} \)
\( = \dfrac{e^{-\sin{x}} + 1}{e^{-\sin{x}} - 1} \)
Payı ve paydayı \( e^{\sin{x}} \) ile genişletelim.
\( = \dfrac{(e^{-\sin{x}} + 1)\ e^{\sin{x}}}{(e^{-\sin{x}} - 1)\ e^{\sin{x}}} \)
\( = \dfrac{e^{-\sin{x}}\ e^{\sin{x}} + e^{\sin{x}}}{e^{-\sin{x}}\ e^{\sin{x}} - e^{\sin{x}}} \)
\( = \dfrac{e^{-\sin{x} + \sin{x}} + e^{\sin{x}}}{e^{-\sin{x} + \sin{x}} - e^{\sin{x}}} \)
\( = \dfrac{e^0 + e^{\sin{x}}}{e^0 - e^{\sin{x}}} = \dfrac{1 + e^{\sin{x}}}{1 - e^{\sin{x}}} \)
\( = -\dfrac{e^{\sin{x}} + 1}{e^{\sin{x}} - 1} = -f(x)\)
\( f(-x) = -f(x) \) olduğu için \( f \) tek fonksiyondur.
\( a, b \in \mathbb{R} \) olmak üzere,
\( f(x) = 9x^4 + ax^2 + b \) fonksiyonunun \( r \lt s \lt t \) olmak üzere üç farklı reel kökü vardır.
Buna göre \( r + s + t \) toplamı kaçtır?
Çözümü Göster\( f \) polinom fonksiyonu \( x \)'in sadece çift kuvvetlerini içerdiği için bir çift fonksiyondur.
\( f \) çift fonksiyon olduğuna göre, her \( x \) için \( f(x) = f(-x) \) eşitliği sağlanır, bir diğer ifadeyle fonksiyon grafiği \( y \) eksenine göre simetriktir.
Buna göre \( x = a \) fonksiyonunun bir kökü ise \( x = -a \) da kökü olur.
4. dereceden reel katsayılı bir polinom fonksiyonunun 3 farklı reel kökü varsa karmaşık kökü olamaz (karmaşık kökler birbirinin eşleniği şeklinde ikili olarak bulunurlar).
Buna göre üç farklı kökten biri çift katlı kök olmak zorundadır.
Hem fonksiyonun üç farklı kökü olabilmesi hem de köklerin \( f(x) = f(-x) \) eşitliğini sağlaması için, iki kök birbirinin ters işaretlisi, çift katlı üçüncü kök de sıfır olmalıdır.
Örnek: \( x \in \{ -5, 0, 5 \} \)
Buna göre \( r + s + t \) toplamı sıfır olur.