Öteleme
Öteleme, bir fonksiyonun grafiğinin belirli bir yönde yer değiştirmesi demektir. Ötelemede fonksiyonun grafiğinin şekli değişmez, sadece analitik düzlemdeki konumu değişir.
Dikey Öteleme
\( k \in \mathbb{R}, \quad k \gt 0 \) olmak üzere,
\( f(x) \longmapsto f(x) + k \)
\( f(x) \longmapsto f(x) - k \)
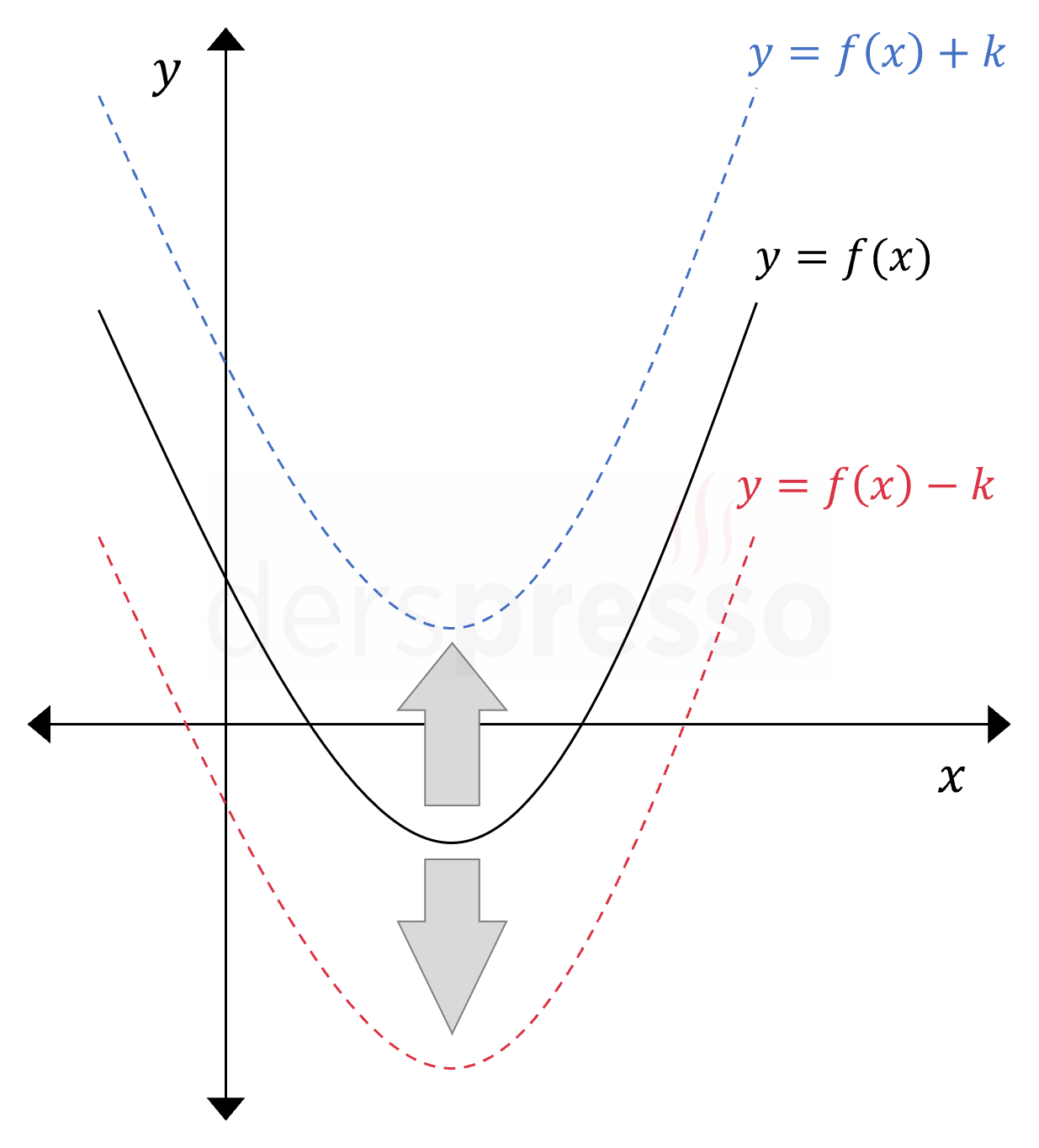
Bir fonksiyonun çıktısına \( k \) birim eklendiğinde grafik \( k \) birim yukarı ötelenir. Bunun sebebi, fonksiyonun bu değişiklik sonucunda aynı \( x \) değeri için daha büyük bir \( y \) değeri üretmesidir.
Bir fonksiyonun çıktısından \( k \) birim çıkarıldığında grafik \( k \) birim aşağı ötelenir. Bunun sebebi, fonksiyonun bu değişiklik sonucunda aynı \( x \) değeri için daha küçük bir \( y \) değeri üretmesidir.
Yatay Öteleme
\( c \in \mathbb{R}, \quad c \gt 0 \) olmak üzere,
\( f(x) \longmapsto f(x + c) \)
\( f(x) \longmapsto f(x - c) \)
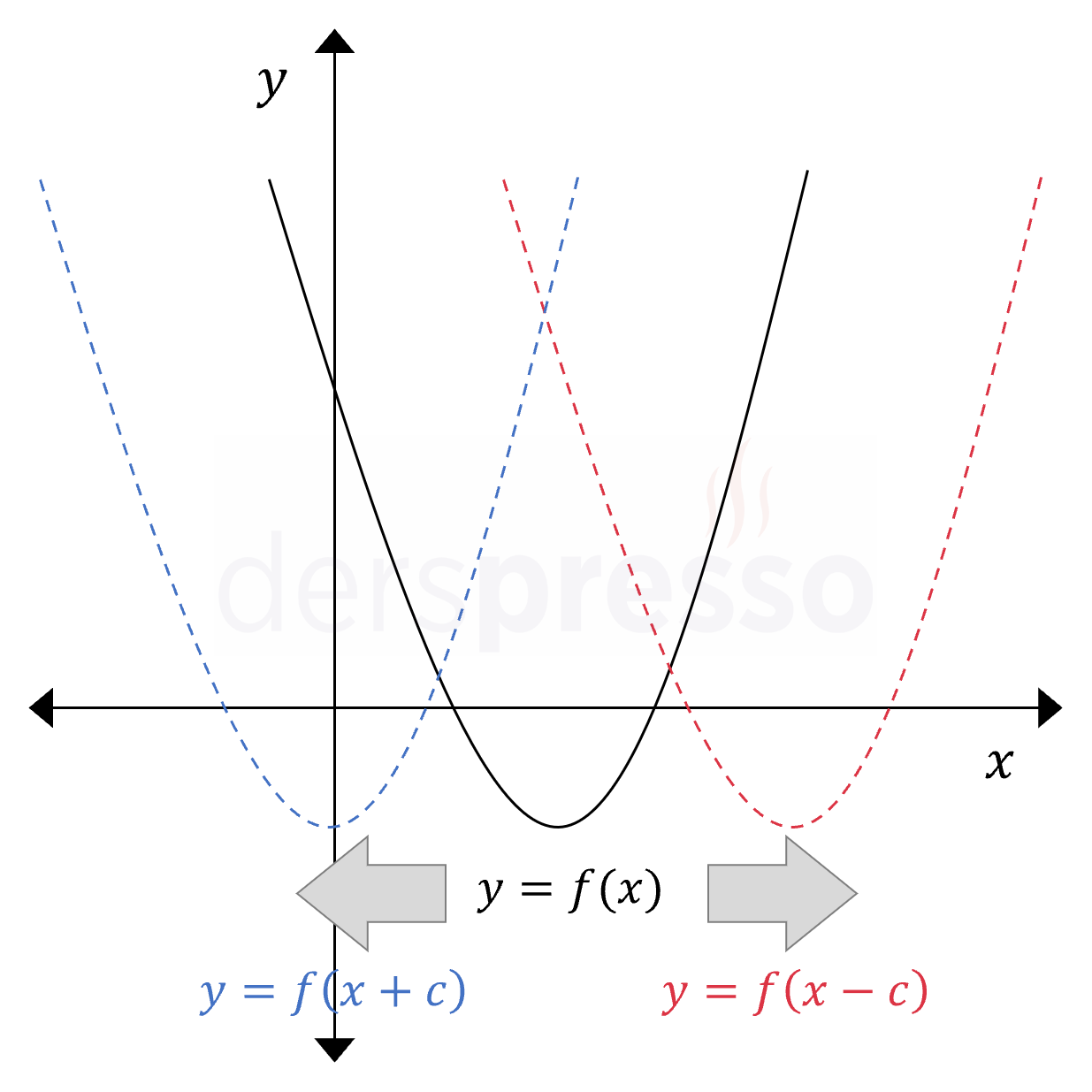
Bir fonksiyonun girdisine \( c \) birim eklendiğinde grafik \( c \) birim sola ötelenir. Bunun sebebi, fonksiyonun bu değişiklik sonucunda aynı \( y \) değerini daha küçük bir \( x \) değeri ile üretmesidir.
Bir fonksiyonun girdisinden \( c \) birim çıkarıldığında grafik \( c \) birim sağa ötelenir. Bunun sebebi, fonksiyonun bu değişiklik sonucunda aynı \( y \) değerini daha büyük bir \( x \) değeri ile üretmesidir.
Aşağıda verilen fonksiyonlara 2. sütunda uygulanan dikey dönüşüm fonksiyonun grafiğini 2 birim yukarı, 3. sütunda uygulanan yatay dönüşüm de 2 birim sola öteler.
| Fonksiyon | Dikey Dönüşüm | Yatay Dönüşüm |
|---|---|---|
| \( f(x) = 2x \) | \( f(x) + 2 = 2x + 2 \) | \( f(x + 2) = 2(x + 2) \) |
| \( f(x) = x^2 \) | \( f(x) + 2 = x^2 + 2 \) | \( f(x + 2) = (x + 2)^2 \) |
| \( f(x) = \sqrt{x} \) | \( f(x) + 2 = \sqrt{x} + 2 \) | \( f(x + 2) = \sqrt{x + 2} \) |
| \( f(x) = \sin{x} \) | \( f(x) + 2 = \sin(x) + 2 \) | \( f(x + 2) = \sin(x + 2) \) |
| \( f(x) = 2^x \) | \( f(x) + 2 = 2^x + 2 \) | \( f(x + 2) = 2^{x + 2} \) |
| \( f(x) = \log{x} \) | \( f(x) + 2 = \log(x) + 2 \) | \( f(x + 2) = \log(x + 2) \) |
| \( f(x) = \abs{x} \) | \( f(x) + 2 = \abs{x} + 2 \) | \( f(x + 2) = \abs{x + 2} \) |
\( f(x) = (x - 1)^2 \) fonksiyonu \( a \) birim sağa \( b \) birim yukarı ötelendiğinde \( g(x) = (x - 4)^2 + 2 \) fonksiyonu elde edildiğine göre, \( a + b \) kaçtır?
Çözümü GösterBir fonksiyonun grafiği \( a \) birim sağa ötelendiğinde \( g(x) = f(x - a) \), \( b \) birim yukarı ötelendiğinde \( g(x) = f(x) + b \) fonksiyonu elde edilir.
Verilen denklemleri karşılaştırdığımızda grafiğin \( a = 3 \) birim sağa ve \( b = 2 \) birim yukarı ötelendiğini görürüz.
\( g(x) = (x - 1 - a)^2 + b \)
\( = (x - 4)^2 + 2 \)
Buna göre \( a + b = 5 \) olarak bulunur.
\( f(x) = \dfrac{1}{2x + 6} - 4 \) fonksiyonuna hangi ötelemeler yapılırsa \( g(x) = \dfrac{1}{2x} \) fonksiyonu elde edilir?
Çözümü GösterFonksiyona \( f(x) \longmapsto f(x) + 4 \) dönüşümü uygulandığında grafiği 4 birim yukarı ötelenir.
\( \dfrac{1}{2x + 6} - 4 \longmapsto \dfrac{1}{2x + 6} \)
Fonksiyona \( f(x) + 4 \longmapsto f(x - 3) + 4 \) dönüşümü uygulandığında grafiği 3 birim sağa ötelenir.
\( \dfrac{1}{2x + 6} \longmapsto \dfrac{1}{2(x - 3) + 6} = \dfrac{1}{2x} \)
\( g(x) = \dfrac{1}{2x} = f(x - 3) + 4 \)
Buna göre istenen fonksiyonu elde etmek için fonksiyon 4 birim yukarı ve 3 birim sağa ötelenmelidir.
\( f(x) = 9x^2 + 15x - b \) parabolü \( a \) birim sola ötelendiğinde \( g(x) = 9x^2 - 21x + 22 \) parabolü elde ediliyor.
Buna göre \( \frac{b}{a} \) kaçtır?
Çözümü GösterFonksiyon grafiğini \( a \) birim sola ötelemek için fonksiyonun girdisine \( a \) eklenir.
\( f(x) \longmapsto f(x + a) \)
\( f(x + a) = 9(x + a)^2 + 15(x + a) - b \)
\( = 9x^2 + 18ax + 9a^2 + 15x + 15a - b \)
\( = 9x^2 + (18a + 15)x + 9a^2 + 15a - b \)
Bu fonksiyon \( g(x) \) fonksiyonuna eşittir.
İki fonksiyonu eşitleyelim.
\( 9x^2 + (18a + 15)x + 9a^2 + 15a - b = 9x^2 - 21x + 22 \)
İki polinomun eşitliğinde aynı dereceli terimlerin katsayıları birbirine eşittir.
\( x \)'li terimlerin katsayılarını birbirine eşitleyelim.
\( 18a + 15 = -21 \)
\( a = -2 \)
Sabit terimleri birbirine eşitleyelim.
\( 9a^2 + 15a - b = 22 \)
\( 9(-2)^2 + 15(-2) - b = 22 \)
\( b = -16 \)
\( \dfrac{b}{a} = \dfrac{-16}{-2} = 8 \) bulunur.
\( f(x) = x^2 - 5x + 1 \) fonksiyonunun grafiği 3 birim sağa ve 5 birim yukarı ötelendiğinde elde edilen grafiğin \( x \) eksenini kestiği noktaların apsisleri toplamı kaçtır?
Çözümü GösterFonksiyon 3 birim sağa ötelendiğinde aşağıdaki fonksiyon elde edilir.
\( f(x - 3) = (x - 3)^2 - 5(x - 3) + 1 \)
Fonksiyon 5 birim yukarı ötelendiğinde aşağıdaki fonksiyon elde edilir.
\( f(x - 3) + 5 = (x - 3)^2 - 5(x - 3) + 1 + 5 \)
\( = x^2 - 6x + 9 - 5x + 15 + 6 \)
\( = x^2 - 11x + 30 \)
Bu fonksiyonun \( x \) eksenini kestiği noktaları bulmak için fonksiyonu sıfıra eşitleyelim.
\( x^2 - 11x + 30 = 0 \)
\( (x - 5)(x - 6) = 0 \)
Buna göre fonksiyon \( x \) eksenini \( x = 5 \) ve \( x = 6 \) apsis değerli noktalarda keser.
\( 5 + 6 = 11 \) olarak bulunur.
\( f(x) = 3x^2 + 12x + 9 \) fonksiyonunun grafiği \( a \) birim yukarı ve 4 birim sağa ötelenerek \( g(x) \) fonksiyonu elde ediliyor.
\( A(-2, 57) \) noktası \( g(x) \) üzerinde olduğuna göre, \( a \) değeri kaçtır?
Çözümü Göster\( f \) fonksiyonunu çarpanlarına ayıralım.
\( f(x) = 3(x + 1)(x + 3) \)
Fonksiyonun grafiğini \( a \) birim yukarı ötelemek için fonksiyonun çıktısına \( a \) eklenir.
\( f(x) \longmapsto f(x) + a \)
\( f(x) + a = 3(x + 1)(x + 3) + a \)
Fonksiyonun grafiğini 4 birim sağa ötelemek için \( x \) yerine \( x - 4 \) yazılır.
\( f(x) + a \longmapsto f(x - 4) + a \)
\( f(x - 4) + a = 3((x - 4) + 1)((x - 4) + 3) + a \)
\( = 3(x - 3)(x - 1) + a \)
Bu fonksiyon \( g(x) \) fonksiyonuna eşittir.
\( g(x) = 3(x - 3)(x - 1) + a \)
\( A(-2, 57) \) noktası \( g(x) \) üzerinde olduğuna göre, koordinatları fonksiyon tanımını sağlar.
\( g(-2) = 57 \)
\( 3(-2 - 3)(-2 - 1) + a = 57 \)
\( a = 12 \) bulunur.
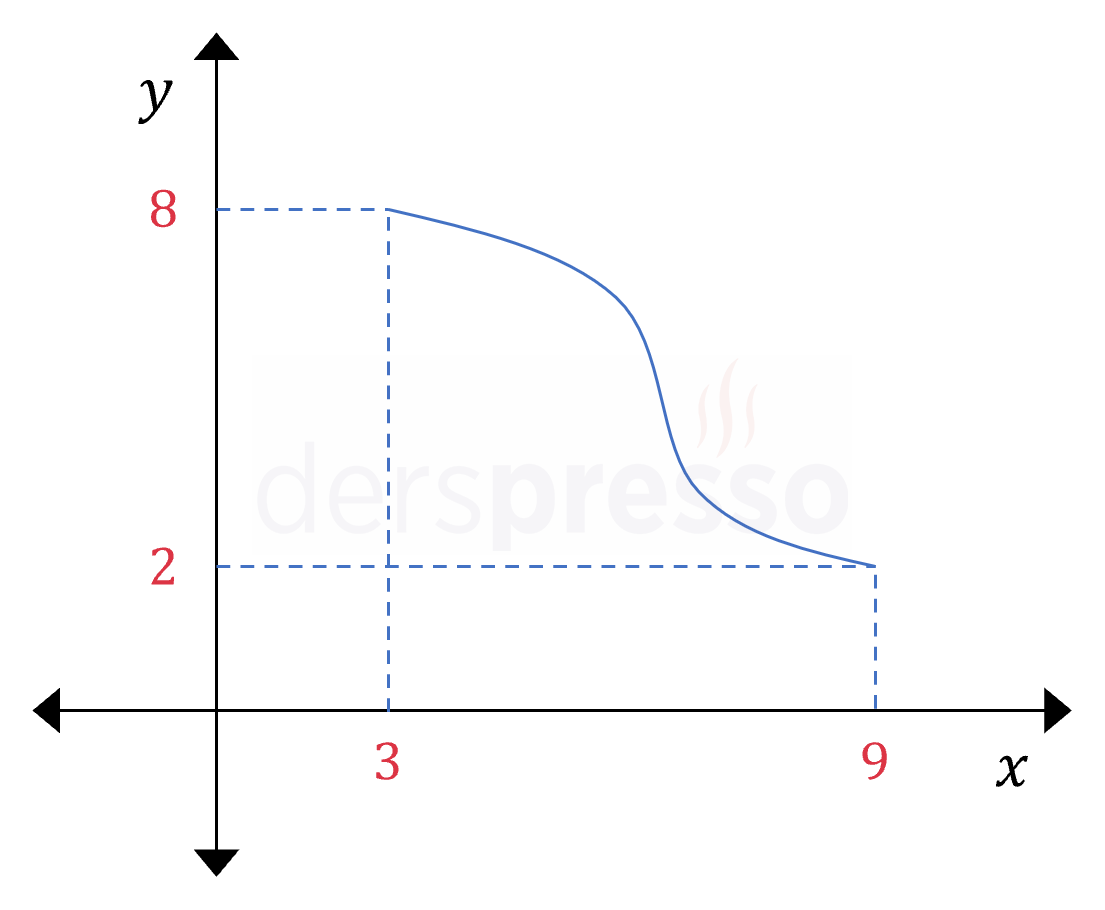
Yukarıda \( y = f(x) \) fonksiyonunun grafiği verilmiştir.
Buna göre \( g(x) = f(x - 2) + f(x + 2) \) fonksiyonunun en geniş tanım kümesi nedir?
Çözümü GösterGrafiği verilen fonksiyonun tanım kümesi \( [3, 9] \) aralığıdır.
\( f(x - 2) \) fonksiyonu \( f(x) \) fonksiyonunun 2 birim sağa ötelenmiş halidir, dolayısıyla tanım kümesi \( [5, 11] \) aralığıdır.
\( f(x + 2) \) fonksiyonu \( f(x) \) fonksiyonunun 2 birim sola ötelenmiş halidir, dolayısıyla tanım kümesi \( [1, 7] \) aralığıdır.
İki fonksiyonun toplamından oluşan fonksiyonun tanım kümesi, iki fonksiyonda da ortak olan \( x \) değerlerinin oluşturduğu kesişim kümesidir.
Buna göre \( g(x) \) fonksiyonunun tanım kümesi \( [1, 7] \cap [5, 11] = [5, 7] \) aralığıdır.
\( a, b \in \mathbb{Z^+} \) olmak üzere,
Orijinden geçen \( f(x) = (x - a)^2 - b \) parabolüne dönüşümler uygulanarak aşağıdaki dört parabol çiziliyor.
- \( f(x + 2a) + 3b \)
- \( f(x + 2a) - b \)
- \( f(x - a) - b \)
- \( f(x - a) + 3b \)
Bu parabollerin tepe noktalarını köşe kabul eden dikdörtgenin alanı 324 olduğuna göre, \( a \) kaçtır?
Çözümü GösterDenklemi \( f(x) = (x - a)^2 - b \) şeklinde verilen bir parabolün tepe noktası \( T(a, -b) \) olur.
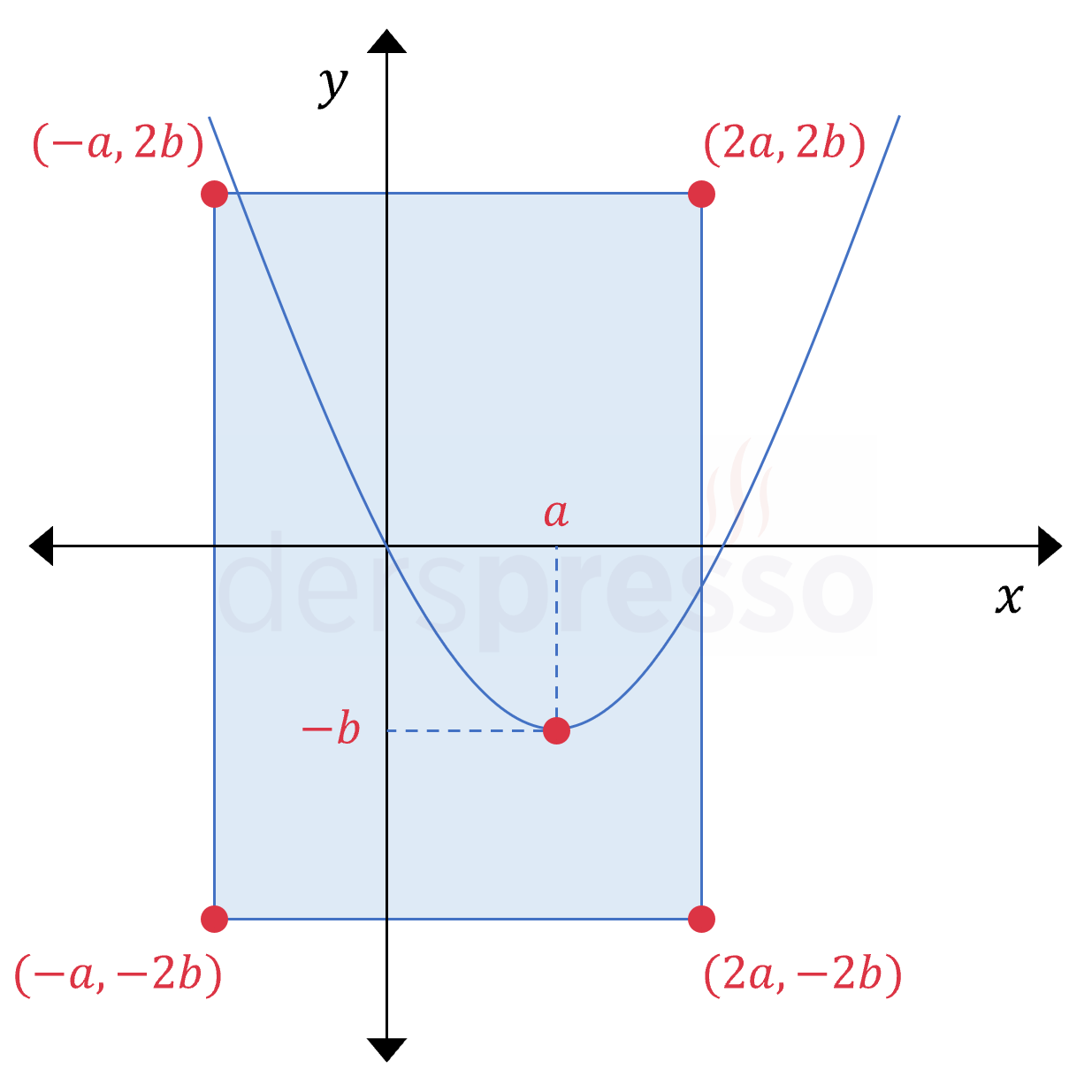
Buna göre \( f(x) \) parabolünün grafiği aşağıdaki gibi olur.
Soruda verilen dikey ve yatay öteleme dönüşümleri fonksiyonun tüm noktalarına aynı şekilde uygulanır.
Buna göre fonksiyona \( f(x) + 3b \) dönüşümü uygulandığında tepe noktası \( 3b \) birim yukarı, \( f(x) - b \) dönüşümü uygulandığında \( b \) birim aşağı ötelenir.
Benzer şekilde fonksiyona \( f(x + 2a) \) dönüşümü uygulandığında tepe noktası \( 2a \) birim sola, \( f(x - a) \) dönüşümü uygulandığında \( a \) birim sağa ötelenir.
Parabolün tepe noktasına bu dönüşümleri uyguladığımızda yukarıdaki şekildeki dikdörtgenin köşe noktalarını elde ederiz. Bu noktalar dönüşümler sonucunda elde edilen parabollerin tepe noktalarıdır.
Bu dikdörtgenin genişliği \( 3a \) birim, yüksekliği \( 4b \) birimdir.
Dikdörtgenin alanı 324 olarak verilmiştir.
\( 3a \cdot 4b = 324 \)
\( a \cdot b = 27 \)
\( f \) parabolü orijinden geçtiği için \( (0, 0) \) noktası parabol denklemini sağlar.
\( f(0) = (0 - a)^2 - b = 0 \)
\( a^2 = b \)
\( b \) değerini bulduğumuz eşitlikte yerine koyalım.
\( a \cdot b = a \cdot a^2 = 27 \)
Buna göre \( a = 3 \) bulunur.