Daralma/Genişleme
Daralma/genişleme, bir fonksiyonun grafiğindeki tüm noktaların \( x \) ya da \( y \) eksenine belirli bir oranda yaklaşması ya da eksenlerden bu oranda uzaklaşması anlamına gelir.
Dikey Daralma/Genişleme
\( a \in \mathbb{R}, \quad a \gt 0 \) olmak üzere,
\( f(x) \longmapsto a \cdot f(x) \)
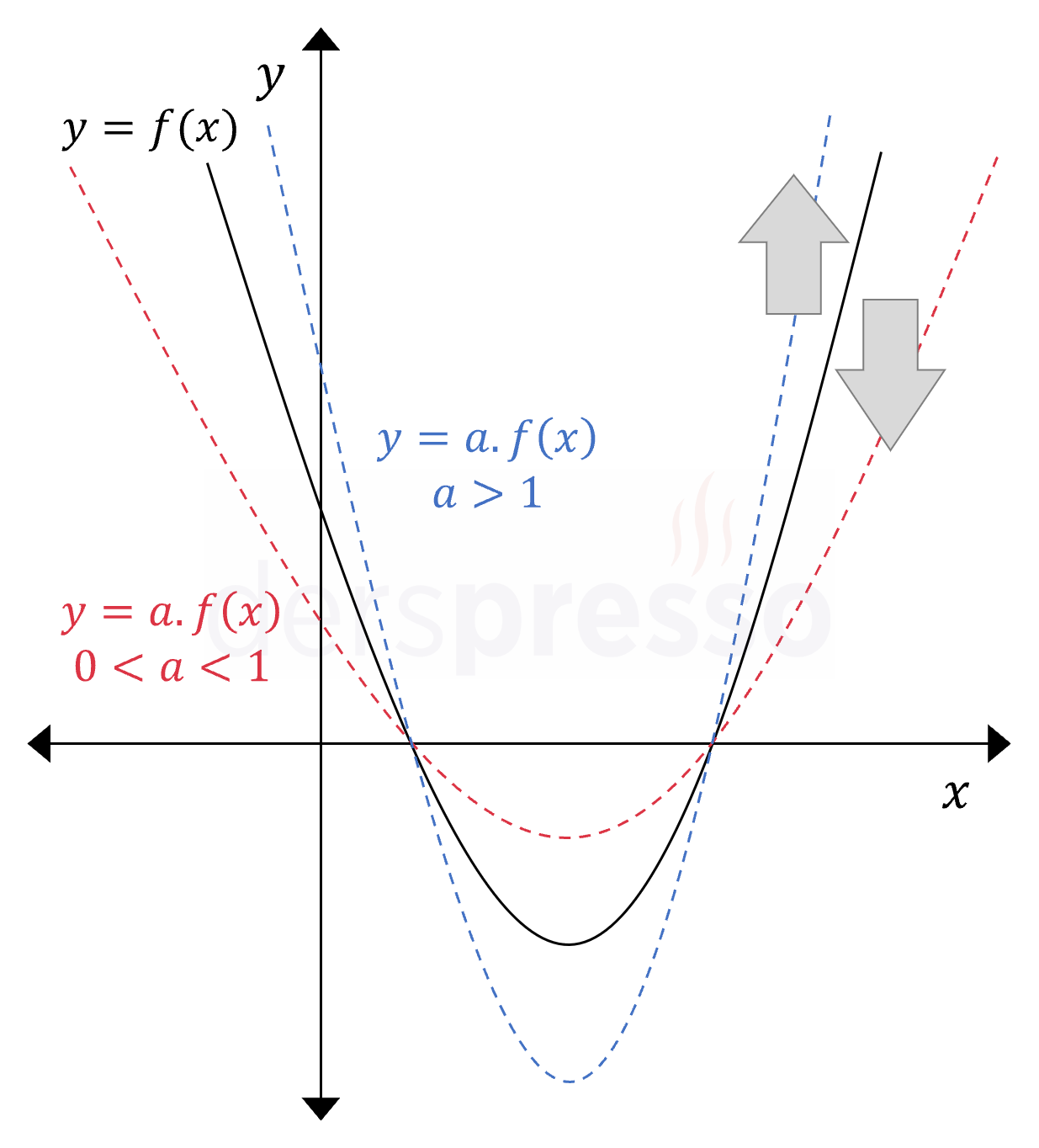
\( a \gt 1 \) olmak üzere, fonksiyonun çıktısı \( a \) ile çarpıldığında grafiğin üzerindeki tüm noktalar \( x \) ekseninden \( a \) kat uzaklaşır. Bunun sebebi, fonksiyonun bu değişiklik sonucunda aynı \( x \) değeri için mutlak değerce daha büyük \( y \) değeri üretmesidir. Örnek olarak \( a = 2 \) ise ordinatı 6 olan bir noktanın ordinatı 12 olur.
\( 0 \lt a \lt 1 \) olmak üzere, fonksiyonun çıktısı \( a \) ile çarpıldığında grafiğin üzerindeki tüm noktalar \( x \) eksenine \( a \) kat yakınlaşır. Bunun sebebi, fonksiyonun bu değişiklik sonucunda aynı \( x \) değeri için mutlak değerce daha küçük \( y \) değeri üretmesidir. Örnek olarak \( a = \frac{1}{2} \) ise ordinatı 6 olan bir noktanın ordinatı 3 olur.
Çıktı değeri olarak \( y = 0 \)'ın sabit bir sayı ile çarpımı yine sıfır olduğu için, bu dönüşümde grafiğin \( x \) eksenini kestiği nokta(lar) değişmez.
Fonksiyonun çıktısı negatif bir \( a \) değeri ile çarpılırsa fonksiyona \( a \)'nın mutlak değeri için yukarıda bahsettiğimiz dikey daralma/genişleme dönüşümü uygulanır. Buna ek olarak katsayının negatif işareti için fonksiyona bir sonraki bölümde bahsedeceğimiz yansıma dönüşümü uygulanır.
Yatay Daralma/Genişleme
\( b \in \mathbb{R}, \quad b \gt 0 \) olmak üzere,
\( f(x) \longmapsto f(bx) \)
\( b \gt 1 \) olmak üzere, fonksiyonun girdisi \( b \) ile çarpıldığında grafiğin üzerindeki tüm noktalar \( y \) eksenine \( \frac{1}{b} \) kat yakınlaşır. Bunun sebebi, fonksiyonun bu değişiklik sonucunda aynı \( y \) değerini mutlak değerce daha küçük bir \( x \) değeri ile üretmesidir. Örnek olarak \( b = 2 \) ise apsisi 6 olan bir nokta aynı fonksiyon değerini 3 apsis değeri ile üretir.
\( 0 \lt b \lt 1 \) olmak üzere, fonksiyonun girdisi \( b \) ile çarpıldığında grafiğin tüm noktaları \( y \) ekseninden \( \frac{1}{b} \) kat uzaklaşır. Bunun sebebi, fonksiyonun bu değişiklik sonucunda aynı \( y \) değerini mutlak değerce daha büyük bir \( x \) değeri ile üretmesidir. Örnek olarak \( b = \frac{1}{2} \) ise apsisi 6 olan bir nokta aynı fonksiyon değerini 12 apsis değeri ile üretir.
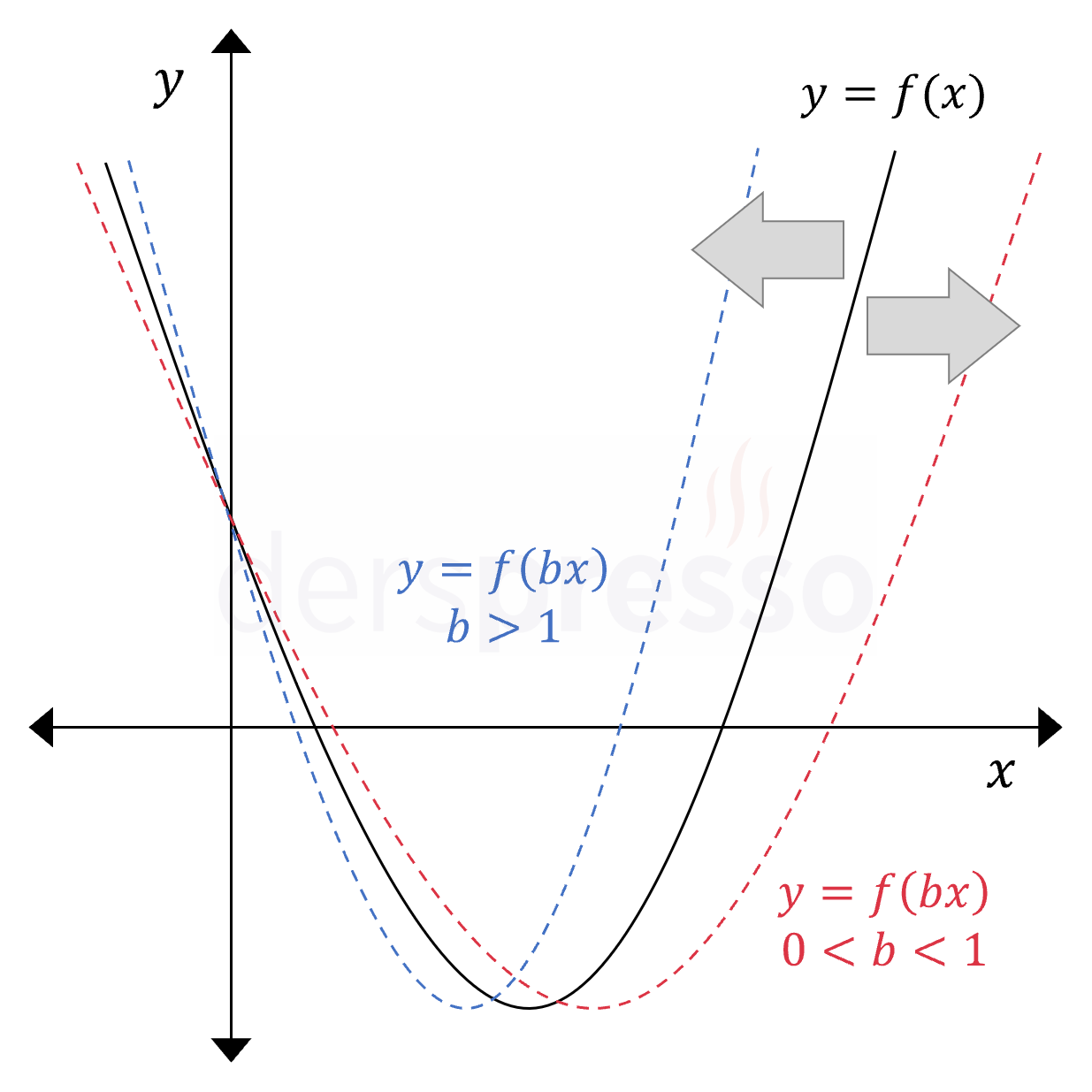
Girdi değeri olarak \( x = 0 \)'ın sabit bir sayı ile çarpımı yine sıfır olduğu için, bu dönüşümde grafiğin \( y \) eksenini kestiği nokta değişmez.
Fonksiyonun girdisi negatif bir \( b \) değeri ile çarpılırsa fonksiyona \( b \)'nin mutlak değeri için yukarıda bahsettiğimiz yatay daralma/genişleme dönüşümü uygulanır. Buna ek olarak katsayının negatif işareti için fonksiyona bir sonraki bölümde bahsedeceğimiz yansıma dönüşümü uygulanır.
Aşağıda verilen fonksiyonlara 2. sütunda uygulanan dikey dönüşüm sonucunda fonksiyon grafiği üzerindeki tüm noktalar \( x \) ekseninden 2 kat uzaklaşır, 3. sütunda uygulanan yatay dönüşüm sonucunda da \( y \) eksenine \( \frac{1}{2} \) kat yakınlaşır.
| Fonksiyon | Dikey Dönüşüm | Yatay Dönüşüm |
|---|---|---|
| \( f(x) = x + 1 \) | \( 2f(x) = 2(x + 1) \) | \( f(2x) = 2x + 1 \) |
| \( f(x) = x^2 \) | \( 2f(x) = 2x^2 \) | \( f(2x) = (2x)^2 \) |
| \( f(x) = \sqrt{x} \) | \( 2f(x) = 2\sqrt{x} \) | \( f(2x) = \sqrt{2x} \) |
| \( f(x) = \sin{x} \) | \( 2f(x) = 2\sin{x} \) | \( f(2x) = \sin(2x) \) |
| \( f(x) = 2^x \) | \( 2f(x) = 2 \cdot 2^x \) | \( f(2x) = 2^{2x} \) |
| \( f(x) = \log{x} \) | \( 2f(x) = 2\log{x} \) | \( f(2x) = \log(2x) \) |
| \( f(x) = \abs{x} \) | \( 2f(x) = 2\abs{x} \) | \( f(2x) = \abs{2x} \) |
Bir kağıda önce \( f(x) = x^2 - 2x - 8 \) parabolü, daha sonra \( f(x - 4) \) ve \( f(-2x) \) parabolleri çiziliyor.
Son çizilen iki parabolün \( x \) eksenini kestiği noktalar arasındaki en büyük uzaklık kaç birimdir?
Çözümü GösterFonksiyonu çarpanlarına ayıralım.
\( f(x) = (x + 2)(x - 4) \)
Buna göre \( f \) fonksiyonu \( x \) eksenini \( x = -2 \) ve \( x = 4 \) noktalarında keser.
\( f(x - 4) \) fonksiyonu \( f(x) \) fonksiyonunun 4 birim sağa ötelenmesi ile elde edilir, dolayısıyla fonksiyonun \( x \) eksenini kestiği noktaların apsis değerleri 4 birim artar.
Buna göre \( f(x - 4) \) fonksiyonu \( x \) eksenini \( x = -2 + 4 = 2 \) ve \( x = 4 + 4 = 8 \) noktalarında keser.
\( f(2x) \) fonksiyonu \( f(x) \) fonksiyonu üzerindeki tüm noktaların apsis değerlerinin yarıya inmesi ile elde edilir.
Buna göre \( f(2x) \) fonksiyonu \( x \) eksenini \( x = -1 \) ve \( x = 2 \) noktalarında keser.
\( f(-2x) \) fonksiyonu \( f(2x) \) fonksiyonunun \( y \) eksenine göre simetriğinin alınması ile elde edilir, dolayısıyla fonksiyonun \( x \) eksenini kestiği noktaların apsis değerlerinin ters işaretlileri alınır.
Buna göre \( f(-2x) \) fonksiyonu \( x \) eksenini \( x = -(-1) = 1 \) ve \( x = -2 \) noktalarında keser.
\( f(x - 4) \) fonksiyonunun \( x \) eksenini kestiği \( x = 2 \) ve \( x = 8 \) noktaları ile \( f(-2x) \) fonksiyonunun \( x \) eksenini kestiği \( x = 1 \) ve \( x = -2 \) noktaları arasındaki en büyük uzaklık \( \abs{8 - (-2)} = 10 \) birim olur.
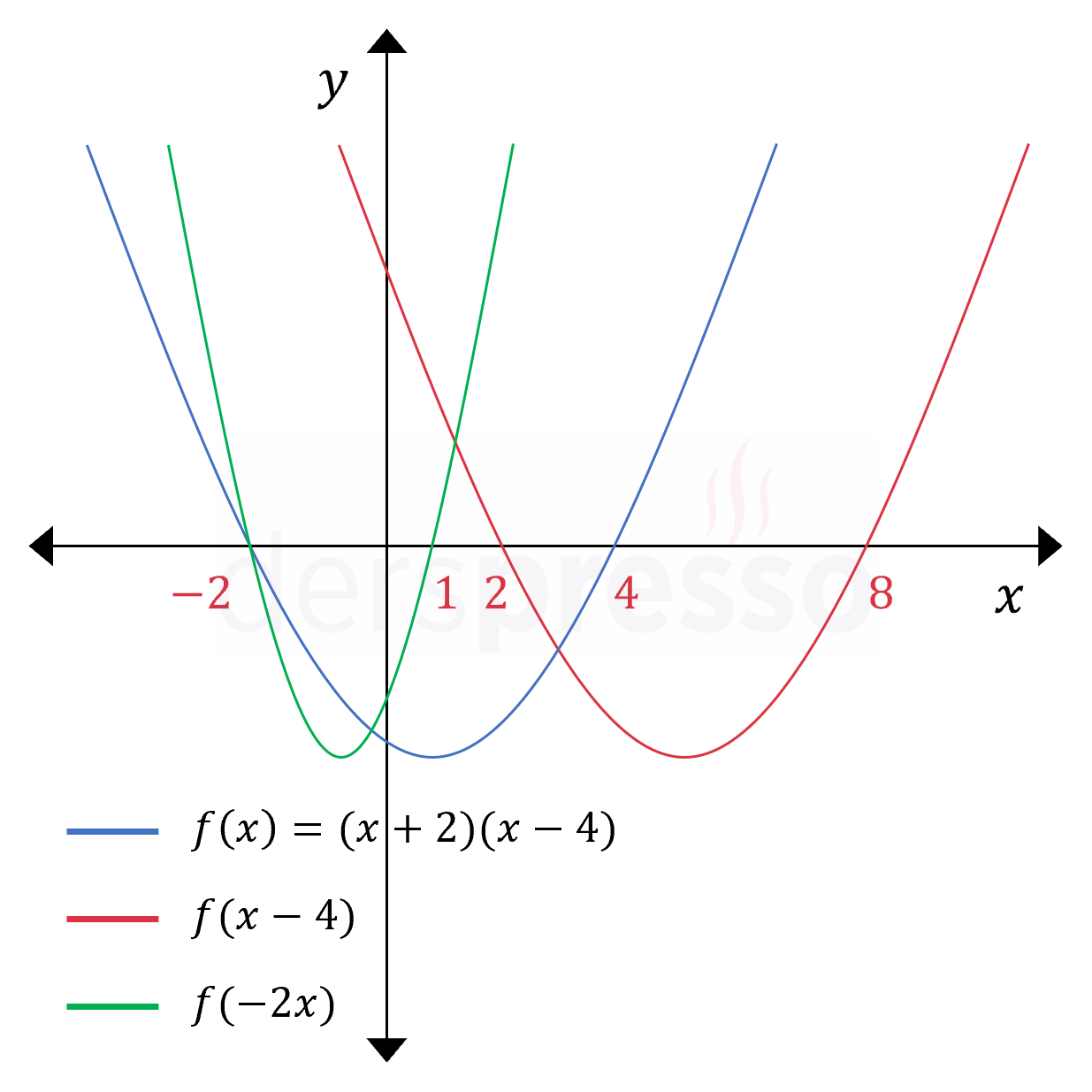
Sorudaki üç fonksiyonun grafikleri aşağıda verilmiştir.
\( y = f(x) \) fonksiyonu üzerindeki \( A(m, -11) \) noktası, \( 2f(x - 5) + 4 \) dönüşümü sonrasında \( B(4, n) \) noktasına öteleniyor.
Buna göre \( \abs{m - n} \) kaçtır?
Çözümü Göster\( f(x - 5) + 4 \) fonksiyonuna ulaşmak için \( f(x) \) fonksiyonuna uygulanan dönüşümleri adım adım uygulayalım.
\( f(x) \) fonksiyonuna \( f(x - 5) \) dönüşümü uygulandığında grafik üzerindeki tüm noktalar 5 birim sağa ötelenir.
\( A(m, -11) \longmapsto A_1(m + 5, -11) \)
\( f(x - 5) \) fonksiyonuna \( 2f(x - 5) \) dönüşümü uygulandığında grafik üzerindeki tüm noktaların ordinat değerleri iki katına çıkar.
\( A_1(m + 5, -11) \longmapsto A_2(m + 5, -22) \)
\( 2f(x - 5) \) fonksiyonuna \( 2f(x - 5) + 4 \) dönüşümü uygulandığında grafik üzerindeki tüm noktalar 4 birim yukarı ötelenir.
\( A_2(m + 5, -22) \longmapsto A_3(m + 5, -18) \)
Tüm bu dönüşümler sonucunda elde ettiğimiz nokta \( B \) noktasıdır.
\( (m + 5, -18) = (4, n) \)
\( m + 5 = 4 \Longrightarrow m = -1 \)
\( n = -18 \)
\( \abs{-1 - (-18)} = 17 \) bulunur.
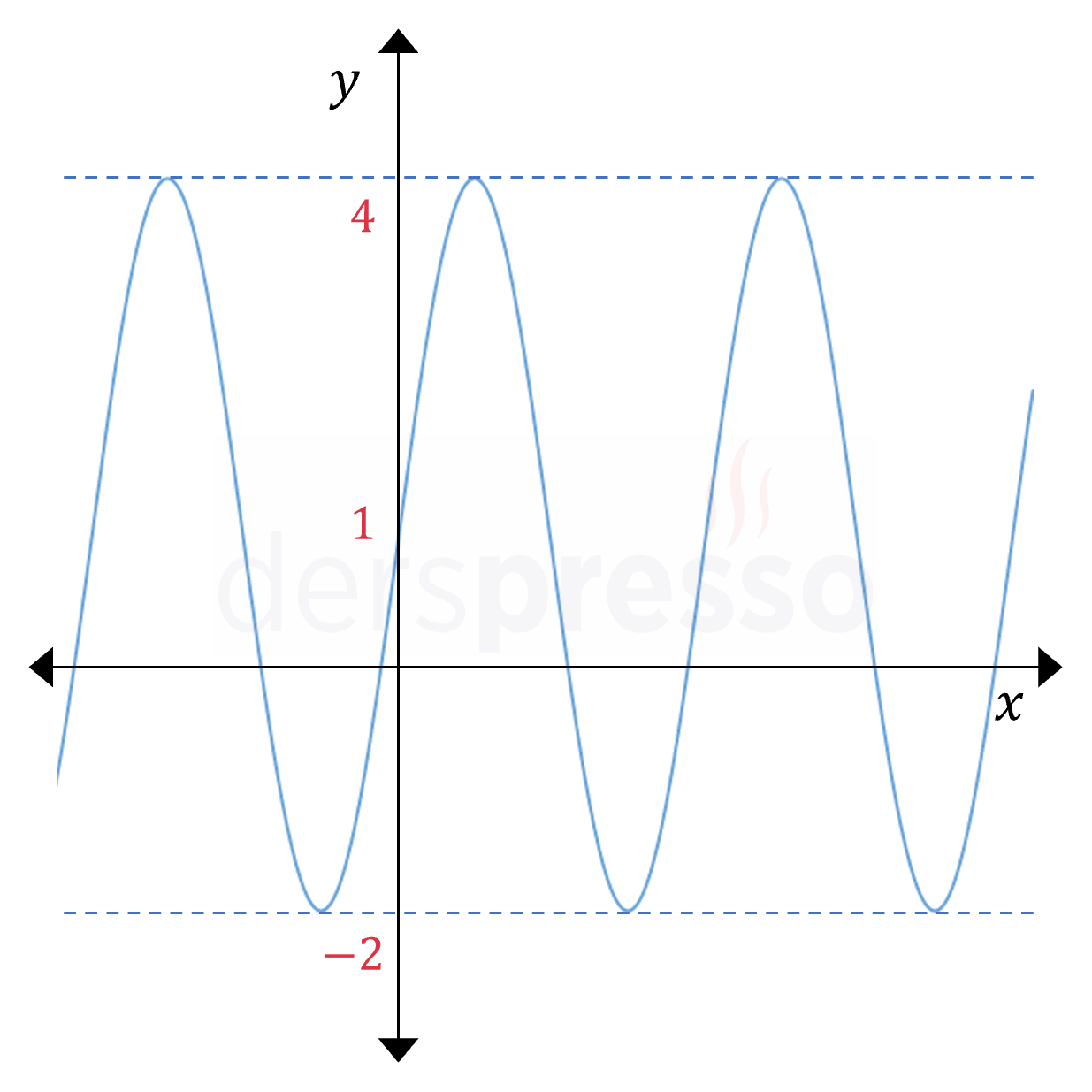
Yukarıda \( f(x) = m\sin{x} + n \) fonksiyonunun grafiği verilmiştir.
Buna göre \( mn \) çarpımı kaçtır?
Çözümü Göster\( \sin{x} \) grafiğine gerekli dönüşümleri uygulayarak \( f \) fonksiyonunu elde etmeye çalışalım.
\( \sin{x} \) fonksiyonunun genliği (fonksiyonun merkez çizgisi ile fonksiyonun en üst veya alt noktası arasındaki mesafe) 1 birimdir. Verilen grafiğin genliği ise \( \frac{4 - (-2)}{2} = 3 \) birimdir.
Fonksiyonun dikey daralmasını ve genişlemesini \( \sin{x} \)'in önündeki katsayı belirler. Bu mesafenin 3 birim olması için fonksiyonun çıktısı 3 ile çarpılmalı, yani fonksiyon \( 3\sin{x} \) şeklinde olmalıdır.
\( 3\sin{x} \) grafiği \( (0, 0) \) noktasından geçer. \( f \) fonksiyonu \( (0, 1) \) noktasından geçtiği için \( 3\sin{x} \) fonksiyonu 1 birim yukarı ötelenmiş olmalıdır.
Buna göre verilen grafik \( f(x) = 3\sin{x} + 1 \) fonksiyonuna ait olmalıdır.
\( mn = 3 \cdot 1 = 3 \) bulunur.