Parabol Grafiği Dönüşümleri
Önceki bölümde bahsettiğimiz dönüşümler bir parabol fonksiyonuna uygulandığında fonksiyon grafiği aşağıdaki şekillerde değişim gösterir.
İnteraktif uygulama: Parabolde Dönüşümler
Dikey Öteleme
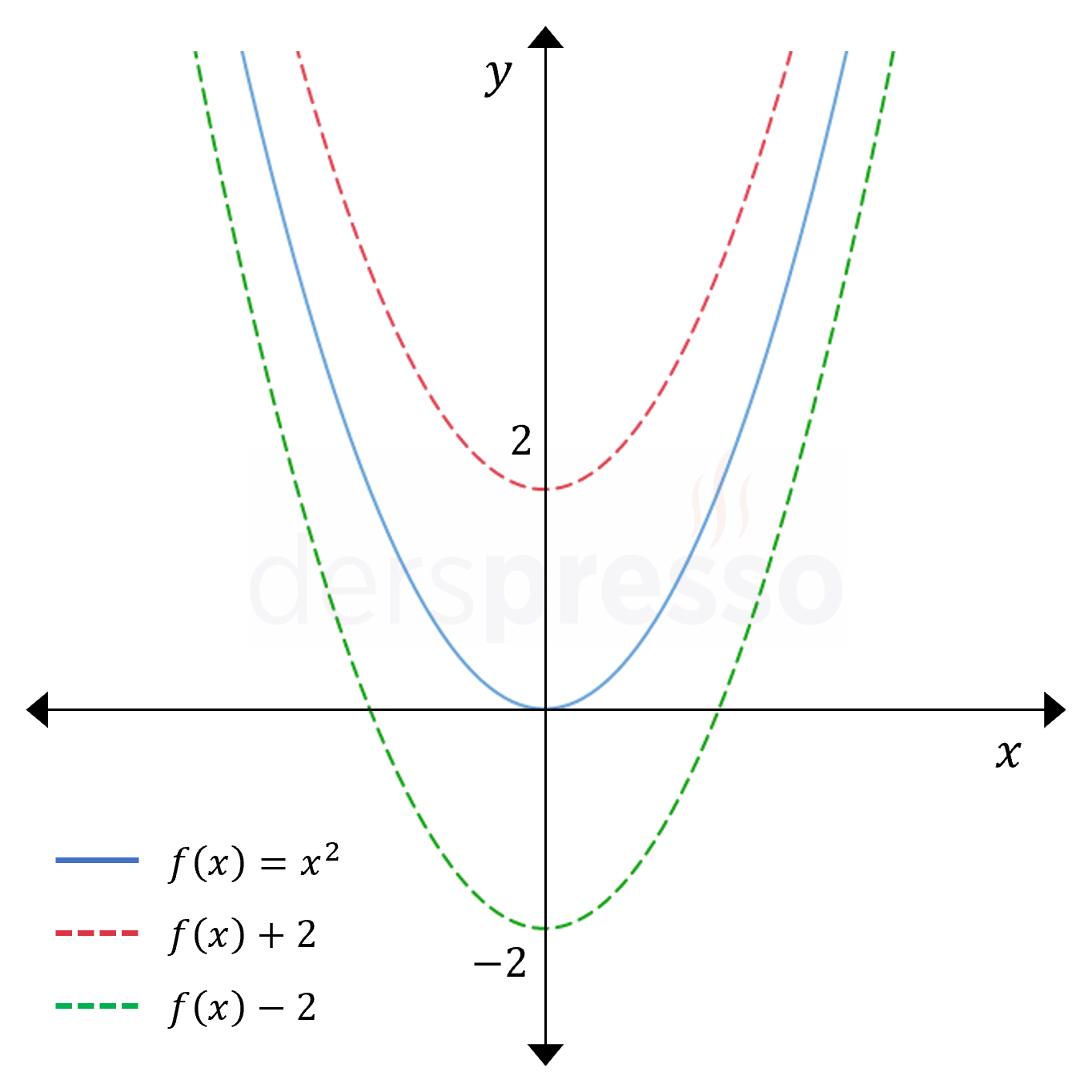
Fonksiyonun çıktısına pozitif sabit bir sayı eklendiğinde, fonksiyon grafiği şeklinde bir değişiklik olmadan \( y \) ekseni boyunca yukarı doğru ötelenir.
Fonksiyonun çıktısından pozitif sabit bir sayı çıkarıldığında, fonksiyon grafiği şeklinde bir değişiklik olmadan \( y \) ekseni boyunca aşağı doğru ötelenir.
Yatay Öteleme
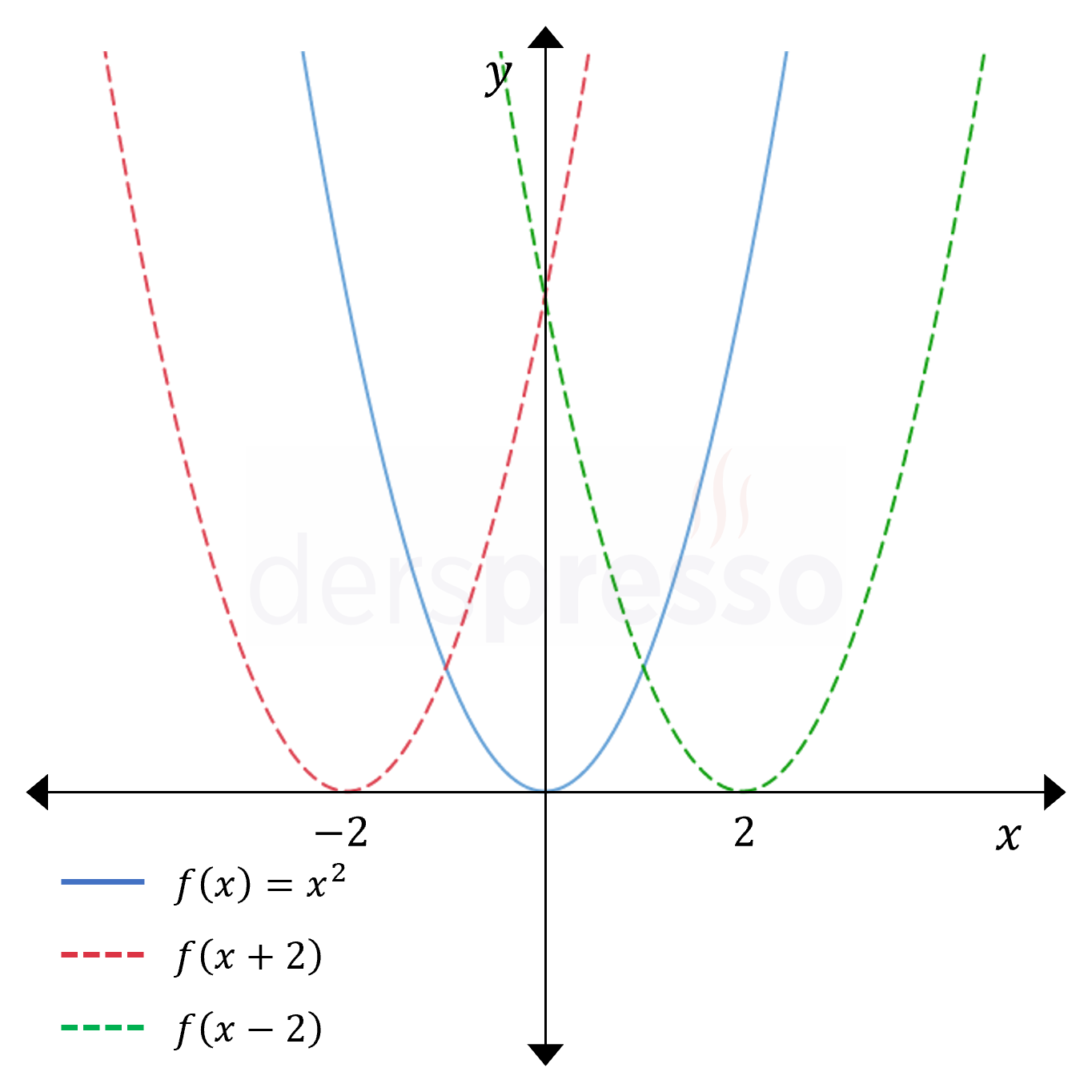
Fonksiyonun girdisine pozitif sabit bir sayı eklendiğinde, fonksiyon grafiği şeklinde bir değişiklik olmadan \( x \) ekseni boyunca sola doğru ötelenir.
Fonksiyonun girdisinden pozitif sabit bir sayı çıkarıldığında, fonksiyon grafiği şeklinde bir değişiklik olmadan \( x \) ekseni boyunca sağa doğru ötelenir.
Dikey Daralma/Genişleme
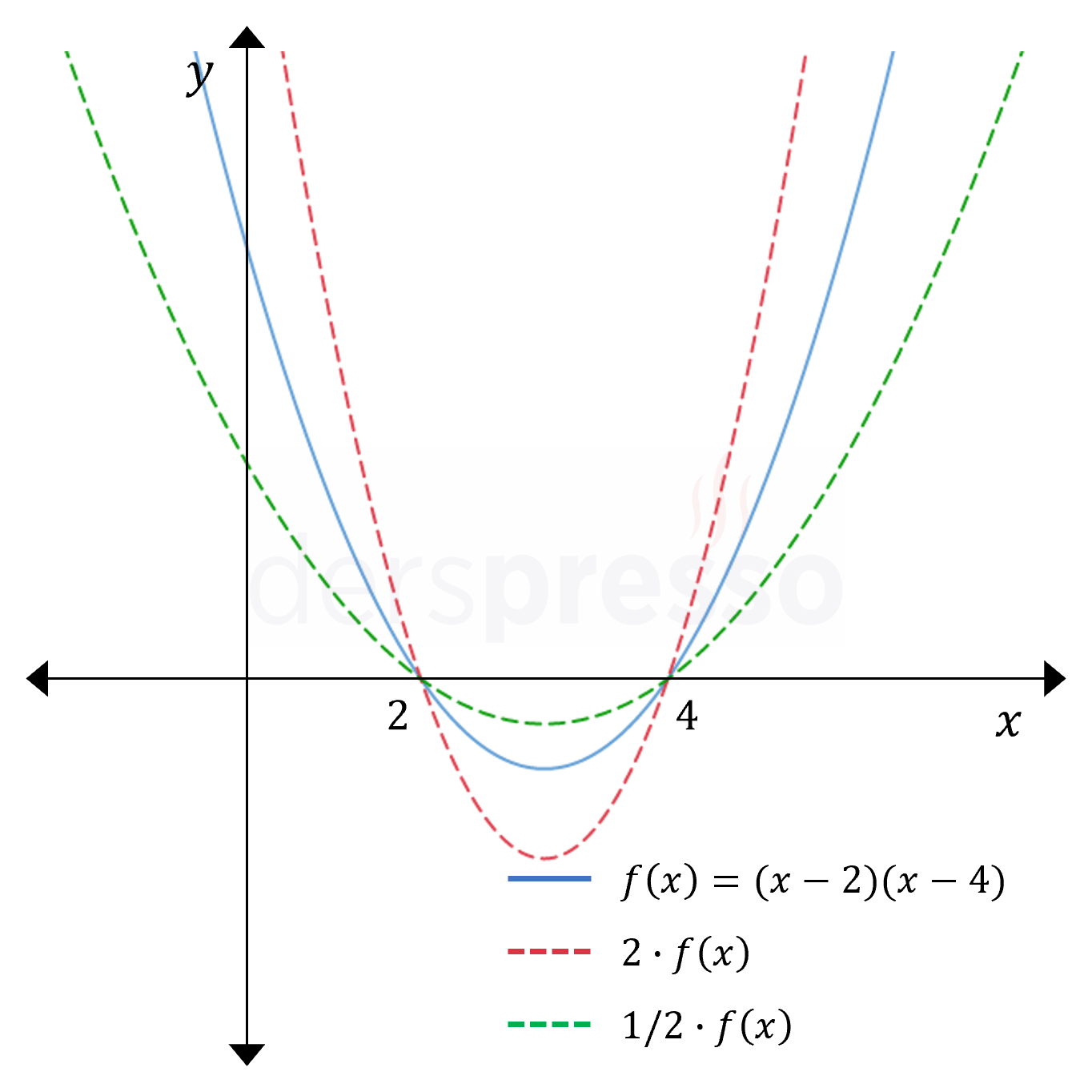
Fonksiyonun çıktısı birden büyük bir sayı ile çarpıldığında (\( a \gt 1 \)), grafiğin üzerindeki tüm noktalar \( x \) ekseninden çarpan oranında uzaklaşır, yani \( y \) değerleri mutlak değerce büyür. Grafiğin \( x \) eksenini kestiği noktalar değişmez.
Fonksiyonun çıktısı sıfır-bir arası bir sayı ile çarpıldığında (\( 0 \lt a \lt 1 \)), grafiğin üzerindeki tüm noktalar \( x \) eksenine çarpan oranında yakınlaşır, yani \( y \) değerleri mutlak değerce küçülür. Grafiğin \( x \) eksenini kestiği noktalar değişmez.
Yatay Daralma/Genişleme
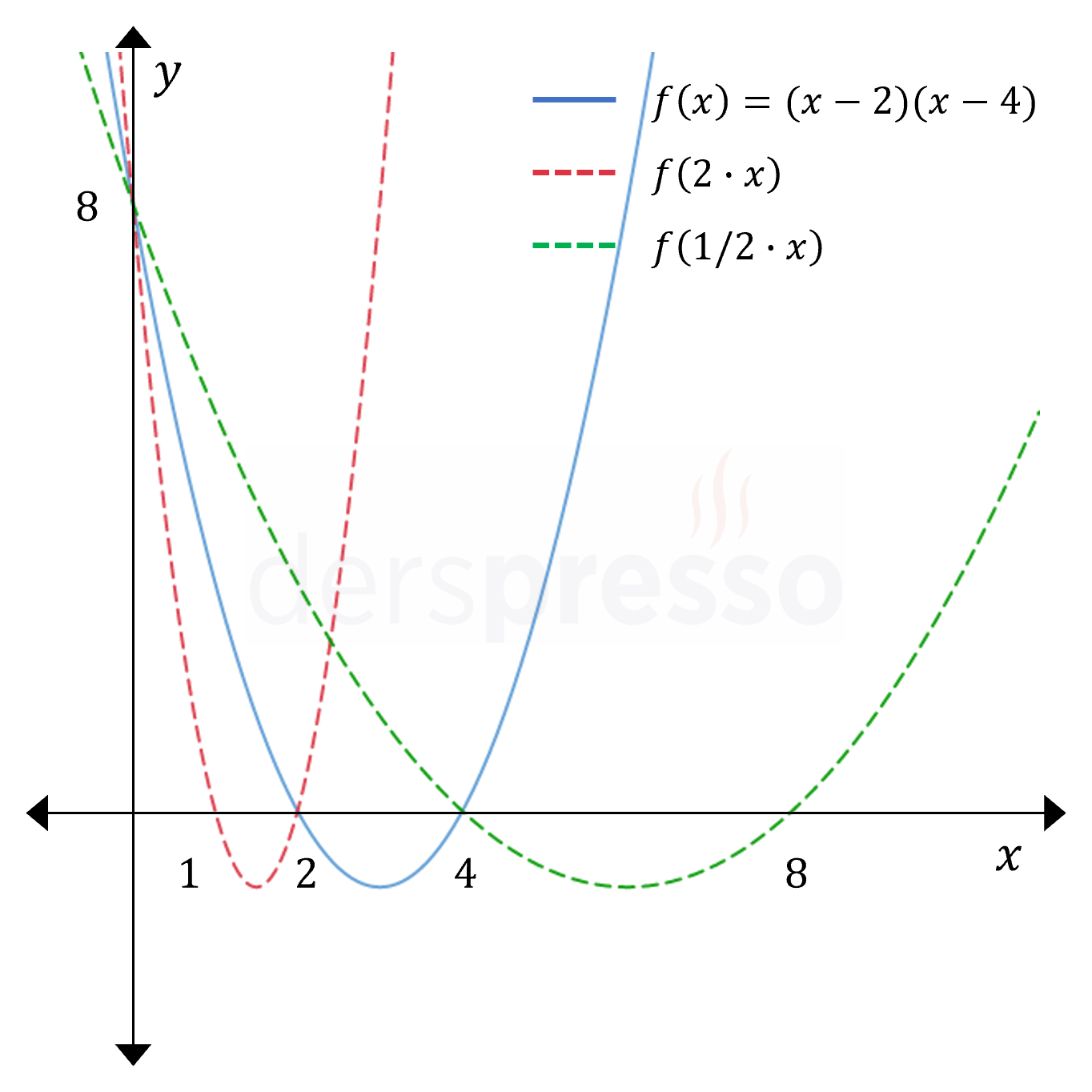
Fonksiyonun girdisi birden büyük bir sayı ile çarpıldığında (\( a \gt 1 \)), grafiğin üzerindeki tüm noktalar \( y \) ekseninine çarpan oranında yakınlaşır, yani \( x \) değerleri mutlak değerce küçülür. Grafiğin \( y \) eksenini kestiği nokta değişmez.
Fonksiyonun girdisi sıfır-bir arası bir sayı ile çarpıldığında (\( 0 \lt a \lt 1 \)), grafiğin üzerindeki tüm noktalar \( y \) eksenininden çarpan oranında uzaklaşır, yani \( x \) değerleri mutlak değerce büyür. Grafiğin \( y \) eksenini kestiği nokta değişmez.
Dikey Yansıma
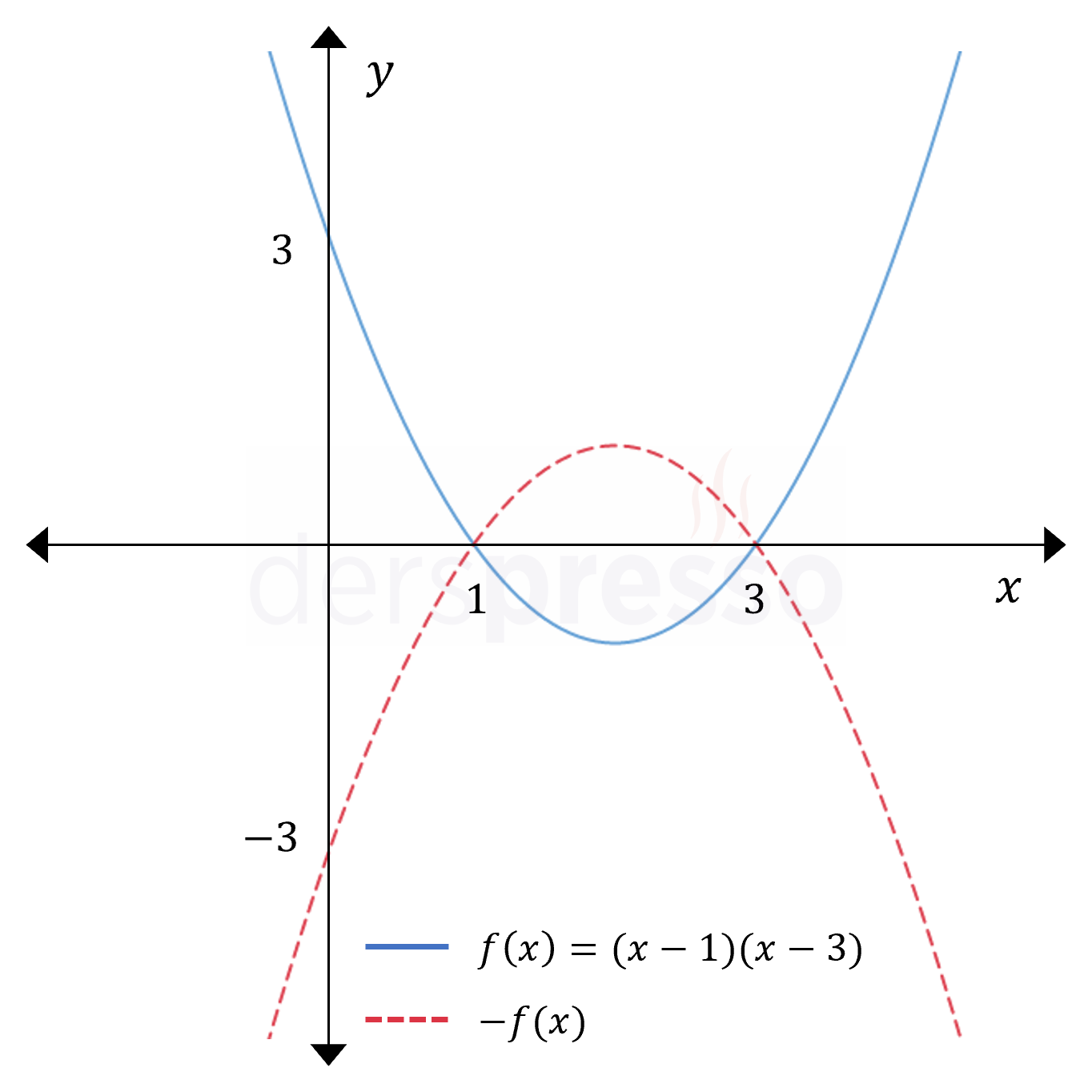
Fonksiyonun çıktısının negatifi alındığında (-1 ile çarpıldığında), tüm \( y \) değerlerinin işareti tersine döner ve grafiğin \( x \) eksenine göre yansıması oluşur. Grafiğin \( x \) eksenini kestiği noktalar değişmez.
Yatay Yansıma
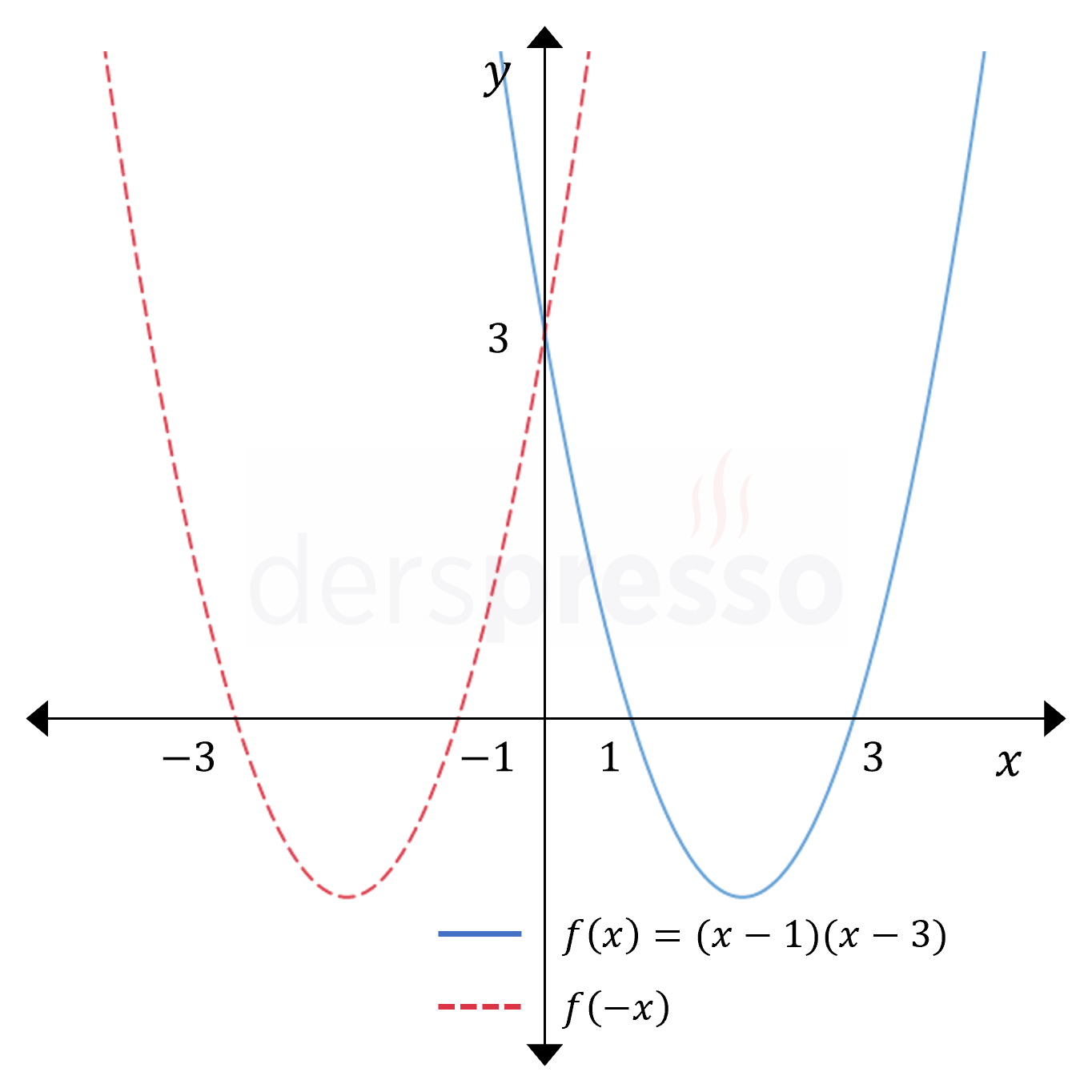
Fonksiyonun girdisinin negatifi alındığında (-1 ile çarpıldığında), fonksiyon bir \( x \) değeri için \( f(-x) \) değerini almaya başlar ve grafiğin \( y \) eksenine göre yansıması oluşur. Grafiğin \( y \) eksenini kestiği nokta değişmez.
Orijine Göre Yansıma
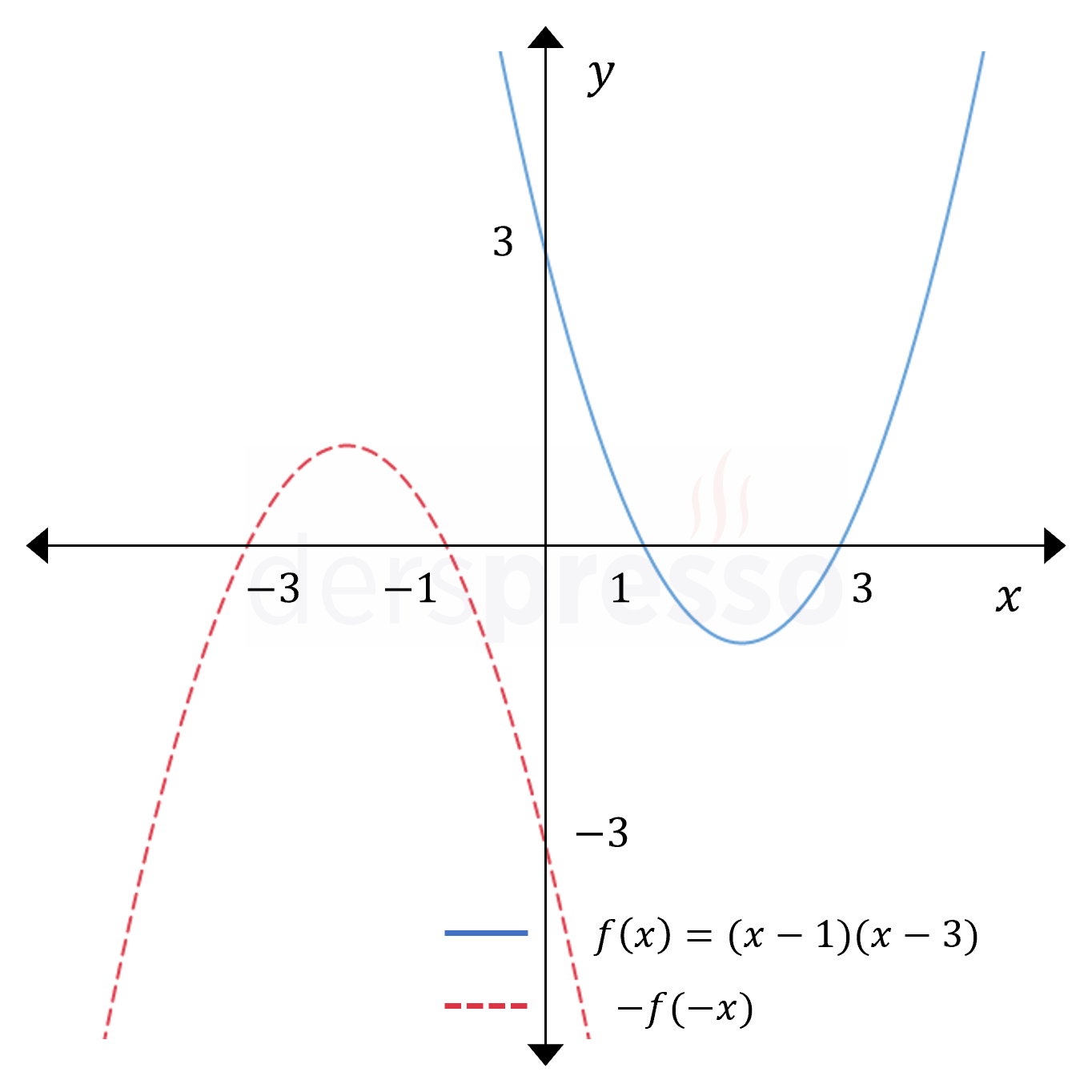
Fonksiyonun hem çıktısının hem de girdisinin negatifi alındığında (-1 ile çarpıldığında), yukarıda bahsettiğimiz dikey ve yatay yansıma dönüşümleri birlikte oluşur ve grafiğin orijine göre yansıması oluşur.
Fonksiyon Çıktısının Mutlak Değeri
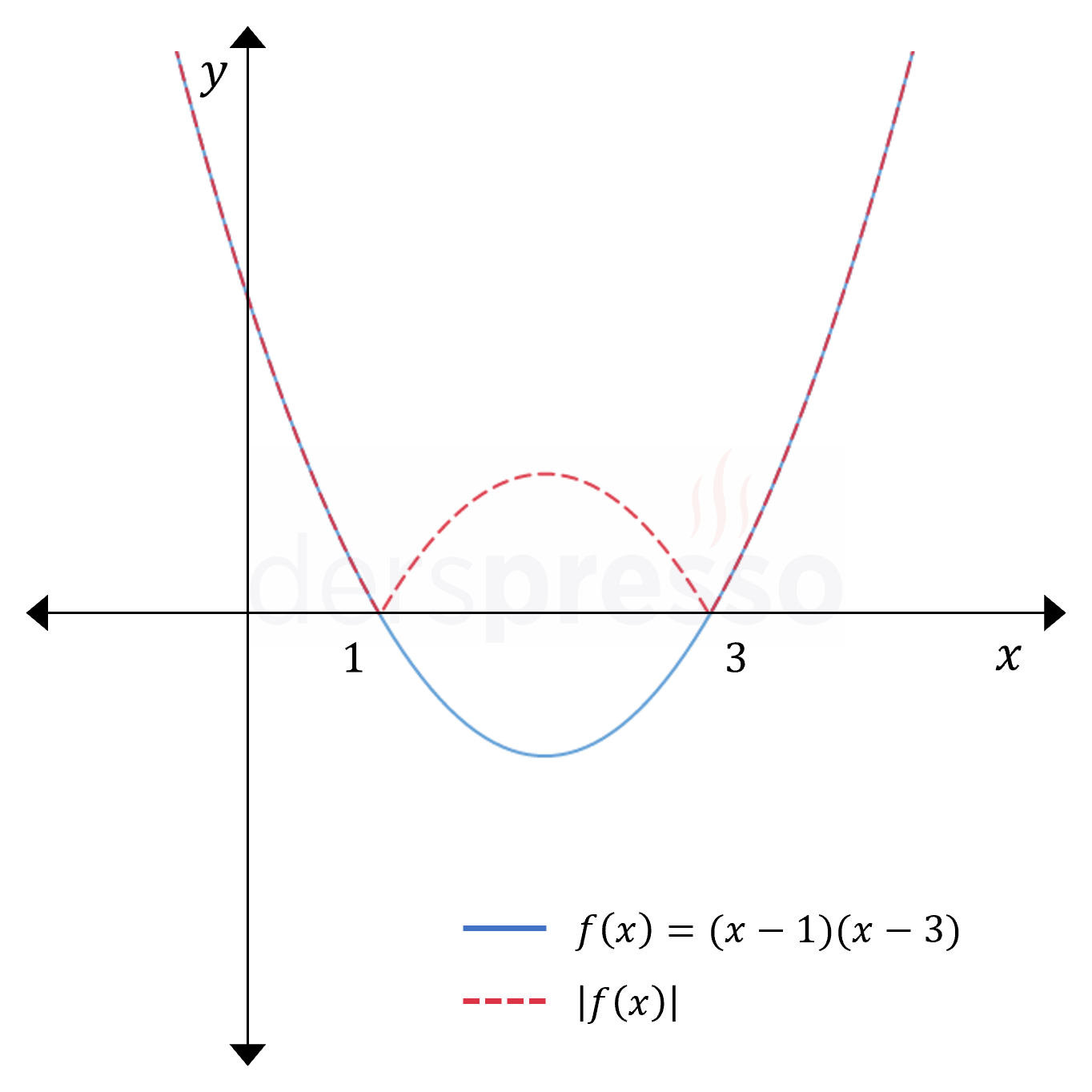
Fonksiyonun çıktısının mutlak değeri alındığında, grafikteki tüm negatif \( y \) değerleri pozitife döner ve grafiğin \( x \) ekseninin altında kalan kısımlarının \( x \) eksenine göre yansıması oluşur. Grafiğin \( x \) ekseninin üstünde kalan kısımlarında değişiklik olmaz.
Fonksiyon Girdisinin Mutlak Değeri
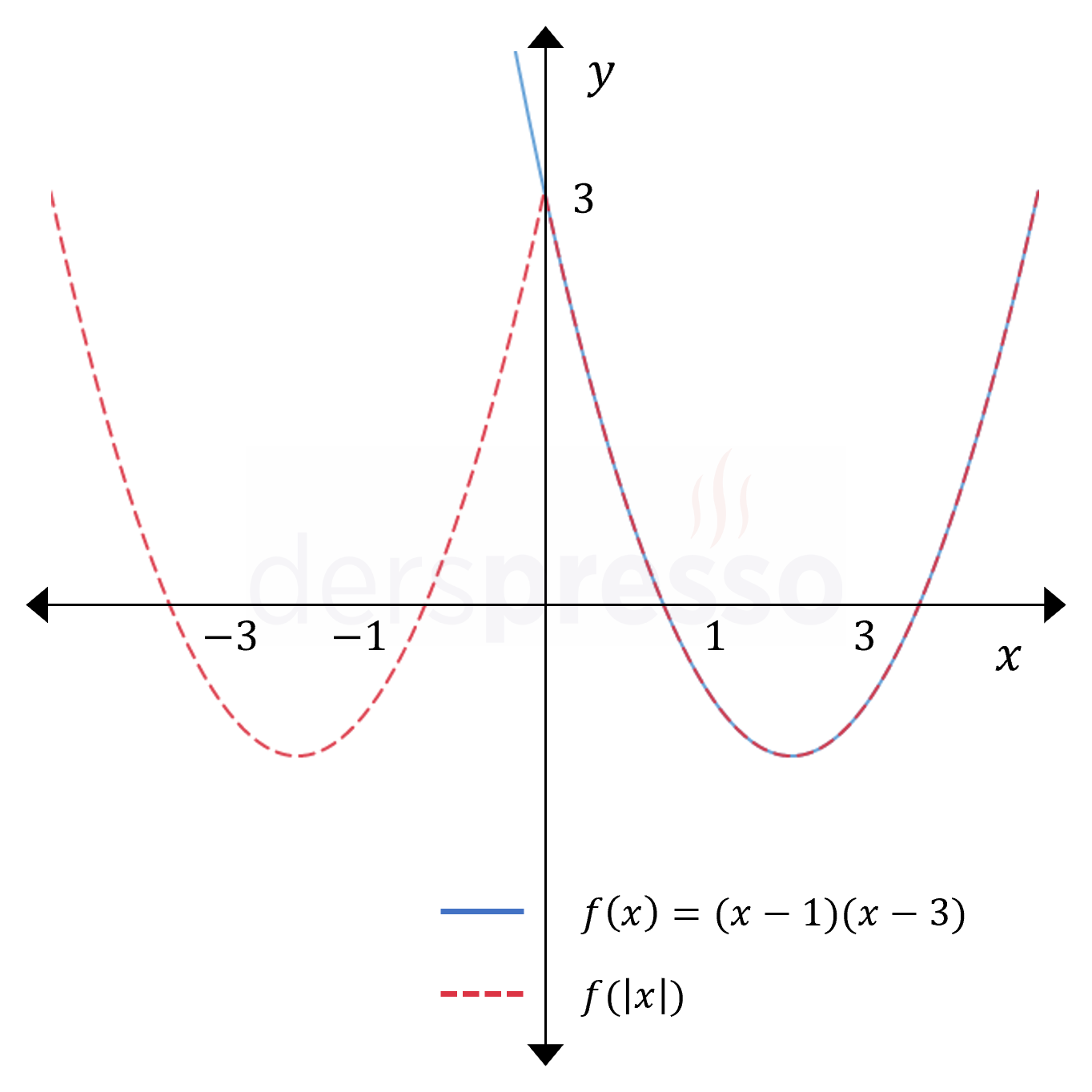
Fonksiyonun girdisinin mutlak değeri alındığında, grafikteki negatif \( x \) değerli noktalar pozitif \( x \) değerli noktalar ile aynı \( y \) değerlerini almaya başlar. Bunun sonucu olarak \( y \) ekseninin solundaki noktalar silinir ve eksenin sağındaki noktaların \( y \) eksenine göre yansıması oluşur. Grafiğin \( y \) ekseninin sağında kalan kısmında değişiklik olmaz.
Fonksiyon Çıktısının ve Girdisinin Mutlak Değeri

Fonksiyonun hem çıktısının hem de girdisinin mutlak değeri alındığında, yukarıdaki iki örnekte bahsettiğimiz dönüşümlerin ikisi birlikte oluşur.