Yansıma, bir fonksiyonun grafiğinin bir nokta, eksen ya da doğruya göre eşit uzaklıktaki ayna görüntüsüdür.
Eksenlere ve Orijine Göre Yansıma
\( x \) eksenine göre yansıma:
\( f(x) \to -f(x) \)
Fonksiyonun çıktısı \( -1 \) ile çarpıldığında grafiğin \( x \) eksenine göre yansıması oluşur. Bunun sebebi, fonksiyonun bu değişiklik sonucunda aynı \( x \) değeri için ters işaretli \( y \) değeri üretmesidir.
\( y \) eksenine göre yansıma:
\( f(x) \to f(-x) \)
Fonksiyonun girdisi \( -1 \) ile çarpıldığında grafiğin \( y \) eksenine göre yansıması oluşur. Bunun sebebi, fonksiyonun bu değişiklik sonucunda aynı \( y \) değerini ters işaretli \( x \) değeri ile üretmesidir.
Orijine göre yansıma:
\( f(x) \to -f(-x) \)
Fonksiyonun hem çıktısı hem de girdisi \( -1 \) ile çarpıldığında grafiğin orijine göre yansıması oluşur. Bunun sebebi, fonksiyonun bu değişiklik sonucunda ters işaretli \( x \) değeri ile ters işaretli \( y \) değeri üretmesidir.
Bu üç dönüşümün grafikleri aşağıdaki şekilde verilmiştir.
Eksenlere ve orijine göre yansıma
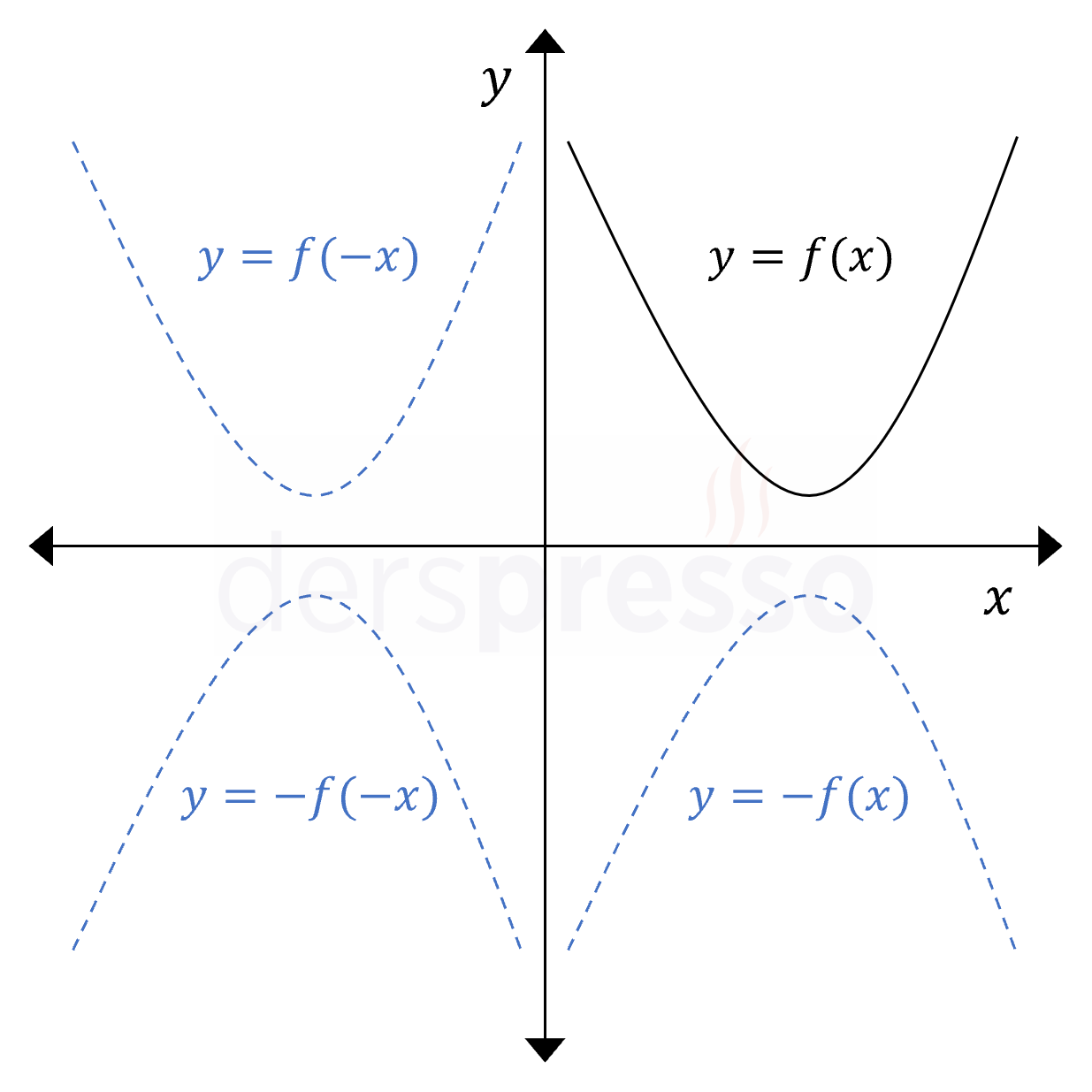
Açıortay Doğrularına Göre Simetri
1. açıortay doğrusuna göre yansıma:
\( y = f(x) \to x = f(y) \)
Fonksiyon denkleminde \( x \) değişkenleri \( y \) ile, \( y \) değişkenleri de \( x \) ile yer değiştirirse grafiğin \( y = x \) doğrusuna göre yansıması oluşur.
2. açıortay doğrusuna göre yansıma:
\( y = f(x) \to -x = f(-y) \)
Fonksiyon denkleminde \( x \) değişkenleri \( -y \) ile, \( y \) değişkenleri de \( -x \) ile yer değiştirirse grafiğin \( y = -x \) doğrusuna göre yansıması oluşur.
Bu iki dönüşümün grafikleri aşağıdaki şekilde verilmiştir.
Açıortay doğrularına göre yansıma
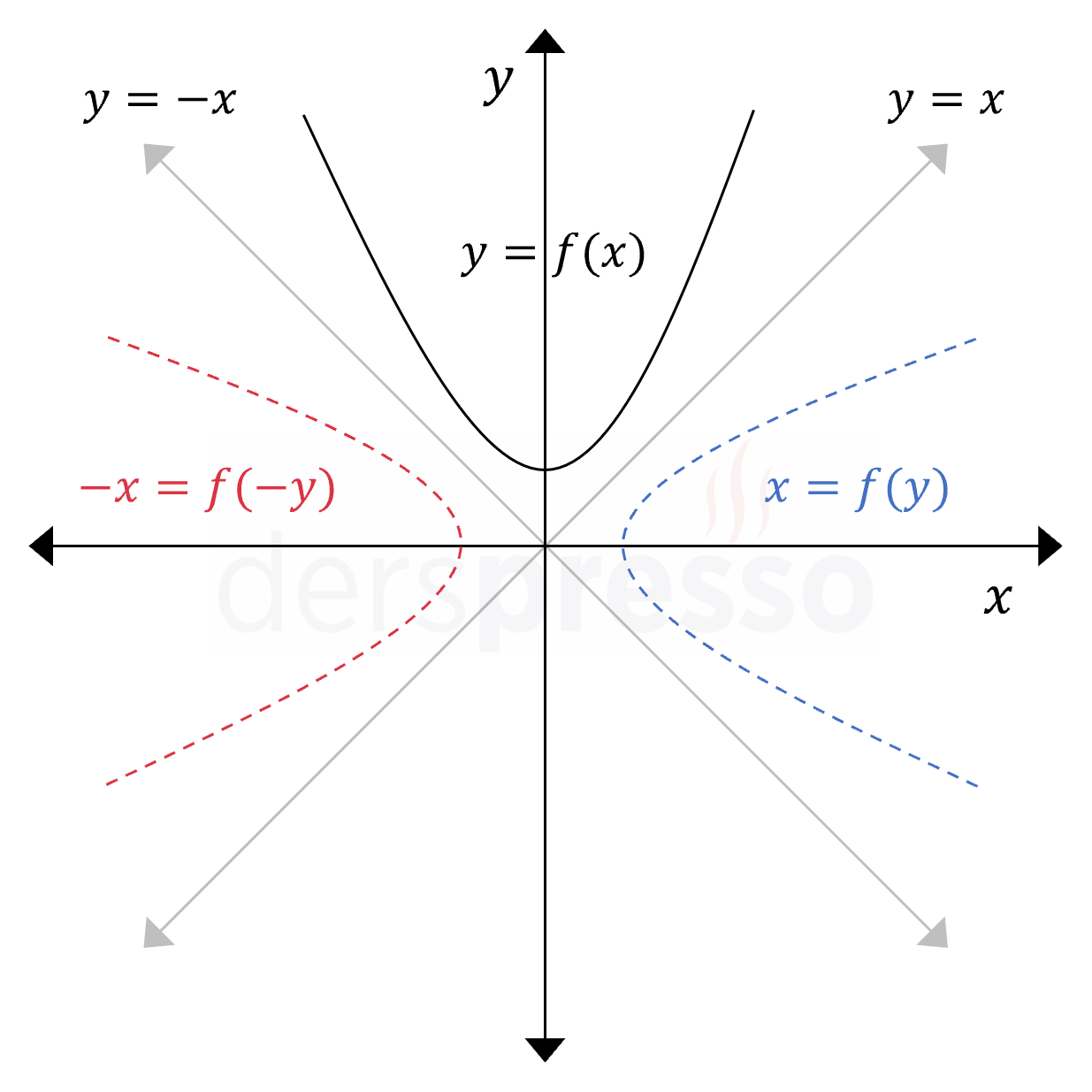
Aşağıda verilen fonksiyonlara 2. sütunda uygulanan dikey dönüşüm sonucunda grafiğin \( x \) eksenine göre, 3. sütunda uygulanan yatay dönüşüm sonucunda da \( y \) eksenine göre yansıması oluşur.
Fonksiyon
Dikey Dönüşüm
Yatay Dönüşüm
\( f(x) = x + 1 \)
\( -f(x) = -(x + 1) \)
\( f(-x) = -x + 1 \)
\( f(x) = x^2 \)
\( -f(x) = -x^2 \)
\( f(-x) = (-x)^2 = x^2 \)
\( f(x) = \sqrt[3]{x} \)
\( -f(x) = -\sqrt[3]{x} \)
\( f(-x) = \sqrt[3]{-x} = -\sqrt[3]{x} \)
\( f(x) = \sin{x} \)
\( -f(x) = -\sin{x} \)
\( f(-x) = \sin(-x) = -\sin{x} \)
\( f(x) = 2^x \)
\( -f(x) = -2^x \)
\( f(-x) = 2^{-x} = (\frac{1}{2})^x \)
\( f(x) = \log{x} \)
\( -f(x) = -\log{x} \)
\( f(-x) = \log(-x) \)
\( f(x) = \abs{x} \)
\( -f(x) = -\abs{x} \)
\( f(-x) = \abs{-x} = \abs{x} \)
SORU 1:
\( f(x) = -x^2 - 6 \) fonksiyonuna aşağıdaki dönüşümler sırasıyla uygulanıyor.
3 birim sağa öteleme
2 birim aşağıya öteleme
\( y \) eksenine göre yansıma
\( x \) eksenine göre yansıma
Buna göre elde edilen fonksiyonun en küçük değeri kaç olur?
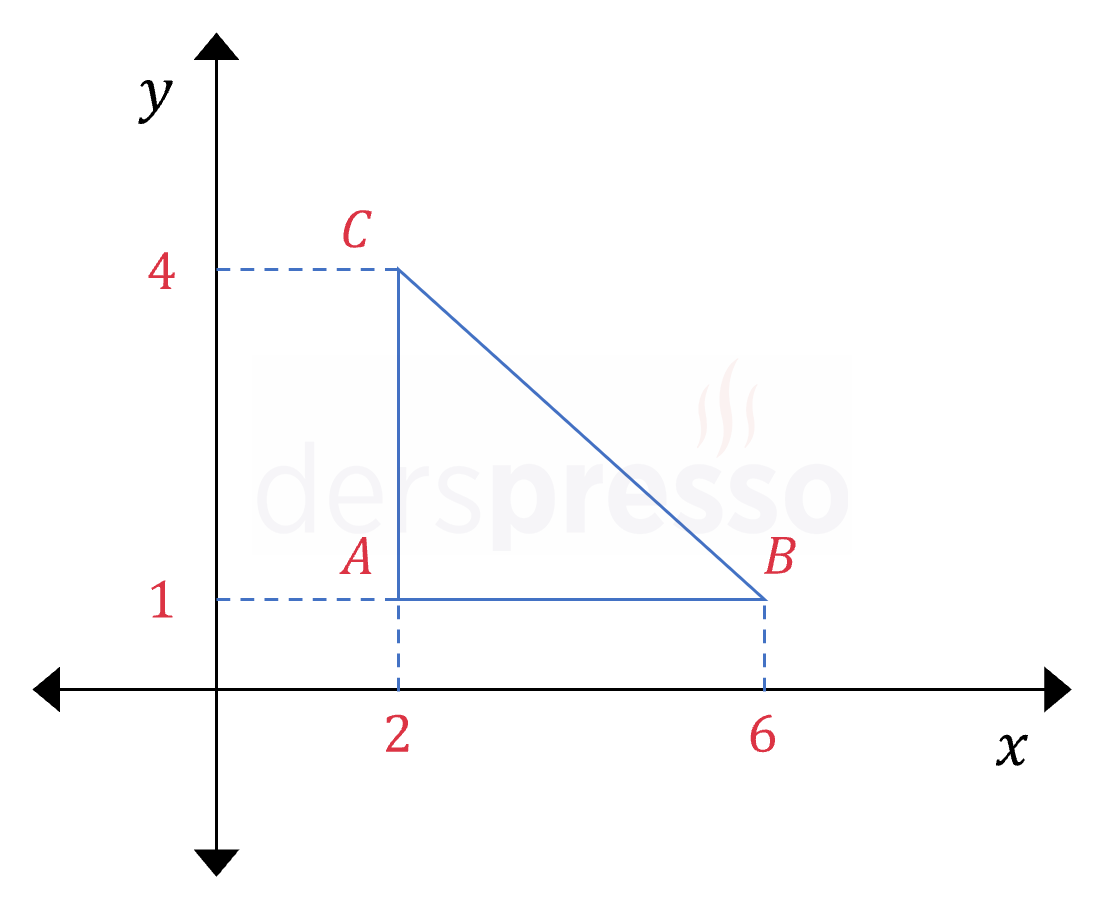
Analitik düzlemde verilen \( ABC \) dik üçgeni önce 3 birim sağa, sonra 2 birim aşağıya ötelendikten sonra \( y = x \) doğrusuna göre yansıması alınıyor.
Yeni üçgenin köşe koordinatlarının ordinatları toplamı kaçtır?
Önce \( \log{x} \) fonksiyonuna iki dönüşüm uygulayarak sorudaki fonksiyonu elde edelim.
\( \log{x} \mapsto \log{\abs{x}} \)
Fonksiyonun girdisinin mutlak değeri alındığında \( y \) ekseninin solunda kalan noktalar (varsa) silinir ve \( y \) ekseninin sağında kalan noktaların \( y \) eksenine göre yansıması oluşur.
\( \log{\abs{x}} \mapsto \log{\abs{x}} + 3 \)
Bir fonksiyonun çıktısına 3 birim eklendiğinde grafiği 3 birim yukarı ötelenir.
Aşağıda bu dönüşümler sonucunda oluşan fonksiyonun ve \( y = x \) doğrusunun grafikleri verilmiştir.
\( y = x \) doğrusunun fonksiyonun \( y \) ekseninin solunda kalan kısmını tek noktada kestiğinden emin olabiliriz, \( y \) ekseninin sağında kalan kısmını kesip kesmediğinden ya da kesiyorsa kaç noktada kestiğinden emin olmak için ya bir programla grafiğini çizmeliyiz ya da iki denklemi ortak çözmeliyiz.
Alternatif olarak \( y = x \) doğrusunun fonksiyonun \( y \) ekseninin sağında kalan kısmını 2 noktada kestiğini daha pratik bir yöntemle bulabiliriz.
Verilen logaritma fonksiyonunda \( y = 0 \) verip \( x \) değerini ve \( x = 1 \) ve \( x = 10 \) verip \( y \) değerlerini hesapladığımızda fonksiyonun aşağıdaki noktalardan geçtiğini buluruz.
\( (10^{-3}, 0), (1, 3), (10, 4) \)
Bu noktalardan 1. ve 3.sünün ordinat değerleri apsis değerlerinden küçük olduğu için \( y = x \) doğrusunun altında kalır, 2. noktanın ise ordinat değeri daha büyük olduğu için \( y = x \) doğrusunun üstünde kalır.
Buna göre fonksiyon grafiğinin doğrunun altındayken doğruyu kesip üstüne geçtiği, sonra tekrar kesip altına indiği sonucuna varabiliriz.
Buna göre verilen fonksiyon ve doğru 3 noktada kesişirler.
Tabanın 1'den büyük olduğu üstel fonksiyonlar tüm reel sayılarda artandır. Fonksiyonun çıktısından 5 çıkarırsak tüm noktalar 5 birim aşağıya öteleneceği için fonksiyon yine artan olur.
I. öncül: \( -f(x) \) fonksiyonu \( f(x) \) fonksiyonunun \( x \) eksenine göre simetriğidir, dolayısıyla artan grafik azalan bir grafiğe dönüşür.
II. öncül: \( f(-x) \) fonksiyonu \( f(x) \) fonksiyonunun \( y \) eksenine göre simetriğidir, dolayısıyla artan grafik azalan bir grafiğe dönüşür.
III. öncül: \( -f(-x) \) fonksiyonu \( f(x) \) fonksiyonunun hem \( x \) hem de \( y \) eksenine göre simetriğidir, dolayısıyla artan grafik yine artan olur.
Buna göre sadece III. önermedeki fonksiyon artandır.
