Özdeş Nesnelerin Farklı Kutulara Dağıtımı
Bu problem tipinde amaç özdeş \( n \) nesnenin birbirinden farklı \( k \) kutuya dağıtım sayısını hesaplamaktır. Nesneler özdeş olduğu için farklı kutulardaki iki nesnenin aralarında yer değiştirmesi yeni bir dağıtım oluşturmaz.
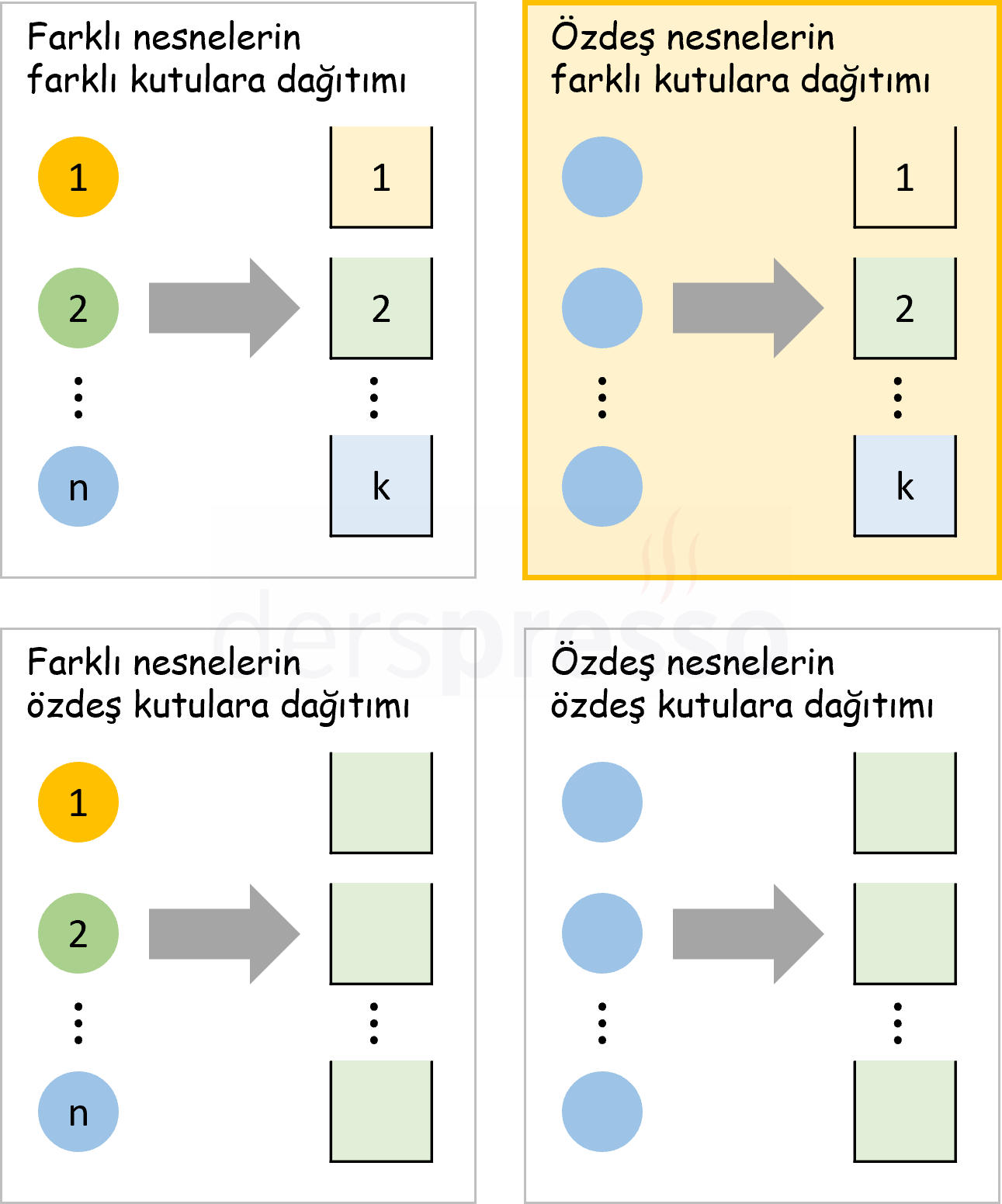
Bu problem tipini her kutuya dağıtılabilecek nesne sayısına göre dört başlık altında inceleyebiliriz.
Her Kutuda Herhangi Bir Sayıda Nesne
Bu problem tipinde nesneler kutulara herhangi bir koşul olmaksızın dağıtılır (bazı kutular boş kalabilir ya da bir kutuya birden fazla nesne konabilir).
\( n \) özdeş nesnenin \( k \) farklı kutuya herhangi bir koşul olmaksızın farklı dağıtım sayısı \( = C(n + k - 1, k - 1) \)
Bu tip problemler "ayraç yöntemi" adı verilen yöntemle çözülebilir. 9 özdeş nesnenin 6 farklı kutuya dağıtımını örnek olarak alırsak, bu yöntemde dağıtılacak nesne sayısı kadar yıldız işareti (\( n = 9 \)) ve kutu sayısının bir eksiği kadar bölü işareti (\( k - 1 = 5 \)) yan yana dizilir.

Bu dizilişte yıldızlar nesneleri temsil ederken bölü işaretleri nesneleri/yıldızları kutu sayısı kadar gruba ayıran birer ayraç görevi görür, dolayısıyla iki bölü işareti arasındaki yıldız sayısı belirli bir kutudaki nesne sayısını verir. Bu problem tipinde bir kutu boş kalabileceği için, iki ya da daha fazla ayraç aralarında yıldız işareti olmayacak şekilde yanyana gelebilir.
Aşağıda 9 özdeş nesnenin 6 farklı kutuya örnek bir dağıtımı verilmiştir. Bu dağıtımda 2. kutuda üç nesne varken 5. kutu boştur.

Bu yöntem ile problem \( n \) özdeş yıldızın (nesnenin) ve \( k - 1 \) özdeş ayracın farklı dizilişi (tekrarlı permütasyonu) problemine dönüşmüş olur. Çoklu kümelerde permütasyon formülünü bu soruya uygularsak, \( n \) ve \( k - 1 \) nesne kendi aralarında özdeş olmak üzere toplamda \( n + k - 1 \) nesnenin farklı diziliş sayısı \( \frac{(n + k - 1)!}{n!\ (k - 1)!} \) olur. Bu da kombinasyon formülü ile \( C(n + k - 1, k - 1) \) ifadesine eşittir.
Her ne kadar problemi özdeş yıldız ve özdeş ayraçların farklı diziliş problemi olarak çözmüş olsak da, özdeş ayraçlar her bir dizilişteki nesneleri elimizdeki problemde olduğu gibi 1. kutu, 2. kutu, ..., k. kutu şeklinde isimlendirebileceğimiz farklı kutulara ayırmaktadır.
10 özdeş muz 5 farklı maymuna kaç farklı şekilde dağıtılabilir?
Çözümü GösterSorudaki özdeş muzlar özdeş nesnelere, farklı maymunlar da muzların dağıtılacağı farklı kutulara karşılık gelmektedir.
Bu açıdan baktığımızda, problemi herhangi bir koşul olmaksızın özdeş nesnelerin farklı kutulara dağıtım problemi olarak modelleyebiliriz ve ayraç yöntemini kullanabiliriz.
Buna göre, 10 özdeş muz 5 farklı maymuna \( C(10 + 5 - 1, 5 - 1) \) farklı şekilde dağıtılabilir.
Farklı dağıtım sayısı \( = C(10 + 5 - 1, 5 - 1) \)
\( = C(14, 4) \)
\( = \dfrac{14!}{4!\ 10!} = 1001 \) bulunur.
Bir baba elindeki 32 adet 100 TL'lik banknotu 3 çocuğuna paylaştıracaktır.
Her çocuk en az 300 TL almak koşuluyla baba bu paylaşımı kaç farklı şekilde yapabilir?
Çözümü GösterBanknotlar özdeş olduğu için baba ilk önce 3'er banknotu 3 çocuğuna 1 farklı şekilde verebilir.
Kalan \( 32 - 9 = 23 \) banknotun 3 çocuğa kaç farklı şekilde dağıtılabileceğini bulalım.
Soruyu 23 özdeş nesnenin (\( n = 23 \)) 3 farklı kutuya (\( k = 3 \)) herhangi bir koşul olmaksızın dağıtım problemi olarak modelleyebiliriz.
Ayraç yöntemini kullanalım.
Farklı dağıtım sayısı \( = C(n + k - 1, k - 1) \)
\( = C(23 + 3 - 1, 3 - 1) \)
\( = C(25, 2) \)
\( = \dfrac{25!}{2!\ 23!} \)
\( = \dfrac{25 \cdot 24}{2} = 300 \) bulunur.
16 özdeş kalem Kadir, Şamil, Öykü ve Alkım isimli dört arkadaşa verilecektir.
Kadir'e en az 5, Şamil'e en az 6 kalem verilecektir.
Herkes en az bir kalem alacağına göre, 16 özdeş kalem bu 4 arkadaşa kaç farklı şekilde dağıtılabilir?
Çözümü GösterHerkes en az bir kalem alacağına göre, Öykü ile Alkım'a da en az 1'er kalem verilecektir.
Önce herkese verilmesi gereken en az kalem sayılarını dağıtırsak geriye dağıtılacak \( 16 - 5 - 6 - 1 - 1 = 3 \) kalem kalır.
\( n \) özdeş nesnenin \( k \) farklı kutuya herhangi bir koşul olmaksızın farklı dağıtım sayısı \( C(n + k - 1, k - 1) \) formülü ile hesaplanır.
Bu örnekte kalemler özdeş nesnelere (\( n = 3 \)), arkadaşlar da farklı kutulara (\( k = 4 \)) karşılık gelir.
Farklı dağıtım sayısı \( = C(n + k - 1, k - 1) \)
\( = C(3 + 4 - 1, 4 - 1) \)
\( = C(6, 3) \)
\( = \dfrac{6!}{3!\ 3!} = 20 \)
Buna göre kalemler dört arkadaşa belirtilen koşullar sağlanacak şekilde 20 farklı şekilde dağıtılabilir.
\( a, b, c, d \in \mathbb{N} \) olmak üzere,
\( a + b + c + d = 7 \) eşitliğini sağlayan kaç \( (a, b, c, d) \) sıralı dörtlüsü vardır?
Çözümü Göster7 sayısını oluşturan 7 adet 1 rakamını dağıtılacak özdeş nesneler, \( a, b, c, d \) değişkenlerini de bu rakamların dağıtılacağı farklı kutular olarak düşünelim. \( a, b, c, d \) birer doğal sayı oldukları için 0 değeri de alabilirler, dolayısıyla problemi \( n \) özdeş nesnenin \( k \) farklı kutuya herhangi bir koşul olmaksızın dağıtım problemi olarak modelleyebiliriz.
Buna göre, örneğin \( (a, b, c, d) = (2, 4, 0, 1) \) çözümü \( a \) kutusuna 2 nesne, \( b \) kutusuna 4 nesne, \( c \) kutusuna 0 nesne, \( d \) kutusuna 1 nesne dağıtılma durumuna karşılık gelir ve ayraç yöntemiyle kutuların sırası a, b, c, d olacak şekilde aşağıdaki gibi gösterilir.
* * \ * * * * \ \ *
Özdeş nesne sayısı \( n = 7 \) ve kutu sayısı \( k = 4 \) olacak şekilde ayraç yöntemi formülünü probleme uygulayalım. Bu formülle 7 özdeş nesne ve 3 özdeş ayracın tekrarlı permütasyon sayısını hesaplıyor oluyoruz.
Farklı dağıtım sayısı \( = C(n + k - 1, k - 1) \)
\( = C(7 + 4 - 1, 4 - 1) \)
\( = C(10, 3) \)
\( = \dfrac{10!}{3!\ 7!} \)
\( = \dfrac{10 \cdot 9 \cdot 8}{3 \cdot 2} = 120 \) bulunur.
Bir pastane 5 farklı renkte makaron üretmektedir. Her renkten makaronun pastanede yeterli sayıda bulunduğunu varsayarsak 8 adetlik bir makaron kutusu kaç farklı şekilde hazırlanabilir (kutudaki makaronların dizilişini değil adetsel dağılımını dikkate alarak)?
Çözümü GösterHer renkteki makarondan kutuya konacak adetlere sırayla \( m_1, m_2, \ldots, m_5 \) diyelim. Buna göre bu 5 değişkenin toplamı kutunun kapasitesi olan 8'e eşit olacaktır.
\( m_1 + m_2 + m_3 + m_4 + m_5 = 8 \)
8 sayısını oluşturan 8 adet 1 sayısını dağıtılacak özdeş nesneler, \( m_1, m_2, \ldots, m_5 \) değişkenlerini de bu sayıların dağıtılacağı farklı kutular olarak düşünelim. Belirli bir renkteki makaron kutuda sıfır dahil herhangi bir sayıda bulunabileceği için problemi \( n \) özdeş nesnenin \( k \) farklı kutuya herhangi bir koşul olmaksızın dağıtım problemi olarak modelleyebiliriz.
Buna göre, örneğin \( (m_1, m_2, m_3, m_4, m_5) = (1, 2, 2, 0, 3) \) seçimi ayraç yöntemiyle kutuların sırası \( m_1, m_2, \ldots, m_5 \) olacak şekilde aşağıdaki gibi gösterilir.
* \ * * \ * * \ \ * * *
Özdeş nesne sayısı \( n = 8 \) ve kutu sayısı \( k = 5 \) olacak şekilde ayraç yöntemi formülünü probleme uygulayalım. Bu formülle 8 özdeş nesne ve 4 özdeş ayracın tekrarlı permütasyon sayısını hesaplıyor oluyoruz.
Farklı dağıtım sayısı \( = C(n + k - 1, k - 1) \)
\( = C(8 + 5 - 1, 5 - 1) \)
\( = C(12, 4) \)
\( = \dfrac{12!}{4!\ 8!} \)
\( = \dfrac{12 \cdot 11 \cdot 10 \cdot 9}{4 \cdot 3 \cdot 2} = 495 \) bulunur.
9 özdeş pet şişe 5 farklı çöp kutusuna atılacaktır.
Her çöp kutusuna en az 1, en fazla 4 şişe atılacağına göre, bu şişeler çöp kutularına kaç farklı şekilde atılabilir?
Çözümü GösterHer çöp kutusuna en az 1 pet şişe atılacaksa özdeş şişelerden birer tanesini en başta çöp kutularına (1 farklı şekilde) attığımızı varsayalım ve işlemi geriye kalan \( 9 - 5 = 4 \) pet şişe için yapalım.
\( n \) özdeş nesnenin \( k \) farklı kutuya herhangi bir koşul olmaksızın farklı dağıtım sayısı \( C(n + k - 1, k - 1) \) formülü ile hesaplanır.
Bu örnekte pet şişeler özdeş nesnelere (\( n = 4 \)), çöp kutuları da farklı kutulara (\( k = 5 \)) karşılık gelir.
Farklı dağıtım sayısı \( = C(n + k - 1, k - 1) \)
\( = C(4 + 5 - 1, 5 - 1) \)
\( = C(8, 4) \)
\( = \dfrac{8!}{4!\ 4!} = 70 \)
Her çöp kutusuna en fazla 4 şişe atılabilir. Her çöp kutusuna en başta 1 pet şişe atıldığı için kalan 4 pet şişenin 4'ü de aynı çöp kutusuna atılamaz.
Kalan 4 pet şişenin dördünün de aynı çöp kutusuna atıldığı (her çöp kutusu için bir tane olmak üzere) 5 durum vardır.
Buna göre istenen farklı durum sayısı \( 70 - 5 = 65 \) olarak bulunur.
Aynı renkteki boncuklar özdeş olmak üzere, 6 mor, 7 siyah ve 8 beyaz boncuk 5 çocuğa dağıtılacaktır.
Her çocuk her boncuktan en az bir tane alacağına göre, bu boncuklar çocuklara kaç farklı şekilde dağıtılabilir?
Çözümü GösterÖnce her çocuğa her boncuktan birer tane dağıtalım. Bu durumda geriye 1 mor, 2 siyah ve 3 beyaz boncuk kalır.
Geriye kalan bu boncuklar çocuklara herhangi bir koşul olmaksızın dağıtılabilir.
\( n \) özdeş nesnenin \( k \) farklı kutuya herhangi bir koşul olmaksızın farklı dağıtım sayısı \( C(n + k - 1, k - 1) \) formülü ile hesaplanır.
1 özdeş mor boncuğun 5 çocuğa farklı dağıtım sayısını bulalım.
\( C(n + k - 1, k - 1) = C(1 + 5 - 1, 5 - 1) \)
\( = C(5, 4) = 5 \)
2 özdeş siyah boncuğun 5 çocuğa farklı dağıtım sayısını bulalım.
\( C(n + k - 1, k - 1) = C(2 + 5 - 1, 5 - 1) \)
\( = C(6, 4) = 15 \)
3 özdeş beyaz boncuğun 5 çocuğa farklı dağıtım sayısını bulalım.
\( C(n + k - 1, k - 1) = C(3 + 5 - 1, 5 - 1) \)
\( = C(7, 4) = 35 \)
Toplam farklı dağıtım sayısı her renkteki bilyenin farklı dağıtım sayılarının çarpımına eşittir.
\( 5 \cdot 15 \cdot 35 = 2625 \) bulunur.
Asya iş yerinden 5 arkadaşına yeni yıl hediyesi olarak 22 özdeş tütsü ve 8 özdeş tütsü kayığı almıştır.
Bu hediyeleri 5 ayrı pakete koyacak olan Asya, her pakette en az 4 tütsü ve bir tütsü kayığı olacak şekilde kaç farklı paketleme yapabilir?
Çözümü GösterBirbirinden farklı iki tip nesne (tütsü ve tütsü kayığı) dağıtılacağından ve birinin dağıtımı diğerini etkilemediğinden bu nesnelerin kaç farklı şekilde dağıtılacağını ayrı ayrı bulup iki sonucu çarpabiliriz.
Tütsülerin dağıtımı:
Her kutuya en az 4 tütsü konacağından \( 5 \cdot 4 = 20 \) özdeş tütsü 5 kutuya 1 farklı şekilde konur.
Geriye kalan \( 22 - 20 = 2 \) özdeş tütsünün 5 farklı kutuya dağıtımını bulalım.
\( n \) özdeş nesnenin \( k \) farklı kutuya herhangi bir koşul olmaksızın farklı dağıtım sayısı \( C(n + k - 1, k - 1) \) formülü ile hesaplanır.
Farklı dağıtım sayısı \( = C(n + k - 1, k - 1) \)
\( = C(2 + 5 - 1, 5 - 1) \)
\( = C(6, 4) \)
\( = \dfrac{6!}{4!\ 2!} = 15 \)
Tütsü kayıklarının dağılımı:
Her kutuya en az 1 tütsü kayığı konacağından \( 5 \) özdeş tütsü kayığı 5 kutuya 1 farklı şekilde konur.
Geriye kalan \( 8 - 5 = 3 \) özdeş tütsünün 5 farklı kutuya dağıtımını bulalım.
Farklı dağıtım sayısı \( = C(n + k - 1, k - 1) = C(3 + 5 - 1, 5 - 1) = C(7, 4) \)
\( = C(3 + 5 - 1, 5 - 1) \)
\( = C(7, 4) \)
\( = \dfrac{7!}{4!\ 3!} = 35 \)
Tütsülerin farklı dağıtım sayısını tütsü kayıklarının farklı dağıtım sayısı ile çarptığımızda hediyelerin kaç farklı şekilde paketleneceğini buluruz.
\( 15 \cdot 35 = 525 \) farklı paketleme yapılabilir.
Rakamları toplamı 9 olan 4 basamaklı kaç farklı sayı yazılabilir?
Çözümü GösterOluşturulacak 4 basamaklı sayıya \( (abcd) \) diyelim. Buna göre bu sayının basamakları toplamı 9'a eşit olmalıdır.
\( a + b + c + d = 9 \)
9 sayısını oluşturan 9 adet 1 sayısını dağıtılacak özdeş nesneler, \( a, b, c, d \) değişkenlerini de bu sayıların dağıtılacağı farklı kutular olarak düşünelim. Binler basamağı dışındaki basamaklara sıfır nesne dağılabileceği için problemi \( n \) özdeş nesnenin \( k \) farklı kutuya herhangi bir koşul olmaksızın dağıtım problemi olarak modelleyebiliriz.
Buna göre, örneğin \( (abcd) = (3042) \) sayısı ayraç yöntemiyle aşağıdaki gibi gösterilir.
111 \ \ 1111 \ 11
Bu soruyu iki farklı yöntemle çözebiliriz.
1. yöntem:
Binler basamağında sıfır bulunma durumunu da dahil edersek özdeş nesne sayısı \( n = 9 \) ve kutu sayısı \( k = 4 \) olacak şekilde ayraç yöntemi formülünü probleme uygulayalım. Bu formülle 9 özdeş nesne ve 3 özdeş ayracın tekrarlı permütasyon sayısını hesaplıyor oluyoruz.
Farklı dağıtım sayısı \( = C(n + k - 1, k - 1) \)
\( = C(9 + 4 - 1, 4 - 1) \)
\( = C(12, 3) \)
\( = \dfrac{12!}{3!\ 9!} \)
Ancak bu sonuç binler basamağı sıfır olan sayıları da içerir, dolayısıyla bu sonuçtan sıfır ile başlayan, yani rakamları toplamı yine 9 olan üç basamaklı sayıları çıkarmamız gerekir. Bu da 9 özdeş nesne ve 2 özdeş ayracın tekrarlı permütasyon sayısına eşittir.
Rakamları toplamı 9 olan 4 basamaklı farklı sayı adedi:
\( = \dfrac{12!}{3!\ 9!} - \dfrac{11!}{2!\ 9!} \)
\( = 220 - 55 = 165 \)
2. yöntem:
Binler basamak sıfır olamayacağı için \( a \) kutusuna en azından bir nesne dağılmalıdır. Bu bir nesneyi en baştan bu kutuya dağıttığımızı düşünelim.
Bu durumda özdeş nesne sayısı \( n = 8 \) ve kutu sayısı \( k = 4 \) olacak şekilde ayraç yöntemi formülünü probleme uygulayalım. Bu formülle 8 özdeş nesne ve 3 özdeş ayracın tekrarlı permütasyon sayısını hesaplıyor oluyoruz.
Farklı dağıtım sayısı \( = C(n + k - 1, k - 1) \)
\( = C(8 + 4 - 1, 4 - 1) \)
\( = C(11, 3) \)
\( = \dfrac{11!}{3!\ 8!} \)
\( = 165 \)
\( P(x) \) polinomunun katsayıları birer rakamdır.
\( P(-1) = -9 \) olduğuna göre, derecesi en fazla 4 olan kaç farklı \( P(x) \) polinomu yazılabilir?
Çözümü Göster\( P(x) = ax^4 + bx^3 + cx^2 + dx + e \)
Soruda \( P(-1) = a - b + c - d + e = -9 \) eşitliğini sağlayan kaç farklı \( (a, b, c, d, e) \) beşlisi olduğunu bulmamız isteniyor.
Negatif katsayıları pozitife çevirelim.
Eşitliğin iki tarafına 18 ekleyelim.
\( 18 + a - b + c - d + e = -9 + 18 \)
\( a + (9 - b) + c + (9 - d) + e = 9 \)
\( b' = 9 - b \) ve \( d' = 9 - d \) şeklinde değişken değiştirelim.
\( b' \) ve \( d' \) sayıları \( b \) ve \( d \) gibi birer rakam olur.
\( a + b' + c + d' + e = 9 \)
Her değişken 0 - 9 arasında değer alabileceği için soruyu 9 özdeş nesnenin (\( n = 9 \)) 5 farklı kutuya (\( k = 5 \)) herhangi bir koşul olmaksızın dağıtımı problemi olarak kurgulayabiliriz.
Bu kurguda nesneler 9 tane 1 sayısının her birine, kutular da katsayılara karşılık gelmektedir. Polinomun derecesi 4 ya da daha az olabileceği için herhangi bir kutuya/katsayıya sıfır nesne gelebilir.
Farklı dağıtım sayısı: \( C(n + k - 1, k - 1) \)
\( = C(9 + 5 - 1, 5 - 1) \)
\( = C(13, 4) \)
\( = \dfrac{13!}{4!\ 9!} \)
\( = \dfrac{13 \cdot 12 \cdot 11 \cdot 10}{4 \cdot 3 \cdot 2} \)
\( = 715 \) bulunur.
Her Kutuda En Fazla Bir Nesne
Bu problem tipinde nesneler kutulara her kutuda en fazla bir nesne olacak şekilde dağıtılır. Her kutuda en fazla bir nesne olabileceği için, bu problemlerde \( n \le k \) koşulunun sağlanması gerekir (nesne sayısı kutu sayısından fazla olamaz), aksi takdirde farklı dağıtım sayısı 0 olur.
\( n \le k \) olmak üzere,
\( n \) özdeş nesnenin \( k \) farklı kutuya her kutuda en fazla bir nesne olacak şekilde farklı dağıtım sayısı \( = C(k, n) \)
Her kutuda sıfır ya da bir nesne olacağı için, bu problemi seçilecek kutulara birer nesne dağıtacak şekilde \( k \) farklı kutu içinden \( n \) kutunun seçimi, yani bir kombinasyon problemi olarak kurgulayabiliriz. Buna göre \( k \) farklı kutu içinden \( n \) kutu \( C(k, n) \) farklı şekilde seçilebilir. Nesneler özdeş olduğu için seçilen kutulara bu nesnelerin dağıtımı sadece 1 şekilde yapılabilir.
4 özdeş oyuncak 6 çocuğa, hiçbir çocuğa birden fazla oyuncak vermemek koşuluyla kaç farklı şekilde dağıtılabilir?
Çözümü GösterSorudaki özdeş oyuncaklar özdeş nesnelere, çocuklar da oyuncakların dağıtılacağı farklı kutulara karşılık gelmektedir.
4 özdeş oyuncak 6 çocuğa, 6 çocuk içinden 4 çocuğun farklı seçim sayısı kadar farklı şekilde dağıtılabilir.
Buna göre farklı dağıtım sayısı \( C(k, n) = C(6, 4) = 15 \) olur.
3 beyaz piyon bir satranç tahtasına kaç farklı şekilde yerleştirilebilir?
Çözümü GösterSorudaki beyaz piyonlar özdeş nesnelere, satranç tahtasının kareleri de (satır ve sütunları numaralandırılmış bir tahta olduğu varsayımıyla) özdeş nesnelerin dağıtılacağı farklı kutulara karşılık gelmektedir.
64 kare içinden 3 kare \( C(64, 3) \) farklı şekilde seçilebilir. 3 özdeş piyon seçilen 3 kareye her kareye bir piyon gelecek şekilde 1 şekilde yerleştirilebilir. Buna göre farklı dağıtım sayısı \( C(64, 3) \) olur.
Her Kutuda En Az Bir Nesne
Bu problem tipinde nesneler kutulara her kutuda en az bir nesne olacak şekilde dağıtılır. Her kutuda en az bir nesne olabileceği için, bu problemlerde \( n \ge k \) koşulunun sağlanması gerekir (nesne sayısı kutu sayısından az olamaz), aksi takdirde farklı dağıtım sayısı 0 olur.
\( n \ge k \) olmak üzere,
\( n \) özdeş nesnenin \( k \) farklı kutuya her kutuda en az bir nesne olacak şekilde dağıtım sayısı \( = C(n - 1, k - 1) \)
Bu tip problemler de yukarıda kullandığımız "ayraç yöntemi" ile çözülebilir. 10 özdeş nesnenin 5 farklı kutuya dağıtımını örnek olarak alırsak, bu yöntemde dağıtılacak nesne sayısı kadar yıldız işareti (\( n = 10 \)) aralarında birer boşluk (alt çizgi) olacak şekilde yan yana dizilir.

Bu 10 yıldız işaretinin arasında kalan 9 boşluğa yerleştireceğimiz \( k - 1 = 4 \) ayraç, nesneleri/yıldızları 5 farklı kutuya ayırmamızı sağlar. Ayraçlar sadece boşluklara yerleştirilebileceği için ve herhangi iki boşluk arasında mutlaka bir nesne olacağı için, problemdeki her kutuda en az bir nesne olma koşulu sağlanmış olur.
Aşağıda 10 özdeş nesneyi 5 farklı kutuya dağıtmak için, 9 boşluk içinden 4 boşluğun örnek bir seçimi verilmiştir. Bu dizilişte nesneler 5 kutuya sırasıyla 2-3-2-2-1 adet dağıtılmış olur.

Problemi bu şekilde kurguladığımızda, nesnelerin kutulara farklı dağıtım sayısı \( n - 1 \) boşluk içinden \( k - 1 \) boşluğun farklı seçim sayısına, yani \( C(n - 1, k - 1) \) ifadesine eşit olur.
10 özdeş muz 5 farklı maymuna, her maymun en az bir muz olacak şekilde kaç farklı şekilde dağıtılabilir?
Çözümü GösterSorudaki özdeş muzlar özdeş nesnelere, maymunlar da muzların dağıtılacağı farklı kutulara karşılık gelmektedir.
Her maymuna en az bir muz dağıtılacağı belirtildiği için, problemi özdeş nesnelerin farklı kutulara her kutuda en az bir nesne olacak şekilde dağıtım problemi olarak modelleyebiliriz.
Farklı dağıtım sayısı \( = C(n - 1, k - 1) \)
\( = C(9, 4) = \dfrac{9!}{4!\ 5!} \)
Bu soruyu alternatif olarak şu şekilde de çözebiliriz: Her maymun en az 1 muz alacağı için önce 5 maymunun her birine 1'er muz verilir. Muzlar özdeş olduğu için bu dağıtım tek bir şekilde yapılabilir. Daha sonra kalan 5 muz yukarıdaki "Her Kutuda Herhangi Bir Sayıda Nesne" yöntemi ile 5 maymuna dağıtılır. O yöntemde kullandığımız formülü 5 özdeş muz ve 5 maymuna uygularsak aynı \( C(n + k - 1, k - 1) = C(9, 4) \) sonucunu elde ederiz.
Özgür elindeki 10 adet 100 TL'lik banknot ile 3 ayrı bankada hesap açtırmak istiyor.
Özgür her hesaptaki bakiyenin en az 100 TL ve 100 TL'nin katları şeklinde olmasını istediğine göre, bu 3 hesabı açılış bakiyeleri açısından kaç farklı şekilde açtırabilir?
Çözümü GösterSorudaki 100 TL'lik banknotlar özdeş nesnelere, banka hesapları da farklı kutulara karşılık gelmektedir.
Hesap açtırmak için her bankaya en az 100 TL yatırmak gerekeceği için problemi özdeş nesnelerin farklı kutulara her kutuda en az bir nesne olacak şekilde dağıtım problemi olarak modelleyebiliriz.
Farklı dağıtım sayısı \( = C(n - 1, k - 1) \)
\( = C(9, 2) = \dfrac{9!}{2!\ 7!} = 36 \) olur.
\( a, b, c, d \in \mathbb{Z^+} \) olmak üzere,
\( a + b + c + d \le 10 \) eşitsizliğini sağlayan kaç \( (a, b, c, d) \) sıralı dörtlüsü vardır?
Çözümü GösterBu sorunun çözümü açısından aşağıdaki iki ifadenin özdeş olduğunu gösterelim.
\( e \in \mathbb{Z^+} \) olmak üzere,
\( a + b + c + d \le 10 \)
\( a + b + c + d + e = 11 \)
İkinci ifadede \( e \) değişkenini sağ tarafa alalım.
\( a + b + c + d = 11 - e \)
\( e \) bir pozitif tam sayı olduğu için en küçük değeri 1 olabilir, dolayısıyla ifadeyi aşağıdaki gibi yazabiliriz.
\( a + b + c + d \le 10 \)
Bu şekilde yukarıdaki iki ifadenin bu soru açısından özdeş ifadeler olduğunu göstermiş olduk.
Buna göre soruyu "aşağıdaki eşitliği sağlayan kaç \( (a, b, c, d, e) \) sıralı beşlisi vardır?" şeklinde yeniden tanımlayalım ve çözelim.
\( a + b + c + d + e = 11 \)
11 sayısını oluşturan 11 adet 1 rakamını dağıtılacak özdeş nesneler, \( a, b, c, d, e \) değişkenlerini de bu rakamların dağıtılacağı farklı kutular olarak düşünelim. \( a, b, c, d, e \) birer pozitif tam sayı oldukları için 0 değeri alamazlar, dolayısıyla problemi \( n \) özdeş nesnenin \( k \) farklı kutuya her kutuda en az bir nesne olacak şekilde dağıtım problemi olarak modelleyebiliriz.
Buna göre, örneğin \( (a, b, c, d, e) = (2, 3, 1, 2, 3) \) çözümü \( a \) kutusuna 2 nesne, \( b \) kutusuna 3 nesne, \( c \) kutusuna 1 nesne, \( d \) kutusuna 2 nesne, \( e \) kutusuna 3 nesne dağıtılma durumuna karşılık gelir ve ayraç yöntemiyle kutuların sırası a, b, c, d, e olacak şekilde aşağıdaki gibi gösterilir.
* * \ * * * \ * \ * * \ * * *
Özdeş nesne sayısı \( n = 11 \) ve kutu sayısı \( k = 5 \) olacak şekilde ayraç yöntemi formülünü probleme uygulayalım.
Farklı dağıtım sayısı \( = C(n - 1, k - 1) \)
\( = C(11 - 1, 5 - 1) \)
\( = C(10, 4) \)
\( = \dfrac{10!}{4!\ 6!} = 210 \) bulunur.
Her Kutuda Tek Bir Nesne
Bu problem tipinde nesneler kutulara her kutuda sadece bir nesne olacak şekilde dağıtılır. Her kutuda sadece bir nesne olabileceği için, bu problemlerde \( n = k \) koşulunun sağlanması gerekir (nesne sayısı kutu sayısına eşit olmalıdır), aksi takdirde farklı dağıtım sayısı 0 olur.
\( n = k \) olmak üzere,
\( n \) özdeş nesnenin \( k \) farklı kutuya her kutuda tek bir nesne olacak şekilde dağıtım sayısı \( = 1 \)
\( n \) özdeş nesnenin \( n \) farklı kutuya her kutuda bir nesne olacak şekilde herhangi bir dağıtımında iki nesne aralarında yer değiştirirse nesneler özdeş olduğu için yeni bir dağıtım oluşmaz. Bu yüzden bu dağıtım sadece bir şekilde yapılabilir.
"Her Kutuda En Fazla Bir Nesne" ve "Her Kutuda En Az Bir Nesne" problem tiplerinde \( n = k \) aldığımızda da aynı \( 1 \) sonucunu elde ederiz.
\( n = k \) ise,
\( C(k, n) = C(n, n) = 1 \)
\( C(n - 1, k - 1) = C(n - 1, n - 1) = 1 \)
5 özdeş gül 5 öğretmene her öğretmen bir gül alacak şekilde kaç farklı şekilde verilebilir?
Çözümü GösterGüller her öğretmen bir gül alacak şekilde dağıtılacağı için farklı dağıtım sayısı 1 olur.
Güller özdeş olduğu için, yapılacak dağıtımda iki öğretmenin aldığı güller aralarında değiştirilirse farklı bir dağıtım oluşmaz.