Parabolün Grafiği
İnteraktif uygulama: Parabolün Katsayıları
Parabolün grafiği kolları yukarı ya da aşağı yönlü olan ve tepe noktasından geçen simetri eksenine göre simetrik olan bir eğridir.
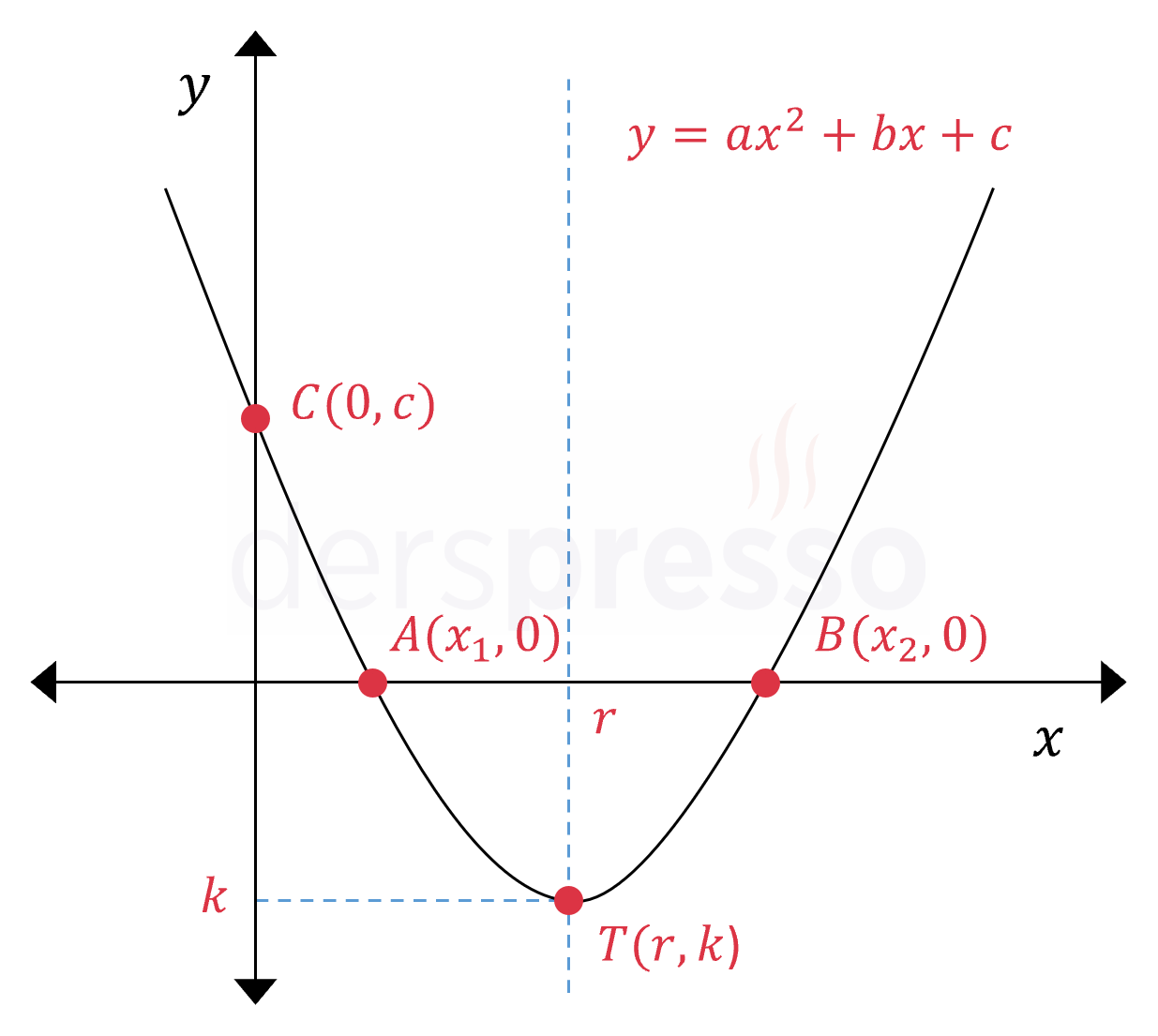
Bir parabol grafiğindeki önemli noktalar şunlardır.
\( T(r, k) \): Parabolün tepe noktası
\( A(x_1, 0) \) ve \( B(x_2, 0) \): Parabolün \( x \) eksenini kestiği noktalar
\( C(0, c) \): Parabolün \( y \) eksenini kestiği nokta
Parabolün Kollarının Yönü
Parabolün kolları denklemin başkatsayısının (\( a \)) işaretine bağlı olarak yukarı ya da aşağı yönlü olur.
Bir parabolün kolları;
- \( a \gt 0 \) ise yukarı yönlüdür,
- \( a \lt 0 \) ise aşağı yönlüdür.
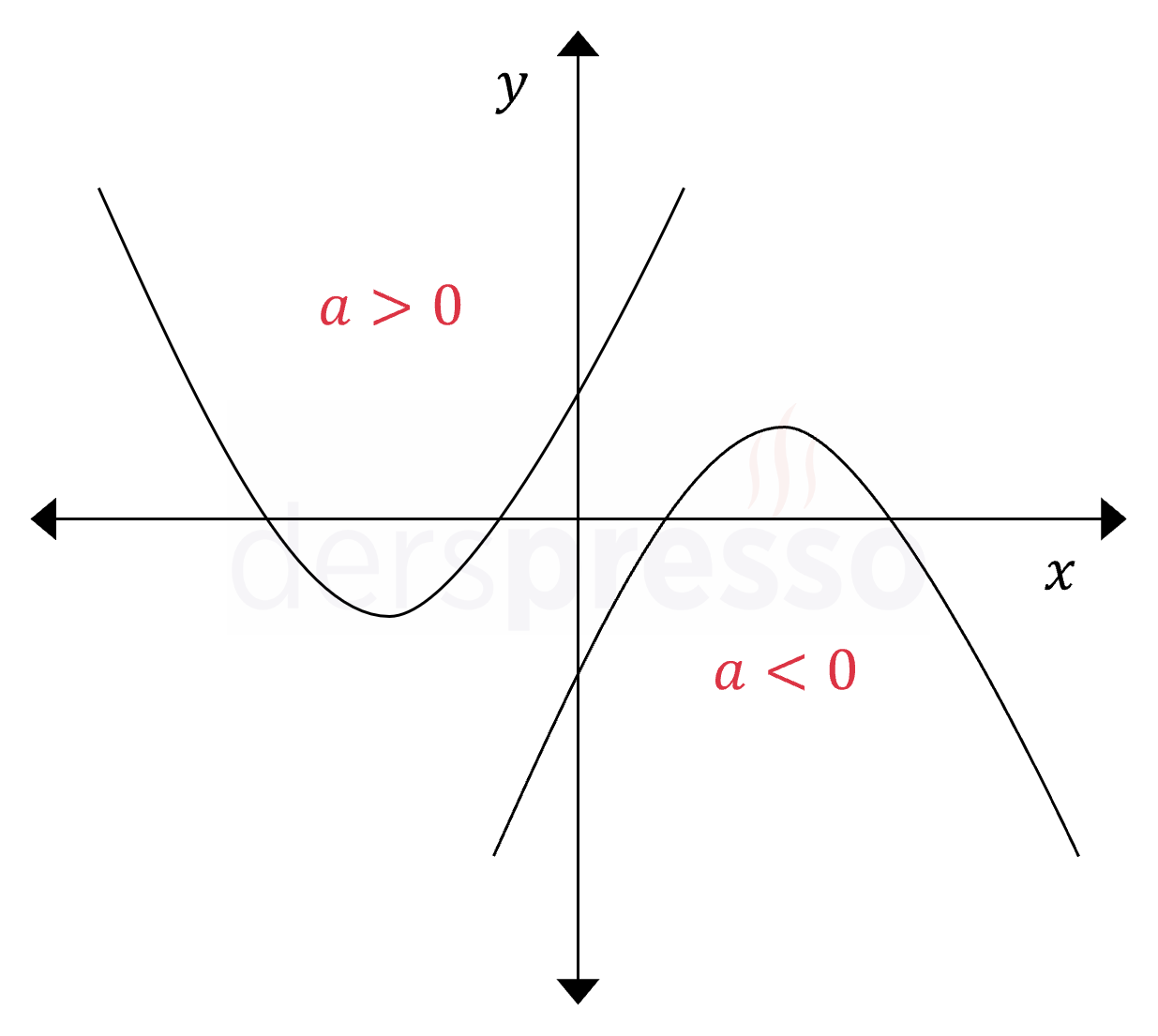
\( x^2 \) ifadesi tüm \( x \) değerleri için pozitif olduğu için, \( x \) pozitif ve negatif sonsuza giderken fonksiyon değerinin işaretini parabolün başkatsayısı belirler. Dolayısıyla \( x \) pozitif ve negatif sonsuza giderken fonksiyon; \( a \gt 0 \) ise pozitif yönde, \( a \lt 0 \) ise negatif yönde büyür.
\( f(x) = x^2 \)
\( f(100) = f(-100) = 10000 \)
\( g(x) = -x^2 \)
\( g(100) = g(-100) = -10000 \)
\( y = (9 - m^2)x^2 - 4x + 3 \) parabolünün kolları yukarı yönlü olduğuna göre, \( m \) değer aralığı nedir?
Çözümü GösterBir parabolün kolları yukarı yönlü ise başkatsayısı pozitiftir.
\( 9 - m^2 \gt 0 \)
\( (3 - m)(3 + m) \gt 0 \)
Negatif başkatsayılı ve birbirinden farklı iki reel kökü olan ikinci dereceden bir ifade köklerin arasındaki aralıkta pozitif olur.
\( m \in (-3, 3) \) bulunur.
Parabolün Kollarının Açıklığı
Başkatsayının işareti parabolün kollarının yönünü belirlerken mutlak değer olarak büyüklüğü kollarının ne kadar açık ya da kapalı olduğunu belirler.
Bir parabolün kolları;
- \( \abs{a} \) büyüdükçe kapanır,
- \( \abs{a} \) küçüldükçe açılır.
Aşağıdaki pozitif başkatsayılı parabolleri incelediğimizde, başkatsayı değeri büyüdükçe parabolün kollarının kapandığı, küçüldükçe de açıldığı görülür. Bunun nedeni; başkatsayı değeri büyüdükçe belirli bir \( x \) değeri için fonksiyonun daha büyük \( y \) değerleri üretmesi, dolayısıyla o \( x \) değeri için parabol üzerindeki noktanın \( x \) ekseninden uzaklaşmasıdır.
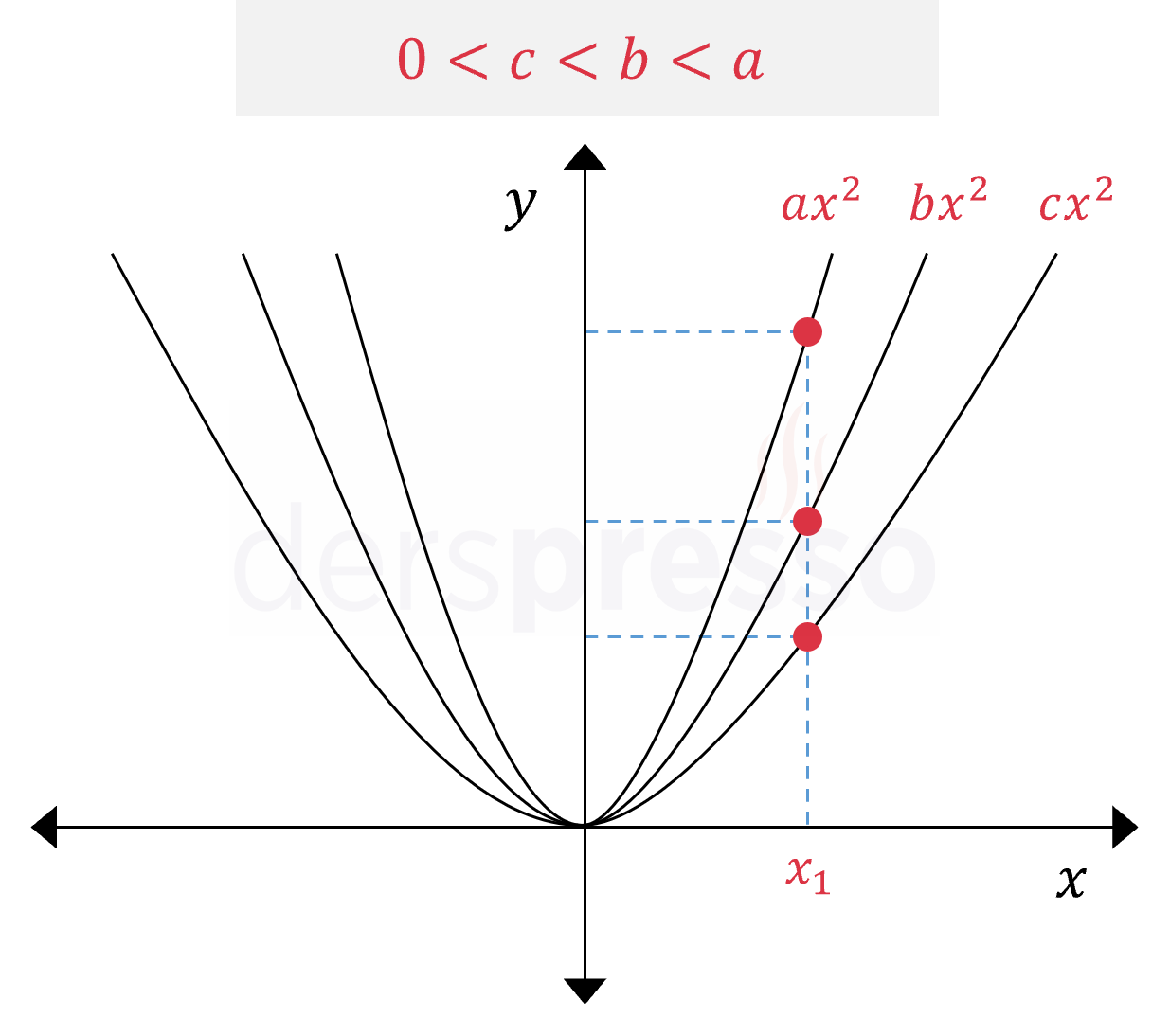
Benzer bir mantıkla, negatif başkatsayılı parabollerde başkatsayının değeri mutlak değer olarak büyüdükçe parabolün kolları kapanır, küçüldükçe de açılır.
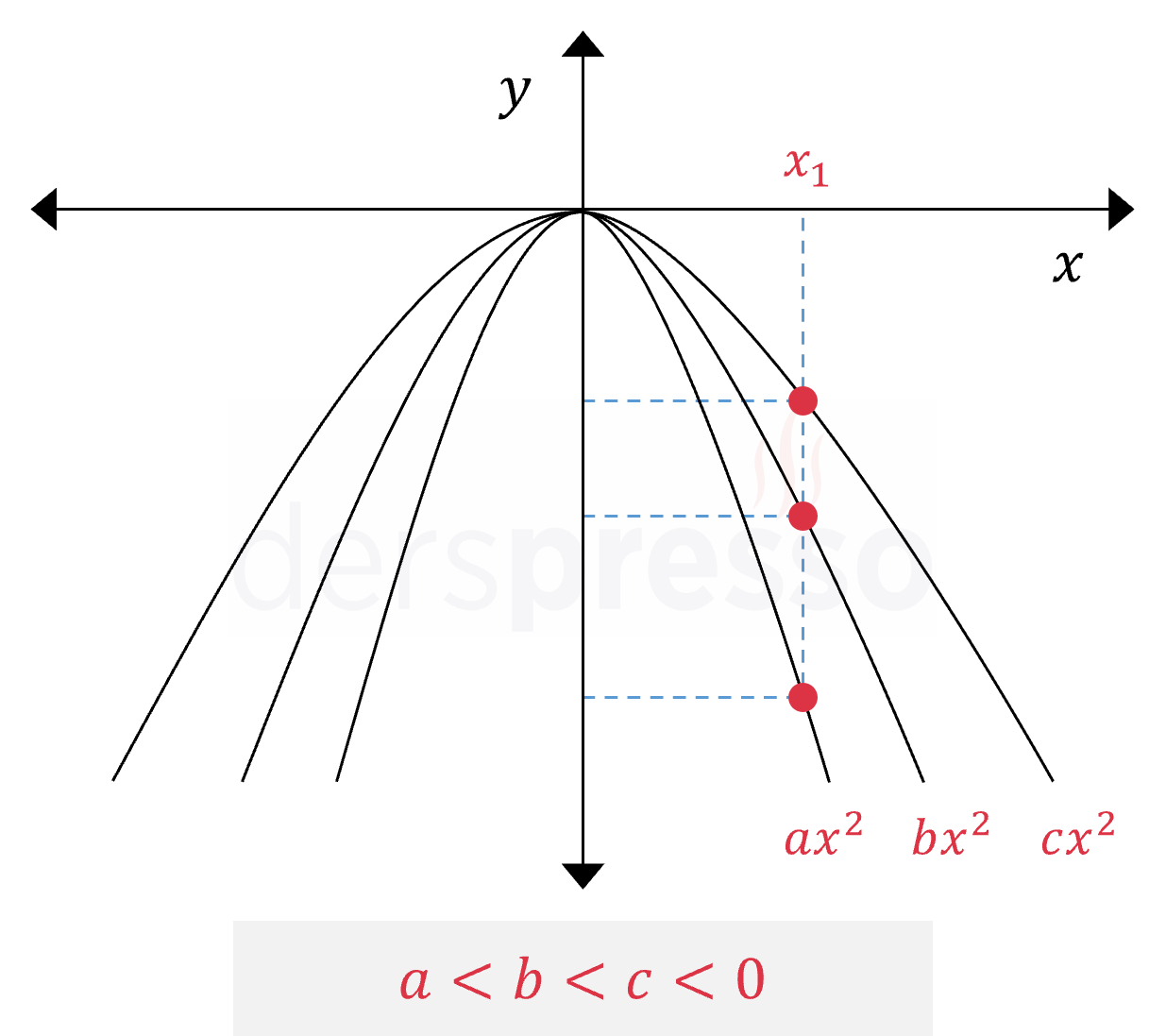
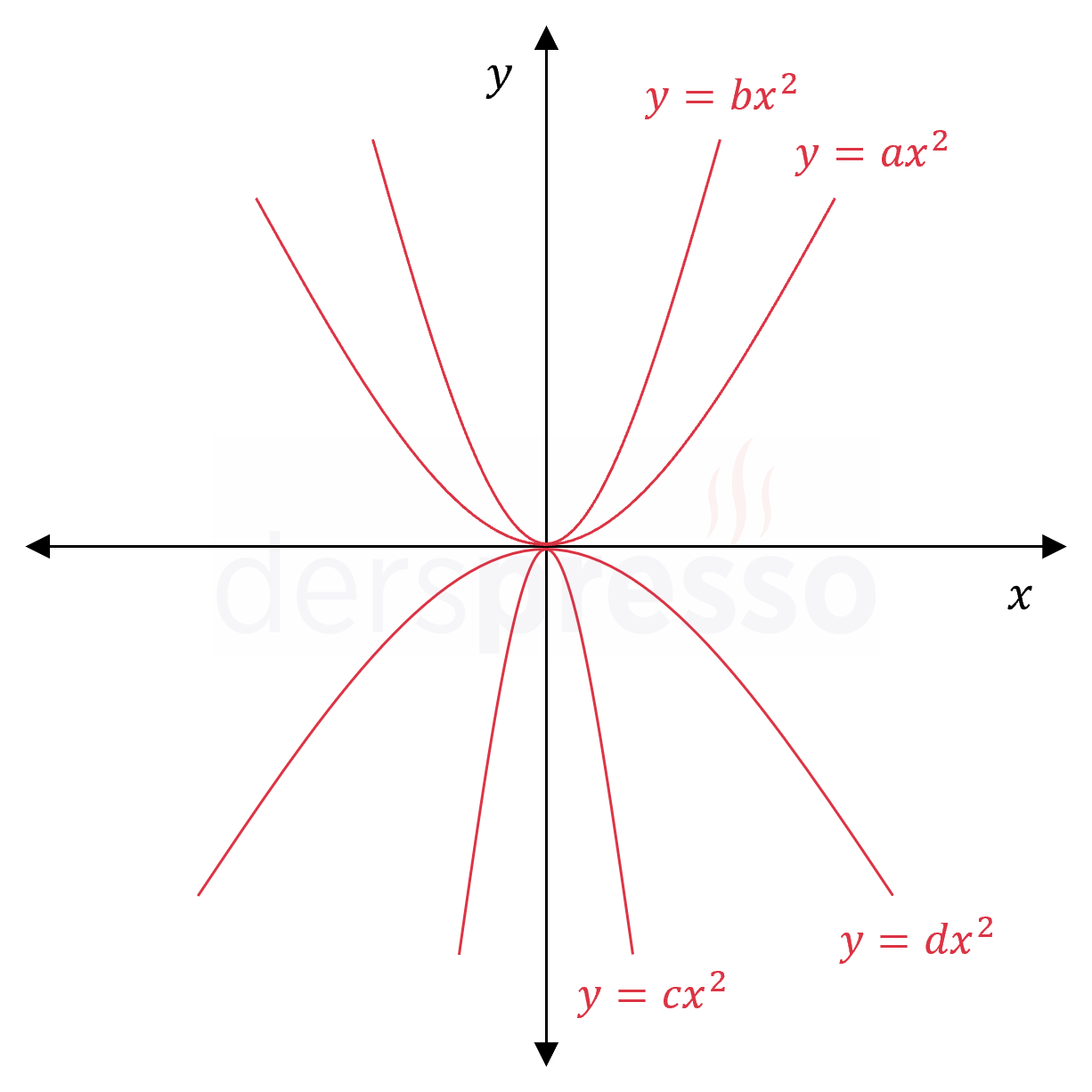
Şekildeki parabol grafikleri için \( a, b, c, d \) değerlerini küçükten büyüğe doğru sıralayınız.
Çözümü GösterKolları yukarı yönlü olan parabollerin başkatsayıları pozitif, aşağı yönlü olan parabollerin başkatsayıları negatiftir.
Pozitif başkatsayılı parabollerde başkatsayı büyüdükçe parabolün kolları kapanır.
\( 0 \lt a \lt b \)
Negatif başkatsayılı parabollerde başkatsayı mutlak değer olarak büyüdükçe parabolün kolları kapanır.
\( 0 \lt \abs{d} \lt \abs{c} \)
\( c \lt d \lt 0 \)
Başkatsayıların sıralaması aşağıdaki gibi olur.
\( c \lt d \lt a \lt b \)
Parabolün x Eksenini Kestiği Noktalar
Bir parabol \( x \) eksenini iki noktada kesebilir (I. parabol), bir noktada kesebilir (II. parabol) ya da kesmeyebilir (III. parabol). Parabolün \( x \) eksenini kestiği noktaları önümüzdeki bölümlerde daha detaylı inceleyeceğiz.

Parabolün y Eksenini Kestiği Nokta
Bir parabol \( y \) eksenini her zaman ve sadece bir noktada keser. Bir parabolün \( y \) eksenini kestiği noktayı bulmak için denklemde \( x = 0 \) konur ve \( y \) değeri bulunur. Bu değer aynı zamanda parabol denkleminin sabit terimi olan \( c \)'ye eşittir.

Bir parabol \( y \) eksenini;
- \( c \gt 0 \) ise eksenin pozitif tarafında keser,
- \( c = 0 \) ise orijinde keser,
- \( c \lt 0 \) ise eksenin negatif tarafında keser.

Sabit terim büyüdükçe parabolün grafiği şekli (kollarının yönü ve açıklığı) değişmeden yukarı doğru, küçüldükçe aşağı doğru ötelenir.
\( y = 2x^2 - 3x + 5 \)
Parabolün \( y \) eksenini kestiği noktayı bulmak için \( x = 0 \) koyalım.
\( y = 2(0)^2 - 3(0) + 5 = 5 \)
Parabol \( y \) eksenini \( (0, 5) \) noktasında keser.
\( f(x) = -x^2 + 6x + 7 \) parabolü için aşağıdaki ifadelerden hangileri doğrudur?
I. Kolları yukarı yönlüdür.
II. Simetri ekseni \( x = 3 \) doğrusudur.
III. En küçük değeri 16'dır.
IV. Tepe noktası II. bölgededir.
V. \( x \) eksenine teğettir.
VI. \( y \) eksenini \( (0, 7) \) noktasında keser.
Çözümü GösterI. öncül:
Parabolün başkatsayısı negatif olduğu için kolları aşağı yönlüdür.
I. öncül yanlıştır.
II. öncül:
Parabolün tepe noktası \( T(r, k) \) olmak üzere, \( x = r \) doğrusu parabolün simetri eksenidir.
\( a = -1, \quad b = 6, \quad c = 7 \)
\( r = -\dfrac{b}{2a} = -\dfrac{6}{2(-1)} = 3 \)
\( x = r = 3 \) doğrusu parabolün simetri eksenidir.
II. öncül doğrudur.
III. öncül:
Parabolün tepe noktasındaki değerini bulalım.
\( k = f(3) \)
\( = -3^2 + 6(3) + 7 = 16 \)
Negatif başkatsayılı (kolları aşağı yönlü olan) bir parabol en küçük değil en büyük değerini tepe noktasında alır, dolayısıyla 16 parabolün en büyük değeridir.
III. öncül yanlıştır.
IV. öncül:
\( T(r, k) = T(3, 16) \)
Buna göre parabolün tepe noktası I. bölgededir.
IV. öncül yanlıştır.
V. öncül:
Parabolün \( x \) eksenine teğet olması için tepe noktasının ordinatı sıfır olmalıdır.
V. öncül yanlıştır.
VI. öncül:
Parabolün \( y \) eksenini kestiği noktayı bulmak için denklemde \( x = 0 \) yazalım.
\( f(0) = -0^2 + 6(0) + 7 = 7 \)
Parabol \( y \) eksenini \( (0, 7) \) noktasında keser.
VI. öncül doğrudur.
Buna göre II. ve VI. öncüller doğrudur.

Grafiği ve denklemi verilen \( f(x) \) parabolü için \( a, b, c \) katsayılarının işaretlerini bulunuz.
Çözümü GösterParabolün kolları yukarı yönlü olduğu için başkatsayısı pozitiftir.
\( a \gt 0 \)
Parabolün tepe noktası I. bölgede yer aldığı için tepe noktasının apsisi pozitiftir.
\( r = -\dfrac{b}{2a} \gt 0 \)
\( a \) pozitif olduğu için eşitsizliğin sağlanması için \( b \) negatif olmalıdır.
\( b \lt 0 \)
Parabolün \( y \) eksenini kestiği noktanın ordinatı pozitif olduğu için denklemin sabit terimi de pozitiftir.
\( c \gt 0 \)
\( a, b, c \) katsayılarının işaretleri sırasıyla aşağıdaki gibidir.
\( +, -, + \)
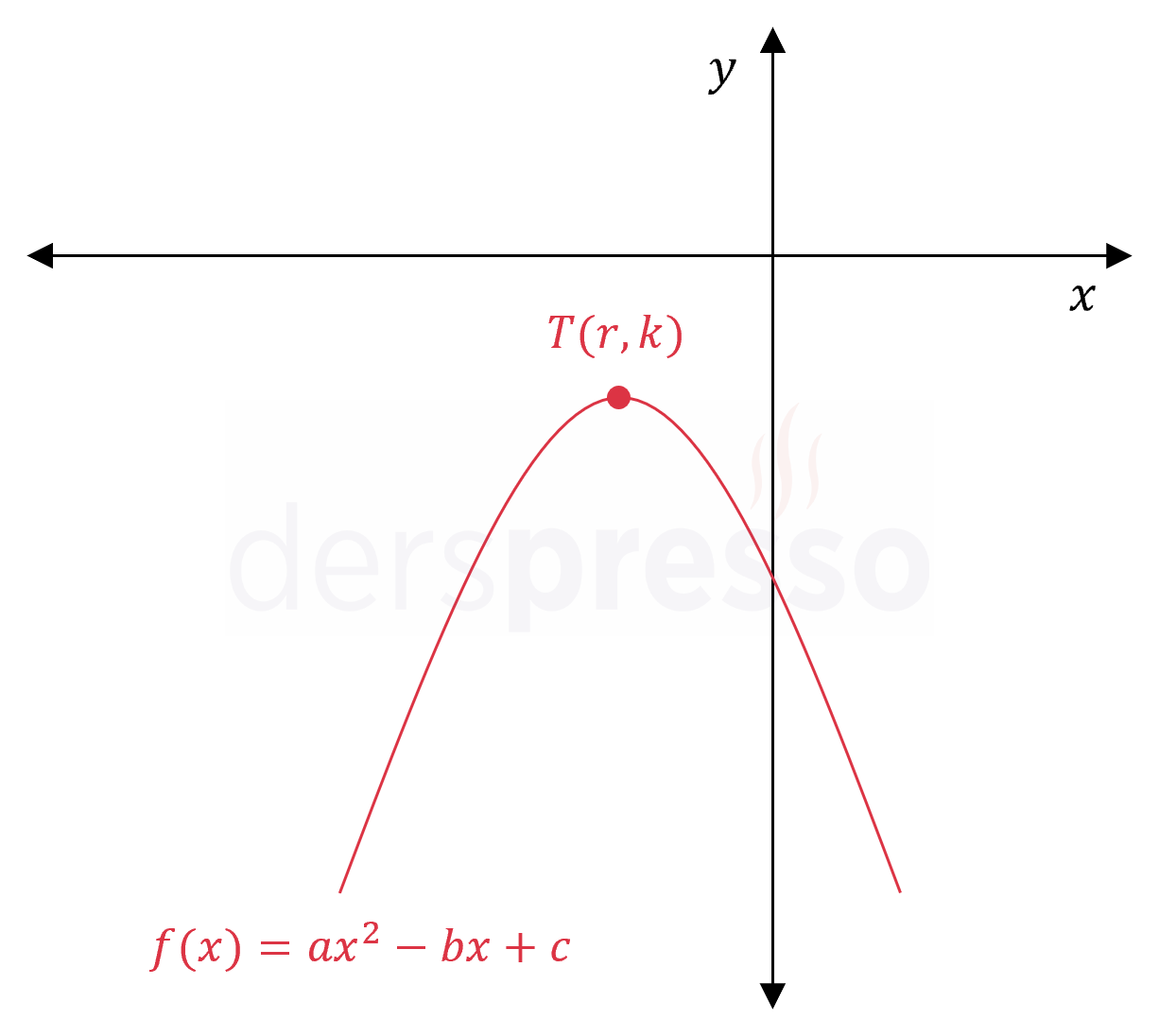
Grafiği ve denklemi verilen \( f(x) \) parabolü için \( a, b, c \) katsayılarının işaretlerini bulunuz.
Çözümü GösterParabolün kolları aşağı yönlü olduğu için başkatsayısı negatiftir.
\( a \lt 0 \)
Parabolün tepe noktası III. bölgede yer aldığı için tepe noktasının apsisi negatiftir.
\( r = -\dfrac{-b}{2a} \lt 0 \)
\( a \) negatif olduğu için eşitsizliğin sağlanması için \( b \) pozitif olmalıdır.
\( b \gt 0 \)
Parabolün \( y \) eksenini kestiği noktanın ordinatı negatif olduğu için denklemin sabit terimi de negatiftir.
\( c \lt 0 \)
\( a, b, c \) katsayılarının işaretleri sırasıyla aşağıdaki gibidir.
\( -, +, - \)
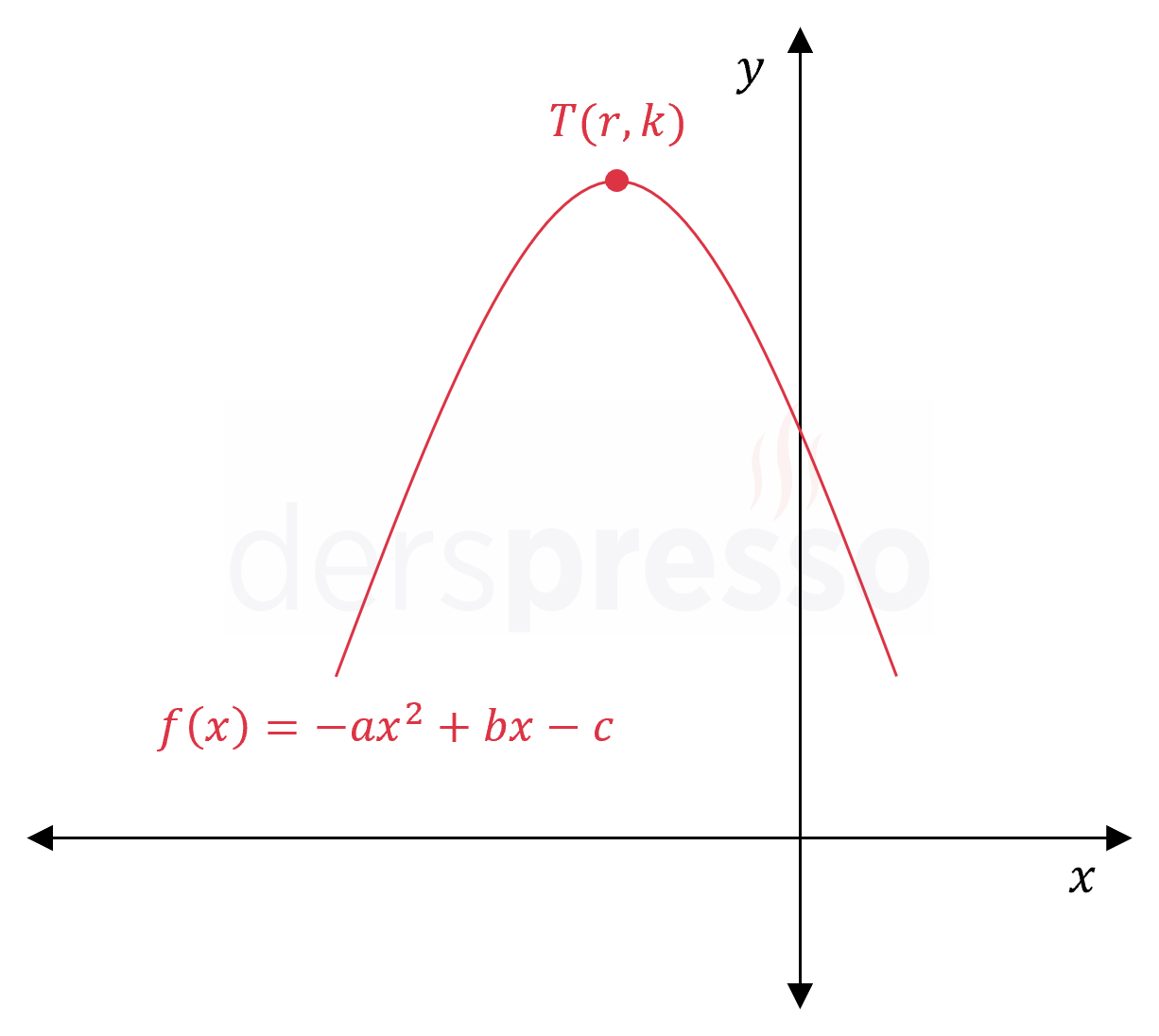
Grafiği ve denklemi verilen \( f(x) \) parabolü için \( a, b, c \) katsayılarının işaretlerini bulunuz.
Çözümü GösterParabolün kolları aşağı yönlü olduğu için başkatsayısı negatiftir.
\( -a \lt 0 \)
\( a \gt 0 \)
Parabolün tepe noktası II. bölgede yer aldığı için tepe noktasının apsisi negatiftir.
\( r = -\dfrac{b}{2(-a)} \lt 0 \)
\( a \) pozitif olduğu için eşitsizliğin sağlanması için \( b \) negatif olmalıdır.
\( b \lt 0 \)
Parabolün \( y \) eksenini kestiği noktanın ordinatı pozitif olduğu için denklemin sabit terimi de pozitiftir.
\( -c \gt 0 \)
\( c \lt 0 \)
\( a, b, c \) katsayılarının işaretleri sırasıyla aşağıdaki gibidir.
\( +, -, - \)

Grafiği ve denklemi verilen \( f(x) \) parabolü için \( a, b, c \) katsayılarının işaretlerini bulunuz.
Çözümü GösterParabolün kolları yukarı yönlü olduğu için başkatsayısı pozitiftir.
\( -a \gt 0 \)
\( a \lt 0 \)
Parabolün tepe noktası IV. bölgede yer aldığı için tepe noktasının apsisi pozitiftir.
\( r = -\dfrac{-b}{2(-a)} \gt 0 \)
\( a \) negatif olduğu için eşitsizliğin sağlanması için \( b \) pozitif olmalıdır.
\( b \gt 0 \)
Parabolün \( y \) eksenini kestiği noktanın ordinatı negatif olduğu için denklemin sabit terimi de negatiftir.
\( -c \lt 0 \)
\( c \gt 0 \)
\( a, b, c \) katsayılarının işaretleri sırasıyla aşağıdaki gibidir.
\( -, +, + \)