Dizi Tanımı
Sıralı sayı listelerine dizi denir. Diziler genellikle \( a_n, b_n, c_n \) şeklinde küçük harflerle ifade edilirler.
Pozitif çift sayılar dizisi:
\( (a_n) = (2, 4, 6, 8, 10, 12, \ldots) \)
Tam kare sayılar dizisi:
\( (b_n) = (1, 4, 9, 16, 25, 36, \ldots) \)
Herhangi bir sayı dizisi:
\( (c_n) = (1, 5, 17, 23, 47, 56, 71, \ldots) \)
Bir dizinin elemanlarına o dizinin terimleri denir. Bir dizinin \( k \). terimi \( a_k \) şeklinde gösterilir. Bir terimin dizinin kaçıncı terimi olduğunu gösteren bu \( k \) sayısına indis denir.
\( (a_n) = (a_1, a_2, \ldots, a_7, \ldots) \)
\( a_2 \): Dizinin 2. terimi
\( a_7 \): Dizinin \( 7 \). terimi
Bir dizinin terimlerini listelemeye gerek kalmadan, tüm terimleri bulmamızı sağlayan ifadeye dizinin genel terimi denir. Bir dizi genellikle \( (a_n) \) ya da \( \{a_n\} \) şeklinde ifade edilir. Belirli bir terimin gösteriminde ise parantez kullanılmaz.
\( (a_n) = 3n + 2 \)
\( a_1 = 3(1) + 2 = 5 \)
\( a_2 = 3(2) + 2 = 8 \)
\( a_3 = 3(3) + 2 = 11 \)
\( a_{10} = 3(10) + 2 = 32 \)
\( (a_n) = (5, 8, 11, \ldots, 32, \ldots) \)
Bir dizinin tanımlı olduğu indis değer aralığı parantez dışında aşağıdaki şekillerde belirtilebilir.
\( (a_n)_{n=0}^{\infty} = 2n - 5 \)
\( (b_n)_{n \in \mathbb{Z^+}} = n^2 \)
Dizilerin indisleri genellikle 1 ile başlasa da, Fibonacci dizisi gibi indisi 0 (ya da herhangi bir pozitif/negatif tam sayı) ile başlayan diziler de tanımlanabilir. Aksi belirtilmediği sürece verilen bir dizinin indisinin 1 ile başladığı varsayılabilir.
Aşağıdaki iki örnekte olduğu gibi, bir dizinin terimlerini üreten matematiksel bir formül her zaman bulunmayabilir.
Asal sayılar dizisi:
\( (a_n) = (2, 3, 5, 7, 11, 13, \ldots) \)
Mükemmel sayılar dizisi:
\( (b_n) = (6, 28, 496, 8128, 33550336, \ldots) \)
Diziler terimlerinin ait oldukları sayı kümelerine göre isimlendirilirler (reel sayı dizisi, tam sayı dizisi, karmaşık sayı dizisi vb.)
Dizilerin Fonksiyon Tanımı
Diziler matematikte doğal sayılar kümesinden (\( \mathbb{N} \)) dizinin terimlerini temsil eden herhangi bir kümeye (\( X \)) birer fonksiyon olarak tanımlanırlar. Bu tanıma göre bir dizinin indis değerleri dizinin tanım kümesini, terimleri de görüntü kümesini oluşturur.
\( f: \mathbb{N} \to \mathbb{X} \)
\( n \mapsto f(n) = a_n \)
Bir dizinin başlangıç indisi herhangi bir tam sayı olabileceği için, tanım kümesi doğal sayılar kümesinin pozitif ya da negatif yönde ötelenmiş bir hali olabilir, burada önemli olan tanım kümesinin bir en küçük elemanının (başlangıç indisinin) olması ve indis değerlerinin hiçbir tam sayıyı atlamadan artarak ilerlemesidir. Buna göre bir dizinin tanım kümesi tüm tam sayılar ya da çift sayılar olamaz.
\( f: \mathbb{Z^+} \to \mathbb{Z} \) olmak üzere,
\( f(n) = 3n + 2 \)
\( f(1) = a_1 = 5 \)
\( f(2) = a_2 = 8 \)
\( f(3) = a_3 = 11 \)
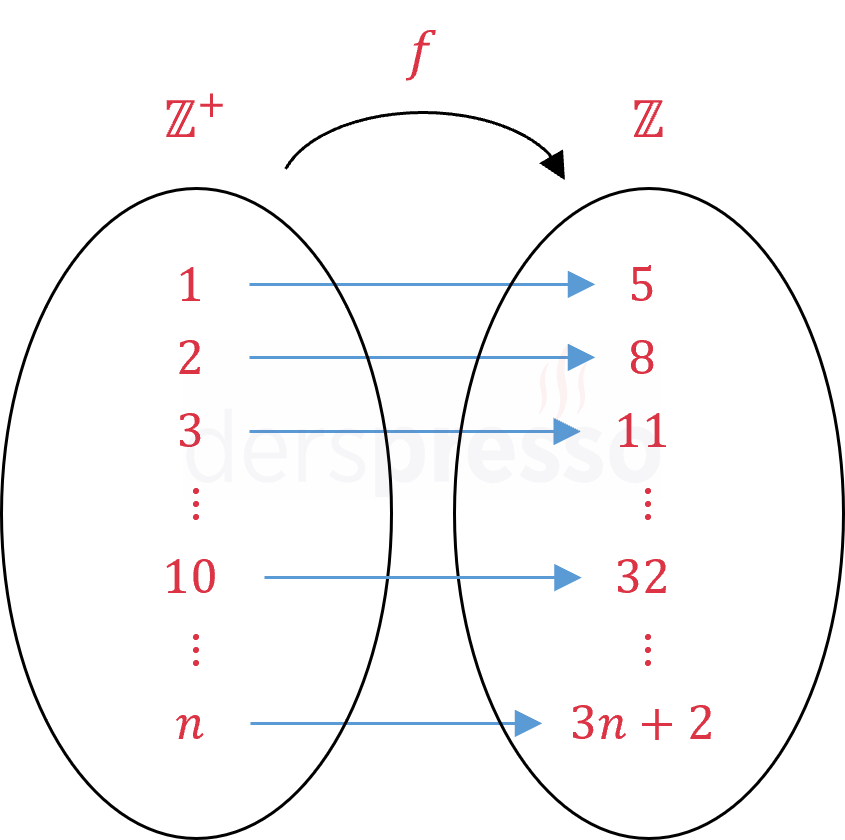
Fonksiyon tanımı gereği, bir dizi tanım kümesindeki her indis değeri için tanımlı olmak zorundadır. Aşağıdaki iki fonksiyon tüm tanım kümelerinde tanımlı oldukları için aynı zamanda birer dizidir.
\( f: \mathbb{N} \to \mathbb{R} \) olmak üzere,
\( f(n) = \dfrac{1}{n + 2} \)
\( f = \{ (0, \frac{1}{2}), (1, \frac{1}{3}), (2, \frac{1}{4}), (3, \frac{1}{5}), \ldots \} \)
\( g: \mathbb{Z^+} \to \mathbb{R} \) olmak üzere,
\( g(n) = \sqrt{n - 1} \)
\( g = \{ (1, 0), (2, 1), (3, \sqrt{2}), (4, \sqrt{3}), \ldots \} \)
Aşağıdaki tanım geçerli bir fonksiyon olsa da, \( n = 5 \) için tanımlı olmadığı için geçerli bir dizi değildir.
\( f: \mathbb{Z^+} - \{5\} \to \mathbb{R} \)
\( f(n) = \dfrac{1}{n - 5} \)
Dizilerin Grafik Gösterimi
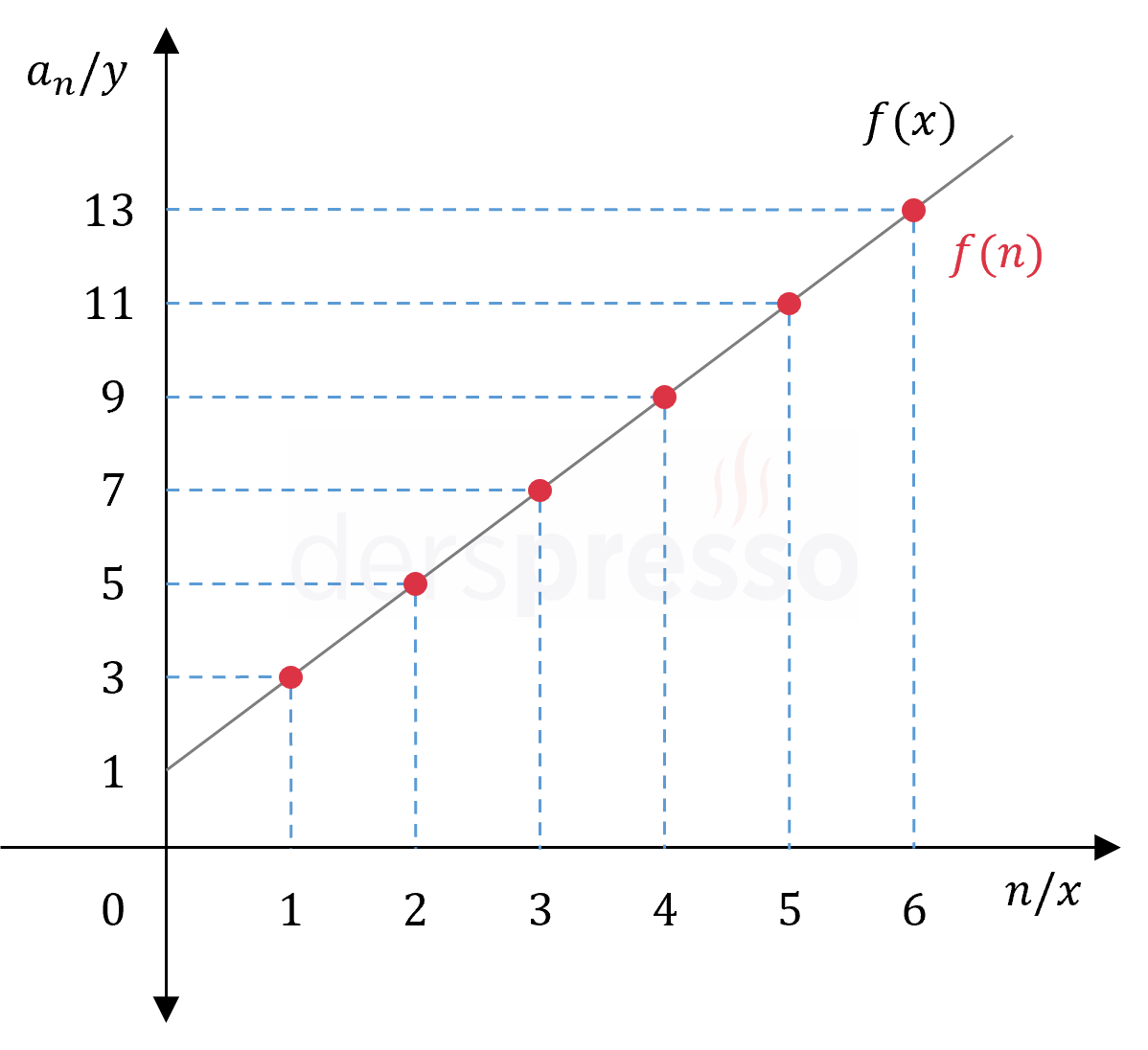
Diziler diğer fonksiyonlar gibi koordinat düzleminde grafiksel olarak gösterilebilir. Böyle bir grafikte yatay eksen dizinin indislerine (\( n \)), dikey eksen de dizinin terimlerine karşılık gelir.
Aşağıdaki örnekte görülebileceği üzere, reel sayılarda tanımlı \( f(x) = 2x + 1 \) fonksiyonunun grafiği her reel sayı için tanımlı ve sürekli iken, \( f(n) = 2n + 1 \) dizisinin grafiği sadece tam sayı indis değerlerindeki noktalardan oluşur ve kesiklidir.
Eşit Diziler
Aynı indisli terimleri birbirine eşit olan dizilere eşit dizi denir.
\( a_1 = b_1, \quad a_2 = b_2, \quad \ldots, \quad a_n = b_n \) ise,
\( (a_n) \) ve \( (b_n) \) eşit dizilerdir.
Aşağıdaki iki dizi aynı indisli terimleri eşit olduğu için eşit dizilerdir.
\( (a_n) = (-1)^n \)
\( = (-1, 1, -1, 1, \ldots) \)
\( (b_n) = \cos(n\pi) \)
\( = (-1, 1, -1, 1, \ldots) \)
\( (a_n) = (b_n) \)
Dizi - Küme Ayrımı
Diziler kümelere benzemekle birlikte bazı açılardan kümelerden ayrılırlar.
- Dizilerin terimleri, kümelerin elemanları vardır.
- Dizilerin terimleri \( ( \ldots ) \), kümelerin elemanları \( \{ \ldots \} \) şeklinde listelenirler.
- Dizilerde terimlerin sırası önemlidir, kümelerde elemanların sırası önemli değildir. Örneğin \( (2, 4, 6, 8, \ldots) \) ve \( (4, 2, 6, 8, \ldots) \) farklı dizilerdir.
- Bir terim bir dizide birden fazla kez yer alabilir, bir eleman bir kümede sadece bir kez yer alabilir.
- Diziler aynı zamanda birer fonksiyondur, kümeler sadece belirli koşullar sağlandığında fonksiyon olurlar.
Aşağıdaki dizilerin ilk 5 terimini yazınız.
(a) \( (a_n) = \dfrac{3 - n}{n^2} \)
(b) \( (b_n) = \dfrac{6 + n}{n!} \)
(c) \( (c_n) = \dfrac{(-1)^{n + 1}}{2n + 1} \)
Çözümü Göster(a) seçeneği:
\( (a_n) = \dfrac{3 - n}{n^2} \)
\( a_1 = \dfrac{3 - 1}{1^2} = 2 \)
\( a_2 = \dfrac{3 - 2}{2^2} = \dfrac{1}{4} \)
\( a_3 = \dfrac{3 - 3}{3^2} = 0 \)
\( a_4 = \dfrac{3 - 4}{4^2} = -\dfrac{1}{16} \)
\( a_5 = \dfrac{3 - 5}{5^2} = -\dfrac{2}{25} \)
(b) seçeneği:
\( (b_n) = \dfrac{6 + n}{n!} \)
\( b_1 = \dfrac{6 + 1}{1!} = 7 \)
\( b_2 = \dfrac{6 + 2}{2!} = 4 \)
\( b_3 = \dfrac{6 + 3}{3!} = \dfrac{3}{2} \)
\( b_4 = \dfrac{6 + 4}{4!} = \dfrac{5}{12} \)
\( b_5 = \dfrac{6 + 5}{5!} = \dfrac{11}{120} \)
(c) seçeneği:
\( (c_n) = \dfrac{(-1)^{n + 1}}{2n + 1} \)
\( c_1 = \dfrac{(-1)^{1 + 1}}{2(1) + 1} = \dfrac{1}{3} \)
\( c_2 = \dfrac{(-1)^{2 + 1}}{2(2) + 1} = -\dfrac{1}{5} \)
\( c_3 = \dfrac{(-1)^{3 + 1}}{2(3) + 1} = \dfrac{1}{7} \)
\( c_4 = \dfrac{(-1)^{4 + 1}}{2(4) + 1} = -\dfrac{1}{9} \)
\( c_5 = \dfrac{(-1)^{5 + 1}}{2(5) + 1} = \dfrac{1}{11} \)
\( (a_n) = \dfrac{n^3 + 18}{6} \) dizisinin kaçıncı terimi \( \dfrac{41}{3} \)'e eşittir?
Çözümü GösterDizinin genel terimini verilen değere eşitleyelim.
\( \dfrac{n^3 + 18}{6} = \dfrac{41}{3} \)
\( n^3 + 18 = 82 \)
\( n^3 = 64 \)
\( n = 4 \)
Dizinin 4. terimi \( \frac{41}{3} \)'e eşittir.
Aşağıdaki dizilerin ilk 5 terimini yazınız.
(a) \( (a_n) = \cos{\dfrac{n\pi}{6}} \)
(b) \( (b_n) = 2\log_{n + 1}(n + 2) \)
(c) \( (c_n) = (-1)^n\sin{\dfrac{n\pi}{4}} \)
Çözümü Göster(a) seçeneği:
\( (a_n) = \cos{\dfrac{n\pi}{6}} \)
\( a_1 = \cos{\dfrac{\pi}{6}} = \dfrac{\sqrt{3}}{2} \)
\( a_2 = \cos{\dfrac{2\pi}{6}} = \dfrac{1}{2} \)
\( a_3 = \cos{\dfrac{3\pi}{6}} = 0 \)
\( a_4 = \cos{\dfrac{4\pi}{6}} = -\dfrac{1}{2} \)
\( a_5 = \cos{\dfrac{5\pi}{6}} = -\dfrac{\sqrt{3}}{2} \)
(b) seçeneği:
\( (b_n) = 2\log_{n + 1}(n + 2) \)
\( b_1 = 2\log_{1 + 1}(1 + 2) = 2\log_2{3} \)
\( b_2 = 2\log_{2 + 1}(2 + 2) = 2\log_3{4} \)
\( b_3 = 2\log_{3 + 1}(3 + 2) = 2\log_4{5} \)
\( b_4 = 2\log_{4 + 1}(4 + 2) = 2\log_5{6} \)
\( b_5 = 2\log_{5 + 1}(5 + 2) = 2\log_6{7} \)
(c) seçeneği:
\( (c_n) = (-1)^n\sin{\dfrac{n\pi}{4}} \)
\( c_1 = (-1)^1\sin{\dfrac{\pi}{4}} = -\dfrac{\sqrt{2}}{2} \)
\( c_2 = (-1)^2\sin{\dfrac{2\pi}{4}} = 1 \)
\( c_3 = (-1)^3\sin{\dfrac{3\pi}{4}} = -\dfrac{\sqrt{2}}{2} \)
\( c_4 = (-1)^4\sin{\dfrac{4\pi}{4}} = 0 \)
\( c_5 = (-1)^5\sin{\dfrac{5\pi}{4}} = \dfrac{\sqrt{2}}{2} \)
Aşağıdaki dizilerin genel terimlerini bulunuz.
(a) \( \dfrac{2}{10}, \dfrac{4}{15}, \dfrac{8}{20}, \dfrac{16}{25}, \ldots \)
(b) \( -\dfrac{2}{9}, -\dfrac{8}{11}, -\dfrac{26}{13}, -\dfrac{80}{15}, \ldots \)
(c) \( -1, \dfrac{8}{9}, -\dfrac{6}{7}, \dfrac{16}{19}, \ldots \)
Çözümü Göster(a) seçeneği:
\( \dfrac{2}{10}, \dfrac{4}{15}, \dfrac{8}{20}, \dfrac{16}{25}, \ldots \)
Dizinin terimlerini düzenleyelim.
\( \dfrac{2^1}{5(1 + 1)}, \dfrac{2^2}{5(2 + 1)}, \dfrac{2^3}{5(3 + 1)}, \dfrac{2^4}{5(4 + 1)}, \ldots \)
\( (a_n) = \dfrac{2^n}{5(n + 1)} \)
(b) seçeneği:
\( -\dfrac{2}{9}, -\dfrac{8}{11}, -\dfrac{26}{13}, -\dfrac{80}{15}, \ldots \)
Dizinin terimlerini düzenleyelim.
\( -\dfrac{3^1 - 1}{2(1) + 7}, -\dfrac{3^2 - 1}{2(2) + 7}, -\dfrac{3^3 - 1}{2(3) + 7}, -\dfrac{3^4 - 1}{2(4) + 7}, \ldots \)
\( (b_n) = -\dfrac{3^{n} - 1}{2n + 7} \)
(c) seçeneği:
\( -1, \dfrac{8}{9}, -\dfrac{6}{7}, \dfrac{16}{19}, \ldots \)
Dizinin terimlerini düzenleyelim.
\( -\dfrac{4}{4}, \dfrac{8}{9}, -\dfrac{12}{14}, \dfrac{16}{19}, \ldots \)
\( -\dfrac{4(1)}{5(1) - 1}, \dfrac{4(2)}{5(2) - 1}, -\dfrac{4(3)}{5(3) - 1}, \dfrac{4(4)}{5(4) - 1}, \ldots \)
Dizinin terimleri bir negatif, bir pozitif şeklinde ilerlediği için terimleri \( (-1)^n \) ile çarpalım.
\( (-1)^1 \cdot \dfrac{4(1)}{5(1) - 1}, (-1)^2 \cdot \dfrac{4(2)}{5(2) - 1}, (-1)^3 \cdot \dfrac{4(3)}{5(3) - 1}, (-1)^4 \cdot \dfrac{4(4)}{5(4) - 1}, \ldots \)
\( (c_n) = (-1)^n \cdot \dfrac{4n}{5n - 1} \)
Aşağıdaki ifadelerden hangileri bir reel sayı dizisinin genel terimidir?
I. \( \dfrac{1}{n^2 - 64} \)
II. \( \dfrac{7}{\sin((n + 1)\pi)} \)
III. \( \dfrac{1}{\cos((n - 1)\pi)} \)
IV. \( \sqrt[4]{100 - n^2} \)
V. \( \sqrt[3]{n^3 - 12n^2} \)
Çözümü GösterI. öncül:
\( \dfrac{1}{n^2 - 64} \)
\( n = 8 \) için ifade tanımsızdır.
\( \dfrac{1}{8^2 - 64} = \dfrac{1}{0} \)
Buna göre ifade bir dizi değildir.
II. öncül:
\( \dfrac{7}{\sin((n + 1)\pi)} \)
Tüm tam sayı \( n \) değerlerinde ifadenin paydası sıfır olduğu için ifade tanımsızdır.
\( \sin(2\pi) = \sin(3\pi) = \sin(4\pi) = \ldots = 0 \)
Buna göre ifade bir dizi değildir.
III. öncül:
\( \dfrac{1}{\cos((n - 1)\pi)} \)
İfadenin paydası farklı \( n \) değerlerinde 1 ve -1 değerleri alır.
\( c_1 = \dfrac{1}{\cos{0}} = 1 \)
\( c_2 = \dfrac{1}{\cos{\pi}} = -1 \)
\( c_3 = \dfrac{1}{\cos(2\pi)} = 1 \)
\( c_4 = \dfrac{1}{\cos(3\pi)} = -1 \)
\( c_5 = \dfrac{1}{\cos(4\pi)} = 1 \)
Bu ifade hiçbir \( n \) değeri için tanımsız değildir.
Buna göre ifade bir dizidir.
IV. öncül:
\( \sqrt[4]{100 - n^2} \)
\( n \gt 10 \) için kök içi sıfırdan küçüktür, dolayısıyla köklü ifade reel sayılarda tanımsız olur.
Buna göre ifade bir dizi değildir.
V. öncül:
\( \sqrt[3]{n^3 - 12n^2} \)
Kök içindeki ifade farklı \( n \) değerlerinde pozitif ya da negatif olabilir, ancak köklü ifadenin derecesi tek sayı olduğu için ifade tüm reel sayılarda tanımlıdır.
Buna göre ifade bir dizidir.
III. ve V. öncüllerdeki ifadeler birer reel sayı dizisinin genel terimidir.
\( (a_n) \) dizisinin ilk 4 teriminin toplamı 119 olduğuna göre, \( k \) kaçtır?
Çözümü GösterDizinin ilk dört terimini bulalım.
\( a_1 = 2k + 3 \)
\( a_2 = 2k + 3 \)
\( a_3 = a_2 + a_1 \)
\( = (2k + 3) + (2k + 3) = 4k + 6 \)
\( a_4 = a_3 + a_2 \)
\( = (4k + 6) + (2k + 3) = 6k + 9 \)
İlk dört terimin toplamını 119'a eşitleyelim.
\( (2k + 3) + (2k + 3) + (4k + 6) + (6k + 9) = 119 \)
\( 14k + 21 = 119 \)
\( k = 7 \) bulunur.
\( (a_n) = \dfrac{3^{2n}}{(n + 3)!} \) dizisi veriliyor.
\( \dfrac{a_{k + 1}}{a_{k + 2}} = \dfrac{4}{3} \)
olduğuna göre, \( k \) kaçtır?
Çözümü GösterDizi genel terimini verilen eşitlikte \( (k + 1) \). ve \( (k + 2) \). terimler için yerine koyalım.
\( \dfrac{\frac{3^{2(k + 1)}}{(k + 1 + 3)!}}{\frac{3^{2(k + 2)}}{(k + 2 + 3)!}} = \dfrac{4}{3} \)
\( \dfrac{\frac{3^{2k + 2}}{(k + 4)!}}{\frac{3^{2k + 4}}{(k + 5)!}} = \dfrac{4}{3} \)
\( \dfrac{3^{2k + 2}}{(k + 4)!} \cdot \dfrac{(k + 5)!}{3^{2k + 4}} = \dfrac{4}{3} \)
\( 3^{-2} \cdot (k + 5) = \dfrac{4}{3} \)
\( k + 5 = \dfrac{4 \cdot 3^2}{3} \)
\( k + 5 = 12 \)
\( k = 7 \) bulunur.
\( (a_n) = -4n^2 + 16n + 5 \) dizisinin en büyük terimi kaçtır?
Çözümü Göster\( -4n^2 + 16n + 5 \) ifadesini sürekli bir fonksiyon olarak düşünürsek grafiği bir paraboldür.
Başkatsayısı negatif (kolları aşağı yönlü) olan bir parabol en büyük değerini tepe noktasında alır.
Parabolün tepe noktası \( T(r, k) \) olmak üzere,
\( r = -\dfrac{b}{2a} = -\dfrac{16}{2(-4)} = 2 \)
Buna göre ifade en büyük değerini \( n = 2 \) değerinde alır.
Bu değeri dizi tanımında yerine koyalım.
\( a_2 = -4(2)^2 + 16(2) + 5 \)
\( = -16 + 32 + 5 = 21 \)
\( (a_n) \) dizisinin en büyük terimi \( a_2 = 21 \) olarak bulunur.
\( (a_n) = \dfrac{n^2 - 4n + k}{n^2 + 1} \)
dizisinin tüm terimlerinin pozitif reel sayı olabilmesi için \( k \)'nın alabileceği en küçük tam sayı değeri kaçtır?
Çözümü GösterGenel terimin paydası her zaman pozitif değer alacağı için, ifadenin pozitif olması için pay pozitif olmalıdır.
Paydaki ikinci dereceden ifadeyi bir sürekli fonksiyon olarak düşünürsek, ifadenin her zaman pozitif olabilmesi için grafiği olan parabol her zaman \( x \) ekseninin üstünde kalmalı, bir diğer ifadeyle bir reel kökü olmamalı, yani ifadenin deltası sıfırdan küçük olmalıdır.
\( \Delta = b^2 - 4ac = (-4)^2 - 4k \lt 0 \)
\( 16 - 4k \lt 0 \)
\( k \gt 4 \)
Buna göre \( k \)'nın alabileceği en küçük tam sayı değeri 5'tir.
\( n \ge 1 \) olmak üzere,
\( (a_n) = 2n^2 + n - 15 \) dizisinin kaç terimi negatiftir?
Çözümü Gösterİkinci dereceden dizinin negatif değer aldığı aralığı bulmak için ifadeyi önce çarpanlarına ayıralım.
\( 2n^2 + n - 15 = (n + 3)(2n - 5) \)
Dizinin genel terimini sürekli bir fonksiyon olarak düşünürsek, grafiği pozitif başkatsayılı bir parabol olan bu ifadenin negatif değer aldığı aralık kökleri arasındaki açık aralık, yani \( n \in (-3, \frac{5}{2}) \) aralığıdır.
Dizinin ilk terimi \( a_1 \) olduğu için dizi sadece \( n = 1 \) ve \( n = 2 \) indis değerlerinde negatif değer alır. Buna göre cevap 2 olur.
\( a_1 = 2(1)^2 + 1 - 15 = -12 \)
\( a_2 = 2(2)^2 + 2 - 15 = -5 \)
\( n = 3 \) indis değerinde dizinin pozitif değer aldığını kontrol edebiliriz.
\( a_3 = 2(3)^2 + 3 - 15 = 6 \)
\( (a_n) = \dfrac{n^2 + 12}{n} \) dizisinin kaç terimi 8'den küçüktür?
Çözümü GösterGenel terimin 8'den küçük değerler ürettiği \( n \) değerlerini bulalım.
\( \dfrac{n^2 + 12}{n} \lt 8 \)
Tüm terimleri eşitsizliğin sol tarafında toplayalım.
\( \dfrac{n^2 + 12}{n} - 8 \lt 0 \)
\( \dfrac{n^2 - 8n + 12}{n} \lt 0 \)
\( \dfrac{(n - 2)(n - 6)}{n} \lt 0 \)
Pay ve paydadaki her bir çarpanı sıfır yapan \( \{ 0, 2, 6 \} \) değerleri eşitsizliğin kritik noktalarıdır.
Bu kritik noktalar reel sayı doğrusunda \( (-\infty, 0) \), \( (0, 2) \), \( (2, 6) \) ve \( (6, \infty) \) aralıklarını oluşturur.
Bir işaret tablosu hazırlayalım.
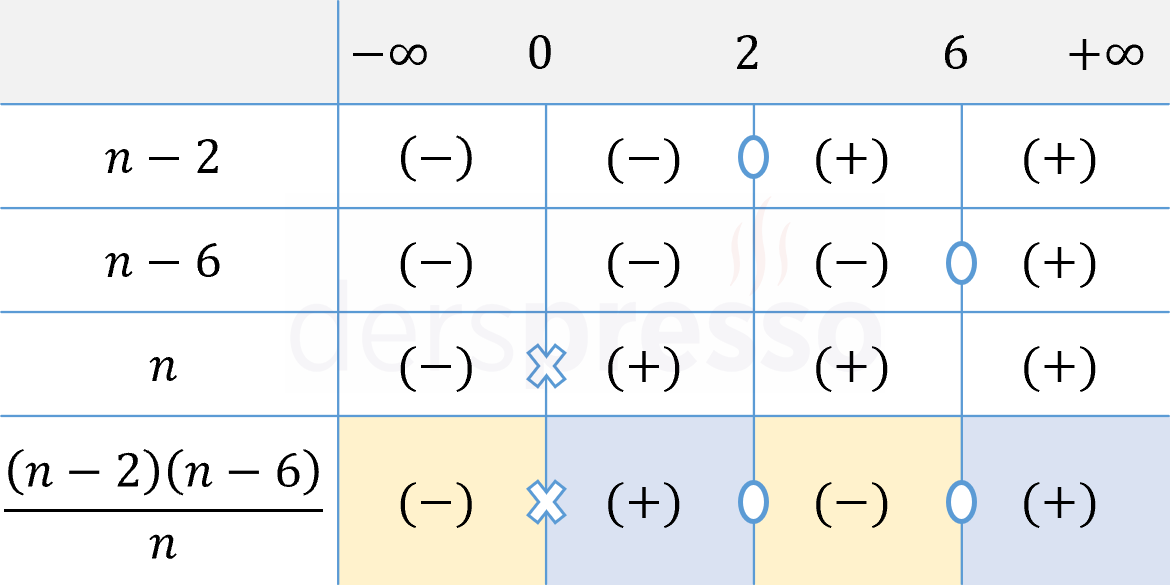
Pay ve paydadaki çarpanları ve her aralıktaki işaretlerini tabloya birer satır olarak ekleyelim.
Rasyonel ifadenin her aralıktaki işareti, çarpanların ilgili aralıktaki işaretlerinin çarpımına eşittir.
Rasyonel ifade paydayı sıfır yapan \( n = 0 \) değerinde tanımsız, payı sıfır yapan \( \{ 2, 6 \} \) değerlerinde sıfır olur.
Verilen eşitsizlikte \( \lt \) sembolü kullanıldığı için rasyonel ifadenin negatif olduğu aralık ve değerler eşitsizliğin çözüm kümesi olur.
Çözüm kümesi: \( n \in (-\infty, 0) \cup (2, 6) \)
\( n \) negatif olamayacağı için alabileceği değerler 3, 4, 5 olur.
Buna göre \( a_n \) dizisinin üç terimi 8'den küçüktür.
\( (a_n) = \dfrac{n^2 + 5n - 126}{n^2 + n + 1} \) dizisinin ilk pozitif terimi kaçıncı terimdir?
Çözümü GösterDizinin genel teriminin payını çarpanlarına ayıralım.
\( (a_n) = \dfrac{(n - 9)(n + 14)}{n^2 + n + 1} \)
Payda tüm \( n \) değerleri için pozitiftir.
Buna göre \( (a_n) \) dizisi payı pozitif yapan \( n \) değerlerinde pozitif, payı negatif yapan \( n \) değerlerinde negatif olur.
Payı (dolayısıyla dizinin terimlerini) pozitif yapan \( n \) değerlerini bulalım.
\( (n - 9)(n + 14) \gt 0 \)
Bu eşitsizliğin sağlandığı aralık, çarpanları sıfır yapan değerlerin dışında kalan \( n \in (-\infty, -14) \cup (9, \infty) \) aralığıdır.
\( n \) negatif olamayacağı için dizinin pozitif terimleri \( n \)'nin \( (9, \infty) \) aralığındaki değerlerdir.
O halde dizinin ilk pozitif terimi 10. terimdir.
\( (a_n) = \log_2(n + 3) \) dizisinin kaç terimi \( [5, 6) \) aralığındadır?
Çözümü Göster\( 5 \le \log_2(n + 3) \lt 6 \)
Eşitsizliğin taraflarının 2 tabanında üssünü alalım.
\( 2^5 \le n + 3 \lt 2^6 \)
\( 32 \le n + 3 \lt 64 \)
\( 29 \le n \lt 61 \)
Bu aralıkta \( 60 - 29 + 1 = 32 \) tane tam sayı \( n \) değeri vardır.
\( (a_n) = (-1)^{n - 5} \cdot \dfrac{4n + 78}{n} \)
dizisinin kaç terimi pozitif tam sayıdır?
Çözümü GösterDizinin genel terimini düzenleyelim.
\( (a_n) = (-1)^{n - 5} \cdot (4 + \dfrac{78}{n}) \)
Dizinin terimlerinin pozitif tam sayı olması için \( (-1)^{n - 5} \) ifadesinde \( n - 5 \) çift sayı, dolayısıyla \( n \) tek sayı olmalıdır.
Ayrıca dizinin terimlerinin tam sayı olması için \( \frac{78}{n} \) ifadesi tam sayı olmalıdır, dolayısıyla \( n \) 78'i tam bölmelidir.
\( 78 = 2 \cdot 3 \cdot 13 \)
78'in pozitif tam bölenleri aşağıdaki gibidir.
\( 1, 2, 3, 6, 13, 26, 39, 78 \)
Bu sayılardan tek sayı olanlar aşağıdaki gibidir.
\( 1, 3, 13, 39 \)
Buna göre dizinin 4 terimi pozitif tam sayıdır.
\( (a_n) = 12n - 20 \) dizisinin kaç terimi üç basamaklıdır?
Çözümü GösterGenel terimin istenen koşulu sağlayan değerler ürettiği \( n \) değerlerini bulalım.
Dizinin genel terimini incelediğimizde negatif üç basamaklı terim olamayacağını görebiliriz.
\( 100 \le 12n - 20 \le 999 \)
\( 120 \le 12n \le 1019 \)
\( 10 \le n \le \dfrac{1019}{12} \)
Buna göre \( n \in [10, 84] \) aralığında dizinin terimleri üç basamaklıdır.
Dizinin genel terimi doğrusal ve artan olduğu için aynı değeri birden fazla \( n \) değerinde alamaz.
O halde dizinin \( 84 - 10 + 1 = 75 \) terimi üç basamaklıdır.
\( (a_n) \) dizisinin ilk \( n \) teriminin toplamı \( S_n = n^2 + 3n \) olduğuna göre, dizinin 20. terimi nedir?
Çözümü Gösterİlk \( n \) teriminin toplam formülü bilinen bir dizinin herhangi bir terimini bu formülü kullanarak bulabiliriz.
Bir dizinin \( n \). terimi, ilk \( n \) terimin toplamının ilk \( (n - 1) \) terimin toplamından farkına eşittir.
\( a_{n} = S_{n} - S_{n - 1} \)
\( S_{20} = 20^2 + 3(20) = 460 \)
\( S_{19} = 19^2 + 3(19) = 418 \)
\( a_{20} = S_{20} - S_{19} \)
\( = 460 - 418 = 42 \) bulunur.
\( (a_n) = \dfrac{2}{n^2 + 2n} \) olmak üzere,
\( (a_n) \) dizisinin ilk 12 teriminin toplamı kaçtır?
Çözümü Göster\( (a_n) \) dizisinin genel terimini basit kesirlerin toplamı şeklinde yazalım.
\( (a_n) = \dfrac{2}{n(n + 2)} = \dfrac{1}{n} - \dfrac{1}{n + 2} \)
\( (a_n) \) dizisinin ilk 12 teriminin toplamını yazalım.
\( \underbrace{\dfrac{1}{1} - \dfrac{1}{3}}_{a_1} + \underbrace{\dfrac{1}{2} - \dfrac{1}{4}}_{a_2} + \underbrace{\dfrac{1}{3} - \dfrac{1}{5}}_{a_3} + \ldots + \underbrace{\dfrac{1}{12} - \dfrac{1}{14}}_{a_{12}} \)
Bu toplamda dizinin her teriminin ilk terimi kendinden iki önceki terimin ikinci terimi ile sadeleşir.
Terimler bu şekilde sadeleşince geriye dizinin ilk iki teriminin birinci terimleri ve son iki terimin ikinci terimleri kalır.
\( = \dfrac{1}{1} + \dfrac{1}{2} - \dfrac{1}{13} - \dfrac{1}{14} \)
\( = \dfrac{246}{182} = \dfrac{123}{91} \) bulunur.
\( (a_n) \) dizisinin herhangi ardışık üç teriminin çarpımı birbirine eşittir.
\( a_3 \cdot a_4 = a_5 = 4 \) eşitliği veriliyor.
\( \dfrac{a_2 \cdot a_3 \cdot a_4 \cdot \ldots \cdot a_{10}}{a_{11} \cdot a_{12} \cdot a_{13}} \) ifadesinin değeri nedir?
Çözümü Göster\( a_3 \cdot a_4 = a_5 = 4 \) eşitliğini kullarak ardışık üç terimin çarpımını bulalım.
\( a_3 \cdot a_4 \cdot a_5 = 4 \cdot 4 = 16 \)
Dizinin herhangi ardışık üç teriminin çarpımı birbirine eşittir.
\( a_2 \cdot a_3 \cdot a_4 = 16 \)
\( a_5 \cdot a_6 \cdot a_7 = 16 \)
\( a_8 \cdot a_9 \cdot a_{10} = 16 \)
\( a_{11} \cdot a_{12} \cdot a_{13} = 16 \)
\( \dfrac{a_2 \cdot a_3 \cdot a_4 \cdot \ldots \cdot a_{10}}{a_{11} \cdot a_{12} \cdot a_{13}} \)
\( = \dfrac{16 \cdot 16 \cdot 16}{16} \)
\( = 256 \) bulunur.
\( (a_n) = \dfrac{3n - 40}{n} \) dizisi veriliyor.
\( a_n \) dizisinin terimlerini tam sayı yapan \( n \) değerlerinin kümesi \( A \), negatif yapan \( n \) değerlerinin kümesi \( B \) olduğuna göre, \( A \cap B \) kümesi kaç elemanlıdır?
Çözümü Göster\( (a_n) = \dfrac{3n - 40}{n} = 3 - \dfrac{40}{n} \)
Dizinin terimlerinin tam sayı olması için \( \frac{40}{n} \) ifadesi tam sayı olmalıdır.
40'ı tam bölen pozitif tam sayı \( n \) değerlerinde dizinin terimleri tam sayı olur.
\( A = \{1, 2, 4, 5, 8, 10, 20, 40\} \)
Dizinin terimlerini negatif yapan \( n \) değerlerini bulalım.
\( 3 - \dfrac{40}{n} \lt 0 \)
\( \dfrac{40}{n} \gt 3 \)
Diziyi negatif yapan değerler aşağıdaki gibidir.
\( B = \{1, 2, 3, \ldots, 13\} \)
\( A \cap B = \{1, 2, 4, 5, 8, 10\} \)
\( s(A \cap B) = 6 \) bulunur.
dizisinin ilk 100 teriminin toplamı kaçtır?
Çözümü GösterDizinin terimlerini hesaplayalım.
\( a_1 = 2(1) + 1 = 3 \)
\( a_2 = 4 - 2(2) = 0 \)
\( a_3 = 2(3) + 1 = 7 \)
\( a_4 = 4 - 2(4) = -4 \)
\( a_5 = 2(5) + 1 = 11 \)
\( a_6 = 4 - 2(6) = -8 \)
\( \vdots \)
\( a_{99} = 2(99) + 1 = 199 \)
\( a_{100} = 4 - 2(100) = -196 \)
\( (a_n) \) dizisinin ilk 100 teriminin toplamını yazalım.
\( \underbrace{3 + 0}_{3} + \underbrace{7 + (-4)}_{3} + \underbrace{11 + (-8)}_{3} \ldots + \underbrace{199 + (-196)}_{3} \)
Bu toplamda terimleri ikişerli gruplarsak ardışık iki terimin toplamı 3 olur.
Dizinin ilk 100 teriminde toplamları 3 olan 50 tane ikili grup vardır.
\( 50 \cdot 3 = 150 \) bulunur.
\( (a_n) \) dizisinin ilk \( n \) teriminin toplamı \( S_n = n^2 + 4n + 2 \) olduğuna göre, \( a_4 + a_7 \) toplamı kaçtır?
Çözümü Gösterİlk \( n \) terim toplam formülü kullanılarak dizinin \( n \). terimi aşağıdaki formülle bulunabilir.
\( a_n = S_n - S_{n-1} \)
\( a_4 = S_4 - S_3 \)
\( = (4^2 + 4(4) + 2) - (3^2 + 4(3) + 2) \)
\( = 34 - 23 = 11 \)
\( a_7 = S_7 - S_6 \)
\( = (7^2 + 4(7) + 2) - (6^2 + 4(6) + 2) \)
\( = 79 - 62 = 17 \)
\( a_4 + a_7 = 11 + 17 = 28 \) bulunur.
\( B = \{1, 2, 3, \ldots, 50\} \) olmak üzere,
\( b_n: B \to \mathbb{R} \)
\( (b_n) = \sin{\frac{n\pi}{2}} \) dizisinin terimlerinin toplamı kaçtır?
Çözümü GösterDizinin ilk terimlerini bulalım.
\( b_1 = \sin{\frac{1\pi}{2}} = 1 \)
\( b_2 = \sin{\frac{2\pi}{2}} = 0 \)
\( b_3 = \sin{\frac{3\pi}{2}} = -1 \)
\( b_4 = \sin{\frac{4\pi}{2}} = 0 \)
\( b_5 = \sin{\frac{5\pi}{2}} = 1 \)
\( b_6 = \sin{\frac{6\pi}{2}} = 0 \)
Buna göre dizinin periyodu 4 olur, yani dizinin her ardışık dört teriminin toplamı 0 olur.
50'nin 4'e bölümünden kalan 2 olduğu için son iki terim \( a_{49} = 1 \) ve \( a_{50} = 0 \) olur.
\( \underbrace{b_1 + b_2 + \ldots + b_{48}}_{0} + b_{49} + b_{50} = 1 + 0 = 1 \) bulunur.
Aşağıdaki dizilerin genel terimlerini bulunuz.
(a) \( 0, -2, 0, 2, 0, \ldots \)
(b) \( \dfrac{\ln{6}}{\sqrt{2}}, \dfrac{\ln{11}}{2}, \dfrac{4\ln{2}}{\sqrt{6}}, \dfrac{\ln{21}}{2\sqrt{2}}, \ldots \)
(c) \( 2\sqrt{5}, \sqrt{7}, 0 , \sqrt{11}, 2\sqrt{13}, \ldots \)
Çözümü Göster(a) seçeneği:
\( 0, -2, 0, 2, 0, \ldots \)
Dizinin terimlerini düzenleyelim.
\( 2(0), 2(-1), 2(0), 2(1), 2(0), \ldots \)
Parantez içerisindeki değerleri kosinüs cinsinden ifade edebiliriz.
\( 2(\cos{\frac{\pi}{2}}), 2(\cos{\frac{2\pi}{2}}), 2(\cos{\frac{3\pi}{2}}), 2(\cos{\frac{4\pi}{2}}), 2(\cos{\frac{5\pi}{2}}), \ldots \)
\( (a_n) = 2\cos{\dfrac{n\pi}{2}} \)
(b) seçeneği:
\( \dfrac{\ln{6}}{\sqrt{2}}, \dfrac{\ln{11}}{2}, \dfrac{4\ln{2}}{\sqrt{6}}, \dfrac{\ln{21}}{2\sqrt{2}}, \ldots \)
Dizinin terimlerini düzenleyelim.
\( \dfrac{\ln{6}}{\sqrt{2}}, \dfrac{\ln{11}}{\sqrt{4}}, \dfrac{\ln{16}}{\sqrt{6}}, \dfrac{\ln{21}}{\sqrt{8}}, \ldots \)
\( \dfrac{\ln(5 + 1)}{\sqrt{2}}, \dfrac{\ln(10 + 1)}{\sqrt{4}}, \dfrac{\ln(15 + 1)}{\sqrt{6}}, \dfrac{\ln(20 + 1)}{\sqrt{8}}, \ldots \)
\( (b_n) = \dfrac{\ln(5n + 1)}{\sqrt{2n}} \)
(c) seçeneği:
\( 2\sqrt{5}, \sqrt{7}, 0 , \sqrt{11}, 2\sqrt{13}, \ldots \)
Dizinin terimlerini düzenleyelim.
\( 2\sqrt{5}, \sqrt{7}, 0\sqrt{9}, \sqrt{11}, 2\sqrt{13}, \ldots \)
\( 2\sqrt{2 + 3}, \sqrt{4 + 3}, 0\sqrt{6 + 3}, \sqrt{8 + 3}, 2\sqrt{10 + 3}, \ldots \)
Köklü ifadelerin katsayıları \( 2, 1, 0, 1, 2, \ldots \) şeklinde ilerlemektedir.
Bu katsayıları sinüs cinsinden ifade edebiliriz.
\( (\sin{\dfrac{\pi}{2}} + 1)\sqrt{2 + 3}, (\sin{\dfrac{2\pi}{2}} + 1)\sqrt{4 + 3}, (\sin{\dfrac{3\pi}{2}} + 1)\sqrt{6 + 3}, (\sin{\dfrac{4\pi}{2}} + 1)\sqrt{8 + 3}, (\sin{\dfrac{5\pi}{2}} + 1)\sqrt{10 + 3}, \ldots \)
\( (c_n) = (\sin(\dfrac{n\pi}{2}) + 1)\sqrt{2n + 3} \)
\( (a_n) = \dfrac{n^2 + 2n + 6}{n + 5} \)
dizisinin tam sayı terimlerinin toplamı kaçtır?
Çözümü GösterDizinin genel teriminin payı ve paydası arasında polinom bölmesi yaparsak bölüm \( n - 3 \), kalan \( 21 \) olur.
\( (a_n) = \dfrac{(n + 5)(n - 3) + 21}{n + 5} \)
\( = n - 3 + \dfrac{21}{n + 5} \)
Bu dizinin bir teriminin tam sayı olması için kesirli ifade tam sayı olmalıdır, bunun için paydadaki ifade 21'i tam bölmelidir.
\( 21 = 3 \cdot 7 \)
21'in pozitif tam bölenleri aşağıdaki gibidir.
\( 1, 3, 7, 21 \)
\( n \ge 1 \) olduğu için, paydadaki \( n + 5 \) ifadesi \( n \)'nin iki değerinde bu değerlerden biri olur.
\( n \in \{2, 16\} \)
Bu iki indis değeri için dizinin terimlerini bulalım.
\( a_2 = \dfrac{2^2 + 2(2) + 6}{2 + 5} = 2 \)
\( a_{16} = \dfrac{16^2 + 2(16) + 6}{16 + 5} = 14 \)
Bu iki terimin toplamı \( 2 + 14 = 16 \) olarak bulunur.
\( (a_n) = \dfrac{1}{n^2 + 5n + 6} \) dizisi tanımlanıyor.
Buna göre, \( (a_n) \) dizisinin ilk 18 teriminin toplamı kaçtır?
Çözümü GösterBasit kesirlere ayırma yöntemiyle dizinin genel terimini basit kesirlerin toplamı şeklinde yazalım.
\( \dfrac{1}{n^2 + 5n + 6} = \dfrac{1}{(n + 3)(n + 2)} \)
\( = \dfrac{A}{n + 3} + \dfrac{B}{n + 2} \)
\( = \dfrac{A(n + 2)}{(n + 3)(n + 2)} + \dfrac{B(n + 3)}{(n + 2)(n + 3)} \)
Kesirlerin paylarını eşitleyelim.
\( An + 2A + Bn + 3B = 1 \)
Bu ifadeyi değişkeni \( n \) olan bir polinom olarak düşünerek polinomların eşitliğini kullanalım.
İki polinomun eşitliğinde dereceleri aynı olan terimlerin katsayıları eşittir.
\( An + Bn = 0 \Longrightarrow A = -B \)
\( 2A + 3B = 1 \)
\( -2B + 3B = 1 \Longrightarrow B = 1 \)
\( A = -1, \quad B = 1 \)
Buna göre genel terimin basit kesirlerin toplamı şeklinde yazılışı aşağıdaki gibi olur.
\( (a_n) = \dfrac{1}{(n + 3)(n + 2)} = \dfrac{-1}{n + 3} + \dfrac{1}{n + 2} \)
İlk 18 terimi yazalım
1. terim: \( \dfrac{-1}{4} + \dfrac{1}{3} \)
2. terim: \( \dfrac{-1}{5} + \dfrac{1}{4} \)
3. terim: \( \dfrac{-1}{6} + \dfrac{1}{5} \)
...
18. terim: \( \dfrac{-1}{21} + \dfrac{1}{20} \)
Tüm terimleri alt alta topladığımızda dizinin her teriminin birinci terimi sonraki terimin ikinci terimi ile birbirini götürür.
Terimlerin toplamını bulalım.
\( \dfrac{1}{3} + \dfrac{-1}{21} = \dfrac{7-1}{21} = \dfrac{2}{7} \) bulunur.
\( a_1 = -3 \) ve \( a_{n+1} - a_n = n - 3 \) olduğuna göre,
\( (a_n) \) dizisinin genel terimi nedir?
Çözümü Göster\( a_{n+1} - a_n = n - 3 \) eşitliğini farklı \( n \) değerleri için yazalım.
\( n = 1 \) için:
\( a_2 - a_1 = 1 - 3 = -2 \)
\( n = 2 \) için:
\( a_3 - a_2 = 2 - 3 = -1 \)
\( n = 3 \) için:
\( a_4 - a_3 = 3 - 3 = 0 \)
\( \vdots \)
\( n = n - 1 \) için:
\( a_n - a_{n-1} = (n - 1) - 3 = n - 4 \)
Bu eşitlikleri taraf tarafa toplayalım.
\( (a_2 - a_1) + (a_3 - a_2) + \ldots + (a_n - a_{n-1}) = (-2) + (-1) + 0 + \ldots + (n - 4) \)
\( a_n - a_1 = (-2) + (-1) + 0 + \ldots + (n - 4) \)
Ardışık sayılarda toplama işlemi formülünü kullanalım.
\( a_n - a_1 = \dfrac{(n - 4)(n - 3)}{2} + (-2) + (-1) \)
\( a_1 = -3 \) değerini yerine yazalım.
\( a_n - (-3) = \dfrac{(n - 4)(n - 3)}{2} - 3 \)
\( (a_n) = \dfrac{(n - 4)(n - 3)}{2} - 6 \)
\( = \dfrac{n^2 - 7n + 12 - 12}{2} \)
\( = \dfrac{n^2 - 7n}{2} \)
\( = \dfrac{n(n - 7)}{2} \) bulunur.
\( K_n = \sin{\dfrac{n\pi}{2}} + 4 \)
\( K_n \) ifadesi bir \( a_n \) dizisinin ilk \( n \) teriminin çarpımını vermektedir.
Buna göre aşağıdaki ifadelerden hangileri doğrudur?
I. \( a_2 = a_6 \)
II. \( a_2 \cdot a_3 = 3 \)
III. \( a_1 \cdot a_6 = 4 \)
Çözümü Gösterİlk \( n \) terimin çarpımını hesaplayarak sırayla \( (a_n) \) dizisinin terimlerini bulalım.
\( K_1 = \sin{\dfrac{\pi}{2}} + 4 = 5 \)
\( a_1 = 5 \)
\( K_2 = \sin{\dfrac{2\pi}{2}} + 4 = 4 \)
\( K_2 = K_1 \cdot a_2 \)
\( 4 = 5 \cdot a_2 \)
\( a_2 = \dfrac{4}{5} \)
\( K_3 = \sin{\dfrac{3\pi}{2}} + 4 = 3 \)
\( K_3 = K_2 \cdot a_3 \)
\( 3 = 4 \cdot a_3 \)
\( a_3 = \dfrac{3}{4} \)
\( K_4 = \sin{\dfrac{4\pi}{2}} + 4 = 4 \)
\( K_4 = K_3 \cdot a_4 \)
\( 4 = 3 \cdot a_4 \)
\( a_4 = \dfrac{4}{3} \)
\( K_5 = \sin{\dfrac{5\pi}{2}} + 4 = 5 \)
\( K_5 = K_4 \cdot a_5 \)
\( 5 = 4 \cdot a_5 \)
\( a_5 = \dfrac{5}{4} \)
\( K_6 = \sin{\dfrac{6\pi}{2}} + 4 = 4 \)
\( K_6 = K_5 \cdot a_6 \)
\( 4 = 5 \cdot a_6 \)
\( a_6 = \dfrac{4}{5} \)
I. ifade \( a_2 = a_6 = \frac{4}{5} \) olduğu için doğrudur.
II. ifade \( a_2 \cdot a_3 = \frac{4}{5} \cdot \frac{3}{4} = \frac{3}{5} \) olduğu için doğru değildir.
III. ifade \( a_1 \cdot a_6 = 5 \cdot \frac{4}{5} = 4 \) olduğu için doğrudur.
Buna göre I. ve III. ifadeler doğrudur.
\( (a_n) = 3^{2^n} + 1 \)
\( a_1 \cdot a_2 \cdot \ldots \cdot a_9 = \dfrac{3^x - 1}{8} \)
olduğuna göre, \( x \) kaçtır?
Çözümü GösterSırayla dizinin terimlerini hesaplayalım.
\( a_1 = 3^{2^1} + 1 \)
\( a_2 = 3^{2^2} + 1 \)
\( a_3 = 3^{2^3} + 1 \)
\( \vdots \)
\( a_9 = 3^{2^9} + 1 \)
İlk 9 terimin çarpımını bulalım.
\( a_1 \cdot a_2 \cdot \ldots \cdot a_9 = \dfrac{3^x - 1}{8} \)
\( (3^2 + 1)(3^{2^2} + 1)(3^{2^3} + 1)\ldots(3^{2^9} + 1) = \dfrac{3^x - 1}{8} \)
Eşitliğin her iki tarafını \( 3^2 - 1 \) ile çarpalım.
\( (3^2 - 1)(3^2 + 1)(3^{2^2} + 1)(3^{2^3} + 1)\ldots(3^{2^9} + 1) = \dfrac{(3^x - 1)(3^2 - 1)}{8} \)
Eşitliğin solundaki ilk 2 çarpan kare farklı özdeşliği oluşturur.
\( (3^2 - 1)(3^2 + 1) = 3^4 - 1 \)
\( (3^4 - 1)(3^4 + 1)(3^{2^3} + 1)\ldots(3^{2^9} + 1) = \dfrac{(3^x - 1)8}{8} \)
Eşitliğin solundaki ilk 2 çarpan kare farklı özdeşliği oluşturur.
\( (3^4 - 1)(3^4 + 1) = 3^8 - 1 \)
\( (3^8 - 1)(3^8 + 1)\ldots(3^{2^9} + 1) = 3^x - 1 \)
Eşitliğin solundaki tüm çarpanlar bu şekilde sadeleşir.
\( 3^{2^{10}} - 1 = 3^x - 1 \)
\( x = 2^{10} \) olarak bulunur.
\( (a_n) = 7n + 2 \) sayı dizisinin ilk 105 terimi \( 91623 \ldots \) şeklinde yan yana yazılarak bir sayı oluşturuluyor.
Oluşan sayının 8 ile bölümünden kalan kaçtır?
Çözümü GösterBir sayının son 3 basamağındaki sayı 8 ile tam bölünüyorsa o sayı 8 ile tam bölünür.
Sayı 8 ile tam bölünmüyorsa son 3 basamağının 8 ile bölümünden kalan, o sayının 8 ile bölümünden kalana eşittir.
Sayının son 3 basamağını bulmak için \( (a_n) \) dizisinin 105. terimini bulalım.
\( a_{105} = 7 \cdot 105 + 2 = 737 \)
737 sayısı 3 basamaklı olduğu için oluşan sayının son üç basamağını oluşturur.
737 sayısının 8 ile bölümünden kalanı bulalım.
\( 737 = 8 \cdot 92 + 1 \)
Buna göre \( 91623 \ldots 737 \) sayısının 8 ile bölümünden kalan 1'dir.
\( (a_n) = \dfrac{37!}{3^n} \)
dizisinin kaç terimi tam sayıdır?
Çözümü GösterFaktöriyel bölümünde gördüğümüz yöntemi kullanarak 37! sayısında kaç tane 3 çarpanı olduğunu bulalım.
\( 37! \) sayısının içinde:
3'ün her katı için \( \floor{37/3} = 12 \) tane,
9'un her katı için \( \floor{12/3} = 4 \) tane,
27'nin her katı için \( \floor{4/3} = 1 \) tane 3 çarpanı vardır.
Toplamda \( 12 + 4 + 1 = 17 \) tane 3 çarpanı vardır.
Buna göre 37! sayısındaki 3 çarpanlarını ayırdığımızda sayıyı \( 37! = 3^{17} \cdot A \) şeklinde yazabiliriz.
\( (a_n) = \dfrac{3^{17} \cdot A}{3^n} \)
Dolayısıyla \( n \le 17 \) için paydadaki 3'ler sadeleşecek ve terim bir tam sayı olacaktır.
Buna göre dizinin 17 terimi tam sayıdır.