Özel Sayı Dizileri
Bu bölümde önceki bölümlerde incelediğimiz aritmetik, geometrik ve ikinci dereceden diziler dışındaki bazı özel dizileri inceleyeceğiz.
Fibonacci Dizisi
İlk iki terimi 0 ve 1 olan ve sonraki her terimi kendisinden önceki iki terimin toplamına eşit olan sayı dizisine Fibonacci dizisi denir.
\( F_n = \begin{cases} 0 & n = 0 \\ 1 & n = 1 \\ F_{n - 1} + F_{n - 2} & n \gt 1 \end{cases} \)
\( (F_n) = (0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, \ldots) \)
Fibonacci dizisinde bir terim ile kendisinden önceki terimlerin toplamı arasında aşağıdaki ilişki vardır.
\( n \gt 2 \) olmak üzere,
\( F_n = F_0 + F_1 + F_2 + \ldots + F_{n - 2} + 1 \)
\( F_7 = F_0 + F_1 + F_2 + \ldots + F_5 + 1 \)
\( 13 = 0 + 1 + 1 + 2 + 3 + 5 + 1 \)
Fibonacci dizisinin terimleri büyüdükçe ardışık terimlerin oranı altın orana yaklaşır.
\( \phi \) altın oran olmak üzere,
\( \lim\limits_{n \to \infty} {\dfrac{F_n}{F_{n-1}}} = \phi = \dfrac{1 + \sqrt{5}}{2} = 1,618... \)
İSPATI GÖSTER
Fibonacci dizisinin ardışık iki teriminin oranını yazalım.
\( \dfrac{F_n}{F_{n-1}} \)
Fibonacci dizisinde her terim önceki iki terimin toplamına eşittir.
\( \dfrac{F_n}{F_{n-1}} = \dfrac{F_{n-1} + F_{n-2}}{F_{n-1}} \)
\( \dfrac{F_n}{F_{n-1}} = 1 + \dfrac{F_{n-2}}{F_{n-1}} \)
Tarafların \( n \to \infty \) iken limitini alalım.
\( \lim\limits_{n \to \infty} {\dfrac{F_n}{F_{n-1}}} = 1 + \lim\limits_{n \to \infty} {\dfrac{F_{n-2}}{F_{n-1}}} \)
Fibonacci dizisinin ardışık iki teriminin oranının \( n \to \infty \) iken limitinin \( L \) olduğunu varsayalım.
\( L \in \mathbb{R} \) olmak üzere,
\( \lim\limits_{n \to \infty} {\dfrac{F_n}{F_{n-1}}} = L \)
\( n \to \infty \) iken \( \frac{F_n}{F_{n-1}} \) ve \( \frac{F_{n-1}}{F_{n-2}} \) oranları aynı limit değerine yaklaşır.
Bu iki limit değerini yukarıdaki eşitlikte yerine koyalım.
\( L = 1 + \dfrac{1}{L} \)
\( L^2 = L + 1 \)
\( L^2 - L - 1 = 0 \)
İkinci dereceden denklemlerin kök bulma formülünü kullanalım.
\( L_{1,2} = \dfrac{-b \pm \sqrt{b^2 - 4ac}}{2a} \)
\( = \dfrac{-(-1) \pm \sqrt{(-1)^2 - 4(1)(-1)}}{2(1)} \)
\( = \dfrac{1 \pm \sqrt{5}}{2} \)
Fibonacci dizisinin terimleri pozitif olduğu için \( L \) negatif olamaz.
\( L = \dfrac{1 + \sqrt{5}}{2} \)
Bulduğumuz değer altın orana eşittir.
\( = \phi = 1,618... \)
Üçgensel Sayı Dizisi
\( 1 \)'den bir \( n \) sayısına kadarki sayma sayılarının toplamına eşit olan sayılara üçgensel sayı, üçgensel sayılardan oluşan sayı dizisine üçgensel sayı dizisi denir.
Üçgensel sayı dizisinin genel terimi ve bazı terimleri aşağıdaki gibidir. Üçgensel sayı dizisinin \( n \). terimi \( T_n \) şeklinde de ifade edilir.
\( T_n = (a_n) = 1 + 2 + 3 + \ldots + n = \dfrac{n(n + 1)}{2} \)
\( = (1, 1 + 2, 1 + 2 + 3, \) \( 1 + 2 + 3 + 4, \ldots) \)
\( = (1, 3, 6, 10, 15, 21, 28, \) \( 36, 45, 55, \ldots) \)
Üçgensel sayı dizisinin \( n \). terimi, \( n \) satırdan oluşan ve \( n \). satırında \( n \) nokta bulunan bir eşkenar üçgendeki toplam nokta sayısına karşılık gelir.

Üçgensel sayı dizileri özyinelemeli dizi şeklinde aşağıdaki şekilde ifade edilebilir.
\( a_1 = 1 \) olmak üzere,
\( a_n = a_{n - 1} + n \)
İSPATI GÖSTER
\( a_n = \dfrac{n(n + 1)}{2} \)
\( a_{n - 1} = \dfrac{(n - 1)n}{2} \)
İki ifadeyi taraf tarafa çıkaralım.
\( a_n - a_{n - 1} = \dfrac{n(n + 1)}{2} - \dfrac{(n - 1)n}{2} \)
\( a_n - a_{n - 1} = \dfrac{n^2 + n - (n^2 - n)}{2} \)
\( a_n - a_{n - 1} = n \)
\( a_{n - 1} \) terimini eşitliğin sağ tarafına alalım.
\( a_n = a_{n - 1} + n \)
Karesel Sayı Dizisi
\( n^2 \) şeklinde yazılabilen sayılara karesel sayı, karesel sayılardan oluşan sayı dizisine karesel sayı dizisi denir.
Karesel sayı dizisinin genel terimi ve bazı terimleri aşağıdaki gibidir.
\( (a_n) = n^2 \)
\( = (1^2, 2^2, 3^2, 4^2, 5^2, \ldots) \)
\( = (1, 4, 9, 16, 25, \ldots) \)
Karesel sayı dizisinin \( n \). terimi, bir kenarı \( n \) birim olan karenin alanına karşılık gelir.
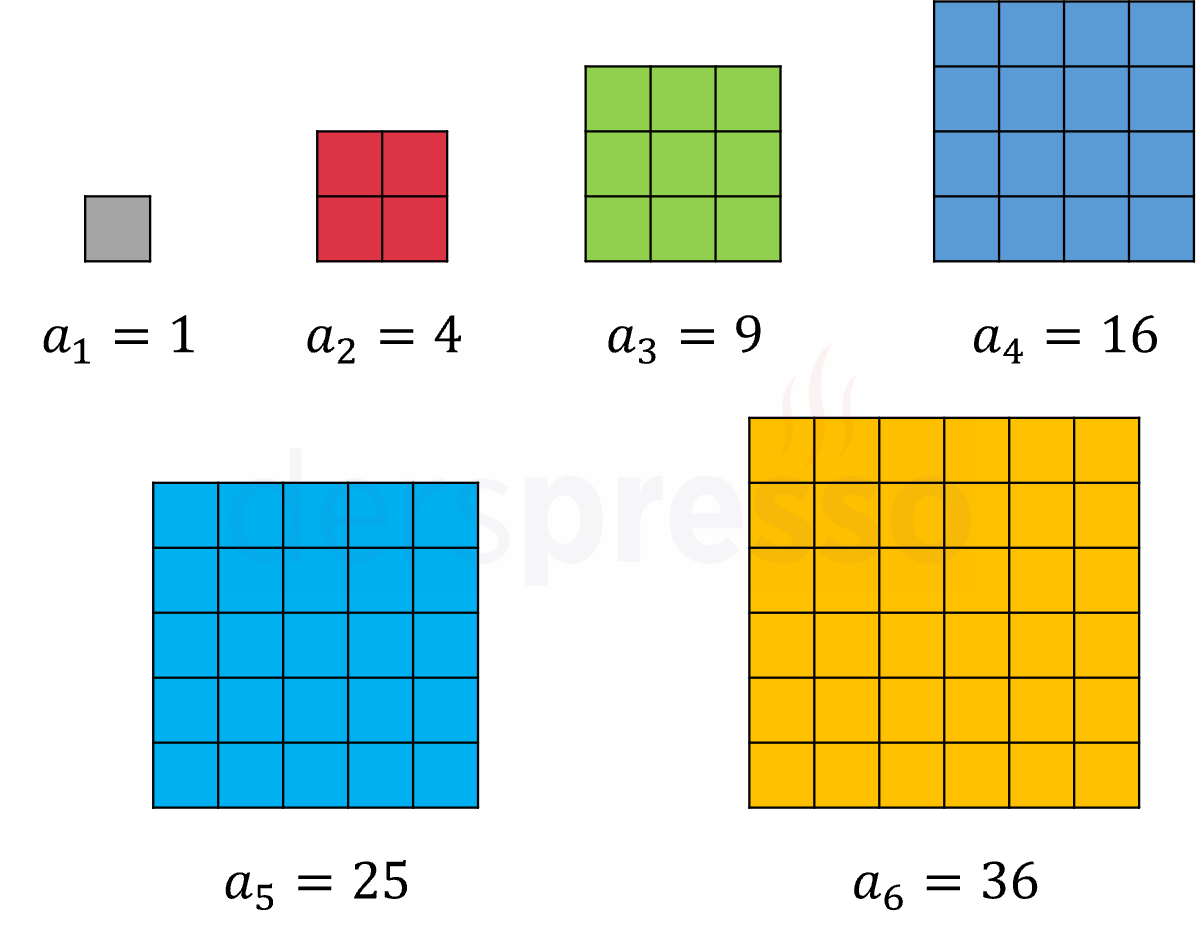
Karesel sayı dizileri özyinelemeli dizi şeklinde aşağıdaki şekilde ifade edilebilir.
\( a_1 = 1 \) olmak üzere,
\( a_n = a_{n - 1} + (2n - 1) \)
İSPATI GÖSTER
\( a_n = n^2 \)
\( a_{n - 1} = (n - 1)^2 = n^2 - 2n + 1 \)
İki ifadeyi taraf tarafa çıkaralım.
\( a_n - a_{n - 1} = n^2 - (n^2 - 2n + 1) \)
\( a_n - a_{n - 1} = 2n - 1 \)
\( a_{n - 1} \) terimini eşitliğin sağ tarafına alalım.
\( a_n = a_{n - 1} + (2n - 1) \)
Aşağıdaki özdeşliğe göre, \( n \). karesel sayı \( n \). ve \( (n - 1) \). üçgensel sayıların toplamına eşittir. Bu ilişki görsel olarak aşağıda gösterilmiştir.
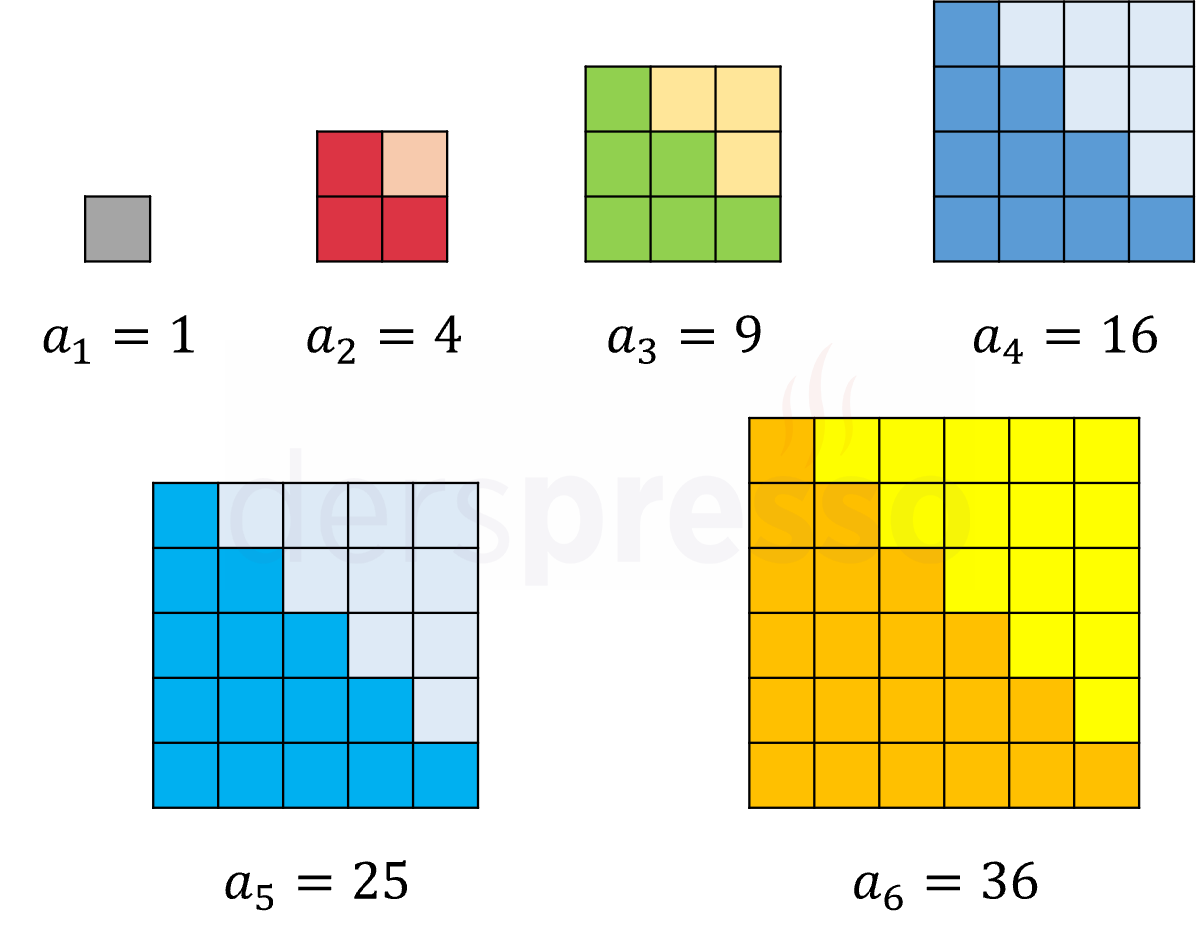
\( n^2 = T_n + T_{n-1} \)
\( 5^2 = T_5 + T_4 = 15 + 10 \)
İSPATI GÖSTER
\( n^2 = T_n + T_{n-1} \)
Üçgensel sayı formülünü kullanarak eşitliğin sağ tarafının açılımını yazalım.
\( T_n + T_{n-1} = \dfrac{n(n + 1)}{2} + \dfrac{(n - 1)(n - 1 + 1)}{2} \)
\( = \dfrac{n(n + 1)}{2} + \dfrac{(n - 1)n}{2} \)
\( = \dfrac{n(n + 1) + n(n - 1)}{2} \)
\( = \dfrac{n(n + 1 + n - 1)}{2} \)
\( = \dfrac{n(2n)}{2} \)
\( = n^2 \)
1'den başlayan üçgensel ve karesel sayı dizileri için aşağıdaki ifadelerden hangileri doğrudur?
I. İki basamaklı en büyük üçgensel sayı, iki basamaklı en büyük karesel sayıdan 10 fazladır.
II. Karesel sayı dizisinin 1'den büyük her elemanı, üçgensel sayı dizisinin ardışık iki elemanının toplamına eşittir.
III. İki dizinin toplamı bir aritmetik dizidir.
Çözümü Gösterİki dizinin de 100'den küçük terimlerini listeleyelim.
Üçgensel sayılar:
\( 1, 3, 6, 10, 15, 21, 28, 36, 45, 55, 66, 78, 91 \)
Karesel sayılar:
\( 1, 4, 9, 16, 25, 36, 49, 64, 81 \)
I. öncül:
\( 91 = 81 + 10 \)
I. ifade doğrudur.
II. öncül:
Yukarıdaki sayı dizisi incelendiğinde II. ifadenin doğru olduğu görülebilir.
III. öncül:
İki dizinin toplamı olan diziyi yazalım.
\( 2, 7, 15, 26, 40, \ldots \)
Dizinin ardışık terimleri arasındaki fark sabit olmadığı için III. öncül yanlıştır.
Buna göre I. ve II. ifadeler doğrudur.
Terimleri doğal sayı olan bir dizide ilk iki terimden sonraki terimler kendinden önceki iki terimin çarpımına eşittir.
Bu dizinin beşinci terimi 1323 olduğuna göre, ilk iki terimin toplamı kaçtır?
Çözümü GösterDiziye \( (a_n) \), dizinin ilk terime \( a \), ikinci terime \( b \) diyelim.
Verilen kuralı kullanarak dizinin ilk 5 terimini yazalım.
\( (a_n) = (a, b, ab, ab^2, a^2b^3, \ldots) \)
\( a_5 = a^2b^3 = 1323 \)
1323 sayısını asal çarpanlarına ayıralım.
\( a^2b^3 = 3^3 \cdot 7^2 \)
Dizinin terimleri doğal sayı olduğu için \( a = 7 \) ve \( b = 3 \) olmalıdır.
\( a + b = 7 + 3 = 10 \) bulunur.
Üçgensel sayılarla ilgili aşağıdaki bilgilerden hangileri doğrudur?
I. Üçgensel sayılar dizisinin 24. terimi 216'dır.
II. 91 bir üçgensel sayıdır.
III. \( (a_n) \) bir üçgensel sayı dizisi ise \( a_{n + 1} - a_n = n + 1 \) olur.
Çözümü GösterBir üçgensel sayı dizisinin genel terimi aşağıdaki gibidir.
\( (a_n) = \dfrac{n(n + 1)}{2} \)
I. öncül:
\( a_{24} = \dfrac{24 \cdot 25}{2} \)
\( = 300 \)
I. öncül yanlıştır.
II. öncül:
91 sayısının üçgensel sayı olabilmesi için genel terim bir \( n \) pozitif tam sayısı için 91'e eşit olmalıdır.
\( (a_n) = \dfrac{n(n + 1)}{2} = 91 \)
\( n(n + 1) = 182 \)
\( n = 13 \)
II. öncül doğrudur.
III. öncül:
\( a_{n + 1} - a_n = \dfrac{(n + 1)(n + 2)}{2} - \dfrac{n(n + 1)}{2} \)
\( = \dfrac{(n + 1)}{2}(n + 2 - n) \)
\( = n + 1 \)
III. öncül doğrudur.
Buna göre II. ve III. öncüller doğrudur.
Terimleri doğal sayı olan bir dizide ilk iki terimden sonraki terimler, kendinden bir önceki terimin kendinden iki önceki terime bölümüne eşittir.
Dizinin 807. terimi \( \frac{1}{3} \) olduğuna göre, 810. terim kaçtır?
Çözümü GösterDiziye \( (a_n) \), dizinin ilk terime \( a \), ikinci terime \( b \) diyelim.
Dizinin ilk birkaç terimini yazarak bir örüntü bulmayan çalışalım.
\( (a_n) = (a, b, \dfrac{b}{a}, \dfrac{1}{a}, \dfrac{1}{b}, \dfrac{a}{b}, a, b, \ldots) \)
Buna göre dizinin terimleri 6 terimde bir kendini tekrar etmektedir.
807'nin 6'ya bölümünden kalan 3'tür.
\( 807 = 6 \cdot 134 + 3 \)
Buna göre dizinin 807. terimi 3. terime eşittir.
\( a_{807} = a_3 = \dfrac{1}{3} \)
Değeri istenen 810. terim ise 6. terime eşittir.
\( a_{810} = a_6 \)
Bulduğumuz örüntüye göre dizinin 3. ve 6. terimleri birbirinin çarpmaya göre tersidir.
\( a_3 = \dfrac{b}{a} \Longrightarrow a_6 = \dfrac{a}{b} \)
\( a_{810} = a_6 = \dfrac{1}{a_{3}} = 3 \) bulunur.
\( A, B, C, D, E, F, G, H, I, J, K, L \) 12 terimden oluşan bir dizidir. Bu dizide ardışık herhangi 4 terimin toplamı 55'tir. Dizinin üçüncü terimi ilk terimin \( -2 \) katı olduğuna ve ikinci terim 7 olduğuna göre, dizinin 4., 7. ve 9. terimlerinin toplamı kaçtır?
Çözümü GösterÖnce verilen bilgileri kullanarak ilk 4 terimi ele alalım.
Dizinin ilk terimi olan \( A \)'nın değerine \( x \) diyelim.
Dizinin üçüncü terimi ilk terimin \( -2 \) katıdır.
\( C = -2x \)
Dizinin ardışık herhangi 4 teriminin toplamı 55 olduğuna göre ilk 4 terimin toplamı da 55'tir.
\( A + B + C + D = x + 7 + (-2x) + D = 55 \)
\( D = 48 + x \)
Dizinin ardışık herhangi 4 teriminin toplamının 55 olması için 5. terim 1. terime, 6. terim 2. terime, 7. terim 3. terime, ..., 12. terim 8. terime eşit olmalıdır.
\( a_n + a_{n+1} + a_{n+2} + a_{n+3} = a_{n+1} + a_{n+2} + a_{n+3} + a_{n+4} = 55 \)
\( a_n = a_{n+4} \)
\( A = x \)
\( B = 7 \)
\( C = -2x \)
\( D = 48 + x \)
\( E = x \)
\( F = 7 \)
\( G = -2x \)
\( H = 48 + x \)
\( I = x \)
\( J = 7 \)
\( K = -2x \)
\( L = 48 + x \)
Dizinin 4., 7. ve 9. terimlerini toplayalım.
\( D + G + I = (48 + x) + (-2x) + x \)
\( = 48 \) bulunur.