Geometrik Dizi
Ardışık terimleri arasındaki oran tüm dizi boyunca sabit olan dizilere geometrik dizi denir. Geometrik dizilerde ardışık terimler arasındaki bu sabit orana ortak oran ya da ortak çarpan denir ve \( r \) ile gösterilir.
\( r \in \mathbb{R} \) olmak üzere, her \( n \) için,
\( \dfrac{a_{n + 1}}{a_n} = r \) ise,
\( (a_n) \) bir geometrik dizidir.
Geometrik dizilerin genel terimi aşağıdaki gibidir. Bu formüle göre, geometrik dizilerde \( n \). terim ortak oranın \( (n - 1) \) kez 1. terimle çarpılmasıyla bulunur.
\( (a_n) = a_1 \cdot r^{n - 1} \)
\( = (a_1, a_1 \cdot r, a_1 \cdot r^2, a_1 \cdot r^3, \ldots) \)
Ortak oranı 2 olan bir geometrik dizi:
\( (a_n) = 5 \cdot 2^n \)
\( = (10, 20, 40, 80, \ldots) \)
Aşağıda genel terimleri verilen bazı dizilerin birer geometrik dizi olup olmadığı belirtilmiştir.
| Genel Terim | Terimler | Geometrik Dizi? |
|---|---|---|
| \( (a_n) = 3^n \) | \( (3, 9, 27, 81, \ldots) \) | Geometrik dizi (\( r = 3 \)) |
| \( (b_n) = 3 \cdot 2^n \) | \( (6, 12, 24, 48, \ldots) \) | Geometrik dizi (\( r = 2 \)) |
| \( (c_n) = {\left( \frac{2}{3} \right)}^{n - 1} \) | \( (1, \frac{2}{3}, \frac{4}{9}, \frac{8}{27}, \ldots) \) | Geometrik dizi (\( r = \frac{2}{3} \)) |
| \( (d_n) = 5 \) | \( (5, 5, 5, 5, \ldots) \) | Geometrik dizi (\( r = 1 \)) |
| \( (e_n) = n^2 \) | \( (1, 4, 9, 16, \ldots) \) | Geometrik dizi değil |
| \( (f_n) = 2^n - 1 \) | \( (1, 3, 7, 15, \ldots) \) | Geometrik dizi değil |
| \( (g_n) = \dfrac{n + 1}{n + 2} \) | \( (\frac{2}{3}, \frac{3}{4}, \frac{4}{5}, \frac{5}{6}, \ldots) \) | Geometrik dizi değil |
Tablodaki ilk dört diziyi incelersek geometrik dizilerin genel terimi \( n \)'nin tabanının ortak orana eşit olduğu bir üstel fonksiyon formundadır (\( f(x) = k \cdot r^x \)).
Bir geometrik dizide ortak oranın değerine göre dizi artan, azalan ya da sabit dizi olur.
\( r \gt 1 \): Artan dizi
\( r = 1 \): Sabit dizi
\( 0 \lt r \lt 1 \): Azalan dizi
Geometrik diziler indirgemeli dizi olarak aşağıdaki şekilde ifade edilebilir.
\( a_n = a_{n - 1} \cdot r \)
\( (a_n) = 3 \cdot 2^n \) dizisinin indirgemeli dizi olarak tanımı:
\( a_1 = 6 \)
\( a_n = a_{n - 1} \cdot 2 \)
Bir geometrik dizide n. terim, birinci ya da herhangi diğer bir terim cinsinden aşağıdaki şekilde ifade edilebilir.
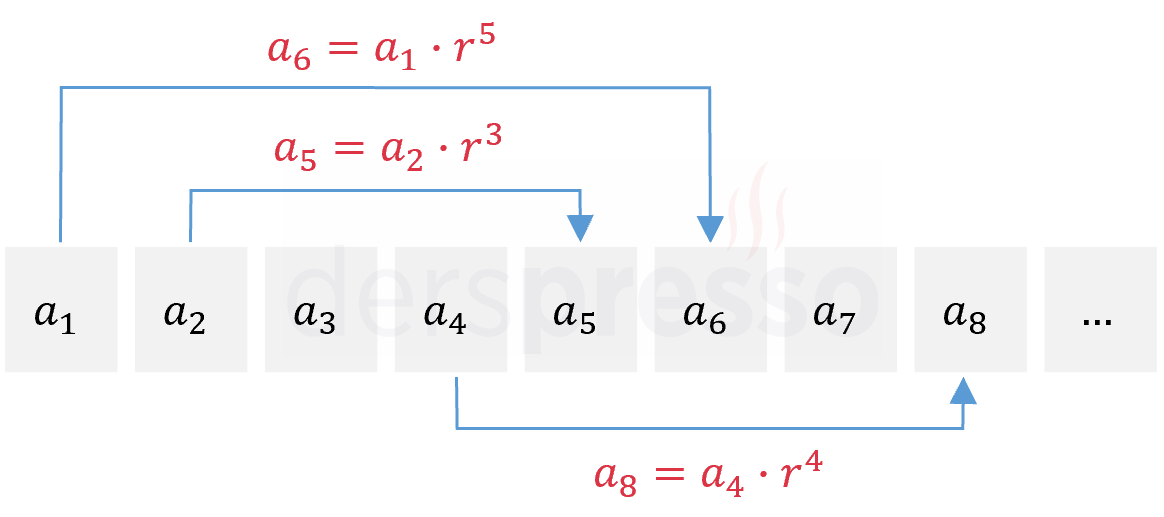
\( a_n = a_1 \cdot r^{n - 1} \)
\( a_n = a_p \cdot r^{n - p} \)
1. terimi 3 ve ortak oranı 2 olan bir geometrik dizinin 8. terimi:
\( a_8 = 3 \cdot 2^{8 - 1} = 384 \)
5. terimi 243 ve ortak oranı \( \frac{1}{3} \) olan bir geometrik dizinin 12. terimi:
\( a_{12} = 243 \cdot (\dfrac{1}{3})^{12 - 5} = 3^5 \cdot \dfrac{1}{3^7} = \dfrac{1}{9} \)
Yukarıdaki formül \( p \). ve \( q \). terimler cinsinden yazılıp ortak oran yalnız bırakıldığında, ortak oranın dizinin herhangi iki teriminin oranının bu iki terimin indislerinin farkı derecesinde köküne eşit olduğu bulunur.
\( q \gt p \) olmak üzere,
\( a_q = a_p \cdot r^{q - p} \)
Terimler ardışık değilse:
\( r = \sqrt[q - p]{\dfrac{a_q}{a_p}} \)
Terimler ardışık ise:
\( r = \dfrac{a_q}{a_p} \)
5. terimi 3 ve 14. terimi 1536 olan bir geometrik dizinin ortak oranı:
\( r = \sqrt[14 - 5]{\dfrac{1536}{3}} \)
\( = \sqrt[9]{512} = 2 \)
Bir geometrik dizide bir terim, kendisinden eşit uzaklıktaki iki terimin geometrik ortalamasına (çarpımlarının kareköküne) eşittir.
\( a_n = \sqrt{a_{n - p} \cdot a_{n + p}} = \sqrt{a_{n - q} \cdot a_{n + q}} \)
Bu kuralın bir sonucu olarak, bir terimden eşit uzaklıktaki terimlerin çarpımı birbirine eşittir.
\( {a_n}^2 = a_{n - p} \cdot a_{n + p} = a_{n - q} \cdot a_{n + q} \)
\( (a_n) = 2^n \) olmak üzere,
\( a_{10} = 2^{10} \)
10. terime 2 terim uzaklıktaki iki terimin çarpımı:
\( a_{8} \cdot a_{12} = 2^8 \cdot 2^{12} = a_{10}^2 = 2^{20} \)
10. terime 5 terim uzaklıktaki iki terimin çarpımı:
\( a_{5} \cdot a_{15} = 2^5 \cdot 2^{15} = a_{10}^2 = 2^{20} \)
Aynı kuralın ikinci bir sonucu olarak, bir geometrik dizinin ardışık üç teriminde ortadaki terim diğer iki terimin geometrik ortalamasına eşittir.
\( a_n = \sqrt{a_{n - 1} \cdot a_{n + 1}} \)
Aynı kuralın üçüncü bir sonucu olarak, bir geometrik dizide indisleri toplamı birbirine eşit olan terimlerin çarpımları birbirine eşittir.
\( p + q = r + s \) ise,
\( a_p \cdot a_q = a_r \cdot a_s \)
\( a_7 \cdot a_8 = a_3 \cdot a_{12} \)
Aynı kuralın dördüncü bir sonucu olarak, sonlu bir geometrik dizide baştan ve sondan eşit uzaklıkta bulunan terimlerin çarpımı birbirine eşittir.
\( a \) ve \( b \) sayılarının arasına \( n \) tane terim yerleştirerek oluşturulan bir geometrik dizinin ortak çarpanı aşağıdaki formülle bulunur.
\( n \gt 0 \) olmak üzere,
\( r = \sqrt[n + 1]{\dfrac{b}{a}} \)
128 ve 8 sayıları arasına 3 terim ekleyerek oluşturulan geometrik dizinin ortak oranı:
\( r = \sqrt[3 + 1]{\dfrac{8}{128}} = \dfrac{1}{2} \)
\( (a_n) = (128, \textcolor{red}{64, 32, 16}, 8) \)
Geometrik dizilerde ilk \( n \) terimin toplamı \( S_n \) ile gösterilir ve aşağıdaki formülle hesaplanır.
\( r \ne 1 \) ve
\( S_n = a_1 + a_2 + a_3 + \ldots + a_n \) olmak üzere,
\( S_n = a_1 \cdot \dfrac{1 - r^n}{1 - r} \)
1. terimi 3 ve ortak oranı 2 olan bir geometrik dizinin ilk 10 teriminin toplamı:
\( S_n = 3 \cdot \dfrac{1 - 2^{10}}{1 - 2} \)
\( = 3 \cdot 1023 = 3069 \)
İSPATI GÖSTER
Dizinin ilk terimine \( a \), dizideki terim sayısına \( n \) diyelim.
Geometrik dizilerde dizinin \( n \). terimi aşağıdaki formülle hesaplanır.
\( a_n = ar^{n - 1} \)
Dizinin terimlerini listeleyelim.
\( (a_n) = (a, ar, ar^2, \ldots, ar^{n - 1}) \)
Terimler toplamını aşağıdaki şekilde yazabiliriz.
\( S_n = a + ar + ar^2 + \ldots + ar^{n - 1} \)
Terimleri \( a \) parantezine alalım.
\( = a(1 + r + r^2 + \ldots + r^{n - 1}) \)
\( r \ne 1 \) olmak üzere, payı ve paydayı \( (1 - r) \) ile çarpalım.
\( = \dfrac{a(1 - r)(1 + r + r^2 + \ldots + r^{n - 1})}{1 - r} \)
Paydaki 2. ve 3. çarpanlar, iki terimin \( n \). dereceden kuvvetlerinin farkı özdeşliğinin çarpanlara ayrılmış halidir.
\( x^n - y^n = (x - y)\) \( (x^{n - 1} + x^{n - 2}y + \ldots + y^{n - 1}) \)
Bu özdeşlikte \( x \) yerine \( 1 \), \( y \) yerine \( r \) yazalım.
\( 1 - r^n = (1 - r)\) \( (1 + r + \ldots + r^{n - 1}) \)
Buna göre, dizinin terimler toplamını aşağıdaki şekilde yazabiliriz.
\( r \ne 1 \) olmak üzere,
\( S_n = a \cdot \dfrac{1 - r^n}{1 - r} \)
Bir dizi hem aritmetik hem de geometrik dizi ise bu dizi sabit dizidir. Sabit bir dizinin aritmetik dizi olarak ortak farkı 0, geometrik dizi olarak ortak çarpanı 1'dir.
İlk üç terimi verilen aşağıdaki geometrik dizilerin ilk 5 teriminin toplamı kaçtır?
(a) \( (a_n) = (\sqrt{3}, -\sqrt{3}, \sqrt{3}, \ldots) \)
(b) \( (b_n) = (-4, 1, -\dfrac{1}{4}, \ldots) \)
(c) \( (c_n) = (\dfrac{12}{25}, \dfrac{6}{5}, 3, \ldots) \)
Çözümü GösterGeometrik dizilerde ardışık terimler arasındaki sabit orana ortak oran denir ve \( r \) ile gösterilir.
Geometrik dizilerde \( r \) aşağıdaki formülle hesaplanır.
\( r = \dfrac{a_{n + 1}}{a_n} \)
Geometrik dizilerde ilk \( n \) terimin toplamı \( S_n \) ile gösterilir ve aşağıdaki formülle hesaplanır.
\( S_n = a_1 \cdot \dfrac{1 - r^n}{1 - r} \)
(a) seçeneği:
\( (a_n) = (\sqrt{3}, -\sqrt{3}, \sqrt{3}, \ldots) \)
Geometrik dizinin ortak çarpanını bulalım.
\( r = \dfrac{a_3}{a_2} \)
\( = \dfrac{\sqrt{3}}{-\sqrt{3}} = -1 \)
İlk 5 teriminin toplamını bulalım.
\( S_5 = \sqrt{3} \cdot \dfrac{1 - (-1)^5}{1 - (-1)} \)
\( = \sqrt{3} \cdot \dfrac{2}{2} \)
\( = \sqrt{3} \)
(b) seçeneği:
\( (b_n) = (-4, 1, -\dfrac{1}{4}, \ldots) \)
Geometrik dizinin ortak çarpanını bulalım.
\( r = \dfrac{b_3}{b_2} \)
\( = \dfrac{-\frac{1}{4}}{1} = -\dfrac{1}{4} \)
İlk 5 teriminin toplamını bulalım.
\( S_5 = -4 \cdot \dfrac{1 - (-\frac{1}{4})^5}{1 - (-\frac{1}{4})} \)
\( = -4 \cdot \dfrac{\frac{1025}{1024}}{\frac{5}{4}} \)
\( = -4 \cdot \dfrac{205}{256} \)
\( = -\dfrac{205}{64} \)
(c) seçeneği:
\( (c_n) = (\dfrac{12}{25}, \dfrac{6}{5}, 3, \ldots) \)
Geometrik dizinin ortak çarpanını bulalım.
\( r = \dfrac{c_3}{c_2} \)
\( = \dfrac{3}{\frac{6}{5}} = \dfrac{5}{2} \)
İlk 5 teriminin toplamını bulalım.
\( S_5 = \dfrac{12}{25} \cdot \dfrac{1 - (\frac{5}{2})^5}{1 - \frac{5}{2}} \)
\( = \dfrac{12}{25} \cdot \dfrac{-\frac{3093}{32}}{-\frac{3}{2}} \)
\( = \dfrac{12}{25} \cdot \dfrac{3093}{32} \cdot \dfrac{2}{3} \)
\( = \dfrac{3093}{100} \)
6 ve 192 sayıları arasına geometrik dizi oluşturacak şekilde 4 sayı ekleniyor.
Buna göre oluşan geometrik dizinin ortak çarpanı kaç olur?
Çözümü GösterOluşan dizinin terimlerini yazalım.
\( 6, a_2, a_3, a_4, a_5, 192 \)
6. terimi 1. terim cinsinden yazalım.
\( a_6 = a_1 \cdot r^5 \)
\( 192 = 6 \cdot r^5 \)
\( r^5 = 32 \)
\( r = 2 \) bulunur.
\( \dfrac{a^3b^5}{16}, -\dfrac{3a^4b^3}{8}, \dfrac{9a^5b}{4} \) geometrik dizisinin dördüncü terimi nedir?
Çözümü GösterDizinin ilk iki teriminin oranını alarak ortak oranı bulalım.
\( \dfrac{a_2}{a_1} = r \)
\( \dfrac{-\frac{3a^4b^3}{8}}{\frac{a^3b^5}{16}} = \dfrac{-6a}{b^2} \)
Dizinin ikinci ve üçüncü terimlerinin aynı ortak oranı verdiğini teyit edebiliriz.
\( \dfrac{a_3}{a_2} = r \)
\( \dfrac{\frac{9a^5b}{4}}{-\frac{3a^4b^3}{8}} = \dfrac{-6a}{b^2} \)
Üçüncü terimle ortak oranı çarparak dizinin dördüncü terimini bulalım.
\( a_4 = a_3r \)
\( = \dfrac{9}{4}a^5b \cdot \dfrac{-6a}{b^2} \)
\( = -\dfrac{27a^6}{2b} \) bulunur.
İlk terimi 3 olan bir geometrik dizinin 4. ve 7. terimlerinin toplamı 216'dır.
Buna göre bu dizinin ortak çarpanının alabileceği tam sayı değeri kaçtır?
Çözümü Göster\( a_1 = 3 \)
\( a_4 + a_7 = 216 \)
Her iki terimi birinci terim cinsinden yazalım.
\( a_1 \cdot r^3 + a_1 \cdot r^6 = 216 \)
\( 3r^3 + 3r^6 = 216 \)
\( r^3 + r^6 = 72 \)
\( r^3 = t \) şeklinde değişken değiştirelim.
\( t^2 + t - 72 = 0 \)
\( (t + 9)(t - 8) = 0 \)
\( t = -9 \) ya da \( t = 8 \)
\( t = r^3 = -9 \)
Bu durumda \( r \) için tam sayı çözüm bulunmaz.
\( t = r^3 = 8 \)
\( r = 2 \) bulunur.
20, 40 ve 70 sayılarına aynı sabit sayı eklendiğinde bir geometrik dizi oluşmaktadır.
Bu geometrik dizinin ortak oranı kaçtır?
Çözümü GösterEklenen sabit sayıya \( c \), oluşan geometrik dizinin ortak oranına \( r \) diyelim.
Oluşan geometrik dizinin terimleri aşağıdaki gibi olur.
\( 20 + c, 40 + c, 70 + c \)
İkinci ve birinci terimlerin oranı ortak oranı verir.
\( r = \dfrac{40 + c}{20 + c} \)
Aynı şekilde, üçüncü ve ikinci terimlerin oranı ortak oranı verir.
\( r = \dfrac{70 + c}{40 + c} \)
\( r \) için bulunan iki denklemi birbirine eşitleyelim.
\( \dfrac{40 + c}{20 + c} = \dfrac{70 + c}{40 + c} \)
\( (40 + c)^2 = (70 + c)(20 + c) \)
\( 1600 + 80c + c^2 = 1400 + 90c + c^2 \)
\( c = 20 \)
\( r \) için bulunan denklemlerden birinde \( c \) değerini yerine koyarak ortak oranı bulalım.
\( r = \dfrac{40 + c}{20 + c} \)
\( = \dfrac{3}{2} \) bulunur.
Pozitif terimli bir geometrik dizide her terim kendisinden önceki iki terimin toplamına eşittir.
Buna göre, bu dizinin ortak oranı kaçtır?
Çözümü Göster\( a, r \in \mathbb{Z^+} \) olmak üzere,
Bu dizinin ilk terimine \( a \), ortak oranına \( r \) diyelim.
Her terim kendisinden önceki iki terimin toplamına eşittir.
\( a + ar = ar^2 \)
\( a(1 + r) = ar^2 \)
Geometrik seride ilk terim sıfır olamayacağı için sadeleştirebiliriz.
\( 1 + r = r^2 \)
\( r^2 - r - 1 = 0 \)
Denklemin deltasını hesaplayalım.
\( \Delta = b^2 - 4ac \)
\( a = 1, \quad b = -1, \quad c = -1 \)
\( = 1^2 - 4(1)(-1) = 5 \)
\( r_{1, 2} = \dfrac{-b \pm \sqrt{\Delta}}{2a} \)
\( = \dfrac{1 \pm \sqrt{5}}{2} \)
Dizi pozitif terimli olduğuna göre \( r \) pozitif olmalıdır.
\( r = \dfrac{1 + \sqrt{5}}{2} \) bulunur.
Pozitif terimlerden oluşan bir geometrik dizide dördüncü ve üçüncü terimler arasındaki fark 96, ikinci ve birinci terimler arasındaki fark 6'dır.
Buna göre, bu dizinin ilk dört teriminin toplamı kaçtır?
Çözümü GösterBu dizinin ilk terimine \( a \), ortak oranına \( r \) diyelim.
Dizinin ilk dört terimi aşağıdaki gibi olur.
\( a, ar, ar^2, ar^3 \)
Dördüncü ve üçüncü terimler arasındaki fark 96'dır.
\( ar^3 - ar^2 = 96 \)
\( ar^2(r - 1) = 96 \)
İkinci ve birinci terimler arasındaki fark 6'dır.
\( ar - a = 6 \)
\( a(r - 1) = 6 \)
Bu iki denklemin birbirine oranını bulalım.
\( \dfrac{ar^2(r - 1)}{a(r - 1)} = \dfrac{96}{6} \)
\( r^2 = 16 \Longrightarrow r = 4 \)
Bu değeri denklemlerden birinde yerine koyarak \( a \) değerini bulalım.
\( a(r - 1) = 6 \)
\( a = 2 \)
Bu iki değeri kullanarak dizinin ilk dört terimini bulalım.
\( a, ar, ar^2, ar^3 \)
\( 2, 8, 32, 128 \)
Dizinin ilk dört teriminin toplamı \( 2 + 8 + 32 + 128 = 170 \) olarak bulunur.
\( x + 2, 2x - 1, 4x - 7, y \) bir geometrik dizinin ardışık 4 terimidir.
Buna göre, \( y \) kaçtır?
Çözümü GösterBir geometrik dizide bir terimin karesi öncesindeki ve sonrasındaki iki terimin çarpımına eşittir.
\( (2x - 1)^2 = (x + 2)(4x - 7) \)
\( 4x^2 - 4x + 1 = 4x^2 + x - 14 \)
\( x = 3 \)
Buna göre verilen geometrik dizinin terimleri aşağıdaki gibi olur.
\( 5, 5, 5, y \)
Bu dizinin ortak çarpanı 1 olduğu için dizi sabit dizidir ve tüm terimleri 5'e eşittir.
Buna göre \( y = 5 \) olarak bulunur.
\( (a_n) \) artan bir geometrik dizidir.
\( \dfrac{a_7 - a_6}{a_5^2 - a_4^2} = \dfrac{1}{7} \)
\( a_1 = \dfrac{1}{8} \)
olduğuna göre, \( a_4 \) kaçtır?
Çözümü Göster\( \dfrac{a_7 - a_6}{(a_5 - a_4)(a_5 + a_4)} = \dfrac{1}{7} \)
Geometrik dizilerde \( n \). terim aşağıdaki formülle hesaplanır.
\( a_n = a_1 \cdot r^{n - 1} \)
Tüm terimleri \( a_1 \) cinsinden yazalım.
\( \dfrac{a_1 \cdot r^6 - a_1 \cdot r^5}{(a_1 \cdot r^4 - a_1 \cdot r^3)(a_1 \cdot r^4 + a_1 \cdot r^3)} = \dfrac{1}{7} \)
\( = \dfrac{a_1 \cdot r^5(r - 1)}{a_1 \cdot r^3(r - 1) \cdot a_1 \cdot r^3(r + 1)} = \dfrac{1}{7} \)
\( = \dfrac{1}{a_1 \cdot r(r + 1)} = \dfrac{1}{7} \)
\( a_1 = \dfrac{1}{8} \) yazalım.
\( \dfrac{1}{\frac{1}{8} \cdot r(r + 1)} = \dfrac{1}{7} \)
\( r(r + 1) = 56 \)
\( r^2 + r - 56 = 0 \)
\( (r + 8)(r - 7) = 0 \)
\( (a_n) \) artan olduğu için \( r = 7 \) olur.
\( a_4 \) terimini bulalım.
\( a_4 = \dfrac{1}{8} \cdot 7^{4 - 1} \)
\( = \dfrac{343}{8} \) bulunur.
\( (a_n) = (4, 20, 100, 500, \ldots) \) geometrik dizisinin 44. teriminin sonunda kaç tane sıfır vardır?
Çözümü GösterGeometrik dizilerde ardışık terimler arasındaki sabit orana ortak oran denir ve \( r \) ile gösterilir.
Geometrik dizilerde \( r \) aşağıdaki formülle hesaplanır.
\( r = \dfrac{a_{n + 1}}{a_n} \)
Geometrik dizinin ortak çarpanını bulalım.
\( \dfrac{a_2}{a_1} = r \)
\( r = \dfrac{20}{4} = 5 \)
Geometrik dizinin 44. terimini bulalım.
\( a_n = a_1 \cdot r^{n - 1} \)
\( a_{44} = 4 \cdot 5^{43} \)
\( = 2^2 \cdot 5^{43} \)
\( = 10^2 \cdot 5^{41} \)
\( = 100 \cdot 5^{41} \)
Buna göre 44. teriminin sonunda 2 tane sıfır bulunur.
Geometrik bir dizinin 7. ve 10. terimleri sırasıyla \( -5! \) ve \( 6! \) olarak veriliyor. Buna göre bu dizinin ilk terimi kaçtır?
Çözümü GösterGeometrik diziye \( a_n \), dizinin ortak çarpanına \( r \) diyelim.
\( a_7 = -5! = -(5!) \)
\( a_{10} = 6! \)
Bir geometrik dizinin \( q \). terimini \( p \). terim cinsinden aşağıdaki şekilde yazabiliriz.
\( a_q = a_p \cdot r^{q - p} \)
\( q = 10 \) ve \( p = 7 \) yazalım.
\( a_{10} = a_7 \cdot r^{10 - 7} \)
\( 6! = -5! \cdot r^3 \)
\( 6 \cdot 5! = -5! \cdot r^3 \)
\( r^3 = -6 \)
\( r = \sqrt[3]{-6} \)
\( a_1 \) değerini bulabilmek için \( a_7 \) terimini \( a_1 \) cinsinden yazalım.
\( a_n = a_1 \cdot r^{n - 1} \)
\( a_7 = a_1 \cdot r^6 \)
\( -5! = a_1 \cdot (\sqrt[3]{-6})^6 \)
\( a_1 = \dfrac{-5!}{(-6)^2} \)
\( = \dfrac{-(5 \cdot 4 \cdot 3 \cdot 2 \cdot 1)}{36} \)
\( = -\dfrac{10}{3} \) bulunur.
Bir altıgenin iç açıları ölçüleri ortak çarpanı 2 olan bir geometrik dizinin ardışık 6 terimidir.
Buna göre bu altıgenin en küçük geniş iç açısının ölçüsü kaçtır?
Çözümü GösterAltıgenin iç açıları toplamı \( 180(6 - 2) = 720 \) derecedir.
6 terimli bir geometrik dizinin terimler toplamı aşağıdaki formülle bulunur.
\( S_n = a_1 \cdot \dfrac{1 - r^n}{1 - r} \)
\( 720 = a_1 \cdot \dfrac{1 - 2^6}{1 - 2} \)
\( 720 = a_1 \cdot 63 \)
\( a_1 = \dfrac{80}{7} \)
Buna göre üçgenin iç açıları aşağıdaki gibi olur.
\( \dfrac{80}{7}, \dfrac{160}{7}, \dfrac{320}{7}, \dfrac{640}{7}, \dfrac{1280}{7}, \dfrac{2560}{7} \)
Derecesi 90 dereceden büyük olan açılara geniş açı denir.
Bu açılar içindeki en küçük geniş açı \( \frac{640}{7} \) açısıdır.
Bir ortamdaki negatif iyonların sayısı her 20 dakikada bir üçte birine inmektedir.
Başlangıçta ortamda \( 9^{40} \) negatif iyon olduğuna göre, 7. saatin sonunda ortamdaki negatif iyon sayısı kaçtır?
Çözümü GösterHer 20 dakikalık periyotlar sonundaki negatif iyon sayılarını, ortak oranı \( r = \frac{1}{3} \) olan bir geometrik dizinin terimleri olarak tanımlayabiliriz.
\( a_1 = 9^{40} = 3^{80} \)
\( r = \dfrac{1}{3} \)
Geometrik dizilerin genel terim formülü aşağıdaki gibidir.
\( (a_n) = a_1 \cdot r^{n - 1} \)
\( (a_n) = 3^{80} \cdot \left( \dfrac{1}{3} \right)^{n - 1} \)
Bir saatte 20 dakikalık periyotlardan üç tane, 7 saatte 21 tane vardır. Birinci periyodun başlangıcına \( a_1 \) dediğimiz için, 21 periyodun sonundaki iyon sayısı 22. terime eşit olur.
\( a_{22} = 3^{80} \cdot \left( \dfrac{1}{3} \right)^{22 - 1} \)
\( = 3^{80} \cdot \left( \dfrac{1}{3} \right)^{21} \)
\( = 3^{59} \) bulunur.
\( a_{2n+3} + a_{n^3} = a_{2n+2} + a_{n^3+1} \)
eşitliğinin sağlandığı \( (a_n) \) dizisi için aşağıdaki ifadelerden hangileri doğru olabilir?
I. Ortak çarpanı 1 olan geometrik dizidir.
II. Aritmetik dizidir.
III. Sabit dizidir.
Çözümü GösterI. öncül:
\( (a_n) \) dizisinin ortak çarpanı 1 olan bir geometrik dizi olduğunu kabul edelim.
\( a_{2n+3} = a_{2n+2} \cdot 1 \)
\( a_{n^3+1} = a_{n^3} \cdot 1 \)
\( a_{2n+2} + a_{n^3} = a_{2n+2} + a_{n^3} \)
Eşitlik sağlandığı için I. öncül doğru olabilir.
II. öncül:
\( (a_n) \) dizisinin bir aritmetik dizi olduğunu kabul edelim.
\( a_{2n+3} = a_{2n+2} + d \)
\( a_{n^3+1} = a_{n^3} + d \)
\( a_{2n+2} + d + a_{n^3} = a_{2n+2} + a_{n^3} + d \)
Eşitlik sağlandığı için II. öncül doğru olabilir.
III. öncül:
\( (a_n) \) dizisinin bir sabit dizi olduğunu kabul edelim.
\( a_{2n+3} = c \)
\( a_{n^3} = c \)
\( a_{2n+2} = c \)
\( a_{n^3+1} = c \)
\( c + c = c + c \)
Eşitlik sağlandığı için III. öncül doğru olabilir.
Buna göre üç öncül de doğru olabilir.
Aşağıdaki ifadelerinden hangileri doğrudur?
I. Bir geometrik dizinin 6. ve 8. terimleri biliniyorsa bu dizinin ortak çarpanı bulunabilir.
II. \( (b_n) \) ortak çarpanı \( r \) olan bir geometrik dizi ise \( b_2 - b_1, b_3 - b_2, \ldots , b_{n+1} - b_n \) dizisi de ortak çarpanı \( r \) olan bir geometrik dizidir.
III. \( (a_n) \) dizisi hem geometrik hem de aritmetik dizi ise sabit dizidir.
Çözümü GösterI. öncül:
\( a_8 = a_6 \cdot r^2 \)
\( r^2 \) ifadesini bu eşitlikle bulabiliriz, ancak \( r \) pozitif ve negatif değer alabileceği için işaretini bilemeyiz. Bu ifade doğru değildir.
II. öncül:
Dizinin terimlerini bulalım.
\( b_2 - b_1 = b_1 \cdot r - b_1 \)
\( = b_1 \cdot (r - 1) \)
\( b_3 - b_2 = b_1 \cdot r^2 - b_1 \cdot r \)
\( = b_1 \cdot (r - 1) \cdot r \)
\( b_4 - b_3 = b_1 \cdot r^3 - b_1 \cdot r^2 \)
\( = b_1 \cdot (r - 1) \cdot r^2 \)
\( b_5 - b_4 = b_1 \cdot r^4 - b_1 \cdot r^3 \)
\( = b_1 \cdot (r - 1) \cdot r^3 \)
Oluşan yeni dizi de ortak çarpanı \( r \) olan bir geometrik dizidir. Bu ifade doğrudur.
III. öncül:
\( a_n \) dizisi hem geometrik hem de aritmetik dizi ise sabit dizidir. Bu ifade doğrudur.
Buna göre II. ve III. ifadeler doğrudur.
Arda internetten 10 kutu siparişi veriyor. Kutuların hacimleri sırasıyla \( a_1, a_2, \ldots, a_{10} \)'dur ve her kutunun hacmi bir önceki kutunun hacminin \( \frac{3}{4} \) katıdır.
\( a_1 \cdot a_2 \cdot a_3 = a_4 \cdot a_5 \cdot a_6 \cdot a_7 \cdot a_8 \)
olduğuna göre, 10. kutunun hacmi nedir?
Çözümü GösterKutuların hacimleri bir ortak çarpan oranında küçüldüğü için bir geometrik dizi oluştururlar.
Bir geometrik dizide \( n \). terim \( k \). terim cinsinden aşağıdaki şekilde ifade edilebilir.
\( a_n = a_k \cdot r^{n - k} \)
Bir geometrik dizide bir terimin karesi, kendisinden eşit uzaklıktaki iki terimin çarpımına eşittir.
\( {a_n}^2 = a_{n - p} \cdot a_{n + p} \)
Buna göre aşağıdaki eşitlikleri yazabiliriz.
\( a_1 \cdot a_3 = a_2^2 \)
\( a_4 \cdot a_8 = a_5 \cdot a_7 = a_6^2 \)
Bu değerleri soruda verilen eşitlikte yerine koyalım.
\( a_1 \cdot a_2 \cdot a_3 = a_4 \cdot a_5 \cdot a_6 \cdot a_7 \cdot a_8 \)
\( a_2 \cdot a_2^2 = a_6 \cdot a_6^2 \cdot a_6^2 \)
\( a_2^3 = a_6^5 \)
\( a_6 \) değerini \( a_2 \) cinsinden yazalım.
\( a_2^3 = (a_2 \cdot r^4)^5 \)
\( a_2^3 = a_2^5 \cdot r^{20} \)
\( a_2^{-2} = r^{20} \)
\( a_2^{-1} = (\dfrac{3}{4})^{10} \)
\( a_2 = (\dfrac{4}{3})^{10} \)
Geometrik dizinin 10. terimini bulalım.
\( a_{10} = a_2 \cdot r^{10 - 2} \)
\( = (\dfrac{4}{3})^{10} \cdot (\dfrac{3}{4})^8 = \dfrac{16}{9} \) bulunur.
Bir geometrik dizide aşağıdaki eşitlik veriliyor.
\( \dfrac{a_{14} + a_{17} + a_{25}}{a_8 + a_{11} + a_{19}} = 64 \)
Buna göre bu dizinin ortak çarpanının alabileceği değerler çarpımı kaçtır?
Çözümü GösterPay ve paydada birbirine karşılık gelen terimlerin indis farkının sabit ve 6 olduğunu görüyoruz.
\( 14 - 8 = 17 - 11 = 25 - 19 = 6 \)
Tüm terimleri 8. terim cinsinden yazalım.
\( \dfrac{a_8 \cdot r^6 + a_8 \cdot r^9 + a_8 \cdot r^{17}}{a_8 + a_8 \cdot r^3 + a_8 \cdot r^{11}} = 64 \)
Pay ve paydadaki ifadeleri ortak çarpan parantezine alalım.
\( \dfrac{a_8 \cdot r^6 (1 + r^3 + r^{11})}{a_8 \cdot (1 + r^3 + r^{11})} = 64 \)
\( r^6 = 64 \)
\( r = 2 \) ya da \( r = -2 \)
\( r \) değerler çarpımı \( 2 \cdot (-2) = -4 \) olarak bulunur.
\( (a_n) \) bir aritmetik dizi, \( (b_n) \) bir geometrik dizidir.
\( b_3 = 18 \)
\( a_1 + a_2 + a_3 = 39 \)
\( a_1 + b_1 - 5 = a_2 + b_2 = 19 \)
olduğuna göre, \( a_4 \) kaçtır?
Çözümü GösterBir aritmetik dizide bir terim, kendisinden eşit uzaklıktaki iki terimin aritmetik ortalamasına eşittir.
\( 2a_2 = a_1 + a_3 \)
\( a_2 + 2a_2 = 3a_2 = 39 \)
\( a_2 = 13 \)
Bu değeri kullanarak diğer terimleri bulalım.
\( a_2 + b_2 = 19 \)
\( 13 + b_2 = 19 \)
\( b_2 = 6 \)
\( b_3 = b_2 \cdot r \) formülü ile geometrik dizinin ortak oranını bulalım.
\( r = \dfrac{b_3}{b_2} = \dfrac{18}{6} = 3 \)
\( b_2 = b_1 \cdot r \) formülü ile \( b_1 \)'i bulalım.
\( 6 = b_1 \cdot 3 \)
\( b_1 = 2 \)
\( a_1 + b_1 - 5 = 19 \)
\( a_1 + 2 - 5 = 19 \)
\( a_1 = 22 \)
\( a_2 = a_1 + d \)
\( 13 = 22 + d \)
\( d = -9 \)
\( a_4 = a_1 + 3d \)
\( = 22 + 3(-9) \)
\( = -5 \) bulunur.
Bir aritmetik dizinin ortak farkı 2'dir.
Aritmetik dizinin 3., 9. ve 11. terimi, bir geometrik dizinin sırasıyla ilk üç terimidir.
(a) Aritmetik dizinin ilk terimini bulunuz.
(b) Geometrik dizinin ortak oranını bulunuz.
Çözümü Göster(a) seçeneği:
Aritmetik dizinin ilk terimine \( a \) diyelim.
Dizinin genel terim formülünü kullanarak 3., 9. ve 11. terimleri bulalım.
\( (a_n) = a_1 + (n - 1)d \)
\( a_3 = a + (3 - 1)2 = a + 4 \)
\( a_9 = a + (9 - 1)2 = a + 16 \)
\( a_{11} = a + (11 - 1)2 = a + 20 \)
Geometrik dizinin ortak oranına \( r \) diyelim.
Geometrik dizilerde ardışık terimlerin oranı ortak orana eşittir.
\( \dfrac{a_9}{a_3} = \dfrac{a_{11}}{a_9} = r \)
\( \dfrac{a + 16}{a + 4} = \dfrac{a + 20}{a + 16} \)
\( (a + 16)(a + 16) = (a + 4)(a + 20) \)
\( a^2 + 32a + 256 = a^2 + 24a + 80 \)
\( a = -22 \)
(b) seçeneği:
Ardışık iki terimin oranını bulalım.
\( r = \dfrac{a_9}{a_3} \)
\( = \dfrac{a + 16}{a + 4} \)
\( = \dfrac{-22 + 16}{-22 + 4} \)
\( = \dfrac{1}{3} \) bulunur.
\( a \), \( a + 10 \), \( a + 16 \), \( b \) bir geometrik dizinin küçükten büyüğe sıralanmış ardışık dört terimidir.
\( 5b + 29 \) ve \( a + 41 \) sayıları arasına yeni bir geometrik dizi oluşturulacak şekilde kaç terim yerleştirilirse oluşan dizinin ortak çarpanı \( \sqrt{2} \) olur?
Çözümü GösterBir geometrik dizide 2. terimin karesi 1. ve 3. terimlerin çarpımına eşittir.
\( (a + 10)^2 = a(a + 16) \)
\( a^2 + 20a + 100 = a^2 + 16a \)
\( a = -25 \)
Buna göre verilen geometrik dizinin terimleri aşağıdaki gibi olur.
\( -25, -15, -9, b \)
Bu dizinin ortak çarpanını bulalım.
\( r = \frac{-15}{-25} = \frac{3}{5} \)
Sonuncu terim 3. terimle ortak çarpanın çarpımına eşittir.
\( b = -9 \cdot \frac{3}{5} = -\frac{27}{5} \)
Oluşturulacak yeni geometrik dizinin verilen iki terimini bulalım.
\( 5b + 29 = 5(-\frac{27}{5}) + 29 = 2 \)
\( a + 41 = -25 + 41 = 16 \)
Bu iki terim arasında \( n \) terim yerleştirildiğinde geometrik dizi aşağıdaki gibi olur.
\( a_1 = 2, \ldots n \text{ terim} \ldots, a_{n + 2} = 16 \)
\( a_{n + 2} = a_1 \cdot r^{n + 1} \)
\( 16 = 2 \cdot (\sqrt{2})^{n + 1} \)
\( 8 = (\sqrt{2})^{n + 1} \)
\( 2^3 = 2^{\frac{1}{2}(n + 1)} \)
\( n = 5 \) bulunur.
\( a, b, c \in \mathbb{R^+} \) olmak üzere,
\( a \), \( b \) ve \( c \) sayıları \( a \gt b \gt c \) olacak şekilde ortak çarpanı \( r \) olan bir geometrik dizi oluşturmaktadır.
Ayrıca \( 7c \), \( 33b \) ve \( 27a \) sayıları ortak farkı \( d \) olan bir sıralı aritmetik dizi oluşturmaktadır.
Buna göre \( r \) kaçtır?
Çözümü GösterGeometrik dizinin terimleri arasındaki ilişkiyi yazalım.
\( c = c \)
\( b = cr \)
\( a = cr^2 \)
Aritmetik dizinin terimleri arasındaki ilişkiyi yazalım.
\( 33b = 7c + d \)
\( 27a = 33b + d \)
İki eşitliği taraf tarafa çıkaralım.
\( 33b - 27a = 7c - 33b \)
\( 27a - 66b + 7c = 0 \)
Sayıları \( r \) cinsinden yazalım.
\( 27cr^2 - 66cr + 7c = 0 \)
\( 27r^2 - 66r + 7 = 0 \)
\( (9r - 1)(3r - 7) = 0 \)
\( r = \dfrac{1}{9} \)ya da \( r = \dfrac{7}{3} \)
\( a \gt b \gt c \) koşulunun sağlanması için \( r \gt 1 \) olmalıdır.
Buna göre geometrik dizinin ortak çarpanı \( r = \frac{7}{3} \) olarak bulunur.
\( a \) ve \( b \) birbirinden farklı sayılardır.
Bir artan geometrik dizinin \( a \). ve \( b \). terimleri sırasıyla \( 5^{-b} \) ve \( 5^{-a} \) olduğuna göre, bu dizinin ortak çarpanı kaçtır?
Çözümü GösterHer iki terimi 1. terim cinsinden yazalım.
\( a_a = a_1 \cdot r^{a-1} = 5^{-b} \)
\( a_b = a_1 \cdot r^{b-1} = 5^{-a} \)
İki eşitliği taraf tarafa birbirine bölelim.
\( \dfrac{a_1 \cdot r^{a-1}}{a_1 \cdot r^{b-1}} = \dfrac{5^{-b}}{5^{-a}} \)
\( r^{a-1-(b-1)} = 5^{-b-(-a)} \)
\( r^{a-b} = 5^{a-b} \)
\( a \) ve \( b \) farklı sayılar olduğu için üsler sıfır olamaz, dolayısıyla tabanlar mutlak değer olarak eşit olur.
\( r = 5 \) veya \( r = -5 \)
Dizinin artan olduğu belirtildiği için \( r \gt 1 \) olmalıdır.
Buna göre \( r = 5 \) olur.
Saatte 70 km hızla giden bir araba ile saatte 20 km hızla giden bir kamyonet aynı noktadan aynı anda yarışa başlıyorlar. Yarışı kazanacağına emin olan araba her saat sonunda hızını yarıya düşürüyor.
Buna göre, kamyonet arabayı kaçıncı saat sonunda geçmiş olur?
Çözümü GösterArabanın her saatte aldığı yolu bulalım.
\( 70, \dfrac{70}{2}, \dfrac{70}{4}, \ldots, \dfrac{70}{2^{t - 1}} \)
\( 70, \dfrac{70}{2^1}, \dfrac{70}{2^2}, \ldots, \dfrac{70}{2^{t - 1}} \)
Arabanın her saatte aldığı yol bir geometrik dizinin terimlerine karşılık geldiği için \( t \) saatte aldığı yolu geometrik dizinin terimler toplamı formülü ile bulabiliriz.
\( S_t = a_1 \cdot \dfrac{1 - r^n}{1 - r} = 70 \cdot \dfrac{1 - (\frac{1}{2})^t}{1 - \frac{1}{2}} \)
\( = 140(1 - \dfrac{1}{2^t}) \)
Kamyonet \( t \) saatte \( 20t \) yol alır.
Kamyonun arabadan daha çok yol katettiği \( t \) zamanını veren eşitsizliği kuralım.
\( 140(1 - \dfrac{1}{2^t}) \lt 20t \)
\( 7(1 - \dfrac{1}{2^t}) \lt t \)
\( t \)'ye farklı değerler vererek eşitsizliğin sağlandığı, yani kamyonetin arabayı geçtiği ilk \( t \) tam sayı değerini bulalım.
\( t = 5 \) için:
\( 7(1 - \dfrac{1}{2^5}) \lt 5 \)
\( 7 \cdot \dfrac{31}{32} \lt 5 \)
Eşitsizlik sağlanmadığı için araba kamyonetin önündedir.
\( t = 6 \) için:
\( 7(1 - \dfrac{1}{2^6}) \lt 6 \)
\( 7 \cdot \dfrac{63}{64} \lt 6 \)
Eşitsizlik sağlanmadığı için araba kamyonetin önündedir.
\( t = 7 \) için:
\( 7(1 - \dfrac{1}{2^7}) \lt 7 \)
\( 7 \cdot \dfrac{127}{128} \lt 7 \)
Eşitsizlik sağlandığı için kamyonet arabayı geçmiştir.
Buna göre kamyonet 7 saat sonunda arabayı geçmiştir.
\( ABC \) bir dik üçgendir.
Üçgenin kenar uzunlukları bir geometrik dizi oluşturduğuna göre, dar açılardan büyük olanın sekant değeri kaçtır?
Çözümü GösterEn kısa kenara \( x \) ve kenar uzunluklarının oluşturduğu geometrik dizinin ortak çarpanına \( r \) diyelim (\( r \gt 1 \)).
Buna göre üçgenin kenar uzunlukları küçükten büyüğe \( x \), \( xr \) ve \( xr^2 \) olur.
Üçgenin en uzun kenarı hipotenüs olduğu için hipotenüs uzunluğu \( xr^2 \) olur.
Üçgenin kenarlarına Pisagor teoremini uygulayalım.
\( (xr^2)^2 = (xr)^2 + x^2 \)
\( x^2r^4 = x^2r^2 + x^2 \)
\( r^4 = r^2 + 1 \)
\( r^2 = t \) şeklinde değişken değiştirelim.
\( t^2 = t + 1 \)
\( t^2 - t - 1 = 0 \)
Denklemin köklerini bulalım.
\( \Delta = b^2 - 4ac \)
\( = (-1)^2 - 4(1)(-1) = 5 \gt 0 \)
Buna göre denklemin birbirinden farklı iki reel kökü vardır.
\( t_{1,2} = \dfrac{-b + \sqrt{\Delta}}{2a} \)
\( t_1 = \dfrac{1 + \sqrt{5}}{2} \)
\( t_2 = \dfrac{1 - \sqrt{5}}{2} \)
\( t = r^2 \) olduğundan \( t \) negatif değer alamaz, dolayısıyla \( t_2 \) geçerli bir çözüm değildir.
\( r^2 = t = \dfrac{1 + \sqrt{5}}{2}\)
Soruda dar açılardan büyük olanın sekant değeri isteniyor. Üçgende açı/kenar bağıntısına göre dar açılardan büyük olan açı \( xr \) kenarını gören açı olur.
\( \sec{\alpha} = \dfrac{xr^2}{x} = r^2 \)
\( = \dfrac{1 + \sqrt{5}}{2} \) bulunur.