Parçalı Fonksiyonların Sürekliliği
Konu tekrarı için: Parçalı Fonksiyonlar | Parçalı Fonksiyonların Limiti
Tanım kümesinin farklı aralıklarında farklı tanımlara sahip olan fonksiyonlara parçalı fonksiyon denir. Bir parçalı fonksiyonun farklı tanıma sahip olduğu alt aralıklara fonksiyonun dalları ya da parçaları, fonksiyon tanımının değiştiği noktalara fonksiyonun geçiş noktaları denir.
Bir parçalı fonksiyonun bir geçiş noktasında sürekli olması için, süreklilik tanımı gereği bu noktanın her iki tarafında tanımlı olan fonksiyonların bu noktadaki soldan ve sağdan limit değerleri ve fonksiyon değeri tanımlı ve birbirine eşit olmalıdır.
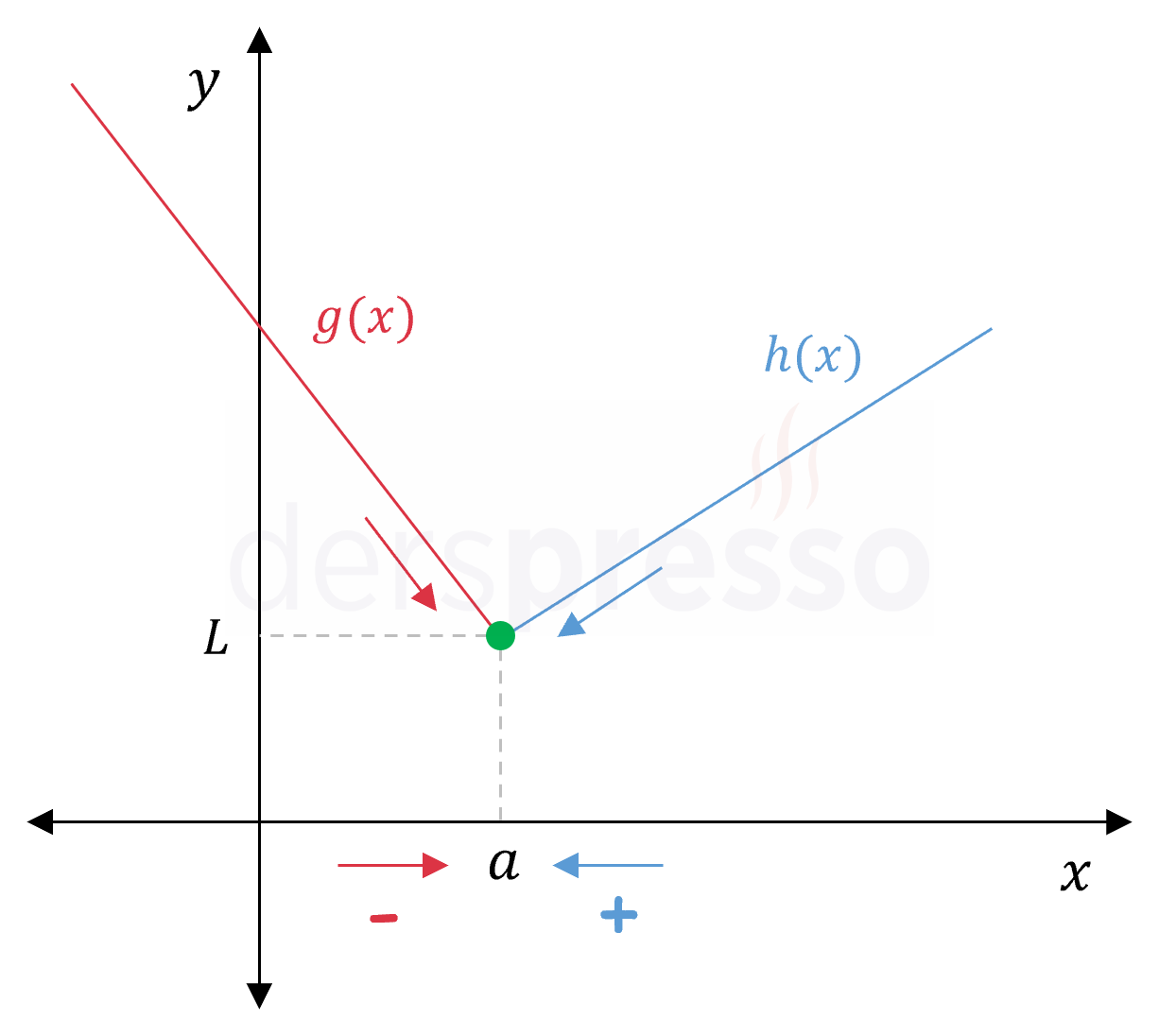
\( a, L \in \mathbb{R} \) olmak üzere,
\( f(x) = \begin{cases} g(x) & x \lt a \\ L & x = a \\ h(x) & x \gt a \end{cases} \)
parçalı fonksiyonunun \( x = a \) geçiş noktasındaki soldan ve sağdan limitleri ve fonksiyon değeri aşağıdaki gibi tanımlı ve birbirine eşit ise,
\( \lim\limits_{x \to a^-} g(x) = \lim\limits_{x \to a^+} h(x) = f(a) = L \)
fonksiyon bu noktada süreklidir.
Aksi takdirde fonksiyon bu noktada süreksizdir.
Parçalı fonksiyonların geçiş noktalarındaki sürekliliğini birkaç örnekle detaylandıralım.
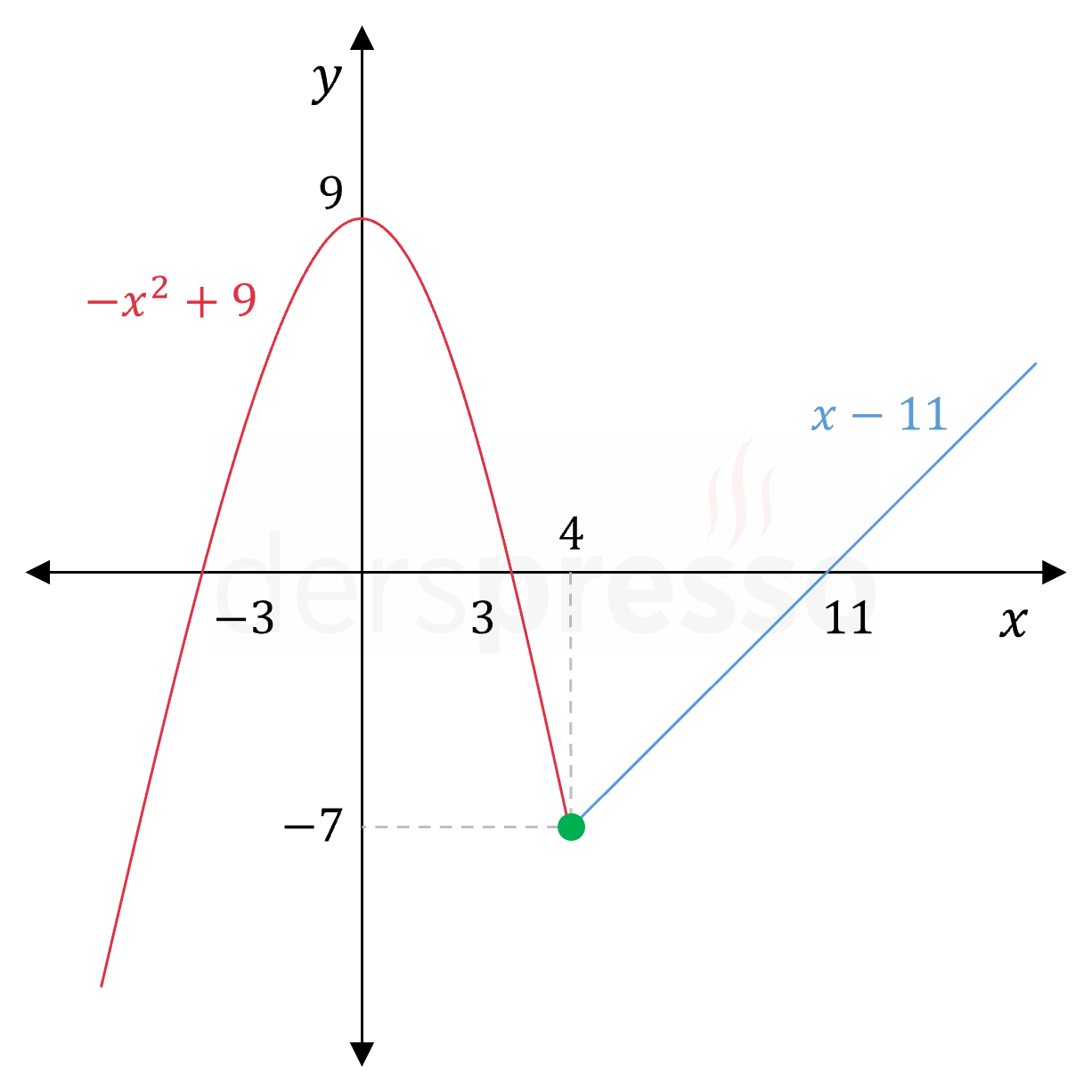
\( f(x) = \begin{cases} -x^2 + 9 & x \lt 4 \\ -7 & x = 4 \\ x - 11 & x \gt 4 \end{cases} \)
fonksiyonunun \( x = 4 \) noktasında sürekli olup olmadığını bulalım.
\( x = 4 \) parçalı fonksiyonun geçiş noktasıdır.
Bir parçalı fonksiyonun bir geçiş noktasında sürekli olması için, bu noktadaki soldan ve sağdan limit değerleri ve fonksiyon değeri tanımlı ve birbirine eşit olmalıdır.
Bu noktadaki soldan limit için \( x \)'in 4'ten küçük olduğu aralıktaki fonksiyon tanımına bakılır. Fonksiyon bu aralıkta ikinci dereceden bir polinom olduğu için süreklidir ve doğrudan yerine koyma yöntemi ile limitini bulabiliriz.
\( \lim\limits_{x \to 4^-} f(x) = \lim\limits_{x \to 4^-} (-x^2 + 9) = -4^2 + 9 = -7 \)
Bu noktadaki soldan limit için \( x \)'in 4'ten büyük olduğu aralıktaki fonksiyon tanımına bakılır. Fonksiyon bu aralıkta doğrusal olduğu için süreklidir ve doğrudan yerine koyma yöntemi ile limitini bulabiliriz.
\( \lim\limits_{x \to 4^+} f(x) = \lim\limits_{x \to 4^+} (x - 11) = 4 - 11 = -7 \)
\( x = 4 \) noktasındaki fonksiyon değeri:
\( f(4) = -7 \)
Bu noktadaki soldan ve sağdan limitler ve fonksiyon değeri tanımlı ve birbirine eşittir, dolayısıyla fonksiyon \( x = 4 \) noktasında süreklidir.
\( \lim\limits_{x \to 4^-} f(x) = \lim\limits_{x \to 4^+} f(x) = f(4) = -7 \)
Aşağıdaki grafikte fonksiyonun bu noktada sürekli olduğu görülebilir.
\( f(x) = \begin{cases} 2x - 4 & x \lt 5 \\ 3 & x = 5 \\ -x + 11 & x \gt 5 \end{cases} \)
fonksiyonunun \( x = 5 \) noktasında sürekli olup olmadığını bulalım.
\( x = 5 \) parçalı fonksiyonun geçiş noktasıdır.
Bir parçalı fonksiyonun bir geçiş noktasında sürekli olması için, bu noktadaki soldan ve sağdan limit değerleri ve fonksiyon değeri tanımlı ve birbirine eşit olmalıdır.
\( x = 5 \) noktasındaki soldan limit:
\( \lim\limits_{x \to 5^-} f(x) = \lim\limits_{x \to 5^-} (2x - 4) = 2(5) - 4 = 6 \)
\( x = 5 \) noktasındaki sağdan limit:
\( \lim\limits_{x \to 5^+} f(x) = \lim\limits_{x \to 5^+} (-x + 11) = -5 + 11 = 6 \)
\( x = 5 \) noktasındaki fonksiyon değeri:
\( f(5) = 3 \)
Bu noktadaki soldan ve sağdan limitler birbirine eşittir, ancak fonksiyon değeri farklıdır, dolayısıyla fonksiyon \( x = 5 \) noktasında sürekli değildir.
Aşağıdaki grafikte fonksiyonun bu noktada sürekli olmadığı görülebilir.
Bir parçalı fonksiyonun geçiş noktası olmayan bir noktasında sürekli olup olmadığını bulmak için, fonksiyonun bu noktanın bulunduğu aralıktaki tanımının bu noktadaki sürekliliğine bakılır.
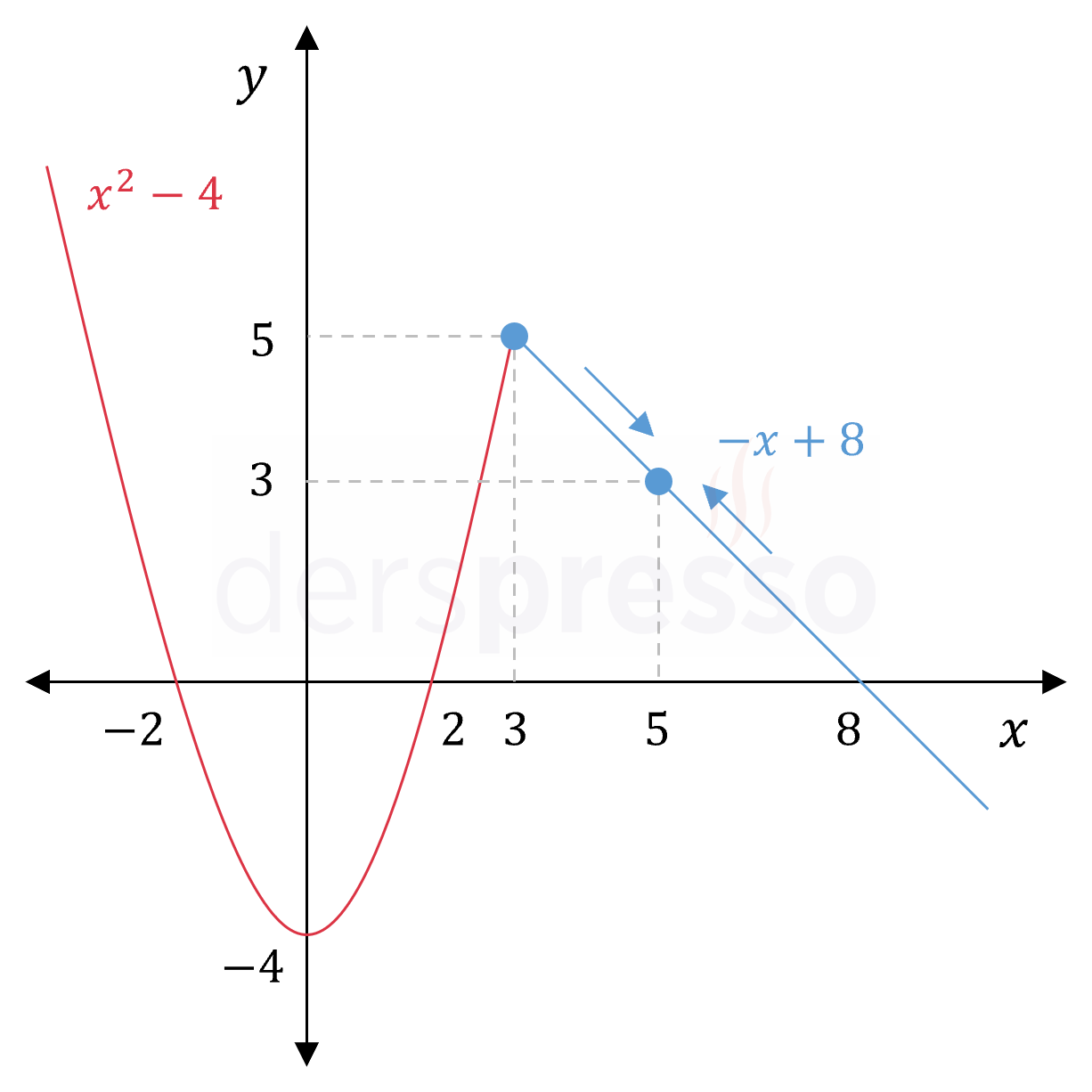
\( f(x) = \begin{cases} x^2 - 4 & x \lt 3 \\ -x + 8 & x \ge 3 \end{cases} \)
fonksiyonunun \( x = 5 \) noktasında sürekli olup olmadığını bulalım.
\( x = 5 \) parçalı fonksiyonun bir geçiş noktası değildir, dolayısıyla fonksiyonun ilgili aralıktaki tanımının bu noktadaki sürekliliğini bulalım.
\( x = 5 \) noktasının bulunduğu aralıktaki \( -x + 8 \) tanımının doğrusal ve sürekli olduğunu bildiğimiz için, bu tanımın geçerli olduğu aralıktaki tüm noktalarda parçalı fonksiyon sürekli olur, dolayısıyla fonksiyon \( x = 5 \) noktasında da süreklidir.
Aşağıdaki grafikte fonksiyonun bu noktada sürekli olduğu görülebilir.
\( f(x) = \begin{cases} -2x + 6, & x \lt 2 \\ -2x + 14, & 2 \le x \lt 6 \\ 2x - 10, & 6 \le x \end{cases} \)
parçalı fonksiyonunun geçiş noktalarında sürekli olup olmadığını bulun.
Çözümü GösterTanımı verilen parçalı fonksiyonun grafiği aşağıdaki gibidir.
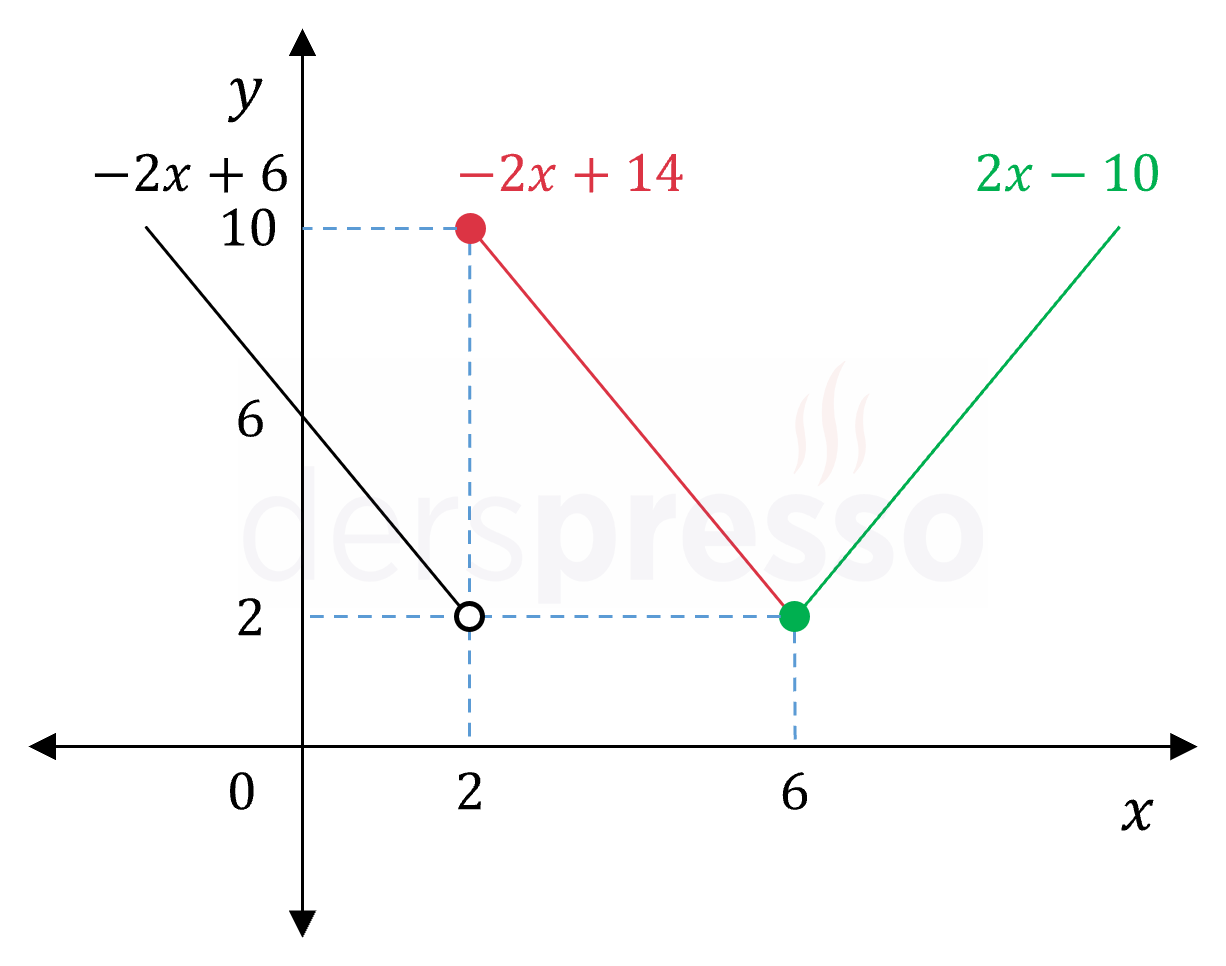
Fonksiyonun \( x = 2 \) ve \( x = 6 \) olmak üzere iki geçiş noktası vardır.
Bir parçalı fonksiyonun bir geçiş noktasında sürekli olması için, bu noktadaki soldan ve sağdan limit değerleri ve fonksiyon değeri tanımlı ve birbirine eşit olmalıdır.
Önce \( x = 2 \) noktasındaki sürekliliği inceleyelim.
\( x = 2 \) noktasındaki soldan limit:
\( \lim\limits_{x \to 2^-} f(x) = \lim\limits_{x \to 2^-} (-2x + 6) = -2(2) + 6 = 2 \)
\( x = 2 \) noktasındaki sağdan limit:
\( \lim\limits_{x \to 2^+} f(x) = \lim\limits_{x \to 2^+} (-2x + 14) = -2(2) + 14 = 10 \)
\( x = 2 \) noktasındaki fonksiyon değeri:
\( f(2) = -2(2) + 14 = 10 \)
Soldan ve sağdan limitler tanımlı olsa da birbirine eşit olmadıkları için fonksiyonun bu noktada limiti tanımlı değildir, dolayısıyla fonksiyon bu noktada sürekli değildir. Nitekim "kalem" testini uyguladığımızda fonksiyon grafiğinin bu noktada bir sıçrama yaptığını görebiliriz.
Şimdi de \( x = 6 \) noktasındaki sürekliliği inceleyelim.
\( x = 6 \) noktasındaki soldan limit:
\( \lim\limits_{x \to 6^-} f(x) = \lim\limits_{x \to 6^-} (-2x + 14) = -2(6) + 14 = 2 \)
\( x = 6 \) noktasındaki sağdan limit:
\( \lim\limits_{x \to 6^+} f(x) = \lim\limits_{x \to 6^+} (2x - 10) = 2(6) - 10 = 2 \)
\( x = 6 \) noktasındaki fonksiyon değeri:
\( f(6) = 2(6) - 10 = 2 \)
Bu noktadaki soldan ve sağdan limit değerleri ve fonksiyon değeri tanımlı ve birbirine eşittir, dolayısıyla fonksiyon bu noktada süreklidir. Nitekim "kalem" testini uyguladığımızda fonksiyon grafiğinin bu noktada herhangi bir kesintiye uğramadığını görebiliriz.
\( \lim\limits_{x \to 6^-} f(x) = \lim\limits_{x \to 6^+} f(x) = f(6) = 2 \)
\( f(x) = \begin{cases} x^2 + a, & x \lt 3 \\ 4, & x = 3 \\ -2x - b, & x \gt 3 \end{cases} \)
parçalı fonksiyonunun sürekli bir fonksiyon olması için \( a \) ve \( b \) reel sayılarının alması gereken değerleri bulun.
Çözümü GösterParçalı fonksiyonun \( x \lt 3 \) aralığında tanımlı fonksiyon ikinci dereceden bir polinom, \( x \gt 3 \) aralığında tanımlı fonksiyon da birinci dereceden bir polinomdur (doğrudur). Her ikisi de sürekli fonksiyonlar oldukları için fonksiyonun sürekliliğini sadece geçiş noktaları için kontrol etmemiz yeterlidir.
Fonksiyonun tek geçiş noktası \( x = 3 \) noktasıdır.
Bir parçalı fonksiyonun bir geçiş noktasında sürekli olması için, bu noktadaki soldan ve sağdan limit değerleri ve fonksiyon değeri tanımlı ve birbirine eşit olmalıdır.
\( x = 3 \) noktasındaki soldan limit:
\( \lim\limits_{x \to 3^-} f(x) = \lim\limits_{x \to 3^-} (x^2 + a) = 3^2 + a = 9 + a \)
\( x = 3 \) noktasındaki sağdan limit:
\( \lim\limits_{x \to 3^+} f(x) = \lim\limits_{x \to 3^+} (-2x - b) = -2(3) - b = -6 - b \)
\( x = 3 \) noktasındaki fonksiyon değeri:
\( f(3) = 4 \)
\( x = 3 \) noktasındaki fonksiyon değerini bildiğimiz için bu noktadaki sürekliliğin sağlanması için soldan ve sağdan limitler bu değere eşit olmalıdır.
\( 9 + a = 4 \)
\( a = -5 \)
\( -6 - b = 4 \)
\( b = -10 \)
Buna göre istenen değerler \( a = -5 \) ve \( b = -10 \) olur.
\( f(x) = \begin{cases} -\dfrac{1}{x} & x \lt -1 \\ 1 - x^2 & -1 \le x \le 1 \\ \dfrac{1}{x} & x \gt 1 \end{cases} \)
şeklinde tanımlanan \( f \) fonksiyonunun süreksiz olduğu noktaları bulup bu noktalardaki süreksizlik tipini belirleyiniz.
Çözümü Göster\( 1 - x^2 \) ifadesi bir polinom fonksiyonudur ve tüm reel sayılarda süreklidir.
\( \frac{1}{x} \) ve \( -\frac{1}{x} \) ifadeleri birer rasyonel fonksiyondur ve paydayı sıfır yapan \( x = 0 \) değeri dışında tüm reel sayılarda süreklidir, ancak verilen parçalı fonksiyonda \( x = 0 \) noktasında \( 1 - x^2 \) fonksiyon tanımı geçerlidir, dolayısıyla \( x = 0 \) değeri için bir tanımsızlık/süreksizlik söz konusu değildir.
\( f \) bir parçalı fonksiyon olduğu için ayrıca geçiş noktalardaki sürekliliğini incelemeliyiz.
Parçalı fonksiyonun tanımının değiştiği \( x = -1 \) ve \( x = 1 \) noktaları fonksiyonun geçiş noktalarıdır.
\( x = -1 \) noktasındaki süreklilik için soldan ve sağdan limit değerlerini ve bu noktadaki fonksiyon değerini bulalım.
\( \lim\limits_{x \to (-1)^-} -\frac{1}{x} = 1 \)
\( \lim\limits_{x \to (-1)^+} (1 - x^2) = 0 \)
\( f(-1) = 0 \)
Soldan ve sağdan limit değerleri farklı olduğu için fonksiyon \( x = -1 \) noktasında süreksizdir.
\( x = 1 \) noktasındaki sürekliliği inceleyelim.
\( \lim\limits_{x \to 1^-} (1 - x^2) = 0 \)
\( \lim\limits_{x \to 1^+} \frac{1}{x} = 1 \)
\( f(1) = 0 \)
Soldan ve sağdan limit değerleri farklı olduğu için fonksiyon \( x = 1 \) noktasında süreksizdir.
Buna göre fonksiyon iki noktada süreksizdir.
Her iki noktada da soldan ve sağdan limit değerleri farklı olduğu için sıçrama süreksizliği vardır.
\( f(x) = \begin{cases} 2\cos{x} & x \lt 0 \\ a\cos{x} + b & 0 \le x \lt \pi \\ - \sin{x} & x \ge \pi \end{cases} \)
fonksiyonunun tüm reel sayılarda sürekli olması için \( a \) ve \( b \) kaç olmalıdır?
Çözümü GösterParçalı fonksiyonun üç tanımındaki sinüs ve kosinüs fonksiyonları tüm reel sayılarda süreklidir, dolayısıyla fonksiyonun sadece geçiş noktalarındaki sürekliliğini kontrol etmemiz yeterlidir.
Parçalı fonksiyonun geçiş noktaları \( x = 0 \) ve \( x = \pi \) noktalarıdır.
Bir parçalı fonksiyonun bir geçiş noktasında sürekli olması için bu noktadaki soldan ve sağdan limit değerleri ve fonksiyon değeri tanımlı ve birbirine eşit olmalıdır.
\( x = 0 \) noktası için:
\( \lim\limits_{x \to 0^-} 2\cos{x} = 2 \cdot 1 = 2 \)
\( \lim\limits_{x \to 0^+} (a\cos{x} + b) = a \cdot 1 + b = a + b \)
\( f(0) = a \cdot 1 + b = a + b \)
Buna göre fonksiyonun bu noktada sürekli olması için aşağıdaki eşitlik sağlanmalıdır.
\( a + b = 2 \)
\( x = \pi \) noktası için:
\( \lim\limits_{x \to \pi^-} (a\cos{x} + b) = a \cdot (-1) + b = -a + b \)
\( \lim\limits_{x \to \pi^+} (-\sin{x}) = 0 \)
\( f(\pi) = -\sin{\pi} = 0 \)
Buna göre fonksiyonun bu noktada sürekli olması için aşağıdaki eşitlik sağlanmalıdır.
\( -a + b = 0 \)
İki bilinmeyenli iki denklemi çözelim.
\( a = 1 \) ve \( b = 1 \) bulunur.
\( f(x) = \begin{cases} x - 3n + m & x \lt 2 \\ 3m + 5 & x = 2 \\ x + 4m & x \gt 2 \end{cases} \)
fonksiyonu tüm reel sayılarda sürekli ise \( m + n \) kaçtır?
Çözümü GösterParçalı fonksiyonun üç tanımındaki doğrusal fonksiyonlar tüm reel sayılarda süreklidir, dolayısıyla fonksiyonun sadece geçiş noktalarındaki sürekliliğini kontrol etmemiz yeterlidir.
Fonksiyonun tek geçiş noktası \( x = 2 \) noktasıdır.
Bir parçalı fonksiyonun bir geçiş noktasında sürekli olması için bu noktadaki soldan ve sağdan limit değerleri ve fonksiyon değeri tanımlı ve birbirine eşit olmalıdır.
\( x = 2 \) noktasındaki soldan limit:
\( \lim\limits_{x \to 2^-} (x - 3n + m) = 2 - 3n + m \)
\( x = 2 \) noktasındaki sağdan limit:
\( \lim\limits_{x \to 2^+} (x + 4m) = 2 + 4m \)
\( x = 2 \) noktasındaki fonksiyon değeri:
\( f(2) = 3m + 5 \)
Bu noktadaki sürekliliğin sağlanması için soldan ve sağdan limitler birbirine ve fonksiyon değerine eşit olmalıdır.
\( 2 - 3n + m = 2 + 4m = 3m + 5 \)
İkinci ve üçüncü eşitliği çözelim.
\( 2 + 4m = 3m + 5 \)
\( m = 3 \)
Bu değeri kullanarak ilk iki eşitliği çözelim.
\( 2 - 3n + 3 = 2 + 4(3) \)
\( n = -3 \)
Buna göre \( m + n = 3 + (-3) = 0 \) bulunur.
\( f(x) = \begin{cases} a^2 - ax^3 & x \lt 1 \\ x^2 + a & x \ge 1 \end{cases} \)
fonksiyonu yalnız bir noktada süreksizdir.
Buna göre, \( a \)'nın alamayacağı değerlerin toplamı kaçtır?
Çözümü GösterVerilen parçalı fonksiyonun iki aralığında tanımlı ifadeler birer polinom fonksiyonudur. Polinom fonksiyonları tüm reel sayılarda süreklidir.
Buna göre fonksiyonun sürekli olmayabileceği tek nokta parçalı fonksiyonun geçiş noktası olan \( x = 1 \) noktasıdır.
Bir parçalı fonksiyonun bir geçiş noktasında sürekli olması için bu noktadaki soldan ve sağdan limit değerleri ve fonksiyon değeri tanımlı ve birbirine eşit olmalıdır.
\( \lim\limits_{x \to 1^-} (a^2 - ax^3) = a^2 - a \)
\( \lim\limits_{x \to 1^+} (x^2 + a) = 1 + a \)
Fonksiyonun bu noktada süreksiz olması için bu iki limit değeri birbirinden farklı olmalıdır.
\( a^2 - a \ne 1 + a \)
\( a^2 - 2a - 1 \ne 0 \)
\( a \)'nın alamayacağı değerler \( a^2 - 2a - 1 = 0 \) denkleminin kökleridir. Bu denklemin kökler toplamı da \( a \)'nın alamayacağı değerlerin toplamını verir.
Kökler toplamı:
\( = -\dfrac{-2}{1} = 2 \) bulunur.
\( f(x) = \begin{cases} \arcsin(\frac{1 - x}{2}) & 0 \lt x \lt 3 \\ \dfrac{\pi}{2} & x = 3 \\ \arctan(\frac{x}{3 - x}) & x \gt 3 \end{cases} \)
şeklinde tanımlı \( f \) fonksiyonunun \( x = 3 \) noktasındaki sürekliliğini inceleyiniz.
Çözümü Göster\( x = 3 \) noktası parçalı fonksiyonun geçiş noktasıdır.
Bu noktadaki soldan ve sağdan limiti bulalım.
\( \lim\limits_{x \to 3^-} f(x) = \lim\limits_{x \to 3^-} \arcsin(\frac{1 - x}{2}) \)
\( = \arcsin(-1) = -\dfrac{\pi}{2} \)
\( \lim\limits_{x \to 3^+} f(x) = \lim\limits_{x \to 3^+} \arctan(\frac{x}{3 - x}) \)
\( = \arctan(-\infty) = -\dfrac{\pi}{2} \)
Fonksiyonun \( x = 3 \) noktasında soldan ve sağdan limitleri tanımlı ve birbirine eşit olduğu için bu noktada iki yönlü limit tanımlıdır ve bu limit değerine eşittir.
\( \lim\limits_{x \to 3} f(x) = -\dfrac{\pi}{2} \)
\( f(3) = \dfrac{\pi}{2} \)
Bu noktadaki fonksiyon değeri limit değerinden farklı olduğu için fonksiyon \( x = 3 \) noktasında süreksizdir. Fonksiyonun bu noktadaki süreksizliği kaldırılabilir süreksizliktir.