Fonksiyonların Sürekliliği
Fonksiyonlar konusunda incelediğimiz aşağıdaki fonksiyonlar en geniş tanım kümelerinde süreklidir. Bu fonksiyonlar ve sürekli oldukları aralıklar aşağıdaki tabloda belirtilmiştir.
Bu fonksiyonların tanımında \( x \) olarak belirtilen ifadelerin yerine bir \( g(x) \) fonksiyonu gelmesi durumunda, bu \( g \) fonksiyonunu süreksiz yapan \( x \) değerleri \( f \) fonksiyonunu da süreksiz yapar.
| Fonksiyon | Denklem | En Geniş Tanım Kümesi |
|---|---|---|
| Sabit fonksiyon | \( f(x) = c \) | Tüm reel sayılar |
| Doğrusal fonksiyon | \( f(x) = mx + c \) | Tüm reel sayılar |
| Kuvvet fonksiyonu | \( f(x) = x^n \) | Tüm reel sayılar |
| Köklü fonksiyon (çift dereceli) | \( f(x) = \sqrt[2n]{x} \) | \( [0, \infty) \) |
| Köklü fonksiyon (tek dereceli) | \( f(x) = \sqrt[2n + 1]{x} \) | Tüm reel sayılar |
| Mutlak değer fonksiyonu | \( f(x) = \abs{x} \) | Tüm reel sayılar |
| Polinom fonksiyonu | \( f(x) = a_nx^n + \ldots + a_0 \) | Tüm reel sayılar |
| Rasyonel fonksiyon | \( f(x) = \dfrac{g(x)}{h(x)} \) | Paydayı sıfır yapan reel kökler dışında tüm reel sayılar |
| Sinüs fonksiyonu | \( f(x) = \sin{x} \) | Tüm reel sayılar |
| Kosinüs fonksiyonu | \( f(x) = \cos{x} \) | Tüm reel sayılar |
| Tanjant fonksiyonu | \( f(x) = \tan{x} \) | \( \{ \ldots, \frac{\pi}{2}, \frac{3\pi}{2}, \ldots \} \) dışında tüm reel sayılar |
| Kotanjant fonksiyonu | \( f(x) = \cot{x} \) | \( \{ \ldots, 0, \pi, \ldots \} \) dışında tüm reel sayılar |
| Sekant fonksiyonu | \( f(x) = \sec{x} \) | \( \{ \ldots, \frac{\pi}{2}, \frac{3\pi}{2}, \ldots \} \) dışında tüm reel sayılar |
| Kosekant fonksiyonu | \( f(x) = \csc{x} \) | \( \{ \ldots, 0, \pi, \ldots \} \) dışında tüm reel sayılar |
| Üstel fonksiyon | \( f(x) = a^x \) | Tüm reel sayılar |
| Logaritma fonksiyonu | \( f(x) = \log_a{x} \) | \( (0, \infty) \) |
\( f(x) = \dfrac{x + 8}{x^2 - 25} \)
\( g(x) = \sqrt{x - 7} \)
\( h(x) = \log_3(x - 5) \)
\( k(x) = 5^{x - 5} \)
Yukarıdaki fonksiyonlardan hangileri \( x = 5 \) noktasında tanımlı ve süreklidir?
Çözümü Göster\( f(x) = \frac{x + 8}{x^2 - 25} \) fonksiyonu rasyonel bir fonksiyondur ve paydayı sıfır yapan değerler hariç tüm reel sayılarda süreklidir. \( x = 5 \) değeri paydayı sıfır yaptığı için \( f \) fonksiyonu bu noktada tanımlı değildir.
\( g(x) = \sqrt{x - 7} \) çift dereceli köklü bir fonksiyondur ve kök içinin sıfıra eşit ya da sıfırdan büyük olduğu durumlarda tanımlı ve sürekli olur. \( x = 5 \) değeri kök içini negatif yaptığı için \( g \) fonksiyonu bu noktada tanımlı değildir.
\( h(x) = \log_3(x - 5) \) bir logaritma fonksiyonudur ve logaritması alınan değerin pozitif olduğu \( x \) değerlerinde tanımlı ve süreklidir. \( x = 5 \) değeri logaritması alınan değeri sıfır yaptığı için \( h \) fonksiyonu bu noktada tanımlı değildir.
\( k(x) = 5^{x - 5} \) fonksiyonu tüm reel sayılarda tanımlı ve süreklidir. Dolayısıyla \( k \) fonksiyonu bu noktada tanımlı ve süreklidir.
Buna göre yalnız \( k \) fonksiyonu \( x = 5 \) noktasında tanımlı ve süreklidir.
\( f(x) = \dfrac{12}{x^2 - (m - 1)x + 9} \)
fonksiyonu tüm reel sayılarda sürekli olduğuna göre, \( m \)'nin alabileceği tam sayı değerlerinin toplamı kaçtır?
Çözümü GösterVerilen rasyonel fonksiyonun tüm reel sayılarda sürekli olabilmesi için fonksiyon tüm reel sayılarda tanımlı olmalı yani paydası sıfır olmamalıdır. Paydadaki ikinci dereceden ifadenin tüm reel sayı \( x \) değerleri için sıfırdan farklı olması için denklem halinin reel kökü bulunmamalıdır, yani deltası sıfırdan küçük olmalıdır.
\( \Delta = b^2 - 4ac \lt 0 \)
\( x^2 - (m - 1)x + 9 = 0 \) denklemi için:
\( a = 1, \quad b = m - 1, \quad c = 9 \)
\( (m - 1)^2 - 4 \cdot 1 \cdot 9 \lt 0 \)
\( (m - 1)^2 - 36 \lt 0 \)
\( \abs{m - 1} \lt 6 \)
\( -6 \lt m - 1 \lt 6 \)
\( -5 \lt m \lt 7 \)
\( m \)'nin alabileceği tam sayı değerlerinin toplamı:
\( (-4) + (-3) + \ldots + 5 + 6 \)
\( = 11 \) bulunur.
\( f(x) = \sqrt{x^2 - 6x - 7} \)
\( g(x) = \dfrac{1}{\sin(2x) + 1} \)
\( h(x) = \tan(4x - \frac{\pi}{2}) \)
\( k(x) = \log_3(5 - x) \)
Yukarıdaki fonksiyonların sürekli oldukları en geniş aralıkları bulunuz.
Çözümü Göster\( f \) fonksiyonu çift dereceli bir köklü fonksiyondur, dolayısıyla kök içini sıfır ya da pozitif yapan değerlerde tanımlı ve süreklidir.
\( x^2 - 6x - 7 \ge 0 \)
\( (x + 1)(x - 7) \ge 0 \)
Buna göre fonksiyon \( (-1, 7) \) aralığı hariç tüm reel sayılarda tanımlı ve süreklidir.
\( g \) fonksiyonu paydasını sıfır yapan değerler için tanımsızdır, diğer tüm değerlerde tanımlı ve süreklidir.
Paydayı sıfır yapan \( x \) değerlerini bulalım.
\( \sin(2x) + 1 = 0 \)
\( \sin(2x) = -1 \)
\( k \in \mathbb{Z} \) olmak üzere,
\( 2x = \dfrac{3\pi}{2} + 2k\pi \)
Buna göre fonksiyon aşağıdaki \( x \) değerleri hariç tüm reel sayılarda tanımlı ve süreklidir.
\( x = \dfrac{3\pi}{4} + k\pi \)
\( h \) fonksiyonu tanjant fonksiyonunu tanımsız yapan değerler için tanımsızdır, diğer tüm değerlerde tanımlı ve süreklidir.
\( 4x - \dfrac{\pi}{2} = \dfrac{\pi}{2} + k\pi \)
\( 4x = \pi + k\pi \)
Buna göre fonksiyon aşağıdaki \( x \) değerleri hariç tüm reel sayılarda tanımlı ve süreklidir.
\( x = \dfrac{\pi}{4} + \dfrac{k\pi}{4} \)
\( k \) fonksiyonu logaritma fonksiyonudur, dolayısıyla logaritma içini pozitif yapan değerlerde tanımlı ve süreklidir.
\( 5 - x \gt 0 \)
\( x \lt 5 \)
Buna göre fonksiyon \( (-\infty, 5) \) aralığında tanımlı ve süreklidir.
Özel fonksiyonlar bölümünde incelediğimiz işaret, taban, tavan ve ondalık kısım fonksiyonlarının süreksiz oldukları noktaları bulup bu noktalardaki süreksizlik tipini belirleyiniz.
Çözümü Gösterİşaret fonksiyonu:
İşaret fonksiyonu \( x \) değeri pozitif bir sayı ise \( +1 \), negatif bir sayı ise \( -1 \), sıfır ise 0 değeri veren bir parçalı fonksiyondur.

Yukarıda grafikte görebileceğimiz gibi işaret fonksiyonu \( x = 0 \) noktasında süreksiz, diğer tüm noktalarda süreklidir. Fonksiyonun bu noktadaki süreksizliği sıçrama süreksizliğidir.
Taban fonksiyonu:
Taban fonksiyonu girdi olarak aldığı \( x \) değerinden küçük ya da \( x \)'e eşit en büyük tam sayıyı verir.
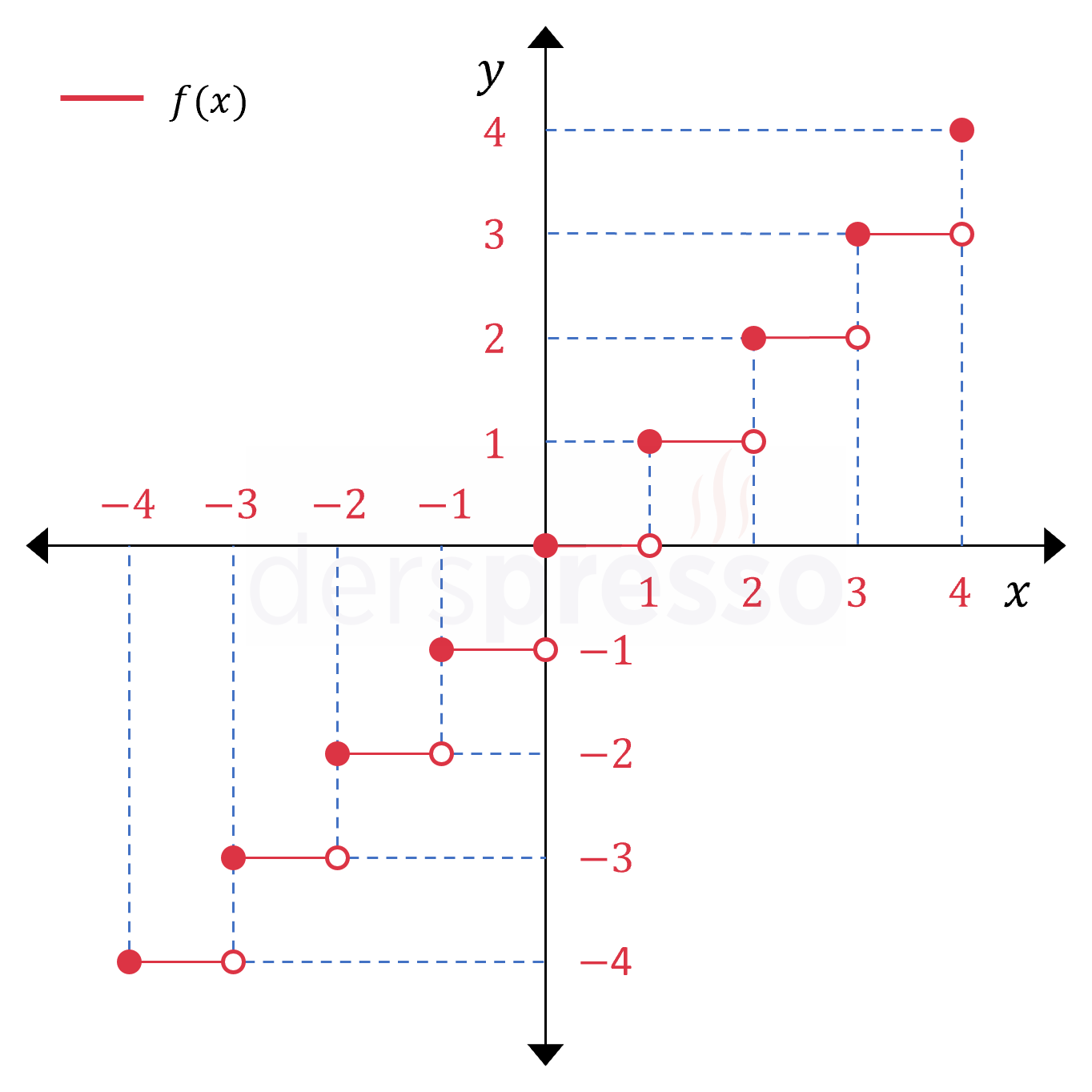
Yukarıda grafikte görebileceğimiz gibi taban fonksiyonu \( x \)'in tam sayı değerlerinde süreksiz, diğer tüm noktalarda süreklidir. Fonksiyonun bu noktadaki süreksizliği sıçrama süreksizliğidir.
Tavan fonksiyonu:
Tavan fonksiyonu girdi olarak aldığı \( x \) değerinden büyük ya da \( x \)'e eşit en küçük tam sayıyı verir.
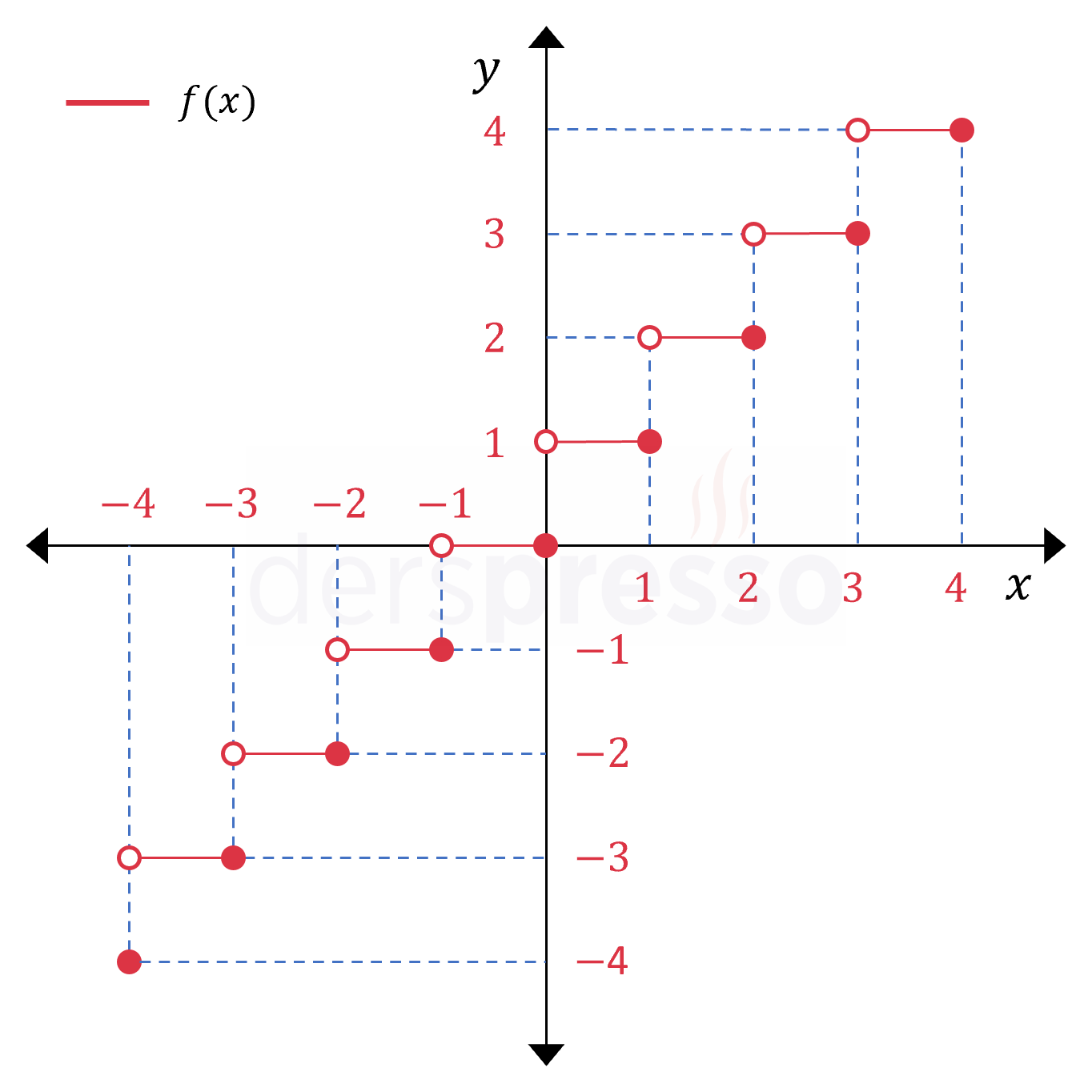
Yukarıda grafikte görebileceğimiz gibi tavan fonksiyonu \( x \)'in tam sayı değerlerinde süreksiz, diğer tüm noktalarda süreklidir. Fonksiyonun bu noktadaki süreksizliği sıçrama süreksizliğidir.
Ondalık kısım fonksiyonu:
Ondalık kısım fonksiyonu girdi olarak aldığı \( x \) değeri ile bu değerin taban fonksiyon değeri arasındaki farkı verir.
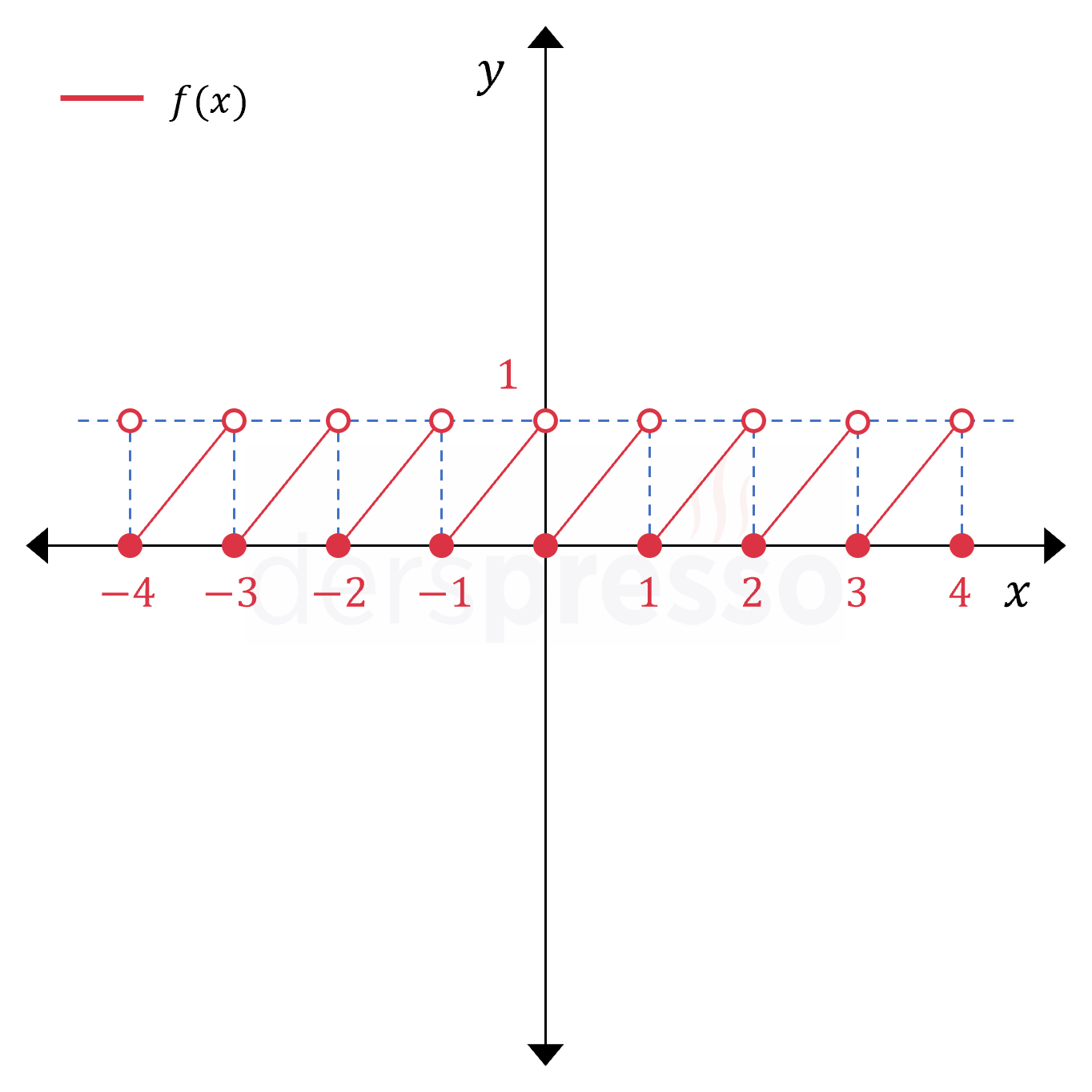
Yukarıda grafikte görebileceğimiz gibi ondalık kısım fonksiyonu \( x \)'in tam sayı değerlerinde süreksiz, diğer tüm noktalarda süreklidir. Fonksiyonun bu noktadaki süreksizliği sıçrama süreksizliğidir.
\( f(x) = \dfrac{\sin{x}}{x} \) fonksiyonunun süreksiz olduğu noktaları ve bu noktalardaki süreksizlik tipini belirleyiniz.
Çözümü Göster\( \dfrac{\sin{x}}{x} \) rasyonel ifadesinin payı ve paydası ayrı ayrı tüm reel sayılarda süreklidir.
\( x = 0 \) değeri paydayı sıfır yaptığı için \( f \) fonksiyonu bu noktada tanımlı değildir, dolayısıyla süreksizdir.
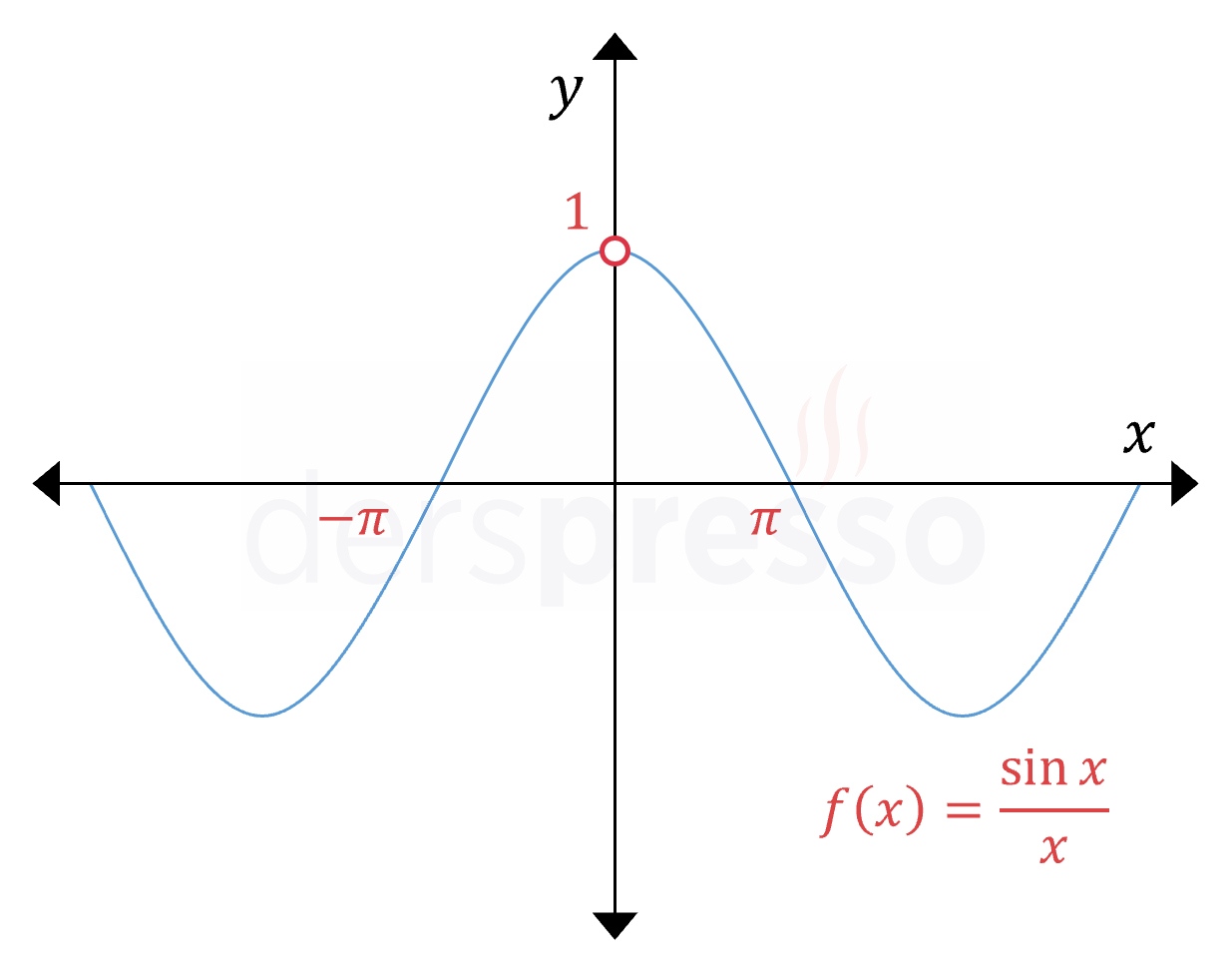
\( \lim\limits_{x \to 0} \dfrac{\sin{x}}{x} = 1 \) olduğunu biliyoruz, bu nedenle \( f \) fonksiyonunun \( x = 0 \) noktasındaki süreksizliği kaldırılabilir süreksizliktir.
Aşağıdaki şekilde tanımlayacağımız \( g \) fonksiyonu \( f \) fonksiyonunun \( x = 0 \) noktasında süreksizliğini giderir.
\( g(x) = \begin{cases} \dfrac{\sin{x}}{x} & x \ne 0 \\ 1 & x = 0 \end{cases} \)
\( f(x) = \dfrac{\sqrt{x^2 - kx + 9}}{x^2 + k} \) fonksiyonunun tüm reel sayılarda sürekli olması için \( k \) değer aralığı ne olmalıdır?
Çözümü GösterBir rasyonel fonksiyon paydasını sıfır yapan veya içerdiği bazı ifadeleri tanımsız yapan \( x \) değerlerinde tanımsız ve süreksiz olur.
Durum 1: Paydayı sıfır yapan değerler
\( x^2 + k \ne 0 \)
\( x^2 \) ifadesi her reel sayı \( x \) değeri için sıfır ya da pozitiftir.
Buna göre paydanın her \( x \) değeri için sıfırdan farklı olması için \( k \gt 0 \) olmalıdır.
Durum 2: Kök içini negatif yapan değerler
Çift dereceli köklü ifadeler kök içini negatif yapan \( x \) değerlerinde tanımsızdır.
\( x^2 - kx + 9 \ge 0 \)
Bu ifade kolları yukarı yönlü bir parabole ait olduğu için tüm reel sayılarda sıfır ya da pozitif olması için deltası sıfır ya da negatif olmalıdır.
\( \Delta = b^2 - 4ac \le 0 \)
\( (-k)^2 - 4 \cdot 1 \cdot 9 \le 0 \)
\( k^2 - 36 \le 0 \)
\( -6 \le k \le 6 \)
Bu iki durumun ikisinin de sağlandığı durumda fonksiyon tanımlı ve sürekli olacağı için \( k \) değer aralığı bulduğumuz iki aralığın kesişim kümesi olur.
\( k \in (0, 6] \)