Olaylarla İşlemler
Bir örnek uzay ve bu örnek uzayın alt kümesi olan tüm olaylar birer kümedir ve elemanları örnek uzayda tanımlı olan sonuçlardır. Buna göre, bir örnek uzayda tanımlı olaylar arasındaki küme işlemlerinin sonuçları da aynı uzayda tanımlı birer olay olur.
Bu açıdan bakınca, kümeler için geçerli olan birleşim, kesişim, tümleyen ve fark işlemlerinin tümü örnek uzay ve olaylar arasında da geçerlidir. Bu bölümde olasılık hesaplamalarında sıklıkla kullanılan bu küme işlemlerini olaylar bağlamında tekrar inceleyeceğiz.
İki Olayın Kesişimi
\( A \) ve \( B \) olaylarının ikisinin de elemanı olan sonuçlardan oluşan olaya \( A \) ve \( B \) olaylarının kesişim olayı denir ve \( A \cap B \) ile gösterilir. \( A \cap B \) olayı \( A \) ve \( B \) olaylarının ikisinin de gerçekleştiği durumlarda gerçekleşmiş olur.
\( A \cap B \) olayının küme gösterimi aşağıdaki gibidir.
\( A \cap B = \{x \mid x \in A \text{ ve } x \in B\} \)
Bir zar atışında sonucun 6 olduğu durumda aşağıdaki gibi tanımlı iki olay gerçekleşmiş olur, dolayısıyla iki olayın kesişim olayı da gerçekleşmiş olur.
\( S = \{1, 2, 3, 4, 5, 6\} \)
\( A \): Zarın çift gelme olayı
\( A = \{2, 4, 6\} \)
\( B \): Zarın 4 ya da daha büyük gelme olayı
\( B = \{4, 5, 6\} \)
\( A \cap B = \{4, 6\} \)
Bu iki olayın kesişim olayı aşağıdaki Venn şemasında yeşil ile gösterilmiştir.
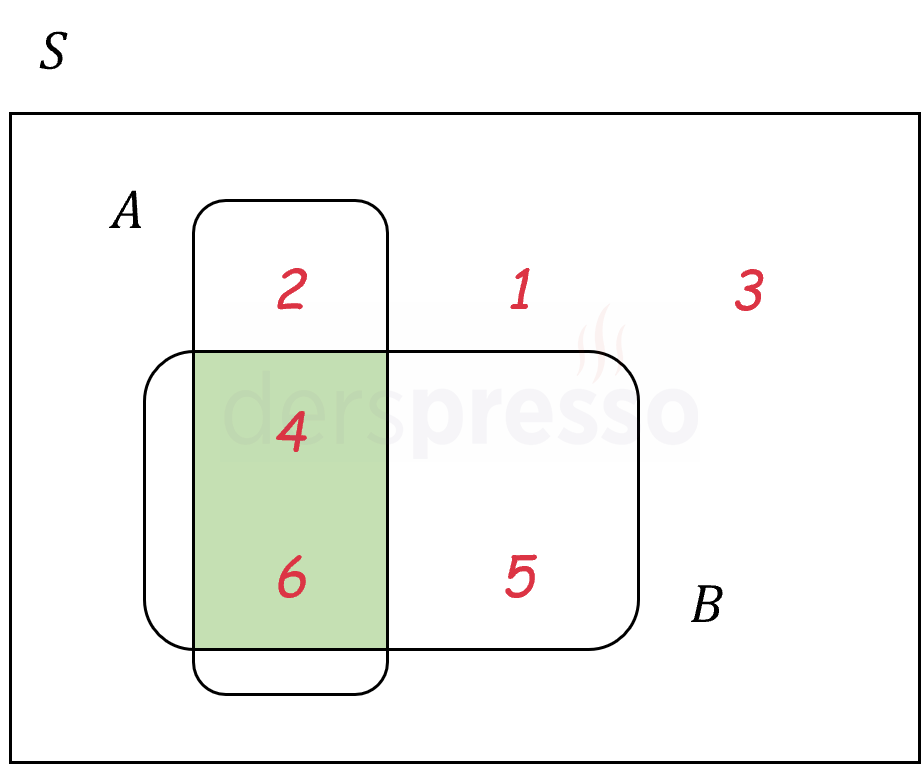
Benzer şekilde, ikiden fazla olayın kesişim olayı bu olayların tümünün elemanı olan sonuçlardan oluşan olaydır. Bu kesişim olayı kesişimi alınan olayların tümünün gerçekleştiği durumlarda gerçekleşmiş olur.
İki Olayın Birleşimi
\( A \) veya \( B \) olaylarının en az birinin elemanı olan sonuçlardan oluşan olaya \( A \) ve \( B \) olaylarının birleşim olayı denir ve \( A \cup B \) ile gösterilir. \( A \cup B \) olayı \( A \) veya \( B \) olaylarının en az birinin gerçekleştiği durumlarda gerçekleşmiş olur.
\( A \cup B \) olayının küme gösterimi aşağıdaki gibidir.
\( A \cup B = \{x \mid x \in A \text{ veya } x \in B\} \)
Bir zarın iki kez atışında zarın iki seferde de 1 gelme durumunda (sonuç: 11) aşağıdaki gibi tanımlı iki olaydan en az biri gerçekleşmiş olur, dolayısıyla iki olayın birleşim olayı da gerçekleşmiş olur.
\( S = \{11, 12, 13, \ldots, 65, 66\} \)
\( A \): İki zarın aynı gelme olayı
\( A = \{11, 22, 33, 44, 55, 66\} \)
\( B \): İki zarın toplamının 10 ya da daha büyük gelme olayı
\( B = \{46, 55, 56, 64, 65, 66\} \)
\( A \cup B = \{11, 22, 33, 44, 46, 55, 56, 64, 65, 66\} \)
Bu iki olayın birleşim olayının tablo şeklinde gösterimi aşağıdaki gibidir. Bu gösterimde satırlar birinci zarın sonucunu, sütunlar ikinci zarın sonucunu göstermekte olup, yeşil kutular iki olayın birleşim olayına karşılık gelmektedir.
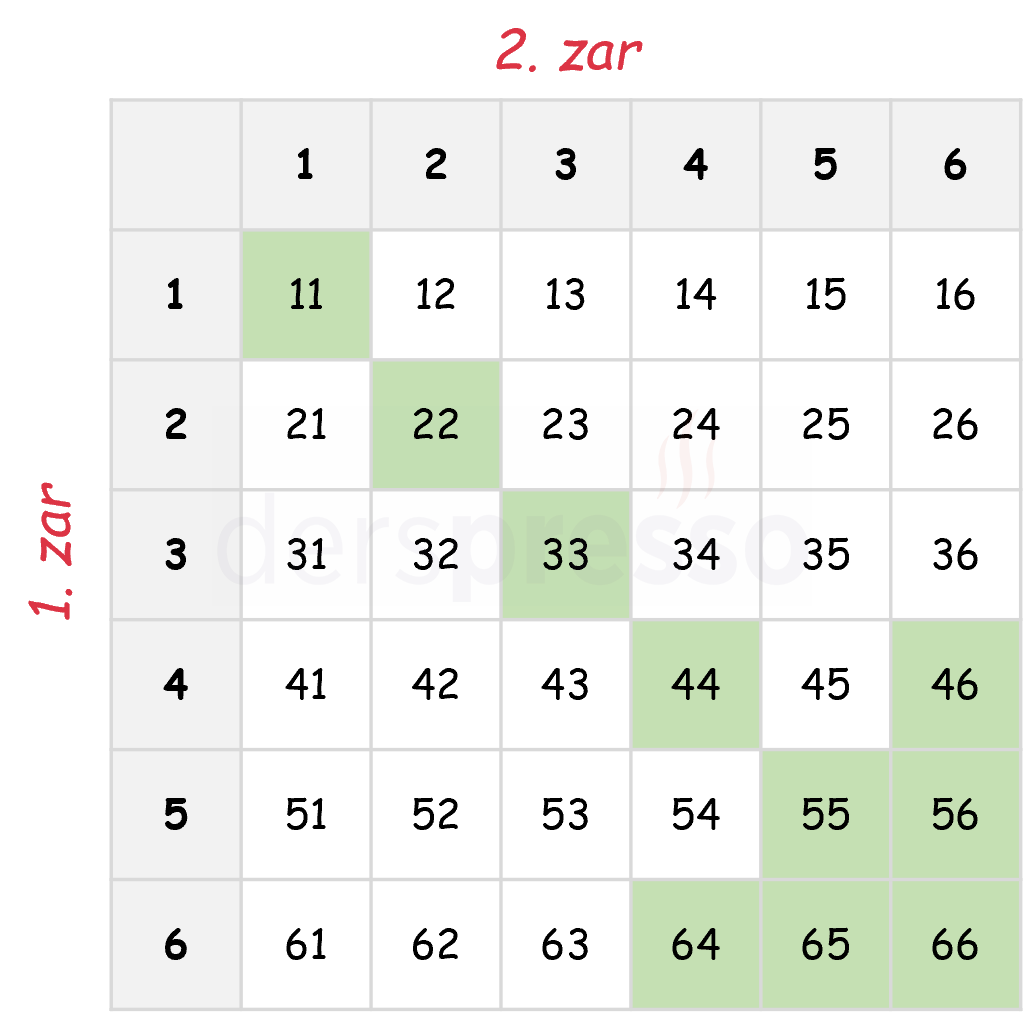
Benzer şekilde, ikiden fazla olayın birleşim olayı bu olayların en az birinin elemanı olan sonuçlardan oluşan olaydır. Bu birleşim olayı birleşimi alınan olaylardan en az birinin gerçekleştiği durumlarda gerçekleşmiş olur.
Birleşim Olayının Eleman Sayısı
İki olayın birleşiminin eleman sayısı aşağıdaki formülle hesaplanır. Bu formülde olayların eleman sayılarının toplamından kesişim kümesinin eleman sayısının çıkarılmasının sebebi, kesişim olayındaki sonuçların iki olayda ortak olması ve bu çıkarma işleminin bu ortak sonuçların iki kez sayılmasının önüne geçmesidir.
\( s(A \cup B) = s(A) + s(B) \textcolor{red}{- s(A \cap B)} \)
\( A = \{1, 2, 3, 4\} \)
\( B = \{3, 4, 5, 6\} \)
\( A \cap B = \{3, 4\} \)
\( A \cup B = \{1, 2, 3, 4, 5, 6\} \)
\( s(A \cup B) = 4 + 4 - 2 = 6 \)
İki ayrık olayın birleşiminde formül aşağıdaki şekilde olur.
\( A \) ve \( B \) ayrık olaylar ise,
\( A \cap B = \emptyset \)
\( s(A \cup B) = s(A) + s(B) \)
Üç ya da daha fazla sayıda olayın birleşiminin eleman sayısını bulmak için sayma konusunda gördüğümüz Dahil Etme - Hariç Tutma Prensibi kullanılır.
Bir Olayın Tümleyeni
\( S \) örnek uzayındaki bir \( A \) olayının elemanı olan sonuçlar dışında kalan sonuçları içeren olaya \( A \) olayının tümleyeni denir ve \( A' \) ile gösterilir. \( A' \) olayı \( A \) olayının gerçekleştiği durumlarda gerçekleşmemiş, \( A \) olayının gerçekleşmediği durumlarda ise gerçekleşmiş olur.
\( A \) olayının tümleyeninin küme gösterimi aşağıdaki gibidir.
\( A' = \{x \mid x \notin A \text{ ve } x \in S\} \)
Tek bir zar atışında zarın 3 gelmesi durumunda aşağıdaki gibi tanımlı \( A \) olayı gerçekleşmemiş olur, dolayısıyla \( A' \) olayı gerçekleşmiş olur.
\( S = \{1, 2, 3, 4, 5, 6\} \)
\( A \): Zarın çift gelme olayı
\( A = \{2, 4, 6\} \)
\( A' = \{1, 3, 5\} \)
Bu olayın tümleyeni olan olay aşağıdaki Venn şemasında yeşil ile gösterilmiştir.
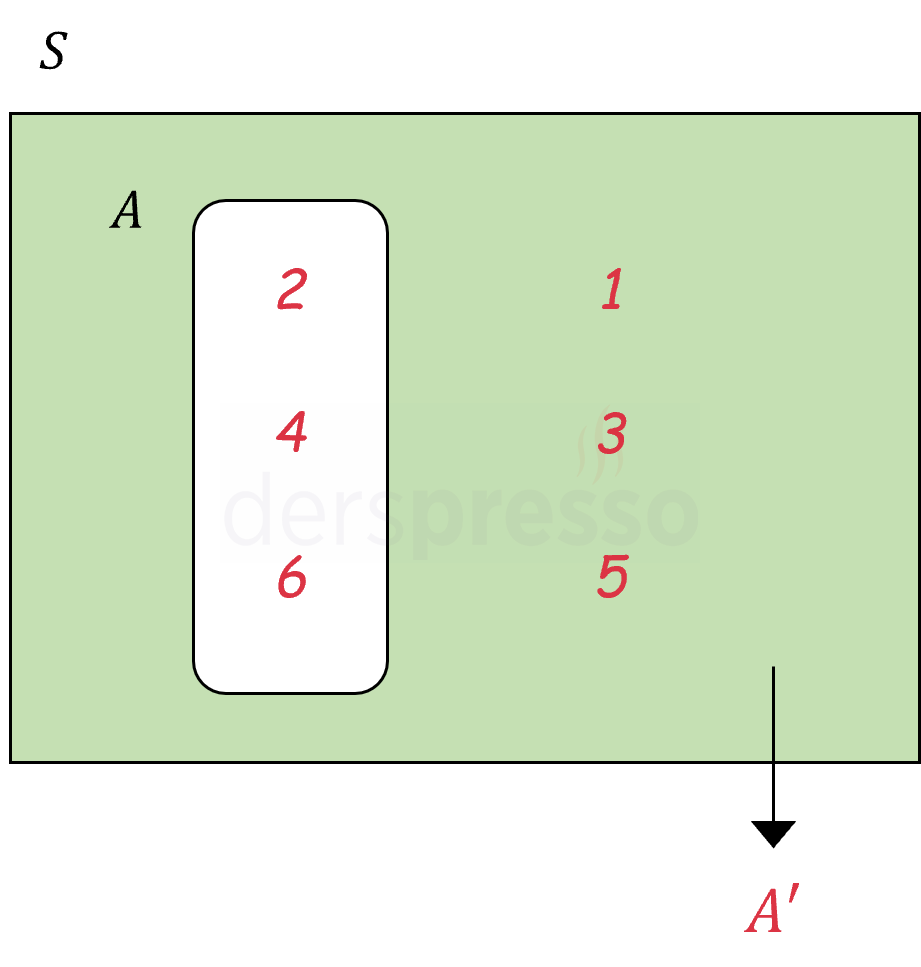
Bir olay ve tümleyeninin kesişimi boş küme olduğu için bu iki olay ayrık olaylardır.
\( A \cap A' = \emptyset \)
\( A \): Çekilen bir kartın maça olması
\( A' \): Çekilen bir kartın maça olmaması
\( A \cap A' = \emptyset \)
Bir olay ve tümleyeninin birleşimi örnek uzaya eşittir.
\( A \cup A' = S \)
\( A' = S - A \)
\( A \): Üç para atışında en az bir yazı gelmesi
\( A' \): Üç para atışında hiç yazı gelmemesi
\( A \cup A' = S \)
İki Olayın Farkı
\( A \) olayının \( B \) olayından farkı, \( A \) olayının elemanı olan ama \( B \) olayının elemanı olmayan sonuçlardan oluşur ve \( A - B \) ile gösterilir. \( A - B \) olayı \( A \) olayının gerçekleştiği ve \( B \) olayının gerçekleşmediği durumlarda gerçekleşmiş olur.
\( A \) olayının \( B \) olayından farkının küme gösterimi aşağıdaki gibidir.
\( A - B = \{x \mid x \in A \land x \notin B\} \)
Bir zar atışında zarın 4 gelme durumunda aşağıdaki gibi tanımlı iki olaydan \( A \) gerçekleşmiş \( B \) gerçekleşmemiş olur, dolayısıyla \( A - B \) olayı gerçekleşmiş olur.
\( S = \{1, 2, 3, 4, 5, 6\} \)
\( A \): Zarın çift gelme olayı
\( A = \{2, 4, 6\} \)
\( B \): Zarın asal sayı gelme olayı
\( B = \{2, 3, 5\} \)
\( A - B = \{4, 6\} \)
\( A \) olayının \( B \) olayından farkı olan olay aşağıdaki Venn şemasında yeşil ile gösterilmiştir.
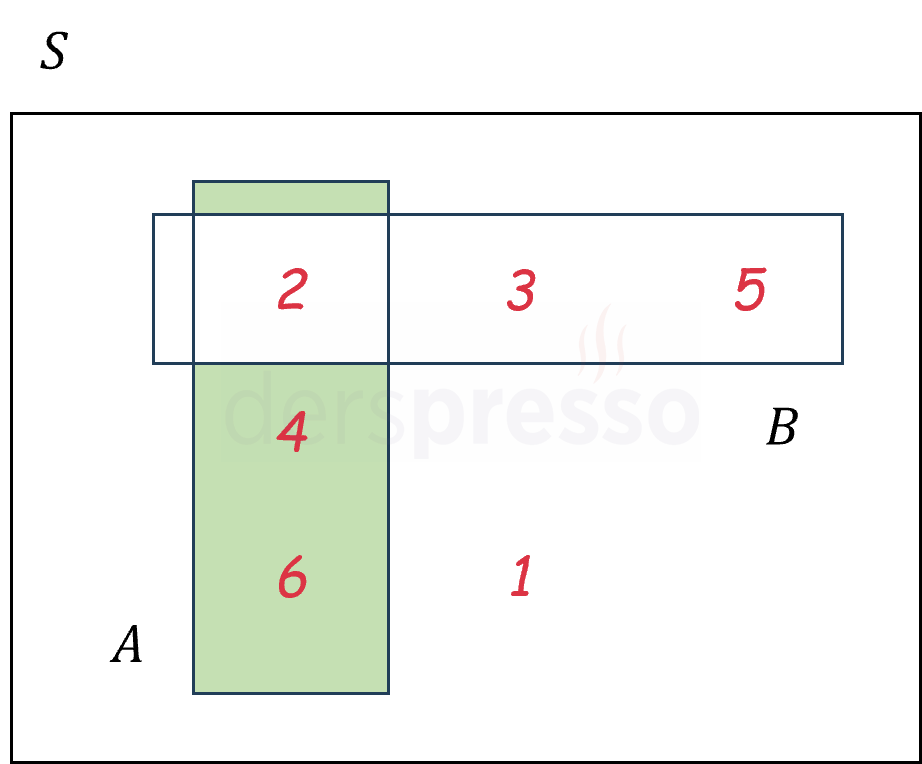
\( A \) olayının \( B \) olayından farkı aşağıdaki şekilde de ifade edilebilir.
\( A - B = A \cap B' \)
Bir olay, diğer bir olaydan farkı ile bu olayla kesişiminin birleşimine eşittir.
\( A = (A - B) \cup (A \cap B) \)
Birbirini Kapsayan Olaylar
\( B \) olayının elemanı olan tüm sonuçlar \( A \) olayının da elemanı ise \( A \) olayı \( B \) olayını kapsıyordur ya da bir diğer ifadeyle \( B \) olayı \( A \) olayının bir alt kümesidir. Bu durumda \( A \) ve \( B \) olayları arasındaki ilişki iki olayın birbirine eşit olabilme ya da olamama durumuna göre \( B \subset A \) ya da \( B \subseteq A \) şeklinde gösterilir. \( A \) olayı \( B \) olayını kapsıyorsa, \( B \) olayı gerçekleştiğinde \( A \) olayı da gerçekleşmiş olur.
Bir zar atışında zarın 6 gelme durumunda aşağıdaki gibi tanımlı iki olaydan \( B \) olayı gerçekleşmiş olur, dolayısıyla \( B \) olayını kapsayan \( A \) olayı da gerçekleşmiş olur.
\( S = \{1, 2, 3, 4, 5, 6\} \)
\( A \): Zarın çift gelme olayı
\( A = \{2, 4, 6\} \)
\( B \): Zarın 6 gelme olayı
\( B = \{6\} \)
\( B \subset A \)
Biri diğerini kapsayan bu iki olay aşağıda Venn şeması şeklinde gösterilmiştir.
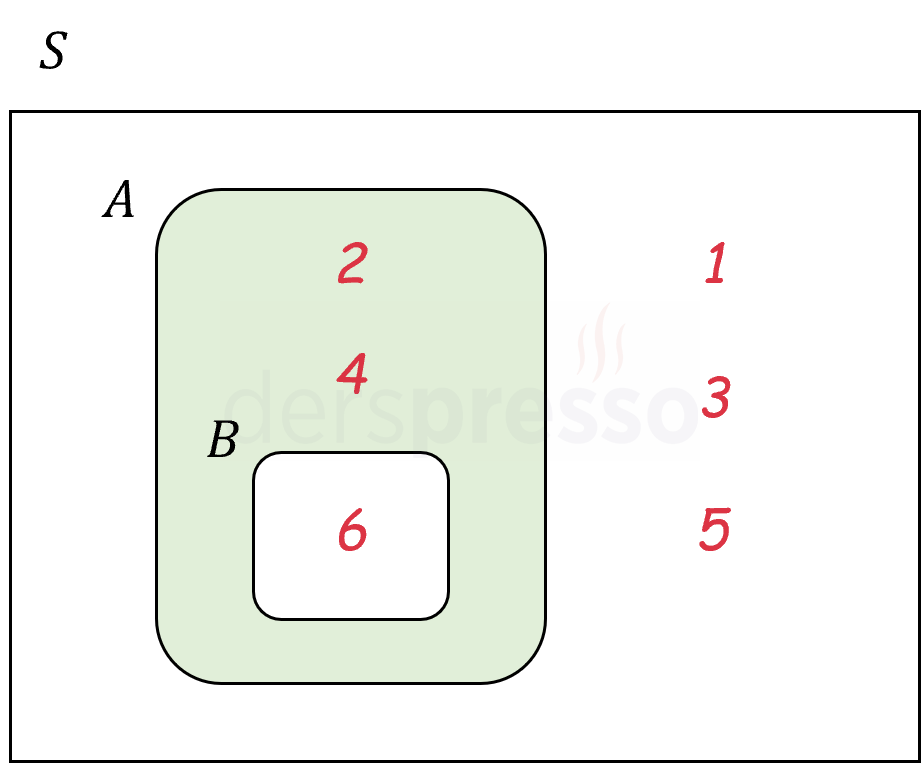
Ayrık Olaylar
\( A \) ve \( B \) olaylarının ortak elemanı olan hiçbir sonuç yoksa, bir diğer ifadeyle iki olayın kesişim kümeleri boş küme ise bu olaylara ayrık olaylar denir. Ayrık olaylar birlikte gerçekleşemezler, ya sadece biri gerçekleşir ya da ikisi de gerçekleşmez.
Bir zar atışında aşağıdaki gibi tanımlı \( A \) ve \( B \) olayları ayrık olaylardır, dolayısıyla birlikte gerçekleşemezler.
\( S = \{1, 2, 3, 4, 5, 6\} \)
\( A = \{1, 3, 5\} \)
\( B = \{2, 4\} \)
\( A \cap B = \emptyset \)
Bu iki ayrık olayın Venn şeması ile gösterimi aşağıdaki gibidir.
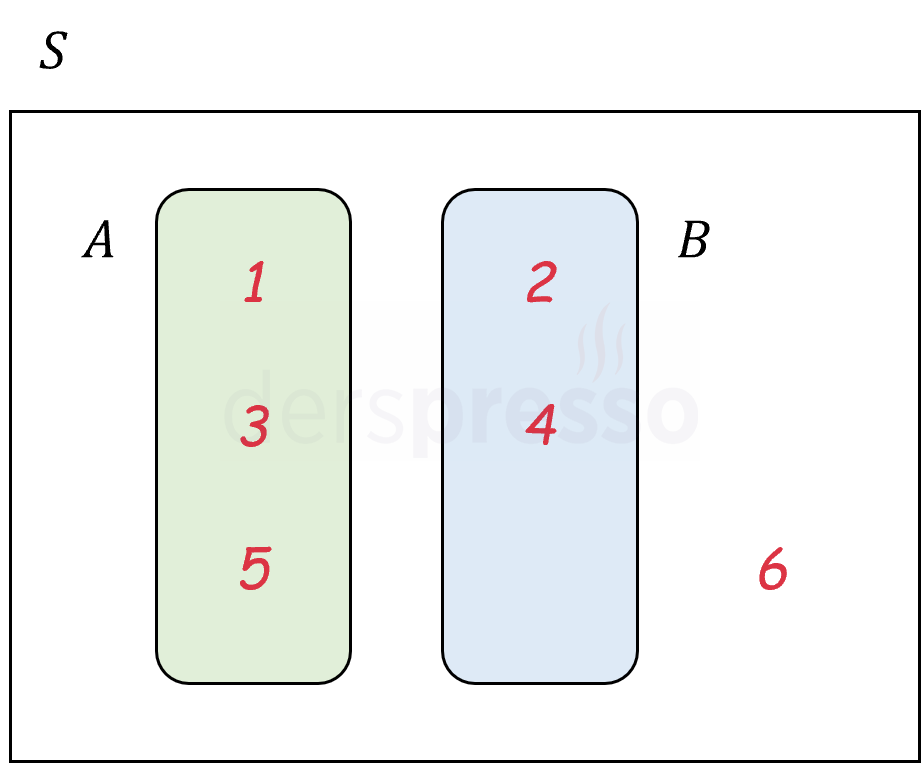
Ayrık olayların kesişim kümesi boş kümedir.
\( A \) ve \( B \) ayrık olaylar ise,
\( A \cap B = \emptyset \)
İkiden fazla olay ikişerli ayrık ise bu olayların arasından seçilecek tüm ikili olaylar aralarında ayrıktır, dolayısıyla bu olayların sadece tümünün ortak kesişim olayı boş küme değildir, aynı zamanda tüm ikili kesişimleri de boş kümedir.

Bütünü Kapsayıcı Olaylar
Birleşimleri örnek uzaya eşit olan olaylara bütünü kapsayıcı olaylar denir. Bir deney gerçekleştirildiğinde bütünü kapsayıcı olaylardan en az biri gerçekleşmiş olur.
\( A_1 \cup A_2 \cup \ldots \cup A_n = S \) ise,
\( A_1, A_2, \ldots, A_n \) bütünü kapsayıcı olaylardır.
Bu tanıma göre, bütünü kapsayıcı olayların kesişimi boş küme olmak zorunda değildir, önemli olan birleşimlerinin örnek uzaya eşit olmasıdır.
Aşağıdaki şekilde tanımlı \( A \) ve \( B \) olayları bütünü kapsayıcı olaylardır.
\( S = \{1, 2, 3, 4, 5, 6\} \)
\( A \): Zarın 2'den büyük gelme olayı
\( A = \{3, 4, 5, 6\} \)
\( B \): Zarın 4'ten küçük gelme olayı
\( B = \{1, 2, 3\} \)
\( A \cup B = S \)
Diğer Kurallar
Kümeler arasındaki değişme, birleşme ve dağılma özellikleri olaylar arasında da geçerlidir.
Değişme özelliği:
\( A \cap B = B \cap A \)
\( A \cup B = B \cup A \)
Birleşme özelliği:
\( (A \cap B) \cap C = A \cap (B \cap C) \)
\( (A \cup B) \cup C = A \cup (B \cup C) \)
Dağılma özelliği:
\( A \cap (B \cup C) = (A \cap B) \cup (A \cap C) \)
\( A \cup (B \cap C) = (A \cup B) \cap (A \cup C) \)
Yine kümeler arasındaki De Morgan kuralları olaylar arasında da geçerlidir.
\( (A \cap B)' = A' \cup B' \)
\( (A \cup B)' = A' \cap B' \)