Koşullu Olasılık
Önceki bölümlerde bir olayın gerçekleşme olasılığını diğer olayların gerçekleşmesinden bağımsız şekilde inceledik. Bir olayın başka olayların gerçekleşmesine bağlı olmadan hesaplanan olasılığına marjinal olasılık denir.
Bazı durumlarda deneyin gerçekleşen (ya da gerçekleşecek) sonucu hakkında ek bazı bilgiler biliyor ve bu bilgiler ışığında bir olayın olasılığı hesaplamak istiyor olabiliriz. Bir örnek vermek gerekirse, bir zarın çift sayı gelme olasılığını \( \frac{1}{2} \) olarak hesaplamıştık.
\( S = \{1, 2, 3, 4, 5, 6\} \)
\( A \): Zarın çift gelme olayı
\( A = \{ 2, 4, 6 \} \)
\( P(A) = \dfrac{s(A)}{s(S)} = \dfrac{3}{6} = \dfrac{1}{2} \)
Farklı bir \( B \) olayını sonucun asal sayı olması şeklinde tanımlayalım.
\( B \): Zarın asal sayı gelme olayı
\( B = \{2, 3, 5\} \)
Eğer zarın atıldığını ve kesin sonucu bilmesek de \( B \) olayının gerçekleştiğini biliyorsak \( A \) olayının gerçekleşme olasılığı artık \( \frac{1}{2} \) olmayacaktır, çünkü kullandığımız olasılık formülünün hem payı hem de paydası bu ek bilgi doğrultusunda değişecektir.
- Payda: \( B \) olayının gerçekleştiğini biliyor olmamız \( B \)'nin elemanı olmayan sonuçların (\( B' \)) gerçekleşmediği anlamına gelir, dolayısıyla deneyin tüm olası sonuçlarını içeren örnek uzay artık \( S \) yerine \( B \) olur.
- Pay: \( B \)'nin elemanı olmayan sonuçların gerçekleşmemiş olması, bu elemanlardan \( A \) olayında tanımlı olanların da gerçekleşmediği anlamına gelir, dolayısıyla \( A \) kümesinde sadece \( B \)'nin de elemanı olan sonuçlar olası birer sonuç olur, bu da iki olayın kesişim olayına karşılık gelir.
\( B \) olayının gerçekleştiği bilindiği durumda \( A \) olayının gerçekleşme olasılığına \( B \) biliniyorken \( A \) olayının koşullu olasılığı denir ve \( P(A \mid B) \) şeklinde gösterilir.
\( B \) olayının bilindiği durum için \( A \) olayının koşullu olasılığı aşağıdaki formülle hesaplanır.
\( P(B) \gt 0 \) olmak üzere,
\( P(A \mid B) = \dfrac{P(A \cap B)}{P(B)} \)
\( B \) olayının gerçekleştiğinin bilinmediği (solda) ve bilindiği (sağda) iki durum arasındaki fark aşağıdaki şekilde gösterilmiştir. Her iki durumda yeşil bölge olasılık formülünde paydaya, kırmızı kenarlı bölge paya karşılık gelmektedir.
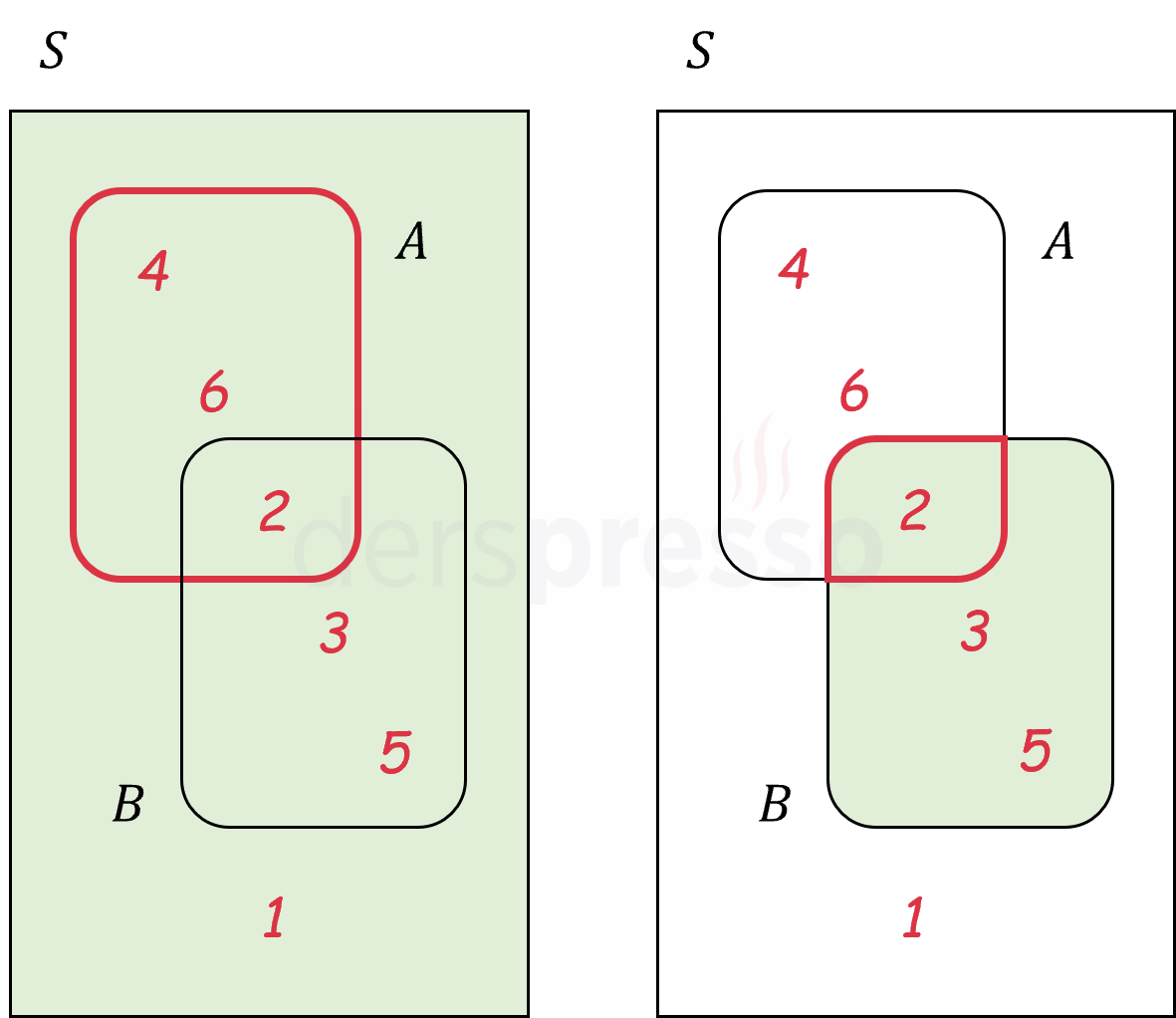
Bu formülü kullanarak \( A \) olayı ve örnek uzayla ilgili aşağıdaki sonuçları çıkarabiliriz.
\( A \) olayının gerçekleştiği biliniyorsa \( A \) olayının gerçekleşme olasılığı 1'dir.
\( P(A \mid A) = \dfrac{P(A \cap A)}{P(A)} = \dfrac{P(A)}{P(A)} = 1 \)
Örnek uzayın gerçekleştiği biliniyorsa \( A \) olayının gerçekleşme olasılığı \( p(A) \)'dır.
\( P(A \mid S) = \dfrac{P(A \cap S)}{P(S)} = \dfrac{P(A)}{P(S)} = P(A) \)
\( A \) olayının gerçekleştiği biliniyorsa örnek uzayın gerçekleşme olasılığı 1'dir.
\( P(S \mid A) = \dfrac{P(S \cap A)}{P(A)} = \dfrac{P(A)}{P(A)} = 1 \)
Bayes Teoremi
Yukarıda tanımladığımız \( P(A \mid B) \) formülünü \( P(B \mid A) \) için de yazdığımızda aşağıdaki Bayes teoremi formülü elde edilir.
\( P(A \mid B) = \dfrac{P(B \mid A)P(A)}{P(B)} \)
İSPATI GÖSTER
\( P(A \mid B) = \dfrac{P(A \cap B)}{P(B)} \)
Yukarıdaki gibi tanımladığımız \( B \) biliniyorken \( A \) olayının koşullu olasılığı formülünü \( A \) biliniyorken \( B \) olayının koşullu olasılığı için de yazalım.
\( P(B \mid A) = \dfrac{P(B \cap A)}{P(A)} \)
Her iki formülde kesişim olayını yalnız bırakalım.
\( P(A \cap B) = P(A \mid B)P(B) \)
\( P(B \cap A) = P(B \mid A)P(A) \)
Kümelerin kesişim işleminin değişim özelliği olduğu için bu iki formülü birbirine eşitleyebiliriz.
\( A \cap B = B \cap A \Longrightarrow P(A \cap B) = P(B \cap A) \)
\( P(A \mid B)P(B) = P(B \mid A)P(A) \)
\( B \) biliniyorken \( A \) olayının koşullu olasılığını yalnız bırakırsak Bayes teoremi formülünü elde ederiz.
\( P(A \mid B) = \dfrac{P(B \mid A)P(A)}{P(B)} \)
Bu formül aynı zamanda \( A \) ve \( B \) olaylarının olasılıkları birbirine eşit olmadığı sürece \( P(A \mid B) \) ve \( P(B \mid A) \) koşullu olasılıklarının birbirine eşit olmadığını gösterir.
\( P(A) \ne P(B) \) ise,
\( \dfrac{P(B \mid A)P(A)}{P(B)} \ne \dfrac{P(A \mid B)P(B)}{P(A)} \)
\( P(A \mid B) \ne P(B \mid A) \)
Bağımsız Olaylar
Bir zar ve bir yazı - tura atışından oluşan bir deney yapıyor olalım.
\( S = \{1Y, 1T, \ldots, 6Y, 6T\} \)
\( s(S) = 6 \cdot 2 = 12 \)
\( A \): Zarın 4 gelme olayı
\( A = \{4Y, 4T\} \)
\( B \): Paranın yazı gelme olayı
\( B = \{1Y, 2Y, \ldots, 6Y\} \)
\( A \) olayının gerçekleşme olasılığını aşağıdaki gibi hesaplayabiliriz.
\( P(A) = \dfrac{s(A)}{s(S)} = \dfrac{2}{12} = \dfrac{1}{6} \)
\( B \) olayının gerçekleştiği durumda \( A \) olayının gerçekleşme olasılığını aşağıdaki gibi hesaplayabiliriz.
\( A \cap B = \{ 4Y \} \)
\( P(A \mid B) = \dfrac{P(A \cap B)}{P(B)} \)
\( = \dfrac{s(A \cap B)}{s(B)} = \dfrac{1}{6} \)
Görebileceğimiz gibi, \( A \) olayının tek başına gerçekleşme olasılığı \( B \)'nin bilindiği durumdaki koşullu olasılığına eşit olmaktadır. Bu şekilde bir olayın gerçekleştiğinin biliniyor olması diğer bir olayın olasılığını değiştirmiyorsa bu iki olaya bağımsız olaylar denir. İki olay bağımsız ise birinin sonucunu biliyor olmamız diğerinin gerçekleşme olasılığını etkilemez.
\( A \) ve \( B \) bağımsız olay değillerse bağımlı olaylardır.
Bağımsız \( A \) ve \( B \) olayları için aşağıdaki ifadeler doğrudur.
\( A \) ve \( B \) bağımsız olaylar ise,
\( P(A \cap B) = P(A)P(B) \)
Bu eşitliği koşullu olasılık formülünde yerine koyduğumuzda bağımsız olayların tanımı olan koşullu olasılığın marjinal olasılığa eşitliğini elde ederiz.
\( P(A \mid B) = P(A) \)
\( P(B \mid A) = P(B) \)
İkiden fazla olay bağımsız ise olasılıkları arasındaki ilişki aşağıdaki şekilde gösterilir.
\( A_1, A_2, \ldots, A_n \) bağımsız olaylar ise,
\( P(A_1 \cap A_2 \cap \ldots \cap A_n) = P(A_1) \cdot P(A_2) \cdot \ldots \cdot P(A_n) \)
\( A \) ve \( B \) olayları ile ilgili aşağıdaki bilgiler veriliyor.
\( P(A) = 0,5 \)
\( P(B) = 0,2 \)
\( P(A \cup B) = 0,6 \)
Buna göre, \( A \) ve \( B \) bağımsız olaylar mıdır?
Çözümü GösterToplama kuralını kullanalım.
\( P(A \cup B) = P(A) + P(B) - P(A \cap B) \)
\( 0,6 = 0,5 + 0,2 - P(A \cap B) \)
\( P(A \cap B) = 0,1 \)
\( A \) ve \( B \) bağımsız olaylar ise aşağıdaki eşitlik sağlanır.
\( P(A \cap B) = P(A) \cdot P(B) \)
\( 0,1 \stackrel{?}{=} 0,5 \cdot 0,2 \)
\( 0,1 = 0,1 \)
Buna göre \( A \) ve \( B \) bağımsız olaylardır.
\( A \) ve \( B \) olayları ile ilgili aşağıdaki bilgiler veriliyor.
\( P(A) = 0,5 \)
\( P(B) = 0,4 \)
\( P(A \cup B) = 0,6 \)
(a) \( A \) ve \( B \) ayrık olaylar mıdır?
(b) \( A \) ve \( B \) bağımsız olaylar mıdır?
Çözümü Göster(a) seçeneği:
\( A \) ve \( B \) ayrık olaylar ise kesişimleri boş küme olur.
Toplama kuralını kullanalım.
\( P(A \cup B) = P(A) + P(B) - P(A \cap B) \)
\( 0,6 = 0,5 + 0,4 - P(A \cap B) \)
\( P(A \cap B) = 0,3 \ne 0 \)
Buna göre \( A \) ve \( B \) ayrık olaylar değildir.
(b) seçeneği:
\( A \) ve \( B \) bağımsız olaylar ise aşağıdaki eşitlik sağlanır.
\( P(A \cap B) = P(A) \cdot P(B) \)
\( 0,3 \stackrel{?}{=} 0,5 \cdot 0,4 \)
\( 0,3 \ne 0,2 \)
Buna göre \( A \) ve \( B \) bağımlı olaylardır.
\( A \) ve \( B \) olayları ile ilgili aşağıdaki bilgiler veriliyor.
\( A \) ve \( B \) bağımsız olaylardır.
\( P(A) = 0,3 \)
\( P(B) = 0,2 \)
Buna göre aşağıdaki olasılıklar nedir?
(a) \( P(A \cup B) \)
(b) \( P(A \cup B) \)
(c) \( P(A \mid B) \)
(d) \( P(B' \mid A) \)
Çözümü Göster(a) seçeneği:
\( P(A \cup B) \)
Bağımsız olayların birlikte gerçekleşme olasılığı her birinin gerçekleşme olasılıklarının çarpımına eşittir.
\( P(A \cap B) = P(A) \cdot P(B) \)
\( = 0,3 \cdot 0,2 = 0,06 \)
(b) seçeneği:
\( P(A \cup B) \)
Toplama kuralını kullanalım.
\( P(A \cup B) = P(A) + P(B) - P(A \cap B) \)
\( = 0,3 + 0,2 - 0,06 = 0,44 \)
(c) seçeneği:
\( P(A \mid B) \)
\( A \) ve \( B \) bağımsız olaylar olduğu için aşağıdaki formülü kullanabiliriz.
\( P(A \mid B) = P(A) = 0,3 \)
(d) seçeneği:
\( P(B' \mid A) \)
\( A \) ve \( B \) bağımsız olaylar olduğu için aşağıdaki formülü kullanabiliriz.
\( P(B' \mid A) = P(B') \)
\( = 1 - P(B) \)
\( = 1 - 0,2 = 0,8 \)
Örnek uzaya \( S \) diyelim.
Bulduğumuz olasılıkları bir Venn şeması üzerinde gösterelim.
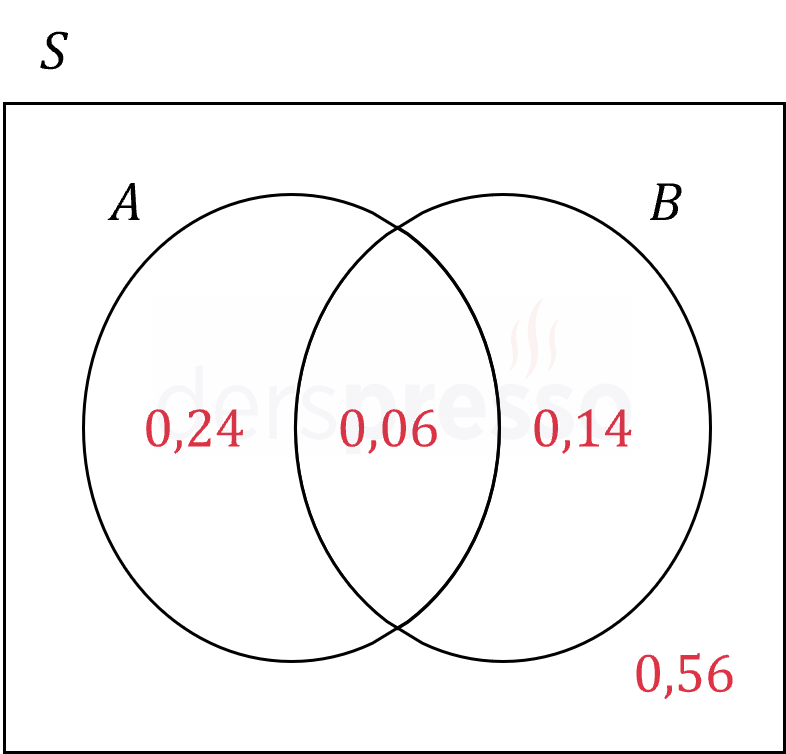
\( A \) ve \( B \) olayları ile ilgili aşağıdaki bilgiler veriliyor.
\( P(A) = 0,22 \)
\( P(B) = 0,44 \)
\( P(A \cap B) = 0,11 \)
(a) \( A \) ve \( B \) bağımsız olaylar mıdır?
(b) \( A \) ve \( B \) olaylarının her ikisinin de gerçekleşmeme olasılığı nedir?
Çözümü Göster(a) seçeneği:
\( A \) ve \( B \) bağımsız olaylar ise aşağıdaki eşitlik sağlanır.
\( P(A \cap B) = P(A) \cdot P(B) \)
\( 0,11 \stackrel{?}{=} 0,22 \cdot 0,44 \)
\( 0,11 \ne 0,0968 \)
Buna göre \( A \) ve \( B \) bağımlı olaylardır.
(b) seçeneği:
Verilen ve bulduğumuz olasılıkları bir Venn şeması üzerinde gösterelim.

\( A \) ve \( B \) olaylarının her ikisinin de gerçekleşmeme olasılığını aşağıdaki şekilde ifade edebiliriz.
\( P(A' \cap B') \)
De Morgan kuralını uygulayalım.
\( = P[(A \cup B)'] \)
Venn şemasını kullanarak ilgili olasılığı yazalım.
\( = 0,45 \)
\( A \) ve \( B \) olayları ile ilgili aşağıdaki bilgiler veriliyor.
\( A \) ve \( B \) bağımsız olaylardır.
\( P(A) = 0,5 \)
\( P(B) = 0,4 \)
Buna göre \( P(A' \cup B') \) olasılığı nedir?
Çözümü Göster\( A \) ve \( B \) bağımsız olaylar ise aşağıdaki eşitlik sağlanır.
\( P(A \cap B) = P(A) \cdot P(B) \)
Verilen değerleri formülde yerine koyalım.
\( P(A \cap B) = 0,5 \cdot 0,4 \)
\( = 0,2 \)
De Morgan kuralını uygulayalım.
\( P(A' \cup B') = P[(A \cap B)'] \)
Bir olay ile tümleyeninin olasılıkları toplamı 1'dir.
\( P(A \cap B) + P[(A \cap B)'] = 1 \)
\( 0,2 + P[(A \cap B)'] = 1 \)
\( P[(A \cap B)'] = P(A' \cup B') = 0,8 \)
\( A \) ve \( B \) olayları ile ilgili aşağıdaki bilgiler veriliyor.
\( A \) ve \( B \) bağımsız olaylardır.
\( P(A') = 0,2 \)
\( P(B') = 0,6 \)
Buna göre aşağıdaki olasılıklar nedir?
(a) \( P(A \cup B) \)
(b) \( P(A' \cup B) \)
Çözümü Göster(a) seçeneği:
\( P(A \cup B) \)
\( A \) ve \( B \) bağımsız olaylar ise aşağıdaki eşitlik sağlanır.
\( P(A \cap B) = P(A) \cdot P(B) \)
Bir olay ile tümleyeninin olasılıkları toplamı 1'dir.
\( P(A) + P(A') = 1 \)
\( P(A) + 0,2 = 1 \)
\( P(A) = 0,8 \)
\( P(B) + P(B') = 1 \)
\( P(B) + 0,6 = 1 \)
\( P(B) = 0,4 \)
Bulduğumuz değerleri formülde yerine koyalım.
\( P(A \cap B) = P(A) \cdot P(B) \)
\( = 0,8 \cdot 0,4 = 0,32 \)
Toplama kuralını kullanalım.
\( P(A \cup B) = P(A) + P(B) - P(A \cap B) \)
\( = 0,8 + 0,4 - 0,32 \)
\( = 0,88 \)
(b) seçeneği:
\( P(A' \cup B) \)
Verilen ve bulduğumuz olasılıkları bir Venn şeması üzerinde gösterelim.
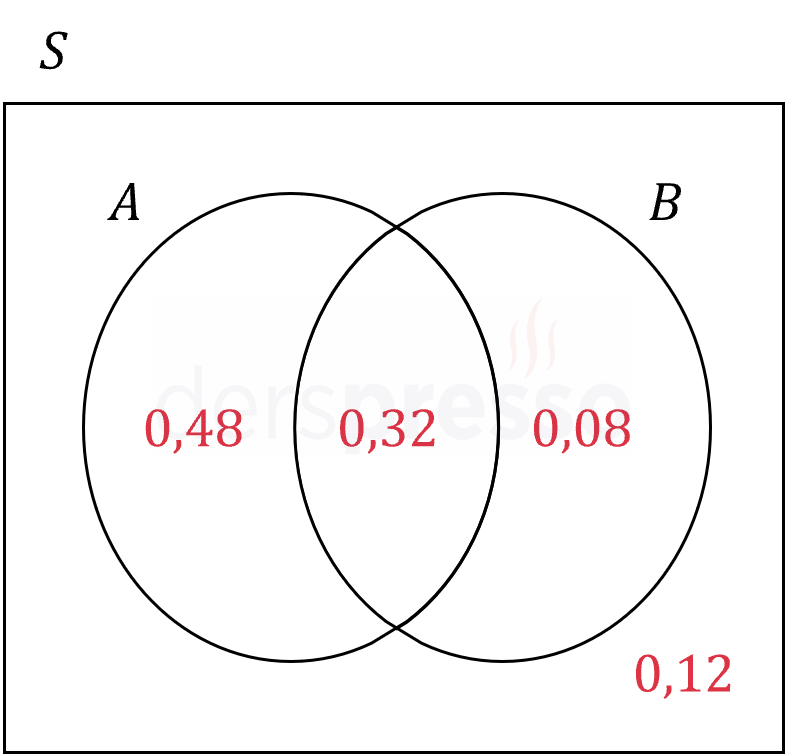
De Morgan kuralını uygulayalım.
\( P(A' \cup B) = P[(A \cap B')'] \)
\( A \cap B' = A - B \) özdeşliğini kullanalım.
\( = P[(A - B)'] \)
Bir olay ile tümleyeninin olasılıkları toplamı 1'dir.
\( = 1 - P(A - B) \)
Venn şemasını kullanarak ilgili olasılığı yazalım.
\( = 1 - 0,48 = 0,52 \)
\( A \) ve \( B \) olayları ile ilgili aşağıdaki bilgiler veriliyor.
\( P(B') = 0,6 \)
\( P(A \cup B) = 0,7 \)
Buna göre aşağıdaki iki durumda \( P(A') \) olasılığı ne olur?
(a) \( A \) ve \( B \) ayrık olaylar
(b) \( A \) ve \( B \) bağımsız olaylar
Çözümü Göster(a) seçeneği:
\( A \) ve \( B \) ayrık olaylar ise kesişimleri boş küme olur.
\( P(A \cap B) = 0 \)
Bir olay ile tümleyeninin olasılıkları toplamı 1'dir.
\( P(B) + P(B') = 1 \)
\( P(B) + 0,6 = 1 \)
\( P(B) = 0,4 \)
Toplama kuralını kullanalım.
\( P(A \cup B) = P(A) + P(B) - P(A \cap B) \)
\( 0,7 = P(A) + 0,4 - 0 \)
\( P(A) = 0,3 \)
Bir olay ile tümleyeninin olasılıkları toplamı 1'dir.
\( P(A) + P(A') = 1 \)
\( 0,3 + P(A') = 1 \)
\( P(A') = 0,7 \)
(b) seçeneği:
Toplama kuralını kullanalım.
\( P(A \cup B) = P(A) + P(B) - P(A \cap B) \)
\( A \) ve \( B \) bağımsız olaylar ise aşağıdaki eşitlik sağlanır.
\( P(A \cap B) = P(A) \cdot P(B) \)
Formülde yerine koyalım.
\( P(A \cup B) = P(A) + P(B) - P(A) \cdot P(B) \)
\( 0,7 = P(A) + 0,4 - P(A) \cdot 0,4 \)
\( P(A) = 0,5 \)
Bir olay ile tümleyeninin olasılıkları toplamı 1'dir.
\( P(A) + P(A') = 1 \)
\( 0,5 + P(A') = 1 \)
\( P(A') = 0,5 \)
\( A \) ve \( B \) bağımsız olaylardır.
\( P(A) = P(B) = a \)
\( P(A \cup B) = \dfrac{9}{25} \)
olduğuna göre, \( a \) kaçtır?
Çözümü GösterToplama kuralını kullanalım.
\( P(A \cup B) = P(A) + P(B) - P(A \cap B) \)
\( A \) ve \( B \) bağımsız olaylar ise aşağıdaki eşitlik sağlanır.
\( P(A \cap B) = P(A) \cdot P(B) \)
Formülde yerine koyalım.
\( P(A \cup B) = P(A) + P(B) - P(A) \cdot P(B) \)
\( \dfrac{9}{25} = a + a - a \cdot a \)
\( 25a^2 - 50a + 9 = 0 \)
\( (5a - 9)(5a - 1) = 0 \)
\( a = \dfrac{9}{5} \) ya da \( a = \dfrac{1}{5} \)
Bir olayın olasılığı 1'den büyük olamaz.
\( a = \dfrac{1}{5} \) bulunur.
\( A \) ve \( B \) olayları bütünü kapsayıcı olaylardır.
\( P(A) = 0,6 \)
\( P(B) = 0,52 \)
olduğuna göre, \( P(B \mid A) \) olasılığı kaçtır?
Çözümü GösterÖrnek uzaya \( S \) diyelim.
Örnek uzayın olasılığı 1'dir.
Bütünü kapsayıcı olayların birleşimi örnek uzaya eşittir.
\( P(A \cup B) = P(S) = 1 \)
Toplama kuralını uygulayalım.
\( P(A \cup B) = P(A) + P(B) - P(A \cap B) \)
\( 1 = 0,6 + 0,52 - P(A \cap B) \)
\( P(A \cap B) = 0,12 \)
Koşullu olasılık formülünü kullanalım.
\( P(B \mid A) = \dfrac{P(B \cap A)}{P(A)} \)
\( = \dfrac{0,12}{0,6} = \dfrac{1}{5} \) bulunur.
\( A \) ve \( B \) olayları ile ilgili aşağıdaki bilgiler veriliyor.
\( P(A') = 0,5 \)
\( P(B') = 0,3 \)
\( P(A' \cap B) = 0,3 \)
Buna göre aşağıdaki olasılıklar nedir?
(a) \( P(A \mid B) \)
(b) \( P(B \mid A) \)
Çözümü Göster\( A' \cap B = B - A \) özdeşliğini kullanalım.
\( P(A' \cap B) = P(B - A) = 0,3 \)
Bir olay ile tümleyeninin olasılıkları toplamı 1'dir.
\( P(A) + P(A') = 1 \)
\( P(A) + 0,5 = 1 \)
\( P(A) = 0,5 \)
\( P(B) + P(B') = 1 \)
\( P(B) + 0,3 = 1 \)
\( P(B) = 0,7 \)
Bir olay birbirinden ayrık iki olayın birleşimi şeklinde aşağıdaki gibi yazılabilir.
\( P(B) = P(B - A) + P(A \cap B) \)
\( 0,7 = 0,3 + P(A \cap B) \)
\( P(A \cap B) = 0,4 \)
Örnek uzaya \( S \) diyelim.
Bulduğumuz olasılıkları bir Venn şeması üzerinde gösterelim.

(a) seçeneği:
\( P(A \mid B) = \dfrac{P(A \cap B)}{P(B)} \)
Venn şemasını kullanarak ilgili olasılıkları yazalım.
\( = \dfrac{0,4}{0,4 + 0,3} \)
\( = \dfrac{4}{7} \)
(b) seçeneği:
\( P(B \mid A) = \dfrac{P(B \cap A)}{P(A)} \)
Venn şemasını kullanarak ilgili olasılıkları yazalım.
\( = \dfrac{0,4}{0,1 + 0,4} \)
\( = \dfrac{4}{5} \)
\( A \) ve \( B \) olayları ile ilgili aşağıdaki bilgiler veriliyor.
\( P(A') = 0,6 \)
\( P(A \cap B) = 0,22 \)
\( P(A' \cap B') = 0,24 \)
Buna göre aşağıdaki olasılıklar nedir?
(a) \( P(A \mid B') \)
(b) \( P(B \mid A') \)
Çözümü GösterBir olay ile tümleyeninin olasılıkları toplamı 1'dir.
\( P(A) + P(A') = 1 \)
\( P(A) + 0,6 = 1 \)
\( P(A) = 0,4 \)
Bir olay birbirinden ayrık iki olayın birleşimi şeklinde aşağıdaki gibi yazılabilir.
\( P(A) = P(A - B) + P(A \cap B) \)
\( 0,4 = P(A - B) + 0,22 \)
\( P(A - B) = 0,18 \)
\( P(A' \cap B') = 0,24 \)
De Morgan kuralını uygulayalım.
\( P[(A \cup B)'] = 0,24 \)
Örnek uzaya \( S \) diyelim.
Bulduğumuz olasılıkları bir Venn şeması üzerinde gösterelim.
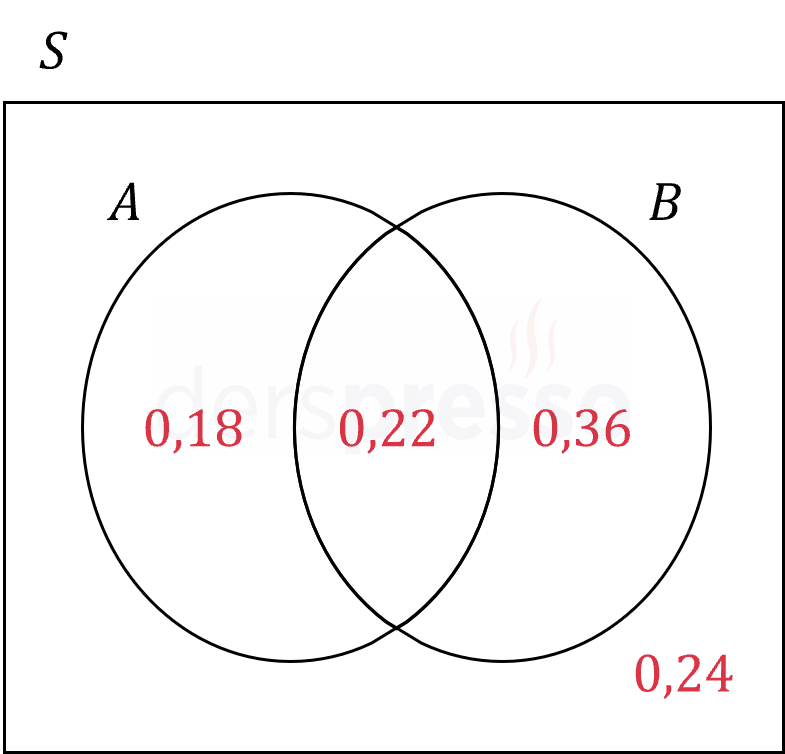
\( P(B - A) = 1 - 0,18 - 0,22 - 0,24 \)
\( = 1 - 0,18 - 0,22 - 0,24 \)
\( = 0,36 \)
(a) seçeneği:
\( P(A \mid B') = \dfrac{P(A \cap B')}{P(B')} \)
\( A \cap B' = A - B \) özdeşliğini kullanalım.
\( = \dfrac{P(A - B)}{P(B')} \)
Venn şemasını kullanalım.
\( = \dfrac{0,18}{0,18 + 0,24} \)
\( = \dfrac{3}{7} \)
(b) seçeneği:
\( P(B \mid A') = \dfrac{P(B \cap A')}{P(A')} \)
\( A' \cap B = B - A \) özdeşliğini kullanalım.
\( = \dfrac{P(B - A)}{P(A')} \)
\( = \dfrac{0,36}{0,36 + 0,24} \)
\( = \dfrac{3}{5} \)
\( A \) ve \( B \) olayları ile ilgili aşağıdaki bilgiler veriliyor.
\( P(A) = 0,5 \)
\( P(B) = 0,25 \)
\( P(A \mid B) = 0,3 \)
Buna göre aşağıdaki olasılıklar nedir?
(a) \( P(A \cap B) \)
(b) \( P(A' \cup B') \)
(c) \( P(A' \mid B) \)
Çözümü Göster(a) seçeneği:
\( P(A \cap B) \)
\( P(A \mid B) = \dfrac{P(A \cap B)}{P(B)} \)
\( 0,3 = \dfrac{P(A \cap B)}{0,25} \)
\( P(A \cap B) = 0,075 \)
(b) seçeneği:
\( P(A' \cup B') \)
Bir olay ile tümleyeninin olasılıkları toplamı 1'dir.
\( P(A' \cup B') + P[(A' \cup B')'] = 1 \)
İkinci terime De Morgan kuralını uygulayalım.
\( P(A' \cup B') + P(A \cap B) = 1 \)
\( P(A' \cup B') + 0,075 = 1 \)
\( P(A' \cup B') = 0,925 \)
Örnek uzaya \( S \) diyelim.
Bir olay birbirinden ayrık iki olayın birleşimi şeklinde aşağıdaki gibi yazılabilir.
\( P(A) = P(A - B) + P(A \cap B) \)
\( 0,5 = P(A - B) + 0,075 \)
\( P(A - B) = 0,425 \)
\( P(B) = P(B - A) + P(A \cap B) \)
\( 0,25 = P(B - A) + 0,075 \)
\( P(B - A) = 0,175 \)
Bulduğumuz olasılıkları bir Venn şeması üzerinde gösterelim.
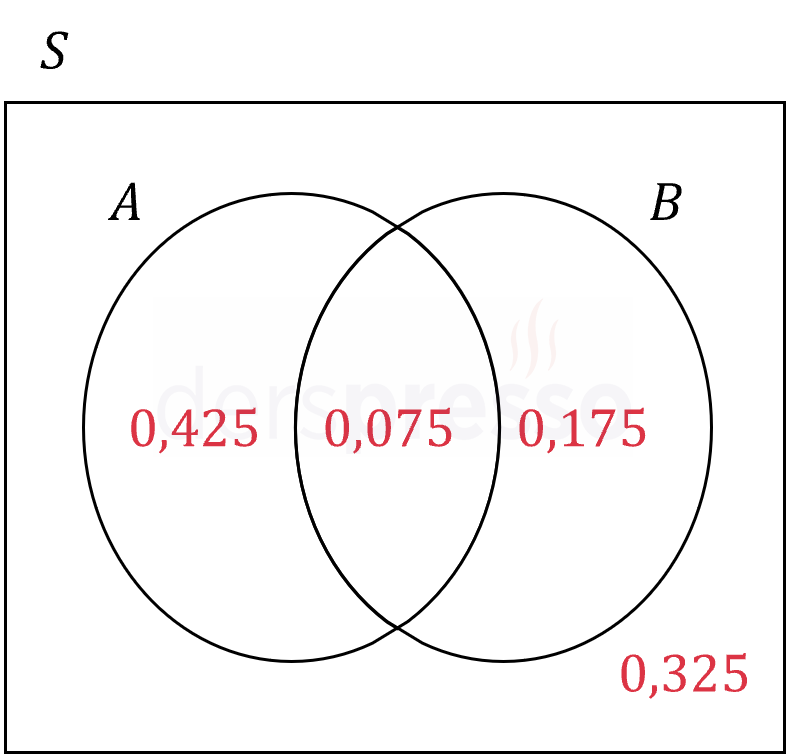
(c) seçeneği:
\( P(A' \mid B) = \dfrac{P(A' \cap B)}{P(B)} \)
\( A' \cap B = B - A \) özdeşliğini kullanalım.
\( = \dfrac{P(B - A)}{P(B)} \)
Venn şemasını kullanarak ilgili olasılıkları yazalım.
\( = \dfrac{0,175}{0,075 + 0,175} \)
\( = \dfrac{7}{10} \)
\( A \) ve \( B \) olayları ile ilgili aşağıdaki bilgiler veriliyor.
\( P(B) = 0,3 \)
\( P(A' \cap B) = 0,2 \)
\( P(A' \cup B) = 0,6 \)
Buna göre aşağıdaki olasılıklar nedir?
(a) \( P(A) \)
(b) \( P(B \mid A) \)
(c) \( P(A' \mid B) \)
Çözümü Göster(a) seçeneği:
\( P(A) \)
\( A' \cap B = B - A \) özdeşliğini kullanalım.
\( P(A' \cap B) = P(B - A) = 0,2 \)
Bir olay birbirinden ayrık iki olayın birleşimi şeklinde aşağıdaki gibi yazılabilir.
\( P(B) = P(B - A) + P(A \cap B) \)
\( 0,3 = 0,2 + P(A \cap B) \)
\( P(A \cap B) = 0,1 \)
Bir olay ile tümleyeninin olasılıkları toplamı 1'dir.
\( P(A' \cup B) + P[(A' \cup B)'] = 1 \)
İkinci terime De Morgan kuralını uygulayalım.
\( P(A' \cup B) + P(A \cap B') = 1 \)
\( A \cap B' = A - B \) özdeşliğini kullanalım.
\( P(A' \cup B) + P(A - B) = 1 \)
\( 0,6 + P(A - B) = 1 \)
\( P(A - B) = 0,4 \)
Bir olay birbirinden ayrık iki olayın birleşimi şeklinde aşağıdaki gibi yazılabilir.
\( P(A) = P(A - B) + P(A \cap B) \)
\( P(A) = 0,4 + 0,1 = 0,5 \)
(b) seçeneği:
\( P(B \mid A) \)
Örnek uzaya \( S \) diyelim.
Bulduğumuz olasılıkları bir Venn şeması üzerinde gösterelim.

Koşullu olasılık formülünü kullanalım.
\( P(B \mid A) = \dfrac{P(B \cap A)}{P(A)} \)
Venn şemasını kullanalım.
\( = \dfrac{0,1}{0,4 + 0,1} \)
\( = \dfrac{1}{5} \)
(c) seçeneği:
\( P(A' \mid B) \)
Koşullu olasılık formülünü kullanalım.
\( P(A' \mid B) = \dfrac{P(A' \cap B)}{P(B)} \)
\( A' \cap B = B - A \) özdeşliğini kullanalım.
\( = \dfrac{P(B - A)}{P(B)} \)
Venn şemasını kullanarak ilgili olasılıkları yazalım.
\( = \dfrac{0,2}{0,1 + 0,2} \)
\( = \dfrac{2}{3} \)
7 kişilik bir arkadaş grubunda 4 kişi bowlinge, 5 kişi sinemaya, 2 kişi ise hem sinemaya hem de bowlinge gitmek istemektedir.
Rastgele seçilen bir kişinin sinemaya gitmek istediği bilindiğine göre, bowlinge gitmek istememe olasığı kaçtır?
Çözümü Göster\( B \): Bowlinge gitmek isteyenlerin kümesi
\( S \): Sinemaya gitmek isteyenlerin kümesi
Verilen bilgileri bir Venn şeması üzerinde gösterelim.

İstenen olasılığı aşağıdaki şekilde ifade edebiliriz.
\( P(B' \mid S) = \dfrac{s(B' \cap S)}{s(S)} \)
\( B' \cap S = S - B \) özdeşliğini kullanalım.
\( = \dfrac{s(S - B)}{s(S)} \)
Venn şemasını kullanarak ilgili olasılıkları yazalım.
\( = \dfrac{3}{5} \)
420 öğrencisi olan bir okulda açılacak bir müzik aleti kursu için öğrencilere keman, gitar ve piyano kursu seçenekleri soruluyor.
350 öğrenci keman, 330 öğrenci gitar, 280 öğrenci piyano, 300 öğrenci keman ve gitar, 220 öğrenci keman ve piyano, 220 öğrenci gitar ve piyano, 200 öğrenci keman, gitar ve piyano kursu cevabını vermiştir.
Buna göre rastgele seçilen bir öğrencinin;
(a) Gitar kursunun açılmasını isteyip keman kursunun açılmasını istememe olasılığı kaçtır?
(b) Yalnızca iki kursun açılmasını isteme olasılığı kaçtır?
(c) Bu üç kurstan ikisinin açılmasını istediği bilindiğine göre, keman kursunun açılmasını isteme olasılığı kaçtır?
Çözümü Göster\( K \): Keman kursunun açılmasını isteyen öğrenciler kümesi
\( G \): Gitar kursunun açılmasını isteyen öğrenciler kümesi
\( P \): Piyano kursunun açılmasını isteyen öğrenciler kümesi
Üçlü kesişim kümesi ile başlayarak ve ikili kesişim kümeleri ile devam ederek kümelerin eleman sayılarını gösteren bir Venn şeması çizelim.

(a) seçeneği:
Örnek uzaya \( S \) diyelim.
Örnek uzay okuldaki tüm öğrencilerden oluşur.
\( s(S) = 420 \)
Bir öğrencinin gitar kursunun açılmasını isteyip keman kursunun açılmasını istememe olayına \( A \) diyelim.
\( A \) olayını aşağıdaki şekilde ifade edebiliriz.
\( A = G - K \)
Venn şemasını kullanarak \( A \) olayının eleman sayısını bulalım.
\( s(A) = s(G - K) \)
\( = 10 + 20 = 30 \)
\( A \) olayının gerçekleşme olasılığı, \( A \) olayındaki sonuç sayısının örnek uzaydaki sonuç sayısına oranına eşittir.
\( P(A) = \dfrac{s(A)}{s(S)} \)
\( = \dfrac{30}{420} \)
\( = \dfrac{1}{14} \)
(b) seçeneği:
Bir öğrencinin yalnızca iki kursun açılmasını isteme olayına \( B \) diyelim.
Bir öğrencinin yalnızca iki kursun açılmasını isteme olayı, yalnızca keman ve gitar kursunun açılmasını isteme, yalnızca keman ve piyano kursunun açılmasını isteme ve yalnızca gitar ve piyano kursunun açılmasını isteme olaylarının birleşimine eşittir.
Venn şemasını kullanarak ilgili eleman sayılarını yazalım.
\( s(B) = 100 + 20 + 20 = 140 \)
\( B \) olayının gerçekleşme olasılığı, \( B \) olayındaki sonuç sayısının örnek uzaydaki sonuç sayısına oranına eşittir.
\( P(B) = \dfrac{s(B)}{s(S)} \)
\( = \dfrac{140}{420} \)
\( = \dfrac{1}{3} \)
(c) seçeneği:
Seçilen kişinin üç kurstan ikisinin açılmasını istediği (\( B \) olayının gerçekleştiği) bilindiğine göre, keman kursunun açılmasını isteme olasılığını aşağıdaki şekilde ifade edebiliriz.
\( P(K \mid B) = \dfrac{s(K \cap B)}{s(B)} \)
Venn şemasını kullanarak ilgili olasılıkları yazalım.
\( = \dfrac{100 + 20}{140} \)
\( = \dfrac{6}{7} \)
Umut kitaplığındaki 50 kitaptan 30'unu okumuştur. Umut'un kitaplıktan rastgele aldığı iki kitaptan biri okuduğu bir kitap olduğuna göre, diğer kitabın da okuduğu bir kitap olma olasılığı nedir?
Çözümü GösterUmut'un seçtiği iki kitaptan (en az) birinin okuduğu bir kitap olma olayına \( A \) diyelim.
Umut'un seçtiği diğer kitabın okuduğu bir kitap olma olayına \( B \) diyelim.
\( A \) olayının gerçekleştiğinin bilindiği durumda \( B \) olayının koşullu olasılığını bulalım.
\( P(B \mid A) = \dfrac{P(B \cap A)}{P(A)} = \dfrac{s(B \cap A)}{s(A)} \)
\( A \) ve \( B \) olaylarının kesişimi, Umut'un seçtiği kitapların ikisini de okuduğu durumdur.
\( s(A \cap B) = C(30, 2) = 435 \)
\( A \) olayı için iki durum vardır.
Durum 1:
Bu durumda Umut seçtiği kitaplardan birini okumuştur, diğerini okumamıştır.
\( C(30, 1) \cdot C(20, 1) = 600 \)
Durum 2:
Bu durumda Umut seçtiği kitaplardan ikisini de okumuştur.
\( C(30, 2) = 435 \)
Bu iki durumun toplamı \( A \) olayındaki toplam sonuç sayısını verir.
\( s(A) = 600 + 435 = 1035 \)
Bulduğumuz değerleri formülde yerine koyalım.
\( P(B \mid A) = \dfrac{s(B \cap A)}{s(A)} \)
\( = \dfrac{435}{1035} = \dfrac{29}{69} \) bulunur.
Bir çift zar birlikte atılıyor. Gelen zarların toplamının 7 olduğu bilindiğine göre, zarlardan birinin 2 gelmiş olma olasılığı kaçtır?
Çözümü Gösterİki zar atıldığında zarların toplamının 7 olma olayına \( B \) diyelim.
\( B = \{(1, 6), (2, 5), (3, 4), (4, 3), (5, 2), (6, 1)\} \)
\( s(B) = 6 \)
Zarlardan birinin 2 gelme olayına \( A \) diyelim.
\( A \) ve \( B \) olaylarının kesişim olayı aşağıdaki gibi olur.
\( A \cap B = \{(2, 5), (5, 2)\} \)
\( s(A \cap B) = 2 \)
\( B \) olayının bilindiği durum için \( A \) olayının koşullu olasılığı:
\( P(A \mid B) = \dfrac{P(A \cap B)}{P(B)} = \dfrac{s(A \cap B)}{s(B)} \)
\( = \dfrac{2}{6} = \dfrac{1}{3} \) bulunur.
\( A \) ve \( B \) olayları ile ilgili aşağıdaki bilgiler veriliyor.
\( P(A) = 0,4 \)
\( P(B) = 0,3 \)
\( P(A \cup B) = 0,58 \)
Buna göre;
(a) \( A \) ve \( B \) bağımsız olaylar mıdır?
(b) \( A \) ve \( B \) olaylarından sadece birinin gerçekleşme olasılığı nedir?
(c) \( A \) ve \( B \) olaylarından sadece birinin gerçekleştiği bilindiğine göre, \( B \) olayının gerçekleşmiş olma olasılığı nedir?
Çözümü Göster(a) seçeneği:
Toplama kuralını kullanalım.
\( P(A \cup B) = P(A) + P(B) - P(A \cap B) \)
\( 0,58 = 0,4 + 0,3 - P(A \cap B) \)
\( P(A \cap B) = 0,12 \)
\( A \) ve \( B \) bağımsız olaylar ise aşağıdaki eşitlik sağlanır.
\( P(A \cap B) = P(A) \cdot P(B) \)
\( 0,12 \stackrel{?}{=} 0,4 \cdot 0,3 \)
\( 0,12 = 0,12 \)
Buna göre \( A \) ve \( B \) bağımsız olaylardır.
(b) seçeneği:
Örnek uzaya \( S \) diyelim.
Örnek uzayın olasılığı 1'dir.
Bir olay ile tümleyeninin birleşimi örnek uzaya eşittir.
\( P(S) = P(A \cup B) + P[(A \cup B)'] \)
\( 1 = 0,58 + P((A \cup B)') \)
\( P((A \cup B)') = 0,42 \)
Verilen ve bulduğumuz olasılıkları bir Venn şeması üzerinde gösterelim.
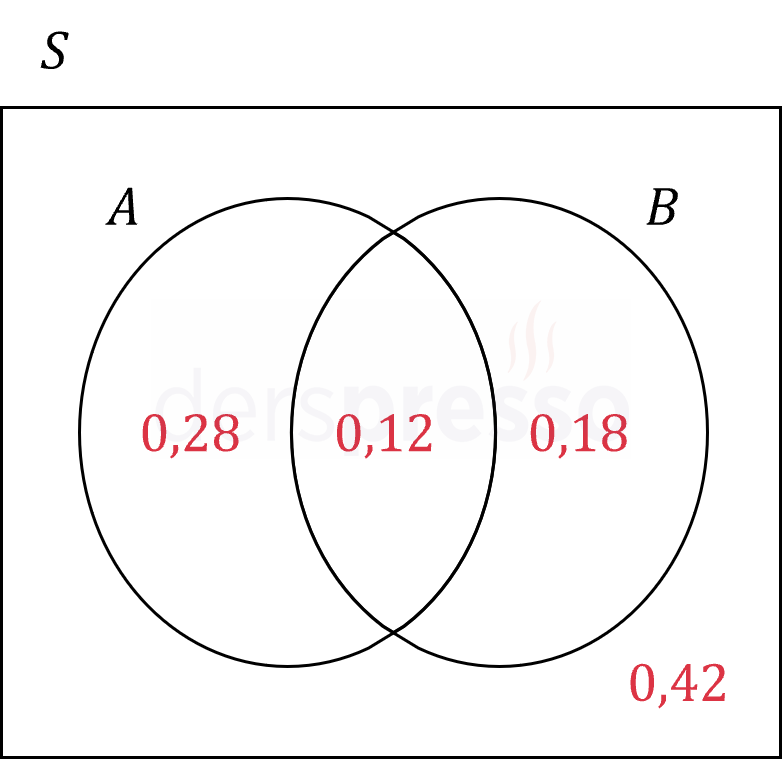
\( A \) ve \( B \) olaylarından sadece birinin gerçekleşme olasılığını aşağıdaki şekilde ifade edebiliriz.
\( P(A \cap B') + P(A' \cap B) \)
\( X \cap Y' = X - Y \) özdeşliğini kullanalım.
\( = P(A - B) + P(B - A) \)
Venn şemasını kullanarak ilgili olasılıkları yazalım.
\( = 0,28 + 0,18 = 0,46 \)
(c) seçeneği:
\( A \) ve \( B \) olaylarından sadece birinin gerçekleme olayına \( C \) diyelim.
\( P(C) = P(A - B) + P(B - A) = 0,46 \)
\( C \) olayının gerçekleştiği durum için \( B \) olayının koşullu olasılığını bulalım.
\( P(B \mid C) = \dfrac{P(B \cap C)}{P(C)} \)
Venn şemasını kullanarak ilgili olasılıkları yazalım.
\( = \dfrac{0,18}{0,46} = \dfrac{9}{23} \)
Bir hastanede bir yıl boyunca Covid olduğu bilinen 6.800 hastaya yapılan testlerin 5.700'ü pozitif, Covid olmadığı bilinen 3.200 hastaya yapılan testlerin 2.300'ü negatif sonuçlanmıştır.
Buna göre bu hastaneye Covid testi için giden bir kişinin testi negatif çıktıysa gerçekten Covid olmama olasılığı nedir?
Çözümü GösterBu soru için örnek uzay hastaneden yapılan tüm testlerdir.
\( s(S) = 10.000 \)
Bir hastanın test sonucundan bağımsız olarak Covid olma olayına \( A \), Covid olma durumundan bağımsız olarak testinin pozitif çıkma olayına \( B \) diyelim.
Soruda verilen bilgiler aşağıdaki tabloda özetlenmiştir.

Soruda istenen test sonucunun negatif çıktığı bilinen bir hastanın gerçekten Covid olmama olasılığıdır, bunu koşullu olasılık olarak aşağıdaki şekilde ifade edebiliriz.
\( P(A' \mid B') = \dfrac{P(A' \cap B')}{P(B')} = \dfrac{s(A' \cap B')}{s(B')} \)
\( A' \cap B' \) kümesi hem Covid olmayan hem de testi negatif çıkan hastalara karşılık gelmektedir ve tabloya göre bu hastaların sayısı 2.300'dür.
\( B' \) kümesi testi negatif çıkan hastaların tümüne karşılık gelmektedir ve tabloya göre bu hastaların sayısı 3.400'dür.
Soruda istenen koşullu olasılığı hesaplayalım.
\( P(A' \mid B') = \dfrac{s(A' \cap B')}{s(B')} \)
\( = \dfrac{2.300}{3.400} = \dfrac{23}{34} \) bulunur.
Bir şirket çalışanları arasında üniversite mezunu olan 46 personelin 6'sının, üniversite mezunu olmayan 54 personelin 22'sinin sigara içtiği biliniyor.
Buna göre şirketteki sigara odasında sigara içtiği görülen bir çalışanın üniversite mezunu olma olasılığı nedir?
Çözümü GösterBu soru için örnek uzay şirketteki tüm çalışanlardır.
\( s(S) = 100 \)
Bir çalışanın üniversite mezunu olma olayına \( A \), sigara içiyor olma olayına \( B \) diyelim.
Soruda verilen bilgiler aşağıdaki tabloda özetlenmiştir.

Soruda istenen sigara içtiği bilinen bir çalışanın üniversite mezunu olma olasılığıdır, bunu koşullu olasılık olarak aşağıdaki şekilde ifade edebiliriz.
\( P(A \mid B) = \dfrac{P(A \cap B)}{P(B)} = \dfrac{s(A \cap B)}{s(B)} \)
\( A \cap B \) kümesi hem üniversite mezunu olan hem de sigara içen çalışanlara karşılık gelmektedir ve tabloya göre bu çalışanların sayısı 6'dır.
\( B \) kümesi sigara içen çalışanların tümüne karşılık gelmektedir ve tabloya göre bu çalışanların sayısı 28'dir.
Soruda istenen koşullu olasılığı hesaplayalım.
\( P(A \mid B) = \dfrac{s(A \cap B)}{s(B)} \)
\( = \dfrac{6}{28} = \dfrac{3}{14} \) bulunur.
Belirli bir markaya ait telefonların \( \% 40 \)'ı A ülkesinde, \( \%60 \)'ı B ülkesinde üretilmektedir. A ülkesinde üretilen telefonların \( \%15 \)'i, B ülkesinde üretilen telefonların \( \%20 \)'si bozuk çıkmaktadır.
Bu telefonlardan rastgele seçilen biri bozuk çıktığına göre, bu telefonun B ülkesinde üretilmiş olma olasılığı A ülkesinde üretilmiş olma olasılığının kaç katıdır?
Çözümü GösterÜretilen toplam telefon sayısına işlem kolaylığı açısından 100 diyelim. Bu telefonların 40'ı A ülkesinde, 60'ı B ülkesinde üretilmiş olur.
A ülkesinde üretilmiş olan bozuk telefon sayısını bulalım.
\( 40 \cdot \dfrac{15}{100} = 6 \)
B ülkesinde üretilmiş olan bozuk telefon sayısını bulalım.
\( 60 \cdot \dfrac{20}{100} = 12 \)
Buradan toplam bozuk telefon sayısını \( 6 + 12 = 18 \) olarak buluruz.
Bu bilgiler aşağıdaki tabloda özetlenmiştir.

Rastgele seçilen bozuk bir telefonun A ülkesinde üretilmiş olma olasılığı \( P(A \mid C') \), B ülkesinde üretilmiş olma olasılığı \( P(B \mid C') \) olur.
İstenen oranı bulalım.
\( \dfrac{P(B \mid C')}{P(A \mid C')} = \dfrac{\frac{P(B \cap C')}{P(C')}}{\frac{P(A \cap C')}{P(C')}} \)
\( = \dfrac{\frac{12}{18}}{\frac{6}{18}} = 2 \) bulunur.
42 kişilik bir sınıfta matematik dersinden geçenlerin sayısı, türkçe dersinden geçenlerin 2 katıdır.
Her iki dersten geçenlerin sayısı her iki dersten kalanların sayısına eşittir. Yalnız türkçe dersinden geçenlerin sayısı 3 kişidir.
Sınıfta rastgele seçilen bir kişinin türkçeden kaldığı bilindiğine göre, matematikten geçme olasılığı kaçtır?
Çözümü Göster\( M \): Matematik dersinden geçen öğrenciler kümesi
\( T \): Türkçe dersinden geçen öğrenciler kümesi
Sınıftaki öğrencilerin dağılımını bir Venn şemasında gösterelim.

Her iki dersten geçen öğrencilerin sayısı her iki dersten kalan öğrenci sayısına eşittir.
\( b = d \)
Yalnız türkçeden geçen öğrencilerin sayısı 3'tür.
\( c = 3 \)
Matematikten geçenlerin sayısı türkçeden geçenlerin 2 katıdır.
\( a + b = 2(b + c) \)
\( a + b = 2b + 6 \)
\( a = b + 6 \)
Sınıftaki toplam öğrenci sayısı 42'dir.
\( a + b + c + d = 42 \)
Tüm değişkenleri \( b \) cinsinden yazalım.
\( (b + 6) + b + 3 + b = 42 \)
\( b = 11 \)
\( a = b + 6 = 17 \)
\( d = b = 11 \)
Türkçeden kaldığı bilinen bir öğrencinin matematikten geçmiş olma olsılığını bulalım.
\( P(M \mid T') = \dfrac{s(M \cap T')}{s(T')} \)
\( = \dfrac{a}{a + d} = \dfrac{17}{17 + 11} = \dfrac{17}{28} \) bulunur.
\( A, B, C \) kutularında farklı renklerde boncuklar vardır.
\( A \) kutusunda 5 adet mavi boncuk vardır.
\( B \) kutusunda 3 adet pembe, 3 adet mavi boncuk vardır.
\( C \) kutusunda 4 adet mavi, 2 adet mavi boncuk vardır.
Rastgele bir kutu seçiliyor ve içinden 2 adet boncuk alınıyor. Boncukların ikisi de mavi renkte olduğuna göre, seçilen kutunun \( B \) kutusu olma olasığı nedir?
Çözümü GösterKutulardan herhangi birinin seçilme olasılığı \( \frac{1}{3} \) olur.
Kutuların seçilme olaylarını kendi isimleriyle adlandıralım (A, B, C).
2 adet mavi boncuk alınması olayına \( M \) diyelim.
\( M \) olayının bilindiği durum için \( B \) olayının koşullu olasılığını bulalım.
\( P(B \mid M) = \dfrac{P(B \cap M)}{P(M)} \)
Paydaki ifade \( B \) kutusunun seçilmesi ve içinden 2 adet mavi boncuk alınması olayıdır.
\( B \) kutusunun seçilme olasılığı \( \frac{1}{3} \)'tür.
\( P(B) = \dfrac{1}{3} \)
\( B \) kutusundan alınan iki boncuğun da mavi renkte olma olasılığını bulalım.
\( \dfrac{C(3, 2)}{C(6, 2)} = \dfrac{1}{5} \)
\( P(B \cap M) = \dfrac{1}{3} \cdot \dfrac{1}{5} = \dfrac{1}{15} \)
\( M \) olayının olasılığını üç kutu için ayrı ayrı bulalım.
Durum 1:
Önce \( A \) kutusu, sonra 2 adet mavi boncuk seçilir.
\( \dfrac{1}{3} \cdot \dfrac{C(5, 2)}{C(5, 2)} = \dfrac{1}{3} \)
Durum 2:
Önce \( B \) kutusu, sonra 2 adet mavi boncuk seçilir.
\( \dfrac{1}{3} \cdot \dfrac{C(3, 2)}{C(6, 2)} = \dfrac{1}{15} \)
Durum 3:
Önce \( C \) kutusu, sonra 2 adet mavi boncuk seçilir.
\( \dfrac{1}{3} \cdot \dfrac{C(4, 2)}{C(6, 2)} = \dfrac{2}{15} \)
Mavi boncuğun seçilmesi olasılığı bu üç olasılığın toplamıdır.
\( P(M) = \dfrac{1}{3} + \dfrac{1}{15} + \dfrac{2}{15} = \dfrac{8}{15} \)
Bulduğumuz değerleri formülde yerine koyalım.
\( P(B \mid M) = \dfrac{P(B \cap M)}{P(M)} \)
\( = \dfrac{\frac{1}{15}}{\frac{8}{15}} = \dfrac{1}{8} \) bulunur.
Bir torbada üçü hileli, biri hilesiz olmak üzere dört madeni para vardır. Hileli paraların iki yüzeyi de yazıdır.
(a) Torbadan rastgele bir madeni para seçiliyor ve iki kez atılıyor. İki kere yazı gelme olasılığı nedir?
(b) Torbadan rastgele bir madeni para seçiliyor ve iki kez atılıyor. Para iki kere yazı geldiğine göre, seçilen paranın hileli olma olasılığı nedir?
(c) Torbadan rastgele bir madeni para seçiliyor ve sekiz kez atılıyor. Paranın sekizinci atışta yazı gelme olasığı nedir?
Çözümü Göster(a) seçeneği:
Seçilen paranın hileli ve hilesiz olma durumlarını ayrı ayrı inceleyelim.
Durum 1: Hileli para
Torbadan rastgele seçilen bir madeni paranın hileli olma olasılığı \( \frac{3}{4} \) olur.
Hileli paranın her atışta yazı gelme olasılığı 1'dir.
Seçilen paranın hileli olma ve paranın iki atışta da yazı gelme olasılığını bulalım.
\( \dfrac{3}{4} \cdot 1 \cdot 1 = \dfrac{3}{4} \)
Durum 2: Hilesiz para
Torbadan rastgele seçilen bir madeni paranın hilesiz olma olasılığı \( \frac{1}{4} \) olur.
Hilesiz paranın her atışta yazı gelme olasılığı \( \frac{1}{2} \)'dir.
Seçilen paranın hilesiz olma ve paranın iki atışta da yazı gelme olasılığını bulalım.
\( \dfrac{1}{4} \cdot \dfrac{1}{2} \cdot \dfrac{1}{2} = \dfrac{1}{16} \)
İstenen olasılık bu iki durumun olasılıklarının toplamına eşittir.
\( \dfrac{3}{4} + \dfrac{1}{16} = \dfrac{13}{16} \)
(b) seçeneği:
Paranın iki kere yazı gelme olayına \( A \) diyelim.
\( A \) olayının olasılığını (a) seçeneğinde hesaplamıştık.
\( P(A) = \dfrac{13}{16} \)
Torbadan hileli para seçilme olayına \( B \) diyelim.
\( A \) olayının bilindiği durum için \( B \) olayının koşullu olasılığını bulalım.
\( P(B \mid A) = \dfrac{P(B \cap A)}{P(A)} \)
Paranın hileli olma ve iki kere yazı gelme olasılığını (a) seçeneğinde hesaplamıştık.
\( P(B \cap A) = \dfrac{3}{4} \cdot 1 \cdot 1 \)
\( = \dfrac{3}{4} \)
Verilen ve bulduğumuz değerleri formülde yerine koyalım.
\( P(B \mid A) = \dfrac{\frac{3}{4}}{\frac{13}{16}} \)
\( = \dfrac{12}{13} \)
(c) seçeneği:
Daha önceki atışların sonucu sekinci atışın sonucu etkilemez.
Torbadan hileli para seçilmesi ve sekizinci atışta yazı gelmesi olasılığını bulalım.
\( \dfrac{3}{4} \cdot 1 = \dfrac{3}{4} \)
Torbadan hilesiz para seçilmesi ve sekizinci atışta yazı gelmesi olasılığını bulalım.
\( \dfrac{1}{4} \cdot \dfrac{1}{2} = \dfrac{1}{8} \)
İstenen olasılık bu iki durumun olasılıklarının toplamına eşittir.
\( \dfrac{1}{8} + \dfrac{3}{4} = \dfrac{7}{8} \)
Hande'nin kahvaltıda portakal suyu içme olasığı 0,6; omlet yeme olasılığı 0,3'tür. Hande'nin portakal suyu içtiği bir kahvaltıda omlet yeme olasılığı 0,5'tir.
Buna göre aşağıdaki olasılıklar nedir?
(a) Hande'nin kahvaltıda omlet yiyip portakal suyu içme olasılığı
(b) Hande'nin kahvaltıda omlet yememe veya portakal suyu içmeme olasığı
(c) Hande'nin portakal suyu içmediği bir kahvaltıda omlet yeme olasılığı
Çözümü GösterÖrnek uzaya \( S \) diyelim.
Örnek uzayın olasılığı 1'dir.
(a) seçeneği:
Hande'nin kahvaltıda portakal suyu içme olayına \( A \), omlet yeme olayına \( B \) diyelim.
Hande'nin kahvaltıda omlet yiyip portakal suyu içme olayını aşağıdaki şekilde ifade edebiliriz.
\( P(A \cap B) \)
Hande'nin portakal suyu içtiği bir kahvaltıda omlet yeme olasılığı soruda verilmiştir.
\( P(B \mid A) = 0,5 \)
\( A \) olayının gerçekleştiğinin bilindiği durumda \( B \) olayının koşullu olasılık formülünü kullanalım.
\( P(B \mid A) = \dfrac{P(B \cap A)}{P(A)} \)
\( P(B \cap A) = P(B \mid A) \cdot P(A) \)
\( = 0,5 \cdot 0,6 = 0,3 \)
(b) seçeneği:
İstenen olasılığı aşağıdaki şekilde ifade edebiliriz.
\( P(A' \cup B') \)
De Morgan kuralını uygulayalım.
\( = P[(A \cap B)'] \)
Bir olay ile tümleyeninin olasılıkları toplamı 1'dir.
\( = 1 - P(A \cap B) \)
\( = 1 - 0,3 = 0,7 \)
(c) seçeneği:
\( A' \) olayının gerçekleştiğinin bilindiği durumda \( B \) olayının koşullu olasılık formülünü kullanalım.
\( P(B \mid A') = \dfrac{P(B \cap A')}{P(A')} \)
\( X \cap Y' = X - Y \) özdeşliğini kullanalım.
\( P(B \mid A') = \dfrac{P(B - A)}{P(A')} \)
Toplama kuralını kullanalım.
\( P(A \cup B) = P(A) + P(B) - P(A \cap B) \)
\( = 0,6 + 0,3 - 0,3 = 0,6 \)
Bir olay ile tümleyeninin birleşimi örnek uzaya eşittir.
\( P(S) = P(A \cup B) + P[(A \cup B)'] \)
\( 1 = 0,6 + P[(A \cup B)'] \)
\( P[(A \cup B)'] = 0,4 \)
Verilen ve bulduğumuz olasılıkları bir Venn şeması üzerinde gösterelim.

\( P(B \mid A') = \dfrac{P(B - A)}{P(A')} \)
Venn şemasını kullanarak ilgili olasılıkları yazalım.
\( = \dfrac{0}{0,4} = 0 \)
Üç kardeş poğaça almak için pastaneye uğruyorlar. Tezgahta görünüşleri aynı 5 adet zeytinli, 7 adet peynirli ve 6 adet sade poğaça vardır, ancak satıcı poğaçaları müşterilerin tercihlerini dikkate almadan rastgele vermektedir.
Buna göre, birer poğaça almak isteyen üç kardeşe de;
(a) Zeytinli poğaça gelme olasılığı nedir?
(b) Aynı çeşit poğaça gelme olasılığı nedir?
(c) Farklı çeşit poğaça gelme olasılığı nedir?
(d) Aynı çeşit poğaça geldiği biliniyorsa zeytinli poğaça gelme olasılığı nedir?
Çözümü GösterTezgahta toplam 18 poğaça vardır.
(a) seçeneği:
Üç kardeşe de zeytinli poğaça gelme olasılığı, her birine zeytinli poğaça gelme olasılıklarının çarpımına eşittir.
\( \dfrac{5}{18} \cdot \dfrac{4}{17} \cdot \dfrac{3}{16} = \dfrac{5}{408} \)
(b) seçeneği:
Üç kardeşe de aynı çeşit poğaça gelme olasılığı, üçüne de zeytinli, peynirli ve sade poğaça gelme olasılıklarının toplamına eşittir.
Bu üç durumun olasılıklarını ayrı ayrı bulalım.
Durum 1:
Üç kardeşe de zeytinli poğaça gelir.
\( \dfrac{5}{18} \cdot \dfrac{4}{17} \cdot \dfrac{3}{16} = \dfrac{60}{4896} \)
Durum 2:
Üç kardeşe de peynirli poğaça gelir.
\( \dfrac{7}{18} \cdot \dfrac{6}{17} \cdot \dfrac{5}{16} = \dfrac{210}{4896} \)
Durum 3:
Üç kardeşe de sade poğaça gelir.
\( \dfrac{6}{18} \cdot \dfrac{5}{17} \cdot \dfrac{4}{16} = \dfrac{120}{4896} \)
İstenen olasılık bu üç durumun olasılıklarının toplamına eşittir.
\( \dfrac{60}{4896} + \dfrac{210}{4896} + \dfrac{120}{4896} = \dfrac{390}{4896} \)
\( = \dfrac{65}{816} \)
(c) seçeneği:
Üç kardeşe de farklı çeşit poğaça gelme olasılığını bulalım.
Örnek uzaya \( S \) diyelim.
Örnek uzay 18 adet poğaça arasından üç poğaçanın tüm farklı seçimlerinden oluşur.
\( s(S) = 18 \cdot 17 \cdot 16 \)
\( = 4896 \)
Her kardeşe farklı çeşit poğaça gelme olayına \( A \) diyelim.
Her çeşitten birer tane poğaça \( C(7, 1) \cdot C(5, 1) \cdot C(6, 1) = 210 \) farklı şekilde seçilebilir.
Seçilen farklı çeşit üç poğaça üç kardeşe \( 3! \) farklı şekilde dağıtılabilir.
\( s(A) = 210 \cdot 3! = 1260 \)
\( A \) olayının gerçekleşme olasılığı \( A \) olayındaki sonuç sayısının örnek uzaydaki sonuç sayısına oranına eşittir.
\( P(A) = \dfrac{s(A)}{s(S)} \)
\( = \dfrac{1260}{4896} = \dfrac{35}{136} \)
(d) seçeneği:
Üç kardeşe de zeytinli poğaça gelme olayına \( Z \), aynı çeşit poğaça gelme olayına \( Y \) diyelim.
\( Y \) olayının gerçekleştiği durum için \( Z \) olayının koşullu olasılığını bulalım.
\( P(Z \mid Y) = \dfrac{P(Z \cap Y)}{P(Y)} \)
Üç kardeşe de zeytinli poğaça gelme olasılığını (a) seçeneğinde bulmuştuk.
\( P(Z \cap Y) = \dfrac{4}{408} \)
Üç kardeşe de aynı çeşit poğaça gelme olasılığı (b) seçeneğinde bulmuştuk.
\( P(Y) = \dfrac{65}{816} \)
Bulduğumuz değerleri formülde yerine koyalım.
\( P(Z \mid Y) = \dfrac{\frac{5}{408}}{\frac{65}{816}} = \dfrac{2}{13} \)
Sena'nın 3 madeni parası vardır. Bu paralardan ikisinin bir yüzü yazı bir yüzü tura, diğerinin her iki yüzü de turadır.
Sena bu paralardan rastgele birini seçiyor ve havaya atıyor. Para tura geldiğine göre, paranın diğer yüzünün de tura olma olasılığı nedir?
Çözümü GösterHer bir sonuçta ilk harf gelen paranın ön yüzü, ikinci harf arka yüzü olmak üzere, örnek uzayı tüm 6 olasılığı içerecek şekilde aşağıdaki şekilde tanımlayabiliriz (ilk iki sonuç 1. para seçildiği durum için, ikinci iki sonuç 2. para seçildiği durum için, üçüncü iki sonuç 3. iki yüzün de tura olduğu para seçildiği durum için).
\( S = \{YT, TY, YT, TY, TT, TT\} \)
\( s(S) = 6 \)
Soruyu çözmek için koşullu olasılık formülünü kullanalım.
\( P(A \mid B) = \dfrac{P(A \cap B)}{P(B)} \)
\( A \): Gelen yüzün arkasının tura olma olayı
\( A = \{YT, YT, TT, TT\} \)
\( s(A) = 4 \)
\( B \): Gelen yüzün tura olma olayı
\( B = \{TY, TY, TT, TT\} \)
\( s(B) = 4 \)
\( P(B) = \dfrac{s(B)}{s(S)} \)
\( = \dfrac{4}{6} = \dfrac{2}{3} \)
\( A \cap B \): Gelen ve arka yüzün ikisinin de tura olma olayı
\( A \cap B = \{TT, TT\} \)
\( s(A \cap B) = 2 \)
\( P(A \cap B) = \dfrac{s(A \cap B)}{s(S)} \)
\( = \dfrac{2}{6} = \dfrac{1}{3} \)
\( A \mid B \): Gelen yüzün tura olduğu bilindiği durumda arkasının tura olma olayı
Bu değerleri koşullu olasılık formülünde yerine koyalım.
\( P(A \mid B) = \dfrac{P(A \cap B)}{P(B)} = \dfrac{s(A \cap B)}{s(B)} \)
\( = \dfrac{\frac{1}{3}}{\frac{2}{3}} = \dfrac{1}{2} \) bulunur.
1 milyonda bir kişide görülen bir hastalığın teşhisinde kullanılan bir test %99 oranında doğru sonuç vermektedir (hastalığa sahip kişi için pozitif, hastalığa sahip olmayan kişi için negatif sonuç).
Bu testi yaptıran bir kişinin sonucu pozitif ise kişinin gerçekten hasta olma olasılığı kaçtır?
Çözümü GösterSoruda verilen bilgiler doğrultusunda bir tablo oluşturalım.
Bu tabloda satırlar bir kişinin gerçekten bu hastalığa sahip olup olmadığını, sütunlar da test sonucunu göstermektedir.

1 milyon kişiyi bu tablonun hücrelerine dağıtalım.
Hastalık 1 milyonda bir kişide görüldüğü için toplam hasta kişi sayısına 1, toplam hasta olmayan kişi sayısına 999999 diyelim.
Test sonucu gerçekten hasta olan bir kişi için pozitif, hasta olmayan bir kişi için negatif olursa doğru olur.
Testin doğruluk oranı %99 olduğu için, gerçekten hasta olan 1 kişi içinde \( \frac{99}{100} \) kişi için test sonucu pozitif (doğru sonuç), \( \frac{1}{100} \) kişi için test sonucu negatif (hatalı sonuç) çıkar.
Benzer şekilde, gerçekten hasta olmayan 999999 kişi içinde \( \frac{999999}{100} \) kişi için test sonucu pozitif (hatalı sonuç), \( \frac{999999 \cdot 99}{100} \) kişi için test sonucu negatif (doğru sonuç) çıkar.
Soruda test sonucu pozitif olduğu bilinen bir kişinin gerçekten hasta olma olasılığı isteniyor.
\( P(\text{Hasta} \mid \text{Pozitif}) = \frac{s(\text{Hasta} \cap \text{Pozitif})}{s(\text{Pozitif})} \)
\( = \dfrac{\frac{99}{100}}{\frac{99}{100} + \frac{999999}{100}} \)
\( = \dfrac{99}{99 + 999999} \approx \%0,01 \)
Görülebileceği üzere, doğruluk oranı %99 olan bir testin pozitif sonuç verdiği bir kişinin gerçekten hasta olma olasılığı yaklaşık %0,01 olmaktadır.
Bir ilçede akşam saat 8 ile sabah saat 8 arasında sürücülerin %10'unun ehliyetsiz olduğu tespit edilmiştir. İstatistiklere göre ehliyetsiz bir sürücünün kaza yapma olasılığı 0,04, ehliyetli bir sürücünün kaza yapma olasılığı ise 0,002'dir.
Bu ilçede gece saat 11'de bir araba ağaca çarpıyor. Bu arabanın sürücüsünün ehliyetsiz olma olasılığı nedir?
Çözümü GösterBir sürücünün kaza yapma olayına \( B \), akşam saat 8 ile sabah saat 8 arasında bir sürücünün ehliyetli olma olayına \( A \) diyelim.
\( P(A) = 1 - 0,1 = 0,9 \)
\( A \) olayının gerçekleştiğinin bilindiği durumda \( B \) olayının koşullu olasılığını bulalım.
\( P(B \mid A) = \dfrac{P(B \cap A)}{P(A)} = 0,002 \)
\( \dfrac{P(B \cap A)}{0,9} = 0,002 \)
\( P(B \cap A) = 0,0018 \)
Bir sürücünün ehliyetsiz olma olayına \( A' \) diyelim.
\( P(A') = 0,1 \)
\( A' \) olayının gerçekleştiğinin bilindiği durumda \( B \) olayının koşullu olasılığını bulalım.
\( P(B \mid A') = \dfrac{P(B \cap A')}{P(A')} = 0,04 \)
\( \dfrac{P(B \cap A')}{0,1} = 0,04 \)
\( P(B \cap A') = 0,004 \)
\( B \) olayının olasılığını hesaplayalım.
\( P(B) = P(B \cap A) + P(B \cap A') \)
\( = 0,0018 + 0,004 = 0,0058 \)
Soruda gece saat 11'de kaza yapan bir sürücünün ehliyetsiz olma olasılığı istenmektedir.
\( B \) olayının gerçekleştiğinin bilindiği durumda \( A' \) olayının koşullu olasılığını bulalım.
\( P(A' \mid B) = \dfrac{P(A' \cap B)}{P(B)} \)
\( = \dfrac{0,004}{0,0058} \)
\( = \dfrac{20}{29} \) bulunur.
Cansu ve Meltem'in oynadığı masa tenisi oyununda toplamda 3 set kazanan oyuncu maçı kazanıyor. Bir seti Cansu'nun kazanma olasılığı \( \frac{2}{5} \)'tir.
Buna göre aşağıdaki olasılıklar nedir?
(a) Cansu'nun maçı 3. sette kazanma olasılığı
(b) Cansu'nun maçı 4. sette kazanma olasılığı
(c) Cansu'nun maçı 5. sette kazanma olasılığı
(d) Cansu'nun maçı kazanma olasılığı
(e) Cansu'nun maçı kazandığı biliniyorsa maçın 3 setten fazla oynanmış olma olasılığı
Çözümü GösterCansu'nun bir seti kaybetme (Meltem'in bir seti kazanma) olasılığı \( \frac{3}{5} \) olur.
Toplamda 3 set kazanan maçı kazandığına göre, maç en az 3, en fazla 5 set sürebilir.
Cansu'nun maçı 3. sette kazanma olayına \( A \), 4. sette kazanma olayına \( B \), 5. sette kazanma olayına \( C \), maçı kazanma olayına \( D \) diyelim.
(a) seçeneği:
Cansu'nun maçı 3. sette kazanabilmesi için 3 seti de kazanmalıdır.
Ceren'in maçı 3-0'a getirdiği durumun olasılığını bulalım.
\( (\dfrac{2}{5})^3 = \dfrac{8}{125} \)
\( P(A) = \dfrac{8}{125} \)
(b) seçeneği:
Cansu'nun maçı 4. sette kazanabilmesi için 3. setin sonunda durum 2-1 olmalıdır.
Ceren'in maçı C-C-M sırasıyla 2-1'e getirdiği durumun olasılığını bulalım.
\( (\dfrac{2}{5})^2 \cdot \dfrac{3}{5} = \dfrac{12}{125} \)
Ceren C-C-M harflerinin farklı diziliş sayısı kadar farklı şekilde maçı 2-1'e getirebilir.
C-C-M harflerinin farklı diziliş sayısı için tekrarlı permütasyon formülünü kullanalım.
\( \dfrac{3!}{2!} = 3 \)
Bu iki sayının çarpımı ile Cansu'nun 4. seti kazanma olasılığının çarpımı, Cansu'nun bu maçı 4. sette kazanma olasılığını verir.
\( P(B) = \dfrac{12}{125} \cdot 3 \cdot \dfrac{2}{5} = \dfrac{72}{625} \)
(c) seçeneği:
Cansu'nun maçı 5. sette kazanabilmesi için 4. setin sonunda durum 2-2 olmalıdır.
Ceren'in maçı C-C-M-M sırasıyla 2-2'ye getirdiği durumun olasılığını bulalım.
\( (\dfrac{2}{5})^2 \cdot (\dfrac{3}{5})^2 = \dfrac{36}{625} \)
Ceren C-C-M-M harflerinin farklı diziliş sayısı kadar farklı şekilde maçı 2-2'ye getirebilir.
C-C-M-M harflerinin farklı diziliş sayısı için tekrarlı permütasyon formülünü kullanalım.
\( \dfrac{4!}{2!\ 2!} = 6 \)
Bu iki sayının çarpımı ile Cansu'nun 5. seti kazanma olasılığının çarpımı, Cansu'nun bu maçı 5. sette kazanma olasılığını verir.
\( P(C) = \dfrac{36}{625} \cdot 6 \cdot \dfrac{2}{5} = \dfrac{432}{3125} \)
(d) seçeneği:
Oyunda 5 setin 3'ünü kazanan oyuncu maçı kazandığı için Cansu maçı 3, 4 ya da 5 sette kazanabilir.
Buna göre Cansu'nun maçı kazanma olasılığı, (a), (b) ve (c) seçeneklerindeki 3 durumun olasılıklarının toplamıdır.
\( P(D) = \dfrac{8}{125} + \dfrac{72}{625} + \dfrac{432}{3125} \)
\( = \dfrac{992}{3125} \)
(e) seçeneği:
Bu durum Cansu'nun maçı 4 ya da 5 sette kazandığı durumda oluşur.
\( D \) olayının bilindiği durum için \( B \cup C \) olayının koşullu olasılığını bulalım.
\( P[(B \cup C) \mid D] = \dfrac{P[(B \cup C) \cap D]}{P(D)} \)
Kesişim işleminin birleşim işlemi üzerinde sağdan dağılma özelliği vardır.
\( = \dfrac{P[(B \cap D) \cup (C \cap D)]}{P(D)} \)
Paydaki ifade Cansu'nun maçı 4. ve 5. sette kazanma olasılıklarının toplamıdır.
\( P[(B \cap D) \cup (C \cap D)] = \dfrac{72}{625} + \dfrac{432}{3125} \)
\( = \dfrac{792}{3125} \)
Verilen ve bulduğumuz değerleri formülde yerine koyalım.
\( P[(B \cup C) \mid D] = \dfrac{\frac{792}{3125}}{\frac{992}{3125}} \)
\( = \dfrac{792}{992} = \dfrac{99}{124} \)
İki çocuklu aileler üzerinde yapılan bir araştırmanın sonuçlarına göre, büyük kardeşin yabancı dil bilme olasılığı \( \frac{5}{12} \), küçük kardeşin yabancı dil bilme olasılığı \( \frac{3}{8} \)'dir. Küçük kardeş yabancı dil biliyor ise büyük kardeşin yabancı dil bilme olasılığı ise \( \frac{1}{3} \)'tür.
Buna göre aşağıdaki olasılıklar nedir?
(a) Rastgele seçilen bir ailede, hem büyük hem de küçük kardeşin yabancı dil bilme olasılığı
(b) Rastgele seçilen bir ailede, kardeşlerden sadece birinin yabancı dil bilme olasılığı
(c) Rastgele seçilen iki ailede, büyük kardeşlerden sadece birinin ve küçük kardeşlerden sadece birinin yabancı dil bilme olasılığı
Çözümü GösterBir ailede büyük kardeşin yabancı dil bilme olayına \( B \) diyelim.
\( P(B) = \dfrac{5}{12} \)
Bir ailede küçük kardeşin yabancı dil bilme olayına \( K \) diyelim.
\( P(K) = \dfrac{3}{8} \)
\( K \) olayının bilindiği durum için \( B \) olayının koşullu olasılığı soruda verilmiştir.
\( P(B \mid K) = \dfrac{P(B \cap K)}{P(K)} = \dfrac{1}{3} \)
\( P(B \cap K) = P(B \mid K) \cdot P(K) \)
\( = \dfrac{1}{3} \cdot \dfrac{3}{8} = \dfrac{1}{8} \)
Toplama kuralını kullanalım.
\( P(B \cup K) = P(B) + P(K) - P(B \cap K) \)
Verilen ve bulduğumuz değerleri formülde yerine koyalım.
\( P(B \cup K) = \dfrac{5}{12} + \dfrac{3}{8} - \dfrac{1}{8} \)
\( = \dfrac{2}{3} \)
Bulduğumuz olasılıkları bir Venn şeması üzerinde gösterelim.

(a) seçeneği:
Rastgele seçilen bir ailede, hem büyük kardeşin hem de küçük kardeşin yabancı dil bilme olasılığını aşağıdaki şekilde ifade edebiliriz.
\( P(B \cap K) \)
Venn şemasını kullanarak ilgili olasılığı yazalım.
\( = \dfrac{1}{8} \)
(b) seçeneği:
Rastgele seçilen bir ailede, kardeşlerden sadece birinin yabancı dil bilme olasılığını aşağıdaki şekilde ifade edebiliriz.
\( P(B \cap K') + P(B' \cap K) \)
Venn şemasını kullanarak ilgili olasılıkları yazalım.
\( = \dfrac{7}{24} + \dfrac{1}{4} = \dfrac{13}{24} \)
(c) seçeneği:
Rastgele seçilen iki ailede, büyük kardeşlerden sadece birinin ve küçük kardeşlerden sadece birinin yabancı dil bilme olayı için 2 durum vardır.
Durum 1:
Ailelerden birinde iki kardeş de yabancı dil biliyor, diğerinde iki kardeş de yabancı dil bilmiyor.
Bir ailede iki kardeşin de yabancı dil bilme olasılığını yukarıda hesaplamıştık.
\( P(B \cap K) = \dfrac{1}{8} \)
Bir ailede iki kardeşin de yabancı dil bilmeme olasılığını bulalım.
\( P[(B \cap K)'] = 1 - P(B \cap K) \)
\( = 1 - \dfrac{1}{8} = \dfrac{7}{8} \)
İki aile için bunun gibi iki durum oluşur.
\( 2 \cdot \dfrac{1}{8} \cdot \dfrac{7}{8} = \dfrac{7}{32} \)
Durum 2:
Ailelerden birinde sadece büyük kardeş yabancı dil biliyor, diğerinde sadece küçük kardeş yabancı dil biliyor.
Bir ailede sadece büyük kardeşin yabancı dil bilme olasılığını bulalım.
\( P(B \cap K') \)
Venn şemasını kullanarak ilgili olasılığı yazalım.
\( = \dfrac{7}{24} \)
Bir ailede sadece küçük kardeşin yabancı dil bilme olasılığını bulalım.
\( P(B' \cap K) \)
Venn şemasını kullanarak ilgili olasılığı yazalım.
\( = \dfrac{1}{4} \)
İki aile için bunun gibi iki durum oluşur.
\( 2 \cdot \dfrac{7}{24} \cdot \dfrac{1}{4} = \dfrac{7}{48} \)
İstenen olasılık bu iki durumun olasılıklarının toplamına eşittir.
\( = \dfrac{7}{32} + \dfrac{7}{48} = \dfrac{35}{96} \) bulunur.
Bir kutuda 2 adet sarı, 3 adet turuncu top vardır. Toplar kutudan 2 sarı top da çekilene kadar rastgele çekiliyor ve çekilen toplar kutuya geri bırakılmıyor.
Çekilen 2. top sarı olduğuna göre, 2 sarı top da çekildiğinde kutudan toplamda 4 top çekilmiş olma olasılığı nedir?
Çözümü GösterÇekilen 2. topun sarı olma olayına \( A \) diyelim.
2 sarı top da çekildiğinde kutudan toplamda 4 top çekilmiş olma olayına \( B \) diyelim.
\( A \) olayının gerçekleştiği bilindiği durumda \( B \) olayının gerçekleşme olasılığını bulalım.
\( P(B \mid A) = \dfrac{P(B \cap A)}{P(A)} \)
\( A \) olayı ilk çekilen topun sarı ya da turuncu olmasına göre iki şekilde gerçekleşebilir.
\( P(A) = \dfrac{2}{5} \cdot \dfrac{1}{4} + \dfrac{3}{5} \cdot \dfrac{2}{4} \)
\( = \dfrac{2}{5} \)
2 sarı top da çekildiğinde \( A \) olayının gerçekleştiği 4 durum vardır.
\( A = \{ SS, TSS, TSTS, TSTTS \} \)
\( B \) olayının gerçekleştiği 3 durum vardır.
\( B = \{ TTSS, TSTS, STTS \} \)
\( B \cap A = \{ TSTS \} \)
\( P(B \cap A) = P(\{ TSTS \}) \)
\( = \dfrac{3}{5} \cdot \dfrac{2}{4} \cdot \dfrac{2}{3} \cdot \dfrac{1}{2} \)
\( = \dfrac{12}{120} = \dfrac{1}{10} \)
Bulduğumuz değerleri formülde yerine koyalım.
\( P(B \mid A) = \dfrac{P(B \cap A)}{P(A)} \)
\( = \dfrac{\frac{1}{10}}{\frac{2}{5}} = \dfrac{1}{4} \) bulunur.
Sefer bazı günler sahile gidiyor ve sahile gittiği günlerde bazen balık tutuyor. Sefer'in belirli bir günde sahile gitme olasılığı \( \frac{4}{5} \), hem sahile gidip hem de balık tutma olasılığı \( \frac{1}{5} \)'tir.
Sefer'in balık tutmadığı bir günde sahile gitmiş olma olasılığı nedir?
Çözümü GösterSefer'in belirli bir günde sahile gitme olayına \( A \) diyelim.
\( P(A) = \dfrac{4}{5} \)
Sefer'in sahilde balık tutma olayına \( B \) diyelim.
Sefer'in belirli bir günde hem sahile gidip hem de balık tutma olasılığı soruda verilmiştir.
\( P(A \cap B) = \dfrac{1}{5} \)
Soruda Sefer'in balık tutmadığı bir günde sahile gitmiş olma olasılığı istenmektedir.
Bu olasılık \( B' \) olayının gerçekleştiğinin bilindiği durumda \( A \) olayının koşullu olasılığına eşittir.
\( P(A \mid B') = ? \)
Bayes teoremi formülünü kullanalım.
\( P(A \mid B') = \dfrac{P(B' \mid A) \cdot P(A)}{P(B')} \)
Bu formülde bilinmeyen iki olasılığı bulalım.
Adım 1: \( P(B' \mid A) \)
\( A \) olayının gerçekleştiğinin bilindiği durumda, \( B \) olayının gerçekleşmesi ve gerçekleşmemesi olaylarının birleşimi örnek uzayı oluşturur.
\( P(B' \mid A) + P(B \mid A) = 1 \)
\( P(B' \mid A) = 1 - P(B \mid A) \)
Koşullu olasılık formülünü kullanalım.
\( P(B \mid A) = \dfrac{P(B \cap A)}{P(A)} \)
\( = \dfrac{\frac{1}{5}}{\frac{4}{5}} = \dfrac{1}{4} \)
\( P(B' \mid A) = 1 - \dfrac{1}{4} = \dfrac{3}{4} \)
Adım 2: \( P(B') \)
\( B' \) olayı için bilinenleri kullanarak bir eşitlik kuralım.
\( P(B) = P(B \cap A) + P(B \cap A') \)
Yukarıdaki toplamı Venn şemasında gösterelim.
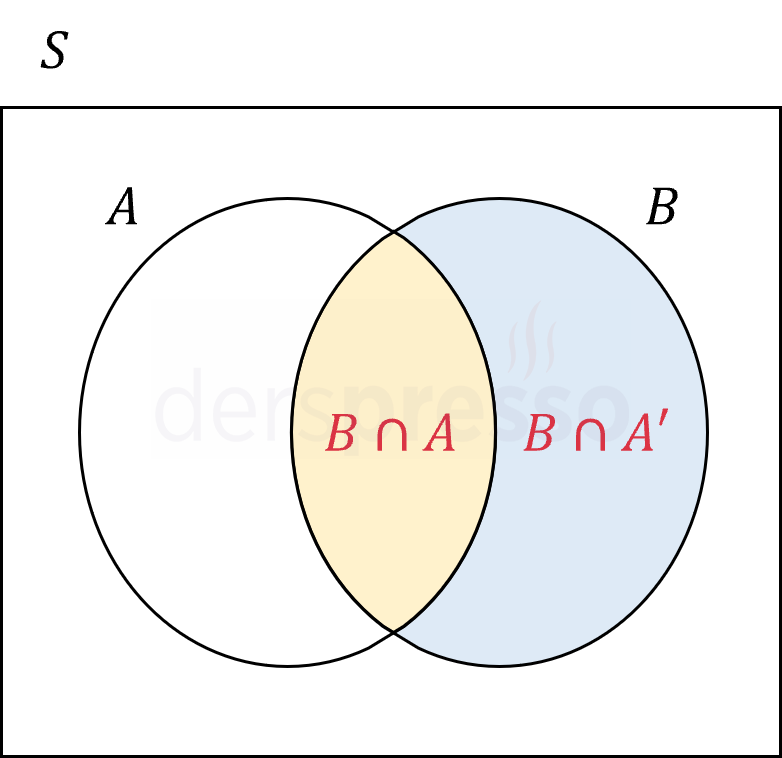
Sefer'in sahile gitmeme ve balık tutma olaylarının kesişimi boş kümedir. Sefer'in balık tutması için sahile gitmesi gerekir.
\( P(B \cap A') = 0 \)
\( P(B) = P(B \cap A) = \dfrac{1}{5} \)
Bir olay ile tümleyeninin birleşimi örnek uzaya eşittir.
\( P(B) + P(B') = 1 \)
\( P(B') = 1 - P(B) \)
\( = 1 - \dfrac{1}{5} = \dfrac{4}{5} \)
Verilen ve bulduğumuz değerleri formülde yerine koyalım.
\( P(A \mid B') = \dfrac{P(B' \mid A) \cdot P(A)}{P(B')} \)
\( = \dfrac{\frac{3}{4} \cdot \frac{4}{5}}{\frac{4}{5}} = \dfrac{3}{4} \) bulunur.