Tam Kareye Tamamlama
\( ax^2 + bx + c \) formundaki ikinci dereceden bir ifadeyi \( a(x - r)^2 + k \) formuna dönüştürme işlemine tam kareye tamamlama denir. Bu ikinci formun ana özelliği, iki yerine tek bir \( x \) değişkeni içermesi ve bunun bir sonucu olarak aşağıda inceleyeceğimiz farklı uygulamalara imkan vermesidir.
İkinci dereceden bir ifadeyi tam kareye tamamlamak için ifadeye sabit bir terim eklenir ve çıkarılır. Bu işlem sonucunda elde edilen ifade orijinal ifade ile özdeş bir ifade olur.
\( ax^2 + bx + c \) ifadesini tam kareye tamamlamak için ifadeye \( \frac{b^2}{4a} \) terimi eklenir ve çıkarılır.
\( ax^2 + bx \textcolor{red}{+ \dfrac{b^2}{4a} - \dfrac{b^2}{4a}} + c \)
Bu işlem sonucunda ifade aşağıdaki forma dönüşür.
\( a(x - r)^2 + k \)
Bu ifadedeki \( r, k \) parametreleri ile orijinal ifadedeki \( a, b, c \) katsayıları arasındaki ilişki aşağıdaki gibidir.
\( r = -\dfrac{b}{2a} \)
\( k = c - \dfrac{b^2}{4a} \)
İSPATI GÖSTER
1. yöntem:
Aşağıdaki gibi bir ikinci dereceden ifade tanımlayalım.
\( ax^2 + bx + c \)
Bu ifadeyi dönüştürmek istediğimiz ifade aşağıdaki formdadır.
\( a(x - r)^2 + k = ax^2 - 2arx + ar^2 + k \)
Bu iki ifadenin özdeş olması istendiğine göre, ifadeleri birbirine eşitleyebiliriz.
\( ax^2 + bx + c = ax^2 - 2arx + ar^2 + k \)
İki polinomun eşitliğinde aynı dereceli terimlerin katsayıları birbirine eşittir.
\( b = -2ar \) için:
\( r = -\dfrac{b}{2a} \)
\( c = ar^2 + k \) için:
\( k = c - ar^2 \)
Bulduğumuz \( r \) değerini yerine koyalım.
\( = c - a\left( -\dfrac{b}{2a} \right)^2 \)
\( = c - \dfrac{b^2}{4a} \)
2. yöntem:
Aşağıdaki gibi bir ikinci dereceden ifade tanımlayalım.
\( ax^2 + bx + c \)
İlk iki terimi \( a \) parantezine alalım.
\( = a\left( x^2 + \dfrac{b}{a}x \right) + c \)
Parantez içindeki iki terimi \( (x + m)^2 = x^2 + 2mx + m^2 \) özdeşliğinin açılımındaki ilk iki terime benzetirsek, parantez içini tam kare bir ifadenin açılımı formuna getirmek için parantez içine üçüncü terim olarak ikinci terimin katsayısının yarısının karesi eklenmelidir. Eşitliğin bozulmaması için de bu terimin aynısı parantez dışında ifadeden çıkarılmalıdır.
\( = a\left( x^2 + \dfrac{b}{a}x + \left( \dfrac{b}{2a} \right)^2 \right) - \dfrac{b^2}{4a} + c \)
Parantez içindeki açılımı kapalı formda yazalım.
\( = a\left( x + \dfrac{b}{2a} \right)^2 + c - \dfrac{b^2}{4a} \)
\( r \) ve \( k \) parametrelerini aşağıdaki gibi tanımlayalım.
\( r = -\dfrac{b}{2a} \)
\( k = c - \dfrac{b^2}{4a} \)
Bu parametreleri yerlerine koyduğumuzda aşağıdaki formu elde ederiz.
\( = a(x - r)^2 + k \)
\( r, k \) parametreleri ile \( a, b, c \) katsayıları arasındaki ilişkinin detayları yukarıdaki ispatta iki farklı yöntemle açıklanmıştır.
\( a = 1 \) olduğu durumda oluşan \( x^2 + bx + c \) ifadesi için tam kareye tamamlama işlemi görsel olarak aşağıda şekilde düşünülebilir.
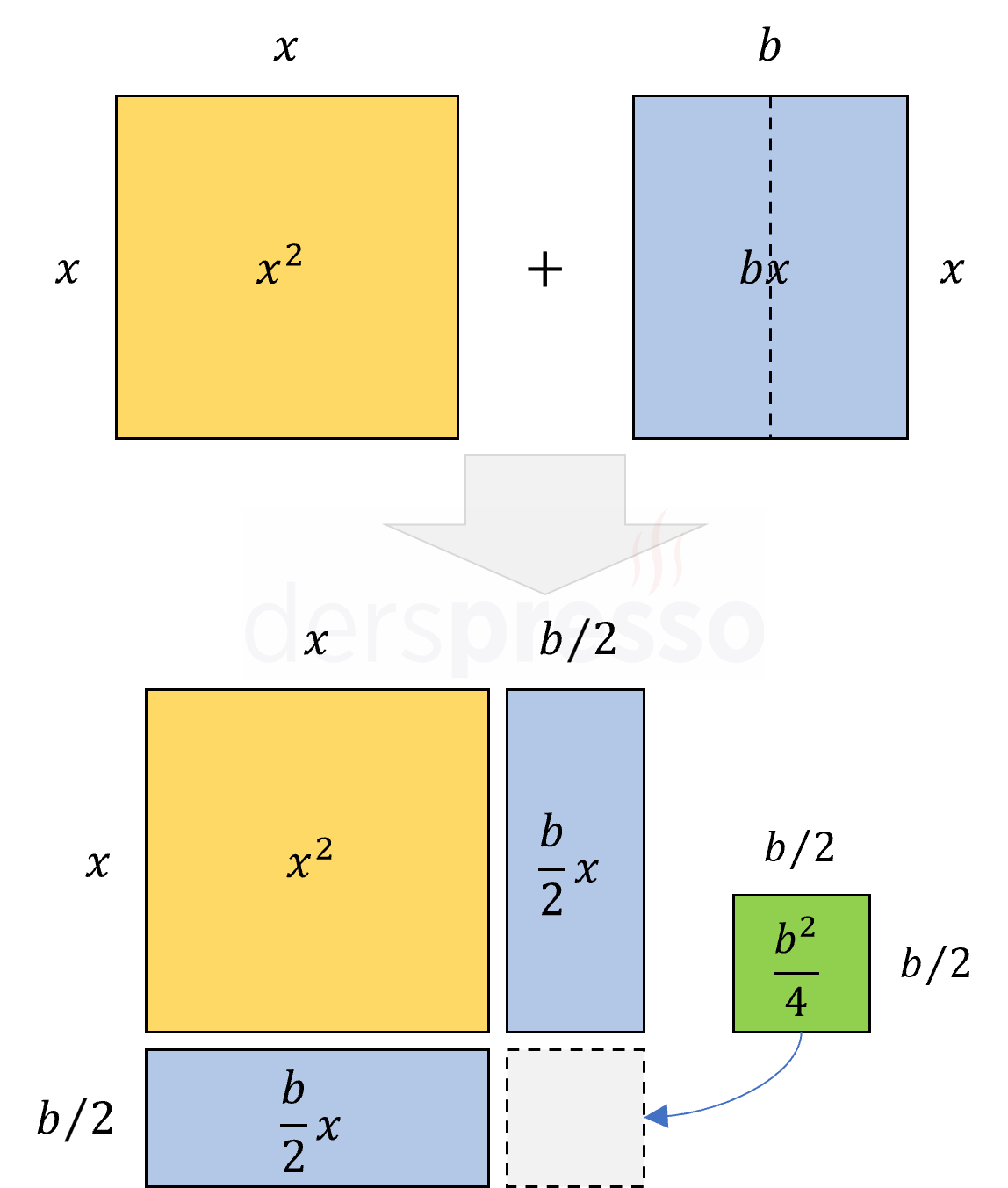
- \( x^2 \) terimini bir kenar uzunluğu \( x \) birim olan bir kare, \( bx \) terimini de kenar uzunlukları \( b \) ve \( x \) birim olan bir dikdörtgen olarak düşünelim.
- \( bx \) dikdörtgenini \( b \) kenarı üzerinden dikey bir doğru ile iki eşit parçaya bölelim ve \( x^2 \) karesinin sağına ve altına yerleştirelim.
- Görselde görülebileceği üzere, şekli bir kareye tamamlamak için eklenmesi gereken parça bir kenar uzunluğu \( \frac{b}{2} \) birim, yani alanı \( \frac{b^2}{4} \) birimkare olan bir karedir.
- Şekil kareye tamamlandığında karenin alanı \( (x + \frac{b}{2})^2 \) olur.
- Eklediğimiz karenin alanını toplam ifadenin değeri değişmeyecek şekilde tüm ifadeden çıkardığımızda tam kare dışındaki terim \( c - \frac{b^2}{4} \) olur.
\( a \ne 1 \) olduğu durum için de benzer bir görsel oluşturulabilir.
Tam kareye tamamlama yöntemini bir örnek üzerinde gösterelim.
\( x^2 - 18x + 12 \) ifadesini tam kareye tamamlayalım.
İfadeyi tam kareye tamamlamak için ekleyip çıkarmamız gereken sabit terimi bulalım.
\( a = 1, \quad b = -18, \quad c = 12 \)
\( \dfrac{b^2}{4a} = \dfrac{(-18)^2}{4(1)} = 81 \)
\( x^2 - 18x \textcolor{red}{+ 81 - 81} + 12 \)
İlk üç terimi gruplayarak tam kare formuna getirelim.
\( = (x^2 - 18x + 81) - 69 \)
\( = (x - 9)^2 - 69 \)
Alternatif olarak, yukarıda \( r \) ve \( k \) için paylaştığımız formülleri de kullanabiliriz.
\( r = -\dfrac{b}{2a} = -\dfrac{-18}{2(1)} = 9 \)
\( k = c - \dfrac{b^2}{4a} = 12 - \dfrac{(-18)^2}{4(1)} = -69 \)
\( a(x - r)^2 + k = (x - 9)^2 - 69 \)
\( a \) katsayısının birden farklı olduğu durum için de bir örnek yapalım.
\( 3x^2 - 12x + 17 \) ifadesini tam kareye tamamlayalım.
İfadeyi tam kareye tamamlamak için ekleyip çıkarmamız gereken sabit terimi bulalım.
\( a = 3, \quad b = -12, \quad c = 17 \)
\( \dfrac{b^2}{4a} = \dfrac{(-12)^2}{4(3)} = 12 \)
\( 3x^2 - 12x \textcolor{red}{+ 12 - 12} + 17 \)
İlk üç terimi gruplayarak tam kare formuna getirelim.
\( = (3x^2 - 12x + 12) + 5 \)
Parantez içindeki terimleri \( x^2 \)'li terimin katsayısı parantezine alalım.
\( = 3(x^2 - 4x + 4) + 5 \)
\( = 3(x - 2)^2 + 5 \)
Aşağıdaki ikinci dereceden ifadeleri tam kareye tamamlayınız.
(a) \( x^2 - 8x - 73 \)
(b) \( x^2 + x - 4 \)
(c) \( x^2 + 5x + 3 \)
Çözümü Göster(a) seçeneği:
\( x^2 - 8x - 73 \)
İfadeyi tam kareye tamamlamak için ekleyip çıkarmamız gereken sabit terimi bulalım.
\( a = 1, \quad b = -8, \quad c = -73 \)
\( \dfrac{b^2}{4a} = \dfrac{(-8)^2}{4(1)} = 16 \)
\( x^2 - 8x \textcolor{red}{+ 16 - 16} - 73 \)
İlk üç terimi gruplayarak tam kare formuna getirelim.
\( = (x^2 - 8x + 16) - 89 \)
\( = (x - 4)^2 - 89 \)
(b) seçeneği:
\( x^2 + x - 4 \)
İfadeyi tam kareye tamamlamak için ekleyip çıkarmamız gereken sabit terimi bulalım.
\( a = 1, \quad b = 1, \quad c = -4 \)
\( \dfrac{b^2}{4a} = \dfrac{1^2}{4(1)} = \dfrac{1}{4} \)
\( x^2 + x \textcolor{red}{+ \dfrac{1}{4} - \dfrac{1}{4}} - 4 \)
İlk üç terimi gruplayarak tam kare formuna getirelim.
\( = \left( x^2 + x + \dfrac{1}{4} \right) - \dfrac{17}{4} \)
\( = \left( x + \dfrac{1}{2} \right)^2 - \dfrac{17}{4} \)
(c) seçeneği:
\( x^2 + 5x + 3 \)
İfadeyi tam kareye tamamlamak için ekleyip çıkarmamız gereken sabit terimi bulalım.
\( a = 1, \quad b = 5, \quad c = 3 \)
\( \dfrac{b^2}{4a} = \dfrac{5^2}{4(1)} = \dfrac{25}{4} \)
\( x^2 + 5x \textcolor{red}{+ \dfrac{25}{4} - \dfrac{25}{4}} + 3 \)
İlk üç terimi gruplayarak tam kare formuna getirelim.
\( = \left( x^2 + 5x + \dfrac{25}{4} \right) - \dfrac{13}{4} \)
\( = \left( x + \dfrac{5}{2} \right)^2 - \dfrac{13}{4} \)
Aşağıdaki ikinci dereceden ifadeleri tam kareye tamamlayınız.
(a) \( 2x^2 + 12x - 5 \)
(b) \( 3x^2 - 2x - 7 \)
(c) \( 4x^2 - 32x - 61 \)
Çözümü Göster(a) seçeneği:
\( 2x^2 + 12x - 5 \)
İfadeyi tam kareye tamamlamak için ekleyip çıkarmamız gereken sabit terimi bulalım.
\( a = 2, \quad b = 12, \quad c = -5 \)
\( \dfrac{b^2}{4a} = \dfrac{12^2}{4(2)} = 18 \)
\( 2x^2 + 12x \textcolor{red}{+ 18 - 18} - 5 \)
İlk üç terimi gruplayarak tam kare formuna getirelim.
\( = (2x^2 + 12x + 18) - 23 \)
\( = 2(x^2 + 6x + 9) - 23 \)
\( = 2(x + 3)^2 - 23 \)
(b) seçeneği:
\( 3x^2 - 2x - 7 \)
İfadeyi tam kareye tamamlamak için ekleyip çıkarmamız gereken sabit terimi bulalım.
\( a = 3, \quad b = -2, \quad c = -7 \)
\( \dfrac{b^2}{4a} = \dfrac{(-2)^2}{4(3)} = \dfrac{1}{3} \)
\( 3x^2 - 2x \textcolor{red}{+ \dfrac{1}{3} - \dfrac{1}{3}} - 7 \)
İlk üç terimi gruplayarak tam kare formuna getirelim.
\( = \left( 3x^2 - 2x + \dfrac{1}{3} \right) - \dfrac{22}{3} \)
\( = 3\left( x^2 - \dfrac{2}{3}x + \dfrac{1}{9} \right) - \dfrac{22}{3} \)
\( = 3\left( x - \dfrac{1}{3} \right)^2 - \dfrac{22}{3} \)
(c) seçeneği:
\( 4x^2 - 32x - 61 \)
İfadeyi tam kareye tamamlamak için ekleyip çıkarmamız gereken sabit terimi bulalım.
\( a = 4, \quad b = -32, \quad c = -61 \)
\( \dfrac{b^2}{4a} = \dfrac{(-32)^2}{4(4)} = 64 \)
\( 4x^2 - 32x \textcolor{red}{+ 64 - 64} - 61 \)
İlk üç terimi gruplayarak tam kare formuna getirelim.
\( = (4x^2 - 32x + 64) - 125 \)
\( = 4(x^2 - 8x + 16) - 125 \)
\( = 4(x - 4)^2 - 125 \)
Aşağıdaki ikinci dereceden ifadeleri tam kareye tamamlayınız.
(a) \( -x^2 + 4x - 19 \)
(b) \( -2x^2 - 3x + 1 \)
(c) \( -5x^2 + 30x - 16 \)
Çözümü Göster(a) seçeneği:
\( -x^2 + 4x - 19 \)
İfadeyi tam kareye tamamlamak için ekleyip çıkarmamız gereken sabit terimi bulalım.
\( a = -1, \quad b = 4, \quad c = -19 \)
\( \dfrac{b^2}{4a} = \dfrac{4^2}{4(-1)} = -4 \)
\( -x^2 + 4x \textcolor{red}{- 4 + 4} - 19 \)
İlk üç terimi gruplayarak tam kare formuna getirelim.
\( = (-x^2 + 4x - 4) - 15 \)
\( = -(x^2 - 4x + 4) - 15 \)
\( = -(x - 2)^2 - 15 \)
(b) seçeneği:
\( -2x^2 - 3x + 1 \)
İfadeyi tam kareye tamamlamak için ekleyip çıkarmamız gereken sabit terimi bulalım.
\( a = -2, \quad b = -3, \quad c = 1 \)
\( \dfrac{b^2}{4a} = \dfrac{(-3)^2}{4(-2)} = -\dfrac{9}{8} \)
\( -2x^2 - 3x \textcolor{red}{- \dfrac{9}{8} + \dfrac{9}{8}} + 1 \)
İlk üç terimi gruplayarak tam kare formuna getirelim.
\( = \left( -2x^2 - 3x - \dfrac{9}{8} \right) + \dfrac{17}{8} \)
\( = -2\left( x^2 + \dfrac{3}{2}x + \dfrac{9}{16} \right) + \dfrac{17}{8} \)
\( = -2\left( x + \dfrac{3}{4} \right)^2 + \dfrac{17}{8} \)
(c) seçeneği:
\( -5x^2 + 30x - 16 \)
İfadeyi tam kareye tamamlamak için ekleyip çıkarmamız gereken sabit terimi bulalım.
\( a = -5, \quad b = 30, \quad c = -16 \)
\( \dfrac{b^2}{4a} = \dfrac{30^2}{4(-5)} = -45 \)
\( -5x^2 + 30x \textcolor{red}{- 45 + 45} - 16 \)
İlk üç terimi gruplayarak tam kare formuna getirelim.
\( = (-5x^2 + 30x - 45) + 29 \)
\( = -5(x^2 - 6x + 9) + 29 \)
\( = -5(x - 3)^2 - 29 \)
Tam kareye tamamlama yöntemi matematikte pek çok alanda sıklıkla kullanılır. Bu uygulama alanlarından (bizim de bu sitede kullandığımız) bazıları şunlardır.
İkinci Dereceden Denklemlerin Çözümü
İkinci dereceden bir denklemin reel ya da karmaşık sayı tüm kökleri tam kareye tamamlama yöntemi ile aşağıdaki adımlar takip edilerek bulunabilir.
- \( ax^2 + bx + c = 0 \) formundaki denklem \( a(x - r)^2 + k = 0 \) formuna dönüştürülür.
- Bu eşitlikte önce \( (x - r)^2 \) ifadesi yalnız bırakılır.
- Parantez karesinden kurtulmak için tarafların karekökü alınır. Bu adımda eşitliğin sağ tarafında pozitif ve negatif işaretli iki değer oluşur.
- Elde edilen eşitlikte \( x \) yalnız bırakıldığında denklemin iki ya da tek (çift katlı) kökü bulunur.
Üçüncü adımda tarafların karekökü alınırken eşitliğin sağ tarafı negatif ise denklemin karmaşık kökleri, aksi durumda reel kökleri vardır.
Tam kareye tamamlama yöntemi ile ikinci dereceden bir denklemin çözüm kümesini bulmayı bir örnek üzerinde gösterelim.
\( x^2 + 22x + 105 = 0 \) denkleminin çözüm kümesini tam kareye tamamlama yöntemiyle bulalım.
İfadeyi tam kareye tamamlamak için ekleyip çıkarmamız gereken sabit terimi bulalım.
\( a = 1, \quad b = 22, \quad c = 105 \)
\( \dfrac{b^2}{4a} = \dfrac{22^2}{4(1)} = 121 \)
\( x^2 + 22x \textcolor{red}{+ 121 - 121} + 105 = 0 \)
İlk üç terimi gruplayarak tam kare formuna getirelim.
\( (x^2 + 22x + 121) - 16 = 0 \)
\( (x + 11)^2 - 16 = 0 \)
Tam kare ifadeyi yalnız bırakalım.
\( (x + 11)^2 = 16 \)
Eşitliğin taraflarının karekökünü alalım.
\( x + 11 = \pm 4 \)
\( x = -11 \pm 4 \)
Çözüm kümesi: \( x \in \{ -15, -7 \} \)
Şimdi de irrasyonel kökleri olan bir denklem örneği verelim.
\( 2x^2 - 8x - 3 = 0 \) denkleminin çözüm kümesini tam kareye tamamlama yöntemiyle bulalım.
İfadeyi tam kareye tamamlamak için ekleyip çıkarmamız gereken sabit terimi bulalım.
\( a = 2, \quad b = -8, \quad c = -3 \)
\( \dfrac{b^2}{4a} = \dfrac{(-8)^2}{4(2)} = 8 \)
\( 2x^2 - 8x \textcolor{red}{+ 8 - 8} - 3 = 0 \)
İlk üç terimi gruplayarak tam kare formuna getirelim.
\( (2x^2 - 8x + 8) - 11 = 0 \)
\( 2(x^2 - 4x + 4) - 11 = 0 \)
\( 2(x - 2)^2 - 11 = 0 \)
Tam kare ifadeyi yalnız bırakalım.
\( 2(x - 2)^2 = 11 \)
\( (x - 2)^2 = \dfrac{11}{2} \)
Eşitliğin taraflarının karekökünü alalım.
\( x - 2 = \pm \sqrt{\dfrac{11}{2}} = \pm \dfrac{\sqrt{22}}{2} \)
\( x = 2 \pm \dfrac{\sqrt{22}}{2} \)
Çözüm kümesi: \( x \in \left\{ 2 - \dfrac{\sqrt{22}}{2}, 2 + \dfrac{\sqrt{22}}{2} \right\} \)
Aşağıdaki ikinci dereceden denklemlerin çözüm kümelerini tam kareye tamamlama yöntemiyle bulunuz.
(a) \( 3x^2 + 10x - 8 = 0 \)
(b) \( 6x^2 - 7x - 24 = 0 \)
(c) \( -2x^2 + 4x + 3 = 0 \)
Çözümü Göster(a) seçeneği:
\( 3x^2 + 10x - 8 = 0 \)
İfadeyi tam kareye tamamlamak için ekleyip çıkarmamız gereken sabit terimi bulalım.
\( a = 3, \quad b = 10, \quad c = -8 \)
\( \dfrac{b^2}{4a} = \dfrac{10^2}{4(3)} = \dfrac{25}{3} \)
\( 3x^2 + 10x \textcolor{red}{+ \dfrac{25}{3} - \dfrac{25}{3}} - 8 = 0 \)
İlk üç terimi gruplayarak tam kare formuna getirelim.
\( \left( 3x^2 + 10x + \dfrac{25}{3} \right) - \dfrac{49}{3} = 0 \)
\( 3\left( x^2 + \dfrac{10}{3}x + \dfrac{25}{9} \right) - \dfrac{49}{3} = 0 \)
\( 3\left( x + \dfrac{5}{3} \right)^2 - \dfrac{49}{3} = 0 \)
Tam kare ifadeyi yalnız bırakalım.
\( 3\left( x + \dfrac{5}{3} \right)^2 = \dfrac{49}{3} \)
\( \left( x + \dfrac{5}{3} \right)^2 = \dfrac{49}{9} \)
Eşitliğin taraflarının karekökünü alalım.
\( x + \dfrac{5}{3} = \pm \dfrac{7}{3} \)
\( x = -\dfrac{5}{3} \pm \dfrac{7}{3} \)
Çözüm kümesi: \( x \in \left\{ -4, \dfrac{2}{3} \right\} \)
(b) seçeneği:
\( 6x^2 - 7x - 24 = 0 \)
İfadeyi tam kareye tamamlamak için ekleyip çıkarmamız gereken sabit terimi bulalım.
\( a = 6, \quad b = -7, \quad c = -24 \)
\( \dfrac{b^2}{4a} = \dfrac{(-7)^2}{4(6)} = \dfrac{49}{24} \)
\( 6x^2 - 7x \textcolor{red}{+ \dfrac{49}{24} - \dfrac{49}{24}} - 24 = 0 \)
İlk üç terimi gruplayarak tam kare formuna getirelim.
\( \left( 6x^2 - 7x + \dfrac{49}{24} \right) - \dfrac{625}{24} = 0 \)
\( 6\left( x^2 - \dfrac{7}{6}x + \dfrac{49}{144} \right) - \dfrac{625}{24} = 0 \)
\( 6\left( x - \dfrac{7}{12} \right)^2 - \dfrac{625}{24} = 0 \)
Tam kare ifadeyi yalnız bırakalım.
\( 6\left( x - \dfrac{7}{12} \right)^2 = \dfrac{625}{24} \)
\( \left( x - \dfrac{7}{12} \right)^2 = \dfrac{625}{144} \)
Eşitliğin taraflarının karekökünü alalım.
\( x - \dfrac{7}{12} = \pm \dfrac{25}{12} \)
\( x = \dfrac{7}{12} \pm \dfrac{25}{12} \)
Çözüm kümesi: \( x \in \left\{ -\dfrac{3}{2}, \dfrac{8}{3} \right\} \)
(c) seçeneği:
\( -2x^2 + 4x + 3 = 0 \)
İfadeyi tam kareye tamamlamak için ekleyip çıkarmamız gereken sabit terimi bulalım.
\( a = -2, \quad b = 4, \quad c = 3 \)
\( \dfrac{b^2}{4a} = \dfrac{4^2}{4(-2)} = -2 \)
\( -2x^2 + 4x \textcolor{red}{- 2 + 2} + 3 = 0 \)
İlk üç terimi gruplayarak tam kare formuna getirelim.
\( (-2x^2 + 4x - 2) + 5 = 0 \)
\( -2(x^2 - 2x + 1) + 5 = 0 \)
\( -2(x - 1)^2 + 5 = 0 \)
Tam kare ifadeyi yalnız bırakalım.
\( -2(x - 1)^2 = -5 \)
\( (x - 1)^2 = \dfrac{5}{2} \)
Eşitliğin taraflarının karekökünü alalım.
\( x - 1 = \pm \sqrt{\dfrac{5}{2}} \)
\( x = 1 \pm \dfrac{\sqrt{5}}{\sqrt{2}} = 1 \pm \dfrac{\sqrt{10}}{2} \)
Çözüm kümesi: \( x \in \left\{ 1 - \dfrac{\sqrt{10}}{2}, 1 + \dfrac{\sqrt{10}}{2} \right\} \)
Parabolde Tepe Noktası Bulma
Tepe noktası \( T(r, k) \) olan bir parabolün denklemi \( y = a(x - r)^2 + k \) şeklinde yazılabilir. Buna göre, denklemi \( y = ax^2 + bx + c \) olan bir parabol tam kareye tamamlandığında elde edilen denklem parabolün tepe noktasının koordinatlarını verir.
\( y = 4x^2 - 16x + 13 \) parabolünün tepe noktasını tam kareye tamamlama yöntemiyle bulalım.
İfadeyi tam kareye tamamlamak için ekleyip çıkarmamız gereken sabit terimi bulalım.
\( a = 4, \quad b = -16, \quad c = 13 \)
\( \dfrac{b^2}{4a} = \dfrac{(-16)^2}{4(4)} = 16 \)
\( y = 4x^2 - 16x \textcolor{red}{+ 16 - 16} + 13 \)
İlk üç terimi gruplayarak tam kare formuna getirelim.
\( = (4x^2 - 16x + 16) - 3 \)
\( = 4(x^2 - 4x + 4) - 3 \)
\( = 4(x - 2)^2 - 3 \)
Buna göre parabolün tepe noktası \( T(r, k) = T(2, -3) \) noktasıdır.
\( y = -2x^2 + 12x + 11 \) parabolünün tepe noktasını tam kareye tamamlama yöntemiyle bulunuz.
Çözümü Gösterİfadeyi tam kareye tamamlamak için ekleyip çıkarmamız gereken sabit terimi bulalım.
\( a = -2, \quad b = 12, \quad c = 11 \)
\( \dfrac{b^2}{4a} = \dfrac{12^2}{4(-2)} = -18 \)
\( y = -2x^2 + 12x \textcolor{red}{- 18 + 18} + 11 \)
İlk üç terimi gruplayarak tam kare formuna getirelim.
\( = (-2x^2 + 12x - 18) + 29 \)
\( = -2(x^2 - 6x + 9) + 29 \)
\( = -2(x - 3)^2 + 29 \)
Buna göre parabolün tepe noktası \( T(r, k) = T(3, 29) \) noktasıdır.
Minimum/Maksimum Değer Bulma
Parabol konusunda gördüğümüz üzere, pozitif başkatsayılı bir parabol en küçük değerini, negatif başkatsayılı bir parabol ise en büyük değerini tepe noktasında alır. Buna göre, \( y = a(x - r)^2 + k \) formundaki denklemi bilinen (dolayısıyla tepe noktasının koordinatları \( T(r, k) \) olan) bir parabol en küçük/en büyük değerini \( x = r \) apsisli noktada alır ve bu değer \( f(r) = k \) olur.
\( f(x) = 3x^2 + 15x + 23 \) fonksiyonunun aldığı en küçük değeri tam kareye tamamlama yöntemiyle bulalım.
İfadeyi tam kareye tamamlamak için ekleyip çıkarmamız gereken sabit terimi bulalım.
\( a = 3, \quad b = 15, \quad c = 23 \)
\( \dfrac{b^2}{4a} = \dfrac{15^2}{4(3)} = \dfrac{75}{4} \)
\( f(x) = 3x^2 + 15x \textcolor{red}{+ \dfrac{75}{4} - \dfrac{75}{4}} + 23 \)
İlk üç terimi gruplayarak tam kare formuna getirelim.
\( = \left( 3x^2 + 15x + \dfrac{75}{4} \right) + \dfrac{17}{4} \)
\( = 3\left( x^2 + 5x + \dfrac{25}{4} \right) + \dfrac{17}{4} \)
\( = 3\left( x + \dfrac{5}{2} \right)^2 + \dfrac{17}{4} \)
Parantez karesi ifadesi hiçbir \( x \) için negatif olamayacağı için en küçük değerini \( x = -\frac{5}{2} \) noktasında sıfır olarak alır.
Buna göre fonksiyonun aldığı en küçük değer bu noktada aldığı \( f(-\frac{5}{2}) = \frac{17}{4} \) değeridir.
Benzer bir örneği negatif başkatsayılı bir parabolün en büyük değeri için yapalım.
\( f(x) = -2x^2 - 16x + 9 \) fonksiyonunun aldığı en büyük değeri tam kareye tamamlama yöntemiyle bulalım.
İfadeyi tam kareye tamamlamak için ekleyip çıkarmamız gereken sabit terimi bulalım.
\( a = -2, \quad b = -16, \quad c = 9 \)
\( \dfrac{b^2}{4a} = \dfrac{(-16)^2}{4(-2)} = -32 \)
\( f(x) = -2x^2 - 16x \textcolor{red}{- 32 + 32} + 9 \)
İlk üç terimi gruplayarak tam kare formuna getirelim.
\( = (-2x^2 - 16x - 32) + 41 \)
\( = -2(x^2 + 8x + 16) + 41 \)
\( = -2(x + 4)^2 + 41 \)
Parantez karesi ifadesi hiçbir \( x \) için negatif olamayacağı için en küçük değerini \( x = -4 \) noktasında sıfır olarak alır.
Buna göre fonksiyonun aldığı en büyük değer bu noktada aldığı \( f(-4) = 41 \) değeridir.
\( f(x) = 4x^2 - 24x - 17 \) fonksiyonunun aldığı en küçük değeri tam kareye tamamlama yöntemiyle bulunuz.
Çözümü Gösterİfadeyi tam kareye tamamlamak için ekleyip çıkarmamız gereken sabit terimi bulalım.
\( a = 4, \quad b = -24, \quad c = -17 \)
\( \dfrac{b^2}{4a} = \dfrac{(-24)^2}{4(4)} = 36 \)
\( f(x) = 4x^2 - 24x \textcolor{red}{+ 36 - 36} - 17 \)
İlk üç terimi gruplayarak tam kare formuna getirelim.
\( = (4x^2 - 24x + 36) - 53 \)
\( = 4(x^2 - 6x + 9) - 53 \)
\( = 4(x - 3)^2 - 53 \)
Parantez karesi ifadesi hiçbir \( x \) için negatif olamayacağı için en küçük değerini \( x = 3 \) noktasında sıfır olarak alır.
Buna göre fonksiyonun aldığı en küçük değer bu noktada aldığı \( f(3) = -53 \) değeridir.
\( f(x) = -3x^2 + 15x - 11 \) fonksiyonunun aldığı en büyük değeri tam kareye tamamlama yöntemiyle bulunuz.
Çözümü Gösterİfadeyi tam kareye tamamlamak için ekleyip çıkarmamız gereken sabit terimi bulalım.
\( a = -3, \quad b = 15, \quad c = -11 \)
\( \dfrac{b^2}{4a} = \dfrac{15^2}{4(-3)} = -\dfrac{75}{4} \)
\( f(x) = -3x^2 + 15x \textcolor{red}{- \dfrac{75}{4} + \dfrac{75}{4}} - 11 \)
İlk üç terimi gruplayarak tam kare formuna getirelim.
\( = \left( -3x^2 + 15x - \dfrac{75}{4} \right) + \dfrac{31}{4} \)
\( = -3\left( x^2 - 5x + \dfrac{25}{4} \right) + \dfrac{31}{4} \)
\( = -3\left(x - \dfrac{5}{2} \right)^2 + \dfrac{31}{4} \)
Parantez karesi ifadesi hiçbir \( x \) için negatif olamayacağı için en küçük değerini \( x = \frac{5}{2} \) noktasında sıfır olarak alır.
Buna göre fonksiyonun aldığı en büyük değer bu noktada aldığı \( f(\frac{5}{2}) = \frac{31}{4} \) değeridir.
İntegral Alma
Tam kareye tamamlama yöntemi aşağıdaki formdaki ifadelerin integralini almakta da kullanılır.
- \( \frac{1}{ax^2 + bx + c} \): Bu formdaki bir ifade, paydası tam kareye tamamlandığında integrali ters tanjant fonksiyonu olan bir forma gelir. Bu yöntem özellikle paydanın çarpanlarına ayrılmadığı (deltasının negatif olduğu) durumlarda kullanılır.
- \( \frac{1}{\sqrt{ax^2 + bx + c}} \): Bu formdaki bir ifade, paydası tam kareye tamamlandığında trigonometrik değişken değiştirme yöntemi bölümünde detaylı incelediğimiz integrali alınabilir standart formlardan birine gelir.
\( \displaystyle\int {\dfrac{dx}{x^2 - 6x + 13}} \) integralinin sonucunu bulalım.
Yukarıda gördüğümüz yöntemle paydadaki ifadeyi tam kareye tamamlayalım.
\( \displaystyle\int {\dfrac{dx}{x^2 - 6x + 13}} = \displaystyle\int {\dfrac{dx}{(x - 3)^2 + 2^2}} \)
Paydadaki ifadenin integrali ters tanjant fonksiyonudur.
\( \displaystyle\int {\dfrac{dx}{a^2 + x^2}} = \dfrac{1}{a}\arctan{\frac{x}{a}} + C \)
\( = \dfrac{1}{2}\arctan{\dfrac{x - 3}{2}} + C \)
Laplace Dönüşümü
Tam kareye tamamlama yöntemi, paydası çarpanlarına ayrılmayan (deltası negatif olan) rasyonel fonksiyonların ters Laplace dönüşümünde de kullanılır.
\( F(s) = \dfrac{1}{s^2 + 4s + 13} \) fonksiyonunun ters Laplace dönüşümünü bulalım.
Yukarıda gördüğümüz yöntemle paydadaki ifadeyi tam kareye tamamlayalım.
\( \mathcal{L}^{-1}\left\{ \dfrac{1}{s^2 + 4s + 13} \right\} = \mathcal{L}^{-1}\left\{ \dfrac{1}{(s + 2)^2 + 9} \right\} \)
\( = \mathcal{L}^{-1}\left\{ \dfrac{1}{(s + 2)^2 + 3^2} \right\} \)
\( = \dfrac{1}{3}e^{-2t}\sin(3t) \)