Dörtgenlere Giriş
Dört kenarı ve dört köşesi olan çokgene dörtgen denir.

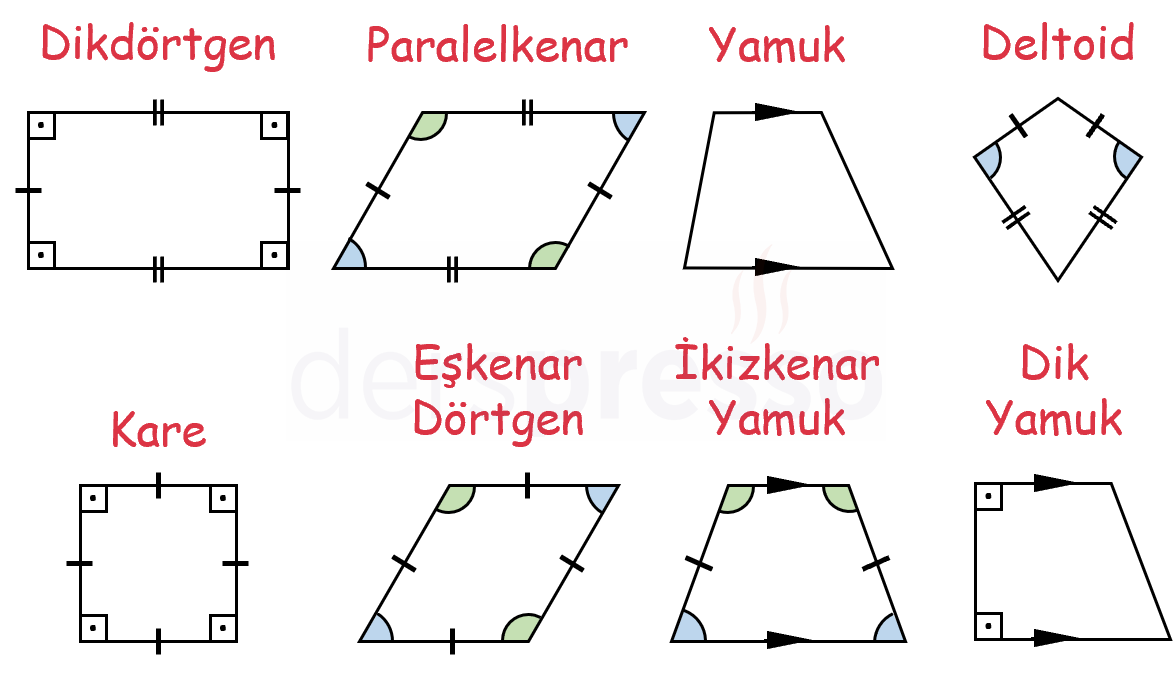
Dörtgenler kenar ve açı özelliklerine göre farklı şekillerde ve isimlerde olabilir. Bu bölümde aşağıdaki basit ve konveks dörtgen çeşitlerini inceleyeceğiz.
Bu dörtgenler arasında aşağıdaki şekilde bir hiyerarşik ilişki kurulabilir. Buna göre, hiyerarşide daha altta bulunan bir dörtgen ok ile bağlı olduğu üstteki bir dörtgenin tüm özelliklerini taşır.
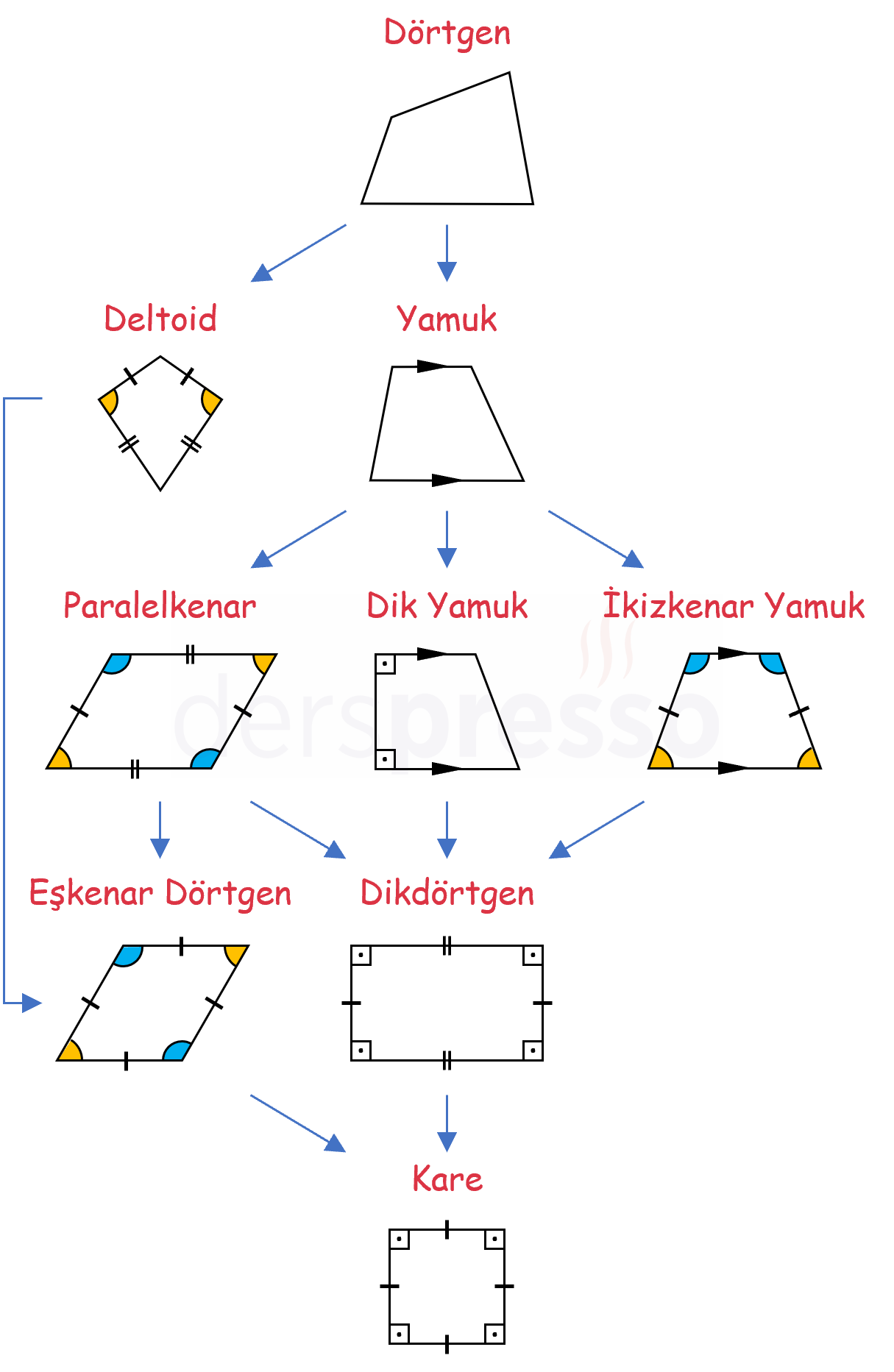
Bu hiyerarşik ilişkiye göre, aşağıdaki dörtgenler belirtilen dörtgenlerin özel birer durumu olarak düşünülebilir.
- Paralelkenar, eşkenar dörtgen, dikdörtgen ve kare özel birer yamuk
- İkizkenar yamuk ve dik yamuk özel birer yamuk
- Eşkenar dörtgen, dikdörtgen ve kare özel birer paralelkenar
- Eşkenar dörtgen ve kare özel birer deltoid
- Kare özel bir eşkenar dörtgen ve dikdörtgen
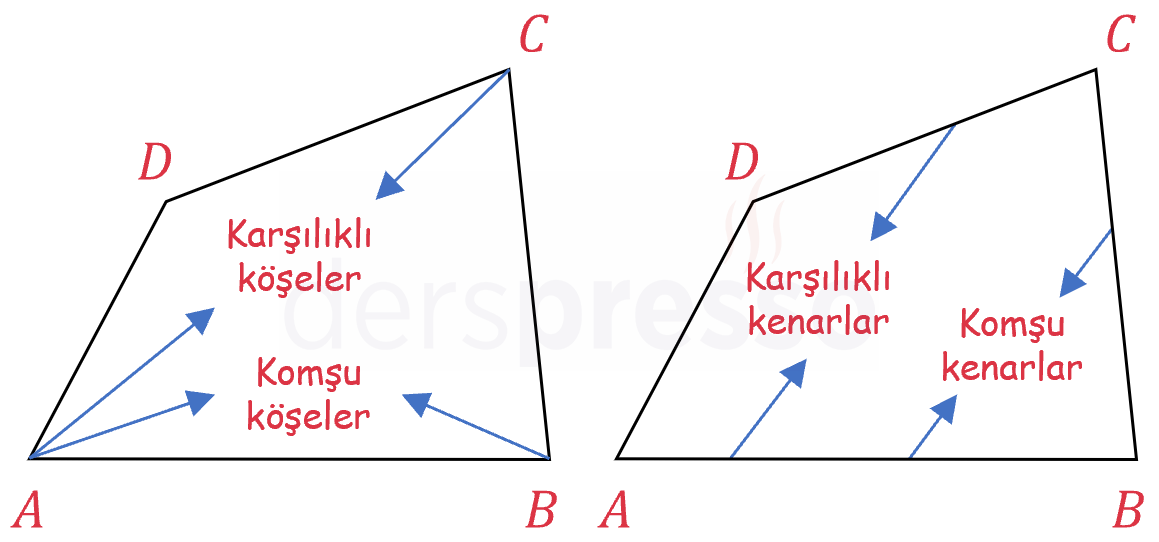
Bir dörtgende aynı kenarın farklı uçlarında bulunan iki köşeye komşu köşe ya da ardışık köşe denir. Komşu olmayan köşelere karşılıklı köşe denir.
Bir dörtgende birer köşesi ortak olan iki kenara komşu kenar ya da ardışık kenar denir. Komşu olmayan kenarlara karşılıklı kenar denir.
Dörtgenin Kenar ve Köşegen Özellikleri
Aşağıdaki şekilde biri konveks diğeri konkav iki dörtgenin köşegenleri (\( p \) ve \( q \)) gösterilmiştir. Buna göre, konveks dörtgenin iki köşegeni de şeklin iç bölgesindeyken konkav dörtgenin bir köşegeni şeklin dış bölgesinde kalır.
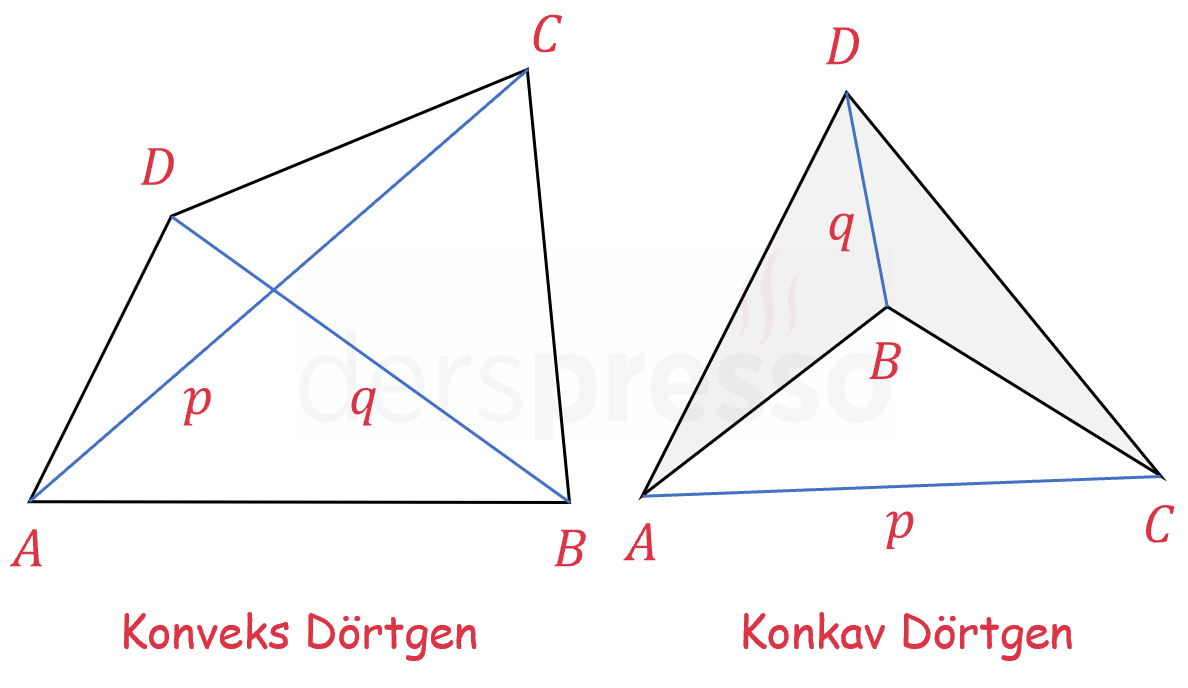
Köşegenler: \( [AC], [BD] \)
Köşegenleri dik kesişen konveks ya da konkav dörtgenlerin karşılıklı kenar uzunluklarının kareleri toplamı birbirine eşittir.
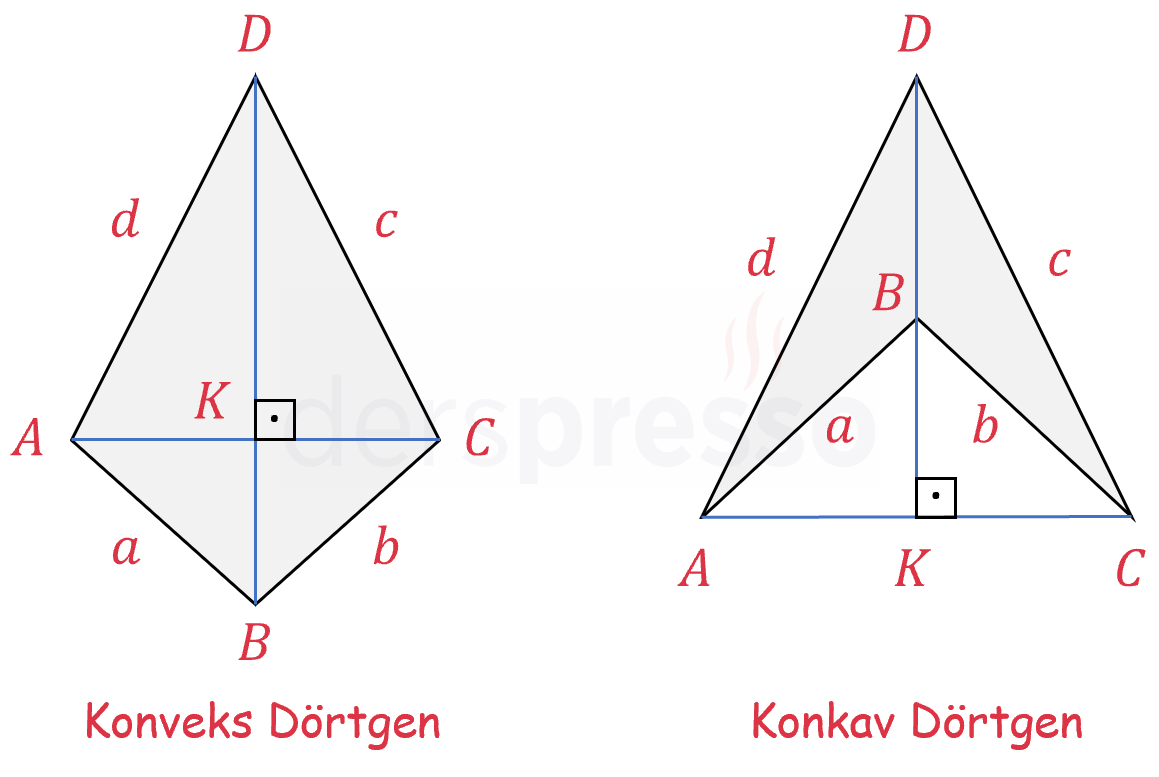
\( a^2 + c^2 = b^2 + d^2 \)
İSPATI GÖSTER
Aşağıdaki yöntem yukarıdaki konveks ve konkav dörtgenlerin ikisi için de geçerlidir.
Köşegenlerin oluşturduğu dört üçgene Pisagor teoremi uygulayalım.
\( a^2 = \abs{AK}^2 + \abs{BK}^2 \)
\( b^2 = \abs{BK}^2 + \abs{CK}^2 \)
\( c^2 = \abs{CK}^2 + \abs{DK}^2 \)
\( d^2 = \abs{DK}^2 + \abs{AK}^2 \)
1. ve 3. satırları ve 2. ve 4. satırları ayrı ayrı taraf tarafa toplayalım.
\( a^2 + c^2 = \abs{AK}^2 + \abs{BK}^2 + \abs{CK}^2 + \abs{DK}^2 \)
\( b^2 + d^2 = \abs{BK}^2 + \abs{CK}^2 + \abs{DK}^2 + \abs{AK}^2 \)
İki eşitliğin sağ tarafları aynı olduğu için, sol tarafları birbirine eşittir.
\( a^2 + c^2 = b^2 + d^2 \)
Varignon Paralelkenarı
Herhangi bir dörtgenin kenar orta noktalarının birleştirilmesiyle oluşan dörtgen bir paralelkenardır. Bu paralelkenara Varignon paralelkenarı denir.

\( ABCD \) dörtgeninin kenarlarının orta noktalarını birleştiren \( KLMN \) dörtgenini çizelim.
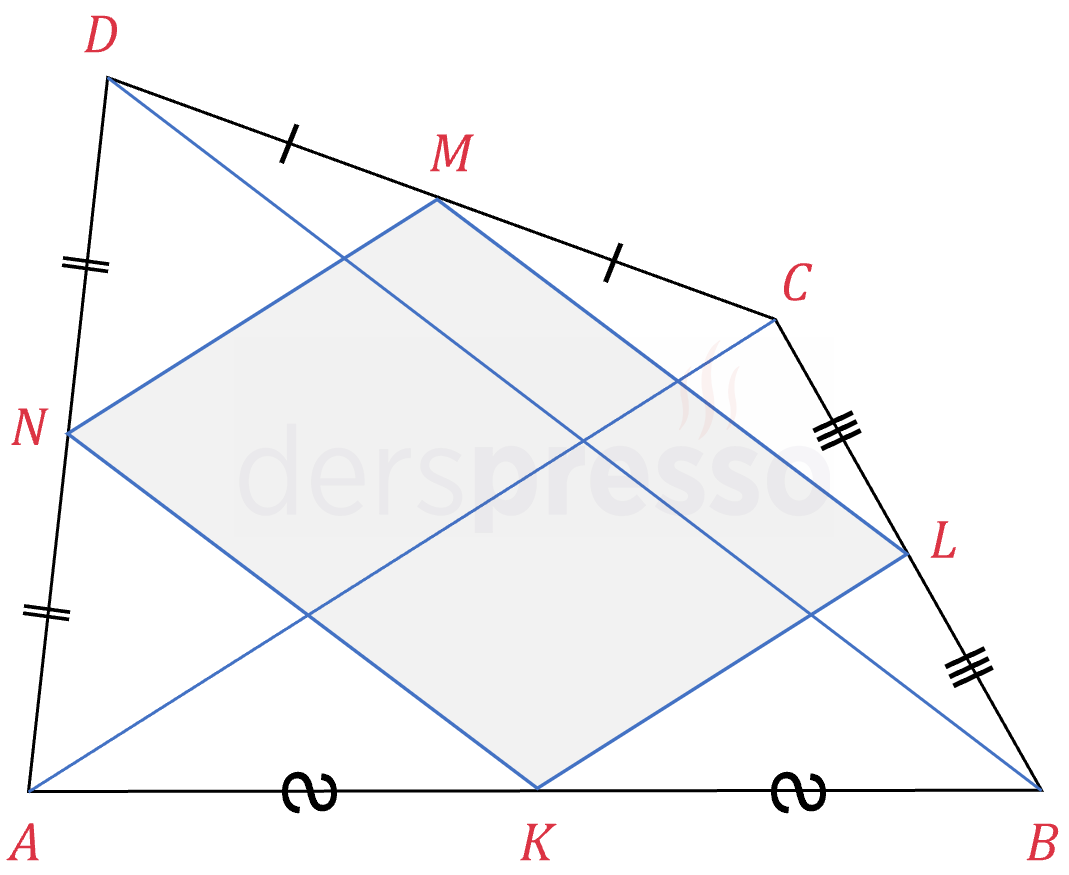
\( [KL] \) doğru parçası \( ABC \) üçgeninin iki kenarının orta noktalarını birleştirdiği için üçgenin orta tabanıdır, dolayısıyla orta taban teoremine göre üçgenin \( [AC] \) kenarına paraleldir ve uzunluğu \( [AC] \) kenar uzunluğunun yarısına eşittir.
\( [KL] \parallel [AC] \)
\( \abs{KL} = \frac{1}{2} \abs{AC} \)
\( [LM] \) doğru parçası \( BCD \) üçgeninin iki kenarının orta noktalarını birleştirdiği için üçgenin orta tabanıdır, dolayısıyla orta taban teoremine göre üçgenin \( [BD] \) kenarına paraleldir ve uzunluğu \( [BD] \) kenar uzunluğunun yarısına eşittir.
\( [LM] \parallel [BD] \)
\( \abs{LM} = \frac{1}{2} \abs{BD} \)
\( [NM] \) doğru parçası \( ACD \) üçgeninin iki kenarının orta noktalarını birleştirdiği için üçgenin orta tabanıdır, dolayısıyla orta taban teoremine göre üçgenin \( [AC] \) kenarına paraleldir ve uzunluğu \( [AC] \) kenar uzunluğunun yarısına eşittir.
\( [NM] \parallel [AC] \)
\( \abs{NM} = \frac{1}{2} \abs{AC} \)
\( [KN] \) doğru parçası \( ABD \) üçgeninin iki kenarının orta noktalarını birleştirdiği için üçgenin orta tabanıdır, dolayısıyla orta taban teoremine göre üçgenin \( [BD] \) kenarına paraleldir ve uzunluğu \( [BD] \) kenar uzunluğunun yarısına eşittir.
\( [KN] \parallel [BD] \)
\( \abs{KN} = \frac{1}{2} \abs{BD} \)
İki doğru parçası ayrı ayrı üçüncü bir doğru parçasına paralel ise bu iki doğru parçası birbirine paraleldir.
\( [KL] \parallel [AC] \) ve \( [NM] \parallel [AC] \) ise \( [KL] \parallel [NM] \) olur.
\( [LM] \parallel [BD] \) ve \( [KN] \parallel [BD] \) ise \( [LM] \parallel [KN] \) olur.
Buna göre \( ABCD \) dörtgeninin kenarlarının orta noktalarını birleştiren \( KLMN \) dörtgeninde karşılıklı kenarlar birbirine paraleldir, dolayısıyla \( KLMN \) dörtgeni bir paralelkenardır.
Aşağıdaki koşulların sağlanması durumunda, oluşan bu paralelkenar belirtilen tipte olur.
- \( ABCD \) dörtgeni bir ikizkenar yamuk ya da dikdörtgen ise köşegenler eşit uzunlukta olur ve \( KLMN \) paralelkenarı bir eşkenar dörtgen olur.
- \( ABCD \) dörtgeni bir deltoid ya da eşkenar dörtgen ise köşegenler birbirine dik olur ve \( KLMN \) paralelkenarı bir dikdörtgen olur.
- \( ABCD \) dörtgeni bir kare ise köşegenler eşit uzunlukta ve birbirine dik olur ve \( KLMN \) paralelkenarı bir kare olur.
Varignon paralelkenarının bazı özellikleri aşağıdaki gibidir.
Paralelkenarın karşılıklı kenarları dörtgenin bir köşegenine paraleldir. Bu kuralın ispatını yukarıda Varignon dörtgeninin bir paralelkenar olduğunu gösterirken yapmıştık.
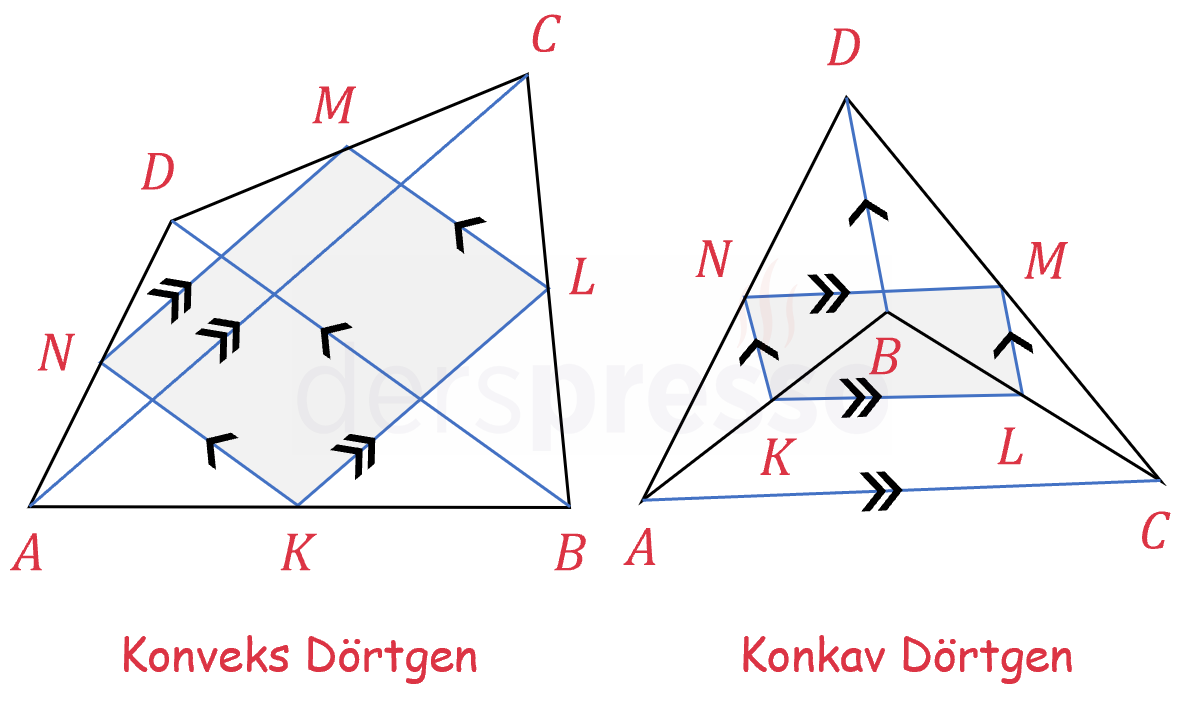
\( [KL] \parallel [NM] \parallel [AC] \)
\( [LM] \parallel [KN] \parallel [BD] \)
Paralelkenarın her kenarı paralel olduğu köşegenin oluşturduğu üçgenin orta tabanıdır, dolayısıyla uzunluğu köşegen uzunluğunun yarısıdır. Bu kuralın ispatını da yukarıda Varignon dörtgeninin bir paralelkenar olduğunu gösterirken yapmıştık.
\( \abs{KL} = \abs{NM} = \frac{1}{2} \abs{AC} \)
\( \abs{LM} = \abs{KN} = \frac{1}{2} \abs{BD} \)
Basit (karmaşık olmayan) dörtgenlerde, paralelkenarın alanı dörtgenin alanının yarısıdır.
\( A(KLMN) = \frac{1}{2} A(ABCD) \)
İSPATI GÖSTER
\( ABCD \) dörtgeninin kenarlarının orta noktalarını birleştiren \( KLMN \) dörtgenini çizelim.

\( KLMN \) dörtgeninin alanını bulmak için \( ABCD \) dörtgeninin alanından 4 üçgenin alanını çıkaralım.
\( A(KLMN) = A(ABCD) - A(AKN) - A(BLK) - A(CML) - A(DNM) \)
Üçgenler başlığı altındaki orta taban konusunda gördüğümüz üzere, bir üçgenin orta tabanının üstünde kalan alan üçgenin alanının dörtte birine eşittir.
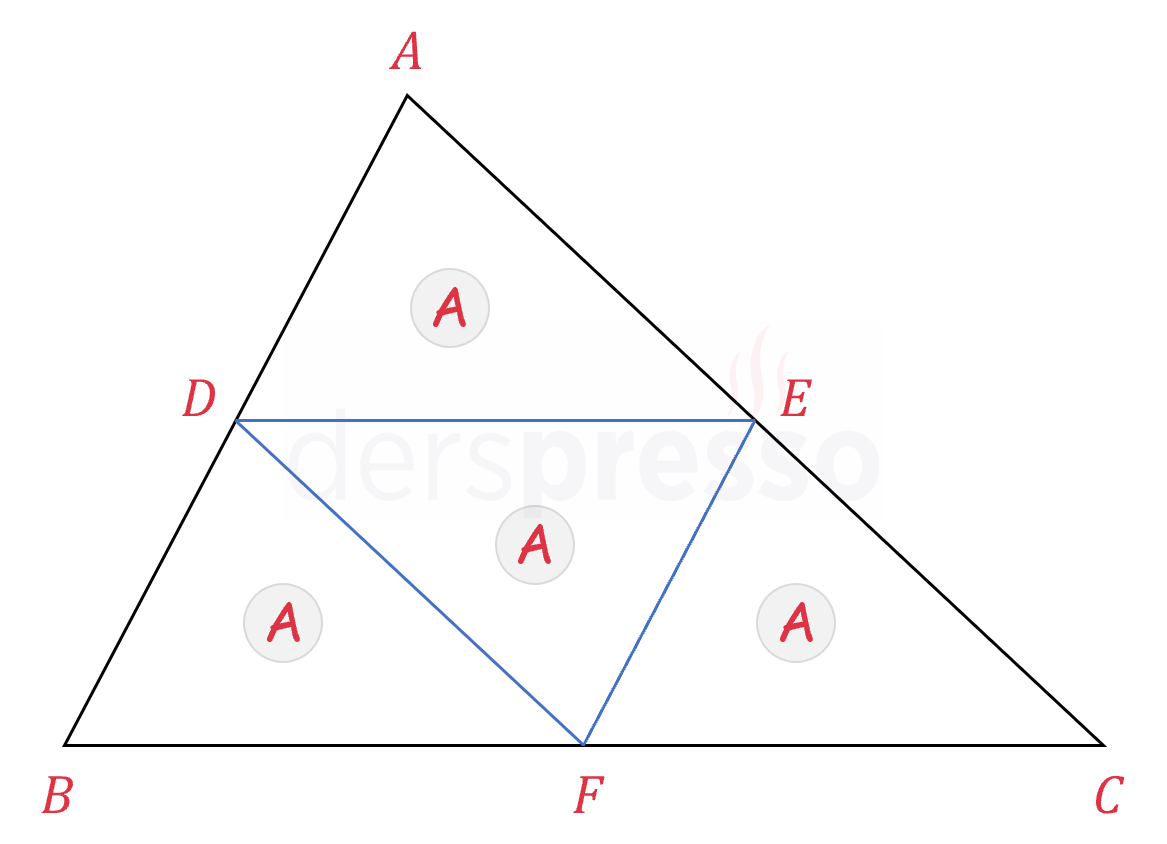
Buna göre yukarıdaki eşitlikteki her bir üçgenin alanını, o üçgenin tabanının orta tabanı olduğu büyük üçgenin alanı cinsinden yazalım.
\( = A(ABCD) - \frac{1}{4} A(ABD) - \frac{1}{4} A(BCA) - \frac{1}{4} A(CDB) - \frac{1}{4} A(DAC) \)
\( = A(ABCD) - \frac{1}{4}(A(ABD) + A(BCA) + A(CDB) + A(DAC)) \)
\( ABD \) ve \( CDB \) üçgenlerinin alanları ile \( BCA \) ve \( DAC \) üçgenlerinin alanlarının toplamı ayrı ayrı \( ABCD \) dörtgeninin alanını verir.
\( = A(ABCD) - \frac{1}{4}(A(ABCD) + A(ABCD)) \)
\( = \frac{1}{2} A(ABCD) \)
Paralelkenarın çevresi dörtgenin köşegen uzunluklarının toplamına eşittir.
\( \text{Ç}(KLMN) = \abs{AC} + \abs{BD} \)
İSPATI GÖSTER
\( ABCD \) dörtgeninin kenarlarının orta noktalarını birleştiren \( KLMN \) dörtgenini çizelim.

Paralelkenarın çevre uzunluk formülünü yazalım.
\( \text{Ç}(KLMN) = \abs{KL} + \abs{LM} + \abs{MN} + \abs{NK} \)
Yukarıda ispatıyla birlikte gösterdiğimiz üzere, paralelkenarın her kenarı paralel olduğu köşegenin oluşturduğu üçgenin orta tabanıdır, dolayısıyla uzunluğu köşegen uzunluğunun yarısıdır.
Örnek vermek gerekirse, paralelkenarın \( [KL] \) kenarı \( ABC \) üçgeninin orta tabanıdır ve uzunluğu \( [AC] \) köşegen uzunluğunun yarısıdır. Aynı durum paralelkenarın tüm kenarları için geçerlidir.
\( = \dfrac{\abs{AC}}{2} + \dfrac{\abs{BD}}{2} + \dfrac{\abs{AC}}{2} + \dfrac{\abs{BD}}{2} \)
\( = \abs{AC} + \abs{BD} \)
Paralelkenarın dışında kalan 4 üçgenden karşılıklı olanların alanları toplamı birbirine eşittir.
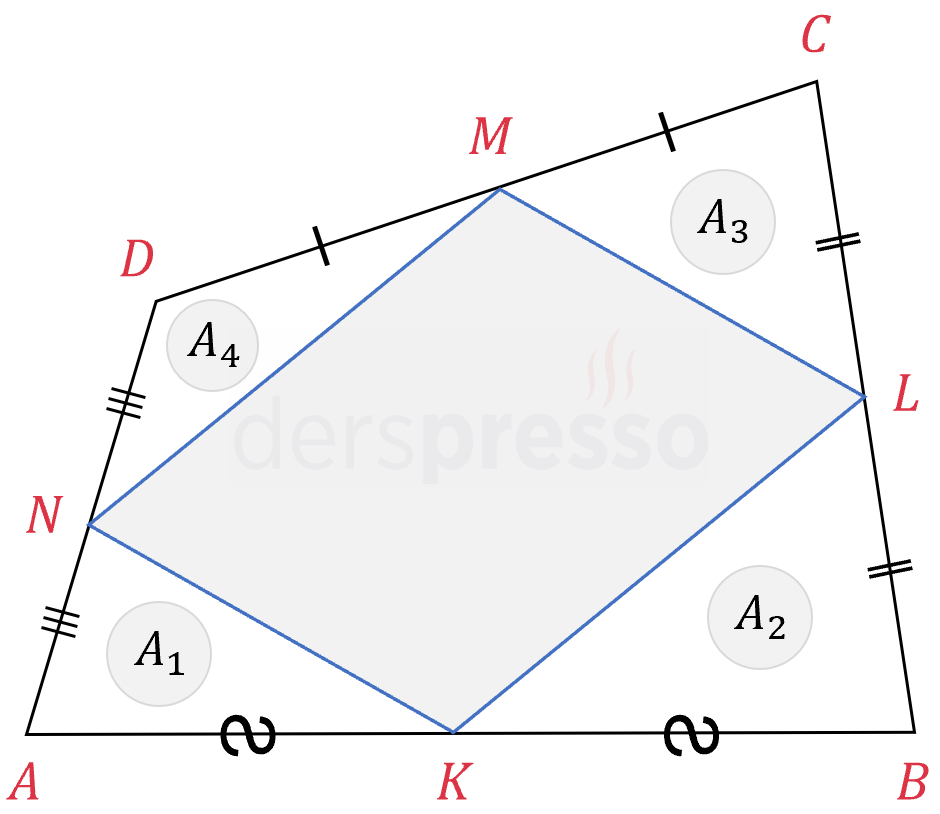
\( A_1 + A_3 = A_2 + A_4 = \frac{1}{4} A(ABCD) \)
İSPATI GÖSTER
\( ABCD \) dörtgeninin köşegenlerini çizelim.
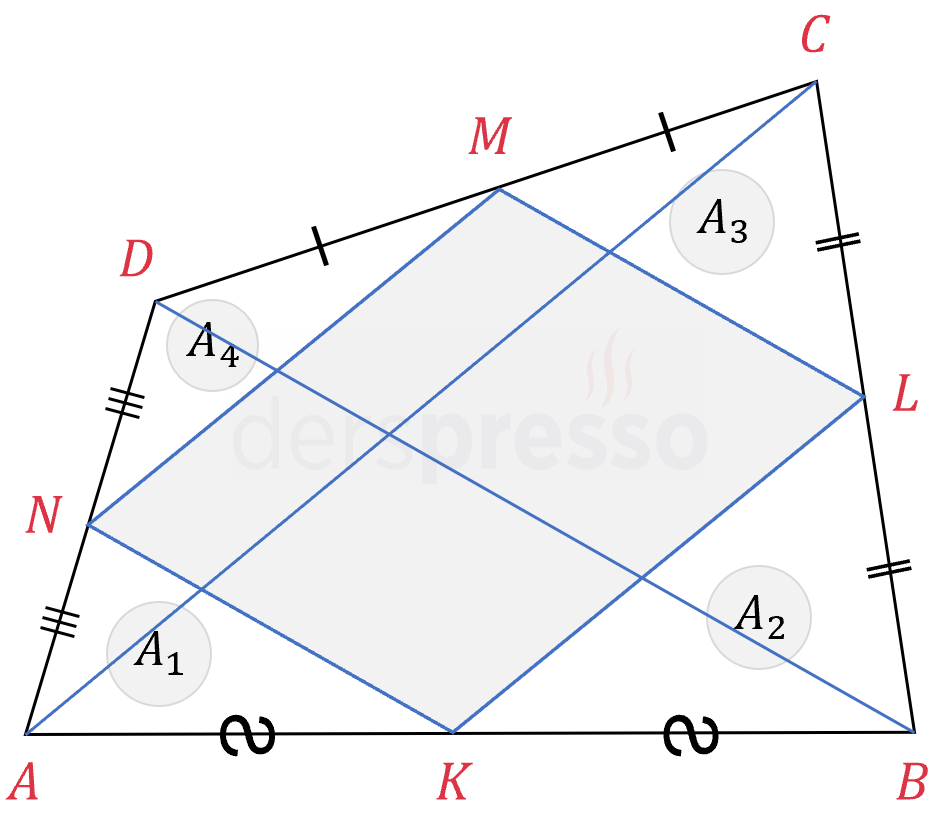
\( A_1 = A(NAK) \)
\( A_2 = A(KBL) \)
\( A_3 = A(LCM) \)
\( A_4 = A(MDN) \)
Yukarıda ispatıyla birlikte gösterdiğimiz üzere; \( [NK] \) kenarı \( DAB \) üçgeninin, \( [KL] \) kenarı \( ABC \) üçgeninin, \( [LM] \) kenarı \( BCD \) üçgeninin, \( [MN] \) kenarı da \( CDA \) üçgeninin orta tabanıdır.
Üçgenler başlığı altındaki orta taban konusunda gördüğümüz üzere, bir üçgenin orta tabanının üstünde kalan alan üçgenin alanının dörtte birine eşittir.

Buna göre her bir üçgenin alanını, o üçgenin tabanının orta tabanı olduğu büyük üçgenin alanı cinsinden yazalım.
\( A_1 = A(NAK) = \frac{1}{4} A(DAB) \)
\( A_2 = A(KBL) = \frac{1}{4} A(ABC) \)
\( A_3 = A(LCM) = \frac{1}{4} A(BCD) \)
\( A_4 = A(MDN) = \frac{1}{4} A(CDA) \)
\( DAB \) ve \( BCD \) üçgenleri ile \( ABC \) ve \( CDA \) üçgenlerinin alanları toplamı ayrı ayrı \( ABCD \) dörtgeninin alanına eşittir.
\( A(DAB) + A(BCD) = A(ABC) + A(CDA) = A(ABCD) \)
Eşitlikteki üçgenlerin alanlarını \( A_i \) cinsinden yazalım.
\( 4A_1 + 4A_3 = 4A_2 + 4A_4 = A(ABCD) \)
Eşitliğin taraflarını 4'e bölelim.
\( A_1 + A_3 = A_2 + A_4 = \frac{1}{4} A(ABCD) \)
Dörtgenin Açı Özellikleri

Dörtgenin iç açıları toplamı \( 360° \)'dir.
\( x + y + z + t = 360° \)
İSPATI GÖSTER
Çokgenler bölümünde gördüğümüz üzere, kenar sayısı \( n \) olan çokgenin iç açıları toplamı aşağıdaki formülle bulunur.
Çokgenlerin iç açıları toplamı: \( (n - 2) \cdot 180° \)
Dörtgenin iç açıları toplamını bulmak için \( n = 4 \) yazalım.
Dörtgenin iç açıları toplamı: \( (4 - 2) \cdot 180° = 360° \)
Tüm çokgenlerde olduğu gibi, dörtgenin dış açıları toplamı \( 360° \)'dir.
\( x' + y' + z' + t' = 360° \)
İSPATI GÖSTER
Bir köşenin iç + dış açıları toplamı \( = 180° \)
Dörtgenin tüm köşelerinin iç + dış açılar toplamı \( = 4 \cdot 180° = 720° \)
Dörtgenin tüm köşelerinin iç açılar toplamı \( = 360° \)
Dörtgenin tüm köşelerinin dış açılar toplamı \( = 720° - 360° = 360° \)
Komşu iki köşenin iç açıortaylarının kesişmesiyle oluşan açının ölçüsü aşağıdaki formülle bulunur.
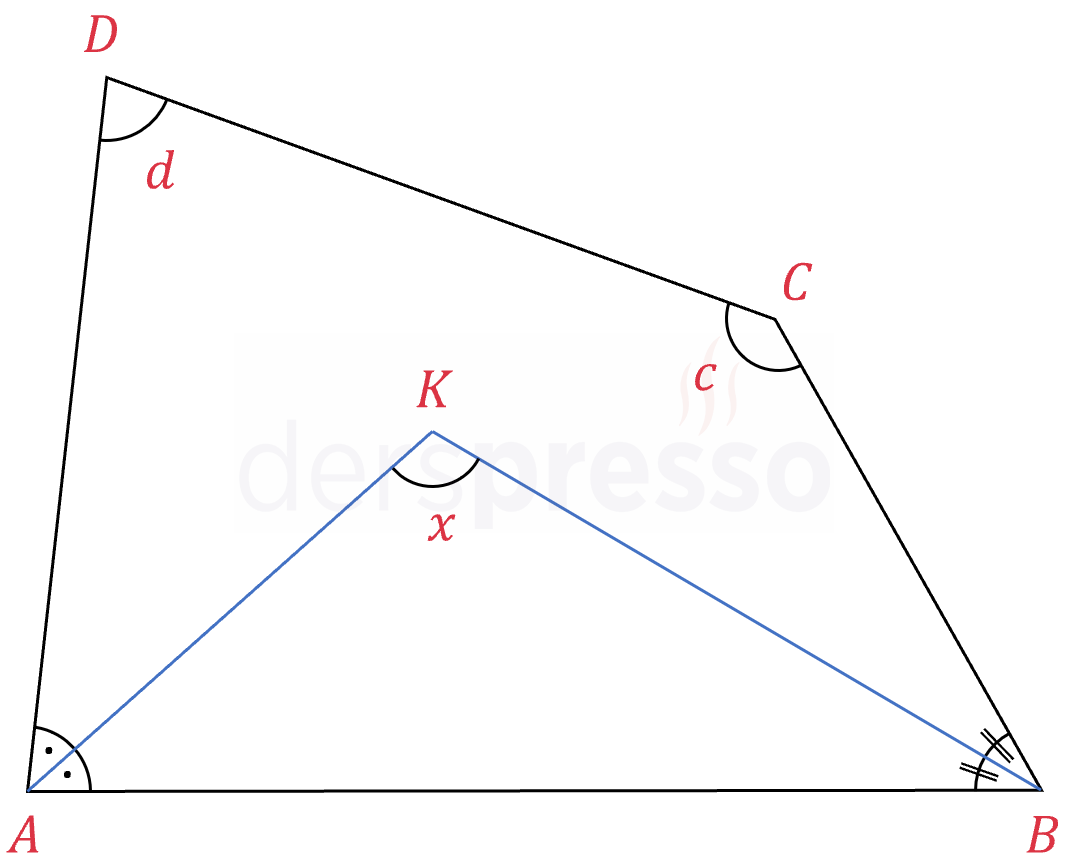
\( x = \dfrac{c + d}{2} \)
İSPATI GÖSTER
\( A \) köşesinin açı ölçüsüne \( a \), \( B \) köşesinin açı ölçüsüne \( b \) diyelim.
\( m(\widehat{DAK}) = m(\widehat{KAB}) = \dfrac{a}{2} \)
\( m(\widehat{ABK}) = m(\widehat{KBC}) = \dfrac{b}{2} \)
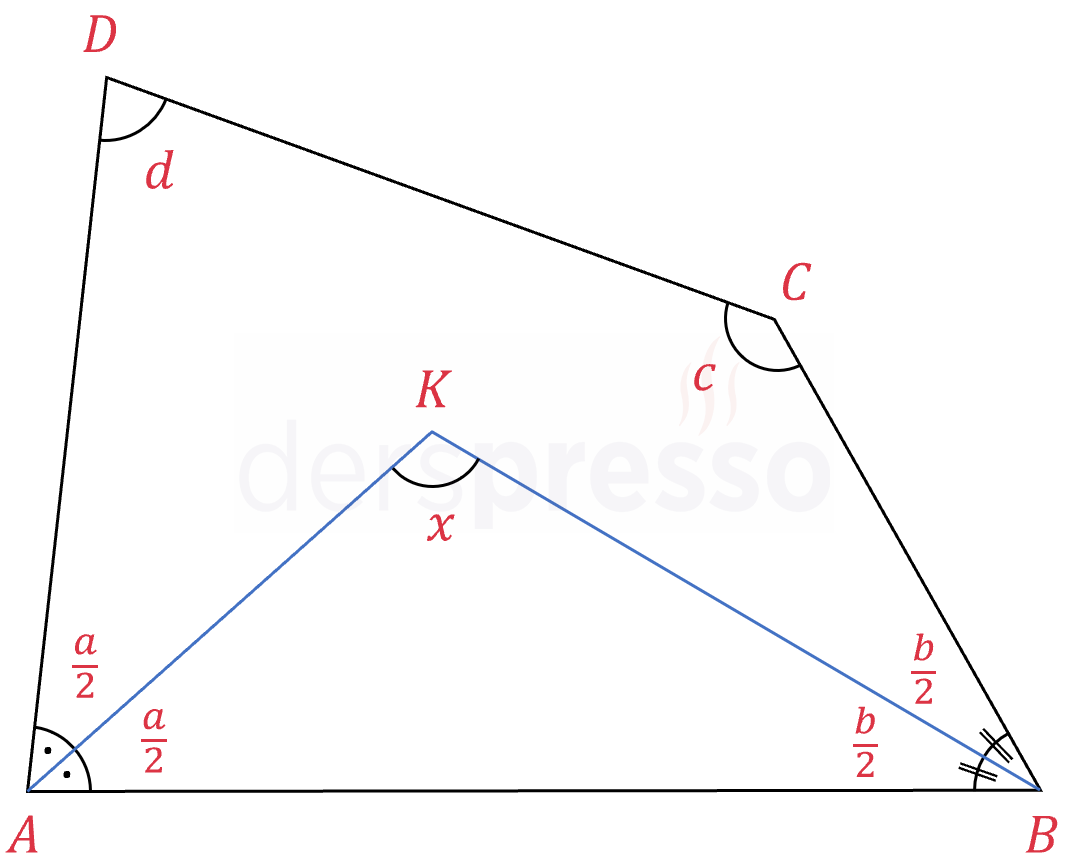
\( ABCD \) dörtgeninin iç açıları toplamı 360°'dir.
\( a + b + c + d = 360 \)
\( AKB \) üçgeninin iç açıları toplamı 180°'dir.
\( x + \dfrac{a}{2} + \dfrac{b}{2} = 180 \)
Eşitliğin taraflarını 2 ile çarpalım.
\( 2x + a + b = 360 \)
Yukarıda bulduğumuz iki ifade de 360°'ye eşit olduğu için birbirine eşitleyebiliriz.
\( 2x + a + b = a + b + c + d \)
\( 2x = c + d \)
\( x = \dfrac{c + d}{2} \)
Karşılıklı iki köşenin iç açıortaylarının kesişmesiyle oluşan açının ölçüsü aşağıdaki formülle bulunur.

\( x = \dfrac{\abs{b - d}}{2} \)
İSPATI GÖSTER
\( A \) köşesinin açı ölçüsüne \( a \), \( C \) köşesinin açı ölçüsüne \( c \) diyelim.
\( m(\widehat{DAK}) = m(\widehat{KAE}) = \dfrac{a}{2} \)
\( m(\widehat{DCK}) = m(\widehat{KCB}) = \dfrac{c}{2} \)

\( ABCD \) dörtgeninin iç açıları toplamı 360°'dir.
\( a + b + c + d = 360 \)
Bir dış açının ölçüsü, kendisine komşu olmayan iki iç açının toplamına eşittir.
\( m(\widehat{AEK}) = b + \dfrac{c}{2} \)
\( AEK \) üçgeninin iç açıları toplamı 180°'dir.
\( x + \dfrac{a}{2} + b + \dfrac{c}{2} = 180 \)
Eşitliğin taraflarını 2 ile çarpalım.
\( 2x + a + 2b + c = 360 \)
Yukarıda bulduğumuz iki ifade de 360°'ye eşit olduğu için birbirine eşitleyebiliriz.
\( 2x + a + 2b + c = a + b + c + d \)
\( 2x = d - b \)
\( x = \dfrac{d - b}{2} \)
Konveks bir dörtgende tüm iç açılar 180°'den küçük iken konkav bir dörtgende en az bir iç açı 180°'den büyüktür.
Dörtgenin Çevresi ve Alanı
Dörtgenin çevresi, dört kenarın uzunlukları toplamına eşittir.
\( \text{Ç}(ABCD) = a + b + c + d \)

Dörtgenin alanı, köşegenlerin uzunlukları ile aralarındaki açının sinüs değerinin çarpımının yarısına eşittir. Birbirini 180°'ye tamamlayan açıların sinüs değerleri eşit olduğu için, köşegenlerin arasında oluşan bütünler açıların ikisi de aynı sonucu verir.

\( A(ABCD) = \frac{1}{2} \abs{AC} \cdot \abs{BD} \cdot \sin{x} \)
\( A(ABCD) = \frac{1}{2} \abs{AC} \cdot \abs{BD} \cdot \sin{y} \)
İSPATI GÖSTER
KONVEKS DÖRTGEN:
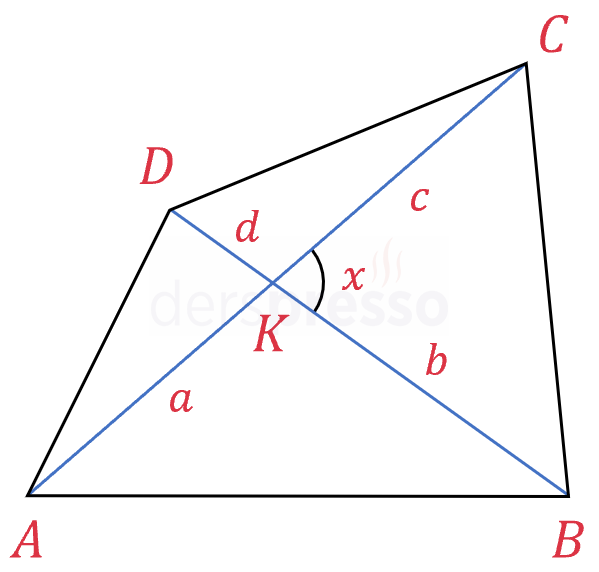
Köşegenlerin ayırdığı dört üçgenin alanlarını sinüs alan formülünü kullanarak hesaplayalım.
\( A(\overset{\triangle}{KAB}) = \dfrac{1}{2} \cdot a \cdot b \cdot \sin(180° - x) \)
\( A(\overset{\triangle}{KBC}) = \dfrac{1}{2} \cdot b \cdot c \cdot \sin{x} \)
\( A(\overset{\triangle}{KCD}) = \dfrac{1}{2} \cdot c \cdot d \cdot \sin(180° - x) \)
\( A(\overset{\triangle}{KDA}) = \dfrac{1}{2} \cdot d \cdot a \cdot \sin{x} \)
Bütünler açıların sinüs değerleri eşittir.
\( \sin{x} = \sin(180° - x) \)
Dört üçgenin alanlarını toplayarak dörtgenin alanını bulalım.
\( A(ABCD) = \dfrac{1}{2} \cdot \sin{x} \cdot (a \cdot b + b \cdot c + c \cdot d + d \cdot a) \)
\( = \dfrac{1}{2} \cdot \sin{x} \cdot [b \cdot (a + c) + d \cdot (a + c)] \)
\( = \dfrac{1}{2} \cdot \sin{x} \cdot (a + c) \cdot (b + d) \)
\( = \dfrac{1}{2} \cdot \abs{AC} \cdot \abs{BD} \cdot \sin{x} \)
KONKAV DÖRTGEN:
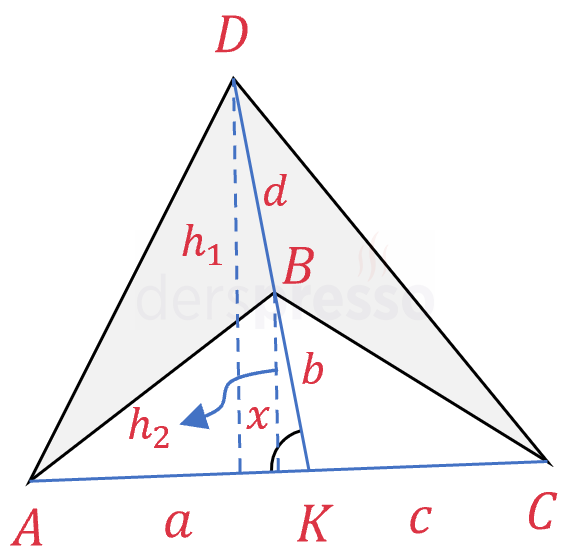
Şekilde oluşan iki üçgenin alanlarını bulalım:
Büyük üçgenin alanı:
\( A(\overset{\triangle}{ACD}) = \dfrac{(a + c) \cdot h_1}{2} \)
\( = \dfrac{(a + c) \cdot (b + d) \cdot \sin{x}}{2} \)
Küçük üçgenin alanı:
\( A(\overset{\triangle}{ACB}) = \dfrac{(a + c) \cdot h_2}{2} \)
\( = \dfrac{(a + c) \cdot b \cdot \sin{x}}{2} \)
Gri renk ile işaretlenmiş konkav dörtgenin alanını, büyük ve küçük üçgenler cinsinden yazalım.
\( A(ABCD) = A(\overset{\triangle}{ACD}) - A(\overset{\triangle}{ACB}) \)
\( = \dfrac{(a + c) \cdot (b + d) \cdot \sin{x}}{2} - \dfrac{(a + c) \cdot b \cdot \sin{x}}{2}\)
\( = \dfrac{(a + c) \cdot d \cdot \sin{x}}{2} \)
\( = \dfrac{1}{2} \cdot \abs{AC} \cdot \abs{BD} \cdot \sin{x} \)
Köşegenleri dik kesişen dörtgenlerin alanı, köşegenlerin uzunlukları çarpımının yarısına eşittir.
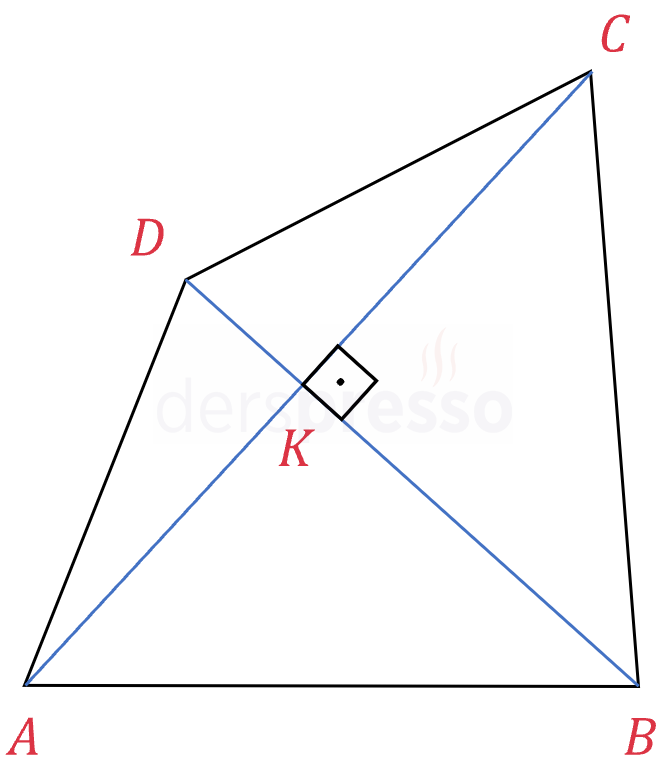
\( A(ABCD) = \frac{1}{2} \abs{AC} \cdot \abs{BD} \)
İSPATI GÖSTER
İspat 1:
Bir dörtgenin alanı, köşegenlerin uzunlukları ile aralarındaki açının sinüs değerinin çarpımının yarısına eşittir.
\( A(ABCD) = \dfrac{1}{2} \cdot \abs{AC} \cdot \abs{BD} \cdot \sin{x} \)
Köşegenleri dik kesişen dörtgenlerde bu açı 90° olur.
\( A(ABCD) = \dfrac{1}{2} \cdot \abs{AC} \cdot \abs{BD} \cdot \sin{90°} \)
\( \sin{90°} = 1 \)
\( A(ABCD) = \frac{1}{2} \abs{AC} \cdot \abs{BD} \)
İspat 2:
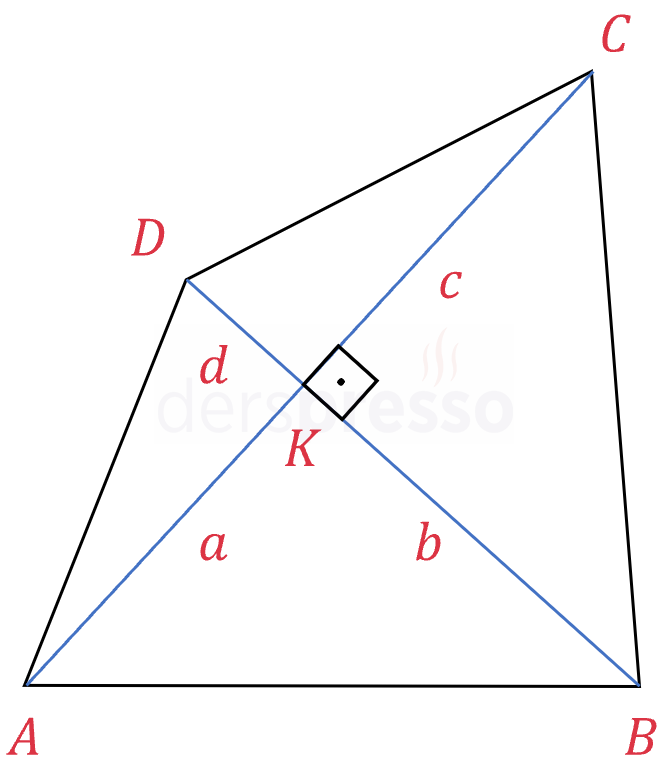
Köşegenlerin oluşturduğu dört üçgenin alanını ayrı ayrı hesaplayalım.
\( A(\overset{\triangle}{AKB}) = \dfrac{a \cdot b}{2} \)
\( A(\overset{\triangle}{BKC}) = \dfrac{b \cdot c}{2} \)
\( A(\overset{\triangle}{CKD}) = \dfrac{c \cdot d}{2} \)
\( A(\overset{\triangle}{DKA}) = \dfrac{d \cdot a}{2} \)
Dörtgenin alanını bulmak için bu dört üçgenin alanlarını toplayalım.
\( A(ABCD) = \dfrac{a \cdot b + b \cdot c + c \cdot d + d \cdot a}{2} \)
\( = \dfrac{b(a + c) + d(a + c)}{2} \)
\( = \dfrac{(a + c)(b + d)}{2} \)
Parantez içindeki toplamlar köşegen uzunluklarına eşittir.
\( A(ABCD) = \frac{1}{2} \abs{AC} \cdot \abs{BD} \)
Bir dörtgenin köşegenlerinin oluşturduğu dört üçgenden karşılıklı olanların alanları çarpımı birbirine eşittir.
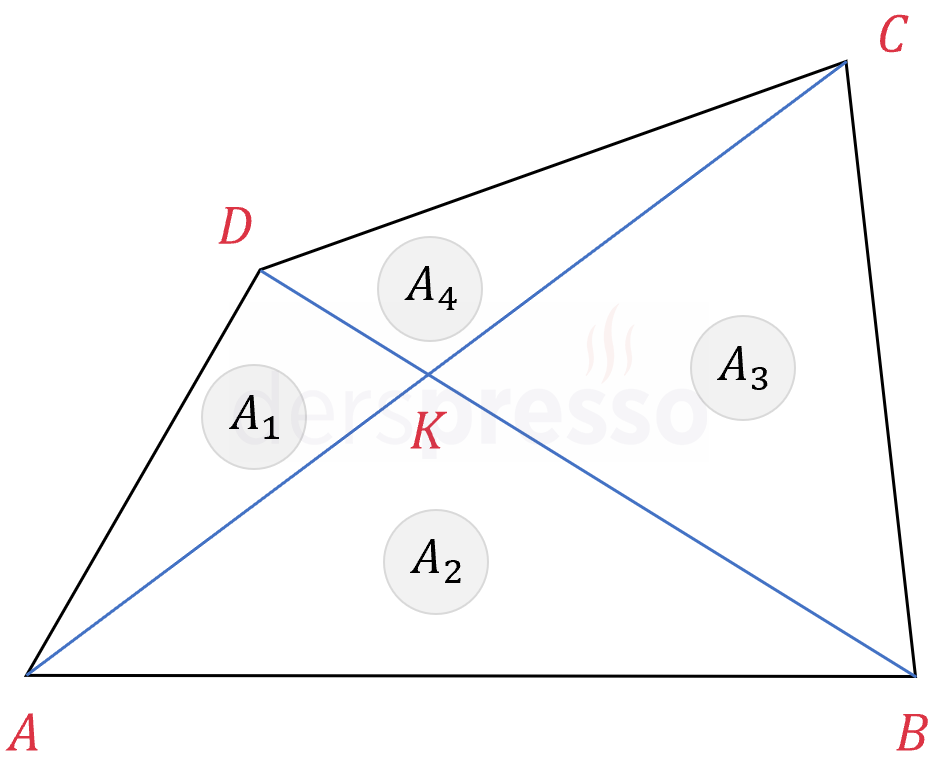
\( A_1 \cdot A_3 = A_2 \cdot A_4 \)
İSPATI GÖSTER
İspat 1:
\( ABD \) ve \( CBD \) üçgenlerinin yüksekliklerini çizelim.
\( h_1 \): \( ABD \) üçgeninin yüksekliği
\( h_2 \): \( CBD \) üçgeninin yüksekliği
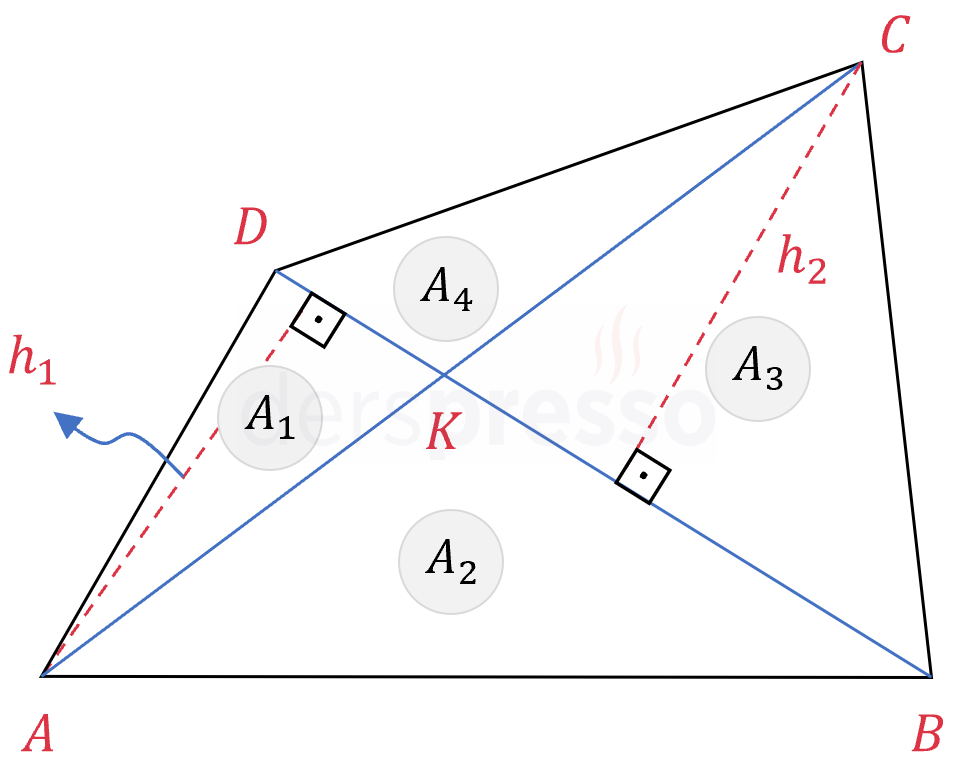
Dört üçgenin alanlarını ayrı ayrı bulalım.
\( A_1 = \dfrac{\abs{DK} \cdot h_1}{2} \)
\( A_2 = \dfrac{\abs{BK} \cdot h_1}{2} \)
\( A_3 = \dfrac{\abs{BK} \cdot h_2}{2} \)
\( A_4 = \dfrac{\abs{DK} \cdot h_2}{2} \)
Formülleri incelediğimizde, aşağıdaki iki ifadenin çarpımının eşit olduğunu görebiliriz.
\( A_1 \cdot A_3 = A_2 \cdot A_4 \)
İspat 2:
Köşegenlerin birbiriyle kesişimi sonucunda oluşan doğru parçalarının uzunluklarına \( x \), \( y \), \( z \) ve \( t \) diyelim.
Köşegenlerin birbiriyle kesişim noktasında oluşan açılara \( \alpha \) ve \( \beta \) diyelim.
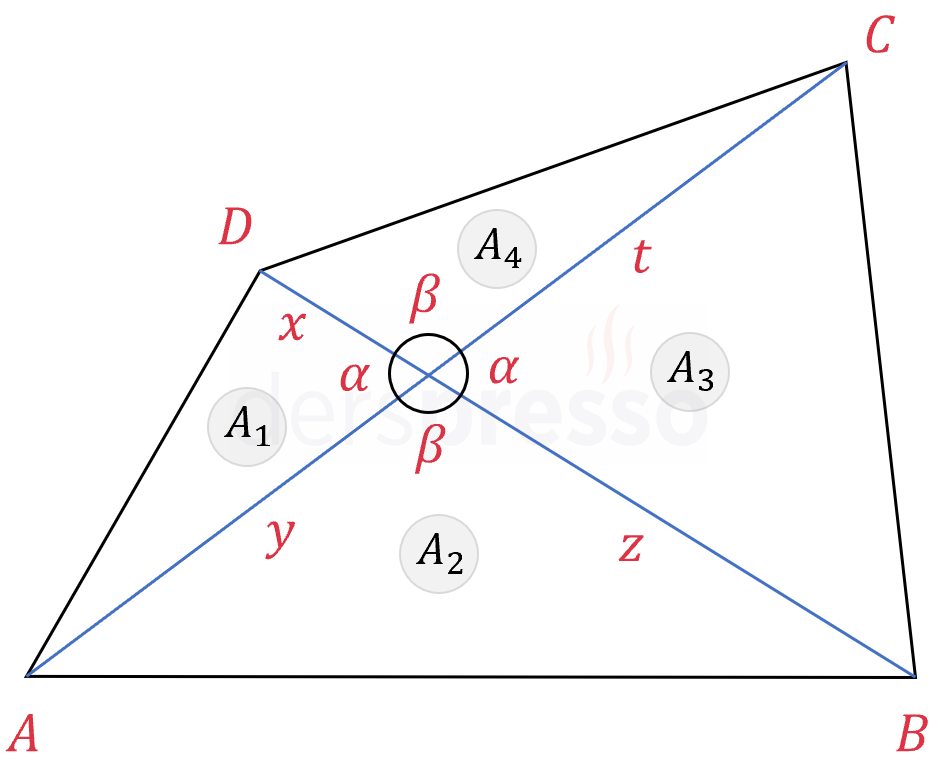
Sinüs alan formülünü kullanarak dört üçgenin alanlarını ayrı ayrı bulalım.
\( A_1 = \dfrac{1}{2} x \cdot y \cdot \sin{\alpha} \)
\( A_2 = \dfrac{1}{2} y \cdot z \cdot \sin{\beta} \)
\( A_3 = \dfrac{1}{2} z \cdot t \cdot \sin{\alpha} \)
\( A_4 = \dfrac{1}{2} t \cdot x \cdot \sin{\beta} \)
\( A_1 \cdot A_3 \) çarpımını bulalım.
\( A_1 \cdot A_3 = \dfrac{1}{2} x \cdot y \cdot \sin{\alpha} \cdot \dfrac{1}{2} z \cdot t \cdot \sin{\alpha} \)
\( = \dfrac{1}{4} x \cdot y \cdot z \cdot t \cdot \sin^2{\alpha} \)
\( A_2 \cdot A_4 \) çarpımını bulalım.
\( A_2 \cdot A_4 = \dfrac{1}{2} y \cdot z \cdot \sin{\beta} \cdot \dfrac{1}{2} t \cdot x \cdot \sin{\beta} \)
\( = \dfrac{1}{4} x \cdot y \cdot z \cdot t \cdot \sin^2{\beta} \)
\( \alpha \) ve \( \beta \) bütünler açılar oldukları için sinüs değerleri birbirine eşittir.
\( \sin{\beta} = \sin(180° - \alpha) = \sin{\alpha} \)
\( = \dfrac{1}{4} x \cdot y \cdot z \cdot t \cdot \sin^2{\alpha} \)
Bulduğumuz iki çarpım birbirine eşittir.
\( A_1 \cdot A_3 = A_2 \cdot A_4 \)
Köşegen uzunlukları 6 ve 8 birim olan basit ve konveks bir dörtgenin alanı 24 birimkaredir.
Buna göre bu dörtgen paralelkenar, eşkenar dörtgen, dikdörtgen, kare, yamuk ve deltoidden hangileri olabilir?
Çözümü GösterBir \( ABCD \) dörtgeninin alanı, köşegenlerinin uzunlukları ve birbiriyle yaptıkları açının sinüs değerinin çarpımının yarısına eşittir.
\( A(ABCD) = \dfrac{1}{2} \cdot \abs{AC} \cdot \abs{BD} \cdot \sin{x} \)
Soruda verilen değerleri yerine koyalım.
\( 24 = \dfrac{1}{2} \cdot 6 \cdot 8 \cdot \sin{x} \)
\( \sin{x} = 1 \)
Buna göre dörtgenin köşegenleri arasındaki açı 90 derecedir, yani köşegenler birbirini dik keser.
Köşegenleri birbirini dik kesen dörtgenler deltoid, eşkenar dörtgen ve karedir. Ancak karenin köşegen uzunlukları da eşit olduğu için verilen dörtgen bir kare olamaz.
Buna göre dörtgen deltoid ya da eşkenar dörtgen olabilir.

Yukarıdaki dörtgenin alanı nedir?
Çözümü GösterDörtgenin \( A \) ve \( C \) köşelerini birleştirelim.

Pisagor teoremini kullanarak \( \abs{AC} \) uzunluğunu bulalım.
\( \abs{AC}^2 = \abs{AD}^2 + \abs{DC}^2 \)
\( \abs{AC}^2 = 7^2 + 9^2 \)
\( \abs{AC} = \sqrt{130} \)
Pisagor teoremini kullanarak \( \abs{AB} \) uzunluğunu bulalım.
\( \abs{AB}^2 + \abs{BC}^2 = \abs{AC}^2 \)
\( \abs{AB}^2 + (\sqrt{13})^2 = (\sqrt{130})^2 \)
\( \abs{AB} = \sqrt{117} = 3\sqrt{13} \)
\( ADC \) ve \( ABC \) üçgenlerinin alanlarının toplamı dörtgenin alanını verir.
\( A(ABCD) = A(ADC) + A(ABC) \)
\( A(ACD) = \dfrac{7 \cdot 9}{2} = \dfrac{63}{2} \)
\( A(ABC) = \dfrac{\sqrt{13} \cdot 3\sqrt{13}}{2} = \dfrac{39}{2} \)
\( A(ABCD) = \dfrac{63}{2} + \dfrac{39}{2} = 51 \) bulunur.