Doğrusal Eşitsizlikler
Analitik düzlemde bir denklemin çözüm kümesi o denklemin grafiği üzerindeki noktalar kümesidir. Bir eşitsizlik ya da eşitsizlik sisteminin çözüm kümesi ise genellikle analitik düzlemde bir bölgeye karşılık gelir.
Eşitsizliklerin Analitik Gösterimi
Bir noktanın bir doğruya (ya da herhangi bir fonksiyona) göre konumu üç farklı şekilde düşünülebilir. Buna göre nokta doğrunun;
- Üzerinde olabilir (\( A \) noktası)
- Üstündeki bölgede olabilir (\( B \) noktası)
- Altındaki bölgede olabilir (\( C \) noktası)

Bir \( (x_1, y_1) \) noktasının bir doğruya göre konumunu bulmak için, noktanın koordinatları doğrunun \( y = ax + b \) formundaki açık denkleminde yerine konur ve oluşan ifadenin tarafları arasındaki eşitlik ya da eşitsizlik durumu incelenir.
\( y_1 = ax_1 + b \Longrightarrow \) Nokta doğrunun üzerindedir (\( A \) noktası)
\( y_2 \gt ax_1 + b \Longrightarrow \) Nokta doğrunun üstündeki bölgededir (\( B \) noktası)
\( y_3 \lt ax_1 + b \Longrightarrow \) Nokta doğrunun altındaki bölgededir (\( C \) noktası)
\( A(12, 60) \) noktasının \( y = 8x - 15 \) doğrusuna göre konumunu bulalım.
\( A \) noktasının koordinatlarını denklemde yerine koyalım ve taraflar arasında oluşan eşitlik ya da eşitsizlik durumunu inceleyelim.
\( 60 \stackrel{?}{\lesseqgtr} 8(12) - 15 \)
\( 60 \lt 81 \)
Buna göre \( A \) noktası verilen doğrunun altındaki bölgededir.
Bunun bir sonucu olarak, bir doğrunun (ya da herhangi bir fonksiyonun) analitik düzlemde oluşturduğu bölgeler ve bu bölgelerin karşılık geldiği eşitlik ya da eşitsizlikler aşağıdaki gibi olur.
| Grafik | Eşitlik/Eşitsizlik |
|---|---|

|
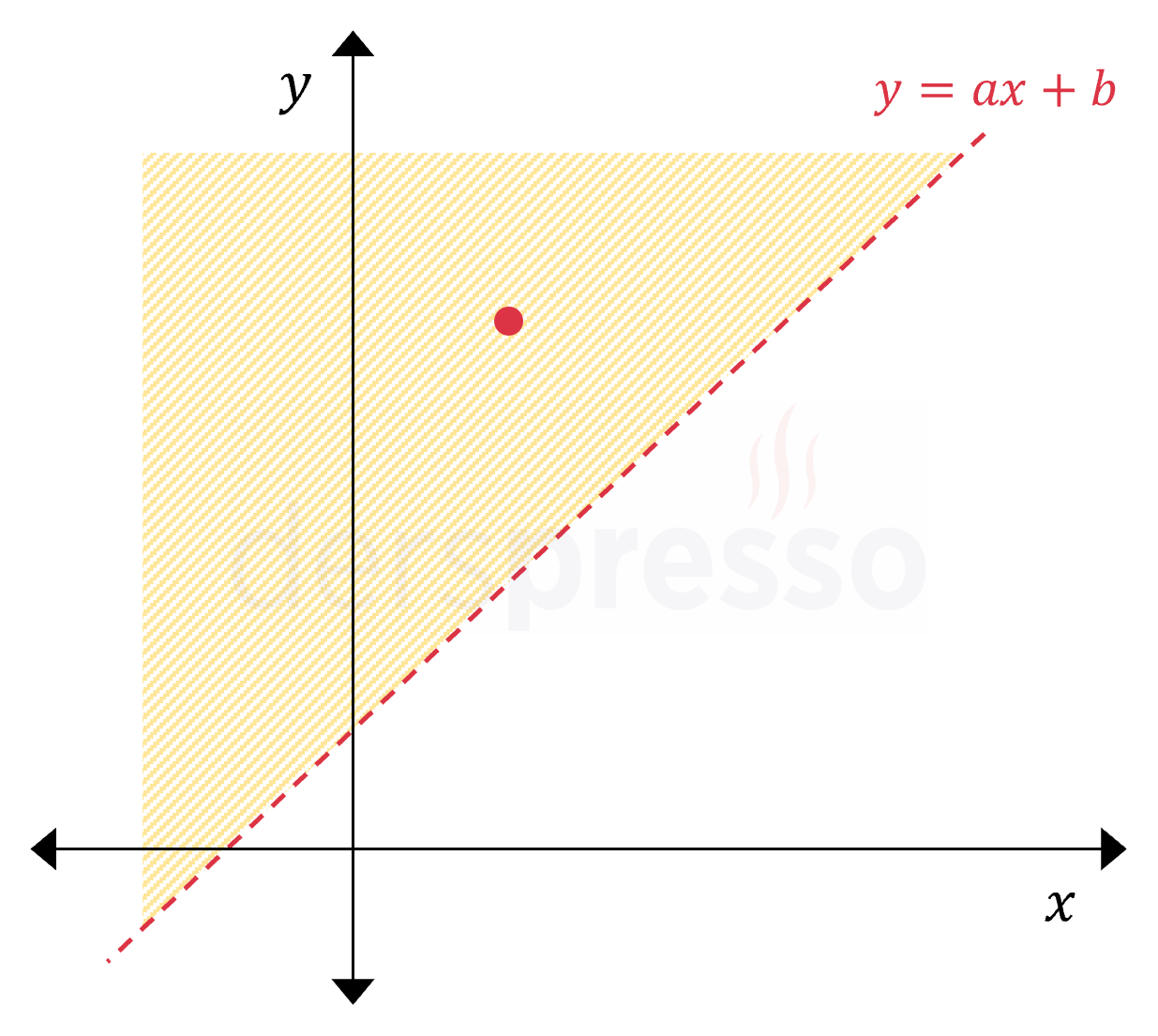
\( y = ax + b \) Doğrunun üzerindeki noktalar |
|
\( y \gt ax + b \) Doğrunun üstündeki bölgedeki noktalar \( \gt \) eşitsizliğinde doğrunun üzerindeki noktaların çözüm kümesine dahil olmadığını vurgulamak için doğru kesikli çizgi ile gösterilir. |
|
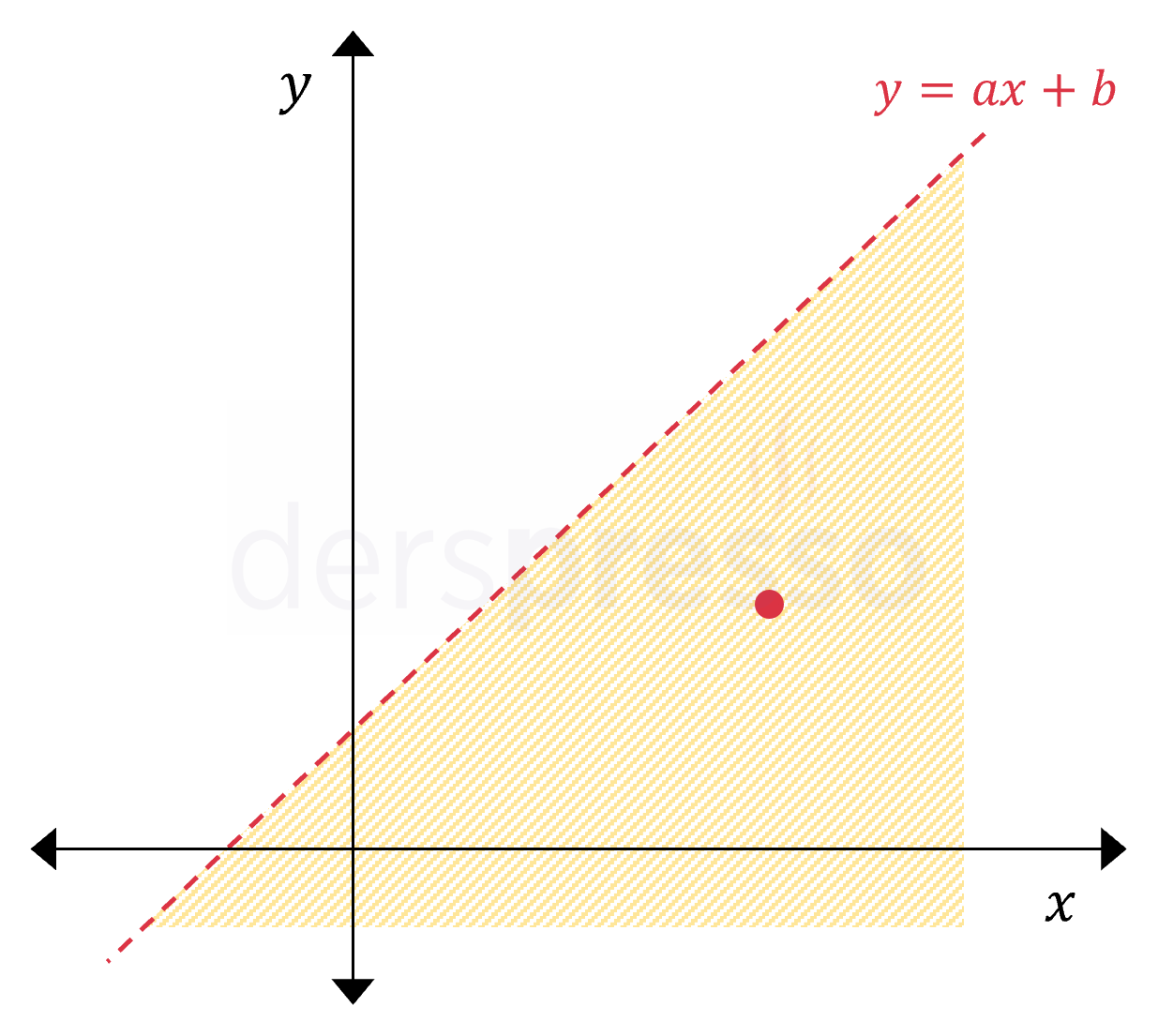
\( y \lt ax + b \) Doğrunun altındaki bölgedeki noktalar \( \lt \) eşitsizliğinde doğrunun üzerindeki noktaların çözüm kümesine dahil olmadığını vurgulamak için doğru kesikli çizgi ile gösterilir. |
|
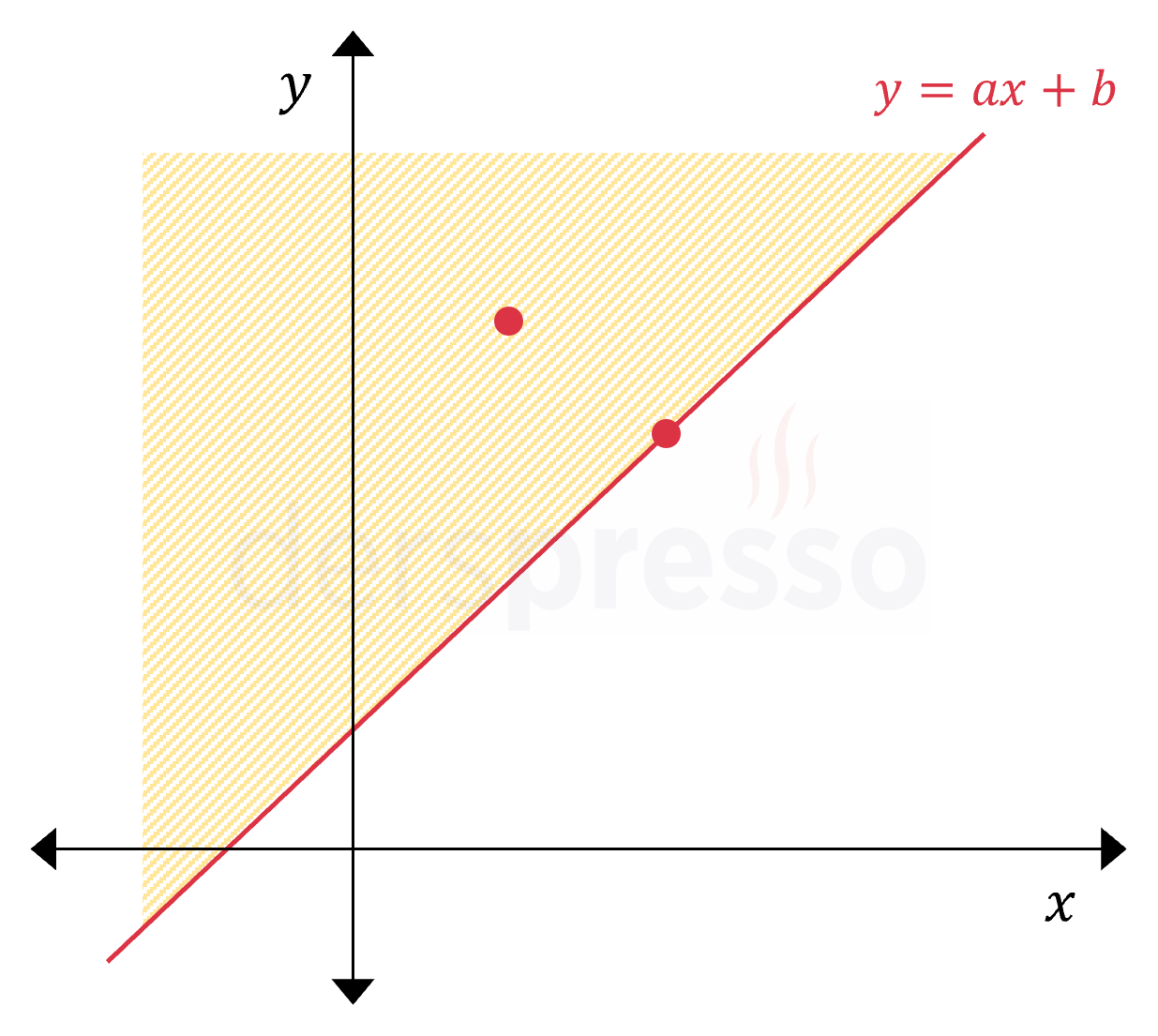
\( y \ge ax + b \) Doğrunun üzerindeki ve üstündeki bölgedeki noktalar \( \ge \) eşitsizliğinde doğrunun üzerindeki noktaların çözüm kümesine dahil olduğunu vurgulamak için doğru sürekli çizgi ile gösterilir. |
|
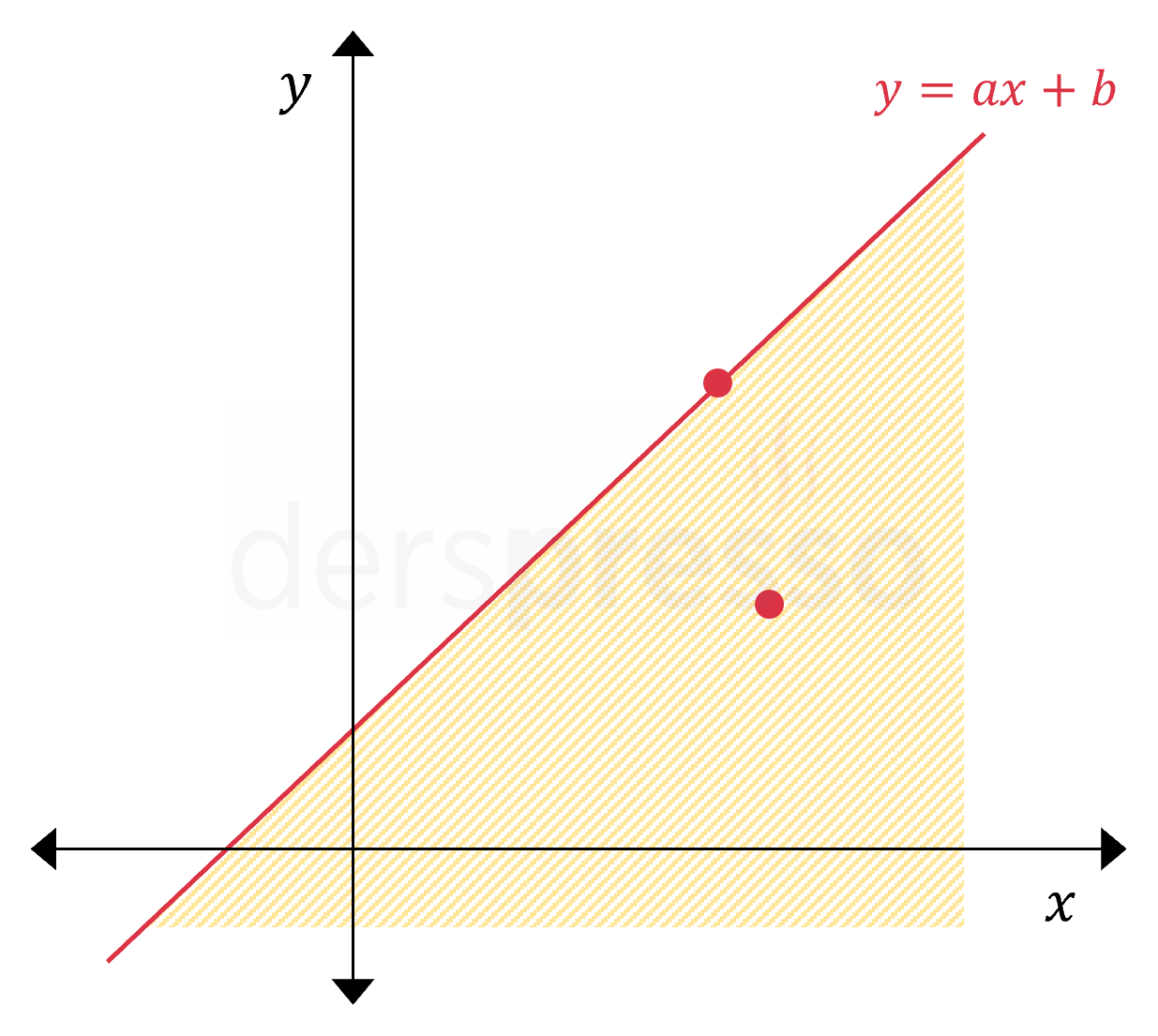
\( y \le ax + b \) Doğrunun üzerindeki ve altındaki bölgedeki noktalar \( \le \) eşitsizliğinde doğrunun üzerindeki noktaların çözüm kümesine dahil olduğunu vurgulamak için doğru sürekli çizgi ile gösterilir. |
Aşağıda örnek bazı doğrusal eşitsizlikler ve analitik düzlemde karşılık geldikleri bölgeler gösterilmiştir.
| Grafik | Eşitsizlik |
|---|---|
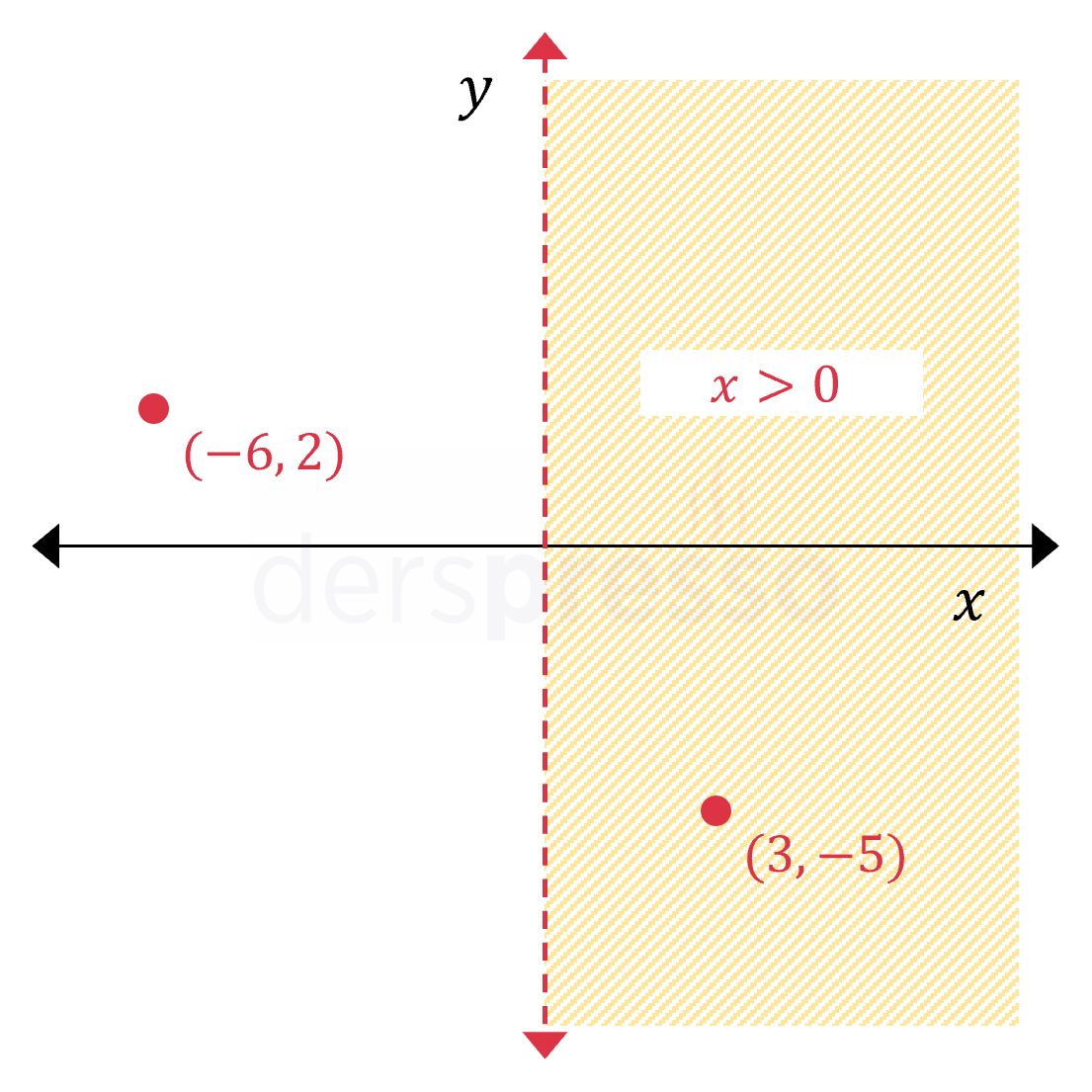
|
\( x \gt 0 \) Bu eşitsizlik apsis değeri sıfırdan büyük olan noktaları içerir. Kesikli çizgi ile gösterilen \( y \) ekseni, üzerindeki apsis değeri sıfır olan noktaların eşitsizliğe dahil olmadığını gösterir. \( (3, -5) \) noktası eşitsizliği sağladığı için taralı bölgeye dahildir. \( (-6, 2) \) noktası eşitsizliği sağlamadığı için taralı bölgeye dahil değildir. |
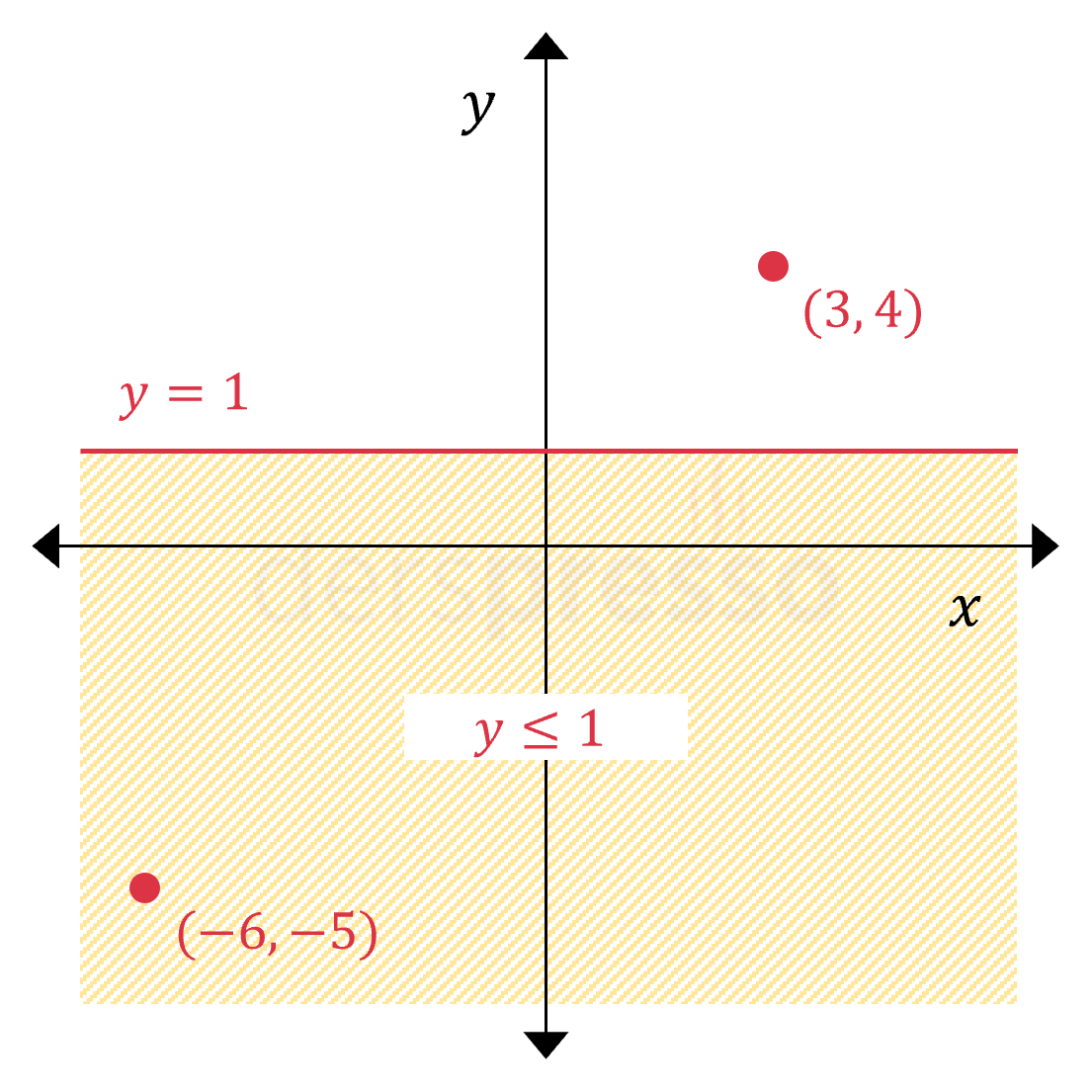
|
\( y \le 1 \) Bu eşitsizlik ordinat değeri 1'e eşit ya da 1'den küçük olan noktaları içerir. Sürekli çizgi ile gösterilen \( y = 1 \) doğrusu, üzerindeki ordinat değeri 1'e eşit olan noktaların eşitsizliğe dahil olduğunu gösterir. \( (-6, -5) \) noktası eşitsizliği sağladığı için taralı bölgeye dahildir. \( (3, 4) \) noktası eşitsizliği sağlamadığı için taralı bölgeye dahil değildir. |
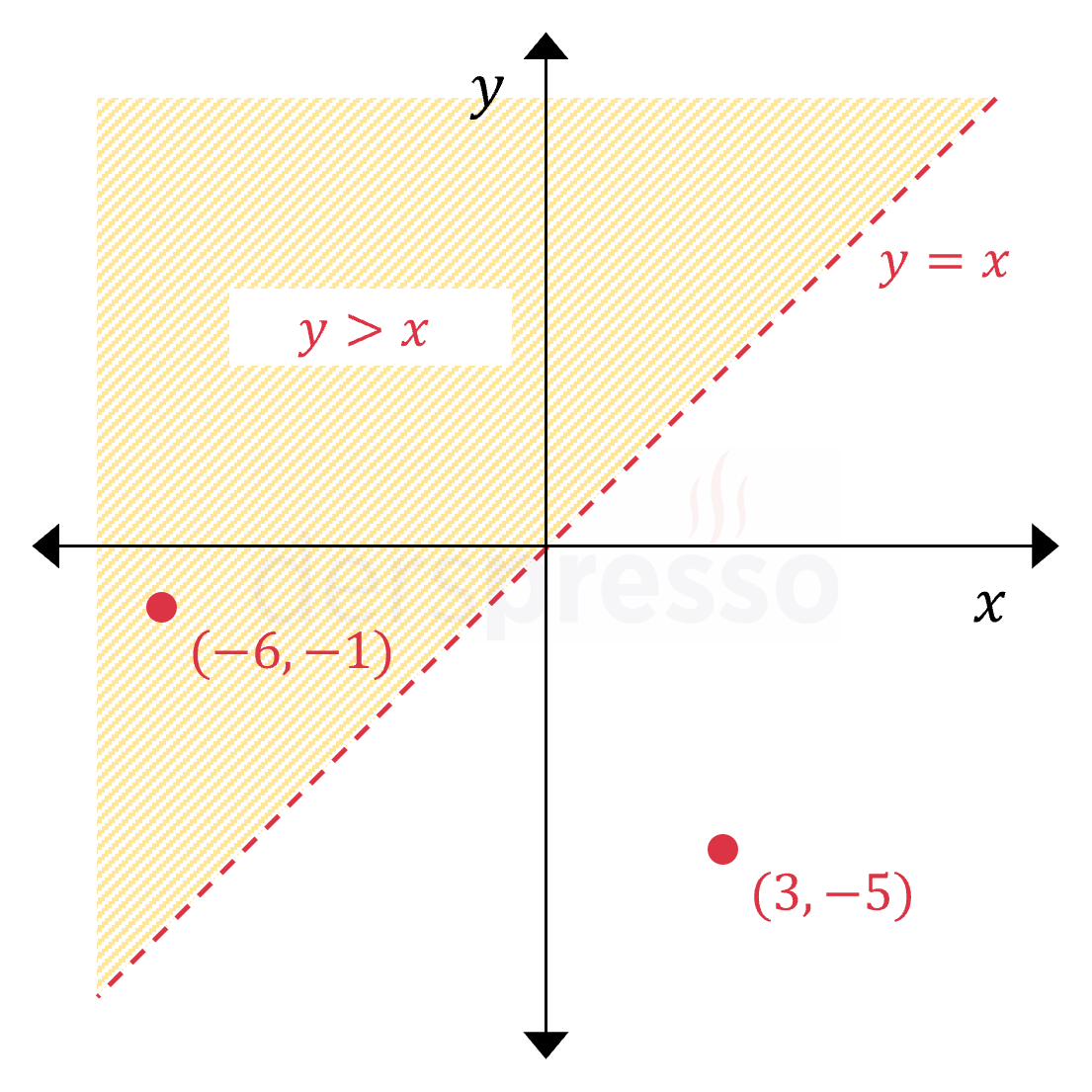
|
\( y \gt x \) Bu eşitsizlik ordinat değeri apsis değerinden büyük olan noktaları içerir. Kesikli çizgi ile gösterilen \( y = x \) doğrusu, üzerindeki apsis ve ordinat değerleri birbirine eşit olan noktaların eşitsizliğe dahil olmadığını gösterir. \( (-6, -1) \) noktası eşitsizliği sağladığı için taralı bölgeye dahildir. \( (3, -5) \) noktası eşitsizliği sağlamadığı için taralı bölgeye dahil değildir. |
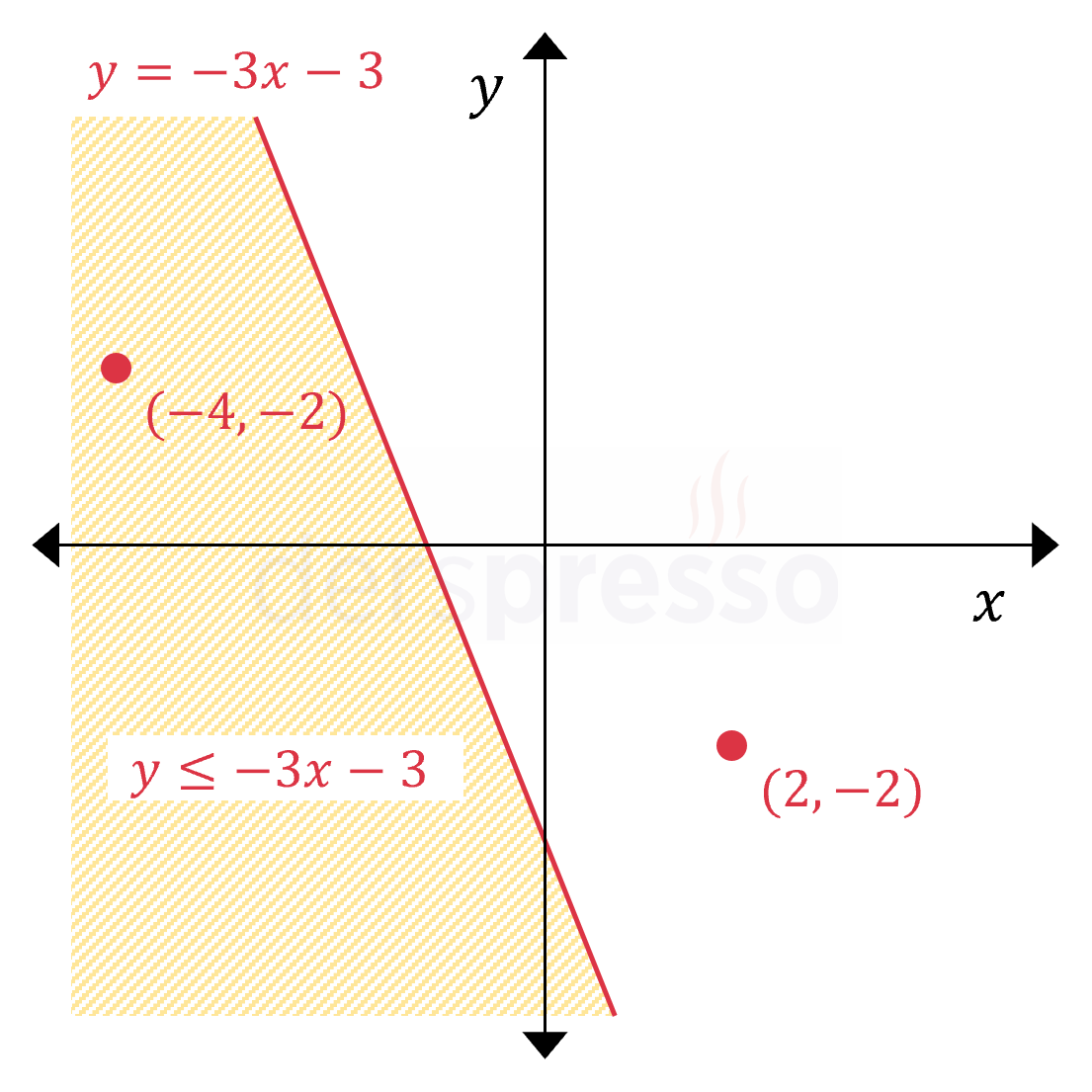
|
\( y \le -3x - 3 \) Bu eşitsizlik \( y = -3x - 3 \) doğrusunun üzerindeki ve altındaki noktaları içerir. Sürekli çizgi ile gösterilen \( y = -3x - 3 \) doğrusu, üzerindeki noktaların eşitsizliğe dahil olduğunu gösterir. \( (-4, -2) \) noktası eşitsizliği sağladığı için taralı bölgeye dahildir. \( (2, -2) \) noktası eşitsizliği sağlamadığı için taralı bölgeye dahil değildir. |
Eşitsizliklerin Analitik Düzlemde Gösterimi
\( y \lesseqgtr ax + b \) formundaki bir eşitsizliğin analitik düzlemde temsil ettiği bölge aşağıdaki şekilde gösterilebilir.
- \( y = ax + b \) doğrusu çizilir. Eşitsizlik sembolü \( \ge \) ya da \( \le \) ise doğru sürekli bir çizgi ile, \( \gt \) ya da \( \lt \) ise kesikli bir çizgi ile çizilir.
- Eşitsizlik sembolü \( \ge \) ya da \( \gt \) ise doğrunun üstünde kalan, \( \le \) ya da \( \lt \) ise altında kalan bölge taranır.
- Özel bir durum olarak, eğer denklem \( x = b \) formunda dikey bir doğru ise \( x \gt b \) için doğrunun sağındaki, \( x \lt b \) için solundaki bölge taranır.
Alternatif ve pratik bir yöntem olarak, koordinat düzleminde seçilecek herhangi bir noktanın koordinatları eşitsizlikte yerine konduğunda eşitsizlik sağlanıyorsa doğrunun noktanın bulunduğu tarafı, sağlanmıyorsa diğer tarafı taranır. İşlem kolaylığı açısından bu noktanın \( (0, 0) \) olarak seçilmesi tercih edilebilir.
Eşitsizlik Sistemlerinin Gösterimi
Eşitsizlik sistemleri birden fazla eşitsizlikten oluşur ve çözüm kümeleri tüm eşitsizlikleri birlikte sağlayan noktaları içerir. Bir diğer ifadeyle, bir eşitsizlik sisteminin karşılık geldiği taralı bölge, sistemi oluşturan eşitsizliklerin ayrı ayrı taradıkları alanların kesişim kümesidir.
Aşağıda örnek bazı eşitsizlik sistemleri ve analitik düzlemde karşılık geldikleri bölgeler gösterilmiştir.
| Grafik | Eşitsizlik Sistemi |
|---|---|
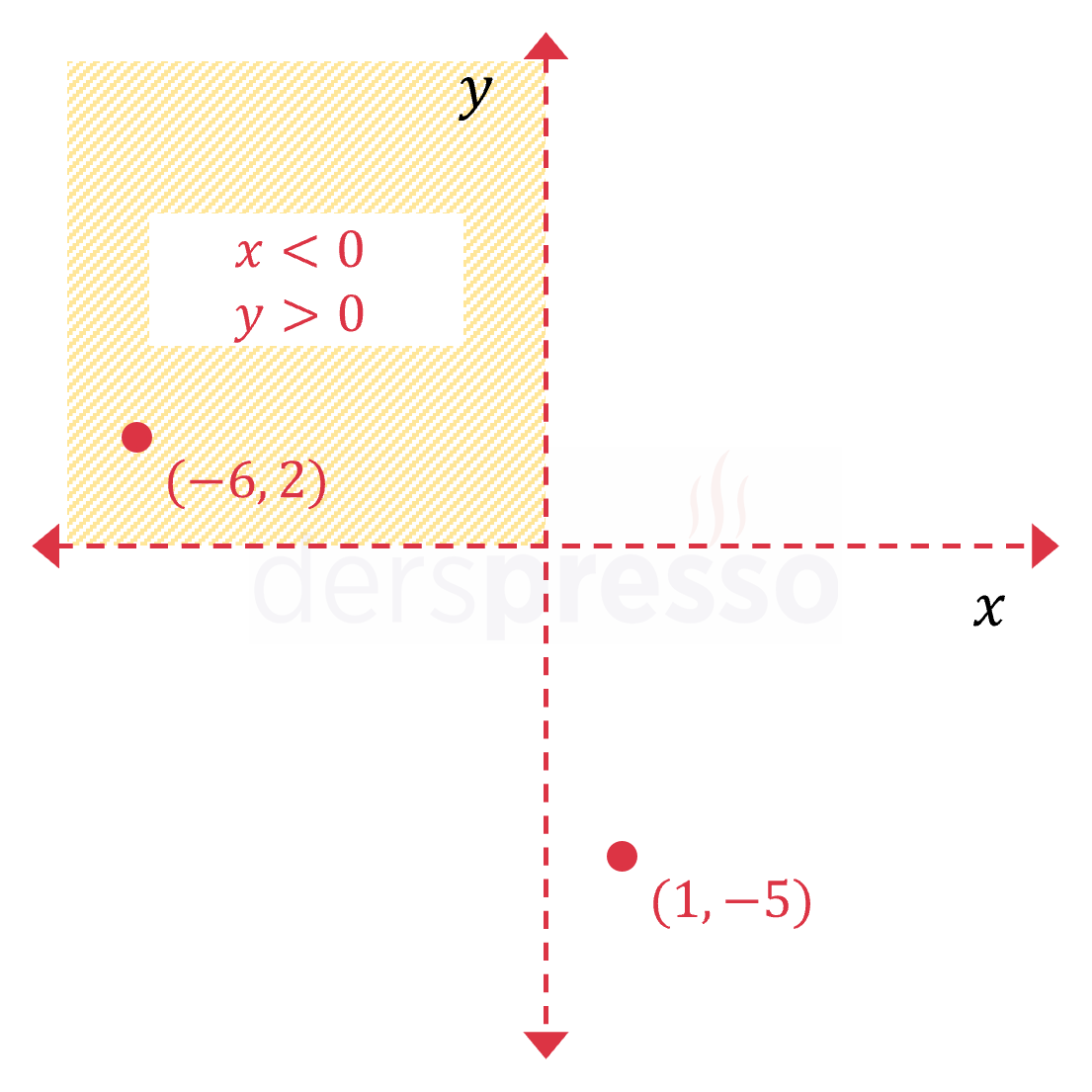
|
\( \begin{cases} x \lt 0 \\ y \gt 0 \end{cases} \) Bu eşitsizlik sistemi apsis değeri negatif ve ordinat değeri pozitif olan noktaları içerir. Kesikli çizgi ile gösterilen \( x \) ve \( y \) eksenleri, üzerlerindeki noktaların eşitsizliğe dahil olmadığını gösterir. \( (-6, -2) \) noktası eşitsizliklerin tümünü sağladığı için taralı bölgeye dahildir. \( (1, -5) \) noktası eşitsizliklerin tümünü sağlamadığı için taralı bölgeye dahil değildir. |
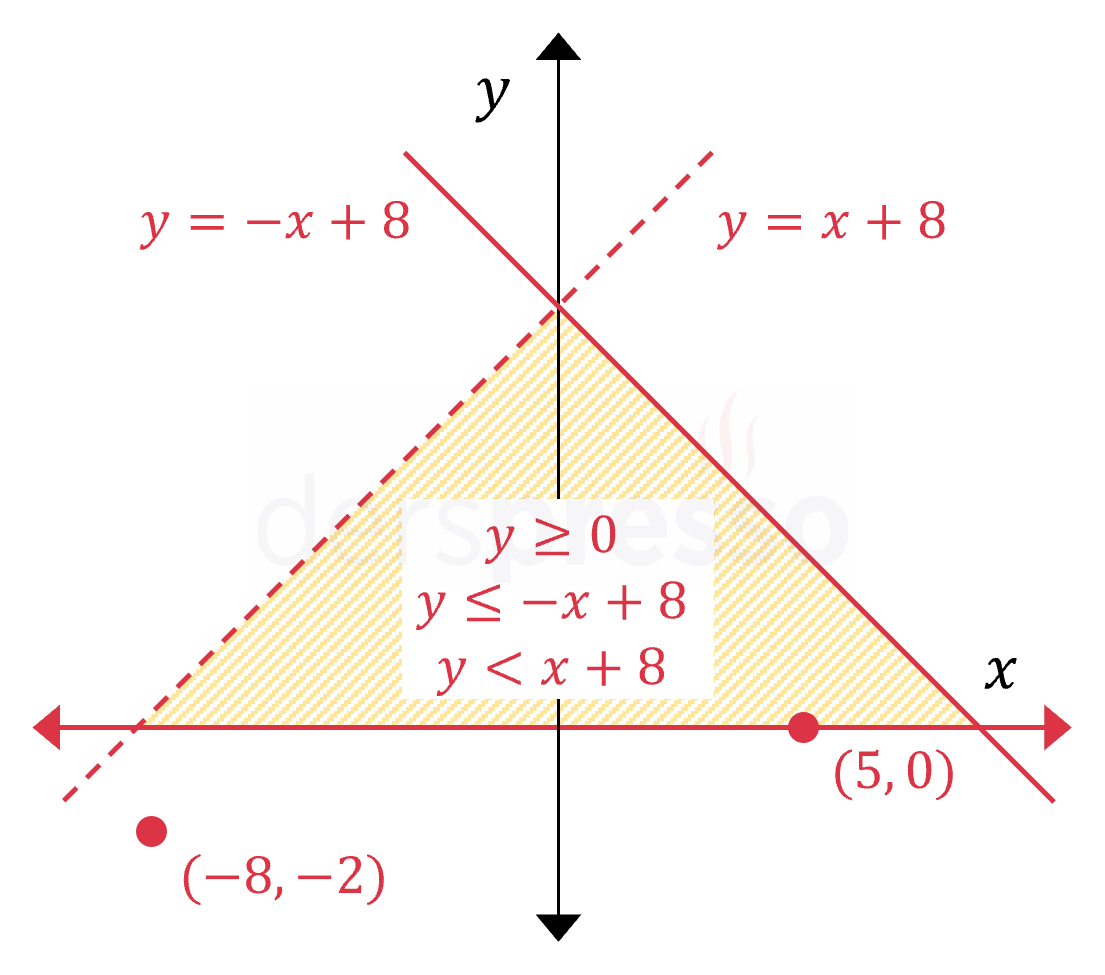
|
\( \begin{cases} y \ge 0 \\ y \le -x + 8 \\ y \lt x + 8 \end{cases} \) Sürekli çizgi ile gösterilen \( x \) ekseni ve \( y = -x + 8 \) doğrusu, üzerlerindeki noktaların eşitsizliğe dahil olduğunu gösterir. Kesikli çizgi ile gösterilen \( y = x + 8 \) doğrusu, üzerindeki noktaların eşitsizliğe dahil olmadığını gösterir. \( (5, 0) \) noktası eşitsizliklerin tümünü sağladığı için taralı bölgeye dahildir. \( (-8, -2) \) noktası eşitsizliklerin tümünü sağlamadığı için taralı bölgeye dahil değildir. |
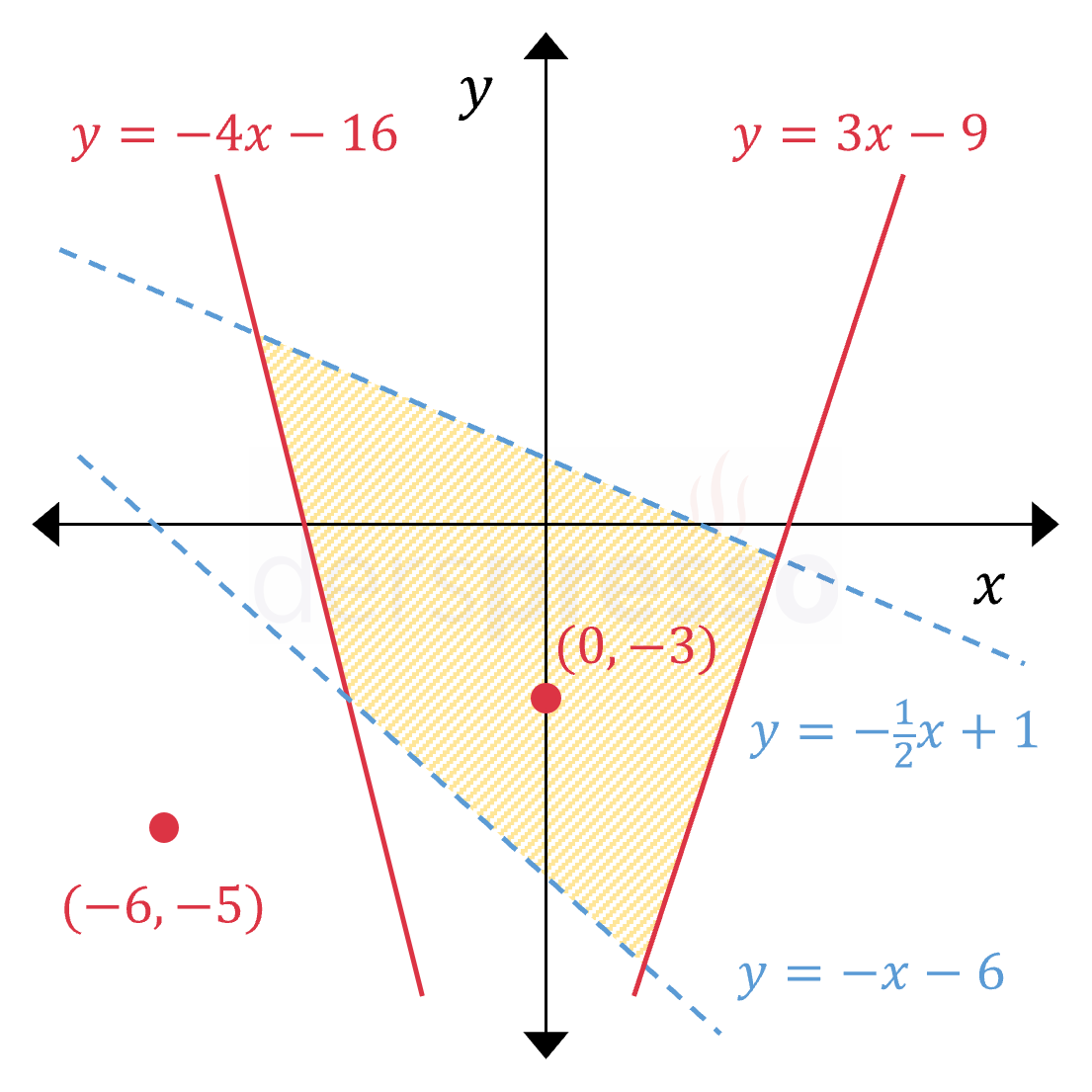
|
\( \begin{cases} y \ge 3x - 9 \\ y \ge -4x - 16 \\ y \lt -\frac{1}{2}x + 1 \\ y \gt -x - 6 \end{cases} \) Sürekli çizgi ile gösterilen \( y = 3x - 9 \) ve \( y = -4x - 16 \) doğruları, üzerlerindeki noktaların eşitsizliğe dahil olduğunu gösterir. Kesikli çizgi ile gösterilen \( y = -\frac{1}{2}x + 1 \) ve \( y = -x - 6 \) doğruları, üzerlerindeki noktaların eşitsizliğe dahil olmadığını gösterir. \( (0, -3) \) noktası eşitsizliklerin tümünü sağladığı için taralı bölgeye dahildir. \( (-6, -5) \) noktası eşitsizliklerin tümünü sağlamadığı için taralı bölgeye dahil değildir. |
Aşağıdaki eşitsizlikleri sağlayan bölgeleri analitik düzlemde gösteriniz.
\( 2x - y \ge 4 \)
\( y \lt -2x + 8 \)
Çözümü GösterHer bir eşitsizliğin karşılık geldiği doğru denkleminin eksenleri kestiği noktaları bulalım.
\( 2x - y = 4 \) doğrusu eksenleri \( (0, -4) \) ve \( (2, 0) \) noktalarında keser. Eşitsizlik sembolü \( \ge \) olduğu için doğru sürekli çizgi ile gösterilir.
\( y = -2x + 8 \) doğrusu eksenleri \( (0, 8) \) ve \( (4, 0) \) noktalarında keser. Eşitsizlik sembolü \( \lt \) olduğu için doğru kesikli çizgi ile gösterilir.
\( (0, 0) \) orijin noktasını kullanarak her bir doğrunun hangi tarafının taranacağını (eşitsizliğin çözüm kümesini gösterdiğini) belirleyelim.
\( 2x - y \ge 4 \) eşitsizliği için:
\( 2(0) - 0 \ge 4 \)
\( 0 \ge 4 \)
\( (0, 0) \) noktası eşitsizliği sağlamadığı için doğrunun orijin tarafında olmayan tarafı taranır.
\( y \lt -2x + 8 \) eşitsizliği için:
\( 0 \lt -2(0) + 8 \)
\( 0 \lt 8 \)
\( (0, 0) \) noktası eşitsizliği sağladığı için doğrunun orijin tarafında kalan tarafı taranır.
Eşitsizliklerin çözüm kümelerinin karşılık geldiği bölgelerin kesişimi eşitsizlik sisteminin çözüm kümesini verir.

Aşağıdaki eşitsizlikleri sağlayan bölgeleri analitik düzlemde gösteriniz.
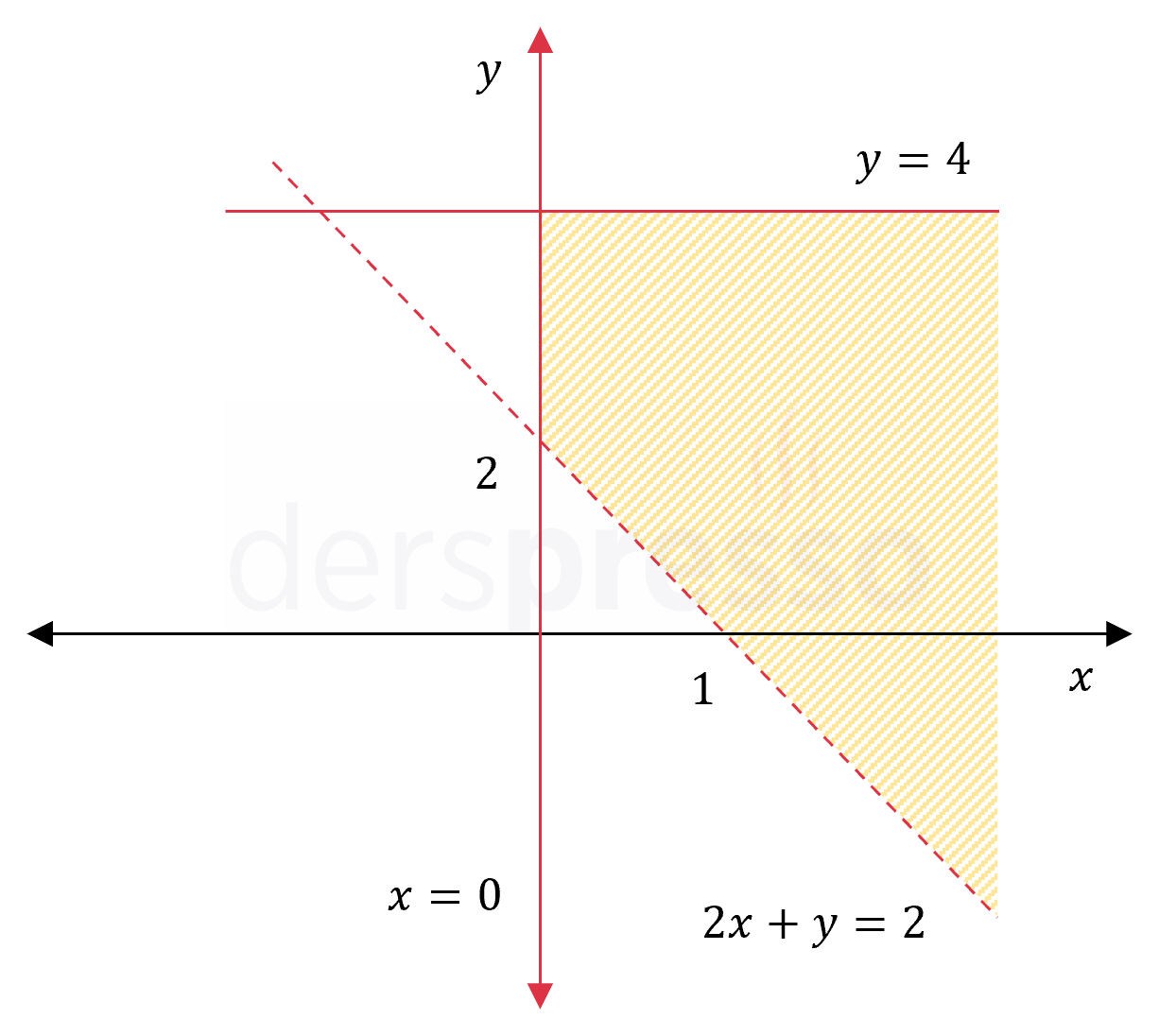
\( x \ge 0 \)
\( y \le 4 \)
\( 2x + y \gt 2 \)
Çözümü GösterHer bir eşitsizliğin karşılık geldiği doğru denkleminin eksenleri kestiği noktaları bulalım.
\( x = 0 \) doğrusu \( y \) eksenidir. Eşitsizlik sembolü \( \ge \) olduğu için doğru sürekli çizgi ile gösterilir.
\( y = 4 \) doğrusu \( y \) eksenini \( (0, 4) \) noktasında keser. Eşitsizlik sembolü \( \le \) olduğu için doğru sürekli çizgi ile gösterilir.
\( 2x + y = 2 \) doğrusu eksenleri \( (0, 2) \) ve \( (1, 0) \) noktalarında keser. Eşitsizlik sembolü \( \gt \) olduğu için doğru kesikli çizgi ile gösterilir.
\( (0, 0) \) orijin noktasını kullanarak her bir doğrunun hangi tarafının taranacağını (eşitsizliğin çözüm kümesini gösterdiğini) belirleyelim.
\( x \ge 0 \) eşitsizliği için:
\( x = 0 \) doğrusunun sağ tarafında bu eşitsizlik sağlandığı için doğrunun sağ tarafı taranır.
\( y \le 4 \) eşitsizliği için:
\( y = 4 \) doğrusunun alt tarafında bu eşitsizlik sağlandığı için doğrunun alt tarafı taranır.
\( 2x + y \gt 2 \) eşitsizliği için:
\( (0, 0) \) orijin noktasını kullanarak hangi bölgenin taranacağını inceleyelim.
\( 2(0) + 0 \gt 2 \)
\( 0 \gt 2 \)
\( (0, 0) \) noktası eşitsizliği sağlamadığı için doğrunun orijin tarafında olmayan tarafı taranır.
Eşitsizliklerin çözüm kümelerinin karşılık geldiği bölgelerin kesişimi eşitsizlik sisteminin çözüm kümesini verir.
Aşağıdaki eşitsizlikleri sağlayan bölgeleri analitik düzlemde gösteriniz.
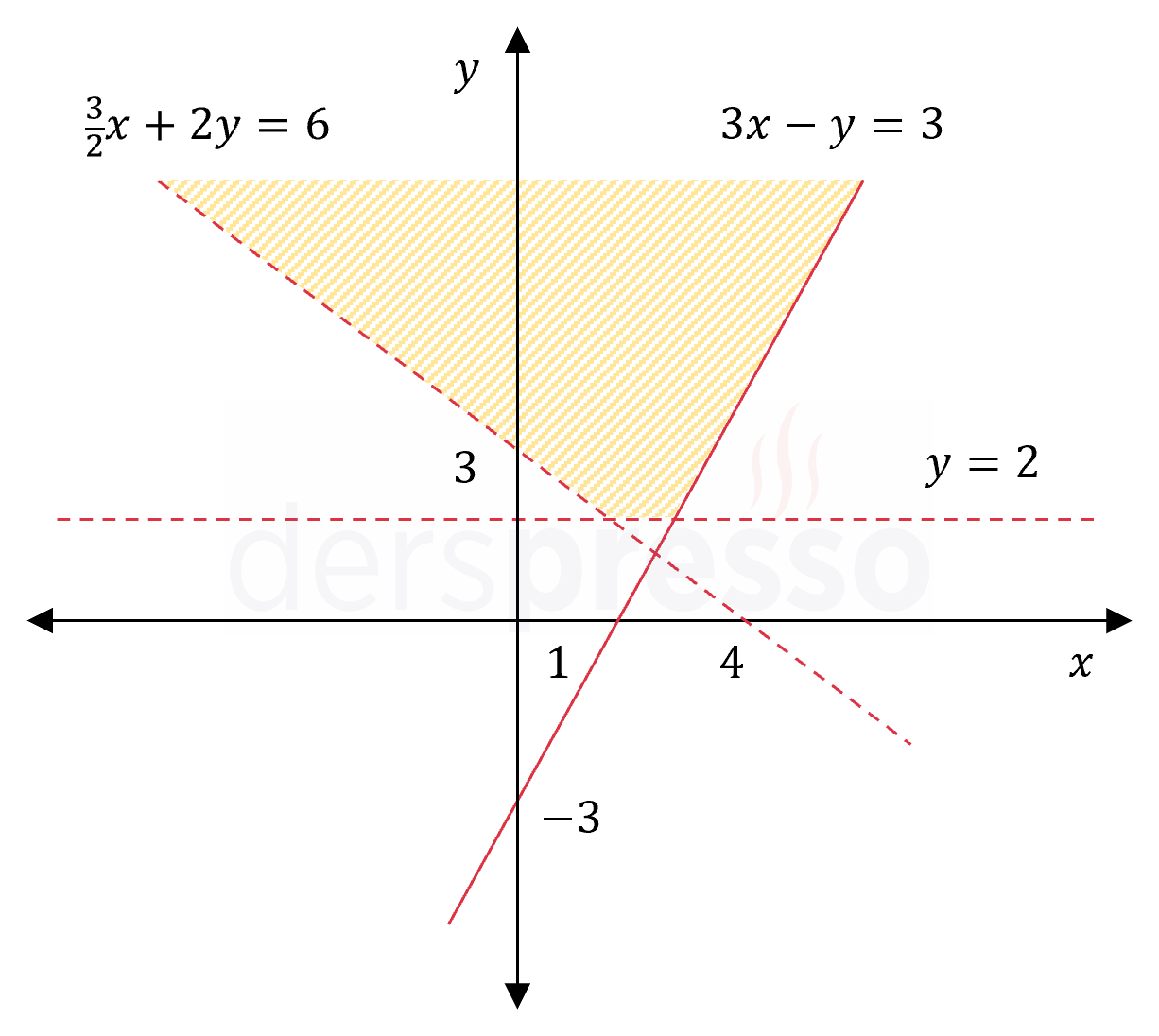
\( \dfrac{3}{2}x + 2y \gt 6 \)
\( 3x - y \le 3 \)
\( y \gt 2 \)
Çözümü GösterHer bir eşitsizliğin karşılık geldiği doğru denkleminin eksenleri kestiği noktaları bulalım.
\( \frac{3}{2}x + 2y = 6 \) doğrusu eksenleri \( (0, 3) \) ve \( (4, 0) \) noktalarında keser. Eşitsizlik sembolü \( \gt \) olduğu için doğru kesikli çizgi ile gösterilir.
\( 3x - y = 3 \) doğrusu eksenleri \( (0, -3) \) ve \( (1, 0) \) noktalarında keser. Eşitsizlik sembolü \( \le \) olduğu için doğru sürekli çizgi ile gösterilir.
\( y = 2 \) doğrusu \( y \) eksenini \( (0, 2) \) noktasında keser. Eşitsizlik sembolü \( \gt \) olduğu için doğru kesikli çizgi ile gösterilir.
\( (0, 0) \) orijin noktasını kullanarak her bir doğrunun hangi tarafının taranacağını (eşitsizliğin çözüm kümesini gösterdiğini) belirleyelim.
\( \dfrac{3}{2}x + 2y \gt 6 \) eşitsizliği için:
\( \dfrac{3}{2}(0) + 2(0) \gt 6 \)
\( 0 \gt 6 \)
\( (0, 0) \) noktası eşitsizliği sağlamadığı için doğrunun orijin tarafında olmayan tarafı taranır.
\( 3x - y \le 3 \) eşitsizliği için:
\( 3(0) - (0) \le 3 \)
\( 0 \le 3 \)
\( (0, 0) \) noktası eşitsizliği sağladığı için doğrunun orijin tarafında kalan tarafı taranır.
\( y \gt 2 \) eşitsizliği için:
\( y = 2 \) doğrusunun üst tarafında bu eşitsizlik sağlandığı için doğrunun üst tarafı taranır.
Eşitsizliklerin çözüm kümelerinin karşılık geldiği bölgelerin kesişimi eşitsizlik sisteminin çözüm kümesini verir.
Aşağıdaki eşitsizlikleri sağlayan bölgeleri analitik düzlemde gösteriniz.
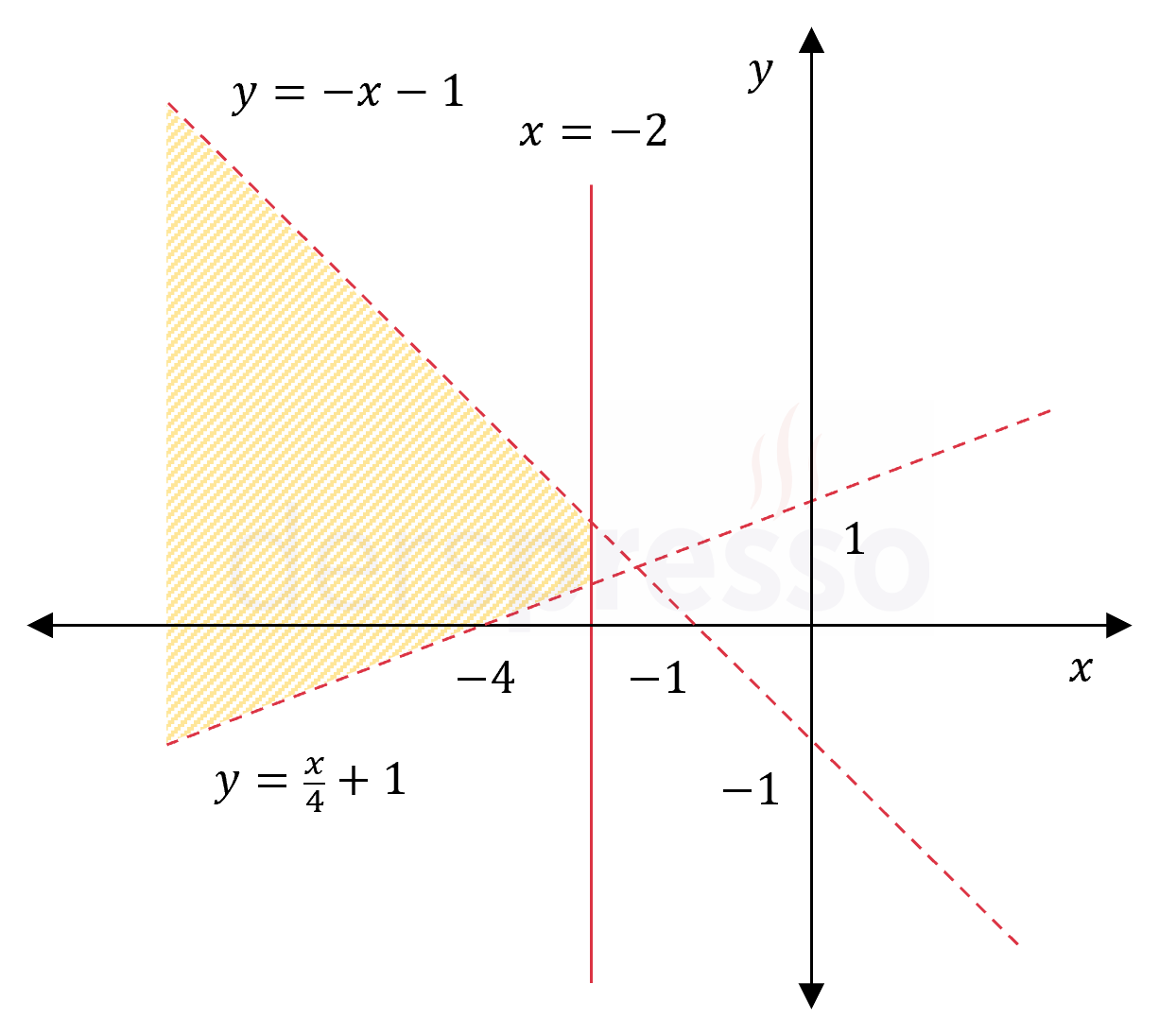
\( x \le -2 \)
\( y \gt \dfrac{x}{4} + 1 \)
\( y \lt -x -1 \)
Çözümü GösterHer bir eşitsizliğin karşılık geldiği doğru denkleminin eksenleri kestiği noktaları bulalım.
\( x = -2 \) doğrusu \( y \) eksenini \( (-2, 0) \) noktasında keser. Eşitsizlik sembolü \( \le \) olduğu için doğru sürekli çizgi ile gösterilir.
\( y = \frac{x}{4} + 1 \) doğrusu eksenleri \( (0, 1) \) ve \( (-4, 0) \) noktalarında keser. Eşitsizlik sembolü \( \gt \) olduğu için doğru kesikli çizgi ile gösterilir.
\( y = -x - 1 \) doğrusu eksenleri \( (0, -1) \) ve \( (-1, 0) \) noktalarında keser. Eşitsizlik sembolü \( \lt \) olduğu için doğru kesikli çizgi ile gösterilir.
\( (0, 0) \) orijin noktasını kullanarak her bir doğrunun hangi tarafının taranacağını (eşitsizliğin çözüm kümesini gösterdiğini) belirleyelim.
\( y \gt \dfrac{x}{4} + 1 \) eşitsizliği için:
\( 0 \gt \dfrac{0}{4} + 1 \)
\( 0 \gt 1 \)
\( (0, 0) \) noktası eşitsizliği sağlamadığı için doğrunun orijin tarafında olmayan tarafı taranır.
\( y \lt -x -1 \) eşitsizliği için:
\( 0 \lt -0 -1 \)
\( 0 \lt -1 \)
\( (0, 0) \) noktası eşitsizliği sağlamadığı için doğrunun orijin tarafında olmayan tarafı taranır.
\( x \le -2 \) eşitsizliği için:
\( x = -2 \) doğrusunun sol tarafında bu eşitsizlik sağlandığı için doğrunun sol tarafı taranır.
Eşitsizliklerin çözüm kümelerinin karşılık geldiği bölgelerin kesişimi eşitsizlik sisteminin çözüm kümesini verir.
Koordinat düzlemindeki \( A(3, -2) \) ve \( B(5, n) \) noktaları \( 2x + y - 7 = 0 \) doğrusunun farklı taraflarında bulunduğuna göre, \( n \)'nin en küçük tam sayı değeri kaçtır?
Çözümü GösterVerilen doğrunun açık denklemini yazalım.
\( y = -2x + 7 \)
\( A(3, -2) \) noktasının bu doğruya göre konumunu bulmak için koordinatlarını doğru denkleminde yerine koyalım.
\( -2 \stackrel{?}{\lesseqgtr} -2(3) + 7 \)
\( -2 \lt 1 \)
\( A \) noktasının ordinatı (\( y = -2 \)), \( x = 3 \) için doğrunun ordinatından (\( y = 1 \)) küçük olduğu için doğrunun altındaki bölgededir.
Buna göre \( B(5, n) \) noktası doğrunun üstündeki bölgede olmalıdır, dolayısıyla \( x = 5 \) için ordinatı doğrunun ordinatından büyük olmalıdır.
\( y \gt -2x + 7 \)
\( n \gt -2(5) + 7 \)
\( n \gt -3 \)
Bu eşitsizliği sağlayan en küçük tam sayı değeri \( n = -2 \)'dir.
Aşağıdaki eşitsizlikleri sağlayan bölgeleri analitik düzlemde gösteriniz.
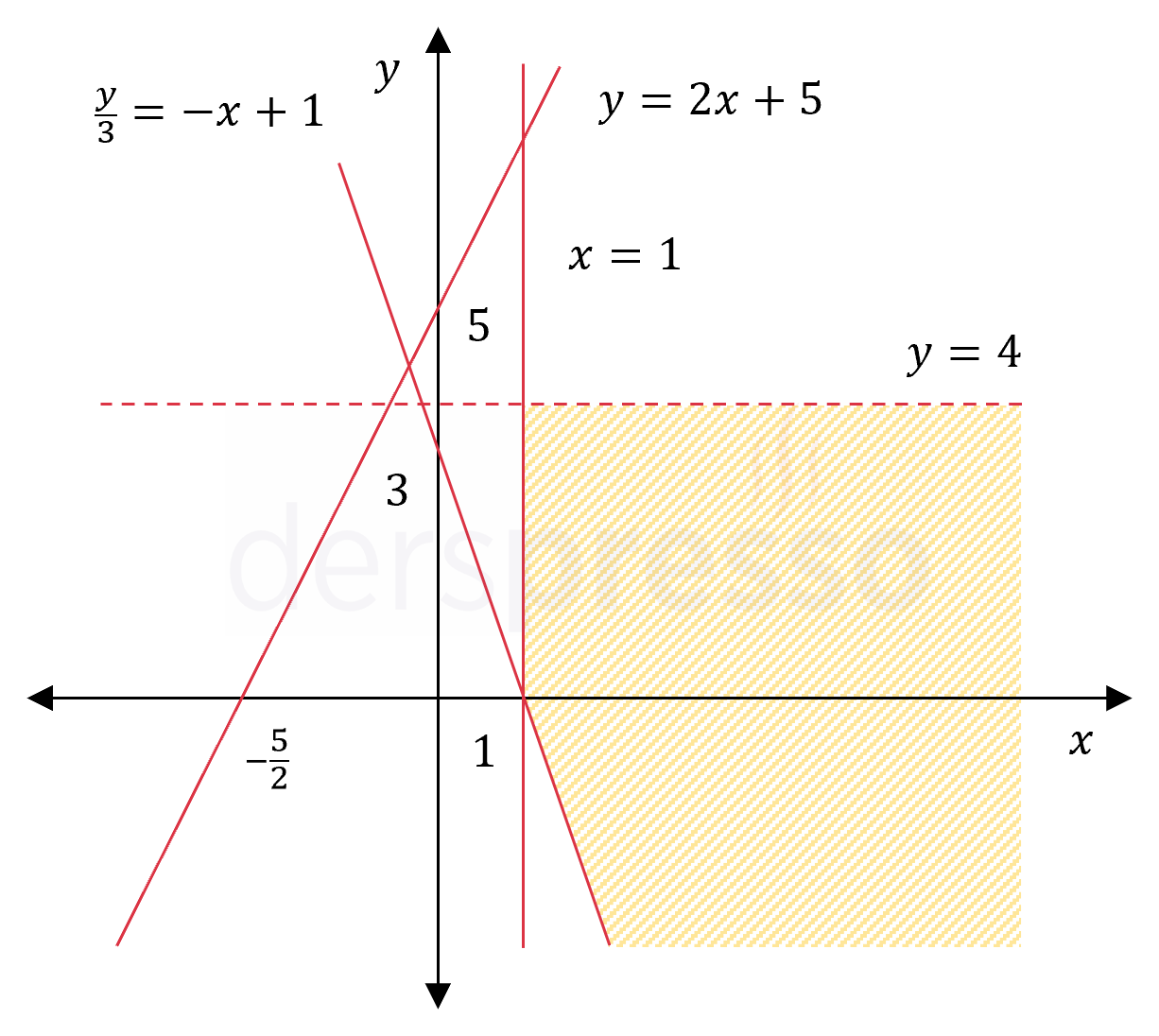
\( y \le 2x + 5 \)
\( \dfrac{y}{3} \ge -x + 1 \)
\( x \ge 1 \)
\( y \lt 4 \)
Çözümü GösterHer bir eşitsizliğin karşılık geldiği doğru denkleminin eksenleri kestiği noktaları bulalım.
\( y = 2x + 5 \) doğrusu eksenleri \( (0, 5) \) ve \( (-\frac{5}{2}, 0) \) noktalarında keser. Eşitsizlik sembolü \( \le \) olduğu için doğru sürekli çizgi ile gösterilir.
\( \frac{y}{3} = -x + 1 \) doğrusu eksenleri \( (0, 3) \) ve \( (1, 0) \) noktalarında keser. Eşitsizlik sembolü \( \ge \) olduğu için doğru sürekli çizgi ile gösterilir.
\( x = 1 \) doğrusu \( x \) eksenini \( (1, 0) \) noktasında keser. Eşitsizlik sembolü \( \ge \) olduğu için doğru sürekli çizgi ile gösterilir.
\( y = 4 \) doğrusu \( y \) eksenini \( (0, 4) \) noktasında keser. Eşitsizlik sembolü \( \lt \) olduğu için doğru kesikli çizgi ile gösterilir.
\( (0, 0) \) orijin noktasını kullanarak her bir doğrunun hangi tarafının taranacağını (eşitsizliğin çözüm kümesini gösterdiğini) belirleyelim.
\( y \le 2x + 5 \) eşitsizliği için:
\( 0 \le 2(0) + 5 \)
\( 0 \le 5 \)
\( (0, 0) \) noktası eşitsizliği sağladığı için doğrunun orijin tarafında kalan tarafı taranır.
\( \dfrac{y}{3} \ge -x + 1 \) eşitsizliği için:
\( \dfrac{0}{3} \ge -0 + 1 \)
\( 0 \ge 1 \)
\( (0, 0) \) noktası eşitsizliği sağlamadığı için doğrunun orijin tarafında olmayan tarafı taranır.
\( x \ge 1 \) eşitsizliği için:
\( x = 1 \) doğrusunun sağ tarafında bu eşitsizlik sağlandığı için doğrunun sağ tarafı taranır.
\( y \lt 4 \) eşitsizliği için:
\( y = 4 \) doğrusunun alt tarafında bu eşitsizlik sağlandığı için doğrunun alt tarafı taranır.
Eşitsizliklerin çözüm kümelerinin karşılık geldiği bölgelerin kesişimi eşitsizlik sisteminin çözüm kümesini verir.
Aşağıdaki eşitsizlikleri sağlayan bölgeleri analitik düzlemde gösteriniz.
\( x + 2y \gt 12 \)
\( \dfrac{x}{2} - \dfrac{y}{3} \ge -6 \)
\( y + 2 \lt 0 \)
Çözümü GösterHer bir eşitsizliğin karşılık geldiği doğru denkleminin eksenleri kestiği noktaları bulalım.
\( x + 2y = 12 \) doğrusu eksenleri \( (0, 6) \) ve \( (12, 0) \) noktalarında keser. Eşitsizlik sembolü \( \gt \) olduğu için doğru kesikli çizgi ile gösterilir.
\( \frac{x}{2} - \frac{y}{3} = -6 \) doğrusu eksenleri \( (0, 18) \) ve \( (-12, 0) \) noktalarında keser. Eşitsizlik sembolü \( \ge \) olduğu için doğru sürekli çizgi ile gösterilir.
\( y + 2 = 0 \) doğrusu \( y \) eksenini \( (0, -2) \) noktasında keser. Eşitsizlik sembolü \( \lt \) olduğu için doğru kesikli çizgi ile gösterilir.
\( (0, 0) \) orijin noktasını kullanarak her bir doğrunun hangi tarafının taranacağını (eşitsizliğin çözüm kümesini gösterdiğini) belirleyelim.
\( x + 2y \gt 12 \) eşitsizliği için:
\( 0 + 2(0) \gt 12 \)
\( 0 \gt 12 \)
\( (0, 0) \) noktası eşitsizliği sağlamadığı için doğrunun orijin tarafında olmayan tarafı taranır.
\( \dfrac{x}{2} - \dfrac{y}{3} \ge -6 \) eşitsizliği için:
\( \dfrac{0}{2} - \dfrac{0}{3} \ge -6 \)
\( 0 \ge -6 \)
\( (0, 0) \) noktası eşitsizliği sağladığı için doğrunun orijin tarafında kalan tarafı taranır.
\( y + 2 \lt 0 \) eşitsizliği için:
\( y + 2 = 0 \) doğrusunun alt tarafında bu eşitsizlik sağlandığı için doğrunun alt tarafı taranır.
Eşitsizliklerin çözüm kümelerinin karşılık geldiği bölgelerin kesişimi eşitsizlik sisteminin çözüm kümesini verir.

Aşağıdaki eşitsizlikleri sağlayan bölgeleri analitik düzlemde gösteriniz.
\( y \ge 3x - 1 \)
\( y \lt 3x - 4 \)
Çözümü GösterHer bir eşitsizliğin karşılık geldiği doğru denkleminin eksenleri kestiği noktaları bulalım.
\( y = 3x - 1 \) doğrusu eksenleri \( (0, -1) \) ve \( (\frac{1}{3}, 0) \) noktalarında keser. Eşitsizlik sembolü \( \ge \) olduğu için doğru sürekli çizgi ile gösterilir.
\( y = 3x - 4 \) doğrusu eksenleri \( (0, -4) \) ve \( (\frac{4}{3}, 0) \) noktalarında keser. Eşitsizlik sembolü \( \lt \) olduğu için doğru kesikli çizgi ile gösterilir.
\( (0, 0) \) orijin noktasını kullanarak her bir doğrunun hangi tarafının taranacağını (eşitsizliğin çözüm kümesini gösterdiğini) belirleyelim.
\( y \ge 3x - 1 \) eşitsizliği için:
\( 0 \ge 3(0) - 1 \)
\( 0 \ge - 1 \)
\( (0, 0) \) noktası eşitsizliği sağladığı için doğrunun orijin tarafında kalan tarafı taranır.
\( y \lt 3x - 4 \) eşitsizliği için:
\( 0 \lt 3(0) - 4 \)
\( 0 \lt -4 \)
\( (0, 0) \) noktası eşitsizliği sağlamadığı için doğrunun orijin tarafında olmayan tarafı taranır.
Eşitsizliklerin çözüm kümelerinin karşılık geldiği bölgelerin kesişimi eşitsizlik sisteminin çözüm kümesini verir.
\( y = 3x - 1 \) ve \( y = 3x - 4 \) doğrularının eğimleri eşit olduğu için doğrular birbirine paraleldir.
Eşitsizliklerin çözüm kümeleri ortak bir taralı alan içermemektedir, dolayısıyla eşitsizlik sisteminin çözüm kümesi boş küme olur.

\( m, n \in \mathbb{Z} \) olmak üzere,
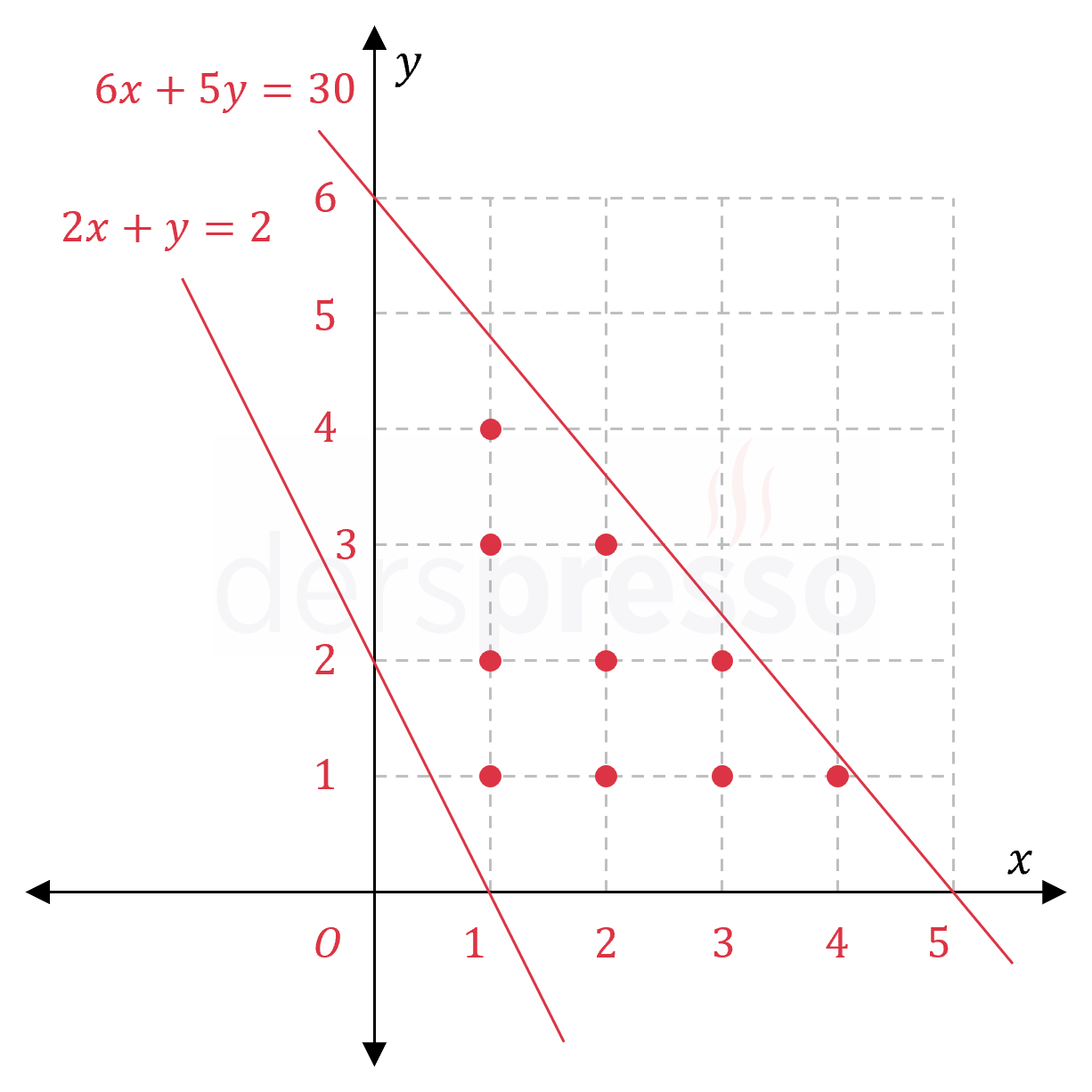
\( 6x + 5y = 30 \), \( 2x + y = 2 \), \( x = 0 \) ve \( y = 0 \) doğrularının sınırlandırdığı bölgenin içinde kaç farklı \( (m, n) \) noktası vardır?
Çözümü GösterVerilen doğruların eksenleri kestiği noktaları bulalım.
Doğruların denklemlerinde \( x = 0 \) koyduğumuzda \( y \) eksenini kestiği nokta, \( y = 0 \) koyduğumuzda \( x \) eksenini kestiği nokta bulunur.
\( 6x + 5y = 30 \) doğrusu \( x \) eksenini \( (5, 0) \), \( y \) eksenini \( (0, 6) \) noktasında keser.
\( 2x + y = 2 \) doğrusu \( x \) eksenini \( (1, 0) \), \( y \) eksenini \( (0, 2) \) noktasında keser.
Verilen doğruların sınırlandırdığı alanı analitik düzlemde çizelim.
Verilen denklemlerde \( y \) değişkenini yalnız bırakalım.
\( y = -\dfrac{6x}{5} + 6 \)
\( y = -2x + 2 \)
\( x \in \{1, 2, 3, 4 \} \) için verilen bölgenin içinde kalan \( y \) değerlerini aşağıdaki eşitsizlikleri kullanarak bulalım.
\( -2x + 2 \lt y \lt -\dfrac{6x}{5} + 6 \)
\( x \gt 0 \)
\( y \gt 0 \)
Durum 1: \( x = 1 \)
\( -2(1) + 2 \lt y \lt -\dfrac{6(1)}{5} + 6 \)
\( 0 \lt y \lt \dfrac{24}{5} \)
Bu durumda aşağıdaki noktalar istenen bölge içinde kalır.
\( (1, 1), (1, 2), (1, 3), (1, 4) \)
Durum 2: \( x = 2 \)
\( -2(2) + 2 \lt y \lt -\dfrac{6(2)}{5} + 6 \)
\( -2 \lt y \lt \dfrac{18}{5} \)
Bu durumda aşağıdaki noktalar istenen bölge içinde kalır.
\( (2, 1), (2, 2), (2, 3) \)
Durum 3: \( x = 3 \)
\( -2(3) + 2 \lt y \lt -\dfrac{6(3)}{5} + 6 \)
\( -4 \lt y \lt \dfrac{12}{5} \)
Bu durumda aşağıdaki noktalar istenen bölge içinde kalır.
\( (3, 1), (3, 2) \)
Durum 4: \( x = 4 \)
\( -2(4) + 2 \lt y \lt -\dfrac{6(4)}{5} + 6 \)
\( -6 \lt y \lt \dfrac{6}{5} \)
Bu durumda aşağıdaki noktalar istenen bölge içinde kalır.
\( (4, 1) \)
Buna göre istenen koşulu sağlayan \( 4 + 3 + 2 + 1 = 10 \) nokta vardır.
Koordinat düzlemindeki \( A(2, -3) \) ve \( B(5, 9) \) noktaları \( ax - 2y + 3 = 0 \) doğrusunun farklı taraflarında bulunduğuna göre, \( a \)'nın alabileceği kaç farklı tam sayı değeri vardır?
Çözümü GösterNoktalar doğrunun farklı taraflarında yer aldığına göre, noktaların koordinatlarını doğrunun kapalı denkleminde yerine yazdığımızda sonuçlar ters işaretli olmalıdır.
\( A(2, -3) \) noktasının koordinatlarını doğru denkleminde yerine koyalım.
\( 2a - 2(-3) + 3 = 2a + 9 \)
\( B(5, 9) \) noktasının koordinatlarını doğru denkleminde yerine koyalım.
\( 5a - 2(9) + 3 = 5a - 15 \)
Bu iki ifade iki durumda ters işaretli olabilir.
Durum 1: \( A \) için pozitif, \( B \) için negatif
\( 5a - 15 \lt 0 \lt 2a + 9 \)
Bu eşitsizliği iki eşitsizliğe ayırarak çözelim.
\( 0 \lt 2a + 9 \Longrightarrow a \gt -\dfrac{9}{2} \)
\( 5a - 15 \lt 0 \Longrightarrow a \lt 3 \)
İki aralığın kesişimi bu durum için geçerli çözümü verir.
\( -\dfrac{9}{2} \lt a \lt 3 \)
Durum 2: \( A \) için negatif, \( B \) için pozitif
\( 2a + 9 \lt 0 \lt 5a - 15 \)
Bu eşitsizliği iki eşitsizliğe ayırarak çözelim.
\( 0 \lt 5a - 15 \Longrightarrow a \gt 3 \)
\( 2a + 9 \lt 0 \Longrightarrow a \lt -\dfrac{9}{2} \)
İki aralığın kesişimi bu durum için geçerli çözümü verir.
\( a \in \emptyset \)
Buna göre \( a \) tam sayı değerleri aşağıdaki aralıkta bulunur.
\( -4 \le a \le 2 \)
\( a \)'nın bu aralıkta alabileceği \( 2 - (-4) + 1 = 7 \) tam sayı değeri vardır.