Doğrunun Denkleminin Bulunması
Bir doğruyu çizebilmek için ya doğrunun iki farklı noktası ya da bir noktası ve eğimi bilinmelidir.
- Doğrunun bir noktası ve eğimi
- Doğrunun herhangi iki farklı noktası
- Doğrunun eksenleri kestiği iki nokta
Bir Noktası ve Eğimi Bilinen Doğru
Bir noktası ve eğimi bilinen doğrunun denklemi aşağıdaki formülle bulunabilir.
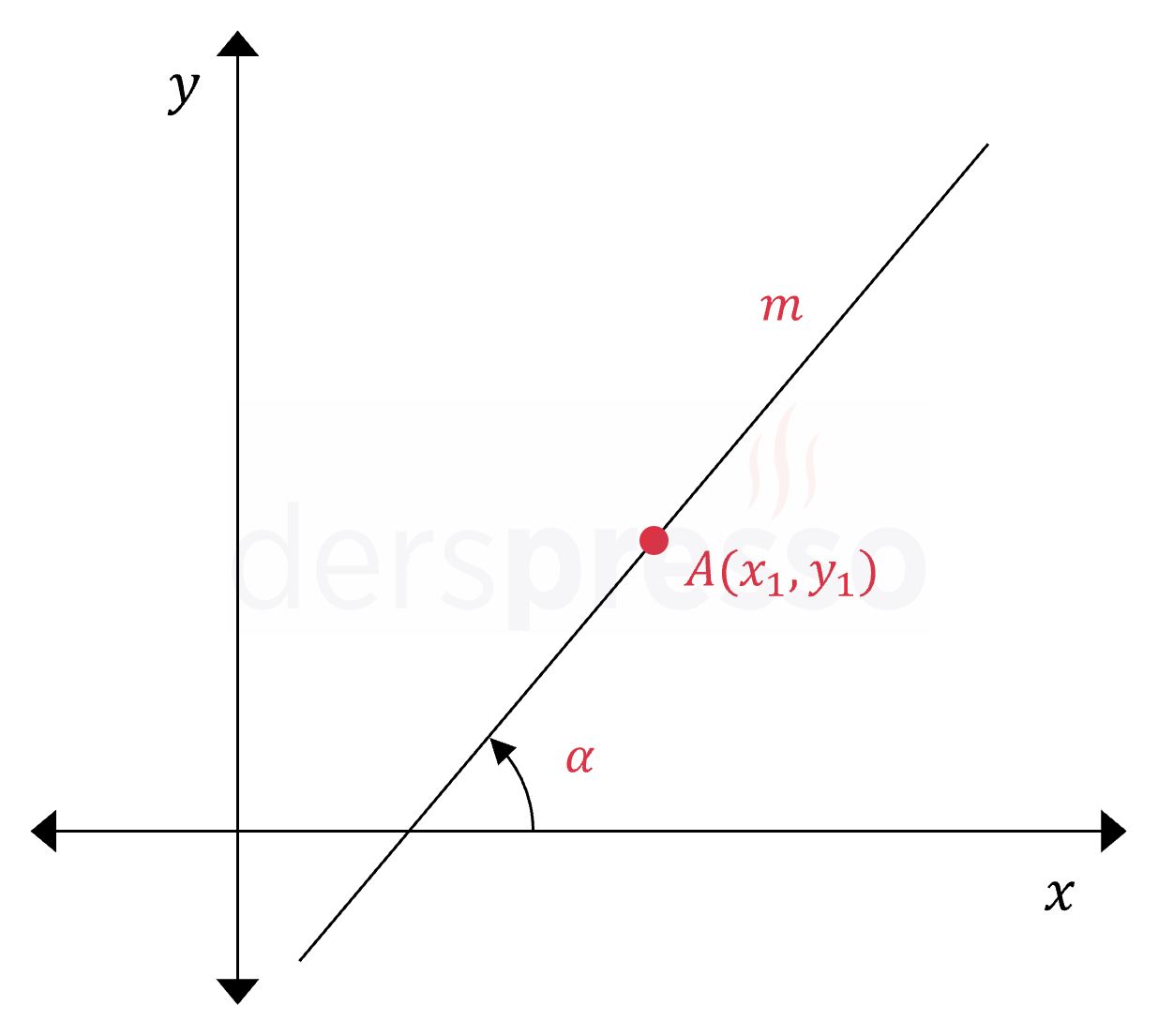
\( A(x_1, y_1) \) noktasından geçen ve eğimi \( m \) olan doğrunun denklemi:
\( y - y_1 = m(x - x_1) \)
\( A(3, -5) \) noktasından geçen ve eğimi \( m = -2 \) olan doğrunun denklemi:
\( y - (-5) = -2(x - 3) \)
\( y + 5 = -2x + 6 \)
\( y = -2x + 1 \)
Bu denklemde \( m \) yalnız bırakıldığında, bu denklemin verilen nokta ile arasındaki eğimin \( m \)'ye eşit olduğu noktaların geometrik yer denklemi olduğu görülebilir.
\( m = \dfrac{y - y_1}{x - x_1} \)
Aşağıda bir noktası ve eğimi verilen doğruların denklemlerini bulunuz.
(a) \( A(5, -2), m = -3 \)
(b) \( A(-6, 7), m = \frac{2}{3} \)
(c) \( A(2, 3), m = 0 \)
Çözümü Göster\( (x_1, y_1) \) noktasından geçen ve eğimi \( m \) olan doğrunun denklemi aşağıdaki formülle bulunur.
\( y - y_1 = m(x - x_1) \)
(a) seçeneği:
\( A(5, -2), m = -3 \)
\( y - (-2) = -3(x - 5) \)
\( y + 2 = -3x + 15 \)
\( y = -3x + 13 \)
(b) seçeneği:
\( A(-6, 7), m = \frac{2}{3} \)
\( y - 7 = \dfrac{2}{3}(x - (-6)) \)
\( y - 7 = \dfrac{2}{3}x + 4 \)
\( y = \dfrac{2}{3}x + 11 \)
(c) seçeneği:
\( A(2, 3), m = 0 \)
\( y - 3 = 0(x - 2) \)
\( y = 3 \)
İki Noktası Bilinen Doğru
Farklı iki noktası bilinen doğrunun denklemi aşağıdaki formülle bulunabilir.

\( A(x_1, y_1) \) ve \( B(x_2, y_2) \) noktalarından geçen doğrunun denklemi:
\( \dfrac{y - y_2}{x - x_2} = \dfrac{y_2 - y_1}{x_2 - x_1} \)
\( A(-2, -3) \) ve \( B(4, 9) \) noktalarından geçen doğrunun denklemi ve eğimi:
\( \dfrac{y - 9}{x - 4} = \dfrac{9 - (-3)}{4 - (-2)} \)
\( \dfrac{y - 9}{x - 4} = \dfrac{12}{6} \)
\( y - 9 = 2(x - 4) \)
\( y = 2x + 1 \)
\( m = 2 \)
Bu formülde eşitliğin sağ tarafı verilen iki nokta arasındaki eğime eşit olduğu için bu formül bir noktası ve eğimi bilinen doğru denklemine de dönüştürülebilir.
\( \dfrac{y - y_2}{x - x_2} = \dfrac{y_2 - y_1}{x_2 - x_1} = m \)
Aşağıda iki noktası verilen doğruların denklemlerini bulunuz.
(a) \( A(-2, 5), B(4, 1) \)
(b) \( A(7, 0), B(-3, -5) \)
(c) \( A(\frac{1}{2}, -\frac{2}{3}), B(-\frac{3}{4}, \frac{1}{3}) \)
Çözümü Göster\( (x_1, y_1) \) ve \( (x_2, y_2) \) noktalarından geçen doğrunun denklemi aşağıdaki formülle bulunur.
\( \dfrac{y - y_2}{x - x_2} = \dfrac{y_2 - y_1}{x_2 - x_1} \)
(a) seçeneği:
\( A(-2, 5), B(4, 1) \)
\( \dfrac{y - 1}{x - 4} = \dfrac{1 - 5}{4 - (-2)} \)
\( \dfrac{y - 1}{x - 4} = -\dfrac{2}{3} \)
\( 3y - 3 = -2x + 8 \)
\( 2x + 3y - 11 = 0 \)
(b) seçeneği:
\( A(7, 0), B(-3, -5) \)
\( \dfrac{y - (-5)}{x - (-3)} = \dfrac{-5 - 0}{-3 - 7} \)
\( \dfrac{y + 5}{x + 3} = \dfrac{1}{2} \)
\( 2y + 10 = x + 3 \)
\( x - 2y - 7 = 0 \)
(c) seçeneği:
\( A(\frac{1}{2}, -\frac{2}{3}), B(-\frac{3}{4}, \frac{1}{3}) \)
\( \dfrac{y - \frac{1}{3}}{x - (-\frac{3}{4})} = \dfrac{\frac{1}{3} - (-\frac{2}{3})}{-\frac{3}{4} - \frac{1}{2}} \)
\( \dfrac{y - \frac{1}{3}}{x + \frac{3}{4}} = -\dfrac{4}{5} \)
\( 5y - \dfrac{5}{3} = -4x - 3 \)
\( 4x + 5y + \dfrac{4}{3} = 0 \)
\( 12x + 15y + 4 = 0 \)
Eksenleri Kestiği Noktalar Bilinen Doğru
Bir doğrunun eksenleri kestiği noktalar biliniyorsa yukarıdaki iki noktası bilinen doğrunun denklem formülüne ek olarak aşağıdaki formül de kullanılabilir.

\( \dfrac{x}{x_1} + \dfrac{y}{y_2} = 1 \)
Bu denklem aşağıdaki biçimde de yazılabilir.
\( y_2\ x + x_1\ y = x_1\ y_2 \)
Doğrunun eğimi: \( m = \tan{\alpha} = -\dfrac{y_2}{x_1} \)
Eksenleri \( A(3, 0) \) ve \( B(0, 4) \) noktalarında kesen doğrunun denklemi ve eğimi:
\( \dfrac{x}{3} + \dfrac{y}{4} = 1 \)
\( 4x + 3y = 12 \)
\( y = -\dfrac{4}{3}x + 4 \)
\( m = -\dfrac{4}{3} \)
İSPATI GÖSTER
İki noktası bilinen doğrunun denklemini yazalım.
\( \dfrac{y - y_2}{x - x_2} = \dfrac{y_2 - y_1}{x_2 - x_1} \)
İçleri aralarında yer değiştirelim.
\( \dfrac{y - y_2}{y_2 - y_1} = \dfrac{x - x_2}{x_2 - x_1} \)
Bu iki noktanın bildiğimiz birer koordinatını denklemde yerine koyalım.
\( A(x_1, y_1) = A(x_1, 0) \)
\( B(x_2, y_2) = A(0, y_2) \)
\( \dfrac{y - y_2}{y_2 - 0} = \dfrac{x - 0}{0 - x_1} \)
\( \dfrac{y - y_2}{y_2} = -\dfrac{x}{x_1} \)
Eşitliğin sol tarafını yeniden düzenleyelim.
\( \dfrac{y}{y_2} - \dfrac{y_2}{y_2} = -\dfrac{x}{x_1} \)
\( \dfrac{y}{y_2} - 1 = -\dfrac{x}{x_1} \)
Değişkenli terimleri sol tarafa alırsak eksenleri kestiği noktalar bilinen doğrunun denklemini elde ederiz.
\( \dfrac{x}{x_1} + \dfrac{y}{y_2} = 1 \)
Aşağıda eksenleri kestiği noktalar verilen doğruların denklemlerini bulunuz.
(a) \( A(3, 0), B(0, -4) \)
(b) \( A(-2, 0), B(0, 7) \)
(c) \( A(\frac{2}{3}, 0), B(0, -\frac{3}{5}) \)
Çözümü GösterEksenleri \( (x_1, 0) \) ve \( (0, y_2) \) noktalarında kesen doğrunun denklemi aşağıdaki formülle bulunur.
\( \dfrac{x}{x_1} + \dfrac{y}{y_2} = 1 \)
(a) seçeneği:
\( A(3, 0), B(0, -4) \)
\( \dfrac{x}{3} + \dfrac{y}{-4} = 1 \)
\( 4x - 3y = 12 \)
\( 4x - 3y - 12 = 0 \)
(b) seçeneği:
\( A(-2, 0), B(0, 7) \)
\( \dfrac{x}{-2} + \dfrac{y}{7} = 1 \)
\( -7x + 2y = 14 \)
\( 7x - 2y + 14 = 0 \)
(c) seçeneği:
\( A(\frac{2}{3}, 0), B(0, -\frac{3}{5}) \)
\( \dfrac{x}{\frac{2}{3}} + \dfrac{y}{-\frac{3}{5}} = 1 \)
\( \dfrac{3x}{2} - \dfrac{5y}{3} = 1 \)
\( 9x - 10y = 6 \)
\( 9x - 10y - 6 = 0 \)
Orijinden Geçen Doğru
Orijinden geçen doğrular \( O(0, 0) \) noktasından geçtiği için sabit terimleri sıfırdır ve denklemleri aşağıdaki formdadır.
\( y = mx + 0 = mx \)
Orijinden geçen ve eğimi \( m = 4 \) olan doğrunun denklemi:
\( y = 4x \)
Analitik düzlemde \( 2x + 3y - 7 = 0 \) doğrusuna paralel olan ve \( A(-1, 2) \) noktasından geçen doğrunun denklemini bulunuz.
Çözümü Göster\( ax + by + c = 0 \) şeklinde kapalı denklemi verilen bir doğrunun eğimi \( m = -\frac{a}{b} \) olur.
\( 2x + 3y - 7 = 0 \)
\( m = -\dfrac{2}{3} \)
Paralel doğruların eğimleri birbirine eşittir.
\( A(-1, 2) \) noktasından geçen ve eğimi \( -\frac{2}{3} \) olan doğrunun denklemini bulalım.
\( y - y_1 = m(x - x_1) \)
\( y - 2 = -\dfrac{2}{3}(x - (-1)) \)
\( 3y - 6 = -2x - 2 \)
İstenen doğrunun denklemi aşağıdaki gibi bulunur.
\( 2x + 3y - 4 = 0 \)

Koordinat düzleminde \( A(2, -1) \) ve \( B(-3, 4) \) noktalarından geçen doğrunun üzerindeki ordinatı 7 olan noktanın apsisi kaçtır?
Çözümü GösterOrdinatı 7 olan noktaya \( C \), apsisine \( a \) diyelim.
\( C(a, 7) \)
\( (x_1, y_1) \) ve \( (x_2, y_2) \) noktalarından geçen doğrunun denklemi aşağıdaki formülle bulunur.
\( \dfrac{y - y_2}{x - x_2} = \dfrac{y_2 - y_1}{x_2 - x_1} \)
\( \dfrac{y - 4}{x - (-3)} = \dfrac{4 - (-1)}{(-3) - 2} \)
\( \dfrac{y - 4}{x + 3} = \dfrac{5}{-5} \)
\( y - 4 = -x - 3 \)
\( y = -x + 1 \)
\( C(a, 7) \) noktası bu doğrunun üzerinde olduğuna göre koordinatları doğru denklemini sağlar.
\( 7 = -a + 1 \)
\( a = -6 \)
\( C \) noktasının apsis değeri \( -6 \) olarak bulunur.

Yukarıdaki şekildeki \( d \) doğrusu üzerinde koordinatları toplamı 20 olan noktanın ordinatı kaçtır?
Çözümü Göster\( d \) doğrusunun denklemini bulalım.
\( y = mx + c \)
\( m = \dfrac{3k}{2k} = \dfrac{3}{2} \)
Orijinden geçen doğrunun sabit terimi sıfır olur.
\( y = \dfrac{3}{2}x \)
Koordinatları toplamı 20 olan noktaya \( A(m, \frac{3}{2}m) \) diyelim.
\( A \) noktasının koordinatları toplamı 20 olarak veriliyor.
\( m + \dfrac{3}{2}m = 20 \)
\( 2m + 3m = 40 \)
\( m = 8 \)
\( A \) noktasının ordinatını bulalım.
\( \dfrac{3}{2}(8) = 12 \) bulunur.
\( x = 3t + 1 \)
\( y = 2t - 3 \)
şeklinde parametrik denklemi olan doğrunun kapalı denklemi nedir?
Çözümü GösterVerilen birinci denklemde \( t \)'yi yalnız bırakalım.
\( x = 3t + 1 \)
\( t = \dfrac{x - 1}{3} \)
Bu \( t \) değerini ikinci denklemde yerine koyalım.
\( y = 2t - 3 \)
\( y = 2(\dfrac{x - 1}{3}) - 3 \)
\( y + 3 = 2(\dfrac{x - 1}{3}) \)
\( 3y + 9 = 2x - 2 \)
\( 3y - 2x + 11 = 0 \) bulunur.

Birim karelerden oluşan şekildeki düzlemde \( K \) noktasının koordinatları \( (-1, -3) \) olduğuna göre, \( [LM] \) doğrusunun denklemini yazınız.
Çözümü Göster\( K \) noktasının koordinatlarını kullanarak bu düzlemde orijinin ve eksenlerin konumunu belirleyelim.

Birim kareleri kullanarak \( L \) ve \( M \) noktalarının koordinatlarını bulalım.
\( L(2, 2) \)
\( M(7, -4) \)
\( (x_1, y_1) \) ve \( (x_2, y_2) \) noktalarından geçen doğrunun denklemi aşağıdaki formülle bulunur.
\( \dfrac{y - y_2}{x - x_2} = \dfrac{y_2 - y_1}{x_2 - x_1} \)
\( \dfrac{y - (-4)}{x - 7} = \dfrac{-4 - 2}{7 - 2} \)
\( \dfrac{y + 4}{x - 7} = \dfrac{-6}{5} \)
\( 5y + 20 = -6x + 42 \)
\( 6x + 5y - 22 = 0 \) bulunur.
\( 2x + y - 4 = 0 \) doğrusundan \( y \) eksenine indirilen dikmelerin orta noktasından geçen doğrunun denklemini bulunuz.
Çözümü GösterVerilen doğrunun eksenleri kestiği noktaları bulalım.
\( x = 0 \) için denklemi çözelim.
\( 2(0) + y - 4 = 0 \)
\( y = 4 \)
\( y = 0 \) için denklemi çözelim.
\( 2x + 0 - 4 = 0 \)
\( x = 2 \)
Buna göre doğru eksenleri \( (0, 4) \) ve \( (2, 0) \) noktalarında keser.

İstenen doğru \( 2x + y - 4 = 0 \) doğrusundan \( y \) eksenine indirilen dikmelerin orta noktasından geçtiğine göre, \( y \) eksenini aynı \( (0, 4) \) noktasında, \( x \) eksenini ise \( (1, 0) \) noktasında keser.
Eksenleri \( (x_1, 0) \) ve \( (0, y_2) \) noktalarında kesen doğrunun denklemi aşağıdaki formülle bulunur.
\( \dfrac{x}{x_1} + \dfrac{y}{y_2} = 1 \)
\( \dfrac{x}{1} + \dfrac{y}{4} = 1 \)
\( y = -4x + 4 \) bulunur.
Uç noktalar dahil olmak üzere, \( (5, 5) \) ve \( (155, 30) \) noktalarını birleştiren doğru parçası üzerinde koordinatları tam sayı olan kaç nokta bulunur?
Çözümü Göster\( (x_1, y_1) \) ve \( (x_2, y_2) \) noktalarından geçen doğrunun denklemi aşağıdaki formülle bulunur.
\( \dfrac{y - y_1}{x - x_1} = \dfrac{y_2 - y_1}{x_2 - x_1} \)
\( \dfrac{y - 5}{x - 5} = \dfrac{30 - 5}{155 - 5} \)
\( \dfrac{y - 5}{x - 5} = \dfrac{1}{6} \)
\( x - 5 = 6(y - 5) \)
\( x = 6y - 25 \)
Bu eşitlikte \( y \)'nin her tam sayı değeri için \( x \) de bir tam sayı değer alır.
Buna göre her \( y \in [5, 30] \) değeri için doğru parçası üzerinde koordinatları tam sayı olan bir nokta bulunur.
Bu aralıkta \( 30 - 5 + 1 = 26 \) tam sayı \( y \) değeri vardır.
Dolayısıyla verilen iki nokta arasında koordinatları tam sayı olan 26 nokta bulunur.
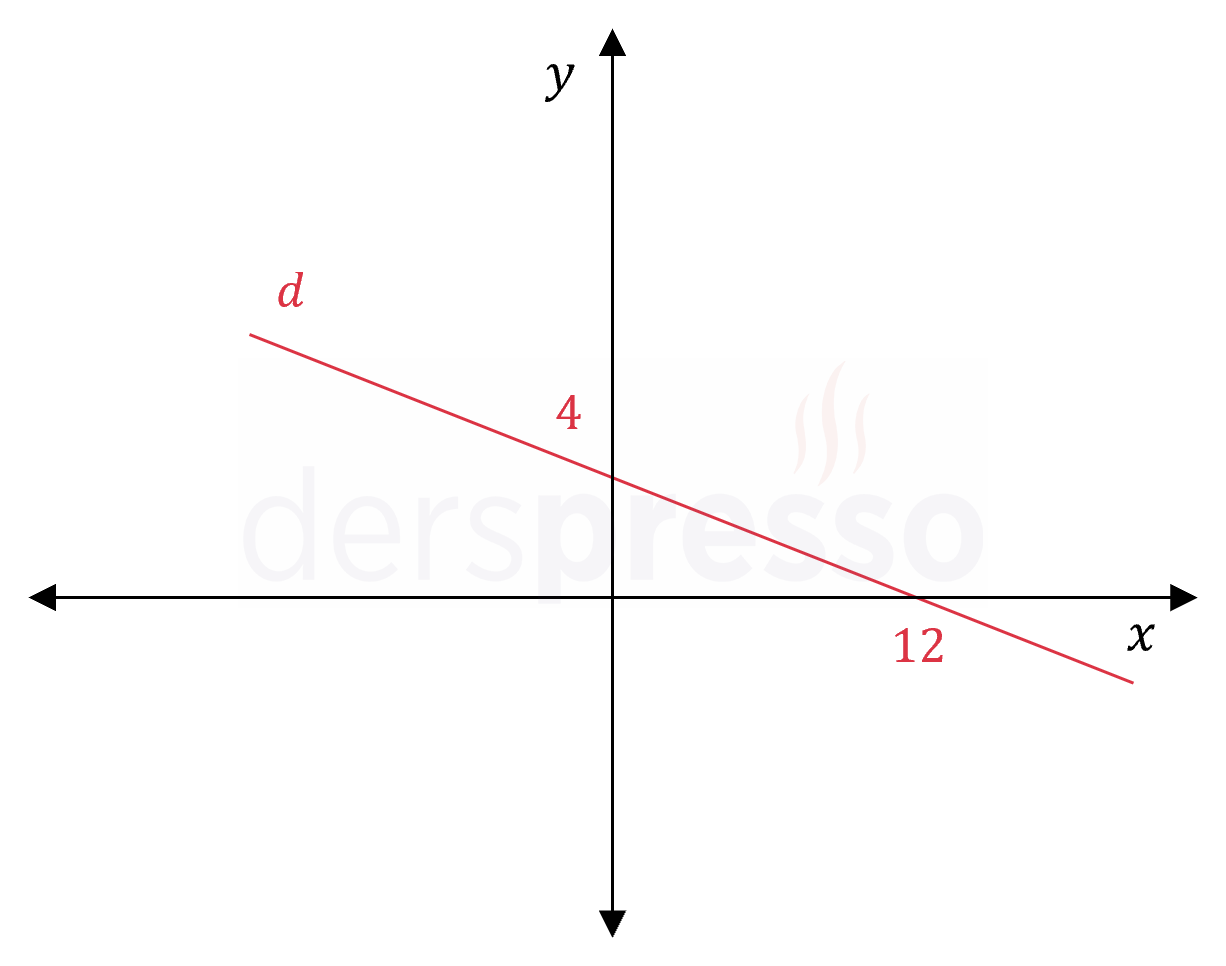
Yukarıdaki şekildeki \( d \) doğrusu üzerinde apsis ve ordinatının mutlak değerleri birbirine eşit olan noktaları bulunuz.
Çözümü GösterEksenleri \( (x_1, 0) \) ve \( (0, y_2) \) noktalarında kesen doğrunun denklemi aşağıdaki formülle bulunur.
\( \dfrac{x}{x_1} + \dfrac{y}{y_2} = 1 \)
\( \dfrac{x}{12} + \dfrac{y}{4} = 1 \)
\( x + 3y = 12 \)
\( y = -\dfrac{1}{3}x + 4 \)
Apsis ve ordinatının mutlak değerleri birbirine eşit olan noktalar \( A(a, a) \) ya da \( B(b, -b) \) formundadır.
\( A(a, a) \) formunda olan noktalar \( y = x \) doğrusu üzerinde, \( B(b, -b) \) formunda olan noktalar \( y = -x \) doğrusu üzerindedir.
\( y = x \) ve \( y = -x \) doğrularını çizelim ve \( d \) doğrusunun bir iki doğru ile kesişim noktalarını bulalım.
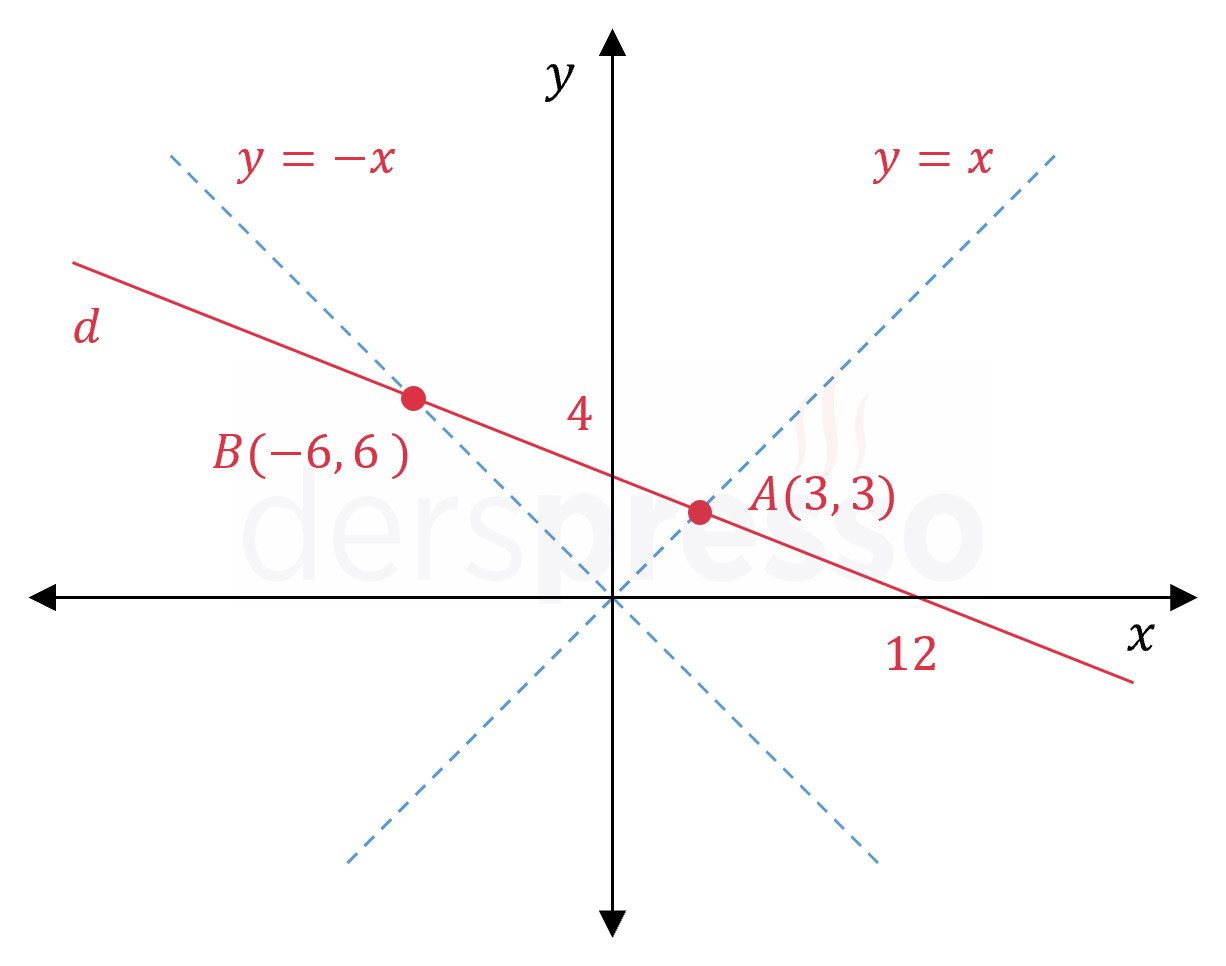
\( A \) noktasının koordinatlarını bulmak için \( d \) doğrusunun denkleminde \( (x, y) = (a, a) \) yazalım.
\( a = -\dfrac{1}{3}a + 4 \)
\( \dfrac{4}{3}a = 4 \)
\( a = 3 \)
\( A(a, a) = A(3, 3) \)
\( B \) noktasının koordinatlarını bulmak için \( d \) doğrusunun denkleminde \( (x, y) = (b, -b) \) yazalım.
\( -b = -\dfrac{1}{3}b + 4 \)
\( -\dfrac{2}{3}b = 4 \)
\( b = -6 \)
\( B(b, -b) = B(-6, 6) \)
\( d \) doğrusu üzerinde apsis ve ordinatının mutlak değeri birbirine eşit olan iki nokta aşağıdaki gibidir.
\( A(3, 3), \quad B(-6, 6) \)
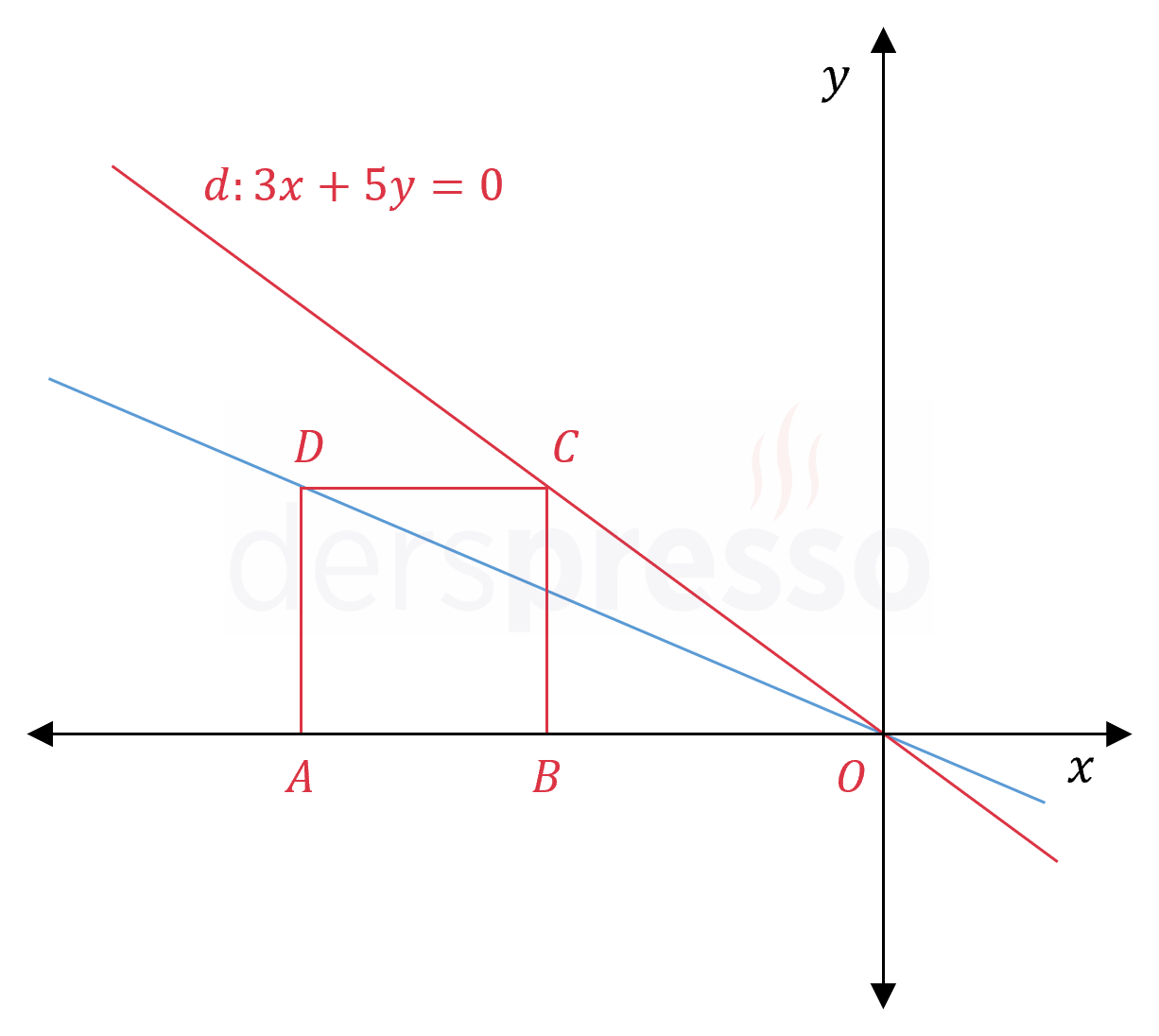
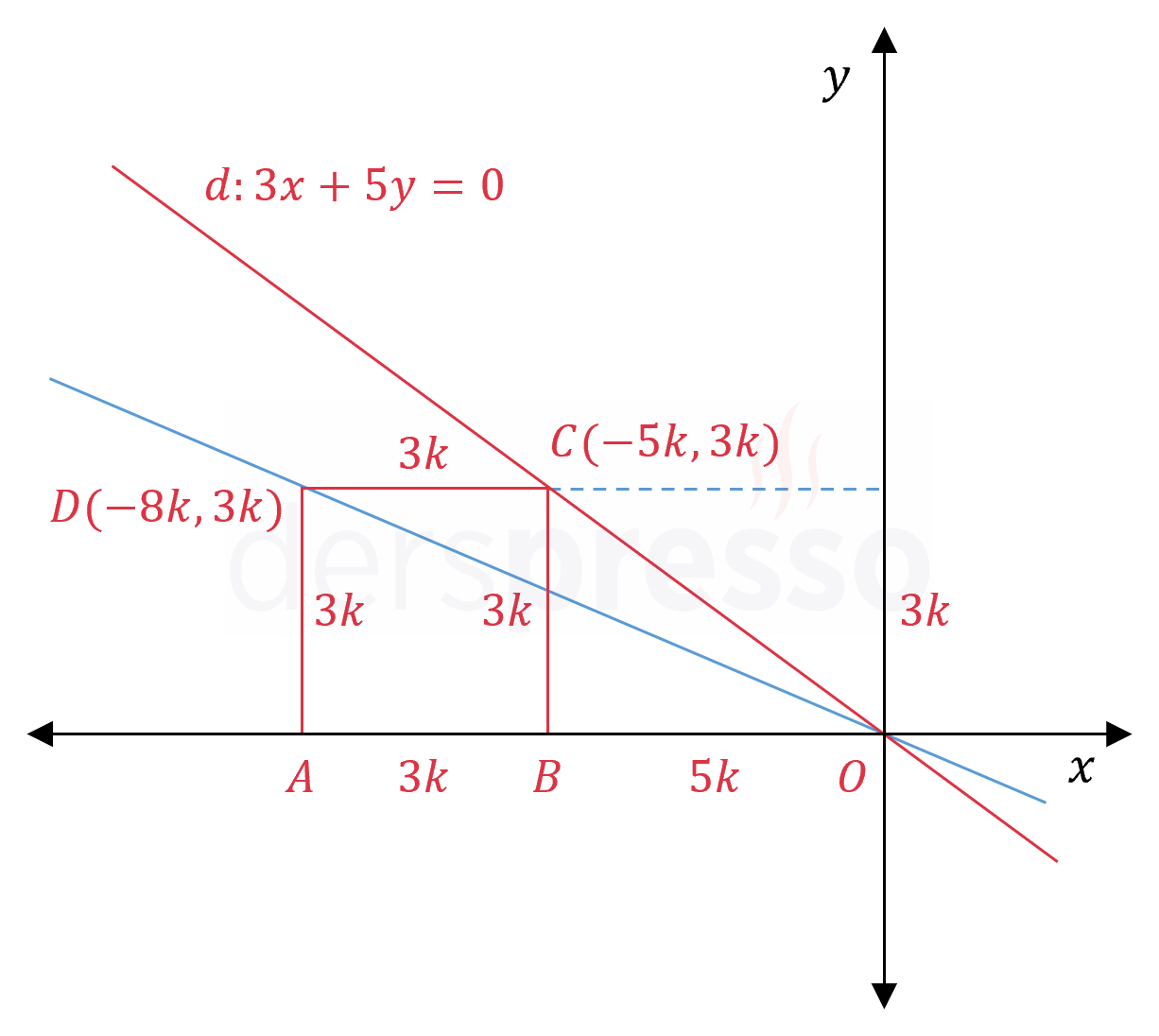
Şekildeki \( ABCD \) karesinin \( C \) köşesi \( d: 3x + 5y = 0 \) doğrusu üzerinde olduğuna göre, \( D \) noktasından ve orijinden geçen doğrunun denklemini bulunuz.
Çözümü Göster\( d \) doğrusunun denkleminini kullanarak \( C \) noktasının koordinatlarını bulalım.
\( C \) noktasının ordinatına \( 3k \) diyelim.
\( 3x = -5(3k) \)
\( x = -5k \)
\( C(-5k, 3k) \)
Buna göre karenin bir kenarının uzunluğu \( 3k \) olur.
\( D(-8k, 3k) \)
\( D \) noktasından ve orijinden geçen doğrunun eğimini bulalım.
\( m = \dfrac{y_2 - y_1}{x_2 - x_1} \)
\( = \dfrac{3k - 0}{-8k - 0} = -\dfrac{3}{8} \)
Orijinden geçen ve eğimi \( m \) olan doğrunun denklemi aşağıdaki formülle bulunur.
\( y = mx \)
\( y = -\dfrac{3}{8}x \)