Doğrunun Analitiği Formülleri
Bir Nokta ve Doğru Arası Uzaklık
Bir doğru ve bu doğru üzerinde bulunmayan bir nokta arasındaki en kısa uzaklık, noktadan doğruya çizilen dikmenin uzunluğudur.
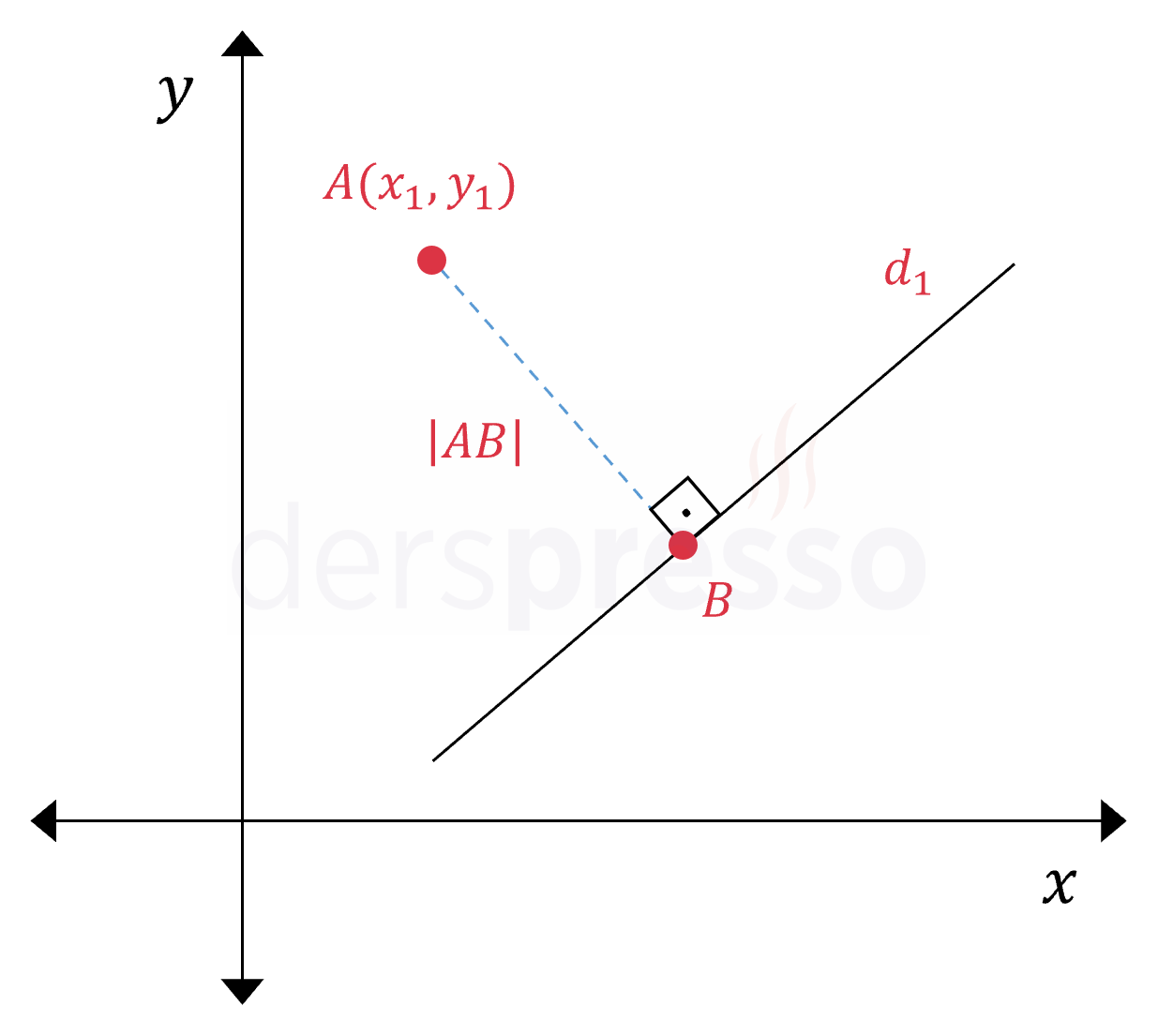
\( A(x_1, y_1) \)
\( d_1: ax + by + c = 0 \) olmak üzere,
\( A \) noktası ve \( d_1 \) doğrusu arasındaki uzaklık:
\( \abs{AB} = \dfrac{\abs{ax_1 + by_1 + c}}{\sqrt{a^2 + b^2}} \)
\( A(-4, 1) \) noktası ve \( 3x - 4y + 6 = 0 \) doğrusu arasındaki uzaklık:
\( = \dfrac{\abs{3(-4) - 4(1) + 6}}{\sqrt{3^2 + (-4)^2}} \)
\( = \dfrac{\abs{-10}}{5} = 2 \)
İki Paralel Doğru Arası Uzaklık
Birbirine paralel iki doğru arasındaki en kısa uzaklık, iki doğruya da dik olan doğru parçasının uzunluğudur.

\( d_1: ax + by + c_1 = 0 \)
\( d_2: ax + by + c_2 = 0 \)
\( d_1 \) ve \( d_2 \) doğruları arasındaki uzaklık:
\( \abs{AB} = \dfrac{\abs{c_2 - c_1}}{\sqrt{a^2 + b^2}} \)
\( 2x - y + 7 = 0 \) ve \( 2x - y - 3 = 0 \) doğruları arasındaki uzaklık:
\( = \dfrac{\abs{-3 - 7}}{\sqrt{2^2 + (-1)^2}} \)
\( = \dfrac{\abs{-10}}{\sqrt{5}} = 2\sqrt{5} \)
Paralel İki Doğruya Eşit Uzaklıktaki Paralel Doğrunun Denklemi
Birbirine paralel iki doğruya eşit uzaklıktaki doğru, yukarıdaki iki doğru arasındaki uzaklık formülüne göre iki doğruya da eşit uzaklıktaki doğrudur.

\( d_1: ax + by + c_1 = 0 \)
\( d_2: ax + by + c_2 = 0 \)
\( d_1 \) ve \( d_2 \) doğrularına eşit uzaklıktaki \( d_3 \) doğrusunun denklemi:
\( d_3: ax + by + \dfrac{c_1 + c_2}{2} = 0 \)
\( 2x - y + 7 = 0 \) ve \( 2x - y - 3 = 0 \) doğrularına eşit uzaklıktaki doğrunun denklemi:
\( 2x - y + \dfrac{7 + (-3)}{2} = 0 \)
\( 2x - y + 2 = 0 \)
Kesişen İki Doğru Arasındaki Açı
Kesişen iki doğru arasında oluşan \( \alpha \) açısının tanjant değeri, doğruların eğimleri cinsinden aşağıdaki formülle bulunur.

Eğimleri \( m_1 \) ve \( m_2 \) olan iki doğru arasındaki açının tanjantı:
\( \tan{\alpha} = \dfrac{m_2 - m_1}{1 + m_1 \cdot m_2} \)
\( y = 3x + 2 \) ve \( y = -x - 5 \) doğruları arasındaki açının tanjantı:
\( m_1 = 3, \quad m_2 = -1 \)
\( \tan{\alpha} = \dfrac{-1 - 3}{1 + (-1) \cdot 3} \)
\( = \dfrac{-4}{-2} = 2 \)
Buna göre iki doğru arasındaki açı tanjant değeri \( 2 \) olan açıdır.
İSPATI GÖSTER

\( d_1 \) ve \( d_2 \) doğrularının eğim açılarına sırasıyla \( \theta \) ve \( \beta \) diyelim.
\( \beta \) açısı \( ABC \) üçgeninin bir dış açısı olduğu için kendisine komşu olmayan iki iç açının toplamına eşittir.
\( \beta = \alpha + \theta \)
\( \alpha = \beta - \theta \)
Eşitliğin iki tarafının tanjantını alalım.
\( \tan{\alpha} = \tan(\beta - \theta) \)
Eşitliğin sağ tarafına tanjant fark formülünü uygulayalım.
\( \tan{\alpha} = \dfrac{\tan{\beta} - \tan{\theta}}{1 + \tan{\beta} \cdot \tan{\theta}} \)
\( d_1 \) ve \( d_2 \) doğrularının eğim açılarının tanjant değerleri doğruların eğimine eşittir.
\( m_1 = \tan{\theta} \)
\( m_2 = \tan{\beta} \)
Bu eğim değerlerini formülde yerine koyalım.
\( \tan{\alpha} = \dfrac{m_2 - m_1}{1 + m_1 \cdot m_2} \)
İki Doğrunun Açıortay Denklemleri
Kesişen iki doğrunun açıortayı olan doğruların denklemleri aşağıdaki formülle bulunur.
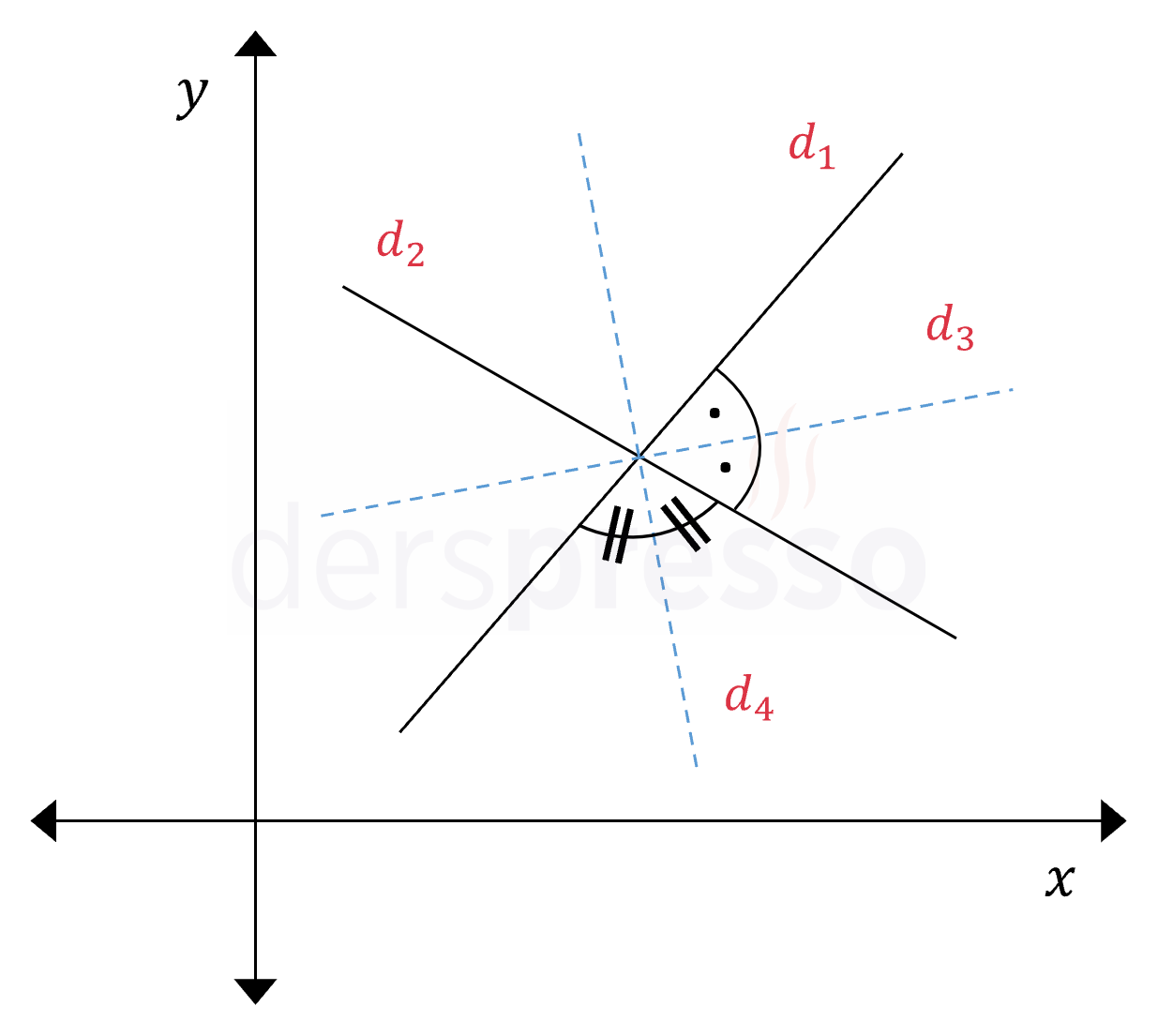
\( d_1: ax + by + c = 0 \)
\( d_2: dx + ey + f = 0 \)
\( d_1 \) ve \( d_2 \) doğrularının açıortayı olan \( d_3 \) ve \( d_4 \) doğrularının denklemleri:
\( d_3: \dfrac{ax + by + c}{\sqrt{a^2 + b^2}} = +\dfrac{dx + ey + f}{\sqrt{d^2 + e^2}} \)
\( d_4: \dfrac{ax + by + c}{\sqrt{a^2 + b^2}} = -\dfrac{dx + ey + f}{\sqrt{d^2 + e^2}} \)
\( d_1: x - 3y - 5 = 0 \) ve \( d_2: 3x + y + 1 = 0 \) doğrularının açıortayı olan doğruların denklemleri:
Birinci açıortay doğrusu (\( d_3 \)):
\( \dfrac{x - 3y - 5}{\sqrt{1^2 + (-3)^2}} = +\dfrac{3x + y + 1}{\sqrt{3^2 + 1^2}} \)
\( \dfrac{x - 3y - 5}{\sqrt{10}} = +\dfrac{3x + y + 1}{\sqrt{10}} \)
\( x - 3y - 5 = 3x + y + 1 \)
\( d_3: x + 2y + 3 = 0 \)
İkinci açıortay doğrusu (\( d_4 \)):
\( \dfrac{x - 3y - 5}{\sqrt{1^2 + (-3)^2}} = -\dfrac{3x + y + 1}{\sqrt{3^2 + 1^2}} \)
\( \dfrac{x - 3y - 5}{\sqrt{10}} = -\dfrac{3x + y + 1}{\sqrt{10}} \)
\( x - 3y - 5 = -3x - y - 1 \)
\( d_4: 2x - y - 2 = 0 \)
\( A(1, m) \) noktasının \( 3x + 2y + 2 = 0 \) doğrusuna en yakın uzaklığı \( \sqrt{13} \text{ br} \) olduğuna göre, \( m \)'nin alabileceği değerlerin toplamı kaçtır?
Çözümü Göster\( (x_1, y_1) \) noktası ve \( ax + by + c = 0 \) doğrusu arasındaki uzaklık aşağıdaki formülle bulunur.
\( d = \dfrac{\abs{ax_1 + by_1 + c}}{\sqrt{a^2 + b^2}} \)
\( \sqrt{13} = \dfrac{\abs{3(1) + 2(m) + 2}}{\sqrt{3^2 + 2^2}} \)
\( \sqrt{13} = \dfrac{\abs{2m + 5}}{\sqrt{13}} \)
\( \abs{2m + 5} = 13 \)
Bu eşitlik iki durumda sağlanır.
Durum 1:
\( 2m + 5 = 13 \)
\( m = 4 \)
Durum 2:
\( 2m + 5 = -13 \)
\( m = -9 \)
\( m \)'nin alabileceği değerler toplamı \( 4 + (-9) = -5 \) olarak bulunur.
Bu iki nokta aşağıdaki şekilde gösterilmiştir.

\( 8x - 6y + 3 = 0 \) doğrusuna uzaklığı 2 birim olan doğruların denklemlerini bulunuz.
Çözümü GösterVerilen doğruya 2 birim uzaklıktaki doğrulara \( d_1 \) ve \( d_2 \) diyelim. Bu doğrular \( d \) doğrusuna sabit uzaklıkta bulunan doğrular oldukları için \( d \) doğrusuna paraleldir, dolayısıyla denklemlerinin \( a \) ve \( b \) katsayıları aynı, \( c \) katsayıları farklı olur.

Verilen doğrulara 2 birim uzaklıktaki doğruların denklemini aşağıdaki gibi yazabiliriz.
\( 8x - 6y + c = 0 \)
Denklemleri \( ax + by + c_1 = 0 \) ve \( ax + by + c_2 = 0 \) olan iki paralel doğru arasındaki uzaklık aşağıdaki formülle bulunur.
\( d = \dfrac{\abs{c_2 - c_1}}{\sqrt{a^2 + b^2}} \)
\( 2 = \dfrac{\abs{c - 3}}{\sqrt{8^2 + (-6)^2}} \)
\( \abs{c - 3} = 20 \)
Bu eşitlik iki durumda sağlanır.
Durum 1:
\( c - 3 = 20 \)
\( c = 23 \)
Durum 2:
\( c - 3 = -20 \)
\( c = -17 \)
Buna göre verilen doğruya 2 birim uzaklıktaki doğruların denklemleri aşağıdaki gibidir.
\( d_1: 8x - 6y + 23 = 0 \)
\( d_2: 8x - 6y - 17 = 0 \)
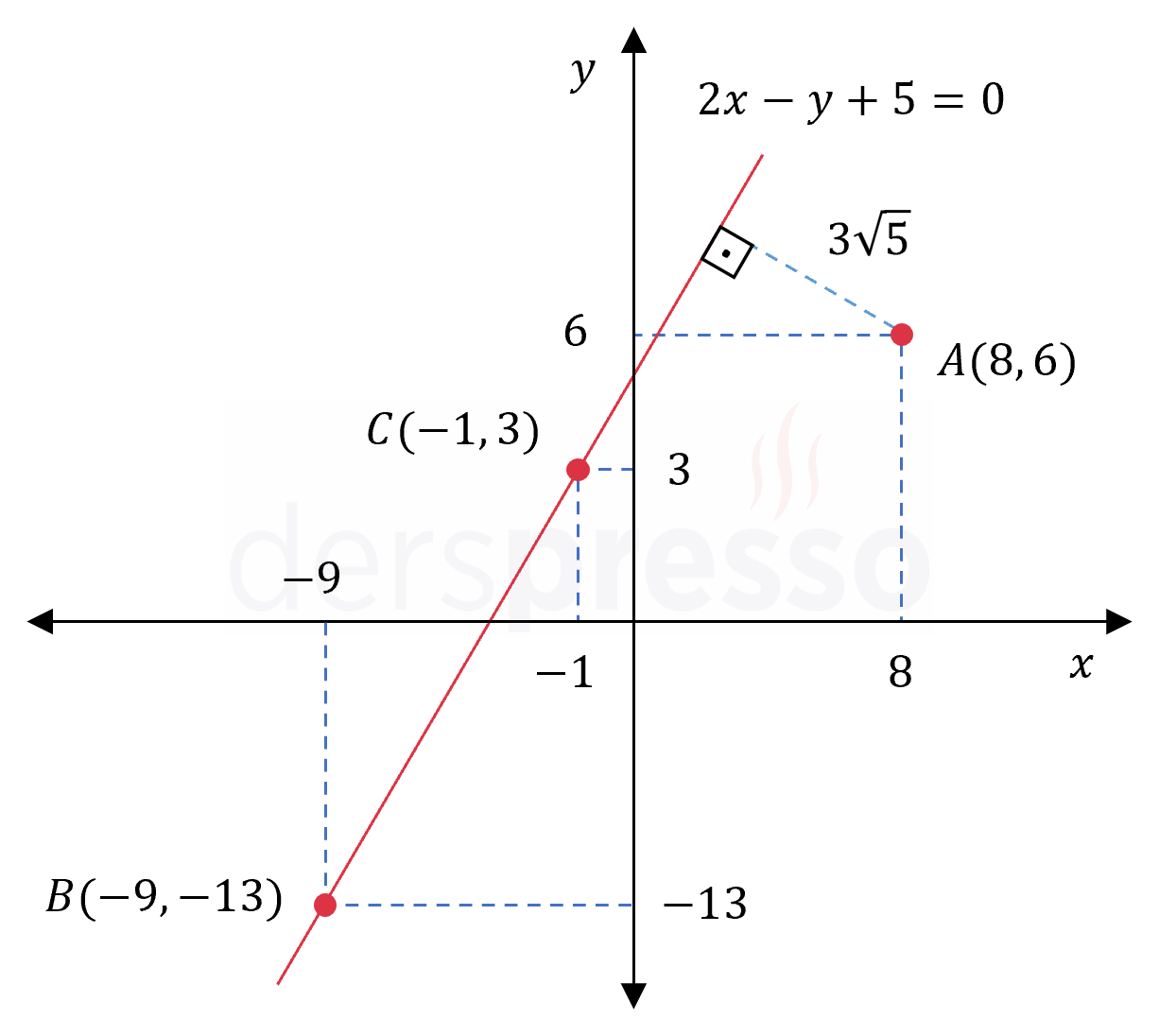
\( A(8, 6) \) noktasının \( B(-9, -13) \) ve \( C(-1, 3) \) noktaları ile aynı doğru üzerinde olabilmesi için konumu en az kaç birim değiştirilmelidir?
Çözümü GösterÖncelikle \( B \) ve \( C \) noktalarından geçen doğrunun denklemini bulalım.
\( (x_1, y_1) \) ve \( (x_2, y_2) \) noktalarından geçen doğrunun denklemi aşağıdaki formülle bulunur.
\( \dfrac{y - y_2}{x - x_2} = \dfrac{y_2 - y_1}{x_2 - x_1} \)
\( \dfrac{y - 3}{x - (-1)} = \dfrac{3 - (-13)}{-1 - (-9)} \)
\( y - 3 = 2x + 2 \)
\( 2x - y + 5 = 0 \)
\( A \) noktasının diğer iki noktanın belirttiği doğru üzerinde olabilmesi için doğru ile arasındaki en kısa uzaklık kadar yer değiştirmelidir.
\( A \) noktasının doğruya dik uzaklığını bulalım.
\( (x_1, y_1) \) noktası ve \( ax + by + c = 0 \) doğrusu arasındaki uzaklık aşağıdaki formülle bulunur.
\( d = \dfrac{\abs{ax_1 + by_1 + c}}{\sqrt{a^2 + b^2}} \)
\( = \dfrac{\abs{2(8) - 6 + 5}}{\sqrt{2^2 + 1^2}} \)
\( = \dfrac{15}{\sqrt{5}} = 3\sqrt{5} \) bulunur.
Koordinat düzlemindeki bir karenin karşılıklı iki kenarı \( d_1: 2x - 3y + 4 = 0 \) ve \( d_2: 4x - 6y + 5 = 0 \) doğruları üzerinde bulunuyor.
Buna göre bu karenin alanı kaçtır?
Çözümü GösterKarenin karşılıklı iki kenarı verilen iki doğru üzerinde bulunduğu için, doğrular arasındaki en kısa uzaklık karenin bir kenar uzunluğuna eşit olur.
Doğru denklemlerinin katsayılarının oranını inceleyelim.
\( \dfrac{2}{4} = \dfrac{-3}{-6} \ne \dfrac{4}{5} \)
\( x \) ve \( y \) katsayılarının oranı eşit, sabit terimlerin oranı bu orandan farklı olduğu için, \( d_1 \) ve \( d_2 \) doğruları (olmasını beklediğimiz gibi) paraleldir.
Denklemleri \( ax + by + c_1 = 0 \) ve \( ax + by + c_2 = 0 \) olan iki paralel doğru arasındaki uzaklık aşağıdaki formülle bulunur.
\( d = \dfrac{\abs{c_2 - c_1}}{\sqrt{a^2 + b^2}} \)
Verilen doğru denklemlerindeki \( x \) ve \( y \) katsayılarını eşitlemek için \( d_1 \) denkleminin taraflarını 2 ile çarpalım.
\( d_1: 4x - 6y + 8 = 0 \)
\( d_2: 4x - 6y + 5 = 0 \)
İki doğru arasındaki uzaklığı bulalım.
\( d = \dfrac{\abs{5 - 8}}{\sqrt{4^2 + (-6)^2}} = \dfrac{3}{\sqrt{52}} \)
Bulduğumuz değer karenin bir kenar uzunluğuna eşittir.
Karenin alanını bulalım.
\( A = (\dfrac{3}{\sqrt{52}})^2 = \dfrac{9}{52} \) bulunur.
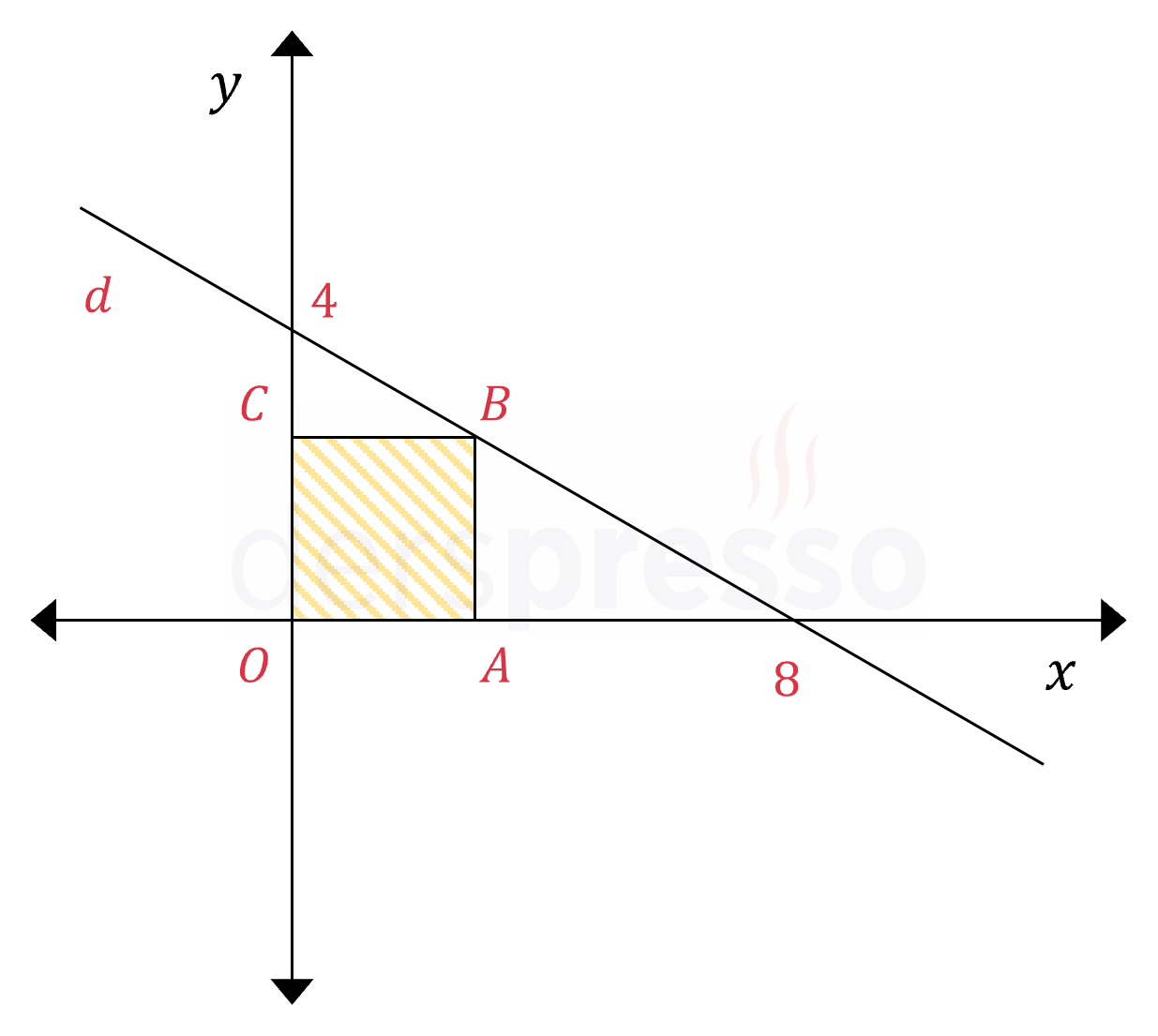
Şekildeki \( OABC \) karesinin \( B \) köşesi \( d \) doğrusu üzerinde olduğuna göre, \( A(OABC) \) kaç birimkaredir?
Çözümü GösterKarenin bir kenar uzunluğuna \( a \) birim diyelim.
\( \abs{OA} = \abs{AB} = a \)
\( B(a, a) \)
Eksenleri \( (x_1, 0) \) ve \( (0, y_2) \) noktalarında kesen doğrunun denklemi aşağıdaki formülle bulunur.
\( \dfrac{x}{x_1} + \dfrac{y}{y_2} = 1 \)
\( \dfrac{x}{8} + \dfrac{y}{4} = 1 \)
\( B \) noktası \( d \) doğrusu üzerinde olduğu için koordinatları doğru denklemini sağlar.
\( \dfrac{a}{8} + \dfrac{a}{4} = 1 \)
\( a = \dfrac{8}{3} \)
Karenin alanını hesaplayalım.
\( A(OABC) = a^2 \)
\( = \left( \dfrac{8}{3} \right)^2 = \dfrac{64}{9} \) birimkare bulunur.

\( KLM \) üçgeninin \( [LM] \) kenarına ait kenarortay doğrusu şekildeki gibidir.
Buna göre bu doğru \( x \) eksenini hangi noktada keser?
Çözümü Göster\( [LM] \) kenarının orta noktasına \( N \) diyelim.

Orta nokta formülünü kullanarak \( N(x_0, y_0) \) noktasının koordinatlarını bulalım.
\( x_0 = \dfrac{x_1 + x_2}{2} \)
\( = \dfrac{-5 + (-1)}{2} = -3 \)
\( y_0 = \dfrac{y_1 + y_2}{2} \)
\( = \dfrac{2 + 2}{2} = 2 \)
\( N(-3, 2) \)
\( K \) ve \( N \) noktalarını kullanarak kenarortay doğrusunun denklemini bulalım.
\( (x_1, y_1) \) ve \( (x_2, y_2) \) noktalarından geçen doğrunun denklemi aşağıdaki formülle bulunur.
\( \dfrac{y - y_2}{x - x_2} = \dfrac{y_2 - y_1}{x_2 - x_1} \)
\( \dfrac{y - 2}{x - (-3)} = \dfrac{2 - 5}{-3 - (-2)} \)
\( \dfrac{y - 2}{x + 3} = 3 \)
\( y = 3x + 11 \)
Bu doğrunun \( x \) eksenini kestiği noktaya \( P(a, 0) \) diyelim.
\( 0 = 3a + 11 \)
\( a = -\dfrac{11}{3} \)
\( P(a, 0) = P(-\dfrac{11}{3}, 0) \) bulunur.
\( A(7, 8) \) noktasının \( d: 2x + 3y - 12 = 0 \) doğrusu üzerinde en yakın olduğu noktanın koordinatları \( B(m, n) \) olduğuna göre, \( m + n \) kaçtır?
Çözümü Göster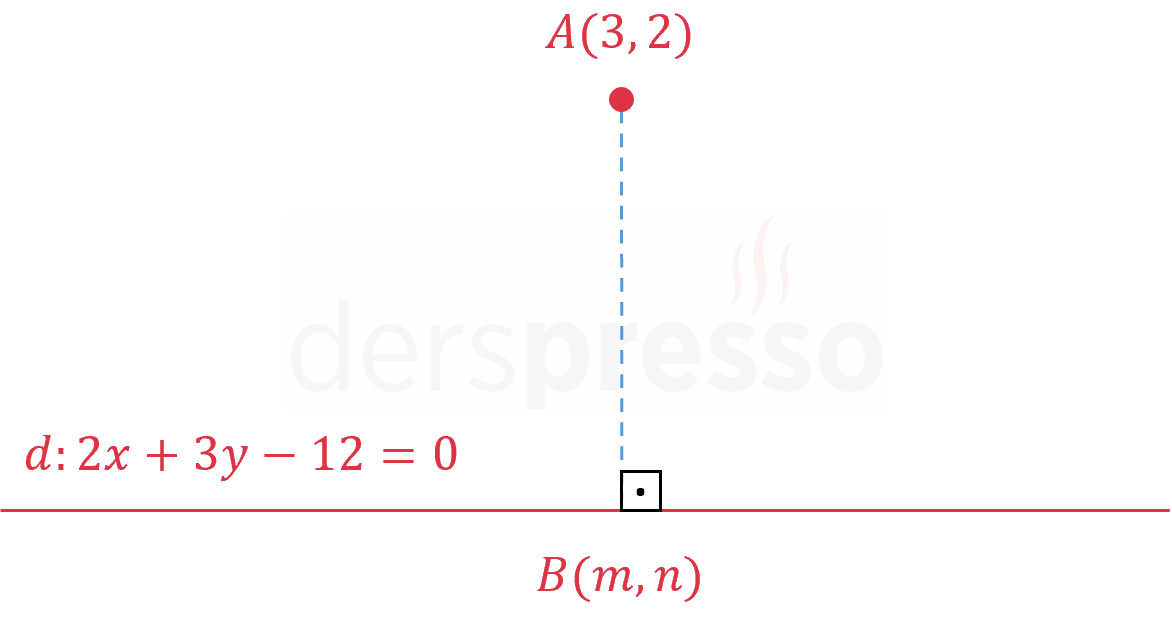
\( A(7, 8) \) noktasının \( d \) doğrusu üzerinde en yakın olduğu nokta \( B(m, n) \) ise çizilecek \( [AB] \) doğru parçası \( d \) doğrusunu dik keser.
\( A \) ve \( B \) noktalarını birleştiren doğru parçasının eğimine \( m_{AB} \) diyelim.
\( (x_1, y_1) \) ve \( (x_2, y_2) \) noktalarından geçen doğrunun eğimi aşağıdaki formülle bulunur.
\( m = \dfrac{y_2 - y_1}{x_2 - x_1} \)
\( m_{AB} = \dfrac{n - 8}{m - 7} \)
\( ax + by + c = 0 \) şeklinde kapalı denklemi verilen bir doğrunun eğimi \( m = -\frac{a}{b} \) olur.
\( m_{d} = -\dfrac{2}{3} \)
Birbirine dik olan doğruların eğimleri çarpımı -1 olur.
\( m_{AB} \cdot m_{d} = -1 \)
\( \dfrac{n - 8}{m - 7} \cdot (-\dfrac{2}{3}) = -1 \)
\( \dfrac{n - 8}{m - 7} = \dfrac{3}{2} \)
\( 2n - 16 = 3m - 21 \)
\( 3m - 2n - 5 = 0 \)
\( m \) ve \( n \) bilinmeyenlerini içeren ikinci bir denklem elde etmeye çalışalım.
\( B \) noktası \( d \) doğrusu üzerinde olduğu için koordinatları \( d \) doğrusunun denklemini sağlar.
\( 2m + 3n - 12 = 0 \)
Bulduğumuz iki bilinmeyenli iki denklemi ortak çözelim.
\( (1) 3m - 2n - 5 = 0 \)
\( (2) 2m + 3n - 12 = 0 \)
Birinci denklemin taraflarını 3 ile, ikinci denklemin taraflarını 2 ile çarpalım ve denklemleri taraf tarafa toplayalım.
\( (1) 9m - 6n - 15 = 0 \)
\( (2) 4m + 6n - 24 = 0 \)
\( 13m - 39 = 0 \)
\( m = 3 \)
Birinci denklemde \( m = 3 \) yazalım.
\( 3(3) - 2n - 5 = 0 \)
\( n = 2 \)
\( m + n = 3 + 2 = 5 \) bulunur.
Koordinat düzlemindeki \( d: x + 2y - 12 = 0 \) doğrusunun orijine en yakın noktasının koordinatları nedir?
Çözümü Göster\( d \) doğrusunun \( y \) eksenini kestiği noktaya \( A(0, a) \), \( x \) eksenini kestiği noktaya \( B(b, 0) \) diyelim.
\( d \) doğrusunun \( y \) eksenini kestiği noktayı bulalım.
\( 0 + 2a - 12 = 0 \)
\( a = 6 \)
\( A(0, 6) \)
\( d \) doğrusunun \( x \) eksenini kestiği noktayı bulalım.
\( b + 2(0) - 12 = 0 \)
\( b = 12 \)
\( B(12, 0) \)

\( \abs{AB} \) uzunluğunu Pisagor teoremi ile bulalım.
\( \abs{AB}^2 = \abs{AO}^2 + \abs{BO}^2 \)
\( \abs{AB}^2 = 6^2 + 12^2 \)
\( \abs{AB} = 6\sqrt{5} \)
\( d \) doğrusunun orijine en yakın noktasını bulmak için orijinden doğruya bir dikme çizelim ve doğruyu kestiği noktaya \( C \) diyelim.
\( \abs{CO} \) uzunluğunu bulalım.
\( AOB \) dik üçgeninde alan bağıntısını yazalım.
\( \abs{AO} \cdot \abs{BO} = \abs{AB} \cdot \abs{CO} \)
\( 6 \cdot 12 = 6\sqrt{5} \cdot \abs{CO} \)
\( \abs{CO} = \dfrac{12\sqrt{5}}{5} \)
\( BCO \) dik üçgeninde \( C \) noktasından \( x \) eksenine bir dikme indirelim ve dikmenin ekseni kestiği noktaya \( D \) diyelim.
\( BCO \) üçgeninde Öklid bağıntısını uygulayalım.
\( \abs{CO}^2 = \abs{OD} \cdot \abs{OB} \)
\( (\dfrac{12\sqrt{5}}{5})^2 = \abs{OD} \cdot 12 \)
\( \dfrac{144 \cdot 5}{25} = \abs{OD} \cdot 12 \)
\( \abs{OD} = \dfrac{12}{5} \)
Buna göre \( C \) noktasının apsisi \( \frac{12}{5} \) olur.
\( C \) noktası \( d \) doğrusu üzerinde olduğu için apsis değerini denklemde yerine yazdığımızda ordinat değerini buluruz.
\( \dfrac{12}{5} + 2y - 12 = 0 \)
\( y = \dfrac{24}{5} \)
\( C(\dfrac{12}{5}, \dfrac{24}{5}) \) bulunur.
\( d_1: 2x + y - 4 = 0 \) doğrusu üzerinde bulunan ve \( d_2: x - y + 1 = 0 \) doğrusuna uzaklığı \( 3\sqrt{2} \) birim olan noktaların koordinatlarını bulunuz.
Çözümü Göster\( d_1 \) doğrusu üzerindeki orijine en yakın noktaya \( A \), apsisine \( n \) diyelim.
\( A \) noktasının ordinatını bulmak için doğru denklemini kullanalım.
\( 2n + y - 4 = 0 \)
\( y = 4 - 2n \)
\( A(n, 4 - 2n) \)
\( d_2 \) doğrusunun \( A(n, 4 - 2n) \) noktasına olan uzaklığını bulalım.
\( (x_1, y_1) \) noktası ve \( ax + by + c = 0 \) doğrusu arasındaki uzaklık aşağıdaki formülle bulunur.
\( d = \dfrac{\abs{ax_1 + by_1 + c}}{\sqrt{a^2 + b^2}} \)
\( 3\sqrt{2} = \dfrac{\abs{1(n) + (-1)(4 - 2n) + 1}}{\sqrt{1^2 + (-1)^2}} \)
\( 3\sqrt{2} = \dfrac{\abs{n + 2n - 4 + 1}}{\sqrt{2}} \)
\( \abs{3n - 3} = 6 \)
\( \abs{n - 1} = 2 \)
Bu eşitlik iki durumda sağlanır.
Durum 1:
\( n - 1 = 2 \)
\( n = 3 \)
Bu değer için \( A \) noktasının koordinatlarını bulalım.
\( A(3, 4 - 2(3)) = A(3, -2) \)
Durum 2:
\( n - 1 = -2 \)
\( n = -1 \)
Bu değer için \( A \) noktasının koordinatlarını bulalım.
\( A(-1, 4 - 2(-1)) = A(-1, 6) \)
Soruda verilen doğrular ve bu iki nokta aşağıdaki şekilde gösterilmiştir.

\( A(2, 3) \) noktasından geçen ve \( B(4, 5) \) noktasına en yakın uzaklığı en büyük olan doğrunun denklemini bulunuz.
Çözümü GösterDenklemi istenen doğruya \( d \) diyelim.
\( A \) noktası \( d \) doğrusu üzerindedir.
\( B \) noktasının \( d \) doğrusuna en yakın uzaklığının en büyük olması için \( [AB] \) doğru parçası \( d \) doğrusunu dik kesmelidir, bir diğer ifadeyle bu en yakın uzaklık \( [AB] \) doğru parçasının uzunluğuna eşit olmalıdır.
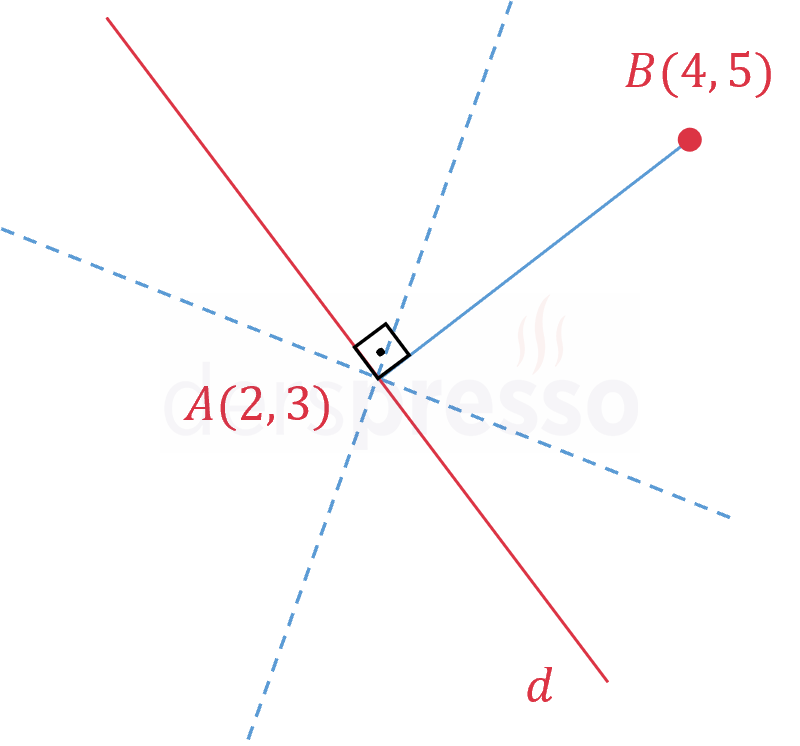
\( [AB] \) doğru parçasının eğimini bulalım.
\( (x_1, y_1) \) ve \( (x_2, y_2) \) noktalarından geçen doğrunun eğimi aşağıdaki formülle bulunur.
\( m = \dfrac{y_2 - y_1}{x_2 - x_1} \)
\( = \dfrac{5 - 3}{4 - 2} = 1 \)
Birbirine dik iki doğrunun eğimleri çarpımı -1 olur.
\( m_{AB} \cdot m_d = -1 \)
\( m_d = -1 \)
\( d \) doğrusunun denklemini bulalım.
\( (x_1, y_1) \) noktasından geçen ve eğimi \( m \) olan doğrunun denklemi aşağıdaki formülle bulunur.
\( y - y_1 = m(x - x_1) \)
\( y - 3 = -1(x - 2) \)
\( y = -x + 5 \) bulunur.
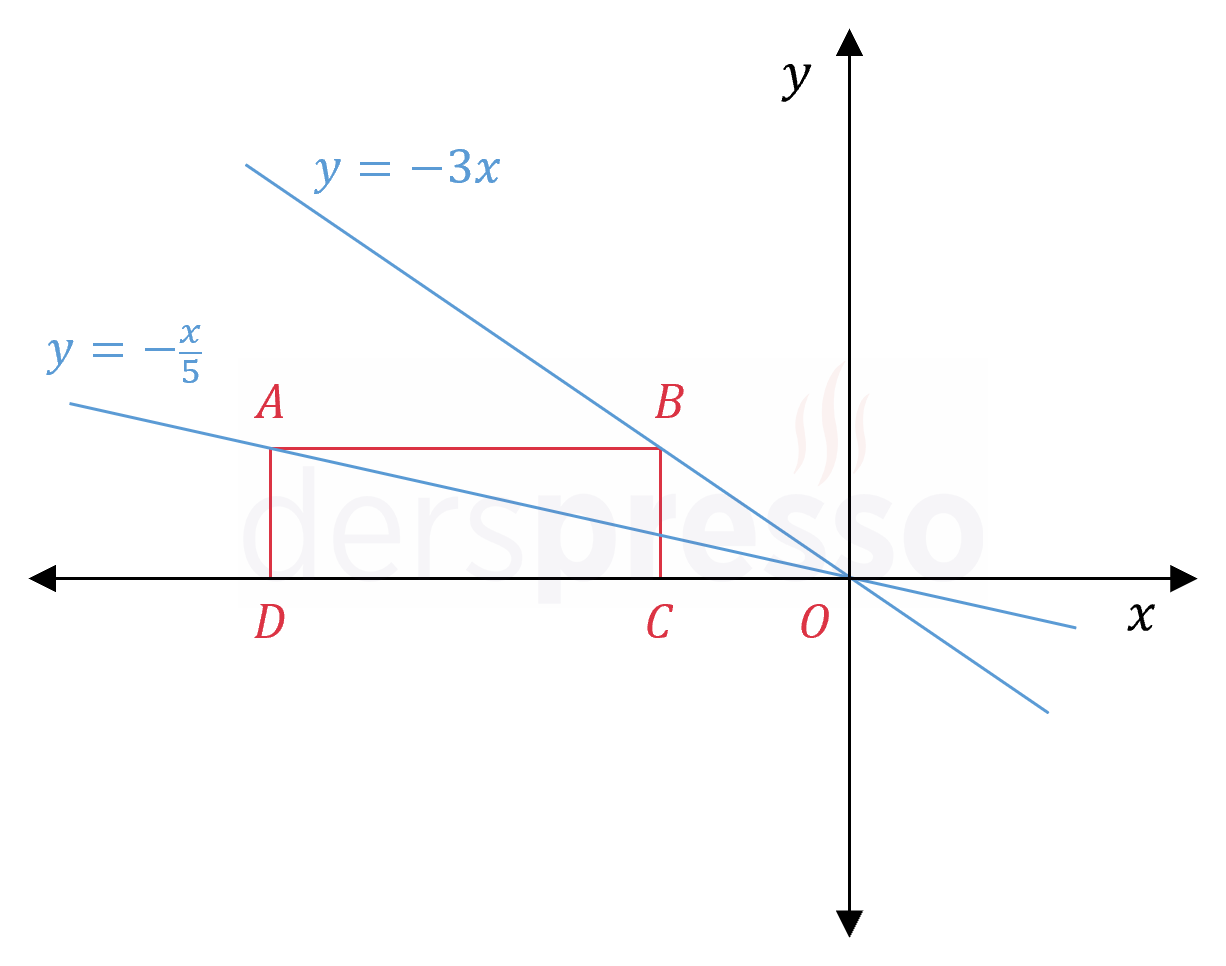
Yukarıdaki şekildeki \( ABCD \) dikdörtgen olup \( A \) köşesi \( y = -\frac{x}{5} \) doğrusu, \( B \) köşesi \( y = -3x \) doğrusu üzerindedir.
\( A(ABCD) = 168 \) olduğuna göre, \( A \) noktasının koordinatları toplamı kaçtır?
Çözümü GösterDoğru denklemlerini kullanarak uzunluklara değer verelim.
\( \abs{OC} = a \) diyelim.
\( B \) noktasının apsisi \( C \) noktası ile aynı olduğundan \( B \) noktasının apsisi \( -a \) olur.

\( B \) köşesi \( y = -3x \) doğrusu üzerinde olduğu için bu denklemi kullanarak ordinat değerini bulalım.
\( y = -3x = -3(-a) = 3a \)
\( B(-a, 3a) \)
\( \abs{BC} = 3a \)
\( A \) ve \( B \) köşeleri aynı yatay doğru üzerinde olduğu için ordinat değerleri eşittir.
\( A \) köşesi \( y = -\frac{x}{5} \) doğrusu üzerinde olduğu için bu denklemi kullanarak apsis değerini bulalım.
\( 3a = -\dfrac{x}{5} \)
\( x = -15a \)
\( A(-15a, 3a) \)
\( D(-15a, 0) \)
\( \abs{OD} = 15a \)
\( \abs{DC} = \abs{AB} = 15a - a = 14a \)
Dikdörtgenin alan formülünü yazalım.
\( A(ABCD) = \abs{AB} \cdot \abs{BC} \)
\( 168 = 14a \cdot 3a \)
\( 42a^2 = 168 \)
\( a^2 = 4 \)
\( a\)'yı \( \abs{OC} \) uzunluk değeri olarak tanımladığımız için değeri pozitiftir.
\( a = 2 \)
\( A(-15a, 3a) = A(-30, 6) \)
\( A \) noktasının koordinatları toplamı \( -30 + 6 = -24 \) olarak bulunur.
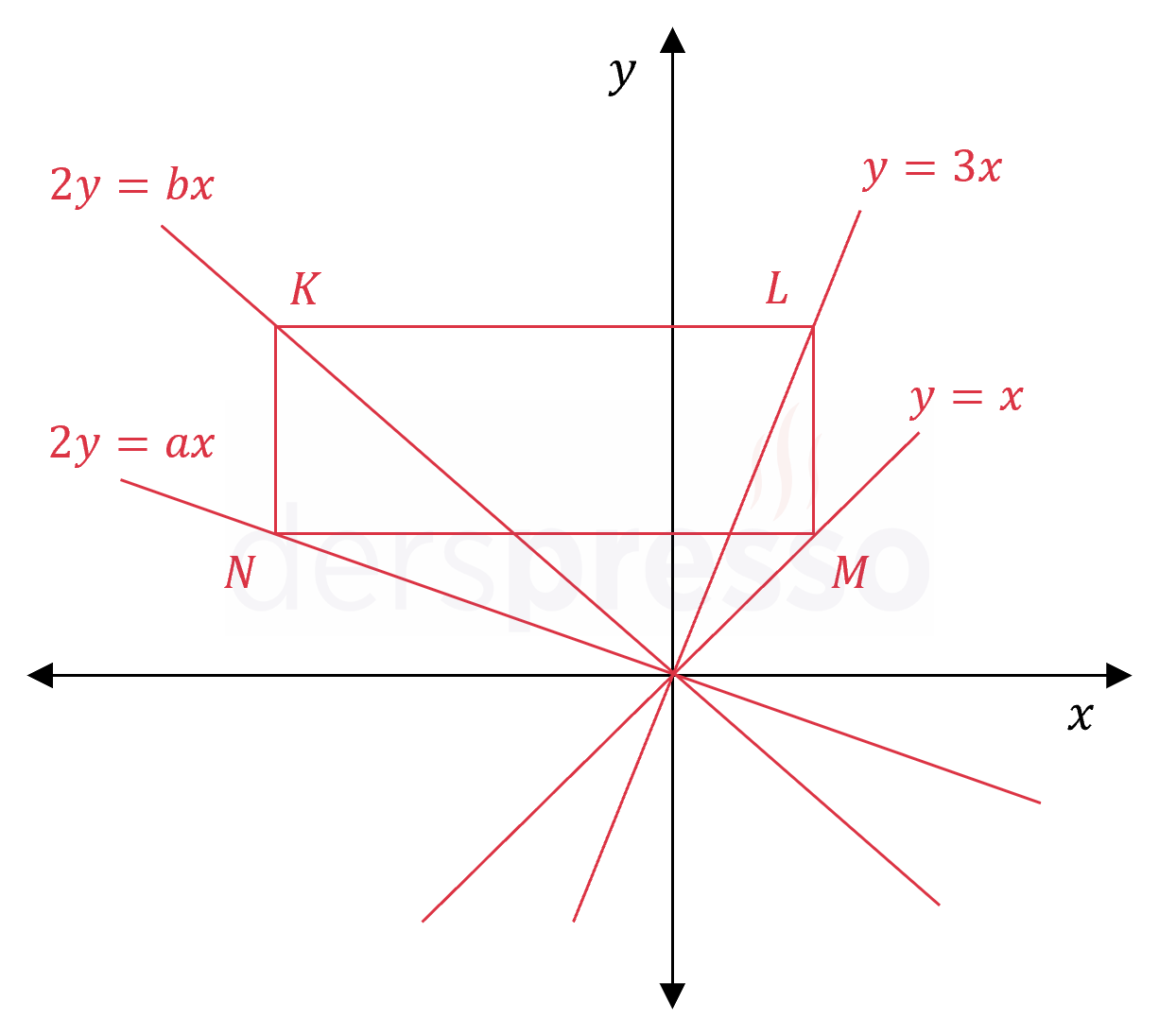
Şekildeki \( KLMN \) dikdörtgeninin köşeleri sırasıyla \( 2y = bx \), \( y = 3x \), \( y = x \) ve \( 2y = ax \) doğruları üzerindedir.
\( [LM] \) kenarı \( y \) eksenine paralel olduğuna göre, \( \frac{a}{b} \) oranı kaçtır?
Çözümü Göster\( KLMN \) dikdörtgeninin köşe noktalarının koordinatlarını doğru denklemlerini kullanarak bulalım.
\( y = x \) doğrusu üzerindeki \( M \) köşesinin apsisine \( p \) diyelim.
\( M(p, p) \)
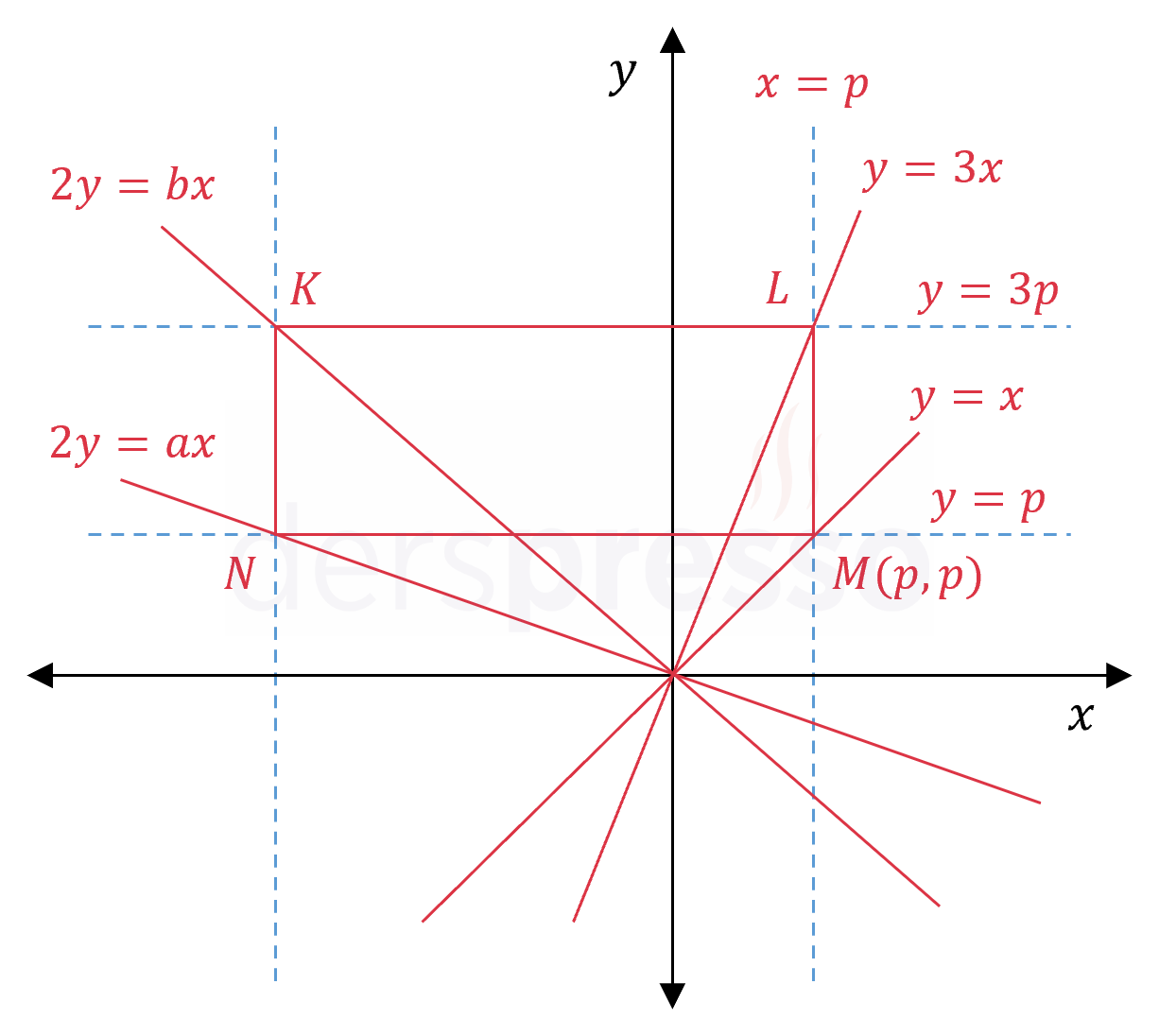
\( y = 3x \) doğrusu üzerindeki \( L \) noktasının apsisi \( M \) noktası ile aynıdır.
\( L(p, 3p) \)
\( 2y = ax \) doğrusu üzerindeki \( N \) noktasının ordinatı \( M \) noktası ile aynıdır.
\( 2p = ax \)
\( x = \dfrac{2p}{a} \)
\( N(\dfrac{2p}{a}, p) \)
\( K \) noktasının apsisi \( N \) noktası ile, ordinatı \( L \) noktası ile aynıdır.
\( K(\dfrac{2p}{a}, 3p) \)
\( K \) noktası \( 2y = bx \) doğrusu üzerinde olduğu için koordinatları doğru denklemini sağlar.
\( 2(3p) = b(\dfrac{2p}{a}) \)
\( 6 = \dfrac{2b}{a} \)
\( \dfrac{a}{b} = \dfrac{1}{3} \) bulunur.
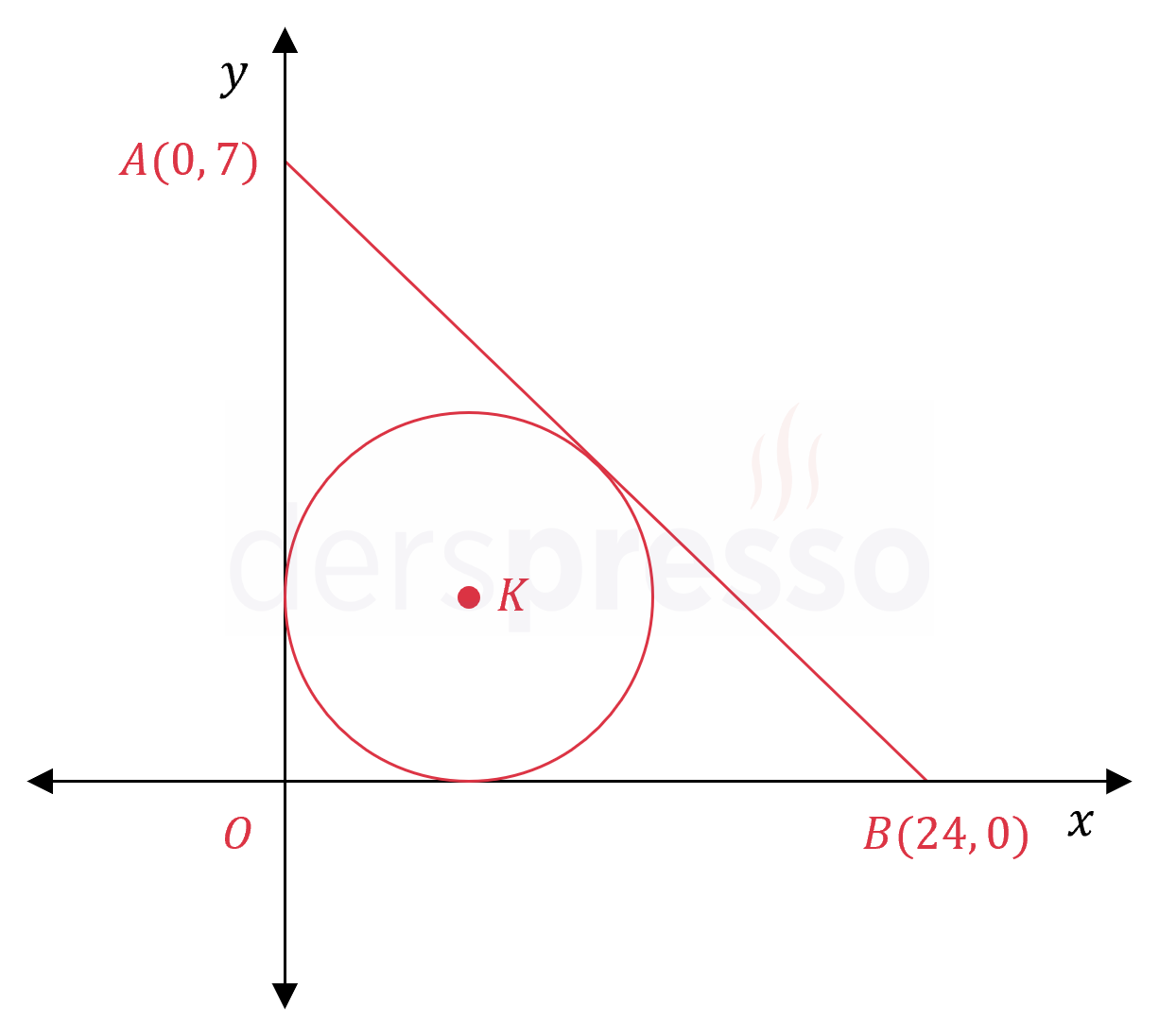
Şekilde \( AOB \) üçgeni ve bu üçgenin \( K \) merkezli iç teğet çemberi verilmiştir.
Buna göre, \( K \) merkezli dairenin alanının \( AOB \) üçgeninin alanına oranı kaçtır?
Çözümü Gösterİç teğet çemberin yarıçapına \( r \) diyelim.
\( x \) ve \( y \) eksenleri bu çembere teğettir.
\( K(r, r) \)
Çemberin \( x \) eksenine teğet olduğu noktaya \( C \), \( y \) eksenine teğet olduğu noktaya \( D \), \( [AB] \) doğrusuna teğet olduğu noktaya \( E \) diyelim.
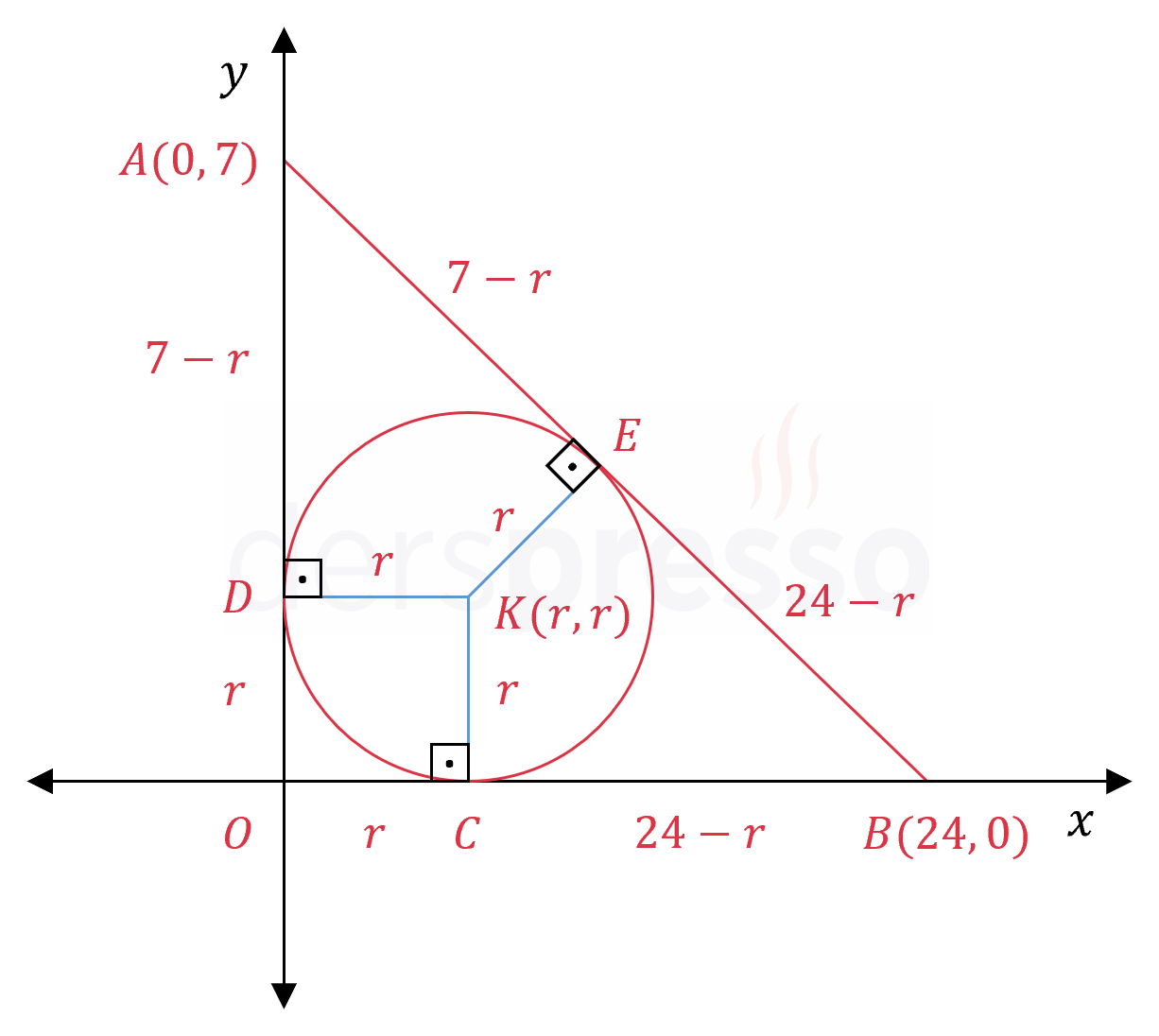
\( AOB \) üçgeninin kenar uzunlukları ile \( K(r, r) \) noktasının koordinatlarını kullanarak doğru parçalarının uzunluklarını yazalım.
\( \abs{DO} = r, \quad \abs{AD} = 7 - r \)
\( \abs{CO} = r, \quad \abs{BC} = 24 - r \)
Dış bir noktadan bir çembere çizilen teğetlerin uzunlukları eşittir.
\( \abs{AD} = \abs{AE} = 7 - r \)
\( \abs{BC} = \abs{BE} = 24 - r \)
\( AOB \) üçgeni 7-24-25 özel üçgeni olduğu için \( \abs{AB} = 25 \) olur.
\( \abs{AB} = \abs{AE} + \abs{BE} \)
\( 25 = 7 - r + 24 - r \)
\( r = 3 \)
\( K(r, r) = K(3, 3) \)
Dairenin alanını bulalım.
\( A = \pi r^2 = 9\pi \)
\( AOB \) üçgeninin alanını bulalım.
\( A(AOB) = \dfrac{\abs{AO} \cdot \abs{BO}}{2} \)
\( = \dfrac{7 \cdot 24}{2} = 84 \)
\( K \) merkezli dairenin alanının \( AOB \) üçgeninin alanına oranını bulalım.
\( \dfrac{9\pi}{84} = \dfrac{3\pi}{28} \) bulunur.
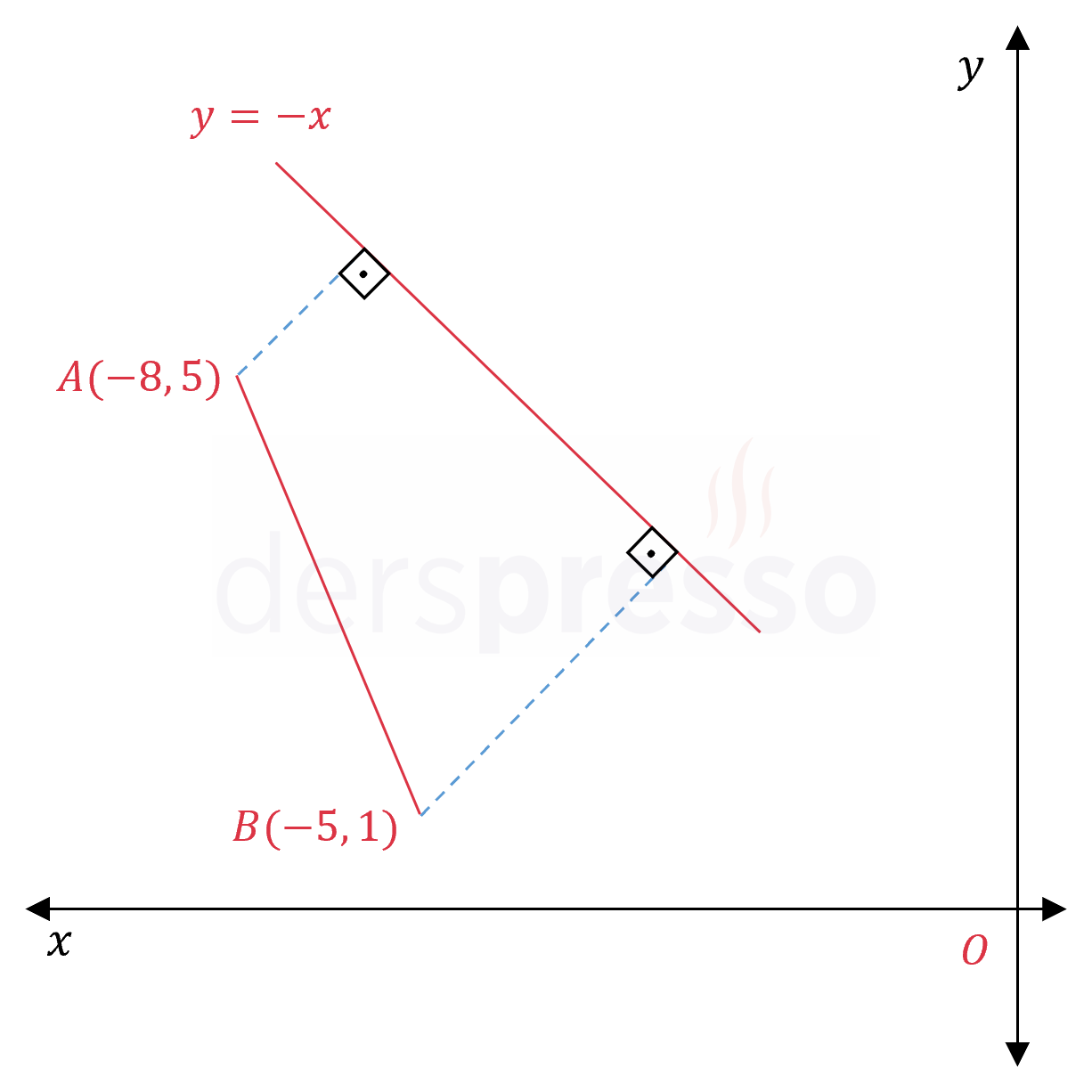
Analitik düzlemde \( A(-8, 5) \) ve \( B(-5, 1) \) noktaları verilmiştir.
Buna göre \( [AB] \) doğru parçasının ve \( d: y = -x \) doğrusu üzerindeki dik izdüşümünün oluşturduğu \( ABB'A' \) yamuğunun alanı kaçtır?
Çözümü Göster\( (x_1, y_1) \) noktası ve \( ax + by + c = 0 \) doğrusu arasındaki uzaklık aşağıdaki formülle bulunur.
\( d = \dfrac{\abs{ax_1 + by_1 + c}}{\sqrt{a^2 + b^2}} \)
\( d \) doğrusunun kapalı denklemini yazalım.
\( x + y = 0 \)
\( \abs{AA'} \) uzaklığını bulalım.
\( \abs{AA'} = \dfrac{\abs{1(-8) + 1(5) + 0}}{\sqrt{1^2 + 1^2}} \)
\( = \dfrac{3\sqrt{2}}{2} \)
\( \abs{BB'} \) uzaklığını bulalım.
\( \abs{BB'} = \dfrac{\abs{1(-5) + 1(1) + 0}}{\sqrt{1^2 + 1^2}} \)
\( = 2\sqrt{2} \)
\( A \) noktasından \( [BB'] \) doğru parçasına bir dikme çizelim ve bu noktaya \( C \) diyelim.
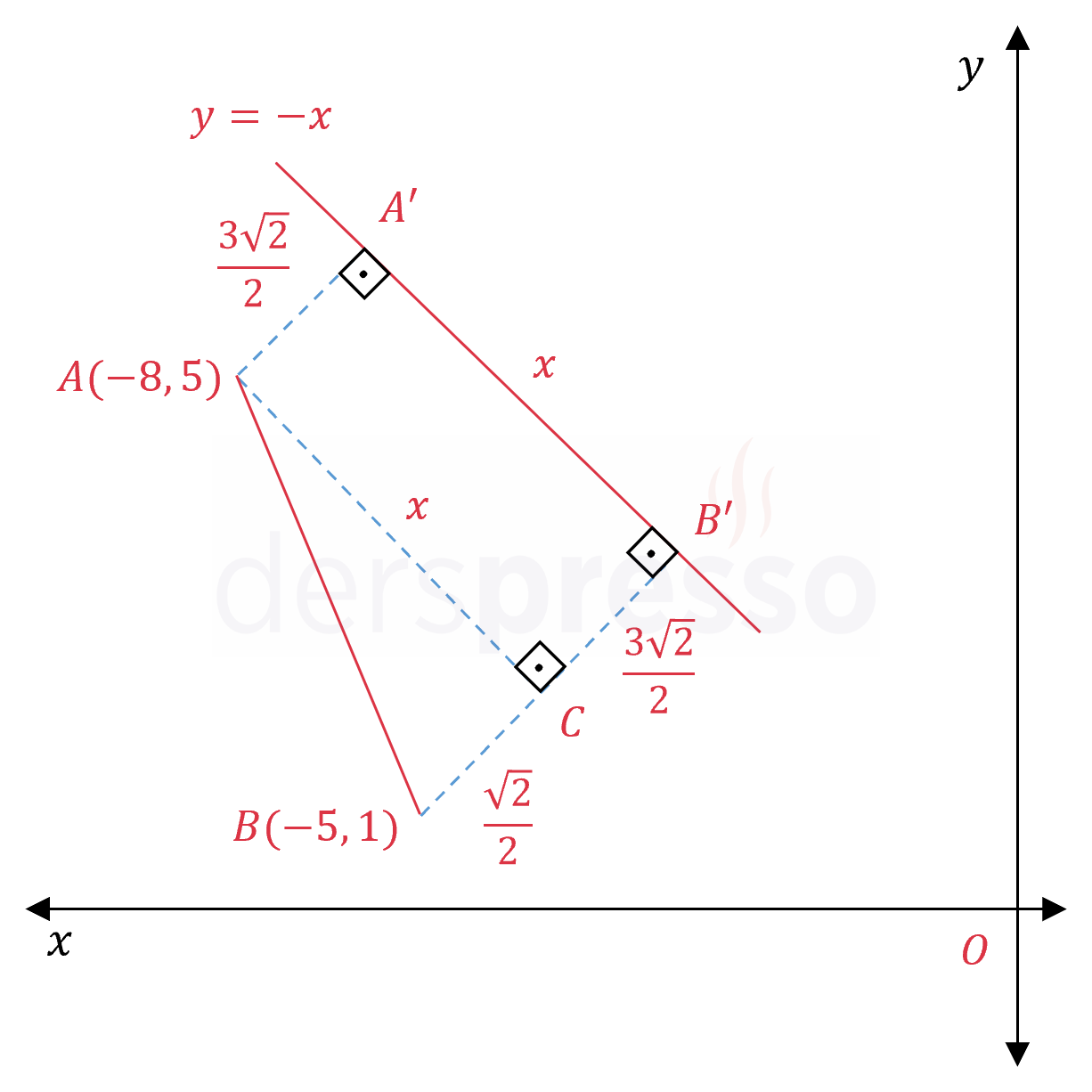
\( [AC] \parallel [A'B'] \)
\( \abs{AA'} = \abs{CB'} = \dfrac{3\sqrt{2}}{2} \)
\( \abs{BB'} = \abs{BC} + \abs{B'C} \)
\( \abs{BC} = \dfrac{\sqrt{2}}{2} \)
\( \abs{AB} \) uzaklığını bulalım.
\( \abs{AB}^2 = (x_2 - x_1)^2 + (y_2 - y_1)^2 \)
\( = (-8 - (-5))^2 + (5 - 1)^2 \)
\( = (-8 + 5)^2 + (5 - 1)^2 \)
\( \abs{AB} = 5 \)
\( \abs{A'B'} = \abs{AC} = x \) diyelim.
\( ACB \) dik üçgeninde Pisagor teoremini uygulayalım.
\( \abs{AC}^2 + \abs{BC}^2 = \abs{AB}^2 \)
\( x^2 + (\dfrac{\sqrt{2}}{2})^2 = 5^2 \)
\( x^2 + \dfrac{1}{2} = 25 \)
\( x = \dfrac{7\sqrt{2}}{2} \)
\( ABB'A' \) yamuğunun alanını hesaplayalım.
\( A(ABB'A') = \dfrac{(\abs{AA'} + \abs{BB'}) \cdot \abs{A'B'}}{2} \)
\( = \dfrac{(\frac{3\sqrt{2}}{2} + 2\sqrt{2}) \cdot \frac{7\sqrt{2}}{2}}{2} \)
\( = \dfrac{49}{4} \) bulunur.
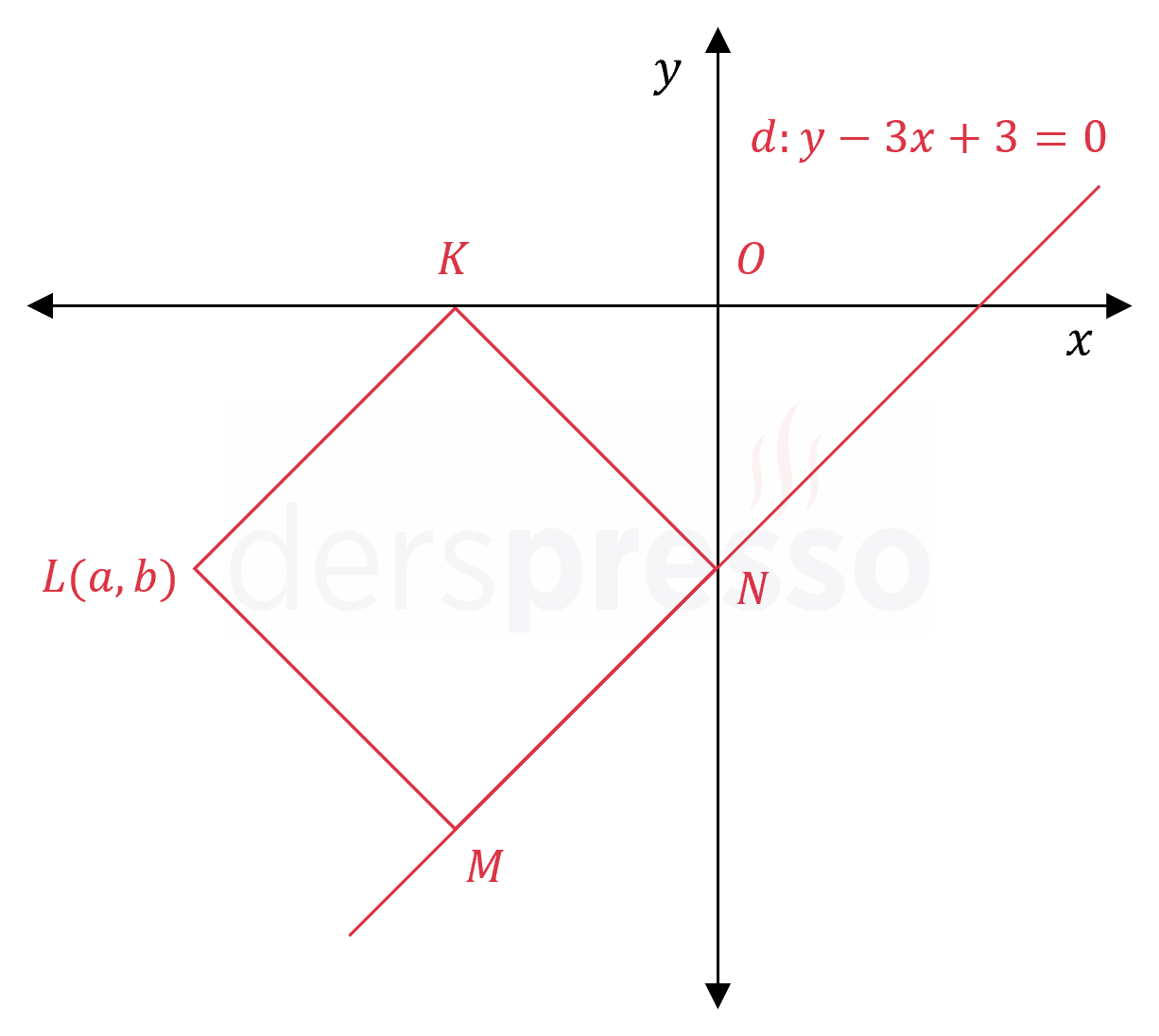
\( KLMN \) karesinin bir kenarı \( d: y - 3x + 3 = 0 \) doğrusu üzerindedir.
Buna göre \( L \) noktasının koordinatları çarpımı kaçtır?
Çözümü Göster\( L \) noktasının koordinatlarına \( L(a, b) \) diyelim.
\( d \) doğrusunun \( x \) eksenini kestiği noktaya \( P \) diyelim.
\( d \) doğrusunun eksenleri kestiği noktaları bulalım.
\( P \) noktasının koordinatlarını bulmak için doğru denkleminde \( y = 0 \) yazalım.
\( 0 - 3x + 3 = 0 \)
\( x = 1 \)
\( P(1, 0) \)
\( N \) noktasının koordinatlarını bulmak için doğru denkleminde \( x = 0 \) yazalım.
\( y - 3(0) + 3 = 0 \)
\( y = -3 \)
\( N(0, -3) \)

\( KON \) ve \( NOP \) üçgenlerinin iç açılarını yazalım.
\( m(\widehat{OKN}) = \alpha \) ve \( m(\widehat{ONK}) = \beta \) diyelim.
\( \alpha + \beta = 90° \)
\( d \) doğrusu \( [MN] \) kenarı üzerinden geçtiğine göre \( m(\widehat{KNP}) = 90° \) olur.
Buna göre, \( m(\widehat{ONP}) = \alpha \) ve \( m(\widehat{OPN}) = \beta \) olur.
\( L \) noktasından \( x \) eksenine bir dikme çizelim ve ekseni kestiği noktaya \( R \) diyelim.
\( m(\widehat{LKN}) = 90° \) olduğuna göre, \( m(\widehat{RKL}) = \beta \) ve \( m(\widehat{RLK}) = \alpha \) olur.
\( ONP \) ve \( OKN \) üçgenleri iç açıları eşit olduğundan benzer üçgenlerdir.
\( \overset{\triangle}{OKN} \sim \overset{\triangle}{ONP} \)
Üçgenler arasındaki benzerliği kullanarak kenar uzunluklarını bulalım.
\( \dfrac{\abs{ON}}{\abs{OP}} = \dfrac{\abs{OK}}{\abs{ON}} \)
\( \dfrac{3}{1} = \dfrac{\abs{OK}}{3} \)
\( \abs{OK} = 9 \)
\( L(a, b) \) olduğundan \( \abs{RL} = -b \), \( \abs{RK} = -a - 9 \) olur.
\( RLK \) ve \( OKN \) üçgenleri iç açıları eşit olduğundan benzer üçgenlerdir.
\( \overset{\triangle}{RLK} \sim \overset{\triangle}{OKN} \)
Üçgenler arasındaki benzerliği kullanarak kenar uzunluklarını bulalım.
\( \dfrac{\abs{RL}}{\abs{OK}} = \dfrac{\abs{LK}}{\abs{KN}} \)
\( [LK] \) ve \( [KN] \) aynı karenin iki kenarı olduğu için uzunlukları eşittir.
\( \abs{LK} = \abs{KN} \)
\( \dfrac{-b}{9} = 1 \)
\( b = -9 \)
\( RLK \) ve \( OKN \) üçgenleri arasındaki benzerliği tekrar kullanarak \( \abs{RK} \) uzunluğunu bulalım.
\( \dfrac{\abs{RK}}{\abs{ON}} = \dfrac{\abs{LK}}{\abs{KN}} \)
\( \dfrac{-a - 9}{3} = 1 \)
\( a = -12 \)
\( L(-12, -9) \)
\( L \) noktasının koordinatları çarpımı \( -12 \cdot (-9) = 108 \) olarak bulunur.