Bilimsel Gösterim
Konu tekrarı için: 10'un Kuvvetleri İle Gösterim
Bir sayının 10'un farklı kuvvetleri ile gösterimleri içinde, katsayının mutlak değer olarak \( [1, 10) \) aralığında olduğu gösterime bilimsel gösterim denir.
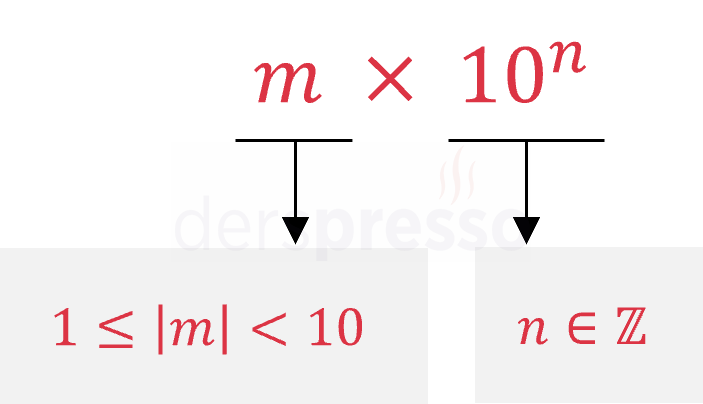
Bilimsel gösterim sayıların 10'un farklı kuvvetleri ile gösterimlerden sadece biridir. 1.234 sayısının aşağıdaki farklı gösterimlerinin tümü doğru ve 1.234'e eşit olmakla birlikte, sadece işaretli olan gösterim bilimsel gösterimdir.
Yukarıdaki örnekte de görülebileceği gibi, bilimsel gösterim çok büyük ve çok küçük sayıların yazılışında genellikle en az sıfırın ve basamağın kullanıldığı gösterimdir.
Bazı çok büyük sayıların bilimsel gösterimi aşağıdaki gibidir.
| Sayı | Bilimsel Gösterim |
|---|---|
| Dünya - güneş arası mesafe | \( 1,51 \times 10^8 \) km |
| Işığın bir yılda katettiği mesafe | \( 9,46 \times 10^{12} \) km |
| Avogadro sayısı | \( 6,02214 \times 10^{23} \) g/mol |
Bazı çok küçük sayıların bilimsel gösterimi aşağıdaki gibidir.
| Sayı | Bilimsel Gösterim |
|---|---|
| Hidrojen atomunun yarıçapı | \( 5,3 \times 10^{-8} \) mm |
| Bir elektronun kütlesi | \( 9,1093 \times 10^{-31} \) kg |
| Planck sabiti | \( 6,626 \times 10^{-34} \) |
Bilimsel Gösterimdeki Sayılarla İşlemler
Bilimsel gösterimin kullanılma sebeplerinden biri çok büyük ve çok küçük sayılar arasındaki işlemlerde kolaylık sağlamasıdır.
Çarpma İşlemi
Bilimsel gösterimdeki iki ya da daha fazla sayının çarpımında, sayıların katsayı ve 10'un kuvveti kısımları kendi aralarında çarpılarak sonucun katsayı ve 10'un kuvveti kısımları ayrı ayrı hesaplanır.
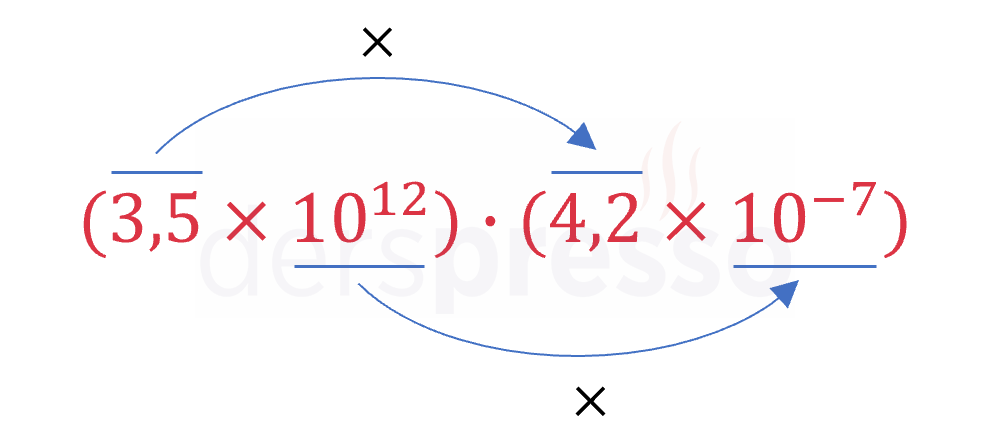
\( (3,5 \cdot 10^{12}) \cdot (4,2 \cdot 10^{-7}) \)
\( = (3,5 \cdot 4,2) \cdot (10^{12} \cdot 10^{-7}) \)
\( = 14,7 \cdot 10^5 \)
Bu sonuç istenirse tekrar bilimsel gösterime çevrilebilir.
\( = 1,47 \cdot 10^6 \)
\( m \) basamaklı bir sayı ile \( n \) basamaklı bir sayının çarpımı en az \( m + n - 1 \) basamaklı, en fazla \( m + n \) basamaklıdır.
\( 10^a \) sayısının basamak sayısı: \( a + 1 \)
\( m \) basamaklı en küçük sayı: \( 10^{m - 1} \)
\( m \) basamaklı en büyük sayı: \( 10^m - 1 \)
\( 4 \) basamaklı en küçük sayı: \( 1.000 = 10^3 \)
\( 4 \) basamaklı en büyük sayı: \( 9.999 = 10^4 - 1 \)
olmak üzere,
\( m \) basamaklı bir sayı ile \( n \) basamaklı bir sayının çarpımının alabileceği en küçük değer:
\( 10^{m - 1} \cdot 10^{n - 1} = 10^{m + n - 2} \)
Bu sayının basamak sayısı üssün 1 fazlası olacağı için \( m + n - 1 \) olur.
\( m \) basamaklı bir sayı ile \( n \) basamaklı bir sayının çarpımının alabileceği en büyük değer:
\( (10^m - 1)(10^n - 1) = 10^{m + n} - 10^m - 10^n + 1 \)
\( 10^{m + n} \) sayısı \( m + n + 1 \) basamaklı en küçük sayıdır. Bu sayıdan \( 10^m + 10^n - 1 \) ifadesini çıkardığımızda basamak sayısı bir azalır ve \( m + n \) olur.
Bölme İşlemi
Bilimsel gösterimdeki iki sayının bölümünde, sayıların katsayı ve 10'un kuvveti kısımları kendi aralarında bölünerek sonucun katsayı ve 10'un kuvveti kısımları ayrı ayrı hesaplanır.
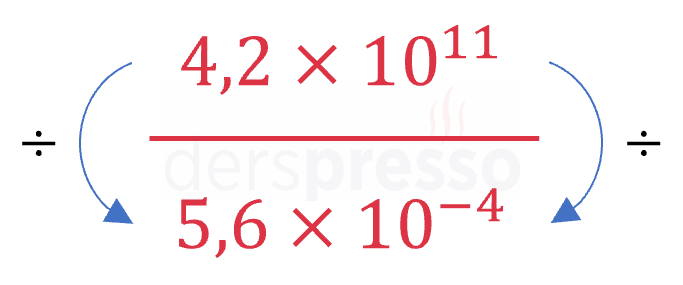
\( (4,2 \cdot 10^{11}) \div (5,6 \cdot 10^{-4}) \)
\( = (4,2 \div 5,6) \cdot (10^{11} \div 10^{-4}) \)
\( = 0,75 \cdot 10^{15} \)
Bu sonuç istenirse tekrar bilimsel gösterime çevrilebilir.
\( = 7,5 \cdot 10^{14} \)
Toplama ve Çıkarma İşlemi
Bilimsel gösterimdeki sayılar arasında toplama/çıkarma işlemi yapılabilmesi için, sayıların 10'un kuvveti kısımlarındaki üsler aynı olmalıdır.
\( 5,2 \cdot 10^{8} + 1,3 \cdot 10^{9} - 3 \cdot 10^{7} \)
10'un kuvvetleri kısmındaki üsleri içlerindeki en küçük değer olan 7'ye getirelim.
\( 5,2 \cdot 10^{8} = 52 \cdot 10^{7} \)
\( 1,3 \cdot 10^{9} = 130 \cdot 10^{7} \)
Sayıların toplamını alalım.
\( 52 \cdot 10^{7} + 130 \cdot 10^{7} - 3 \cdot 10^{7} \)
\( = (52 + 130 - 3) \cdot 10^{7} \)
\( = 179 \cdot 10^{7} \)
Bu sonuç istenirse tekrar bilimsel gösterime çevrilebilir.
\( = 1,79 \cdot 10^{9} \)
Bir Sayının Basamak Sayısı
Bilimsel gösterimdeki bir tam sayının basamak sayısı, 10'un kuvveti kısmındaki üs değerinin bir fazlasına eşittir.
\( 2 \cdot 10^{9} = 2.000.000.000 \)
Basamak sayısı = 10
\( 3,5 \cdot 10^{9} = 3.500.000.000 \)
Basamak sayısı = 10
\( 7,92 \cdot 10^{9} = 7.920.000.000 \)
Basamak sayısı = 10
Aşağıda verilen ifadeleri bilimsel gösterimde yazınız.
(a) \( 16811,124 \cdot 10^{-6} \)
(b) \( 0,000367 \)
(c) \( 91560,01 \)
Çözümü Göster(a) seçeneği:
\( 16811,124 \cdot 10^{-6} \)
\( = 1681,1124 \cdot 10^{-5} \)
\( = 168,11124 \cdot 10^{-4} \)
\( = 16,811124 \cdot 10^{-3} \)
\( = 1,6811124 \cdot 10^{-2} \)
(b) seçeneği:
\( 0,000367 = 0,000367 \cdot 10^0 \)
\( = 0,00367 \cdot 10^{-1} \)
\( = 0,0367 \cdot 10^{-2} \)
\( = 0,367 \cdot 10^{-3} \)
\( = 3,67 \cdot 10^{-4} \)
(c) seçeneği:
\( 91560,01 = 91560,01 \cdot 10^0 \)
\( = 9156,001 \cdot 10^1 \)
\( = 915,6001 \cdot 10^2 \)
\( = 91,56001 \cdot 10^3 \)
\( = 9,156001 \cdot 10^4 \)
Aşağıdaki sayılardan hangileri \( 457,3 \cdot 10^{-4} \) sayısına eşittir?
I. \( 45,73 \cdot 10^{-3} \)
II. \( 4,573 \cdot 10^{-2} \)
III. \( 0,4573 \cdot 10^{-4} \)
IV. \( 4573000 \cdot 10^{-8} \)
Çözümü GösterTüm sayıları bilimsel gösterimde yazalım.
\( 457,3 \cdot 10^{-4} = 4,573 \cdot 10^{-2} \)
I. \( 45,73 \cdot 10^{-3} = 4,573 \cdot 10^{-2} \)
II. \( 4,573 \cdot 10^{-2} \)
III. \( 0,4573 \cdot 10^{-4} = 4,573 \cdot 10^{-5} \)
IV. \( 4573000 \cdot 10^{-8} = 4,573 \cdot 10^{-2} \)
Buna göre verilen sayı I., II. ve IV. öncüllerdeki sayılara eşittir.
\( 0,00016 \) sayısının bilimsel gösterimi \( A \cdot 10^x \) ve 120.000.000 sayısının bilimsel gösterimi \( B \cdot 10^y \) şeklindedir.
Buna göre \( (A + B) - (x + y) \) işleminin sonucu kaçtır?
Çözümü GösterBirinci sayıyı bilimsel gösterimde yazalım.
\( 0,00016 = 0,00016 \cdot 10^0 \)
\( = 0,0016 \cdot 10^{-1} \)
\( = 0,016 \cdot 10^{-2} \)
\( = 0,16 \cdot 10^{-3} \)
\( = 1,6 \cdot 10^{-4} = A \cdot 10^x \)
\( A = 1,6, \quad x = -4 \)
İkinci sayıyı bilimsel gösterimde yazalım.
\( 120.000.000 = 12 \cdot 10^7 \)
\( = 1,2 \cdot 10^8 = B \cdot 10^y \)
\( B = 1,2 \quad y = 8 \)
Bulduğumuz değerleri sorudaki ifadede yerine yazalım.
\( (A + B) - (x + y) \)
\( = (1,6 + 1,2) - (-4 + 8) \)
\( 2,8 - 4 = -1,2 \) bulunur.
Işık bir saniyede yaklaşık 300 bin km yol katettiğine göre, ışığın cm/sn cinsinden hızını bilimsel gösterimde yazınız.
Çözümü GösterIşığın km/sn cinsinden verilen hızını cm/sn cinsinden yazalım.
\( 300000 = 3 \cdot 10^5 \) km/sn
1 kilometre 1000 metredir.
\( = 3 \cdot 10^8 \) m/sn
1 metre 100 santimetredir.
\( = 3 \cdot 10^{10} \) cm/sn
\( 57,3 \cdot 10^8 - 0,17 \cdot 10^{10} \) işleminin sonucu için aşağıdakilerden hangileri doğrudur?
I. Bilimsel gösterimi \( 4,03 \cdot 10^9 \) şeklindedir.
II. Sondan 7 basamağı sıfırdır.
III. 11 basamaklı bir sayıdır.
IV. \( 0,00403 \cdot 10^6 \) ifadesine eşittir.
Çözümü GösterI. Öncül:
İşlemin terimlerini 10'un aynı kuvvetleri şeklinde yazalım.
\( 57,3 \cdot 10^8 - 17 \cdot 10^8 \)
\( = (57,3 - 17) \cdot 10^8 \)
\( = 40,3 \cdot 10^8 \)
Sonucu bilimsel gösterimde yazalım.
\( = 4,03 \cdot 10^9 \)
I. öncül doğrudur.
II. Öncül:
İşlem sonucunu katsayısı tam sayı olacak şekilde yazalım.
\( 4,03 \cdot 10^9 = 403 \cdot 10^7 \)
\( a \cdot 10^b \) şeklindeki bir sayının açılımında \( a \)'nın sonuna \( b \) tane sıfır eklenir.
Buna göre işlem sonucunun sondan 7 basamağı sıfır olur.
II. öncül doğrudur.
III. Öncül:
İşlem sonucunu bilimsel gösterimde \( 4,03 \cdot 10^9 \) olarak bulmuştuk.
Bilimsel gösterimdeki bir tam sayının basamak sayısı, 10'un kuvveti kısmındaki üs değerinin bir fazlasına eşittir.
Buna göre işlem sonucu \( 9 + 1 = 10 \) basamaklı olur.
III. öncül yanlıştır.
VI. Öncül:
İşlem sonucunu bilimsel gösterimde \( 4,03 \cdot 10^9 \) olarak bulmuştuk.
Katsayı \( 0,00403 \) olana kadar sayıyı 10'un artan kuvvetleri şeklinde yazalım.
\( = 0,403 \cdot 10^{10} \)
\( = 0,0403 \cdot 10^{11} \)
\( = 0,00403 \cdot 10^{12} \ne 0,00403 \cdot 10^6 \)
IV. öncül yanlıştır.
Buna göre I. ve II. öncüller doğrudur.
Türkiye'nin yüzölçümü bakımından en büyük şehri olan Konya'nın yüzölçümü 39.000 km\( ^2 \), en küçük şehri olan Yalova'nın yüzölçümü 403 km\( ^2 \)'dir.
Buna göre, Konya ve Yalova illerinin yüzölçümlerinin metrekare cinsinden farkını bilimsel gösterimde yazınız.
Çözümü GösterBu iller arasındaki yüzölçümü farkını bulalım.
\( 39.000 - 403 = 38597 \) km\( ^2 \)
1 kilometrekare 1.000.000 metrekareye eşittir.
\( = 38597 \cdot 1000000 \) m\( ^2 \)
\( = 38597 \cdot 10^6 \) m\( ^2 \)
Bu değeri bilimsel gösterimde yazalım.
\( = 3859,7 \cdot 10^7 \)
\( = 385,97 \cdot 10^8 \)
\( = 38,597 \cdot 10^9 \)
\( = 3,8597 \cdot 10^{10} \) bulunur.
Bir tahmine göre, evrende yaklaşık 2 trilyon galaksi ve her galakside yaklaşık 120 milyar yıldız bulunmaktadır.
Buna göre evrendeki yıldız sayısının yaklaşık değerini bilimsel gösterimde yazınız.
Çözümü Göster1 trilyonu 10'un kuvveti biçiminde yazalım.
\( 1.000.000.000.000 = 10^{12} \)
1 milyarı 10'un kuvveti biçiminde yazalım.
\( 1.000.000.000 = 10^9 \)
Buna göre evrende yaklaşık \( 2 \cdot 10^{12} \) galaksi ve her galakside yaklaşık \( 120 \cdot 10^9 \) yıldız vardır.
Evrendeki yaklaşık yıldız sayısını bulalım.
\( 2 \cdot 10^{12} \cdot 120 \cdot 10^9 \)
\( = 240 \cdot 10^{21} \)
Bu sayıyı bilimsel gösterime çevirelim.
\( = 2,4 \cdot 10^{23} \) bulunur.
1 dolar 30 TL iken 45,6 milyar doların TL karşılığını bilimsel gösterimle ifade ediniz.
Çözümü Göster45,6 milyar USD = 45.600.000.000 USD
\( = 456 \cdot 10^8 \) USD
Bu sayının TL karşılığını bulmak için 30 ile çarpalım.
\( = 456 \cdot 10^8 \cdot 30 \)
\( = 1368 \cdot 10^9 \) TL
Bu sayıyı bilimsel gösterimde yazalım.
\( = 136,8 \cdot 10^{10} \)
\( = 13,68 \cdot 10^{11} \)
\( = 1,368 \cdot 10^{12} \) bulunur.
\( 8^{15} \cdot 25^{23} \cdot 7 \) sayısı kaç basamaklıdır?
Çözümü GösterTabanları asal sayılar cinsinden yazalım.
\( 8^{15} \cdot 25^{23} \cdot 7 = (2^3)^{15} \cdot (5^2)^{23} \cdot 7 \)
\( = 2^{45} \cdot 5^{46} \cdot 7 \)
2 ve 5 tabanlı ifadelerden 10 tabanlı bir ifade oluşturalım.
\( = 2^{45} \cdot 5^{45} \cdot 5 \cdot 7 = 35 \cdot (2 \cdot 5)^{45} \)
\( = 35 \cdot 10^{45} \)
Sayıyı bilimsel gösterimde yazalım.
\( = 3,5 \cdot 10^{46} \)
Bilimsel gösterimdeki bir tam sayının basamak sayısı, 10'un kuvveti kısmındaki üs değerinin bir fazlasına eşittir.
Buna göre verilen sayı \( 46 + 1 = 47 \) basamaklıdır.
\( 3 \cdot 2^{18} \cdot 5^{15} + 10^{11} \) sayısı kaç basamaklıdır?
Çözümü GösterBirinci terimdeki 2 ve 5 tabanlı ifadelerden 10 tabanlı bir ifade oluşturalım.
\( 3 \cdot 2^3 \cdot 2^{15} \cdot 5^{15} + 10^{11} \)
\( = 24 \cdot (2 \cdot 5)^{15} + 10^{11} \)
\( = 24 \cdot 10^{15} + 10^{11} \)
Birinci terimi bilimsel gösterimde yazalım.
\( = 2,4 \cdot 10^{16} + 10^{11} \)
Bilimsel gösterimdeki bir tam sayının basamak sayısı, 10'un kuvveti kısmındaki üs değerinin bir fazlasına eşittir.
Buna göre \( 2,4 \cdot 10^{16} \) sayısı \( 16 + 1 = 17 \) basamaklıdır.
Bu sayıya 11 basamaklı \( 10^{11} \) sayısının eklenmesi basamak sayısını değiştirmez.