Çarpma Yoluyla Sayma
Çarpma yoluyla saymaya göre, birbirinden bağımsız \( A \) ve \( B \) olayları sırasıyla \( m \) ve \( n \) farklı şekilde sonuçlanabiliyorsa bu olayların ikisi birlikte \( m \cdot n \) farklı şekilde sonuçlanabilir.
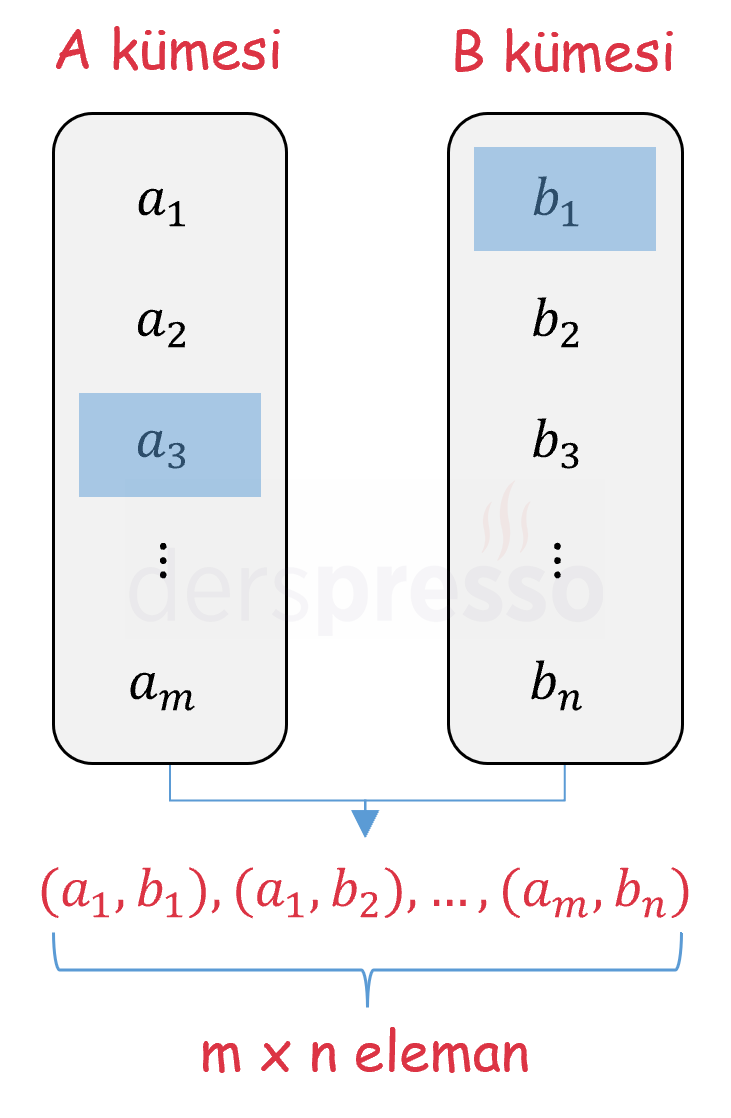
Çarpma yoluyla saymayı kümeler üzerinden tanımlarsak, \( A \) kümesi \( m \) elemanlı ve \( B \) kümesi \( n \) elemanlı ise birinci bileşeni \( A \) kümesinden ikinci bileşeni \( B \) kümesinden gelen \( (a, b) \) sıralı ikililerinin sayısı \( m \cdot n \) olur.
\( A \) ve \( B \) sonlu iki küme olmak üzere,
\( s(A \times B) = s(A) \cdot s(B) \)
\( A = \{ a_1, a_2, a_3, a_4 \} \)
\( B = \{ b_1, b_2, b_3 \} \)
\( A \times B = \{ (a_1, b_1), (a_1, b_2), (a_1, b_3), \)
\( \quad (a_2, b_1), (a_2, b_2), (a_2, b_3), \)
\( \quad (a_3, b_1), (a_3, b_2), (a_3, b_3), \)
\( \quad (a_4, b_1), (a_4, b_2), (a_4, b_3) \} \)
\( s(A \times B) = 4 \cdot 3 = 12 \)
Benzer şekilde, her bir bileşeni sonlu \( n \) tane kümeden gelen \( (a_1, a_2, \ldots, a_n) \) sıralı \( n \)'lilerinin sayısı bu kümelerin eleman sayılarının çarpımına eşit olur.
\( A_1, A_2, \ldots, A_n \) sonlu kümeler olmak üzere,
\( s(A_1 \times A_2 \times \ldots \times A_n) \) \( = s(A_1) \cdot s(A_2) \ldots s(A_n) \)
Çarpma yoluyla saymaya saymanın temel prensibi ya da kısaca çarpma kuralı da denir.
Çarpma yoluyla saymanın uygulamalarında bu kümelerin elemanları olayların farklı sonuçlarına, tamamlanması gereken işlere, oluşturulacak sayıların basamaklarına, kelimelerin harflerine ya da arasından seçim yapılacak farklı seçeneklere karşılık gelebilir.
Çarpma yoluyla sayma yönteminin kullanılabilmesi için iki koşul sağlanmalıdır.
- Her kümeden birer eleman seçiliyor olmalıdır.
- Her kümeden yapılan seçimler birbirinden bağımsız olmalıdır. Seçimlerin bağımsız olması, bir kümeden yapılan seçimin diğer bir kümeden yapılan seçimi etkilememesi anlamına gelir.
Bir problemin çözümünde çarpma kuralının kullanılabileceğine işaret eden bir ipucu, problem tanımındaki her kümeden bir eleman seçilmesi gerektiğini belirten "VE" bağlacı olmaktadır.
Önce İstanbul'dan Ankara'ya, oradan da Gaziantep'e uçacak olan Öykü'nün İstanbul-Ankara arası 4, Ankara-Gaziantep arası 3 farklı uçuş seçeneği vardır.
Buna göre Öykü seyahat planını kaç farklı şekilde oluşturabilir?
Çözümü GösterYolculuğun her iki ayağından birer uçuş seçileceği ve bir ayakta yapılan seçim diğer ayakta yapılan seçimi etkilemeyeceği için çarpma kuralını kullanabiliriz.
İstanbul-Ankara arası 4, Ankara-Gaziantep arası 3 farklı uçuş seçeneği vardır, dolayısıyla tüm yolculuk için toplamda \( 4 \cdot 3 = 12 \) farklı uçuş seçeneği olur.
Bu 12 farklı seyahat planını bir şekil yardımı ile aşağıdaki gibi gösterebiliriz.
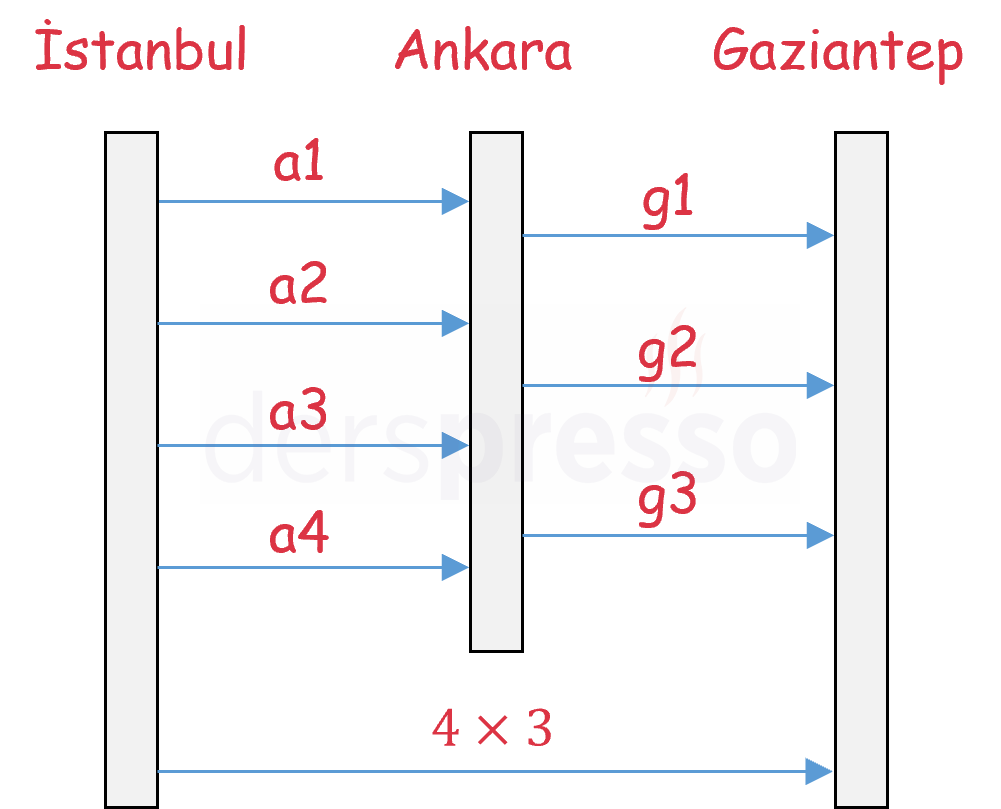
Her uçuşa ait seçeneklerin ve iki uçuşun kartezyen çarpımının küme şeklinde gösterimleri aşağıdaki gibidir.
\( A \) ve \( G \) sırasıyla İstanbul-Ankara ve Ankara-Gaziantep arası uçuş seçeneklerini içeren kümeler olmak üzere,
\( A = \{ a1, a2, a3, a4 \} \)
\( G = \{ g1, g2, g3 \} \)
\( A \times G = \{ (a1, g1), (a1, g2), (a1, g3), \)
\( \quad (a2, g1), (a2, g2), (a2, g3), \)
\( \quad (a3, g1), (a3, g2), (a3, g3), \)
\( \quad (a4, g1), (a4, g2), (a4, g3) \} \)
\( s(A \times G) = s(A) \cdot s(G) = 4 \cdot 3 = 12 \)
Bir okulda 10. sınıflarda 3 şube, her şubede sırasıyla 30, 32, 34 öğrenci vardır. Her şubeden bir sınıf başkanı seçilmek isteniyor. Bu seçim kaç farklı şekilde yapılabilir?
Çözümü GösterHer şubeden bir başkan seçileceği ve bir şubede yapılan seçim diğer şubelerdeki seçimi etkilemeyeceği için çarpma kuralını kullanabiliriz.
Verilen bilgiler doğrultusunda sınıf başkanları \( 30 \cdot 32 \cdot 34 = 32640 \) farklı şekilde seçilebilir.
Bir restoranın menüsünde 3 çeşit çorba, 5 çeşit ana yemek ve 4 çeşit tatlı vardır. Birer çeşit çorba, ana yemek ve tatlıdan oluşan bir menü kaç farklı şekilde oluşturulabilir?
Çözümü GösterHer menü çorba, ana yemek ve tatlıdan birer çeşit içereceği ve bir yemekte yapılan seçim diğer yemekte yapılan seçimi etkilemeyeceği için çarpma kuralını kullanabiliriz.
Verilen bilgiler doğrultusunda toplamda \( 3 \cdot 5 \cdot 4 = 60 \) farklı menü oluşturulabilir.
Menüdeki seçeneklerin ve tüm menünün kartezyen çarpımının küme şeklinde gösterimleri aşağıdaki gibidir.
\( C \), \( A \) ve \( T \) sırasıyla çorba, ana yemek ve tatlı seçeneklerini içeren kümeler olmak üzere,
\( C = \{ c1, c2, c3 \} \)
\( A = \{ a1, a2, a3, a4, a5 \} \)
\( T = \{ t1, t2, t3, t4 \} \)
\( C \times A \times T = \{ (c1, a1, t1), \) \( (c1, a1, t2), \cdots, (c3, a5, t4) \} \)
\( s(C \times A \times T) = s(C) \cdot s(A) \cdot s(T) = 60 \)
Doğan'ın gardrobunda birbirinden farklı 8 tişört, 4 kot pantolon ve 3 spor ayakkabı vardır. Tişört, pantolon ve spor ayakkabı giymek istediği bir günde Doğan'ın oluşturabileceği kombin sayısı kaçtır?
Çözümü GösterHer kombin tişört, pantolon ve spor ayakkabıdan birer tane içereceği ve bir kıyafette yapılan seçim diğer kıyafette yapılan seçimi etkilemeyeceği için çarpma kuralını kullanabiliriz.
Verilen bilgiler doğrultusunda toplamda \( 8 \cdot 4 \cdot 3 = 96 \) farklı kombin oluşturulabilir.
AVM'ye giden Elif ve Duru'nun yemek için 7 restoran, sinema için 10 film ve sonrasında kahve için 4 kafe seçeneği vardır. Bu üç aktiviteyi de yapmak isteyen Elif ve Duru, aktiviteleri kaç farklı şekilde seçebilirler (aktivitelerin sırası önemli değildir.)?
Çözümü GösterRestoran, film ve kafe seçeneklerinden birer tane seçileceği ve bir aktivitede yapılan seçim diğer aktivitelerde yapılan seçimi etkilemeyeceği için çarpma kuralını kullanabiliriz.
Verilen bilgiler doğrultusunda aktiviteler toplamda \( 7 \cdot 10 \cdot 4 = 280 \) farklı şekilde organize edilebilir.
Bir tişört markasının koleksiyonunda 9 farklı model, her modelin 4 farklı rengi ve her rengin 3 farklı bedeni vardır.
Buna göre, bu koleksiyonda kaç farklı tişört ürünü vardır?
Çözümü GösterHer tişört için bir model, renk ve beden seçimi yapılması gerektiği ve yapılan model seçimi renk seçeneklerini, renk seçimi de beden seçeneklerini etkilemediği için çarpma kuralını kullanabiliriz.
Verilen bilgiler doğrultusunda toplamda \( 9 \cdot 4 \cdot 3 = 108 \) farklı tişört ürünü vardır.
\( 1, 2, 3, 4, 5 \) rakamlarını kullanarak 4 basamaklı kaç sayı yazılabilir?
Çözümü GösterHer basamak için bir rakam seçileceği ve bir basamaktaki rakam seçimi diğer basamaklardaki seçimi etkilemeyeceği için çarpma kuralını kullanabiliriz.
Verilen bilgiler doğrultusunda toplamda \( 5 \cdot 5 \cdot 5 \cdot 5 = 625 \) farklı seçim yapılabilir, dolayısıyla 4 basamaklı 625 farklı sayı yazılabilir.
Bir çiçekçinin elinde renkleri dışında özdeş 8 kırmızı, 6 beyaz ve 4 pembe gül vardır. Buna göre çiçekçi harhangi bir sayıda gül içeren bir buketi kaç farklı şekilde oluşturabilir?
Çözümü GösterÇiçekçinin elinde toplam 18 gül vardır ve buketi 1'den 18'e kadar herhangi bir sayıda gülle oluşturabilir.
Çiçekçinin yapması gereken 3 seçim vardır ve bu üç seçimi birbirini etkilemeyen bağımsız olaylar olarak düşünebiliriz.
- Bukete konacak kırmızı gül sayısı (0, 1, 2, ..., 8 tane)
- Bukete konacak beyaz gül sayısı (0, 1, 2, ..., 6 tane)
- Bukete konacak pembe gül sayısı (0, 1, 2, ..., 4 tane)
Buna göre çiçekçinin kırmızı güller için \( 8 + 1 = 9 \), beyaz güller için \( 6 + 1 = 7 \), pembe güller için de \( 4 + 1 = 5 \) farklı seçeneği vardır.
Bu bilgiler doğrultusunda çiçekçi \( 9 \cdot 7 \cdot 5 = 315 \) farklı seçim yapabilir. Üç renkten de sıfır gül seçilen durum bir buket oluşturmayacağı için bu çarpımdan bu tek durumu çıkararak toplam farklı buket sayısını \( 315 - 1 = 314 \) olarak buluruz.
8 elemanlı bir \( A \) kümesinin alt kümelerinin sayısı kaçtır?
Çözümü Göster\( A \) kümesinin her bir elemanının belirli bir alt kümede bulunup bulunmama durumunu "Var (V)/Yok (Y)" olarak işaretlersek soruyu tümünün gerçekleşmesi gereken birbirinden bağımsız 8 olay şeklinde kurgulayabiliriz.
Örneğin, boş küme için olaylar "YYYYYYYY" şeklinde gerçekleşirken, sadece kümenin birinci ve sonuncu elemanından oluşan bir alt küme için bu olaylar "VYYYYYYV" şeklinde gerçekleşir.
Çarpma kuralını bu 8 bağımsız olaya uygularsak toplam alt küme sayısını \( 2 \cdot 2 \cdot \ldots \cdot 2 = 2^8 \) olarak buluruz. Hatırlayacak olursak, \( 2^n \) aynı zamanda "Kümeler" konusunda gördüğümüz \( n \) elemanlı bir kümenin toplam alt küme sayısı formülüdür.
360 sayısının pozitif tam bölenlerinin sayısı kaçtır?
Çözümü Göster360'ı asal çarpanlarına ayıralım.
\( 360 = 2^3 \cdot 3^2 \cdot 5^1 \)
Görülebileceği gibi, 360 sayısının içinde asal çarpan olarak 3 tane 2, 2 tane 3 ve 1 tane 5 vardır ve 360'ın bir pozitif tam böleni bu asal çarpanları en fazla bu adetlerde içerebilir.
Bir tam bölenin belirli bir asal çarpanı hiç içermeme durumunu da düşünürsek, 360'ın bir pozitif tam böleninde 2 çarpanı \( 3 + 1 \) farklı şekilde, 3 çarpanı \( 2 + 1 \) farklı şekilde ve 5 çarpanı \( 1 + 1 \) farklı şekilde bulunabilir.
Çarpma kuralını bu farklı olaylara uygularsak toplam pozitif bölen sayısını \( (3 + 1)(2 + 1)(1 + 1) = 24 \) olarak buluruz, bu da "Asal Sayılar" konusunda gördüğümüz aşağıdaki pozitif bölen sayısı formülüne eşittir.
\( A = x^a \cdot y^b \cdot z^c \) şeklinde asal çarpanlarına ayrılmış bir sayı için,
Pozitif tam bölenlerin sayısı \( = (a + 1)(b + 1)(c + 1) \)
Ali'nin okulunda kostüm partisi düzenlenmektedir. Ali'nin partide giyebileceği 5 farklı kostümü, 4 farklı maskesi, 3 farklı şapkası ve 1 pelerini vardır.
Kostüm giymek zorunlu, diğer aksesuarlar isteğe bağlı olduğuna göre, Ali partiye kaç farklı kombinle gidebilir?
Çözümü GösterKostüm zorunlu olduğu için Ali'nin 5 kostüm seçeneği vardır.
Maske, şapka ve pelerin zorunlu olmadığı için seçeneklere Ali'nin bu aksesuarları takmama durumunu da eklemeliyiz.
Dolayısıyla, Ali'nin maske için 5, şapka için 4, pelerin için 2 farklı seçeneği vardır.
Buna göre Ali, kombini için \( 5 \cdot 5 \cdot 4 \cdot 2 = 200 \) farklı seçim yapabilir.
Annesinin 7 rakamdan oluşan telefon numarasını unutan Semih numarayla ilgili şunları hatırlamaktadır.
- En ortadaki rakam asaldır.
- İlk 3 basamaktaki rakamlar soldan sağa doğru ikişer azalan çift sayılardır.
- Son 3 basamaktaki sayı rakamları soldan sağa doğru ardışık artan bir tek sayıdır.
Semih tüm olasılıkları araması durumunda en fazla kaçıncı denemesinde annesine ulaşabilir?
Çözümü GösterEn ortadaki rakam, ilk 3 rakam ve son 3 rakam için farklı olasılıkları bulalım.
En ortadaki rakam asal olduğuna göre bu rakam için 4 olasılık vardır.
2, 3, 5, 7
İlk 3 basamaktaki rakamlar soldan sağa doğru ikişer azalan çift sayılar olduğuna göre bu basamaklar için 3 olasılık vardır.
420, 642, 864
Son 3 basamaktaki sayı rakamları soldan sağa doğru ardışık artan bir tek sayı olduğuna göre bu basamaklar için 4 olasılık vardır.
123, 345, 567, 789
İlk 3 rakam, ortadaki rakam ve son üç rakam birbirinden bağımsız seçimler olduğundan bu farklı olasılıkların çarpımı kadar farklı telefon numarası oluşturulabilir.
\( 4 \cdot 3 \cdot 4 = 48 \)
Buna göre Semih tüm olasılıkları araması durumunda en fazla 48. denemesinde annesine ulaşabilir.
Kenarları tam sayı ve alanı 180 birimkare olan kaç farklı dikdörtgen çizilebilir?
Çözümü Göster180'i asal çarpanlarına ayıralım.
\( 180 = 2^2 \cdot 3^2 \cdot 5 \)
180'in pozitif bölen sayısını bulalım.
Bir sayının pozitif bölen sayısı (PBS), asal çarpanlarının kuvvetlerinin birer fazlasının çarpımına eşittir.
\( PBS = (2 + 1)(2 + 1)(1 + 1) = 18 \)
Verilen dikdörtgenin 180'in her pozitif böleni kadar farklı kenar uzunluğu olabilir. Örneğin bir kenar uzunluğu 12 ise diğer kenar uzunluğu 12'de bulunmayan asal çarpanlardan oluşan 15 olur.
\( 180 = \underbrace{2 \cdot 2 \cdot 3}_{12} \cdot \underbrace{3 \cdot 5}_{15} \)
Oluşan dikdörtgenlerde genişlik ve yükseklik ikilisi aralarında yer değiştirdiğinde yeni bir dikdörtgen oluşmadığı için 18 dikdörtgenin yarısı birbirinin aynısıdır.
Buna göre kenarları tam sayı ve alanı 180 birimkare olan 9 farklı dikdörtgen çizilebilir.
3 katlı bir binadaki asansör her seferinde bir kat aşağı iniyor ya da yukarı çıkıyor ve her gün sonunda o gün bulunduğu katların sıralı listesini içeren bir rapor üretiyor.
Günün başında çalışmaya 1. kattan başlayan asansör gün boyunca 125 kez kat değiştirdiğine göre, bu rapor kaç farklı şekilde oluşabilir?
Çözümü GösterAsansör 1. ve 3. katlarda iken sadece 2. kata gidebilir, dolayısıyla gidebileceği tek kat seçeneği olur.
Asansör 2. katta iken 1. ya da 3. katlara gidebilir, dolayısıyla gidebileceği iki kat seçeneği olur.
Asansör 125 kez kat değiştirdiyse en başta bulunduğu 1. kat dahil toplam 126 kata uğramıştır, buna göre gün sonu raporu 126 satırdan oluşur.
Asansörün bir günlük operasyonuna ait örnek bir rapor aşağıdaki gibi olabilir.
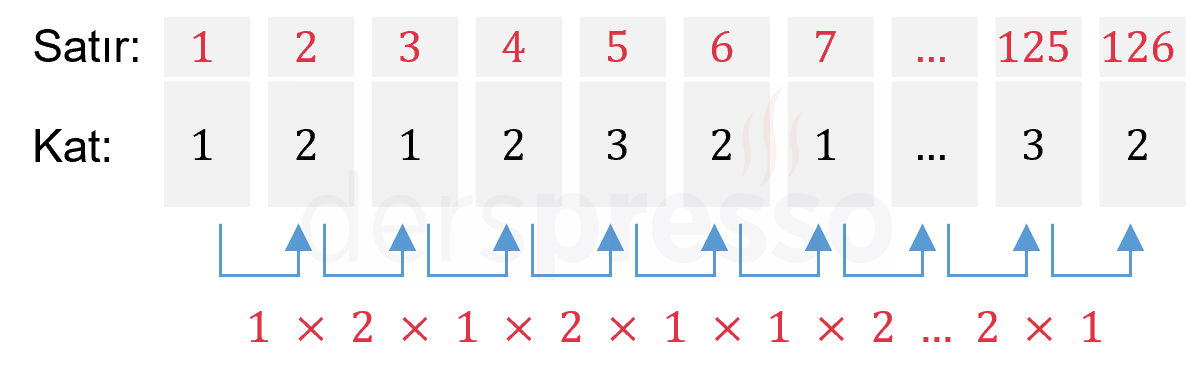
Buna göre asansörün gün boyunca 125 kat değişikliğinin 63'ünde tek değişiklik seçeneği vardır, 62'sinde ise iki değişiklik seçeneği vardır.
Asansör 2. kattayken 1. ya da 3. kata gitmesi, sonraki duraklardaki seçenek sayılarını değiştirmez.
Buna göre 125 kat değişikliği, dolayısıyla gün sonu raporu aşağıdaki sayıda farklı şekilde olabilir.
\( \underbrace{1 \cdot 2 \cdot 1 \cdot 2 \cdot \ldots \cdot 1}_\text{125 kez} \)
\( = \underbrace{1 \cdot 1 \cdot \ldots \cdot 1}_\text{63 kez} \cdot \underbrace{2 \cdot 2 \cdot \ldots \cdot 2}_\text{62 kez} \)
\( = 2^{62} \) bulunur.
Tekrarlayan Olaylar
Çarpma kuralının bir diğer uygulaması tek bir olayın pek çok kez tekrarlandığı durumdur.
\( m \) farklı sonucu olan bir olay \( n \) kez tekrarlandığında oluşabilecek farklı sonuç sayısı \( m^n \) olur.
\( \underbrace{m \cdot m \cdot m \ldots m}_\text{n adet} = m^n \)
Bir madeni para 10 kez atıldığında, sonuçların sırası da gözetilerek kaç farklı sonuç oluşabilir?
Çözümü GösterHer madeni para atışında 2 olası sonuç vardır (Y: yazı, T: tura).
Her atış birbirinden bağımsız olaylar olduğu için para 10 kez atıldığında toplamda \( \underbrace{2 \cdot 2 \cdot \ldots \cdot 2}_\text{10 kere} = 2^{10} \) farklı sonuç oluşur (örneğin YTTYTYYTYT).
Bir zar 5 kez atıldığında, sonuçların sırası da gözetilerek kaç farklı sonuç oluşabilir?
Çözümü GösterHer zar atışında 6 olası sonuç vardır (1, 2, 3, 4, 5, 6).
Her atış birbirinden bağımsız olaylar olduğu için zar 5 kez atıldığında toplamda \( \underbrace{6 \cdot 6 \cdot \ldots \cdot 6}_\text{5 kere} = 6^5 \) farklı sonuç oluşur (örneğin 13256).
Bir futbol liginde her hafta 10 maç yapılmaktadır. Her maçın 3 olası sonucu olduğuna göre (ev sahibi takımın galibiyeti, beraberlik, konuk takımın galibiyeti), belirli bir haftada oynanan maçlar kaç farklı şekilde sonuçlanabilir?
Çözümü GösterHer maçın 3 olası sonucu vardır (1: ev sahibi takımın galibiyeti, 0: beraberlik, 2: konuk takımın galibiyeti).
Her maç birbirinden bağımsız olaylar olduğu için 10 maçta toplamda \( \underbrace{3 \cdot 3 \cdot \ldots \cdot 3}_\text{10 tane} = 3^{10} \) farklı sonuç oluşur (örneğin 1101201021).
12 kişinin katıldığı bir ehliyet sınavı sonucunda her aday ya başarılı ya da başarısız olmaktadır.
Buna göre bu sınav kaç farklı şekilde sonuçlanabilir?
Çözümü GösterSınava giren her aday ya başarılı ya da başarısız olacağı için her aday için 2 farklı sonuç vardır.
Adayların sınav sonucu birbirinden bağımsız olaylar olduğu için çarpma kuralı gereği 12 aday için \( \underbrace{2 \cdot 2 \cdot \ldots \cdot 2}_\text{12 tane} = 2^{12} \) farklı sonuç oluşur.
5 farklı oyuncak 3 çocuğa herhangi bir koşul olmadan kaç farklı şekilde dağıtılabilir?
Çözümü GösterHer çocuk en az bir oyuncak almalı gibi bir koşul verilmediği için her oyuncağın dağıtımını bağımsız olaylar olarak düşünebiliriz.
Buna göre her oyuncak 3 farklı şekilde dağıtılabilir. Çarpım kuralı gereği 5 oyuncak 3 çocuğa toplamda \( 3 \cdot 3 \cdot 3 \cdot 3 \cdot 3 = 3^5 \) farklı şekilde dağıtılabilir.
Seçimlerin Bağımsızlığı
Çarpma kuralının kullanılabilmesi için yapılan seçimlerin birbirinden bağımsız olması, yani bir kümeden yapılan seçimin diğer bir kümeden yapılan seçimi etkilememesi gerektiğini belirtmiştik.
Bu koşulu daha esnek bir şekilde ifade edebiliriz. Buna göre, bir kümeden yapılan seçim diğer bir kümedeki seçenekleri değiştirse de seçenek sayısı aynı kalıyorsa çarpma kuralını kullanabilmemiz için gerekli koşul sağlanmış olur. Bir diğer ifadeyle, çarpma yoluyla saymada kümelerin elemanlarının değil eleman sayılarının değişmemesi yeterlidir.
A şehrinden B şehrine 5, B şehrinden C şehrine 4, C şehrinden D şehrine 3 farklı yol vardır. A şehrinden D şehrine gidip geri dönecek bir kişi, aynı yolu iki kez kullanmamak koşuluyla bunu kaç farklı şekilde yapabilir?
Çözümü GösterHer iki şehir arasındaki yollar birbirinden bağımsız seçenekler olduğu için, A'dan D'ye bu yol sayılarının çarpımı kadar farklı şekilde gidilebilir.
Gidişteki farklı yol sayısı \( = 5 \cdot 4 \cdot 3 = 60 \)
Gidişte kullanılan bir yol dönüşte kullanılamayacağı için, D'den A'ya bu yol sayılarının bir eksiklerinin çarpımı kadar farklı şekilde dönülebilir. Örneğin A'dan B'ye 2 no'lu yol kullanıldıysa dönüşte bu yol bir seçenek olmamaktadır.
Dönüşteki farklı yol sayısı \( = (5 - 1)(4 - 1)(3 - 1) = 24 \)
Gidişte kullanılabilecek 60 yolun her biri için dönüşte 24 farklı seçenek olduğu için A'dan D'ye gidiş ve dönüşte kullanılabilecek farklı yol sayısı bu iki sayının çarpımına eşittir.
Gidiş-dönüşteki farklı yol sayısı \( = 60 \cdot 24 = 1440 \)
Dikkat edilirse dönüşte kullanılabilecek yol seçenekleri gidişte kullanılan yollara bağlı olarak değişmektedir, ancak dönüşteki seçenek sayıları gidişte hangi yollar seçilmiş olursa olsun aynı kalmaktadır. Bu yüzden çarpma kuralını kullanmamıza engel bir durum oluşmamaktadır.
A binasının 6, B binasının 8 farklı giriş çıkış kapısı bulunmaktadır. Önce A binasına sonra da B binasına girip çıkacak olan Zeynep, farklı giriş çıkışları kullanmak üzere bu işlemi kaç farklı şekilde yapabilir?
Çözümü GösterZeynep A binasına 6 farklı kapıdan girebilir ve girişte kullandığı kapıyı kullanamayacağı için 5 farklı kapıdan çıkabilir. Buna göre Zeynep A binasına \( 6 \cdot 5 = 30 \) farklı şekilde girip çıkabilir.
Zeynep B binasına 8 farklı kapıdan girebilir ve girişte kullandığı kapıyı kullanamayacağı için 7 farklı kapıdan çıkabilir. Buna göre Zeynep B binasına \( 8 \cdot 7 = 56 \) farklı şekilde girip çıkabilir.
A binasındaki 30 farklı giriş-çıkış seçeneğinin her biri için B binasında 56 farklı giriş-çıkış seçenek olduğu için, Zeynep iki binaya \( 30 \cdot 56 = 1680 \) farklı şekilde girip çıkabilir.
Her binaya girişte kullanılan kapı çıkıştaki kapı seçeneklerini değiştirmektedir, ancak çıkıştaki seçenek sayısı girişte hangi kapı kullanılmış olursa olsun aynı kalmaktadır. Bu yüzden çarpma kuralını kullanmamıza engel bir durum oluşmamaktadır.
40 soruluk bir testte her sorunun 5 seçeneği vardır. Ardışık 3 sorunun doğru cevapları farklı olmak koşuluyla cevap anahtarı kaç farklı şekilde hazırlanabilir?
Çözümü GösterBirinci sorunun doğru cevabı 5 seçenekten biri olabilir.
İkinci sorunun doğru cevabı ilk soruyla aynı olamayacağı için ilk sorunun doğru cevabı dışındaki 4 seçenekten biri olabilir.
Üçüncü sorunun doğru cevabı ilk iki soruyla aynı olamayacağı için ilk iki sorunun doğru cevabı dışındaki 3 seçenekten biri olabilir.
Sonraki soruların doğru cevabı da kendinden önceki iki sorununki ile aynı olamayacağı için yine 3 seçenekten biri olabilir.
Buna göre cevap anahtarında ilk soru için 5, ikinci soru için 4, sonraki sorular için 3 doğru cevap seçeneği vardır.
Dolayısıyla farklı cevap anahtarı sayısı \( 5 \cdot 4 \cdot 3^{38} \) olur.
Dikkat edilirse ilk iki sorunun doğru cevabı sonraki soruların doğru cevap seçeneklerini değiştirmektedir, ancak seçenek sayıları ilk iki soruda doğru cevap ne olursa olsun aynı kalmakta ve 3 olmaktadır. Bu yüzden çarpma kuralını kullanmamıza engel bir durum oluşmamaktadır.
\( A = \{0, 2, 3, 5, 7, 9\} \) kümesinin elemanlarıyla rakamları farklı dört basamaklı kaç doğal sayı yazılabilir?
Çözümü GösterHer basamakta arasından seçim yapabileceğimiz rakam sayılarını belirleyelim.
1. basamak: 0'ı ilk basamakta kullanamayacağımız için 5 rakam seçeneği vardır.
2. basamak: Bu ve bundan sonraki basamaklarda 0'ı kullanabiliriz. 6 rakamdan birini 1. basamakta kullandığımız için 5 rakam seçeneği vardır.
3. basamak: İki rakamı ilk iki basamakta kullandığımız için 4 rakam seçeneği vardır.
4. basamak: Üç rakamı ilk üç basamakta kullandığımız için 3 rakam seçeneği vardır.
Bir basamakta yaptığımız seçim diğer basamaklardaki seçenekleri değiştirse de seçenek sayısını değiştirmediği için bu seçimleri bağımsız olarak düşünebiliriz ve çarpma kuralını kullanabiliriz.
Buna göre rakamları farklı dört basamaklı \( 5 \cdot 5 \cdot 4 \cdot 3 = 300 \) doğal sayı yazılabilir.
Bu soruda uyguladığımız yöntemi daha detaylı şekilde permütasyon konusunda inceleyeceğiz.
\( N \) 100'den büyük üç basamaklı bir tam sayıdır.
\( N \)'nin basamaklarındaki rakamlar ters sırayla yazıldığında oluşan yeni sayı \( N \)'den 297 daha fazla olmaktadır. Bu koşulları sağlayan kaç \( N \) sayısı vardır?
Çözümü Göster\( N \) sayısını \( (abc) \) şeklinde yazalım. Bu durumda basamakları tersten yazıldığında sayı \( (cba) \) olur.
\( (cba) - (abc) = 297 \)
Üç basamaklı sayıların çözümlemesini yapalım.
\( 100c + 10b + a - (100a + 10b + c) = 297 \)
\( 99c - 99a = 297 \)
\( c - a = 3 \)
\( a \) üç basamaklı bir sayının yüzler basamağında olduğundan 0 olamaz. Ayrıca \( c \)'nin bir rakam olabilmesi için \( a \) en fazla 6 olabilir.
Buna göre \( a \) aşağıdaki değerleri alabilir.
\( a \in \{1, 2, 3, 4, 5, 6\} \)
\( b \) herhangi bir kurala bağlı olmadığı için 10 rakamdan herhangi biri olabilir.
\( c \), \( a \)'nın her farklı değeri için tek bir değer alabilir.
Bir basamakta yaptığımız seçim diğer basamaklardaki seçenekleri değiştirse de seçenek sayısını değiştirmediği için bu seçimleri bağımsız olarak düşünebiliriz ve çarpma kuralını kullanabiliriz.
Her basamakta kullanabileceğimiz rakam sayılarını çarparak kaç farklı \( N \) sayısı oluşturabileceğimizi bulalım.
\( 6 \cdot 10 \cdot 1 = 60 \) farklı \( N \) sayısı oluşturulabilir.
Bir kümeden yapılan seçim diğer bir kümedeki seçenek sayısını değiştiriyorsa ya çarpma kuralını kullanamayız ya da önümüzdeki bölümde göreceğimiz üzere problemi birden fazla parçaya bölerek çarpma ve toplama kurallarını birlikte kullanabiliriz.