Mutlak Değer Tanımı
Mutlak değer üç farklı şekilde tanımlanabilir. Mutlak değerin uzaklık tanımı karmaşık sayılara da uygulanabilir olup diğer iki tanımı sadece reel sayılarda geçerlidir.
"Negatif Olmayan" Büyüklük Tanımı
Bu tanıma göre; negatif reel sayılar için mutlak değer sayının işaretinden bağımsız büyüklüğü, sıfır ve pozitif reel sayılar için sayının kendisidir. Bu tanım bir parçalı fonksiyon olarak aşağıdaki şekilde ifade edilebilir.
\( x \in \mathbb{R} \) olmak üzere,
\( \abs{x} = \begin{cases} x & x \ge 0 \\ -x & x \lt 0 \end{cases} \)
\( \abs{4} = \abs{-4} = 4 \)
\( \abs{0} = 0 \)
Aşağıdaki ifadelerin sonucunu bulunuz.
(a) \( \abs{-5} + \abs{-(-5)} + \abs{-(-(-5))} \)
(b) \( \abs{5 - 3} + \abs{3 - 5} + \abs{-5 + 3} \)
(c) \( \abs{(-2) \cdot 5} + \abs{(-2) \cdot (-5)} + \abs{2 \cdot (-5)} \)
Çözümü GösterMutlak değer içindeki bir ifade mutlak değerden, değeri sıfır ya da pozitif ise olduğu gibi, negatif ise önünde negatif işareti ile çıkar.
(a) seçeneği:
\( \abs{-5} + \abs{-(-5)} + \abs{-(-(-5))} \)
\( = \abs{-5} + \abs{5} + \abs{-5} \)
\( = 5 + 5 + 5 = 15 \)
(b) seçeneği:
\( \abs{5 - 3} + \abs{3 - 5} + \abs{-5 + 3} \)
\( = \abs{2} + \abs{-2} + \abs{-2} \)
\( = 2 + 2 + 2 = 6 \)
(c) seçeneği:
\( \abs{(-2) \cdot 5} + \abs{(-2) \cdot (-5)} + \abs{2 \cdot (-5)} \)
\( = \abs{-10} + \abs{10} + \abs{-10} \)
\( = 10 + 10 + 10 = 30 \)
\( c \lt b \lt a \) olduğuna göre,
\( \abs{c - b} + \abs{a - b} \) işleminin sonucu nedir?
Çözümü GösterMutlak değer içindeki ifadeleri işaretlerini dikkate alarak mutlak değer dışına çıkaralım.
Daha küçük sayıdan daha büyük sayı çıkardığımızda sonuç negatif olur ve ifade mutlak değerden önünde negatif işareti ile çıkar.
\( \abs{c - b} = -(c - b) = b - c \)
Daha büyük sayıdan daha küçük sayı çıkardığımızda sonuç pozitif olur ve ifade mutlak değerden olduğu gibi çıkar.
\( \abs{a - b} = a - b \)
İşlem sonucunu bulalım.
\( \abs{c - b} + \abs{a - b} = b - c + a - b \)
\( = a - c \) bulunur.
\( 4 \lt x \lt 10 \) olduğuna göre,
\( 3\abs{x - 4} - 2\abs{x - 10} \) işleminin sonucu nedir?
Çözümü GösterMutlak değer içindeki ifadeleri işaretlerini dikkate alarak mutlak değer dışına çıkaralım.
\( x \) için verilen değer aralığına göre; \( x - 4 \) ifadesi pozitiftir, dolayısıyla mutlak değerden olduğu gibi çıkar. \( x - 10 \) ifadesi ise negatiftir, dolayısıyla mutlak değerden önünde negatif işareti ile çıkar.
\( 3\abs{x - 4} - 2\abs{x - 10} = 3(x - 4) - 2[-(x - 10)] \)
\( = 3x - 12 + 2x - 20 \)
\( = 5x - 32 \) bulunur.
Aşağıdaki ifadelerin sonucunu bulunuz.
(a) \( \abs{3\sqrt{2} - 4} + \abs{2\sqrt{3} - 4} \)
(b) \( \abs{\pi - 3} - \abs{2\pi - 7} + \abs{10 - 3\pi} \)
(c) \( \abs{-5 + 2e} - \abs{8 - 3e} \)
Çözümü GösterMutlak değer içindeki bir ifade mutlak değerden, değeri sıfır ya da pozitif ise olduğu gibi, negatif ise önünde negatif işareti ile çıkar.
(a) seçeneği:
\( \abs{3\sqrt{2} - 4} + \abs{2\sqrt{3} - 4} \)
\( \sqrt{2} \approx 1,41\ldots \)
\( 3\sqrt{2} - 4 \gt 0 \)
\( \sqrt{3} \approx 1,73\ldots \)
\( 2\sqrt{3} - 4 \lt 0 \)
Mutlak değer içindeki ifadeleri işaretlerini dikkate alarak mutlak değer dışına çıkaralım.
\( = (3\sqrt{2} - 4) + [-(2\sqrt{3} - 4)] \)
\( = 3\sqrt{2} - 4 - 2\sqrt{3} + 4 \)
\( = 3\sqrt{2} - 2\sqrt{3} \)
(b) seçeneği:
\( \abs{\pi - 3} - \abs{2\pi - 7} + \abs{10 - 3\pi} \)
\( \pi = 3,1415\ldots \)
\( \pi - 3 \gt 0 \)
\( 2\pi - 7 \lt 0 \)
\( 10 - 3\pi \gt 0 \)
Mutlak değer içindeki ifadeleri işaretlerini dikkate alarak mutlak değer dışına çıkaralım.
\( = (\pi - 3) - [-(2\pi - 7)] + (10 - 3\pi) \)
\( = \pi - 3 + 2\pi - 7 + 10 - 3\pi \)
\( = 0 \)
(c) seçeneği:
\( \abs{-5 + 2e} - \abs{8 - 3e} \)
\( e = 2,7182\ldots \) (Euler sayısı)
\( -5 + 2e \gt 0 \)
\( 8 - 3e \lt 0 \)
Mutlak değer içindeki ifadeleri işaretlerini dikkate alarak mutlak değer dışına çıkaralım.
\( = (-5 + 2e) - [-(8 - 3e)] \)
\( = -5 + 2e + 8 - 3e \)
\( = 3 - e \)
Uzaklık Tanımı
Bu tanıma göre; bir reel sayının mutlak değeri, sayının sayı doğrusunda sıfır noktasına (orijine) olan uzaklığına eşittir ve sayının orijine göre hangi tarafta olduğundan bağımsız olarak her zaman pozitiftir.

İki reel sayının farkının mutlak değeri ise bu iki sayının sayı doğrusunda aralarındaki uzaklığa eşittir. İki sayının farkı sayıların çıkarma işlemindeki sırasına göre farklılık gösterse de, aralarındaki uzaklık ve farklarının mutlak değeri işlem sırasından bağımsız olarak her zaman pozitiftir.

\( 5 - 1 \ne 1 - 5 \)
\( \abs{5 - 1} = \abs{4} = 4 \)
\( \abs{1 - 5} = \abs{-4} = 4 \)
Bir karmaşık sayının mutlak değeri, o sayının iki boyutlu karmaşık düzlemde orijine olan uzaklığına eşittir. Karmaşık sayılarda mutlak değer ifadesi yerine modül ifadesi de kullanılmaktadır. Bu konuyu detaylı olarak karmaşık sayıların grafiksel gösterimi sayfasında inceleyeceğiz.
\( a \) sayısının sayı doğrusu üzerinde orijine uzaklığı 9 birim, \( b \) sayısına uzaklığı 13 birim olduğuna göre,
\( \abs{b - a} - \abs{-a} \) ifadesinin sonucu kaçtır?
Çözümü GösterSayı doğrusu üzerinde bir \( x \) sayısının \( y \) sayısına uzaklığı \( \abs{x - y} \) ile ifade edilir.
Sayı doğrusu üzerinde bir \( x \) sayısının orijine uzaklığı \( \abs{x - 0} = \abs{x} \) ile ifade edilir.
\( x \) sayısının \( y \) sayısına olan uzaklığı, \( y \) sayısının \( x \) sayısına olan uzaklığına eşittir.
\( \abs{x - y} = \abs{y - x} \)
\( a \) sayısının orijine olan uzaklığı 9 birimdir.
\( \abs{a} = 9 \)
\( a \) sayısının \( b \) sayısına olan uzaklığı 13 birimdir.
\( \abs{a - b} = 13 \)
İstenen ifadenin sonucunu bulalım.
\( \abs{b - a} - \abs{-a} = \abs{a - b} - \abs{a} \)
\( = 13 - 9 = 4 \) bulunur.
"\( a \) sayısının sayı doğrusu üzerinde -8 noktasına olan uzaklığı, 5 noktasına olan uzaklığının 3 katıdır." ifadesini denklem şeklinde yazınız.
Çözümü GösterSayı doğrusu üzerinde bir \( x \) sayısının \( y \) sayısına uzaklığı \( \abs{x - y} \) ile ifade edilir.
Buna göre \( a \) sayısının -8 noktasına olan uzaklığı \( \abs{a - (-8)} = \abs{a + 8} \) ile, 5 noktasına olan uzaklığı \( \abs{a - 5} \) ile ifade edilir.
Verilen ifadeyi denklem şeklinde yazalım.
\( \abs{a + 8} = 3\abs{a - 5} \)
\( \abs{x + 2} + \abs{x - 8} = 10 \)
eşitliğini sağlayan kaç tam sayı \( x \) değeri vardır?
Çözümü GösterSoruyu mutlak değerin uzaklık tanımını kullanarak çözelim.
Bu tanıma göre, iki reel sayının farkının mutlak değeri bu iki sayının sayı doğrusunda aralarındaki uzaklığı verir.
Verilen eşitliği düzenleyelim.
\( \abs{x - (-2)} + \abs{x - 8} = 10 \)
Buna göre \( \abs{x - (-2)} \) ifadesi \( x \)'in sayı doğrusu üzerinde \( -2 \) noktasına olan uzaklığını, \( \abs{x - 8} \) ifadesi \( x \)'in sayı doğrusu üzerinde \( 8 \) noktasına olan uzaklığını verir.
Sayı doğrusu üzerinde \( -2 \) ve \( 8 \) noktaları arasındaki uzaklık \( \abs{8 - (-2)} = 10 \) olduğu için, bu iki noktaya olan uzaklıkları toplamı 10 olan sayı sadece bu iki sayı arasında olabilir.
\( 8 \)'den büyük bir sayının \( -2 \) sayısına uzaklığı ve \( -2 \)'den küçük bir sayının \( 8 \) sayısına uzaklığı 10'dan büyük olacağı için, bu aralığın dışındaki bir sayı için bu toplam her zaman 10'dan büyük olacaktır.
Çözüm kümesi: \( -2 \le x \le 8 \)
Bu aralıkta \( x \)'in alabileceği \( 8 - (-2) + 1 = 11 \) tam sayı değer vardır.
Karekök Tanımı
Mutlak değerin bir diğer tanımı, bir sayının ya da değişkenin karesinin kareköküne eşit olmasıdır. Pozitif ve negatif reel sayıların karesi pozitiftir, pozitif sayıların karekökü de pozitiftir. Dolayısıyla, hem pozitif hem de negatif sayıların karesinin karekökü sayılardan pozitif olana eşit olur, bu da sayının mutlak değerine karşılık gelir.
\( x \in \mathbb{R} \) olmak üzere,
\( \sqrt{x^2} = \abs{x} \)
\( \sqrt{4^2} = \abs{4} = 4 \)
\( \sqrt{(-4)^2} = \abs{-4} = 4 \)
\( \sqrt{(x - 2)^2} = \abs{x - 2} \)
\( b \lt 0 \) olmak üzere,
\( \abs{b - 4 + \sqrt{(b - 1)^2}} \) ifadesinin sonucu kaçtır?
Çözümü GösterReel sayılar kümesinde tanımlı her ifadenin karesinin karekökü o ifadenin mutlak değerine eşittir.
\( \abs{b - 4 + \sqrt{(b - 1)^2}} = \abs{b - 4 + \abs{b - 1}} \)
Negatif \( b \) sayısından 1 çıkardığımızda sonuç yine negatif olur, dolayısıyla bu ifade mutlak değerden önünde negatif işareti ile çıkar.
\( = \abs{b - 4 + [-(b - 1)]} \)
\( = \abs{b - 4 + (1 - b)} \)
\( = \abs{-3} = 3 \) bulunur.
\( x \lt y \lt z \lt 0 \) olduğuna göre,
\( \sqrt{x^2 - 2xz + z^2} - \sqrt{(x + y - z)^2} + \sqrt{9 - 6x + x^2} \) ifadesinin sonucu nedir?
Çözümü Gösterİfadeyi düzenleyelim.
\( \sqrt{(x - z)^2} - \sqrt{(x + y - z)^2} + \sqrt{(3 - x)^2} \)
Bir ifadenin karesinin karekökü o ifadenin mutlak değerine eşittir.
\( = \abs{x - z} - \abs{x + y - z} + \abs{3 - x} \)
Daha büyük sayıdan daha küçük sayı çıkardığımızda sonuç pozitif olur ve ifade mutlak değerden olduğu gibi çıkar.
Daha küçük sayıdan daha büyük sayı çıkardığımızda sonuç negatif olur ve ifade mutlak değerden önünde negatif işareti ile çıkar.
\( x - z \) ifadesi negatiftir.
\( \abs{x - z} = -(x - z) = z - x \)
\( x + y - z \) ifadesi negatiftir.
\( \abs{x + y - z} = -(x + y - z) = z - x - y \)
\( 3 - x \) ifadesi pozitiftir.
\( \abs{3 - x} = 3 - x \)
Bulduğumuz değerleri yerine koyalım.
\( = (z - x) - (z - x - y) + (3 - x) \)
\( = z - x - z + x + y + 3 - x \)
\( = -x + y + 3 \) bulunur.
\( \abs{x - 3} = x - 3 \)
\( \abs{4x - 72} = 72 - 4x \)
eşitliklerini sağlayan kaç farklı \( x \) tam sayı değeri vardır?
Çözümü GösterBirinci ifade mutlak değerden olduğu gibi çıktığına göre değeri sıfır ya da pozitiftir.
\( x - 3 \ge 0 \)
\( x \ge 3 \)
İkinci ifade mutlak değerden ters işaretli çıktığına göre değeri sıfır ya da negatiftir.
Mutlak değer içindeki ifade sıfıra eşit olduğunda \( \abs{a - b} = a - b = b - a \) olacağı için burada küçük değil küçük eşit sembolü kullanmalıyız.
\( 4x - 72 \le 0 \)
\( x \le 18 \)
Bulduğumuz aralıkların kesişimi denklem sisteminin çözüm kümesini verir.
\( 3 \le x \le 18 \)
\( x \)'in bu aralıkta alabileceği \( 18 - 3 + 1 = 16 \) farklı tam sayı değeri vardır.
\( a \lt b \lt 0 \lt c \) olduğuna göre, aşağıdaki ifadelerin sonucu nedir?
(a) \( 2\abs{a - c} - \abs{b - a} - \abs{b - c} \)
(b) \( \abs{a - 6} + \abs{b + a} - 3\abs{a - b - 2} \)
(c) \( \abs{c - 2b} - \abs{-c + a} + \abs{a - 2c} \)
Çözümü GösterDaha büyük sayıdan daha küçük sayı çıkardığımızda sonuç pozitif olur ve ifade mutlak değerden olduğu gibi çıkar.
Daha küçük sayıdan daha büyük sayı çıkardığımızda sonuç negatif olur ve ifade mutlak değerden önünde negatif işareti ile çıkar.
Mutlak değer içindeki ifadeleri işaretlerini dikkate alarak mutlak değer dışına çıkaralım.
(a) seçeneği:
\( 2\abs{a - c} - \abs{b - a} - \abs{b - c} \)
Negatif sayıdan pozitif sayı çıkardığımızda sonuç negatif olur.
\( \abs{a - c} = -(a - c) = c - a \)
Daha büyük sayıdan daha küçük sayı çıkardığımızda sonuç pozitif olur.
\( \abs{b - a} = b - a \)
Negatif sayıdan pozitif sayı çıkardığımızda sonuç negatif olur.
\( \abs{b - c} = -(b - c) = c - b \)
Bulduğumuz değerleri yerine koyalım.
\( = 2(c - a) - (b - a) - (c - b) \)
\( = 2c - 2a - b + a - c + b \)
\( = -a + c \)
(b) seçeneği:
\( \abs{a - 6} + \abs{b + a} - 3\abs{a - b - 2} \)
Negatif sayıdan pozitif sayı çıkardığımızda sonuç negatif olur.
\( \abs{a - 6} = -(a - 6) = 6 - a \)
Negatif sayıların toplamı negatiftir.
\( \abs{b + a} = -(b + a) = -b - a \)
\( a \lt b \) olduğu için \( a - b \) negatiftir, bu değerden pozitif bir sayı çıkardığımızda sonuç yine negatif olur.
\( \abs{a - b - 2} = -(a - b - 2) = -a + b + 2 \)
Bulduğumuz değerleri yerine koyalım.
\( = (6 - a) + (-b - a) - 3(-a + b + 2) \)
\( = 6 - a - b - a + 3a - 3b - 6 \)
\( = a - 4b \)
(c) seçeneği:
\( \abs{c - 2b} - \abs{-c + a} + \abs{a - 2c} \)
Pozitif sayıdan negatif sayı çıkardığımızda sonuç pozitif olur.
\( \abs{c - 2b} = c - 2b \)
Negatif sayıların toplamı negatiftir.
\( \abs{-c + a} = -(-c + a) = c - a \)
Negatif sayıdan pozitif sayı çıkardığımızda sonuç negatif olur.
\( \abs{a - 2c} = -(a - 2c) = 2c - a \)
Bulduğumuz değerleri yerine koyalım.
\( = (c - 2b) - (c - a) + (2c - a) \)
\( = c - 2b - c + a + 2c - a \)
\( = -2b + 2c \)
\( a, b \in \mathbb{R} \) olmak üzere,
\( a = \abs{9b - 45} - 41 \) olduğuna göre,
\( a \)'nın en küçük değeri için \( ab \) çarpımı kaçtır?
Çözümü Göster\( a \) en küçük değerini mutlak değer ifadesi en küçük değerini aldığında alır.
Bir mutlak değer ifadesinin alabileceği en küçük değer sıfırdır.
\( \abs{9b - 45} = 0 \)
\( 9b - 45 \) ifadesi sıfır yapan \( b \) değerini bulalım.
\( 9b - 45 = 0 \)
\( b = 5 \)
\( b = 5 \) için \( a \) değerini bulalım.
\( a = 0 - 41 = -41 \)
\( a \)'nın en küçük değeri için \( ab \) çarpımını bulalım.
\( ab = 5 \cdot (-41) = -205 \) bulunur.
\( x \lt \abs{x} \) ve \( \abs{y} \le y \) olduğuna göre,
\( \sqrt[3]{-8y^3} - \sqrt{x^2 - 2xy + y^2} \) ifadesinin sonucu nedir?
Çözümü GösterBir sayının mutlak değeri kendisinden büyükse sayı negatiftir.
\( x \lt \abs{x} \Longrightarrow x \lt 0 \)
Bir sayı mutlak değerinden büyük ya da ona eşitse sayı sıfır ya da pozitiftir.
\( \abs{y} \le y \Longrightarrow y \ge 0 \)
Köklü ifadelerin içini düzenleyelim.
\( \sqrt[3]{(-2y)^3} - \sqrt{(x - y)^2} \)
Köklü ifadeleri kök dışına çıkaralım.
Birinci ifade tek dereceli kök içinden olduğu gibi, ikinci ifade çift dereceli kök içinden mutlak değer içinde çıkar.
\( = -2y - \abs{x - y} \)
Daha küçük sayıdan daha büyük sayı çıkardığımızda sonuç negatif olur ve ifade mutlak değerden önünde negatif işareti ile çıkar.
\( = -2y - [-(x - y)] \)
\( = -2y + x - y \)
\( = x - 3y \) bulunur.
\( x \in \mathbb{R} \) olmak üzere,
Aşağıdaki ifadelerin alabilecekleri değer aralıklarını bulunuz.
(a) \( \abs{2x - 8} + 5 \)
(b) \( 3 - \abs{x + 7} \)
(c) \( 3\abs{4 - 5x} - 10 \)
Çözümü GösterBir mutlak değer ifadesi sıfır ya da pozitif değer alabilir.
(a) seçeneği:
\( \abs{2x - 8} \ge 0 \)
Eşitsizliğin taraflarına 5 ekleyelim.
\( \abs{2x - 8} + 5 \ge 5 \)
(b) seçeneği:
\( \abs{x + 7} \ge 0 \)
Eşitsizliğin taraflarını \( -1 \) ile çarpalım.
\( -\abs{x + 7} \le 0 \)
Eşitsizliğin taraflarına 3 ekleyelim.
\( 3 - \abs{x + 7} \le 3 \)
(c) seçeneği:
\( \abs{4 - 5x} \ge 0 \)
Eşitsizliğin taraflarını 3 ile çarpalım.
\( 3\abs{4 - 5x} \ge 0 \)
Eşitsizliğin taraflarından 10 çıkaralım.
\( 3\abs{4 - 5x} - 10 \ge -10 \)
\( x, y, z \in \mathbb{Z^-} \) olmak üzere,
\( \dfrac{1}{x} \lt \dfrac{1}{y} \lt \dfrac{1}{z} \) olduğuna göre,
\( \abs{x + y} + \abs{z - y} - \abs{x - z} \) ifadesinin sonucu nedir?
Çözümü GösterVerilen eşitsizliğe göre \( x, y, z \) arasındaki sıralama aşağıdaki gibi olur.
\( z \lt y \lt x \lt 0 \)
Mutlak değer içindeki ifadeleri işaretlerini dikkate alarak mutlak değer dışına çıkaralım.
Negatif sayıların toplamı negatiftir.
\( \abs{x + y} = -(x + y) \)
Daha küçük sayıdan daha büyük sayı çıkardığımızda sonuç negatif olur.
\( \abs{z - y} = -(z - y) = y - z \)
Daha büyük sayıdan daha küçük sayı çıkardığımızda sonuç pozitif olur.
\( \abs{x - z} = x - z \)
Bulduğumuz değerleri yerine koyalım.
\( \abs{x + y} + \abs{z - y} - \abs{x - z} \)
\( = -(x + y) + (y - z) - (x - z) \)
\( = -x - y + y - z - x + z \)
\( = -2x \) bulunur.
\( x \ne 0 \) olmak üzere,
\( \abs{3x - 7y - 2z} \) ifadesinin en küçük değeri için \( \frac{14x - 28y - 8z}{15x + 42y + 12z} \) ifadesinin eşiti nedir?
Çözümü GösterBir mutlak değer ifadesinin alabileceği en küçük değer sıfırdır.
\( \abs{3x - 7y - 2z} = 0 \)
\( 3x - 7y - 2z = 0 \)
\( 3x = 7y + 2z \)
Bulduğumuz değeri verilen ifadede yerine yazalım.
\( \dfrac{14x - 28y - 8z}{15x + 42y + 12z} \)
\( = \dfrac{14x - 4(7y + 2z)}{15x + 6(7y + 2z)} \)
\( = \dfrac{14x - 4 \cdot 3x}{15x + 6 \cdot 3x} \)
\( = \dfrac{14x - 12x}{15x + 18x} \)
\( = \dfrac{2x}{33x} = \dfrac{2}{33} \) bulunur.
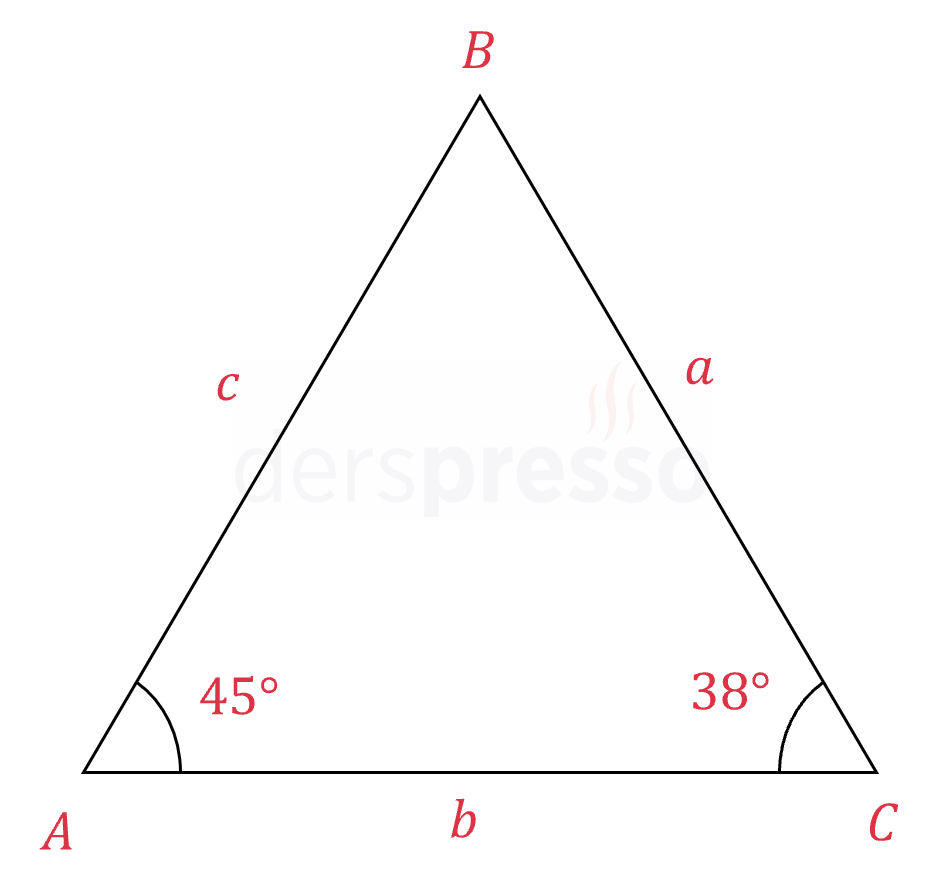
\( \abs{BC} = a, \quad \abs{AC} = b, \quad \abs{AB} = c \)
olduğuna göre, \( \abs{b - a} + \abs{c + a} - \abs{c - b} \) ifadesinin sonucu nedir?
Çözümü GösterBir üçgende daha büyük (küçük) açı daha uzun (kısa) kenarı görür.
Verilen üçgenin kenar ve açıları arasındaki ilişkileri buna göre inceleyelim.
\( m(\hat{B}) = 180 - 45 - 38 = 97° \)
Üçgenin iç açıları arasındaki sıralama aşağıdaki gibidir.
\( m(\hat{C}) \lt m(\hat{A}) \lt m(\hat{B}) \)
Buna göre, üçgenin kenar uzunlukları arasındaki sıralama aşağıdaki gibi olur.
\( c \lt a \lt b \)
Mutlak değer ifadelerinin işaretlerini buna göre düzenleyelim.
\( \abs{b - a} + \abs{c + a} - \abs{c - b} \)
\( = (b - a) + (c + a) - [-(c - b)] \)
\( = (b - a) + (c + a) + (c - b) \)
\( = 2c \) bulunur.
\( x, y \in \mathbb{Z} \) olmak üzere,
\( \abs{x - 1}^{\abs{y + 2}} = 64 \)
olduğuna göre, \( xy \) çarpımının en küçük değeri kaçtır?
Çözümü GösterTaban ve üs birer pozitif tam sayı olmak üzere, 64 sayısını 4 farklı şekilde yazabiliriz.
\( 64 = 2^6 = 4^3 = 8^2 = 64^1 \)
Her bir durum için \( x \) ve \( y \) değerlerini bulalım.
Durum 1:
\( 64 = 2^6 \)
\( \abs{x - 1} = 2 \Longrightarrow x \in \{-1, 3\} \)
\( \abs{y + 2} = 6 \Longrightarrow y \in \{-8, 4\} \)
Bu durum için \( xy \) çarpımının en küçük değeri \( -8 \cdot 3 = -24 \) olur.
Durum 2:
\( 64 = 4^3 \)
\( \abs{x - 1} = 4 \Longrightarrow x \in \{-3, 5\} \)
\( \abs{y + 2} = 3 \Longrightarrow y \in \{-5, 1\} \)
Bu durum için \( xy \) çarpımının en küçük değeri \( -5 \cdot 5 = -25 \) olur.
Durum 3:
\( 64 = 8^2 \)
\( \abs{x - 1} = 8 \Longrightarrow x \in \{-7, 9\} \)
\( \abs{y + 2} = 2 \Longrightarrow y \in \{-4, 0\} \)
Bu durum için \( xy \) çarpımının en küçük değeri \( -4 \cdot 9 = -36 \) olur.
Durum 4:
\( 64 = 64^1 \)
\( \abs{x - 1} = 64 \Longrightarrow x \in \{-63, 65\} \)
\( \abs{y + 2} = 1 \Longrightarrow y \in \{-3, -1\} \)
Bu durum için \( xy \) çarpımının en küçük değeri \( -3 \cdot 65 = -195 \) olur.
Buna göre \( xy \) çarpımının en küçük değeri \( -195 \) olur.