Karmaşık Sayıların Grafiksel Gösterimi
Karmaşık sayıların koordinat düzleminde gösteriminde sayıların reel kısımları yatay eksenle, sanal kısımları da dikey eksenle eşlenir. Daha sonra bir \( z = a + bi \) karmaşık sayısının karşılık geldiği \( (a, b) \) noktası koordinat düzleminde işaretlenir ve orijinden bu noktaya bir doğru parçası çizilir.
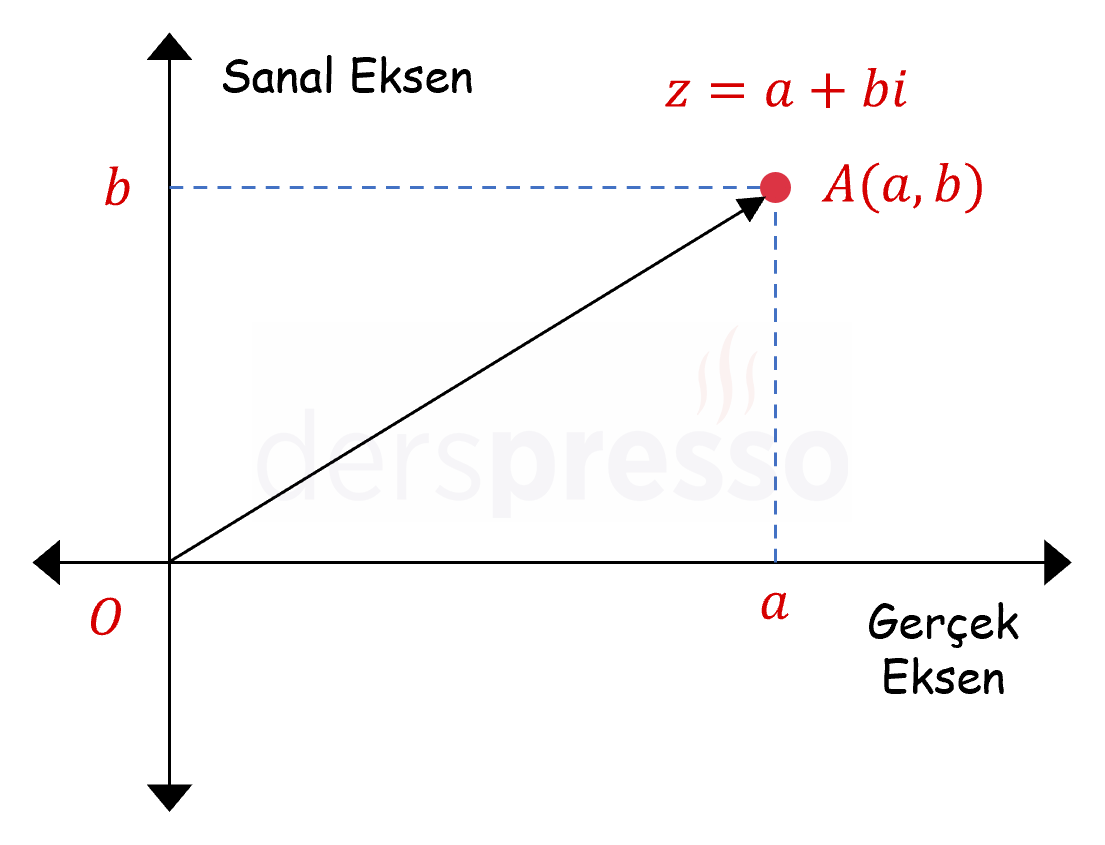
Karmaşık sayıları göstermek için kullanılan bu düzleme karmaşık düzlem, yatay eksene gerçek eksen, dikey eksene de sanal eksen denir.
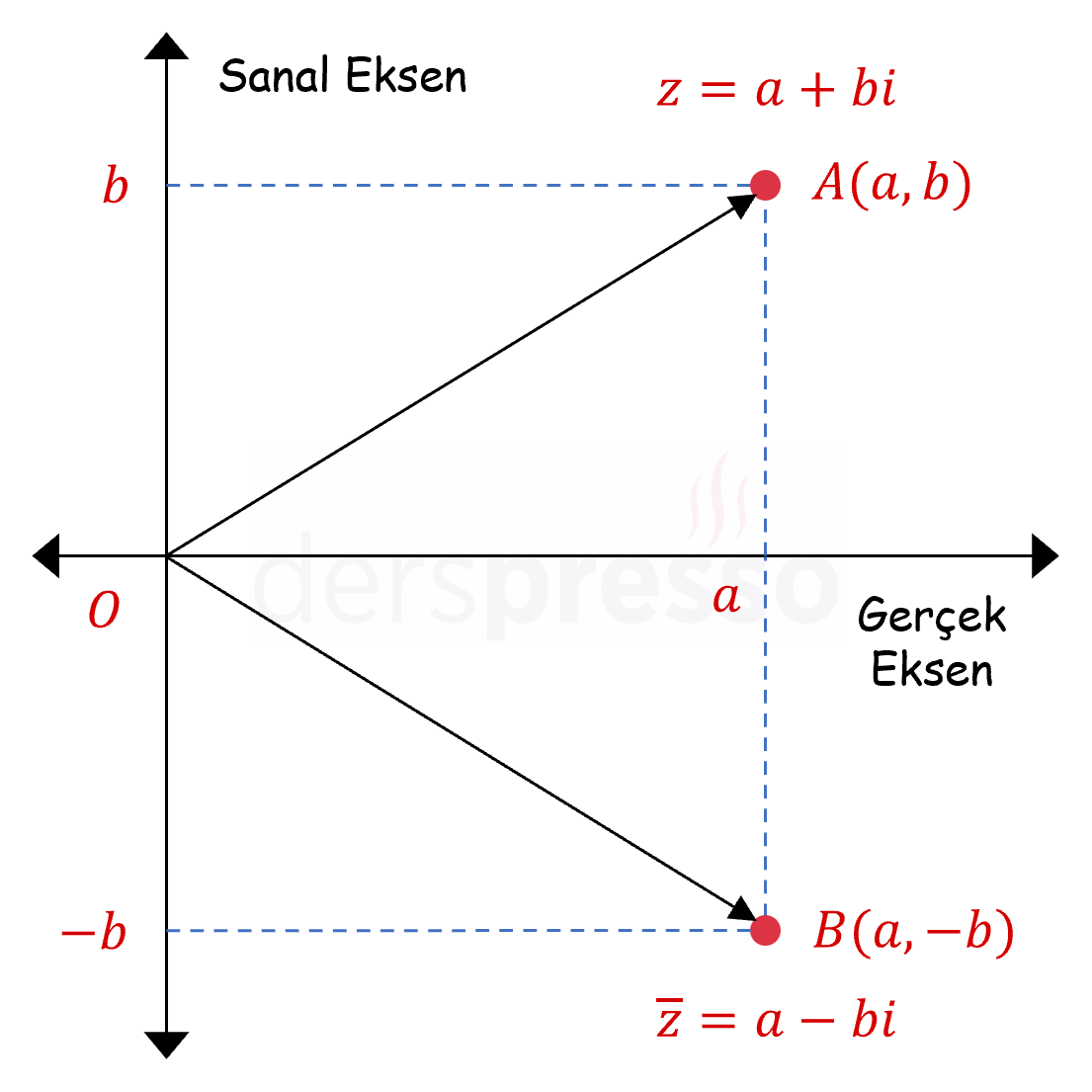
Bir karmaşık sayının eşleniğinin grafiği, o sayının gerçek eksene göre simetriğidir.
SORU 1:
Yukarıdaki grafiğe göre, \( \dfrac{z_1^2 \cdot \overline{z_2}}{z_3^3} \) ifadesinin eşiti nedir?
Çözümü Göster