Karmaşık Sayı Tanımı
Aşağıdaki formda yazılabilen sayılara karmaşık sayı denir. Karmaşık sayılar genellikle \( z \) ve \( w \) harfleri ile gösterilirler.
\( a, b \in \mathbb{R}, \quad i \) sanal birim olmak üzere,
\( z = a + bi \)
\( z_1 = 3 + 2i \)
\( z_2 = 0 - 3i = -3i \)
\( z_3 = 5 + 0i = 5 \)
Görülebileceği üzere, karmaşık sayıların reel ve sanal bileşenleri vardır. Yukarıdaki \( z \) karmaşık sayısında \( a \) sayının reel (gerçek) bileşeni, \( b \) sanal (imajiner) bileşenidir.
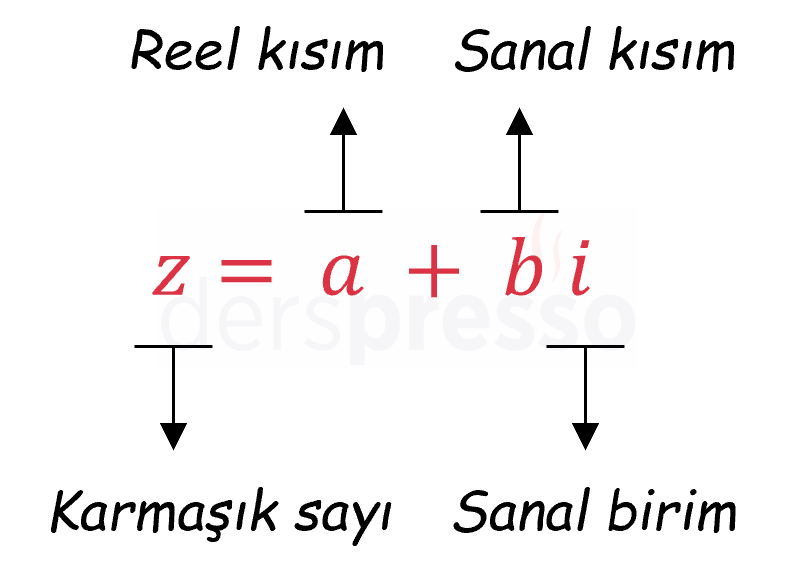
Karmaşık sayılar kümesi \( \mathbb{C} \) ile gösterilir.
\( \mathbb{C} = \{ a + bi \mid a, b \in \mathbb{R} \} \)
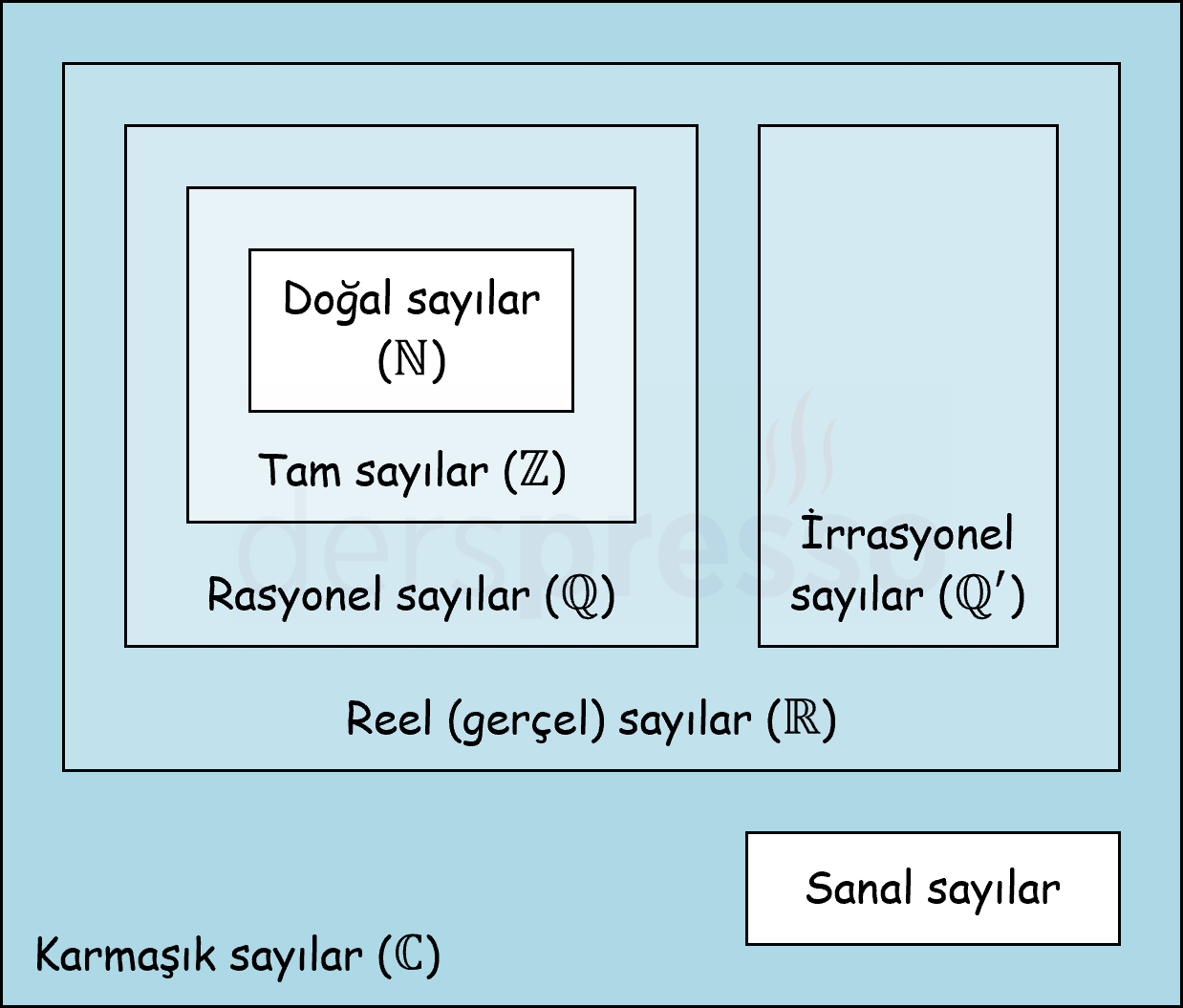
Bir karmaşık sayı reel ve sanal bileşenlerden oluşabildiği gibi, sadece reel ya da sadece sanal bileşenden de oluşabilir. Bunun bir sonucu olarak, tüm reel sayılar aynı zamanda sanal bileşeni sıfır olan birer karmaşık sayıdır ve karmaşık sayılar kümesi reel sayılar kümesini kapsar.
Aşağıdaki şekil karmaşık sayılar, sanal sayılar ve diğer sayı kümeleri arasındaki ilişkiyi göstermektedir.
\( z \) sayısının reel bileşeni \( Re(z) \), sanal bileşeni \( Im(z) \) şeklinde gösterilir.
\( z = a + bi \) olmak üzere,
\( Re(z) = a \)
\( Im(z) = b \)
\( z = 3 - 7i \)
\( Re(z) = 3, \quad Im(z) = -7 \)
\( z = -2 \)
\( Re(z) = -2, \quad Im(z) = 0 \)
\( z = 4i \)
\( Re(z) = 0, \quad Im(z) = 4 \)
\( Im(z) \) ifadesinin sadece \( b \) katsayısını verdiğine ve \( i \) sanal birimini içermediğine dikkat edilmelidir. Buna göre bir karmaşık sayı aşağıdaki şekilde ifade edilebilir.
\( z = Re(z) + Im(z)i \)
Karmaşık Sayıların Eşitliği
İki karmaşık sayının eşitliğinde sayıların reel ve sanal bileşenleri ayrı ayrı birbirine eşittir. Benzer şekilde, iki karmaşık sayının reel ve sanal bileşenleri ayrı ayrı birbirine eşitse bu iki sayı birbirine eşittir.
\( z_1 = a_1 + b_1i \)
\( z_2 = a_2 + b_2i \) olmak üzere,
\( z_1 = z_2 \Longleftrightarrow (a_1 = a_2 \text{ ve } b_1 = b_2) \)
\( z_1 = a - \sqrt{2}i \)
\( z_2 = 4 + bi \)
\( z_1 = z_2 \) ise,
\( a = 4, \quad b = -\sqrt{2} \)
Bir karmaşık sayı sıfıra eşitse sayının reel ve sanal bileşenleri ayrı ayrı sıfıra eşittir. Benzer şekilde, bir karmaşık sayının reel ve sanal bileşenleri ayrı ayrı sıfıra eşitse bu sayı sıfıra eşittir.
\( z = a + bi \) olmak üzere,
\( z = 0 \Longleftrightarrow (a = 0 \text{ ve } b = 0) \)
\( z = a - 2 + (b + 1)i \)
\( z = 0 \) ise,
\( a = 2, \quad b = -1 \)
Reel sayılarda geçerli olan büyüklük/küçüklük ilişkisi karmaşık sayılarda geçerli değildir. Buna göre iki karmaşık sayı arasında \( z_1 \lt z_2 \) ya da \( z_1 \ge z_2 \) şeklinde karşılaştırma yapılamaz.
\( z = 1 + i + i^2 + \ldots + i^{1002} \)
karmaşık sayısı için \( Im(z) + Re(z) \) toplamı kaçtır?
Çözümü GösterSanal birimin ardışık 4 tam sayı kuvvetinin toplamı her zaman sıfırdır.
\( i^n + i^{n + 1} + i^{n + 2} + i^{n + 3} = 0 \)
Verilen sayıda \( 1002 - 0 + 1 = 1003 \) terim vardır.
\( 1003 = 4 \cdot 250 + 3 \)
Buna göre ilk üç terimden sonraki 1000 terimi 4'erli grupladığımızda her gruptaki terimlerin toplamı sıfır olur, dolayısıyla verilen sayının değeri ilk üç terimin toplamına eşittir.
\( z = 1 + i^1 + i^2 + 0 \)
\( = 1 + i + (-1) = i \)
\( Re(z) = 0 \)
\( Im(z) = 1 \)
\( Re(z) + Im(z) = 0 + 1 = 1 \) bulunur.
\( z = (2 + 2i)^8 \) ve \( w = (8 - 8i)^4 \) olmak üzere,
\( Re(zw) \) işleminin sonucu kaçtır?
Çözümü Göster\( z \) karmaşık sayısını sadeleştirelim.
\( z = (2 + 2i)^8 \)
\( = [2(1 + i)]^8 \)
\( = 2^8(1 + i)^8 \)
\( = 2^8[(1 + i)^2]^4 \)
\( = 2^8(1 + 2i + i^2)^4 \)
\( = 2^8(2i)^4 \)
\( = 2^82^4i^4 \)
\( = 2^{12} \)
\( w \) karmaşık sayısını sadeleştirelim.
\( = (8 - 8i)^4 \)
\( = [8(1 - i)]^4 \)
\( = 8^4(1 - i)^4 \)
\( = 2^{12}[(1 - i)^2]^2 \)
\( = 2^{12}(1 - 2i + i^2)^2 \)
\( = 2^{12}(-2i)^2 \)
\( = 2^{12}(-2)^2i^2 \)
\( = 2^{12}2^2i^2 \)
\( = -2^{14} \)
İki karmaşık sayının çarpımını bulalım.
\( zw = 2^{12} \cdot (-2^{14}) = -2^{26} \)
\( Re(zw) = -2^{26} \) bulunur.