Vektörlerle Toplama ve Çıkarma
Skaler büyüklükler arasında olduğu gibi, vektörler arasında da toplama ve çıkarma işlemleri yapılabilir. Skaler büyüklükler arasındaki işlemlerden farklı olarak, vektörler arasındaki toplama/çıkarma işleminin sonucu yine bir vektördür.
Vektörlerle Toplama
İki vektör arasındaki toplama işleminde, vektörlerin birbirine karşılık gelen bileşenlerinin ayrı ayrı toplamı alınır.
\( \vec{a} = (x_1, y_1) \)
\( \vec{b} = (x_2, y_2) \) olmak üzere,
\( \vec{a} + \vec{b} = (x_1, y_1) + (x_2, y_2) \)
\( = (x_1 + x_2, y_1 + y_2) \)
\( \vec{a} = (3, 2) \)
\( \vec{b} = (-4, 3) \) olmak üzere,
\( \vec{a} + \vec{b} = (3, 2) + (-4, 3) \)
\( = (3 + (-4), 2 + 3) \)
\( = (-1, 5) \)
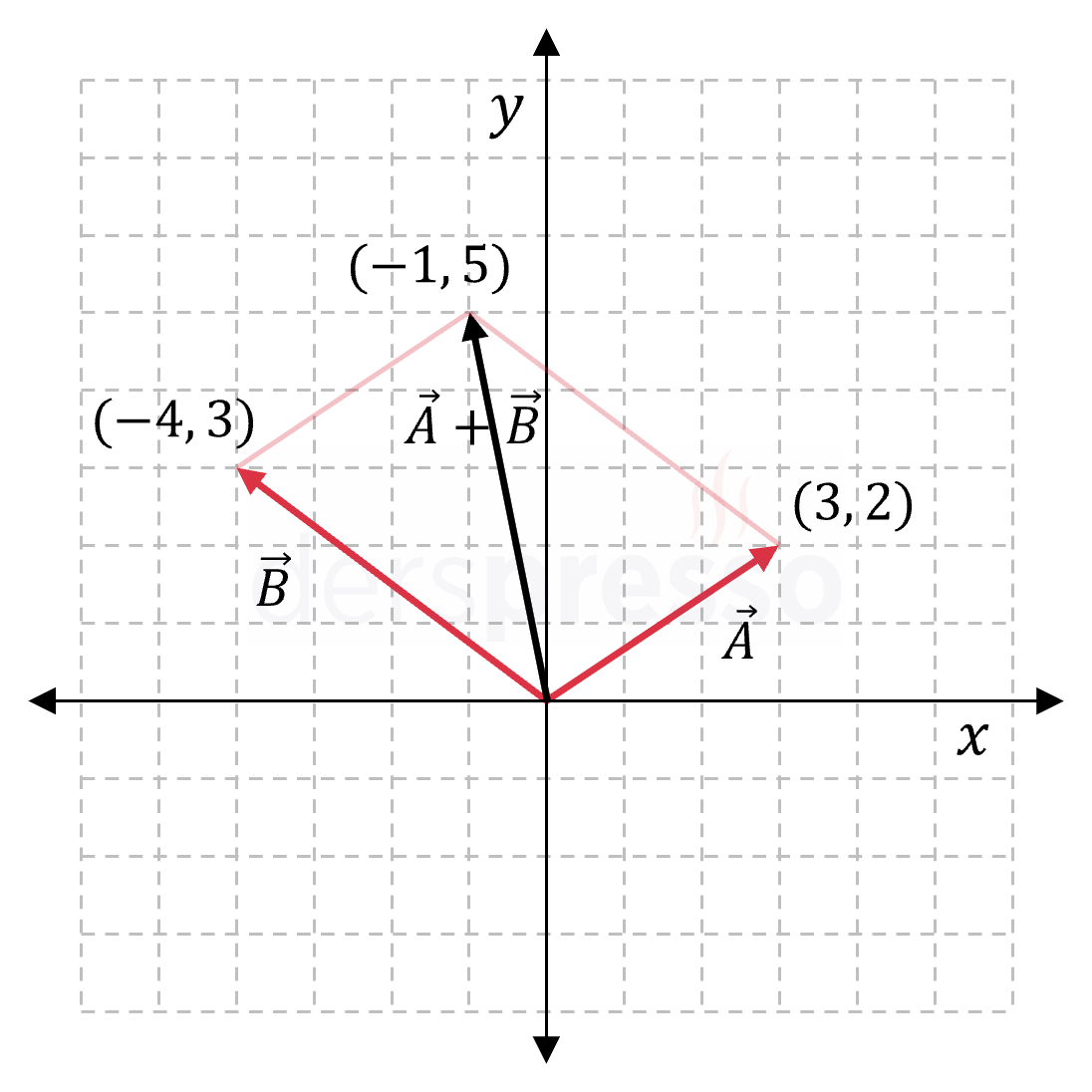
Vektörler arasında toplama işlemi geometrik olarak iki farklı yöntemle yapılabilir.
Uç Uca Ekleme Yöntemi
Uç uca ekleme yönteminde; ikinci vektör, başlangıç noktası birinci vektörün bitiş noktasına denk gelecek şekilde yerleştirilir ve ilk vektörün başlangıç noktasından ikinci vektörün bitiş noktasına bir ok çizilir. Çizilen bu ok iki vektörün toplam vektörüdür.
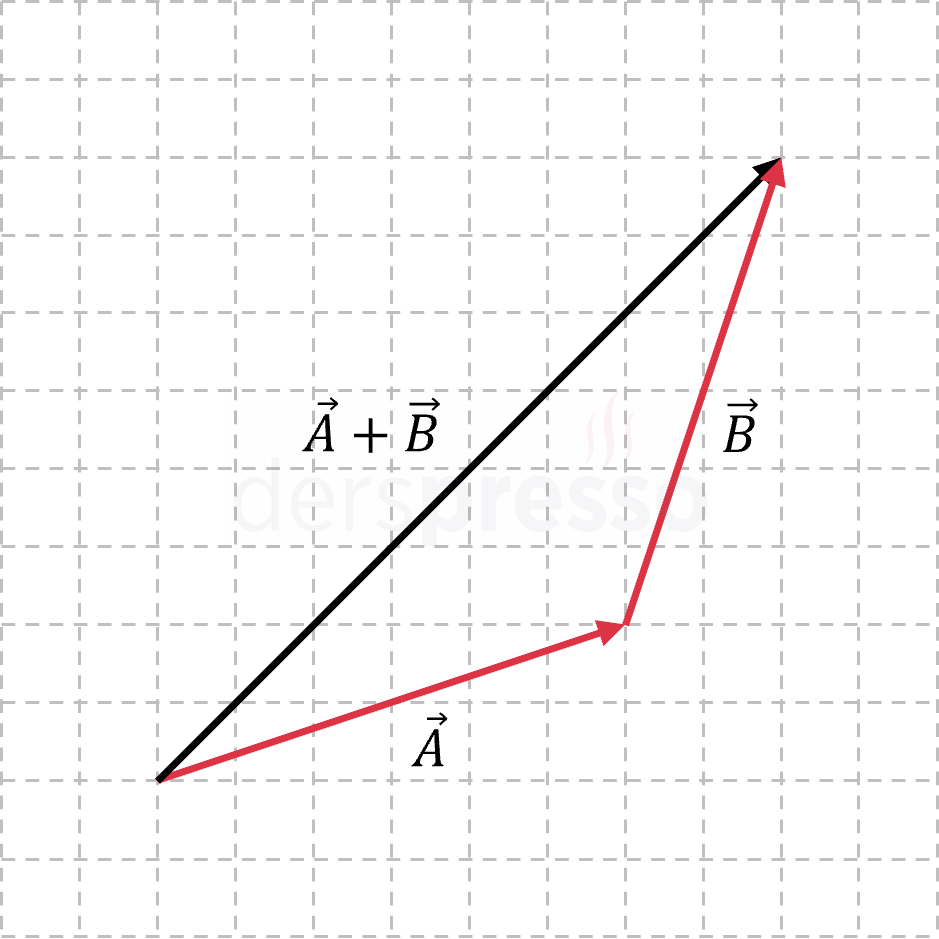
İki vektörün farklı sırada uç uca eklenmesi sonucu değiştirmez. Birinci vektör ikinci vektörün ucuna eklendiğinde yön ve büyüklük olarak aynı toplam vektörünün elde edildiği aşağıdaki şekilde görülebilir.

Paralelkenar Yöntemi
Paralelkenar yönteminde iki vektör başlangıç noktaları denk gelecek şekilde yerleştirilir ve bu iki vektöre paralel birer vektör çizilerek şekil bir paralelkenara tamamlanır. İki vektörün başlangıç noktalarından paralelkenarın karşı köşesine bir ok çizilir. Bu çizilen ok iki vektörün toplam vektörüdür.
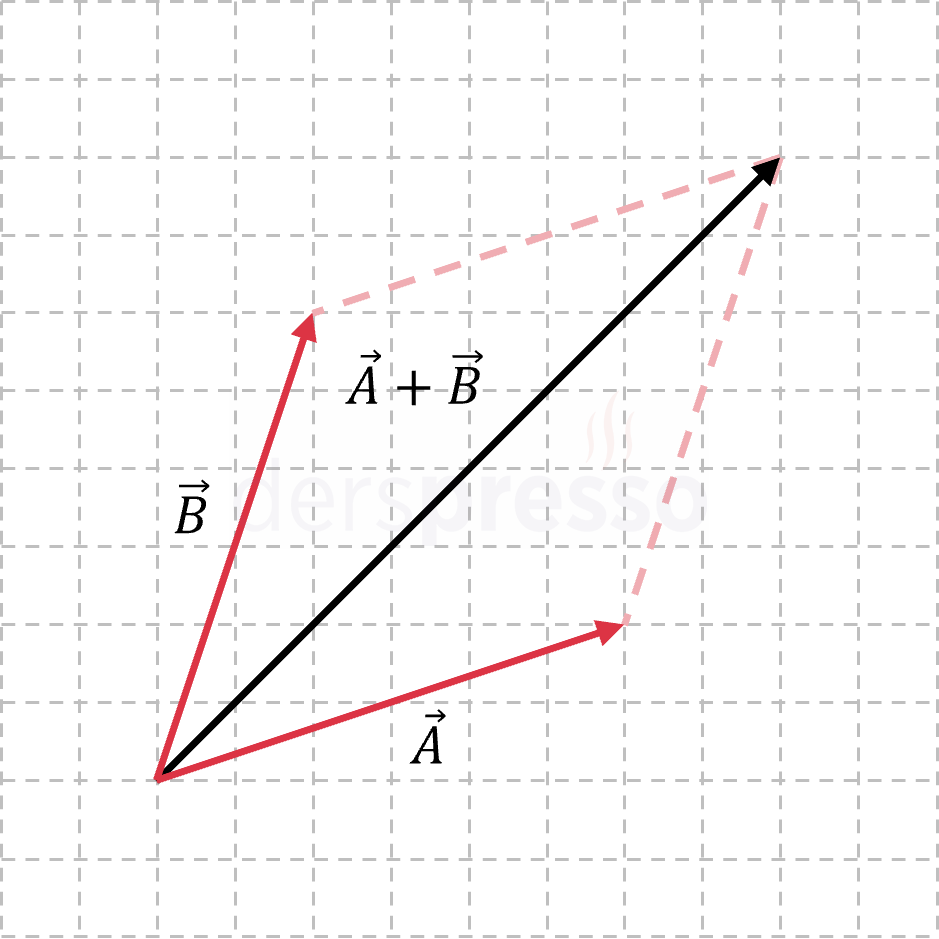
Bu iki yöntem ile elde edilen toplam vektörlerinin eşit vektörler oldukları yukarıdaki şekillerde görülebilir.
Kosinüs Teoremi ile Toplam Vektörünün Normu
İki vektörün toplamının normu kosinüs teoremi kullanılarak hesaplanabilir. Kosinüs teoremi özetle iki kenar uzunluğu ve bu iki kenar arasındaki açı bilinen bir üçgenin üçüncü kenar uzunluğunu bulmamızı sağlar.

Uç uca ekleme yöntemi kullanıldığında vektörler arasında oluşan açıya \( \alpha \), paralelkenar yöntemi kullanıldığında oluşan açıya \( \beta \) diyelim. Toplam vektörünün normu \( \alpha \) açısı kullanılarak aşağıdaki kosinüs teorem formülü ile bulunabilir.
\( \norm{\vec{c}}^2 = \norm{\vec{a}}^2 + \norm{\vec{b}}^2 - 2 \norm{\vec{a}}\norm{\vec{b}}\cos{\alpha} \)
\( \alpha \) ve \( \beta \) açıları bütünler açılar oldukları için, \( \alpha \) açısı yerine \( \beta \) kullanıldığında son terimin işareti negatiften pozitife döner.
\( \alpha + \beta = 180° \)
\( \cos{\alpha} = \cos(180° - \beta) = -\cos{\beta} \)
\( \norm{\vec{c}}^2 = \norm{\vec{a}}^2 + \norm{\vec{b}}^2 \textcolor{red}{+} 2 \norm{\vec{a}}\norm{\vec{b}}\cos{\beta} \)
Toplamanın İşlem Özellikleri
Yukarıdaki örnekte gördüğümüz üzere, vektörlerle toplama işleminin değişme özelliği vardır.
\( \vec{a} + \vec{b} = \vec{b} + \vec{a} \)
\( (4, 3) + (5, 1) = (5, 1) + (4, 3) \)
\( (4 + 5, 3 + 1) = (5 + 4, 1 + 3) \)
\( (9, 4) = (9, 4) \)
İSPATI GÖSTER
\( \vec{a} \) ve \( \vec{b} \) vektörleri tanımlayalım.
\( \vec{a} = (a_1, a_2, a_3) \)
\( \vec{b} = (b_1, b_2, b_3) \)
\( \vec{a} + \vec{b} = (a_1, a_2, a_3) + (b_1, b_2, b_3) \)
\( = (a_1 + b_1, a_2 + b_2, a_3 + b_3) \)
Reel sayılarda toplama işleminin değişme özelliği vardır.
\( = (b_1 + a_1, b_2 + a_2, b_3 + a_3) \)
\( = (b_1, b_2, b_3) + (a_1, a_2, a_3) \)
\( = \vec{b} + \vec{a} \)
Vektörlerle toplama işleminin birleşme özelliği vardır. Buna göre, ikiden fazla sayıda vektörün toplama işleminde vektörlerin hangi sırada toplandığının bir önemi yoktur.
\( (\vec{a} + \vec{b}) + \vec{c} = \vec{a} + (\vec{b} + \vec{c}) \)
\( [(1, 2) + (6, 3)] + (-2, 5) = (1, 2) + [(6, 3) + (-2, 5)] \)
\( (7, 5) + (-2, 5) = (1, 2) + (4, 8) \)
\( (5, 10) = (5, 10) \)
İSPATI GÖSTER
\( \vec{a} \), \( \vec{b} \) ve \( \vec{c} \) vektörleri tanımlayalım.
\( \vec{a} = (a_1, a_2, a_3) \)
\( \vec{b} = (b_1, b_2, b_3) \)
\( \vec{c} = (c_1, c_2, c_3) \)
\( (\vec{a} + \vec{b}) + \vec{c} = [(a_1, a_2, a_3) + (b_1, b_2, b_3)] + (c_1, c_2, c_3) \)
\( = (a_1 + b_1, a_2 + b_2, a_3 + b_3) + (c_1, c_2, c_3) \)
\( = ((a_1 + b_1) + c_1, (a_2 + b_2) + c_2, (a_3 + b_3) + c_3) \)
Reel sayılarda toplama işleminin birleşme özelliği vardır.
\( = (a_1 + (b_1 + c_1), a_2 + (b_2 + c_2), a_3 + (b_3 + c_3)) \)
\( = (a_1, a_2, a_3) + (b_1 + c_1, b_2 + c_2, b_3 + c_3) \)
\( = (a_1, a_2, a_3) + [(b_1, b_2, b_3) + (c_1, c_2, c_3)] \)
\( = \vec{a} + (\vec{b} + \vec{c}) \)
Vektörlerle toplama işleminin birim (etkisiz) elemanı sıfır vektörüdür.
\( \vec{a} + \vec{0} = \vec{0} + \vec{a} = \vec{a} \)
\( (7, -2) + (0, 0) = (7 + 0, -2 + 0) \)
\( = (7, -2) \)
Bir vektörün zıt vektörü ile toplamı sıfır vektörüne eşittir.
\( \vec{a} + (-\vec{a}) = (-\vec{a}) + \vec{a} = \vec{0} \)
\( (4, -3) + [-(4, -3)] = (4, -3) + (-4, 3) \)
\( = (4 + (-4), -3 + 3) = (0, 0) \)
Vektörlerle Çıkarma
İki vektör arasındaki çıkarma işleminde, vektörlerin birbirine karşılık gelen bileşenlerinin ayrı ayrı farkı alınır.
\( \vec{a} = (x_1, y_1) \)
\( \vec{b} = (x_2, y_2) \) olmak üzere,
\( \vec{a} - \vec{b} = (x_1, y_1) - (x_2, y_2) \)
\( = (x_1 - x_2, y_1 - y_2) \)
\( \vec{a} = (1, -4) \)
\( \vec{b} = (-4, 1) \) olmak üzere,
\( \vec{a} - \vec{b} = (1, -4) - (-4, 1) \)
\( = (1 - (-4), -4 - 1) \)
\( = (5, -5) \)

Vektörler arasında çıkarma işlemi geometrik olarak üç farklı yöntemle yapılabilir.
Zıt Vektörle Toplama
Önceki bölümde zıt vektörleri büyüklükleri aynı, yönleri zıt yönlü vektörler olarak tanımlamıştık. Bu yöntemde, çıkarma işleminin ikinci terimi olan vektörün zıt vektörü birinci vektörle toplanır.
\( \vec{a} - \vec{b} = \vec{a} + (-\vec{b}) \)

Başlangıç Noktalarını Birleştirme
Bu yöntemde birbirinden çıkarılacak vektörler başlangıç noktaları denk gelecek şekilde yerleştirilir ve ikinci vektörün bitiş noktasından birinci vektörün bitiş noktasına bir ok çizilir. Çizilen bu ok iki vektörün fark vektörüdür.

Bitiş Noktalarını Birleştirme
Bu yöntemde birbirinden çıkarılacak vektörler uçları denk gelecek şekilde yerleştirilir ve birinci vektörün başlangıç noktasından ikinci vektörün başlangıç noktasına bir ok çizilir. Çizilen bu ok iki vektörün fark vektörüdür.

Bu üç yöntem ile elde edilen fark vektörlerinin eşit vektörler oldukları yukarıdaki şekillerde görülebilir.
Çıkarmanın İşlem Özellikleri
Vektörlerle çıkarma işleminin değişme özelliği yoktur.
\( (5, 2) - (2, 1) \ne (2, 1) - (5, 2) \)
\( (3, 1) \ne (-3, -1) \)
Vektörlerle çıkarma işleminin birleşme özelliği yoktur.
Üç Boyutta Toplama ve Çıkarma
Üç boyutlu vektörler arasında toplama işlemi iki boyutlu vektörlere benzer şekilde yapılır.
\( \vec{a} = (x_1, y_1, z_1) \)
\( \vec{b} = (x_2, y_2, z_2) \) olmak üzere,
\( \vec{a} + \vec{b} = (x_1, y_1, z_1) + (x_2, y_2, z_2) \)
\( = (x_1 + x_2, y_1 + y_2, z_1 + z_2) \)
\( \vec{a} = (2, 4, 3) \)
\( \vec{b} = (3, 2, 4) \) olmak üzere,
\( \vec{a} + \vec{b} = (2, 4, 3) + (3, 2, 4) \)
\( = (2 + 3, 4 + 2, 3 + 4) \)
\( = (5, 6, 7) \)

Üç boyutlu vektörler arasında çıkarma işlemi iki boyutlu vektörlere benzer şekilde yapılır.
\( \vec{a} = (x_1, y_1, z_1) \)
\( \vec{b} = (x_2, y_2, z_2) \) olmak üzere,
\( \vec{a} - \vec{b} = (x_1, y_1, z_1) - (x_2, y_2, z_2) \)
\( = (x_1 - x_2, y_1 - y_2, z_1 - z_2) \)
\( \vec{a} = (3, -1, 4) \)
\( \vec{b} = (-1, 0, 2) \) olmak üzere,
\( \vec{a} - \vec{b} = (3, -1, 4) - (-1, 0, 2) \)
\( = (3 - (-1), -1 - 0, 4 - 2) \)
\( = (4, -1, 2) \)
\( O \) orijin olmak üzere, koordinat düzlemindeki \( A \) ve \( B \) noktaları ile ilgili aşağıdaki bilgiler veriliyor.
\( \vec{OA} = (5, 8) \)
\( \vec{AB} = (7, -3) \)
Buna göre, \( \norm{\vec{OB}} \) uzunluğu nedir?
Çözümü GösterVerilen nokta ve vektörleri koordinat düzleminde gösterelim.

\( \vec{AB} \) vektörü başlangıç noktası \( A \) ve bitiş noktası \( B \) olan vektörü temsil eder.
\( \vec{AB} \) vektörü \( \vec{OB} \) konum vektöründen \( \vec{OA} \) konum vektörünün çıkarılması ile elde edilir.
\( \vec{AB} = \vec{OB} - \vec{OA} \)
\( \vec{OB} = \vec{OA} + \vec{AB} \)
\( = (5, 8) + (7, -3) \)
\( = (12, 5) \)
\( \vec{OB} \) vektörünün normunu bulalım.
\( \norm{\vec{OB}} = \sqrt{12^2 + 5^2} \)
\( = \sqrt{169} = 13 \) bulunur.
Koordinat uzayındaki \( A \) ve \( B \) noktaları ile ilgili aşağıdaki bilgiler veriliyor.
\( A(-1, 3, 2) \)
\( \vec{AB} = (-3, -3, 1) \)
Buna göre, \( B \) noktasının orijine olan uzaklığı nedir?
Çözümü Göster\( O \) orijin olmak üzere,
\( \vec{OA} \) konum vektörünü tanımlayalım.
\( \vec{OA} = (-1, 3, 2) \)
\( \vec{AB} \) vektörü başlangıç noktası \( A \) ve bitiş noktası \( B \) olan vektörü temsil eder.
\( \vec{OB} \) vektörü başlangıç noktası orijin ve bitiş noktası \( B \) olan vektörü temsil eder.
\( \vec{AB} \) vektörü \( \vec{OB} \) konum vektöründen \( \vec{OA} \) konum vektörünün çıkarılması ile elde edilir.
\( \vec{AB} = \vec{OB} - \vec{OA} \)
\( \vec{OB} = \vec{OA} + \vec{AB} \)
\( = (-1, 3, 2) + (-3, -3, 1) \)
\( = (-4, 0, 3) \)
\( B \) noktasının orijine olan uzaklığı \( \vec{OB} \) vektörünün normuna eşittir.
\( \vec{OB} \) vektörünün normunu bulalım.
\( \norm{\vec{OB}} = \sqrt{(-4)^2 + 0^2 + 3^2} \)
\( = \sqrt{25} = 5 \) bulunur.
\( O \) noktası orijin olmak üzere, koordinat uzayındaki \( A, B, C, D \) noktaları ile ilgili aşağıdaki bilgiler veriliyor.
\( A(3, 2, 1) \)
\( \vec{AB} = (-1, 3, 0) \)
\( \vec{BC} = (1, 0, 3) \)
\( \vec{CD} = (0, 1, -2) \)
Buna göre, \( \vec{OD} \) konum vektörü nedir?
Çözümü Göster\( \vec{OA} \) konum vektörünü tanımlayalım.
\( \vec{OA} = (3, 2, 1) \)
Verilen ve istenen vektörleri çizelim.

\( \vec{OD} \) konum vektörü \( \vec{OA} \), \( \vec{AB} \), \( \vec{BC} \) ve \( \vec{CD} \) vektörlerinin toplamına eşittir.
\( \vec{OD} = \vec{OA} + \vec{AB} + \vec{BC} + \vec{CD} \)
\( = (3, 2, 1) + (-1, 3, 0) + (1, 0, 3) + (0, 1, -2) \)
\( = (3 + (-1) + 1 + 0, 2 + 3 + 0 + 1, 1 + 0 + 3 + (-2)) \)
\( = (3, 6, 2) \) bulunur.
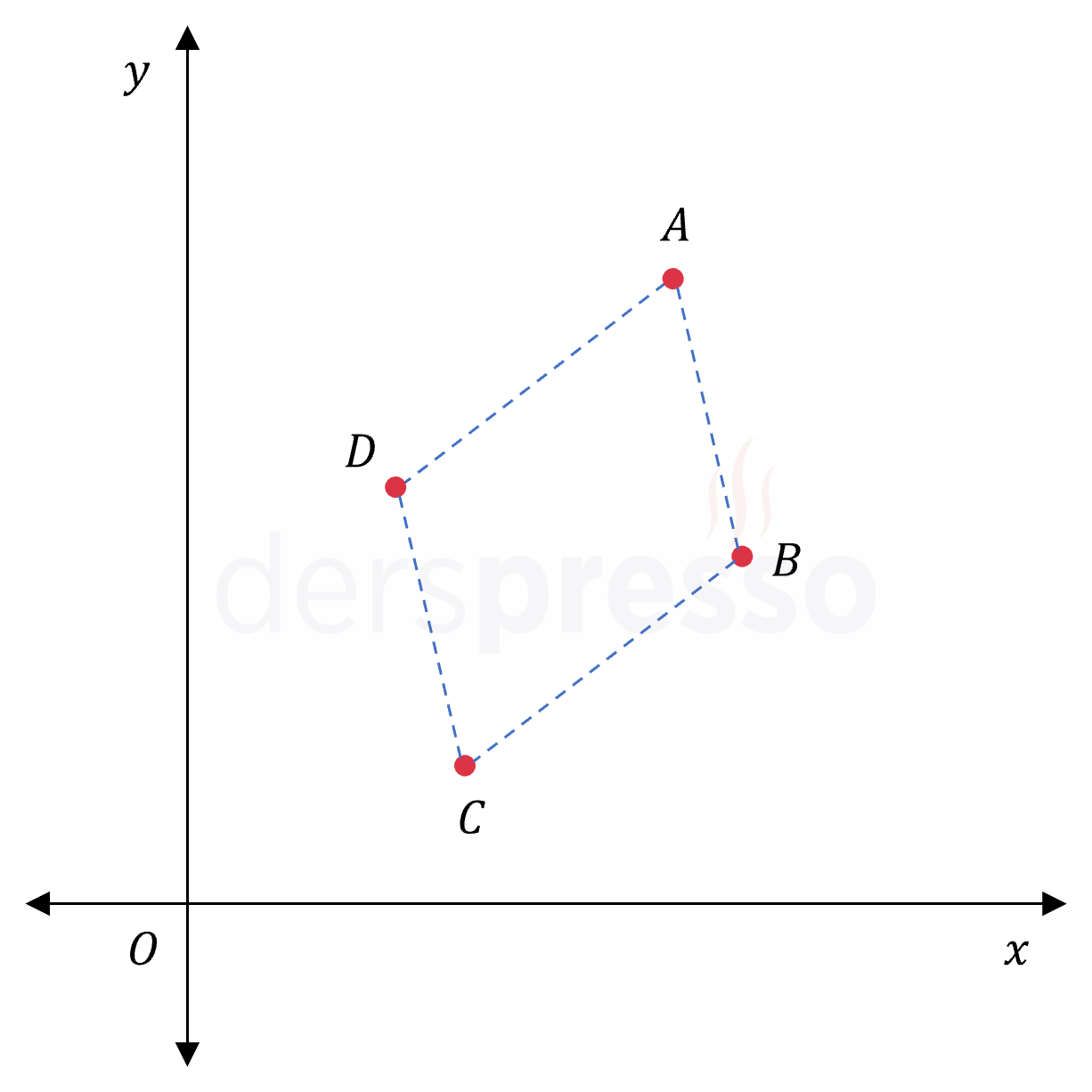
\( O \) noktası orijin olmak üzere, koordinat düzlemindeki \( A, B, C, D \) noktaları ile ilgili aşağıdaki bilgiler veriliyor.
\( ABCD \) bir paralelkenardır.
\( \vec{OA} = (7, 9) \)
\( \vec{OB} = (8, 5) \)
\( \vec{OC} = (4, 2) \)
Buna göre, \( \vec{OD} \) konum vektörü nedir?
Çözümü GösterUç uca ekleme yöntemini kullanarak \( \vec{OD} \) vektörünü yazalım.

\( \vec{OD} = \vec{OC} + \vec{CD} \)
Paralelkenarda karşılıklı kenarlar birbirine paraleldir ve uzunlukları birbirine eşittir.
Buna göre \( \vec{CD} \) ile \( \vec{BA} \) vektörleri yönleri ve büyüklükleri aynı olan vektörlerdir.
\( \vec{CD} = \vec{BA} \)
Eşitlikte yerine koyalım.
\( \vec{OD} = \vec{OC} + \vec{BA} \)
\( \vec{BA} \) vektörü başlangıç noktası \( B \) ve bitiş noktası \( A \) olan vektörü temsil eder.
\( \vec{BA} \) vektörü \( \vec{OA} \) konum vektöründen \( \vec{OB} \) konum vektörünün çıkarılması ile elde edilir.
\( \vec{BA} = \vec{OA} - \vec{OB} \)
Eşitlikte yerine koyalım.
\( \vec{OD} = \vec{OC} + \vec{BA} \)
\( = \vec{OC} + (\vec{OA} - \vec{OB}) \)
İki vektör arasındaki toplama/çıkarma işleminde, vektörlerin birbirine karşılık gelen bileşenlerinin ayrı ayrı toplamı/farkı alınır.
\( = (4, 2) + [(7, 9) - (8, 5)] \)
\( = (4 + 7 - 8, 2 + 9 - 5) \)
\( = (3, 6) \) bulunur.
\( m, n \in \mathbb{R} \) olmak üzere,
Koordinat uzayındaki \( A, B, C, D \) noktaları ile ilgili aşağıdaki bilgiler veriliyor.
\( A(2, 6, m) \)
\( D(m, 1, 5) \)
\( \vec{AB} = (1, -n, 2 + m) \)
\( \vec{CB} = (-1, -1, -2) \)
\( \vec{DC} = (3, 1, 1) \)
Buna göre, \( \vec{AB} \) vektörü nedir?
Çözümü Göster\( \vec{DA} \) vektörü \( A \) noktasının koordinatlarından \( D \) noktasının koordinatları çıkarılarak elde edilir.
\( \vec{DA} = A - D \)
\( = (2, 6, m) - (m, 1, 5) \)
\( = (2 - m, 5, m - 5) \)
Başlangıç ve bitiş noktaları aynı \( A \) noktası olan aşağıdaki vektör toplama işlemi sıfır vektörüne eşittir.

\( \vec{AB} + \vec{BC} + \vec{CD} + \vec{DA} = \vec{0} \)
\( \vec{AB} + (-\vec{CB}) + (-\vec{DC}) + \vec{DA} = \vec{0} \)
\( \vec{AB} - \vec{CB} - \vec{DC} + \vec{DA} = \vec{0} \)
\( (1, -n, 2 + m) - (-1, -1, -2) - (3, 1, 1) + (2 - m, 5, m - 5) = (0, 0, 0) \)
\( (1 - (-1) - 3 + 2 - m, -n - (-1) - 1 + 5, 2 + m - (-2) - 1 + m - 5) = (0, 0, 0) \)
\( (1 - m, -n + 5, 2m - 2) = (0, 0, 0) \)
Eşit vektörlerin tüm bileşenleri birbirine eşittir.
\( 1 - m = 0 \)
\( m = 1 \)
\( -n + 5 = 0 \)
\( n = 5 \)
Bulduğumuz değerleri \( \vec{AB} \) vektöründe yerine koyalım.
\( \vec{AB} = (1, -n, 2 + m) \)
\( = (1, -5, 3) \) bulunur.