Vektörlerle Çarpma
Çarpanlarından en az biri bir vektör olan farklı çarpma işlemleri vardır.
- Bir vektörün bir skaler ile çarpımı
- Nokta çarpımı (skaler çarpım)
- Vektörel çarpım
- Üçlü (Karma) vektörel çarpım
Bu bölümde bir vektörün bir skaler ile çarpımını, önümüzdeki iki bölümde sırasıyla nokta çarpımını ve vektörel çarpımı inceleyeceğiz.
Bir Vektörün Skaler ile Çarpımı
Bir vektörün bir skaler büyüklükle çarpımında, vektörün tüm bileşenlerinin bu skaler büyüklükle ayrı ayrı çarpımı alınır.
\( k \in \mathbb{R} \) olmak üzere,
\( \vec{a} = (x_1, y_1) \)
\( k\vec{a} = k(x_1, y_1) \)
\( = (kx_1, ky_1) \)
\( \vec{a} = (2, 1) \) olmak üzere,
\( 3\vec{a} = 3 (2, 1) \)
\( = (3 \cdot 2, 3 \cdot 1) \)
\( = (6, 3) \)
\( \vec{b} = (2, -2) \) olmak üzere,
\( -2 \vec{b} = -2 (2, -2) \)
\( = (-2 \cdot 2, -2 \cdot (-2)) \)
\( = (-4, 4) \)

Bir vektör pozitif bir skaler büyüklükle çarpıldığında vektörün yönü değişmez, büyüklüğü skalerin büyüklüğü oranında artar ya da azalır. Aşağıda bir \( \vec{a} \) vektörünün farklı pozitif skaler büyüklüklerle çarpımı sonucunda oluşan vektörler gösterilmiştir.

Bir vektör negatif bir skaler büyüklükle çarpıldığında vektörün yönü zıt yöne döner, büyüklüğü skalerin büyüklüğünün mutlak değeri oranında artar ya da azalır. Aşağıda bir \( \vec{a} \) vektörünün farklı negatif skaler büyüklüklerle çarpımı sonucunda oluşan vektörler gösterilmiştir.

Bir vektörün 1 ile skaler çarpımının sonucu vektörün kendisidir.
\( 1\vec{a} = \vec{a} \)
\( 1 (5, 2) = (1 \cdot 5, 1 \cdot 2) \)
\( = (5, 2) \)
Bir vektörün 0 ile skaler çarpımının sonucu sıfır vektörüdür.
\( 0\vec{a} = \vec{0} \)
\( 0 (3, 4) = (0 \cdot 3, 0 \cdot 4) \)
\( = (0, 0) \)
Bir vektörün -1 ile skaler çarpımının sonucu vektörün zıt vektörüdür.
\( -1\vec{a} = -\vec{a} \)
\( -(3, -2) = (-1 \cdot 3, -1 \cdot (-2)) \)
\( = (-3, 2) \)
Skaler çarpma işleminin birleşme özelliği vardır.
\( c(d\vec{a}) = (cd)\vec{a} = d(c\vec{a}) \)
İSPATI GÖSTER
\( \vec{a} \) vektörü ve \( c, d \) reel sayıları tanımlayalım.
\( \vec{a} = (a_1, a_2, a_3) \)
\( c, d \in \mathbb{R} \)
İSPAT 1:
\( c(d\vec{a}) = (cd)\vec{a} \) eşitliğini ispatlayalım.
\( c(d\vec{a}) = c[d(a_1, a_2, a_3)] \)
\( = c(da_1, da_2, da_3) \)
\( = (c(da_1), c(da_2), c(da_3)) \)
Reel sayılarda çarpma işleminin birleşme özelliği vardır.
\( = ((cd)a_1, (cd)a_2, (cd)a_3) \)
\( = cd(a_1, a_2, a_3) \)
\( = (cd)\vec{a} \)
İSPAT 2:
\( c(d\vec{a}) = d(c\vec{a}) \) eşitliğini ispatlayalım.
\( c(d\vec{a}) = c[d(a_1, a_2, a_3)] \)
\( = c(da_1, da_2, da_3) \)
\( = (c(da_1), c(da_2), c(da_3)) \)
Reel sayılarda çarpma işleminin birleşme özelliği vardır.
\( = ((cd)a_1, (cd)a_2, (cd)a_3) \)
Reel sayılarda çarpma işleminin değişme özelliği vardır.
\( = ((dc)a_1, (dc)a_2, (dc)a_3) \)
\( = (d(ca_1), d(ca_2), d(ca_3)) \)
\( = d(ca_1, ca_2, ca_3) \)
\( = d[c(a_1, a_2, a_3)] \)
\( = d(c\vec{a}) \)
Skaler çarpma işleminin toplama işlemi üzerinde soldan ve sağdan dağılma özelliği vardır.
\( c(\vec{a} + \vec{b}) = c\vec{a} + c\vec{b} \)
\( (c + d)\vec{a} = c\vec{a} + d\vec{a} \)
İSPATI GÖSTER
\( \vec{a} \), \( \vec{b} \) vektörleri ve bir \( c \) reel sayısı tanımlayalım.
\( \vec{a} = (a_1, a_2, a_3) \)
\( \vec{b} = (b_1, b_2, b_3) \)
\( c \in \mathbb{R} \)
Skaler çarpma işleminin toplama işlemi üzerinde soldan dağılma özelliğini ispatlayalım.
\( c(\vec{a} + \vec{b}) = c[(a_1, a_2, a_3) + (b_1, b_2, b_3)] \)
\( = c(a_1 + b_1, a_2 + b_2, a_3 + b_3) \)
\( = (c(a_1 + b_1), c(a_2 + b_2), c(a_3 + b_3)) \)
Reel sayılarda çarpma işleminin toplama işlemi üzerinde soldan dağılma özelliği vardır.
\( = (ca_1 + cb_1, ca_2 + cb_2, ca_3 + cb_3) \)
\( = (ca_1, ca_2, ca_3) + (cb_1, cb_2, cb_3) \)
\( = c(a_1, a_2, a_3) + c(b_1, b_2, b_3) \)
\( = c\vec{a} + c\vec{b} \)
Skaler çarpma işleminin toplama işlemi üzerinde sağdan dağılma özelliği de benzer şekilde ispatlanabilir.
Bir vektörün tüm reel sayılarla skaler çarpımlarının kümesi bir doğru oluşturur.

\( l = \{ k\vec{a} \mid k \in \mathbb{R} \} \)
Üç boyutlu bir vektörün bir skaler büyüklükle çarpımı iki boyutlu vektörlere benzer şekilde yapılır.
\( k \in \mathbb{R} \) olmak üzere,
\( \vec{a} = (x_1, y_1, z_1) \)
\( k\vec{a} = k(x_1, y_1, z_1) \)
\( = (kx_1, ky_1, kz_1) \)
\( \vec{a} = (3, -2, 1) \) olmak üzere,
\( 3\vec{a} = 3(3, -2, 1) \)
\( = (3 \cdot 3, 3 \cdot (-2), 3 \cdot 1) \)
\( = (9, -6, 3) \)
Koordinat düzlemindeki \( \vec{a} \) ve \( \vec{b} \) vektörleri ile ilgili aşağıdaki bilgiler veriliyor.
\( \vec{a} = (4x^2 - 4y + 5, y^2 + 4x) \)
\( \vec{b} = (-1, 1) \)
\( \vec{a} \) ve \( \vec{b} \) vektörleri birbirine paralel olduğuna göre, \( xy \) çarpımı kaçtır?
Çözümü Göster\( \vec{a} \parallel \vec{b} \)
Paralel iki vektörün bileşenlerinin oranı birbirine eşittir.
\( \dfrac{4x^2 - 4y + 5}{-1} = \dfrac{y^2 + 4x}{1} \)
İçler - dışlar çarpımı yapalım.
\( 4x^2 - 4y + 5 = -y^2 - 4x \)
\( 4x^2 - 4y + 5 + y^2 + 4x = 0 \)
Terimleri düzenleyelim.
\( (4x^2 - 4x + 1) + (y^2 + 4y + 4) = 0 \)
\( (2x - 1)^2 + (y + 2)^2 = 0 \)
İki kare ifadesinin toplamı sıfır ise iki ifade ayrı ayrı sıfıra eşittir.
\( 2x - 1 = 0 \Longrightarrow x = \dfrac{1}{2} \)
\( y + 2 = 0 \Longrightarrow y = -2 \)
\( xy = \dfrac{1}{2} \cdot (-2) = -1 \) bulunur.
Koordinat uzayındaki \( A, B, C \) noktaları ile ilgili aşağıdaki bilgiler veriliyor.
\( A(6, 10, 14) \)
\( B(18, 19, 29) \)
\( C(26, 25, 39) \)
Buna göre;
(a) \( A, B, C \) noktaları doğrusal mıdır?
(b) \( \dfrac{\norm{\vec{AB}}}{\norm{\vec{BC}}} \) oranı kaçtır?
Çözümü Göster(a) seçeneği:
\( \vec{AB} \) vektörü \( B \) noktasının koordinatlarından \( A \) noktasının koordinatları çıkarılarak elde edilir.
\( \vec{AB} = B - A \)
\( = (18, 19, 29) - (6, 10, 14) \)
\( = (12, 9, 15) \)
\( \vec{BC} \) vektörü \( C \) noktasının koordinatlarından \( B \) noktasının koordinatları çıkarılarak elde edilir.
\( \vec{BC} = C - B \)
\( = (26, 25, 39) - (18, 19, 29) \)
\( = (8, 6, 10) \)
\( \vec{AB} \) vektörünü \( \vec{BC} \) vektörünün bir skaler ile çarpımı şeklinde yazabiliriz.
\( \vec{AB} = \dfrac{3}{2}\vec{BC} \)
\( (12, 9, 15) = \dfrac{3}{2}(8, 6, 10) \)
Buna göre \( \vec{AB} \) ve \( \vec{BC} \) yönleri aynı vektörlerdir.
İki vektör ayrıca ortak bir \( B \) noktası içerdikleri için \( A, B, C \) noktaları doğrusaldır.
(b) seçeneği:
\( \vec{AB} \) ve \( \vec{BC} \) aynı yönlü vektörlerdir, dolayısıyla vektörler arasındaki oran normları için de geçerlidir.
\( \vec{AB} = \dfrac{3}{2}\vec{BC} \)
\( \dfrac{\norm{\vec{AB}}}{\norm{\vec{BC}}} = \dfrac{3}{2} \)
\( O \) noktası orijin olmak üzere, koordinat düzlemindeki \( A, B, C \) noktaları ile ilgili aşağıdaki bilgiler veriliyor.
\( \vec{OA} = (2, 3) \)
\( \vec{OB} = (-9, 1) \)
\( \vec{AB} = \dfrac{3}{4}\vec{AC} \)
Buna göre, \( \vec{OC} \) konum vektörü nedir?
Çözümü Göster\( \vec{AB} \) vektörü başlangıç noktası \( A \) ve bitiş noktası \( B \) olan vektörü temsil eder.
\( \vec{AB} \) vektörü \( \vec{OB} \) konum vektöründen \( \vec{OA} \) konum vektörünün çıkarılması ile elde edilir.
\( \vec{AB} = \vec{OB} - \vec{OA} \)
\( = (-9, 1) - (2, 3) \)
\( = (-11, -2) \)
\( \vec{AB} = \dfrac{3}{4}\vec{AC} \)
\( \vec{AC} = \dfrac{4}{3}\vec{AB} \)
\( = \dfrac{4}{3}(-11, -2) \)
\( = (-\dfrac{44}{3}, -\dfrac{8}{3}) \)
\( \vec{AC} \) vektörü başlangıç noktası \( A \) ve bitiş noktası \( C \) olan vektörü temsil eder.
\( \vec{AC} \) vektörü \( \vec{OC} \) konum vektöründen \( \vec{OA} \) konum vektörünün çıkarılması ile elde edilir.
\( \vec{AC} = \vec{OC} - \vec{OA} \)
\( \vec{OC} = \vec{OA} + \vec{AC} \)
\( = (2, 3) + (-\dfrac{44}{3}, -\dfrac{8}{3}) \)
\( = (-\dfrac{38}{3}, \dfrac{1}{3}) \) bulunur.
\( m, n \in \mathbb{R} \) olmak üzere,
\( \vec{a} \) ve \( \vec{b} \) vektörleri ile ilgili aşağıdaki bilgiler veriliyor.
\( 3\vec{a} + m\vec{b} + 2m\vec{a} = 4\vec{b} + 3n\vec{b} + n\vec{a} \)
\( \vec{a} \) ve \( \vec{b} \) vektörleri paralel olmadığına göre, \( m + n \) toplamı kaçtır?
Çözümü Gösterİki vektöre ait terimleri eşitliğin farklı taraflarında toplayalım.
\( 3\vec{a} + 2m\vec{a} - n\vec{a} = 4\vec{b} + 3n\vec{b} - m\vec{b} \)
\( (3 + 2m - n)\vec{a} = (4 + 3n - m)\vec{b} \)
\( \vec{a} \) ve \( \vec{b} \) vektörleri paralel olmadığına göre birbirinin bir skaler katı değildir.
Buna göre elde ettiğimiz eşitlik ancak \( \vec{a} \) ve \( \vec{b} \) vektörlerinin katsayıları sıfır olduğunda sağlanır.
\( 3 + 2m - n = 0 \)
\( 4 + 3n - m = 0 \)
İki bilinmeyenli denklem sistemini çözelim.
İkinci denklemde \( n \) yerine \( 3 + 2m \) yazalım.
\( 4 + 3(3 + 2m) - m = 0 \)
\( m = -\dfrac{13}{5} \)
\( m \) değerini birinci denklemde yerine koyalım.
\( 3 + 2(-\dfrac{13}{5}) - n = 0 \)
\( n = -\dfrac{11}{5} \)
\( m + n = -\dfrac{13}{5} + (-\dfrac{11}{5}) \)
\( = -\dfrac{24}{5} \) bulunur.
Koordinat düzlemindeki \( A, B, C, D \) noktaları ile ilgili aşağıdaki bilgiler veriliyor.
\( A(2, 1), B(1, 3), C(-1, 7) \)
\( D \) noktası \( [BC] \) doğru parçası üzerindedir.
\( \vec{BD} = \dfrac{1}{4}\vec{BC} \)
Buna göre;
(a) \( A, B, C \) noktaları doğrusal mıdır?
(b) \( D \) noktasının koordinatları nedir?
Çözümü Göster(a) seçeneği:
\( \vec{AB} \) vektörü \( B \) noktasının koordinatlarından \( A \) noktasının koordinatları çıkarılarak elde edilir.
\( \vec{AB} = B - A \)
\( = (1, 3) - (2, 1) \)
\( = (-1, 2) \)
\( \vec{BC} \) vektörü \( C \) noktasının koordinatlarından \( B \) noktasının koordinatları çıkarılarak elde edilir.
\( \vec{BC} = C - B \)
\( = (-1, 7) - (1, 3) \)
\( = (-2, 4) \)
\( \vec{AB} \) vektörünü \( \vec{BC} \) vektörünün bir skaler ile çarpımı şeklinde yazabiliriz.
\( \vec{BC} = 2 \vec{AB} \)
\( (-2, 4) = 2(-1, 2) \)
Buna göre \( \vec{AB} \) ve \( \vec{BC} \) yönleri aynı vektörlerdir.
İki vektör ayrıca ortak bir \( B \) noktası içerdikleri için \( A, B, C \) noktaları doğrusaldır.
(b) seçeneği:
\( \vec{BD} = \dfrac{1}{4}\vec{BC} \)
\( = \dfrac{1}{4}(-2, 4) \)
\( = (-\dfrac{1}{2}, 1) \)
\( \vec{BD} \) vektörü \( D \) noktasının koordinatlarından \( B \) noktasının koordinatları çıkarılarak elde edilir.
\( D \) noktasının koordinatlarına \( (x, y) \) diyelim.
\( \vec{BD} = D - B \)
\( (-\dfrac{1}{2}, 1) = (x, y) - (1, 3) \)
\( (x, y) = (-\dfrac{1}{2}, 1) + (1, 3) \)
\( = (\dfrac{1}{2}, 4) \)
Koordinat uzayındaki \( A, B, C, D \) noktaları ile ilgili aşağıdaki bilgiler veriliyor.
\( A(9, 5, 1) \)
\( B(4, 5, 6) \)
\( C(3, -7, 1) \)
\( \vec{AC} = 6\vec{BD} \)
Buna göre, \( \norm{\vec{CD}} \) uzunluğu nedir?
Çözümü Göster\( \vec{AC} \) vektörü \( C \) noktasının koordinatlarından \( A \) noktasının koordinatları çıkarılarak elde edilir.
\( \vec{AC} = C - A \)
\( = (3, -7, 1) - (9, 5, 1) \)
\( = (-6, -12, 0) \)
\( \vec{BD} \) vektörü \( D \) noktasının koordinatlarından \( B \) noktasının koordinatları çıkarılarak elde edilir.
\( \vec{BD} = D - B \)
\( D \) noktasının koordinatlarına \( (x, y, z) \) diyelim.
\( = (x, y, z) - (4, 5, 6) \)
\( = (x - 4, y - 5, z - 6) \)
Bulduğumuz değerleri verilen eşitlikte yerine koyalım.
\( \vec{AC} = 6\vec{BD} \)
\( (-6, -12, 0) = 6(x - 4, y - 5, z - 6) \)
\( (-6, -12, 0) = (6x - 24, 6y - 30, 6z - 36) \)
Eşit vektörlerin tüm bileşenleri birbirine eşittir.
\( -6 = 6x - 24 \)
\( x = 3 \)
\( -12 = 6y - 30 \)
\( y = 3 \)
\( 0 = 6z - 36 \)
\( z = 6 \)
\( D \) noktasının koordinatları aşağıdaki gibi bulunur.
\( D(3, 3, 6) \)
\( \vec{CD} \) vektörü \( D \) noktasının koordinatlarından \( C \) noktasının koordinatları çıkarılarak elde edilir.
\( \vec{CD} = D - C \)
\( = (3, 3, 6) - (3, -7, 1) \)
\( = (0, 10, 5) \)
\( \vec{CD} \) vektörünün normunu bulalım.
\( \norm{\vec{CD}} = \sqrt{0^2 + 10^2 + 5^2} \)
\( = 5\sqrt{5} \) bulunur.
Koordinat düzlemindeki \( A, B, C, D \) noktaları ile ilgili aşağıdaki bilgiler veriliyor.
\( D \) noktası \( [BC] \) doğru parçası üzerindedir.
\( \vec{AB} = (7, 3) \)
\( \vec{AC} = (9, -7) \)
\( \dfrac{\norm{\vec{BD}}}{\norm{\vec{DC}}} = \dfrac{2}{3} \)
Buna göre;
(a) \( \vec{BD} \) vektörünü bulunuz.
(b) \( \vec{AD} \) vektörünü bulunuz.
Çözümü Göster(a) seçeneği:
\( \dfrac{\norm{\vec{BD}}}{\norm{\vec{DC}}} = \dfrac{2}{3} \)
\( k \in \mathbb{R} \) ve \( k \ne 0 \) olmak üzere,
\( \norm{\vec{BD}} = 2k \)
\( \norm{\vec{DC}} = 3k \)
\( D \) noktası \( [BC] \) doğru parçası üzerindedir.
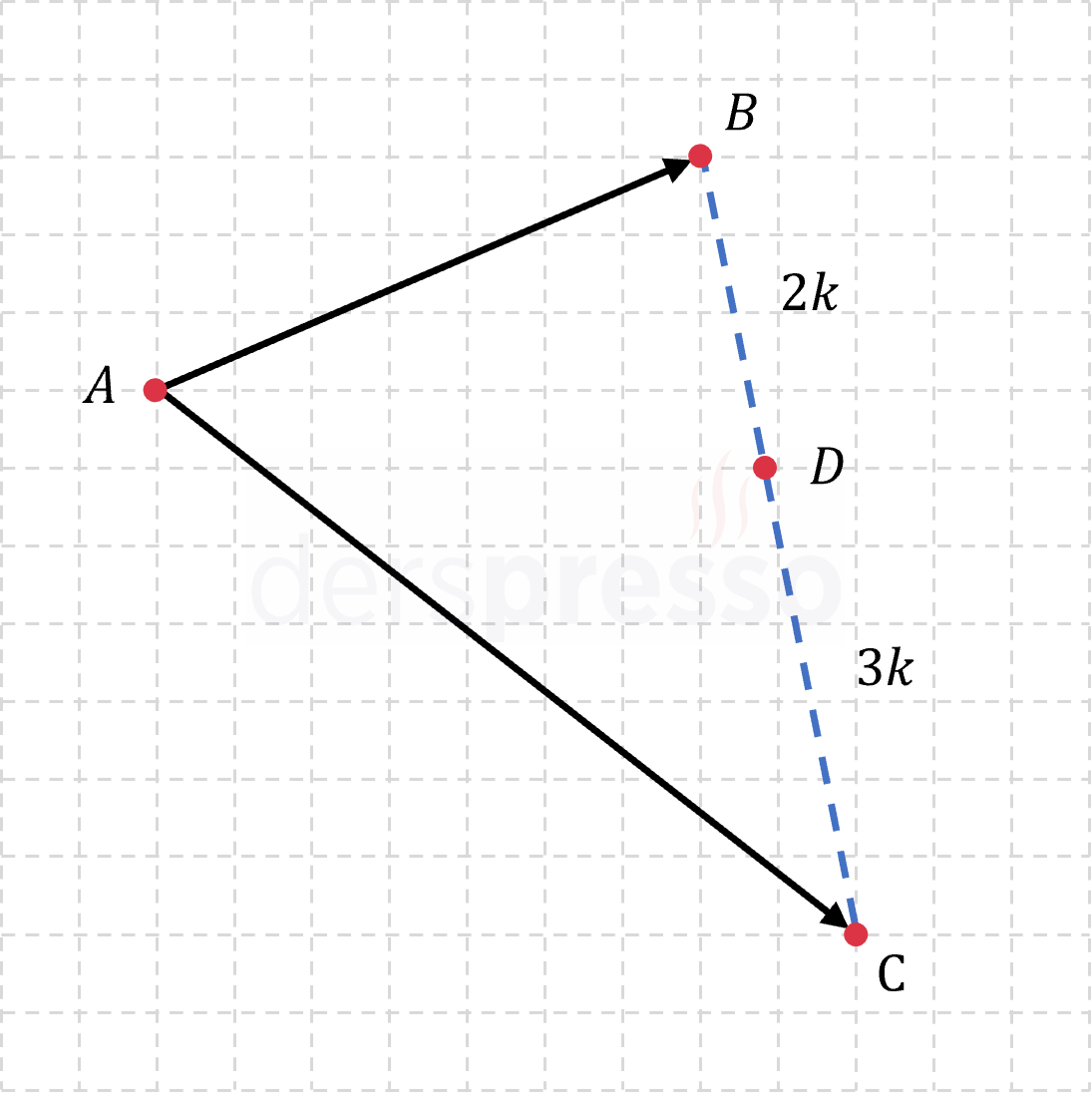
\( \norm{\vec{BC}} = 2k + 3k = 5k \)
\( \vec{BC} \) vektörünü uç uca ekleme yöntemini kullanarak yazalım.

\( \vec{BC} = \vec{BA} + \vec{AC} \)
\( = -\vec{AB} + \vec{AC} \)
\( = -(7, 3) + (9, -7) \)
\( = (-7, -3) + (9, -7) \)
\( = (2, -10) \)
\( \vec{BD}, \vec{DC} \) ve \( \vec{BC} \) aynı yönlü vektörlerdir, dolayısıyla normları arasındaki oran vektörler için de geçerlidir.
\( \dfrac{\norm{\vec{BD}}}{\norm{\vec{BC}}} = \dfrac{2k}{5k} \)
\( \vec{BD} = \dfrac{2}{5}\vec{BC} \)
Bir vektörün bir skaler büyüklükle çarpımında, vektörün bileşenlerinin bu skaler büyüklükle çarpımı alınır.
\( = \dfrac{2}{5}(2, -10) \)
\( = (\dfrac{4}{5}, -4) \)
(b) seçeneği:
\( \vec{AD} \) vektörünü uç uca ekleme yöntemini kullanarak yazalım.
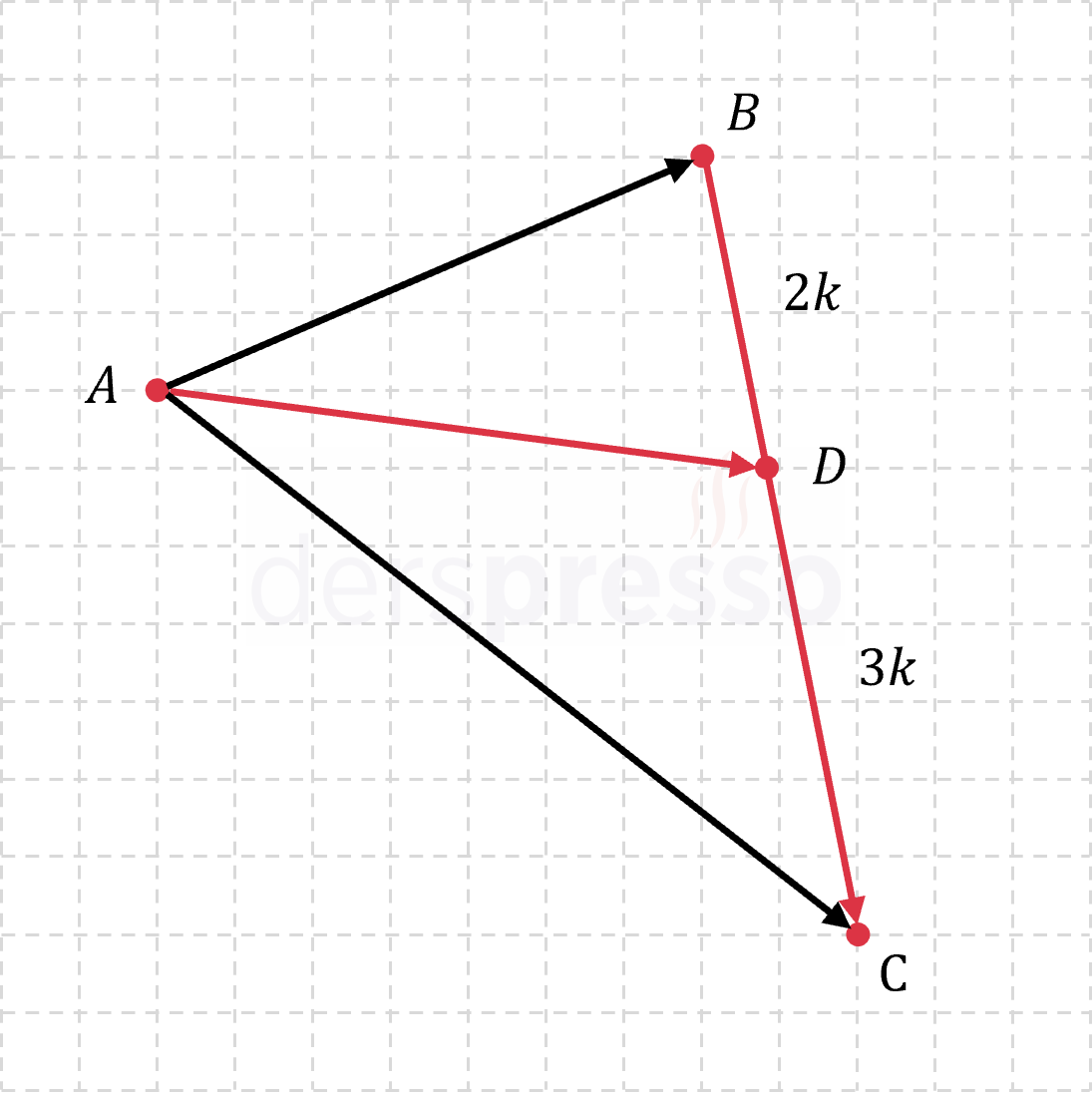
\( \vec{AD} = \vec{AB} + \vec{BD} \)
\( = (7, 3) + (\dfrac{4}{5}, -4) \)
\( = (\dfrac{39}{5}, -1) \)
\( O \) noktası orijin olmak üzere, koordinat uzayındaki \( A, B, C \) noktaları ile ilgili aşağıdaki bilgiler veriliyor.
\( C \) noktası \( [AB] \) doğru parçası üzerindedir.
\( \vec{OA} = (10, -20, -15) \)
\( \vec{OB} = (20, 5, 15) \)
\( \dfrac{\norm{\vec{AC}}}{\norm{\vec{CB}}} = \dfrac{1}{4} \)
Buna göre, \( \vec{OC} \) konum vektörü nedir?
Çözümü Göster\( \dfrac{\norm{\vec{AC}}}{\norm{\vec{CB}}} = \dfrac{1}{4} \)
\( k \in \mathbb{R} \) ve \( k \ne 0 \) olmak üzere,
\( \norm{\vec{AC}} = k \)
\( \norm{\vec{CB}} = 4k \)
\( C \) noktası \( [AB] \) doğru parçası üzerindedir.

\( \norm{\vec{AB}} = k + 4k = 5k \)
\( \vec{AB} \) vektörünü yazalım.
\( \vec{AB} \) vektörü başlangıç noktası \( A \) ve bitiş noktası \( B \) olan vektörü temsil eder.
\( \vec{AB} \) vektörü \( \vec{OB} \) konum vektöründen \( \vec{OA} \) konum vektörünün çıkarılması ile elde edilir.
\( \vec{AB} = \vec{OB} - \vec{OA} \)
\( = (20, 5, 15) - (10, -20, -15) \)
\( = (10, 25, 30) \)
\( \vec{AC}, \vec{CB} \) ve \( \vec{AB} \) aynı yönlü vektörlerdir, dolayısıyla normları arasındaki oran vektörler için de geçerlidir.
\( \dfrac{\norm{\vec{AC}}}{\norm{\vec{AB}}} = \dfrac{k}{5k} \)
\( \vec{AC} = \dfrac{1}{5}\vec{AB} \)
\( = \dfrac{1}{5}(10, 25, 30) \)
\( = (2, 5, 6) \)
\( \vec{AC} \) vektörü başlangıç noktası \( A \) ve bitiş noktası \( C \) olan vektörü temsil eder.
\( \vec{AC} \) vektörü \( \vec{OC} \) konum vektöründen \( \vec{OA} \) konum vektörünün çıkarılması ile elde edilir.
\( \vec{AC} = \vec{OC} - \vec{OA} \)
\( \vec{OC} = \vec{OA} + \vec{AC} \)
\( = (10, -20, -15) + (2, 5, 6) \)
\( = (12, -15, -9) \) bulunur.
\( O \) noktası orijin olmak üzere, koordinat uzayındaki \( A, B, C \) noktaları ile ilgili aşağıdaki bilgiler veriliyor.
\( A \) noktası \( [CB] \) doğru parçası üzerindedir.
\( \vec{OA} = (12, -16, 4) \)
\( \vec{OB} = (20, -4, -8) \)
\( \dfrac{\norm{\vec{CA}}}{\norm{\vec{AB}}} = \dfrac{3}{4} \)
Buna göre, \( \vec{OC} \) konum vektörü nedir?
Çözümü Göster\( \dfrac{\norm{\vec{CA}}}{\norm{\vec{AB}}} = \dfrac{3}{4} \)
\( k \in \mathbb{R} \) ve \( k \ne 0 \) olmak üzere,
\( \norm{\vec{CA}} = 3k \)
\( \norm{\vec{AB}} = 4k \)
\( A \) noktasının \( [CB] \) doğru parçası üzerindedir.

\( \vec{CA} \) ve \( \vec{AB} \) aynı yönlü vektörlerdir, dolayısıyla normları arasındaki oran vektörler için de geçerlidir.
\( \vec{CA} = \dfrac{3}{4}\vec{AB} \)
\( \vec{AB} \) vektörü başlangıç noktası \( A \) ve bitiş noktası \( B \) olan vektörü temsil eder.
\( \vec{AB} \) vektörü \( \vec{OB} \) konum vektöründen \( \vec{OA} \) konum vektörünün çıkarılması ile elde edilir.
\( \vec{AB} = \vec{OB} - \vec{OA} \)
\( = (20, -4, -8) - (12, -16, 4) \)
\( = (8, 12, -12) \)
Eşitlikte yerine koyalım.
\( \vec{CA} = \dfrac{3}{4}\vec{AB} \)
\( = \dfrac{3}{4}(8, 12, -12) \)
\( = (6, 9, -9) \)
\( \vec{CA} \) vektörü başlangıç noktası \( C \) ve bitiş noktası \( A \) olan vektörü temsil eder.
\( \vec{CA} \) vektörü \( \vec{OA} \) konum vektöründen \( \vec{OC} \) konum vektörünün çıkarılması ile elde edilir.
\( \vec{CA} = \vec{OA} - \vec{OC} \)
\( \vec{OC} = \vec{OA} - \vec{CA} \)
\( = (12, -16, 4) - (6, 9, -9) \)
\( = (6, -25, 13) \) bulunur.
\( O \) noktası orijin olmak üzere, koordinat uzayındaki \( A, B, C \) noktaları ile ilgili aşağıdaki bilgiler veriliyor.
\( \vec{OA} = (-2, -1, -3) \)
\( \vec{OB} = (-6, 5, -1) \)
\( B \) noktası \( [AC] \) doğru parçası üzerindedir.
\( \dfrac{\norm{\vec{AB}}}{\norm{\vec{BC}}} = \dfrac{2}{3} \)
Buna göre, \( \vec{OC} \) konum vektörü nedir?
Çözümü Göster\( \dfrac{\norm{\vec{AB}}}{\norm{\vec{BC}}} = \dfrac{2}{3} \)
\( k \in \mathbb{R} \) ve \( k \ne 0 \) olmak üzere,
\( \norm{\vec{AB}} = 2k \)
\( \norm{\vec{BC}} = 3k \)
\( B \) noktası \( [AC] \) doğru parçası üzerindedir.

\( \vec{AB} \) ve \( \vec{BC} \) aynı yönlü vektörlerdir, dolayısıyla normları arasındaki oran vektörler için de geçerlidir.
\( \vec{AB} = \dfrac{2}{3}\vec{BC} \)
\( \vec{BC} = \dfrac{3}{2}\vec{AB} \)
\( \vec{AB} \) vektörü başlangıç noktası \( A \) ve bitiş noktası \( B \) olan vektörü temsil eder.
\( \vec{AB} \) vektörü \( \vec{OB} \) konum vektöründen \( \vec{OA} \) konum vektörünün çıkarılması ile elde edilir.
\( \vec{AB} = \vec{OB} - \vec{OA} \)
\( = (-6, 5, -1) - (-2, -1, -3) \)
\( = (-4, 6, 2) \)
Eşitlikte yerine koyalım.
\( \vec{BC} = \dfrac{3}{2}\vec{AB} \)
\( = \dfrac{3}{2}(-4, 6, 2) \)
\( = (-6, 9, 3) \)
\( \vec{BC} \) vektörü başlangıç noktası \( B \) ve bitiş noktası \( C \) olan vektörü temsil eder.
\( \vec{BC} \) vektörü \( \vec{OC} \) konum vektöründen \( \vec{OB} \) konum vektörünün çıkarılması ile elde edilir.
\( \vec{BC} = \vec{OC} - \vec{OB} \)
\( \vec{OC} = \vec{OB} + \vec{BC} \)
\( = (-6, 5, -1) + (-6, 9, 3) \)
\( = (-12, 14, 2) \) bulunur.
\( O \) noktası orijin olmak üzere, koordinat uzayındaki \( A, B, C, D \) noktaları ile ilgili aşağıdaki bilgiler veriliyor.
\( A(12, 2, 4) \)
\( B(6, 10, 1) \)
\( C(2, 2, 8) \)
\( \vec{DA} - \vec{DB} = 4\vec{DC} \)
Buna göre, \( \vec{OD} \) konum vektörü nedir?
Çözümü Göster\( D \) noktasının koordinatlarına \( (x, y, z) \) diyelim.
\( \vec{DA} \) vektörü başlangıç noktası \( D \) ve bitiş noktası \( A \) olan vektörü temsil eder.
\( \vec{DA} \) vektörü \( A \) noktasının koordinatlarından \( D \) noktasının koordinatları çıkarılarak elde edilir.
\( \vec{DA} = A - D \)
\( = (12, 2, 4) - (x, y, z) \)
\( = (12 - x, 2 - y, 4 - z) \)
\( \vec{DB} \) vektörü başlangıç noktası \( D \) ve bitiş noktası \( B \) olan vektörü temsil eder.
\( \vec{DB} \) vektörü \( B \) noktasının koordinatlarından \( D \) noktasının koordinatları çıkarılarak elde edilir.
\( \vec{DB} = B - D \)
\( = (6, 10, 1) - (x, y, z) \)
\( = (6 - x, 10 - y, 1 - z) \)
\( \vec{DA} - \vec{DB} \) farkını hesaplayalım.
\( \vec{DA} - \vec{DB} = (12 - x, 2 - y, 4 - z) - (6 - x, 10 - y, 1 - z) \)
\( = (6, -8, 3) \)
\( \vec{DC} \) vektörü başlangıç noktası \( D \) ve bitiş noktası \( C \) olan vektörü temsil eder.
\( \vec{DC} \) vektörü \( C \) noktasının koordinatlarından \( D \) noktasının koordinatları çıkarılarak elde edilir.
\( \vec{DC} = C - D \)
\( = (2, 2, 8) - (x, y, z) \)
\( = (2 - x, 2 - y, 8 - z) \)
\( 4\vec{DC} \) çarpımını hesaplayalım.
\( 4\vec{DC} = 4(2 - x, 2 - y, 8 - z) \)
\( = (8 - 4x, 8 - 4y, 32 - 4z) \)
Bulduğumuz değerleri verilen eşitlikte yerine koyalım.
\( \vec{DA} - \vec{DB} = 4\vec{DC} \)
\( (6, -8, 3) = (8 - 4x, 8 - 4y, 32 - 4z) \)
\( 6 = 8 - 4x \)
\( x = \dfrac{1}{2} \)
\( -8 = 8 - 4y \)
\( y = 4 \)
\( 3 = 32 - 4z \)
\( z = \dfrac{29}{4} \)
\( D(\dfrac{1}{2}, 4, \dfrac{29}{4}) \)
\( \vec{OD} = (\dfrac{1}{2}, 4, \dfrac{29}{4}) \) bulunur.

Şekildeki \( ABCD \) dikdörtgeni ve \( E, F \) noktaları ile ilgili aşağıdaki bilgiler veriliyor.
\( \dfrac{\norm{\vec{BC}}}{\norm{\vec{CF}}} = 2 \)
\( \dfrac{\norm{\vec{CE}}}{\norm{\vec{ED}}} = \dfrac{1}{2} \)
Buna göre, \( A, E, F \) noktaları doğrusal mıdır?
Çözümü Göster\( \dfrac{\norm{\vec{BC}}}{\norm{\vec{CF}}} = 2 \)
\( \norm{\vec{BC}} = 2\norm{\vec{CF}} \)
\( \vec{BC} \) ve \( \vec{CF} \) aynı yönlü vektörlerdir, dolayısıyla normları arasındaki oran vektörler için de geçerlidir.
\( \vec{BC} = 2\vec{CF} \)
\( \dfrac{\norm{\vec{CE}}}{\norm{\vec{ED}}} = \dfrac{1}{2} \)
\( \norm{\vec{ED}} = 2\norm{\vec{CE}} \)
\( \vec{CE} \) ve \( \vec{ED} \) aynı yönlü vektörlerdir, dolayısıyla normları arasındaki oran vektörler için de geçerlidir.
\( \vec{ED} = 2\vec{CE} \)
\( \vec{AE} \) vektörünü uç uca ekleme yöntemini kullanarak yazalım.

\( \vec{AE} = \vec{AD} + \vec{DE} \)
\( = \vec{AD} + (-\vec{ED}) \)
Dikdörtgende karşılıklı kenarlar birbirine paraleldir ve uzunlukları birbirine eşittir. Buna göre \( \vec{AD} \) ile \( \vec{BC} \) vektörleri yönleri ve büyüklükleri aynı olan eşit vektörlerdir.
\( = \vec{BC} - \vec{ED} \)
\( \vec{EF} \) vektörünü uç uca ekleme yöntemini kullanarak yazalım.

\( \vec{EF} = \vec{EC} + \vec{CF} \)
\( = -\vec{CE} + \vec{CF} \)
\( = \vec{CF} - \vec{CE} \)
\( \vec{BC} = 2\vec{CF} \) ve \( \vec{ED} = 2\vec{CE} \) eşitliklerini kullanalım.
\( = \dfrac{\vec{BC}}{2} - \dfrac{\vec{ED}}{2} \)
\( = \dfrac{1}{2}(\vec{BC} - \vec{ED}) \)
Buna göre, \( \vec{AE} \) vektörünü \( \vec{EF} \) vektörünün bir skaler ile çarpımı şeklinde yazabiliriz.
\( \vec{BC} - \vec{ED} = 2[\dfrac{1}{2}(\vec{BC} - \vec{ED})] \)
\( \vec{AE} = 2 \vec{EF} \)
Buna göre \( \vec{AE} \) ve \( \vec{EF} \) yönleri aynı vektörlerdir.
İki vektör ayrıca ortak bir \( E \) noktası içerdiği için \( A, E, F \) noktaları doğrusaldır.
\( O \) noktası orijin olmak üzere, koordinat uzayındaki \( A, B \) ve \( C \) noktaları ile ilgili aşağıdaki bilgiler veriliyor.
\( A(3, 7, -11) \)
\( B(-1, -1, 5) \)
\( C \) noktası \( A \) ve \( B \) noktalarından geçen doğru üzerindedir.
\( \norm{\vec{AC}} = 3\norm{\vec{CB}} \)
Buna göre, \( \vec{OC} \) konum vektörü hangi değerleri alabilir?
Çözümü Göster\( \vec{OA} \) ve \( \vec{OB} \) konum vektörlerini tanımlayalım.
\( \vec{OA} = (3, 7, -11) \)
\( \vec{OB} = (-1, -1, 5) \)
\( \norm{\vec{AC}} = 3\norm{\vec{CB}} \)
\( k \in \mathbb{R} \) ve \( k \ne 0 \) olmak üzere,
\( \norm{\vec{AC}} = 3k \)
\( \norm{\vec{CB}} = k \)
O halde, \( C \) noktasının konumu için 2 durum oluşur.
Durum 1:
\( C \) noktası \( [AB] \) doğru parçası üzerindedir.

\( \norm{\vec{AB}} = 3k + k = 4k \)
\( \vec{AB} \) vektörünü yazalım.
\( \vec{AB} \) vektörü başlangıç noktası \( A \) ve bitiş noktası \( B \) olan vektörü temsil eder.
\( \vec{AB} \) vektörü \( \vec{OB} \) konum vektöründen \( \vec{OA} \) konum vektörünün çıkarılması ile elde edilir.
\( \vec{AB} = \vec{OB} - \vec{OA} \)
\( = (-1, -1, 5) - (3, 7, -11) \)
\( = (-4, -8, 16) \)
\( \vec{AC}, \vec{CB} \) ve \( \vec{AB} \) aynı yönlü vektörlerdir, dolayısıyla normları arasındaki oran vektörler için de geçerlidir.
\( \norm{\vec{AC}} = \dfrac{3}{4}\norm{\vec{AB}} \)
\( \vec{AC} = \dfrac{3}{4}\vec{AB} \)
\( = \dfrac{3}{4}(-4, -8, 16) \)
\( = (-3, -6, 12) \)
\( \vec{AC} \) vektörü başlangıç noktası \( A \) ve bitiş noktası \( C \) olan vektörü temsil eder.
\( \vec{AC} \) vektörü \( \vec{OC} \) konum vektöründen \( \vec{OA} \) konum vektörünün çıkarılması ile elde edilir.
\( \vec{AC} = \vec{OC} - \vec{OA} \)
\( \vec{OC} = \vec{OA} + \vec{AC} \)
\( = (3, 7, -11) + (-3, -6, 12) \)
\( = (0, 1, 1) \) bulunur.
Durum 2:
\( B \) noktası \( [AC] \) doğru parçası üzerindedir.

\( \vec{AB} \) ve \( \vec{BC} \) aynı yönlü vektörlerdir, dolayısıyla normları arasındaki oran vektörler için de geçerlidir.
\( \norm{\vec{AB}} = 2\norm{\vec{BC}} \)
\( \vec{AB} = 2\vec{BC} \)
\( \vec{BC} = \dfrac{1}{2}\vec{AB} \)
\( \vec{AB} \) vektörü başlangıç noktası \( A \) ve bitiş noktası \( B \) olan vektörü temsil eder.
\( \vec{AB} \) vektörü \( \vec{OB} \) konum vektöründen \( \vec{OA} \) konum vektörünün çıkarılması ile elde edilir.
\( \vec{AB} = \vec{OB} - \vec{OA} \)
\( = (-1, -1, 5) - (3, 7, -11) \)
\( = (-4, -8, 16) \)
Eşitlikte yerine koyalım.
\( \vec{BC} = \dfrac{1}{2}\vec{AB} \)
\( = \dfrac{1}{2}(-4, -8, 16) \)
\( = (-2, -4, 8) \)
\( \vec{BC} \) vektörü başlangıç noktası \( B \) ve bitiş noktası \( C \) olan vektörü temsil eder.
\( \vec{BC} \) vektörü \( \vec{OC} \) konum vektöründen \( \vec{OB} \) konum vektörünün çıkarılması ile elde edilir.
\( \vec{BC} = \vec{OC} - \vec{OB} \)
\( \vec{OC} = \vec{OB} + \vec{BC} \)
\( = (-1, -1, 5) + (-2, -4, 8) \)
\( = (-3, -5, 13) \) bulunur.