Vektör Tanımı

Skaler ve Vektörel Büyüklükler

Bir yönü olmayan, sadece sayısal değeri ile ifade edilen büyüklüklere skaler büyüklük denir. Uzunluk, hacim, zaman, kütle, sıcaklık ve enerji birer skaler büyüklüktür.

Skaler büyüklüklerle toplama, çıkarma, çarpma ve bölme gibi işlemler sadece sayısal değerleri kullanılarak yapılabilir. Basit bir örnek vermek gerekirse, 3 lt suya 2 lt su ilave edildiğinde 5 lt su elde edilir.

Sayısal değerine ek olarak bir yönü olan büyüklüklere vektörel büyüklük denir. Hız, ivme, ağırlık ve kuvvet birer vektörel büyüklüktür.

Vektör Tanımı

Bir yönü ve büyüklüğü olan doğru parçalarına vektör denir. Vektörler geometrik olarak aşağıdaki şekilde gösterilir. Bu gösterimde doğru parçasının uzunluğu vektörün büyüklüğünü, okun yönü de vektörün yönünü gösterir.

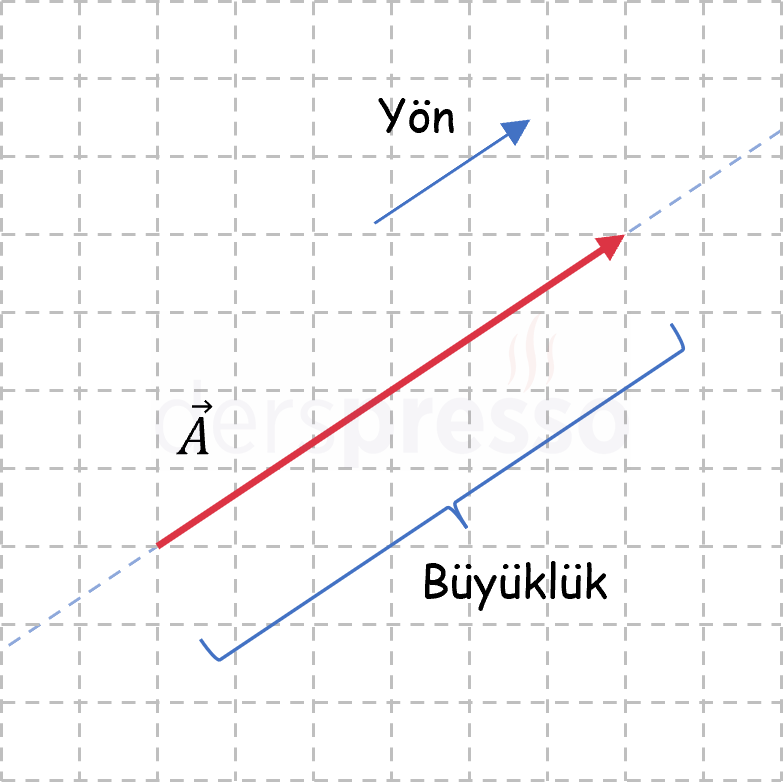
Vektörler genellikle küçük harflerle ve üzerlerinde birer ok işareti ile, \( \vec{a} \), \( \vec{b} \), \( \vec{c} \) şeklinde gösterilir.

Aşağıdaki şekilde yönleri aynı, büyüklükleri farklı üç vektör verilmiştir. Büyüklük vektörlerin ayırt edici bir özelliği olduğu için bu üç vektör birbirinden farklıdır.

Aşağıdaki şekilde büyüklükleri aynı, yönleri farklı üç vektör verilmiştir. Yön de vektörlerin ayırt edici bir özelliği olduğu için bu üç vektör birbirinden farklıdır.

Büyüklükleri ve yönleri eşit aşağıdaki üç vektör, konumları farklı olsa da birbirine eşittir.