Bir Vektörün Normu
Bir vektörün uzunluğuna o vektörün büyüklüğü ya da normu denir ve \( \norm{\vec{a}} \) ya da \( \abs{\vec{a}} \) şeklinde gösterilir.
İki boyutlu bir vektörün normu, Pisagor teoremi kullanılarak aşağıdaki formülle hesaplanır.
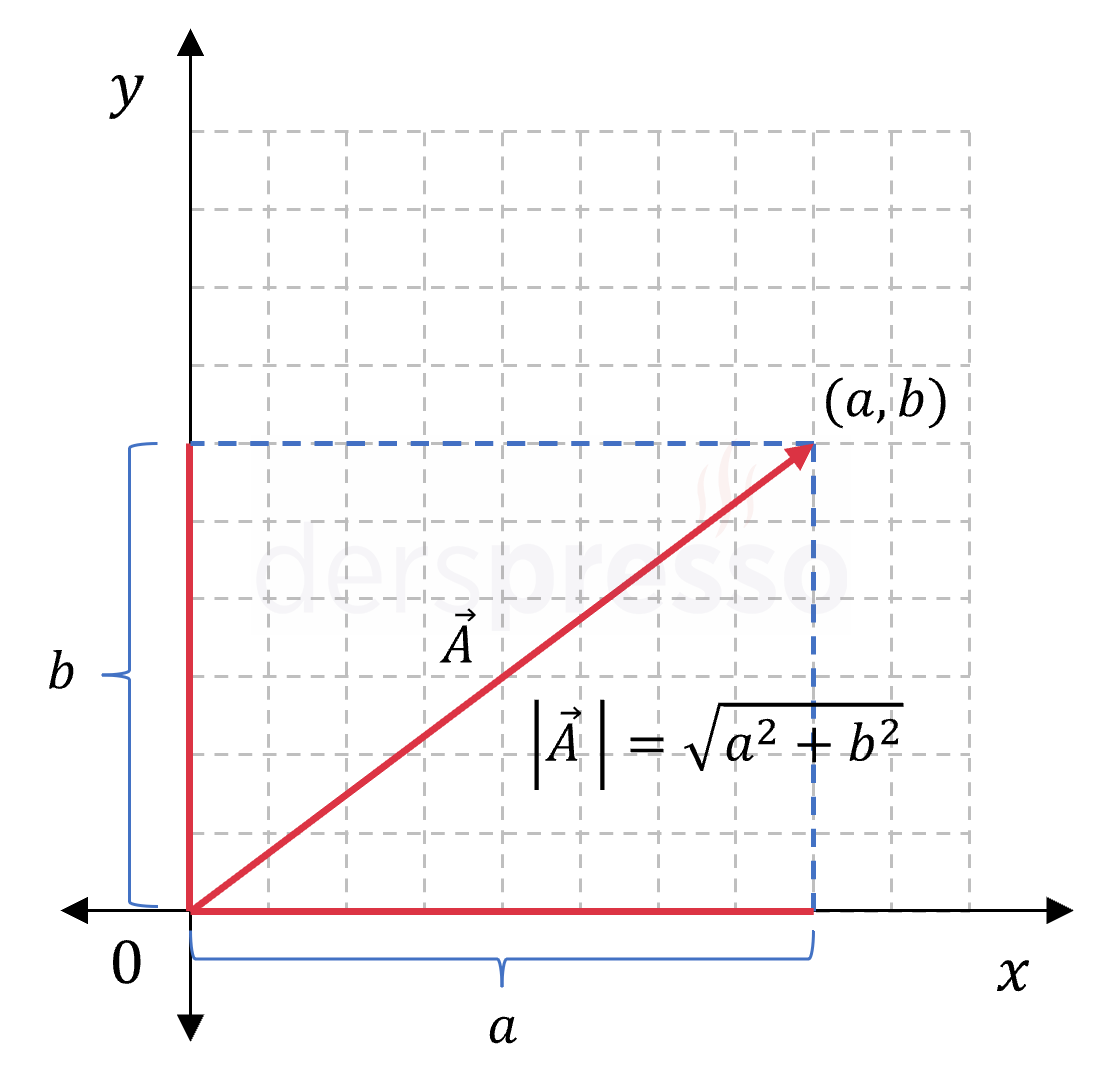
\( \vec{a} = (x_1, y_1) \) olmak üzere,
\( \norm{\vec{a}} = \sqrt{x_1^2 + y_1^2} \)
\( \vec{a} = (12, -5) \)
\( \norm{\vec{a}} = \sqrt{12^2 + (-5)^2} = 13 \)
\( \vec{b} = (-8, 0) \)
\( \norm{\vec{b}} = \sqrt{(-8)^2 + 0^2} = 8 \)
Bir vektörün normu, kendisini temsil eden doğru parçasının uzunluğuna karşılık geldiği için skaler bir büyüklüktür ve negatif değer alamaz.
\( \norm{\vec{a}} \ge 0 \)
Norm pozitif bir büyüklük olduğu için, bir vektörün önündeki katsayı normun dışına mutlak değer içinde çıkar.
\( \norm{k\vec{a}} = \abs{k}\norm{\vec{a}} \)
\( \vec{a} = (-3, 4) \) olmak üzere,
\( \norm{-2\vec{a}} = \norm{-2(-3, 4)} \)
\( = 2\norm{(-3, 4)} \)
\( = 2\sqrt{(-3)^2 + 4^2} \)
\( = 2 \cdot 5 = 10 \)

Üç boyutlu bir vektörün büyüklüğü, iki kez Pisagor teoremi kullanılarak aşağıdaki formülle hesaplanır.
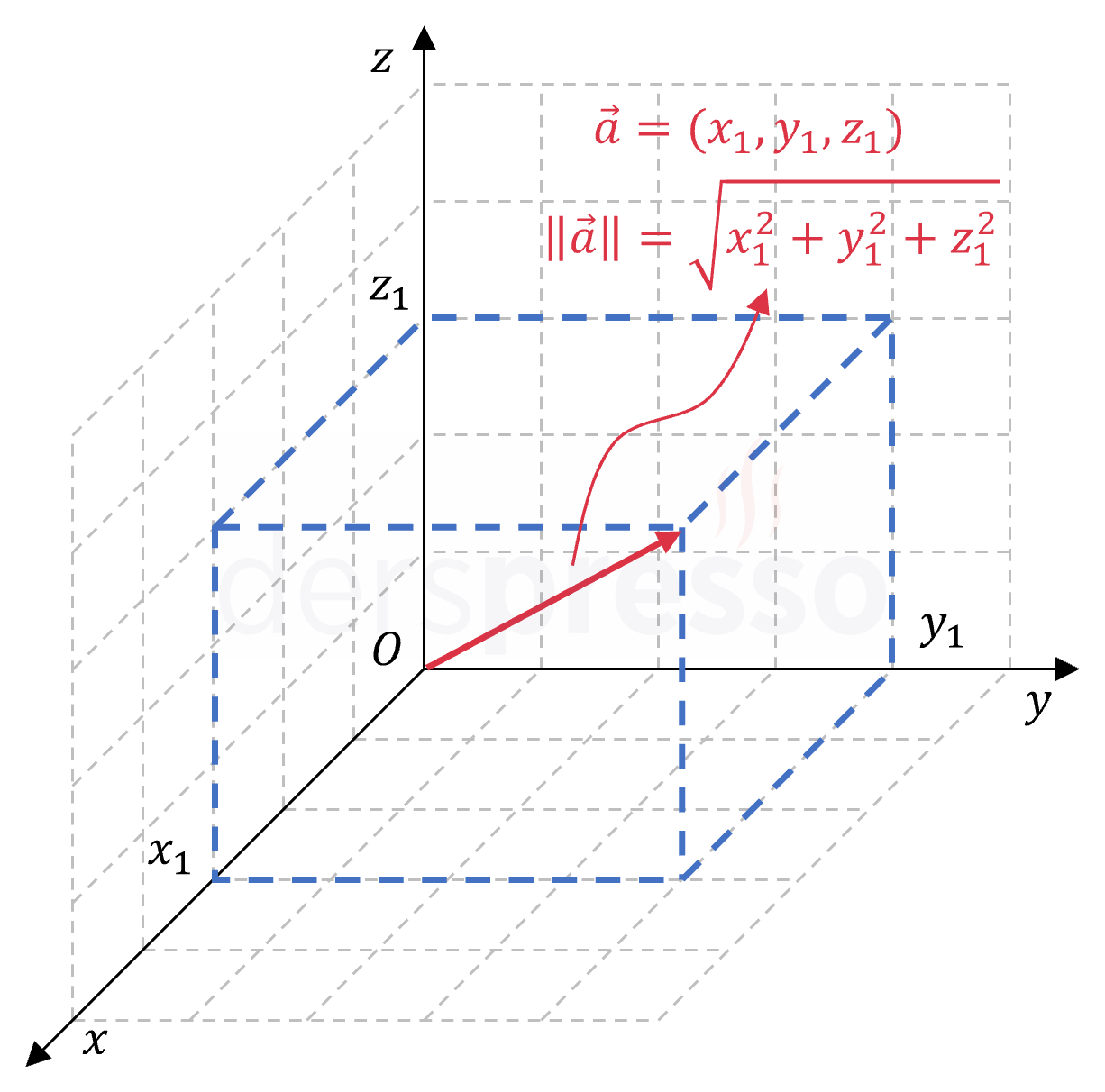
\( \vec{a} = (x_1, y_1, z_1) \) olmak üzere,
\( \norm{\vec{a}} = \sqrt{x_1^2 + y_1^2 + z_1^2} \)
\( \vec{a} = (6, -3, 2) \)
\( \norm{\vec{a}} = \sqrt{6^2 + (-3)^2 + 2^2} = 7 \)
\( \vec{b} = (4, 0, -3) \)
\( \norm{\vec{b}} = \sqrt{(4^2 + 0^2 + (-3)^2} = 5 \)
İSPATI GÖSTER
\( \vec{a} \) vektörünün uç noktasına \( A \), bu noktanın \( xy \) düzlemi üzerindeki izdüşümü olan noktaya \( B \) diyelim.

\( xy \) düzleminde bulunan ve \( z \) koordinatları aynı olan \( O \) ve \( B \) noktaları arasındaki \( \abs{OB} \) uzaklığını iki boyutlu kartezyen düzlemi uzaklık formülü ile bulabiliriz.
\( \abs{OB}^2 = x_1^2 + y_1^2 \)
\( [BA] \) doğru parçasının uzunluğu \( \vec{a} \) vektörünün \( z \) bileşenine eşittir.
\( \abs{BA} = z_1 \)
\( O \), \( B \) ve \( A \) noktaları bir dik üçgen oluşturur.
\( OBA \) dik üçgenine Pisagor teoremini uygulayalım.
\( \abs{OA}^2 = \abs{OB}^2 + \abs{BA}^2 \)
\( \norm{\vec{a}}^2 = (x_1^2 + y_1^2) + z_1^2 \)
\( \norm{\vec{a}} = \sqrt{x_1^2 + y_1^2 + z_1^2} \)
Uzunlukları aynı, yönleri farklı vektörler birbirine eşit değildir, ancak normları birbirine eşittir.
\( \vec{a} = (3, 4) \)
\( \vec{b} = (-5, 0) \)
\( \vec{c} = (-4, -3) \)
\( \vec{d} = (2, -\sqrt{21}) \)

\( \vec{a} \ne \vec{b} \ne \vec{c} \ne \vec{d} \)
\( \norm{\vec{a}} = \norm{\vec{b}} = \norm{\vec{c}} = \norm{\vec{d}} \)
Koordinat uzayındaki \( A \) ve \( B \) noktaları ile ilgili aşağıdaki bilgiler veriliyor.
\( k \in \mathbb{R} \) olmak üzere,
\( A(4, 2, 4) \)
\( B(3k, 4, k) \)
\( \norm{\vec{AB}} = \sqrt{30} \)
Buna göre, \( k \) hangi değerleri alabilir?
Çözümü Göster\( \vec{AB} \) vektörü başlangıç noktası \( A \) ve bitiş noktası \( B \) olan vektörü temsil eder.
\( \vec{AB} \) vektörü \( B \) noktasının koordinatlarından \( A \) noktasının koordinatları çıkarılarak elde edilir.
\( \vec{AB} = B - A \)
\( = (3k, 4, k) - (4, 2, 4) \)
\( = (3k - 4, 2, k - 4) \)
\( \vec{AB} \) vektörünün normunu bulalım.
\( \norm{\vec{AB}} = \sqrt{(3k - 4)^2 + 2^2 + (k - 4)^2} \)
\( = \sqrt{9k^2 - 24k + 16 + 4 + k^2 - 8k + 16} \)
\( = \sqrt{10k^2 - 32k + 36} \)
\( \norm{\vec{AB}} \) uzunluğu soruda verilmiştir.
\( \sqrt{10k^2 - 32k + 36} = \sqrt{30} \)
Eşitliğin taraflarının karesini alalım.
\( 10k^2 - 32k + 36 = 30 \)
\( 10k^2 - 32k + 6 = 0 \)
\( (5k - 1)(k - 3) = 0 \)
\( k \in \{ \frac{1}{5}, 3 \} \) bulunur.
Koordinat uzayındaki \( A \) ve \( B \) noktaları ile ilgili aşağıdaki bilgiler veriliyor.
\( k \in \mathbb{R} \) olmak üzere,
\( A(2k, k, 1) \)
\( B(k + 1, 3, 6) \)
Buna göre, \( \norm{\vec{AB}} \) uzunluğunun alabileceği en küçük değer nedir?
Çözümü Göster\( \vec{AB} \) vektörü başlangıç noktası \( A \) ve bitiş noktası \( B \) olan vektörü temsil eder.
\( \vec{AB} \) vektörü \( B \) noktasının koordinatlarından \( A \) noktasının koordinatları çıkarılarak elde edilir.
\( \vec{AB} = B - A \)
\( = (k + 1, 3, 6) - (2k, k, 1) \)
\( = (1 - k, 3 - k, 5) \)
\( \vec{AB} \) vektörünün normunu bulalım.
\( \norm{\vec{AB}} = \sqrt{(1 - k)^2 + (3 - k)^2 + 5^2} \)
\( = \sqrt{1 - 2k + k^2 + 9 - 6k + k^2 + 25} \)
\( = \sqrt{2k^2 - 8k + 35} \)
Bir karekök ifadesi en küçük değerini kök içindeki ifade en küçük değerini aldığında alır.
Kareköklü ifadenin en küçük değerini bulmak için kök içini tam kareye tamamlayalım.
\( = \sqrt{2(k - 2)^2 + 27} \)
Buna göre kök içindeki ifade en küçük değerini \( k = 2 \) olduğunda alır.
Bu değeri norm formülünde yerine koyalım.
\( \norm{\vec{AB}} = \sqrt{2(2)^2 - 8(2) + 35} \)
\( = \sqrt{27} = 3\sqrt{3} \) bulunur.
Alternatif olarak, kök içindeki ifade bir fonksiyon olarak tanımladıktan sonra birinci türevi sıfıra eşitleyerek de minimum değeri bulabiliriz.