Üstel Fonksiyon Tanım ve Görüntü Kümesi
\( a \gt 0 \) olmak üzere, \( a^x \) şeklindeki bir ifadeyi tanımsız yapan bir \( x \) değeri olmadığı için üstel fonksiyonların en geniş tanım kümesi tüm reel sayılardır.
Pozitif bir tabanın herhangi bir reel sayı kuvveti hiçbir zaman sıfır ya da negatif olamayacağı için üstel fonksiyonların en geniş görüntü kümesi pozitif reel sayılardır.
| Fonksiyon | Tanım Kümesi | Görüntü Kümesi |
|---|---|---|
|
\( y = a^x \) \( a \in \mathbb{R^+} - \{ 1 \} \) |
\( \mathbb{R} \) | \( \mathbb{R^+} \) |
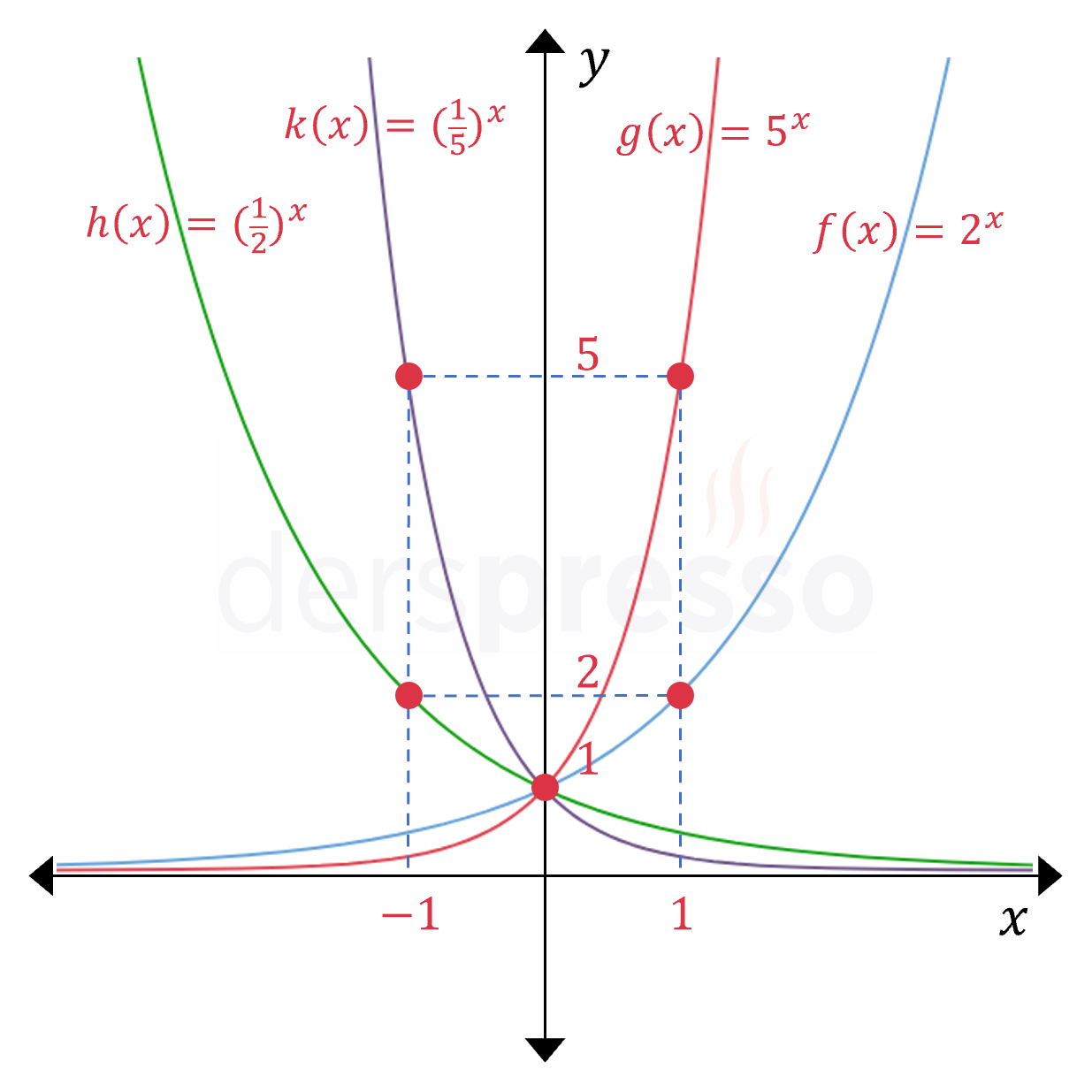
Üstel fonksiyonların tanım kümesinin tüm reel sayılar, görüntü kümesinin de pozitif reel sayılar olduğu farklı tabanlara ait aşağıdaki grafikler üzerinden de teyit edilebilir.
\( f(x) = \dfrac{1}{9^x - 6 \cdot 3^x + 17} \) fonksiyonunun alabileceği en büyük reel sayı değeri kaçtır?
Çözümü GösterFonksiyonu düzenleyelim.
\( f(x) = \dfrac{1}{3^{2x} - 6 \cdot 3^x + 17} \)
\( t = 3^x \) şeklinde değişken değiştirelim.
\( g(t) = \dfrac{1}{t^2 - 6t + 17} \)
Paydadaki ifadenin değer aralığını bulabilmek için ifadeyi tam kareye tamamlayalım.
\( = \dfrac{1}{t^2 - 6t + 9 - 9 + 17} \)
\( = \dfrac{1}{(t - 3)^2 + 8} \)
Payda ne kadar küçük olursa \( g \) fonksiyonunun değeri o kadar büyük olur.
Payda en küçük değerini tam kare ifade sıfır olduğunda, yani \( t = 3 \) olduğunda alır.
\( t = 3 \) değerinin fonksiyonun orijinal değişkenini tanımsız yapmadığından emin olalım.
\( t = 3 = 3^x \Longrightarrow x = 1 \)
\( t = 3 \) vererek fonksiyonun en büyük değerini bulalım.
\( g(3) = \dfrac{1}{(3 - 3)^2 + 8} = \dfrac{1}{8} \) bulunur.