Üstel Fonksiyonların Grafiği

Üstel fonksiyonların grafiği taban değerinin \( (0, 1) \) aralığında olma ya da 1'den büyük olma durumuna göre farklılık gösterir.

Taban Birden Büyükse

Tabanın birden büyük olduğu durumda (\( a \gt 1 \)) üstel fonksiyonların grafiği aşağıdaki şekilde oluşur.

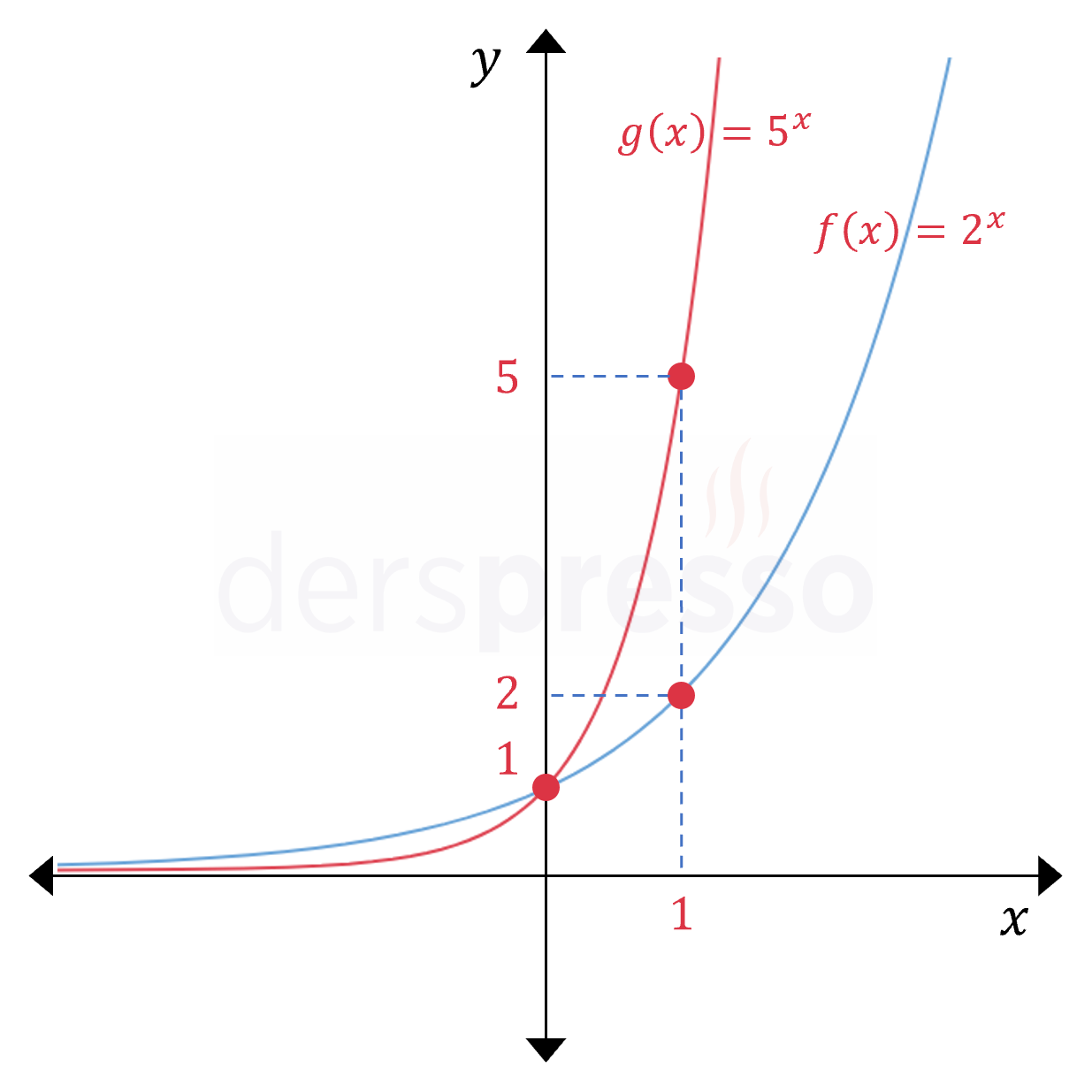
\( a \gt 1 \) için üstel fonksiyonların grafikleri ile ilgili önemli bazı noktalar aşağıdaki gibidir:

Grafik tüm tanım aralığında artandır.
Grafik \( x \) eksenine yaklaşır ama kesmez, dolayısıyla \( x \) ekseni grafiğin bir yatay asimptotudur.
Grafik \( y \) eksenini her zaman \( (0, 1) \) noktasında keser ( \( a^0 = 1 \)).
\( x \)'in negatif olduğu II. bölgede daha büyük tabanlı fonksiyonların grafiği daha küçük tabanlı fonksiyonların grafiğinin altında kalır.
\( x \)'in pozitif olduğu I. bölgede daha büyük tabanlı fonksiyonların grafiği daha küçük tabanlı fonksiyonların grafiğinin üstünde kalır.
Fonksiyon birebirdir.
Fonksiyon \( \mathbb{R} \to \mathbb{R^+} \) için örtendir.

Tabanın sıfır ve bir aralığında olduğu durumda (\( 0 \lt a \lt 1 \)) üstel fonksiyonların grafiği aşağıdaki şekilde oluşur.

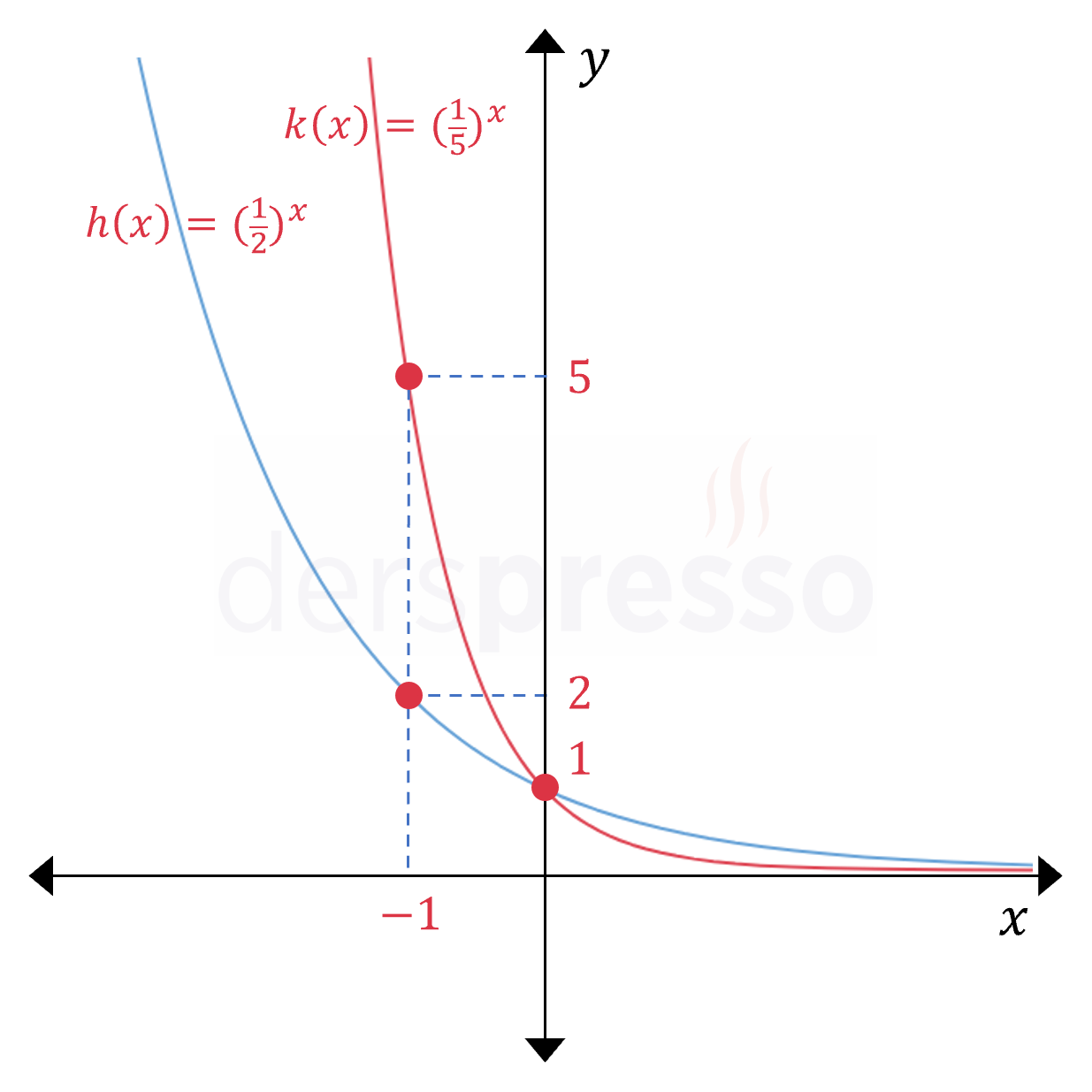
\( 0 \lt a \lt 1 \) için üstel fonksiyonların grafikleri ile ilgili önemli bazı noktalar aşağıdaki gibidir:

Grafik tüm tanım aralığında azalandır.
Grafik \( x \) eksenine yaklaşır ama kesmez, dolayısıyla \( x \) ekseni grafiğin bir yatay asimptotudur.
Grafik \( y \) eksenini her zaman \( (0, 1) \) noktasında keser ( \( a^0 = 1 \)).
\( x \)'in negatif olduğu II. bölgede daha büyük tabanlı fonksiyonların grafiği daha küçük tabanlı fonksiyonların grafiğinin altında kalır.
\( x \)'in pozitif olduğu I. bölgede daha büyük tabanlı fonksiyonların grafiği daha küçük tabanlı fonksiyonların grafiğinin üstünde kalır.
Fonksiyon birebirdir.
Fonksiyon \( \mathbb{R} \to \mathbb{R^+} \) için örtendir.

Çarpmaya göre birbirinin tersi olan tabanlara ait üstel fonksiyon grafikleri \( y \) eksenine göre simetriktir.

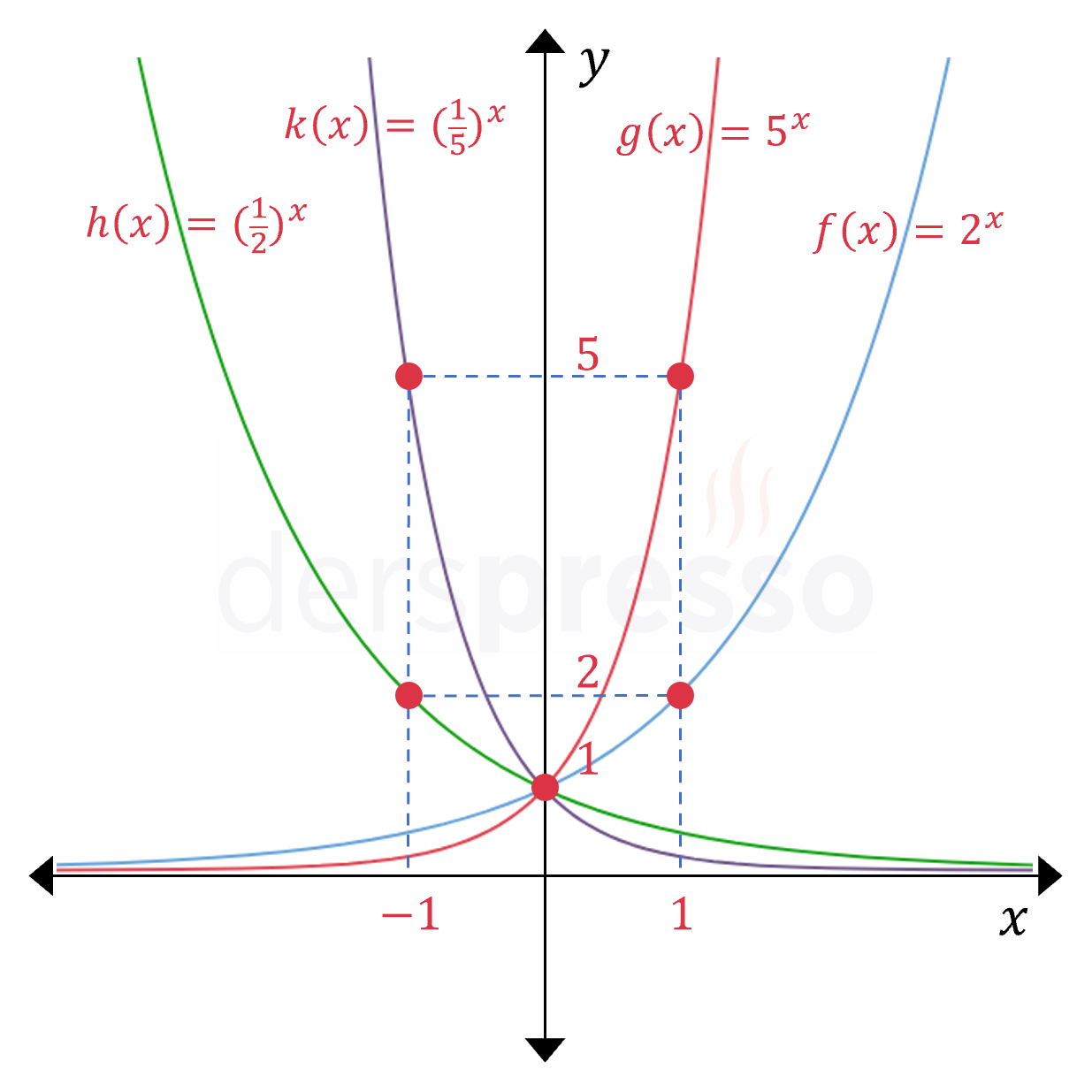
Bu simetrinin sebebi, çarpmaya göre birbirinin tersi olan tabanların çift fonksiyon olma koşulunu sağlıyor olmasıdır.

\( f(x) = 2^x \)

\( h(x) = (\frac{1}{2})^x \) olmak üzere,

\( h(-x) = (\frac{1}{2})^{-x} = 2^x = f(x) \)

SORU 1:

\( f: \mathbb{R} \to \mathbb{R^+} \)

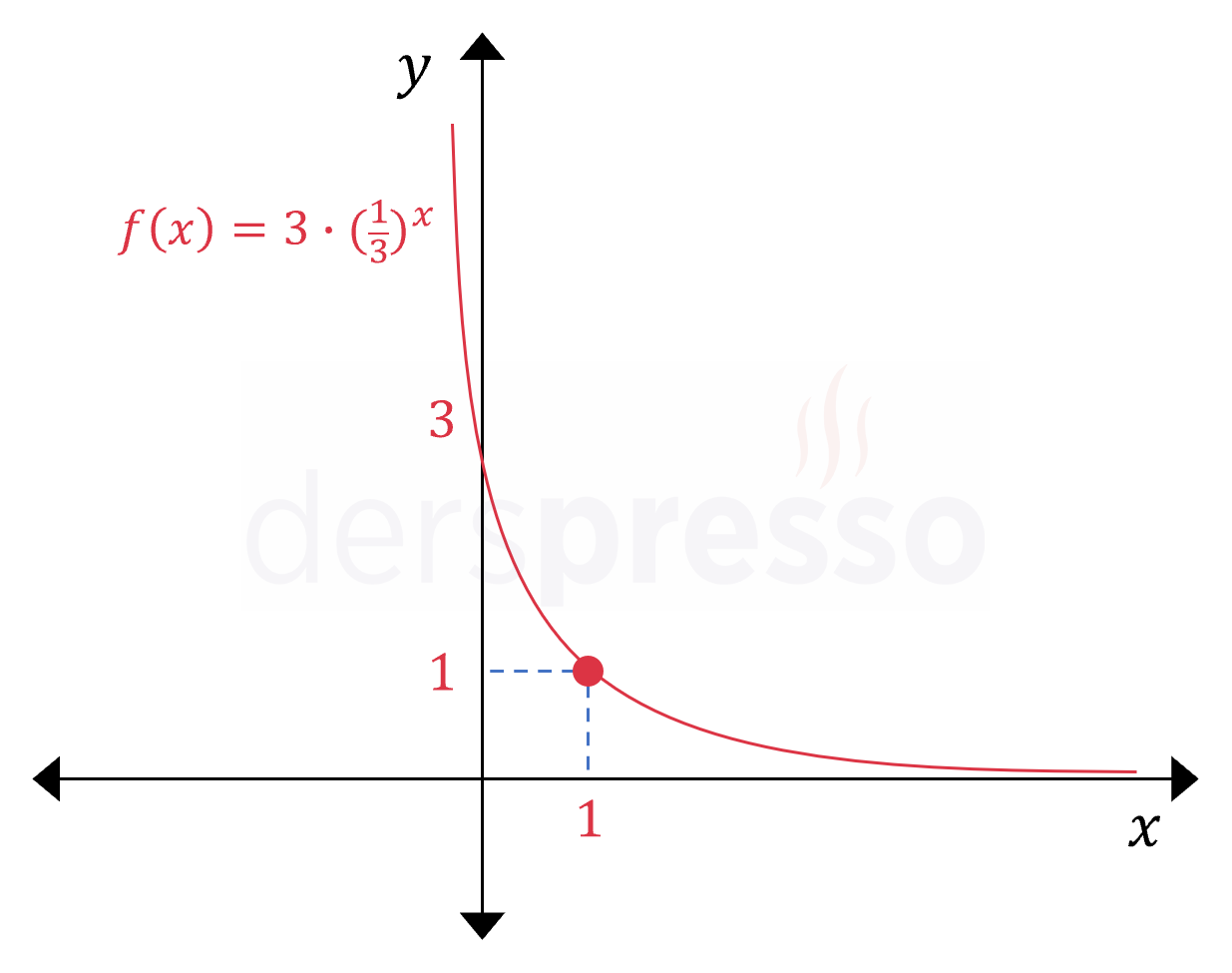
\( f(x) = 3^{1 - x} \) fonksiyonunun grafiğini çiziniz.