Üstel Fonksiyon Denklemleri
Bu bölümde bazı üstel fonksiyon denklem tiplerini ve her biri için çözüm yöntemlerini inceleyeceğiz.
Sabit Değer
Bir üstel ifadenin sabit bir reel sayıya eşitliğinde denklem logaritma ifadesine çevrilir ve değişken yalnız bırakılır.
\( a^x = k \) ise,
\( x = \log_a{k} \)
\( 3 \cdot 5^{2x + 1} = 9 \) denkleminin çözüm kümesini bulalım.
\( 5^{2x + 1} = 3 \)
\( 2x + 1 = \log_5{3} \)
\( x = \dfrac{\log_5{3} - 1}{2} \)
Eşit Tabanlar
Tabanları aynı iki üstel ifadenin eşitliğinde üsler birbirine eşittir.
Bu noktada üstel fonksiyonların tabanlarının sıfırdan büyük ve birden farklı olma koşulunu tekrar hatırlatalım, çünkü bu kural tabanın \( 0 \), \( 1 \) ya da negatif olma durumlarında geçerli olmayacaktır.
\( a^x = a^y \Longrightarrow x = y \)
\( 3^{3x - 1} = 3^{x + 3} \) denkleminin çözüm kümesini bulalım.
\( 3x - 1 = x + 3 \)
\( x = 2 \)
Eşitlenebilir Tabanlar
Tabanları farklı ama eşitlenebilir iki üstel ifadenin eşitliğinde önce tabanlar eşitlenir. Elde edilen üstel ifadelerin üsleri birbirine eşittir.
\( 2^{2x + 4} = (\frac{1}{2})^{2x} \) ise,
\( 2^{2x + 4} = 2^{-2x} \)
\( 2x + 4 = -2x \)
\( x = -1 \)
\( 27^{x + 2} = (\frac{1}{81})^{1 - 2x} \) denkleminin çözüm kümesini bulalım.
\( 3^{3(x + 2)} = 3^{-4(1 - 2x)} \)
\( 3x + 6 = -4 + 8x \)
\( x = 2 \)
Farklı Tabanlar
Tabanları farklı ve eşitlenebilir olmayan iki üstel ifadenin eşitliğinde iki tarafın uygun bir tabanda logaritması alınır ve değişken yalnız bırakılır. Çözüm değerleri logaritma cinsinden bulunur.
\( 2^{2x - 1} = 3^{x + 4} \) denkleminin çözüm kümesini bulalım.
\( \log{2^{2x - 1}} = \log{3^{x + 4}} \)
\( (2x - 1)\log{2} = (x + 4)\log{3} \)
\( 2x\log{2} - \log{2} = x\log{3} + 4\log{3} \)
\( 2x\log{2} - x\log{3} = 4\log{3} + \log{2} \)
\( x(2\log{2} - \log{3}) = 4\log{3} + \log{2} \)
\( x = \dfrac{4\log{3} + \log{2}}{2\log{2} - \log{3}} \)
Değişken Değiştirme
Bir denklemde değişken içeren tüm üstel ifadeler ortak bir ifade cinsinden yazılabiliyorsa denklem aşağıdaki adımlar takip edilerek değişken değiştirme yöntemi ile çözülebilir.
- Üstel ifadelerin yerine geçecek ifade için yeni bir değişken tanımlanır.
- Üstel ifadeler bu yeni değişken cinsinden yazılır ve bu şekilde üstel ifade içermeyen daha sade bir denklem elde edilir.
- Elde edilen denklem standart denklem çözme yöntemleri ile çözülür.
- Yeni değişken için bulunan çözüm değerleri tanım kümesi kontrolleri yapılarak denklemin orijinal değişkenine dönüştürülür.
\( 9^x - 3^x = 6 \) denkleminin çözüm kümesini bulalım.
\( 3^{2x} - 3^x - 6 = 0 \)
\( 3^x = t \) şeklinde değişken değiştirelim.
\( t^2 - t - 6 = 0 \)
\( (t + 2)(t - 3) = 0 \)
\( t = -2 \) ya da \( t = 3 \) olur.
\( t \) değişkenini denklemin orijinal değişkenine dönüştürelim.
\( 3^x = t = -2 \)
Üstel bir ifade negatif değer alamayacağı için \( t = -2 \) geçerli bir çözüm değildir.
\( 3^x = t = 3 \Longrightarrow x = 1 \)
Çözüm kümesi: \( x \in \{1\} \)
\( 3^{2x - 12} = \dfrac{1}{81} \) denkleminin çözüm kümesini bulunuz.
Çözümü Göster\( 3^{2x - 12} = \dfrac{1}{81} \)
\( = \dfrac{1}{3^4} = 3^{-4} \)
Tabanları aynı iki üstel ifadenin eşitliğinde üsler birbirine eşittir.
\( 2x - 12 = -4 \)
\( x = 4 \)
Çözüm kümesi: \( x = 4 \)
\( 5^{4x + 11} = 125^{x - 3} \) denkleminin çözüm kümesini bulunuz.
Çözümü Göster\( 5^{4x + 11} = 125^{x - 3} \)
\( = (5^3)^{x - 3} = 5^{3x -9} \)
Tabanları aynı iki üstel ifadenin eşitliğinde üsler birbirine eşittir.
\( 4x + 11 = 3x - 9 \)
\( x = -20 \)
Çözüm kümesi: \( x = -20 \)
\( \dfrac{(e^{2x + 4})^3}{e^4} = e^{3x - 1} \) eşitliğini sağlayan \( x \) değeri kaçtır?
Çözümü Göster\( e^{3(2x + 4)}e^{-4} = e^{3x - 1} \)
\( e^{6x + 12 - 4} = e^{3x - 1} \)
\( e^{6x + 8} = e^{3x - 1} \)
Tabanları aynı iki üstel ifadenin eşitliğinde üsler birbirine eşittir.
\( 6x + 8 = 3x - 1 \)
\( x = -3 \) bulunur.
\( 2^{x + 3} - 5\cdot 2^{x + 1} + 3 \cdot 2^{x + 2} = 80 \)
olduğuna göre, \( x \) kaçtır?
Çözümü Göster\( 2^2 \cdot 2^{x + 1} - 5 \cdot 2^{x + 1} + 3 \cdot 2^1 \cdot 2^{x + 1} = 80 \)
\( 2^{x + 1} \cdot (2^2 - 5 + 3 \cdot 2) = 80 \)
\( 2^{x + 1} \cdot 5 = 80 \)
\( 2^{x + 1} = 16 = 2^4 \)
Tabanları aynı iki üstel ifadenin eşitliğinde üsler birbirine eşittir.
\( x + 1 = 4 \)
\( x = 3 \) bulunur.
\( 25^x + 5^x - 30 = 0 \) denkleminin çözüm kümesini bulunuz.
Çözümü Göster\( (5^x)^2 + 5^x - 30 = 0 \)
\( 5^x = t \) şeklinde değişken değiştirelim.
\( t^2 + t - 30 = 0 \)
\( (t + 6)(t - 5) = 0 \)
\( t = -6 \) veya \( t = 5 \)
Bu değerleri \( 5^x = t \) ifadesinde yerine koyarak \( x \) değerlerini bulalım.
\( 5^x = t = -6 \)
Üstel ifadenin sonucu negatif olamayacağı için bu eşitliği sağlayan \( x \) değeri yoktur, dolayısıyla \( t = -6 \) geçerli bir çözüm değildir.
\( 5^x = t = 5 \Longrightarrow x = 1 \)
Çözüm kümesi: \( x = 1 \)
\( e^{2x} - 8e^x + 15 = 0 \) denkleminin çözüm kümesini bulunuz.
Çözümü Göster\( (e^x)^2 - 8e^x + 15 = 0 \)
\( e^x = t \) şeklinde değişken değiştirelim.
\( t^2 - 8t + 15 = 0 \)
\( (t - 3)(t - 5) = 0 \)
\( t = 3 \) veya \( t = 5 \)
Bu değerleri \( e^x = t \) ifadesinde yerine koyarak \( x \) değerlerini bulalım.
\( e^x = t = 3 \Longrightarrow x = \ln{3} \)
\( e^x = t = 5 \Longrightarrow x = \ln{5} \)
Çözüm kümesi: \( x \in \{\ln{3}, \ln{5}\} \)
\( e^x + 4e^{-x} = 5 \) denkleminin çözüm kümesini bulunuz.
Çözümü Göster\( e^x + \dfrac{4}{e^x} = 5 \)
\( e^x = t \) şeklinde değişken değiştirelim.
\( t + \dfrac{4}{t} = 5 \)
\( t^2 - 5t + 4 = 0 \)
\( (t - 1)(t - 4) = 0 \)
\( t = 1 \) veya \( t = 4 \)
Bu değerleri \( e^x = t \) ifadesinde yerine koyarak \( x \) değerlerini bulalım.
\( e^x = t = 1 \Longrightarrow x = \ln{1} = 0 \)
\( e^x = t = 4 \Longrightarrow x = \ln{4} \)
Çözüm kümesi: \( x \in \{0, \ln{4}\} \)
\( 2^x + 7^{y + 1} = 407 \)
\( 2^{x + 1} - 7^y = 79 \)
denklem sisteminin çözüm kümesini bulunuz.
Çözümü Göster\( 2^x + 7 \cdot 7^y = 407 \)
\( 2 \cdot 2^x - 7^y = 79 \)
\( 2^x = s \) ve \( 7^y = t \) şeklinde değişken değiştirelim.
\( s + 7t = 407 \)
\( 2s - t = 79 \)
İkinci eşitliği 7 ile çarpıp birinci eşitlikle taraf tarafa toplayalım.
\( 15s + 0 = 407 + 7 \cdot 79 = 960 \)
\( s = 64 = 2^x \)
\( x = 6 \)
Bulduğumuz değeri birinci eşitlikte yerine yazalım.
\( 2^6 + 7 \cdot 7^y = 407 \)
\( 7^y = 49 \Longrightarrow y = 2 \)
Çözüm kümesi: \( (x, y) = (6, 2) \)
\( 2^x + 2^{y+2} = 17\sqrt{2} \)
\( 2^{x+3}+ 2^y = 12\sqrt{2} \)
olduğuna göre, \( x + y \) kaçtır?
Çözümü Göster\( 2^x + 4 \cdot 2^y = 17\sqrt{2} \)
\( 8 \cdot 2^x + 2^y = 12\sqrt{2} \)
\( 2^x = a \) ve \( 2^y = b \) şeklinde değişken değiştirelim.
\( a + 4b = 17\sqrt{2} \)
\( 8a + b = 12\sqrt{2} \)
Bu iki denklemi ortak çözdüğümüzde aşağıdaki değerleri buluruz.
\( a = \sqrt{2} \)
\( b = 4\sqrt{2} \)
\( x \) ve \( y \) değerlerini ayrı ayrı bulmadan toplamlarını kısa yoldan bulalım.
\( ab = 2^x \cdot 2^y = 2^{x+y} \)
\( \sqrt{2} \cdot 4\sqrt{2} = 2^{x+y} \)
\( 8 = 2^3 = 2^{x+y} \)
Tabanları aynı iki üstel ifadenin eşitliğinde üsler birbirine eşittir.
\( x + y = 3 \) bulunur.
\( e^a + e^b = 6 \)
\( 2e^a + e^{2b} = 11 \)
denklem sisteminin çözüm kümesini bulunuz.
Çözümü Göster\( e^a = s \) ve \( e^b = t \) şeklinde değişken değiştirelim.
\( s + t = 6 \)
\( 2s + t^2 = 11 \)
İkinci denklemde \( t = 6 - s \) yazalım.
\( 2s + (6 - s)^2 = 11 \)
\( 2s + 36 - 12s + s^2 = 11 \)
\( s^2 - 10s + 25 = 0 \)
\( (s - 5)^2 = 0 \)
\( s = 5 \)
\( t = 6 - s = 1 \)
Bu değerleri yukarıdaki ifadelerde yerine koyarak \( a \) ve \( b \) değerlerini bulalım.
\( e^a = s = 5 \)
\( a = \ln{5} \)
\( e^b = t = 1 \)
\( b = \ln{1} = 0 \)
Çözüm kümesi: \( (a, b) = (\ln{5}, 0) \)
\( 27^x + 9 = 9^x + 3^{x + 2} \) denkleminin kaç reel çözümü vardır?
Çözümü GösterVerilen fonksiyonu düzenleyelim.
\( 3^{3x} + 9 = 3^{2x} + 9 \cdot 3^x \)
\( 3^x = t \) şeklinde değişken değiştirelim.
\( t^3 + 9 = t^2 + 9t \)
Tüm terimleri tek tarafta toplayıp denklemi sıfıra eşitleyelim.
\( t^3 - t^2 - 9t + 9 = 0 \)
İfadeyi çarpanlarına ayıralım.
\( t^2(t - 1) - 9(t - 1) = 0 \)
\( (t - 1)(t^2 - 9) = 0 \)
\( (t - 1)(t - 3)(t + 3) = 0 \)
Denklemin çözüm kümesi her bir çarpanı sıfır yapan değerlerden oluşur.
\( t = 1 \), \( t = 3 \) ya da \( t = -3 \)
\( 3^x = t = 1 \Longrightarrow x = 0 \)
\( 3^x = t = 3 \Longrightarrow x = 1 \)
\( 3^x = t = -3 \)
Bir üstel ifadenin sonucu negatif olamayacağı için bu durum için geçerli bir çözüm yoktur.
Çözüm kümesi: \( x \in \{ 0, 1 \} \)
Buna göre verilen denklemin 2 reel kökü vardır.
\( 7^a2^a - 8 \cdot 2^a - 7 \cdot 7^a + 7 \cdot 8 = 0 \)
Eşitliğin sol tarafını çarpanlarına ayıralım.
\( 2^a(7^a - 8) - 7(7^a - 8) = 0 \)
\( (7^a - 8)(2^a - 7) = 0 \)
Bu eşitlik iki durumda sağlanır.
Durum 1:
\( 7^a - 8 = 0 \)
\( 7^a = 8 \)
\( a = \log_7{8} \)
Durum 2:
\( 2^a - 7 = 0 \)
\( 2^a = 7 \)
\( a = \log_2{7} \)
Bu iki değerin çarpımını bulalım.
\( \log_7{8} \cdot \log_2{7} = \log_2{8} \)
\( = \log_2{2^3} = 3 \) bulunur.
\( 6^x - 2^{x + 1} = 3^{x + 1} - 6 \) denkleminin çözüm kümesini bulunuz.
Çözümü GösterTüm terimleri eşitliğin sol tarafında toplayalım ve ifadeyi çarpanlarına ayıralım.
\( 3^x2^x - 2 \cdot 2^x - 3 \cdot 3^x + 6 = 0 \)
\( 2^x(3^x - 2) - 3(3^x - 2) = 0 \)
\( (2^x - 3)(3^x - 2) = 0 \)
Bu eşitlik iki durumda sağlanır.
Durum 1:
\( 2^x - 3 = 0 \)
\( 2^x = 3 \)
\( x = \log_2{3} \)
Durum 2:
\( 3^x - 2 = 0 \)
\( 3^x = 2 \)
\( x = \log_3{2} \)
Çözüm kümesi: \( x \in \{ \log_2{3}, \log_3{2} \} \)
\( \dfrac{2^x - 2}{2^{1 - x} - 1} = -8 \) denkleminin çözüm kümesini bulunuz.
Çözümü Göster\( \dfrac{2^x - 2}{2 \cdot 2^{-x} - 1} = -8 \)
\( \dfrac{2^x - 2}{\frac{2}{2^x} - 1} = -8 \)
\( 2^x = t \) şeklinde değişken değiştirelim.
\( \dfrac{t - 2}{\frac{2}{t} - 1} = -8 \)
\( t - 2 = -\dfrac{16}{t} + 8 \)
Eşitliğin iki tarafını \( t \) ile çarpalım.
\( t^2 - 2t = -16 + 8t \)
\( t^2 - 10t + 16 = 0 \)
\( (t - 2)(t - 8) = 0 \)
\( t = 2 \) ya da \( t = 8 \)
Bu değerleri \( 2^x = t \) ifadesinde yerine koyarak \( x \) değerlerini bulalım.
\( 2^x = t = 2 \Longrightarrow x = 1 \)
\( 2^x = t = 8 \Longrightarrow x = 3 \)
Çözüm adımlarında eşitliğin iki tarafını \( t \) ile çarparak ifadelerin derecesini artırdığımız için denkleme geçersiz bir çözüm eklenmiş olabilir, bu yüzden bulduğumuz iki değeri orijinal denklemde yerine koyarak sağlamasını yapalım.
\( x = 1 \) için:
\( \dfrac{2^1 - 2}{2^{1 - 1} - 1} = -8 \)
Eşitliğin sol tarafının paydası sıfır olduğu için \( x = 1 \) geçersiz bir çözümdür.
\( x = 3 \) için:
\( \dfrac{2^3 - 2}{2^{1 - 3} - 1} = -8 \)
\( \dfrac{6}{-\frac{3}{4}} = -8 \)
Eşitlik sağlandığı için \( x = 3 \) geçerli bir çözümdür.
Çözüm kümesi: \( x = 3 \)
\( e^{\cos{\ln{x}}} = 1 \) denkleminin genel çözümünü bulunuz.
Çözümü GösterEşitliğin her iki tarafının doğal logaritmasını alalım.
\( \ln{e^{\cos{\ln{x}}}} = \ln{1} \)
\( \cos{\ln{x}} = 0 \)
Kosinüs fonksiyonu periyodik bir fonksiyondur ve aşağıdaki değerlerde sıfır olur.
\( k \in \mathbb{Z} \) olmak üzere,
\( \ln{x} = \dfrac{\pi}{2} + \pi k \)
\( x = e^{\frac{\pi}{2} + \pi k} \)
Çözüm kümesi: \( x \in \{\ldots, e^{-\frac{\pi}{2}}, e^{\frac{\pi}{2}}, e^{\frac{3\pi}{2}}, e^{\frac{5\pi}{2}}, \ldots\} \)
\( 7^x(7^x - 14) + 3^y(3^y - 18) = -130 \)
olduğuna göre, \( xy \) çarpımının değeri kaçtır?
Çözümü Göster\( 7^x = a \) ve \( 3^y = b \) şeklinde değişken değiştirelim.
\( a(a - 14) + b(b - 18) + 130 = 0 \)
\( a^2 - 14a + b^2 - 18b + 130 = 0 \)
\( a \) ve \( b \) değişkenlerine bağlı ifadeleri ayrı ayrı tam kareye tamamlamak için 130 sayısını 49 + 81 şeklinde ikiye bölelim.
\( a^2 - 14a + 49 + b^2 - 18b + 81 = 0 \)
\( (a - 7)^2 + (b - 9)^2 = 0 \)
İki tam kare ifadenin toplamının sıfır olması için ifadeler ayrı ayrı sıfır olmalıdır.
\( a - 7 = 0 \) ve \( b - 9 = 0 \)
\( a = 7 \) ve \( b = 9 \)
Bu denklemin \( a \) ve \( b \) kök değerlerini kullanarak orijinal denklemin \( x \) ve \( y \) kök değerlerini bulalım.
\( a = 7 \) için:
\( a = 7^x = 7 \Longrightarrow x = 1 \)
\( b = 9 \) için:
\( b = 3^y = 9 \Longrightarrow y = 2 \)
\( xy = 1 \cdot 2 = 2 \) bulunur.
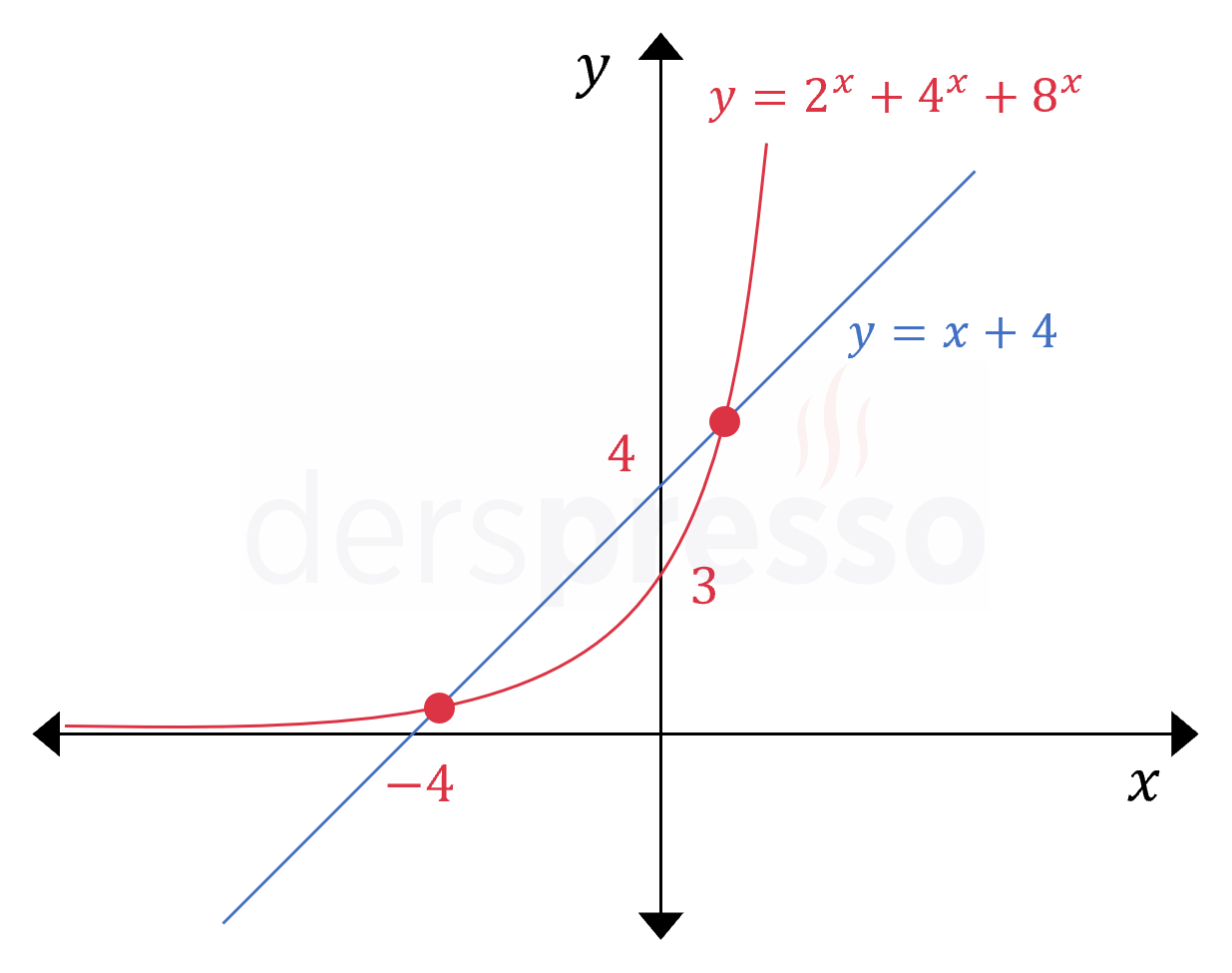
\( 2^x + 4^x + 8^x - x = 4 \) denklemini sağlayan kaç \( x \) değeri vardır?
Çözümü Göster\( x \) terimini eşitliğin sağ tarafına alalım.
\( 2^x + 4^x + 8^x = x + 4 \)
Eşitliğin iki tarafını ayrı fonksiyonlar olarak düşünürsek eşitliği sağlayan \( x \) değerleri bu iki fonksiyonun grafiklerinin kesişim noktalarının apsis değerleridir.
\( y = 2^x + 4^x + 8^x \) fonksiyonu tabanı birden büyük, dolayısıyla artan üç üstel ifadenin toplamından oluşur, dolayısıyla artandır.
\( a^x \) formundaki tüm üstel ifadeler \( y \) eksenini \( (0, 1) \) noktasında kestiği için bu fonksiyon \( y \) eksenini \( (0, 3) \) noktasında keser ve tüm reel sayılarda pozitiftir.
\( 2^0 + 4^0 + 8^0 = 3 \)
Eşitliğin sağ tarafı \( y = x + 4 \) doğrusal fonksiyonudur.
Doğru \( x \) eksenini \( (-4, 0) \) noktasında kestiği için bu noktada üstel fonksiyonun altındadır. Üstel fonksiyon tüm reel sayılarda pozitif olduğu için doğru \( x \lt -4 \) için üstel fonksiyonun altında kalmaya devam eder.
Doğru \( y \) eksenini \( (0, 4) \) noktasında kestiği için bu noktada üstel fonksiyonun üstündedir. \( x \) pozitif sonsuza giderken üstel fonksiyon çok hızlı büyüdüğü için doğrunun tekrar üstüne çıkacağından emin olabiliriz.
Buna göre iki grafiğin kesiştiği, birincisi \( x_1 \in (-4, 0) \) aralığında, ikincisi \( x_2 \in (0, \infty) \) aralığında olmak üzere iki nokta olmalıdır.
Her iki grafiği çizdiğimizde fonksiyonların tam kesişim noktalarını bulamasak da iki noktada kesiştiklerini görebiliriz.
