Orantı
İki ya da daha fazla oranın eşitliğine orantı denir. Bu oranların eşit oldukları değere orantı sabiti denir ve genellikle \( k \) ile ifade edilir.
\( \dfrac{a}{b} = \dfrac{c}{d} = k \)
Orantının bir diğer gösterimi aşağıdaki gibidir.
\( a:b = c:d \)
Orantıdaki değişkenler orantı sabiti cinsinden aşağıdaki şekilde ifade edilebilir.
\( a = k \cdot b \)
\( c = k \cdot d \)
\( \frac{a}{b} = \frac{c}{d} \) şeklindeki bir orantıda \( a \) ve \( d \) orantının dış terimleri/dışları, \( b \) ve \( c \) orantının iç terimleri/içleridir. İçler - dışlar çarpımı olarak adlandırılan yöntemdeki terimler de isimlerini buradan almaktadır.
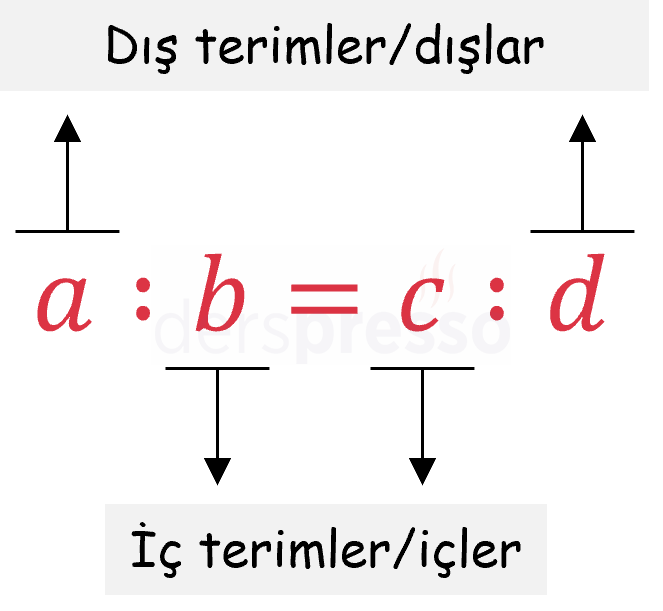
Bu şekildeki gibi bir orantıda \( d \) sayısına \( a \), \( b \) ve \( c \) sayılarının dördüncü orantılısı denir.
\( \dfrac{a}{b} = \dfrac{c}{\textcolor{red}{d}} \)
\( \dfrac{9}{5} = \dfrac{36}{d} \)
Verilen orantının dördüncü orantılısını bulalım.
\( 9 \cdot d = 5 \cdot 36 \)
\( d = 20 \)
İç terimlerin birbirine eşit olduğu bir orantıda, bu iç terime \( a \) ve \( d \) sayılarının orta orantılısı ya da geometrik ortalaması denir.
\( b = c \) ise,
\( \dfrac{a}{\textcolor{red}{b}} = \dfrac{\textcolor{red}{b}}{d} \)
\( b^2 = a \cdot d \)
\( b = \sqrt{a \cdot d} \)
\( \dfrac{4}{b} = \dfrac{b}{36} \)
Verilen orantının orta orantılısını bulalım.
\( b^2 = 4 \cdot 36 \)
\( b = 12 \)
Bir orantı ikiden fazla oranın eşitliğinden oluşabilir.
\( \dfrac{a}{b} = \dfrac{c}{d} = \dfrac{e}{f} = \ldots = k \)
\( a:c:e = b:d:f \)
\( a = k \cdot b \)
\( c = k \cdot d \)
\( e = k \cdot f \)
Orantıya örnek olarak, farklı boyutlardaki üç Türk bayrağı ve bu bayrakların boyutlarının oranları arasındaki eşitlik verilebilir.
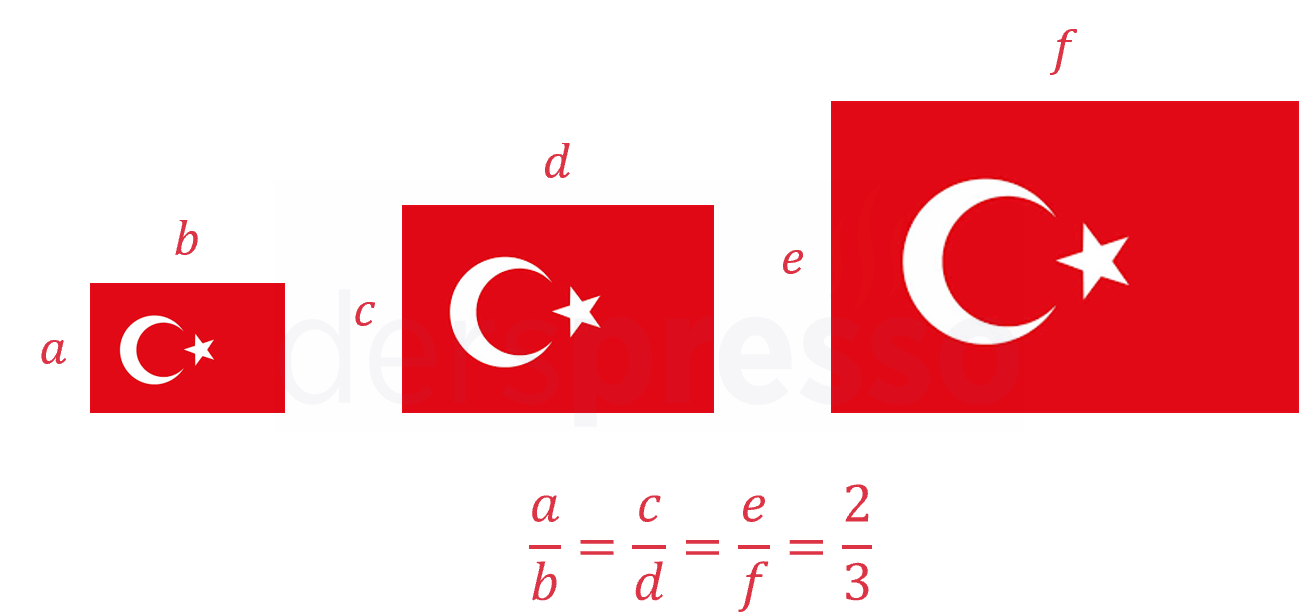
Aşağıda paylaşacağımız orantı özelliklerinde kullanmak üzere bu üç bayrağın ölçülerini aşağıdaki gibi alacağız.
| Bayrak | Yükseklik | Genişlik | Oran |
|---|---|---|---|
| Küçük boy | \( a = 10 \text{ cm} \) | \( b = 15 \text{ cm} \) | \( \frac{10}{15} = \frac{2}{3} \) |
| Orta boy | \( c = 30 \text{ cm} \) | \( d = 45 \text{ cm} \) | \( \frac{30}{45} = \frac{2}{3} \) |
| Büyük boy | \( e = 60 \text{ cm} \) | \( f = 90 \text{ cm} \) | \( \frac{60}{90} = \frac{2}{3} \) |
Orantı Özellikleri
Bir orantıda içlerin çarpımı dışların çarpımına eşittir.
\( \dfrac{a}{b} = \dfrac{c}{d} \) ise,
\( a \cdot d = b \cdot c \)
\( \dfrac{10}{15} = \dfrac{x}{45} \) ise,
\( 10 \cdot 45 = 15 \cdot x \)
\( x = 30 \)
Bir orantıda çapraz terimler aralarında yer değiştirirse eşitlik bozulmaz, ancak oluşan yeni orantının orantı sabiti farklı olur.
\( \dfrac{a}{b} = \dfrac{c}{d} = k_1 \) ise,
\( \dfrac{\textcolor{red}{d}}{b} = \dfrac{c}{\textcolor{red}{a}} = k_2 \)
\( \dfrac{a}{\textcolor{red}{c}} = \dfrac{\textcolor{red}{b}}{d} = k_3 \)
\( \dfrac{10}{15} = \dfrac{30}{45} = k_1 = \dfrac{2}{3} \) ise,
\( \dfrac{\textcolor{red}{45}}{15} = \dfrac{30}{\textcolor{red}{10}} = k_2 = 3 \)
\( \dfrac{10}{\textcolor{red}{30}} = \dfrac{\textcolor{red}{15}}{45} = k_3 = \dfrac{1}{3} \)
Bir orantıda oranların çarpmaya göre tersi alınırsa (pay ve paydadaki sayılar aralarında yer değiştirirse) orantı sabitinin de çarpmaya göre tersi alınır.
\( \dfrac{a}{b} = \dfrac{c}{d} = k \) ise,
\( \dfrac{b}{a} = \dfrac{d}{c} = \dfrac{1}{k} \)
\( \dfrac{10}{15} = \dfrac{30}{45} = \dfrac{2}{3} \) ise,
\( \dfrac{15}{10} = \dfrac{45}{30} = \dfrac{3}{2} \)
Bir orantıda oranların paylarının kendi aralarında, paydalarının da kendi aralarında toplamı ya da farkı alınırsa orantı sabiti değişmez.
\( \dfrac{a}{b} = \dfrac{c}{d} = k \) ise,
\( \dfrac{a + c}{b + d} = \dfrac{a - c}{b - d} = k \)
\( \dfrac{10}{15} = \dfrac{30}{45} = \dfrac{2}{3} \) ise,
\( \dfrac{10 + 30}{15 + 45} = \dfrac{40}{60} = \dfrac{2}{3} \)
\( \dfrac{10 - 30}{15 - 45} = \dfrac{-20}{-30} = \dfrac{2}{3} \)
Yukarıdaki orantı özellikleri kullanılarak aşağıdaki ek özellikler elde edilebilir. Bu işlemler sonucunda eşitliğin sağlandığına, ancak orantı sabitinin aynı kalmadığına dikkat edilmelidir.
\( \dfrac{a}{b} = \dfrac{c}{d} = k_1 \) ise,
\( \dfrac{a + b}{b} = \dfrac{c + d}{d} = k_2 \)
\( \dfrac{a - b}{b} = \dfrac{c - d}{d} = k_3 \)
\( k \ne 1 \) olmak üzere,
\( \dfrac{a + b}{a - b} = \dfrac{c + d}{c - d} = k_4 \)
\( \dfrac{10}{15} = \dfrac{30}{45} = \dfrac{2}{3} \) ise,
\( \dfrac{10 + 15}{15} = \dfrac{30 + 45}{45} = \dfrac{5}{3} \)
\( \dfrac{10 - 15}{15} = \dfrac{30 - 45}{45} = -\dfrac{1}{3} \)
İSPATI GÖSTER
\( \dfrac{a}{b} = \dfrac{c}{d} = k \) ise,
Orantıdaki iki orana 1 ekleyelim.
\( \dfrac{a}{b} + 1 = \dfrac{c}{d} + 1 \)
\( \dfrac{a}{b} + \dfrac{b}{b} = \dfrac{c}{d} + \dfrac{d}{d} \)
\( \dfrac{a + b}{b} = \dfrac{c + d}{d} \)
Orantıdaki iki orandan 1 çıkaralım.
\( \dfrac{a}{b} - 1 = \dfrac{c}{d} - 1 \)
\( \dfrac{a}{b} - \dfrac{b}{b} = \dfrac{c}{d} - \dfrac{d}{d} \)
\( \dfrac{a - b}{b} = \dfrac{c - d}{d} \)
Yukarıda elde ettiğimiz iki orantıyı taraf tarafa bölelim.
\( \dfrac{\frac{a + b}{b}}{\frac{a - b}{b}} = \dfrac{\frac{c + d}{d}}{\frac{c - d}{d}} \)
\( \dfrac{a + b}{a - b} = \dfrac{c + d}{c - d} \)
Bir orantıdaki oranlar sabit sayılarla genişletildiğinde orantı sabiti değişmez.
\( m, n \in \mathbb{R} \) ve \( (m, n) \ne (0, 0) \) olmak üzere,
\( \dfrac{a}{b} = \dfrac{c}{d} = k \) ise,
\( \dfrac{ma}{mb} = \dfrac{nc}{nd} = k \)
\( \dfrac{ma \pm nc}{mb \pm nd} = k \)
\( m = 4, n = 2 \) olmak üzere,
\( \dfrac{10}{15} = \dfrac{30}{45} = \dfrac{2}{3} \) ise,
\( \dfrac{40}{60} = \dfrac{60}{90} = \dfrac{2}{3} \)
\( \dfrac{40 + 60}{60 + 90} = \dfrac{100}{150} = \dfrac{2}{3} \)
Bir orantıda belirli sayıda oranın çarpımı, orantı sabitinin aynı sayıda kuvvetine eşittir.
\( \dfrac{a}{b} = \dfrac{c}{d} = \dfrac{e}{f} = k \) ise,
\( \dfrac{a \cdot c}{b \cdot d} = k^2 \)
\( \dfrac{a \cdot c \cdot e}{b \cdot d \cdot f} = k^3 \)
\( \dfrac{10}{15} = \dfrac{30}{45} = \dfrac{2}{3} \) ise,
\( \dfrac{10 \cdot 30}{15 \cdot 45} = {\left( \dfrac{2}{3} \right)}^2 = \dfrac{4}{9} \)
Bir orantıda oranların paylarının ve paydalarının kendi aralarında bölümlerinin oranı bire eşittir.
\( \dfrac{a}{b} = \dfrac{c}{d} = k \) ise,
\( \dfrac{a \div c}{b \div d} = 1 \)
\( \dfrac{10}{15} = \dfrac{30}{45} = \dfrac{2}{3} \) ise,
\( \dfrac{10 \div 30}{15 \div 45} = 1 \)
Bir orantıda oranların belirli bir kuvveti/kökü, orantı sabitinin aynı sayıda kuvvetine/köküne eşittir.
\( \dfrac{a}{b} = \dfrac{c}{d} = k \) ise,
\( \dfrac{a^2}{b^2} = \dfrac{c^2}{d^2} = k^2 \)
\( \dfrac{a^n}{b^n} = \dfrac{c^n}{d^n} = k^n \)
\( \dfrac{\sqrt[n]{a}}{\sqrt[n]{b}} = \dfrac{\sqrt[n]{c}}{\sqrt[n]{d}} = \sqrt[n]{k} \)
\( \dfrac{10}{15} = \dfrac{2}{3} \) ise,
\( \dfrac{10^2}{15^2} = \dfrac{2^2}{3^2} \)
\( \dfrac{100}{225} = \dfrac{4}{9} \)
Aşağıdaki oran ikililerinden hangileri orantı oluşturur?
I. \( \dfrac{1}{7}, \dfrac{8}{42} \)
II. \( \dfrac{6}{5}, \dfrac{54}{45} \)
III. \( \dfrac{\sqrt{3}}{2}, \dfrac{3}{2\sqrt{3}} \)
Çözümü GösterBir oran ikilisinin orantı oluşturması için içlerin çarpımı dışların çarpımına eşit olmalıdır.
\( \dfrac{a}{b} = \dfrac{c}{d} = k \) ise,
\( a \cdot d = b \cdot c \) olmalıdır.
I. öncül:
\( \dfrac{1}{7}, \dfrac{8}{42} \)
\( 1 \cdot 42 = 42 \)
\( 7 \cdot 8 = 56 \)
Bu ikili orantı oluşturmaz.
II. öncül:
\( \dfrac{6}{5}, \dfrac{54}{45} \)
\( 6 \cdot 45 = 270 \)
\( 5 \cdot 54 = 270 \)
Bu ikili orantı oluşturur.
III. öncül:
\( \dfrac{\sqrt{3}}{2}, \dfrac{3}{2\sqrt{3}} \)
\( \sqrt{3} \cdot 2\sqrt{3} = 6 \)
\( 2 \cdot 3 = 6 \)
Bu ikili orantı oluşturur.
Buna göre II. ve III. öncüllerdeki ikililer orantı oluşturur.
Aşağıdaki orantılarda bilinmeyeni bulunuz.
(a) \( \dfrac{9}{17} = \dfrac{x}{34} \)
(b) \( \dfrac{39}{y} = \dfrac{117}{\frac{2}{5}} \)
(c) \( \dfrac{z}{4,5} = -\dfrac{0,8}{6,4} \)
Çözümü GösterBir orantıda içler çarpımı dışlar çarpımına eşittir.
\( \dfrac{a}{b} = \dfrac{c}{d} = k \) ise,
\( a \cdot d = b \cdot c \)
(a) seçeneği:
\( \dfrac{9}{17} = \dfrac{x}{34} \)
\( 9 \cdot 34 = 17 \cdot x \)
\( x = \dfrac{9 \cdot 34}{17} \)
\( = 9 \cdot 2 = 18 \)
(b) seçeneği:
\( \dfrac{39}{y} = \dfrac{117}{\frac{2}{5}} \)
\( 39 \cdot \dfrac{2}{5} = y \cdot 117 \)
\( y = \dfrac{39 \cdot \frac{2}{5}}{117} \)
\( = \dfrac{1}{3} \cdot \dfrac{2}{5} = \dfrac{2}{15} \)
(c) seçeneği:
\( \dfrac{z}{4,5} = \dfrac{-0,8}{6,4} \)
\( z \cdot 6,4 = 4,5 \cdot (-0,8) \)
\( z = -\dfrac{4,5 \cdot 0,8}{6,4} \)
Eşitliğin sağ tarafını 100 ile genişletelim.
\( z = -\dfrac{45 \cdot 8}{640} \)
\( = -\dfrac{45}{80} = -\dfrac{9}{16} \)
\( \dfrac{a}{7} = \dfrac{b}{3} = \dfrac{c}{22} = 6 \)
olduğuna göre, \( a \cdot b - c \) ifadesinin sonucu kaçtır?
Çözümü GösterOrantı sabitini kullanarak değişkenlerin değerini bulalım.
\( a = 7 \cdot 6 = 42 \)
\( b = 3 \cdot 6 = 18 \)
\( c = 22 \cdot 6 = 132 \)
Bu değerleri verilen ifadede yerine koyalım.
\( a \cdot b - c = 42 \cdot 18 - 132 \)
\( = 624 \) bulunur.
\( \dfrac{x}{5} = \dfrac{y}{7} \)
\( x + y = 156 \)
olduğuna göre, \( x - y \) ifadesinin sonucu kaçtır?
Çözümü GösterVerilen orantıyı bir orantı sabitine eşitleyelim.
\( \dfrac{x}{5} = \dfrac{y}{7} = k \)
Değişkenleri orantı sabiti cinsinden yazalım.
\( x = 5k, \quad y = 7k \)
Bu değerleri verilen eşitlikte yerine koyalım.
\( x + y = 156 \)
\( 5k + 7k = 156 \)
\( 12k = 156 \)
\( k = 13 \)
\( x - y \) farkını bulalım.
\( x - y = 5k - 7k \)
\( = -2k = -2 \cdot 13 = -26 \) bulunur.
\( x = \dfrac{y}{3} = \dfrac{z}{4} \)
\( 4x + 3y - 2z = 15 \)
olduğuna göre, \( y \) kaçtır?
Çözümü GösterVerilen orantıyı bir orantı sabitine eşitleyelim.
\( x = \dfrac{y}{3} = \dfrac{z}{4} = k \)
Değişkenleri orantı sabiti cinsinden yazalım.
\( x = k, \quad y = 3k, \quad z = 4k \)
Bu değerleri verilen eşitlikte yerine koyalım.
\( 4x + 3y - 2z = 15 \)
\( 4k + 3(3k) - 2(4k) = 15 \)
\( 5k = 15 \)
\( k = 3 \)
\( y = 3k = 9 \) bulunur.
\( a, b, c \) sayıları sırasıyla \( -3, -2, 5 \) sayıları ile orantılıdır.
\( 2a + 5b + 3c = -15 \)
olduğuna göre, \( c \) kaçtır?
Çözümü Göster\( a, b, c \) sayıları arasındaki orantıyı yazalım ve orantıyı bir orantı sabitine eşitleyelim.
\( \dfrac{a}{-3} = \dfrac{b}{-2} = \dfrac{c}{5} = k \)
Değişkenleri orantı sabiti cinsinden yazalım.
\( a = -3k, \quad b = -2k, \quad c = 5k \)
Bu değerleri verilen eşitlikte yerine yazalım.
\( 2a + 5b + 3c = -15 \)
\( 2(-3k) + 5(-2k) + 3(5k) = -15 \)
\( -6k - 10k + 15k = -15 \)
\( k = 15 \)
\( c \) değerini bulalım.
\( c = 5k = 75 \) bulunur.
Üç doğal sayı sırasıyla \( 2 : 3 : 5 \) sayıları ile orantılıdır.
Bu sayıların karelerinin toplamı 15200 olduğuna göre, sayılardan en küçüğü kaçtır?
Çözümü GösterSayılara sırasıyla \( 2k \), \( 3k \) ve \( 5k \) diyelim.
Sayıların karelerinin toplamı 15200'dür.
\( (2k)^2 + (3k)^2 + (5k)^2 = 15200 \)
\( 4k^2 + 9k^2 + 25k^2 = 15200 \)
\( 38k^2 = 15200 \)
\( k^2 = 400 \)
Sayılar doğal sayı olduğu için \( k = 20 \) olur.
Buna göre sayıların en küçüğü \( 2k = 40 \) olarak bulunur.
\( \dfrac{a}{b} = \dfrac{c}{d} = \dfrac{e}{f} = k \) olduğuna göre,
\( \dfrac{a^2 \cdot d \cdot f^3}{b^2 \cdot c \cdot e^3} \) ifadesi \( k \) cinsinden kaçtır?
Çözümü Gösterİfadeyi düzenleyelim.
\( \dfrac{a^2 \cdot d \cdot f^3}{b^2 \cdot c \cdot e^3} = \dfrac{a^2}{b^2} \cdot \dfrac{d}{c} \cdot \dfrac{f^3}{e^3} \)
\( = {\left( \dfrac{a}{b} \right)}^2 \cdot \dfrac{d}{c} \cdot {\left( \dfrac{f}{e} \right)}^3 \)
Verilen orantıdaki oranları yerine koyalım.
\( = k^2 \cdot \dfrac{1}{k} \cdot {\left( \dfrac{1}{k} \right)}^3 \)
\( = \dfrac{k^2}{k \cdot k^3} \)
\( = \dfrac{1}{k^2} \) bulunur.
\( a, b, c \in \mathbb{Z^-} \) olmak üzere,
\( \dfrac{a}{b} = \dfrac{3}{7} \) ve \( \dfrac{b}{c} = \dfrac{2}{9} \)
olduğuna göre, \( a, b, c \) sayılarını küçükten büyüğe doğru sıralayın.
Çözümü GösterSoruda aşağıdaki oranlar veriliyor.
\( a:b = 3:7, \quad b:c = 2:9 \)
Birinci oranı 2 ile, ikinci oranı 7 ile genişleterek \( b \)'nin iki orandaki katsayısını eşitleyelim.
\( a:b = 6:14, \quad b:c = 14:63 \)
\( b \) katsayısı iki oranda eşit olduğu için iki oranı tek bir oran şeklinde yazabiliriz.
\( a:b:c = 6:14:63 \)
Buna göre \( a, b, c \) sayılarına sırasıyla \( 6k, 14k, 63k \) diyebiliriz.
Sayılar negatif olduğu için katsayısı daha küçük olan sayı daha büyük olur.
Buna göre sayıların sıralaması aşağıdaki gibi olur.
\( c \lt b \lt a \)
\( x, y, z, t \) birer rakam olmak üzere,
\( \dfrac{x}{4} = \dfrac{y}{2} = \dfrac{z}{3} = t \)
olduğuna göre, \( x + y + z + t \) ifadesinin değeri en fazla kaçtır?
Çözümü Göster\( x, y, z \) birer rakam olacak şekilde \( t \)'nin alabileceği en büyük değer 2'dir.
\( t = 2 \)
\( \dfrac{x}{4} = \dfrac{y}{2} = \dfrac{z}{3} = 2 \)
Orantı sabitini kullanarak değişkenlerin değerlerini bulalım.
\( x = 4 \cdot 2 = 8 \)
\( y = 2 \cdot 2 = 4 \)
\( z = 3 \cdot 2 = 6 \)
Bulduğumuz değerlerin toplamını alalım.
\( x + y + z + t = 8 + 4 + 6 + 2 \)
\( = 20 \) bulunur.
\( (a + b) : (b + c) : (a + c) = 5 : 9 : 13 \)
\( a + b + c = 15 \)
olduğuna göre, \( a \) kaçtır?
Çözümü Göster\( \dfrac{a + b}{5} = \dfrac{b + c}{9} = \dfrac{a + c}{13} = k \)
Paylardaki ifadeleri orantı sabiti cinsinden yazalım.
\( a + b = 5k \)
\( b + c = 9k \)
\( a + c = 13k \)
Eşitlikleri taraf tarafa toplayalım.
\( 2a + 2b + 2c = 5k + 9k + 13k \)
\( 2(a + b + c) = 27k \)
\( 2 \cdot 15 = 27k \)
\( k = \dfrac{10}{9} \)
\( b + c \) toplamını bulalım.
\( b + c = 9k = 10 \)
\( b + c \) toplamını \( a + b + c = 15 \) eşitliğinde yerine koyalım.
\( a = 5 \) bulunur.
\( A : B = \frac{3}{23} : \frac{1}{4} \) ve \( B : C = \frac{1}{3} : \frac{1}{2} \) oranları veriliyor.
Buna göre \( \dfrac{C - A}{A + B} \) oranı kaçtır?
Çözümü Göster\( A \) ve \( B \) sayıları arasındaki oranı sadeleştirelim.
\( \dfrac{A}{B} = \dfrac{3}{23} : \dfrac{1}{4} \)
\( = \dfrac{\frac{3}{23}}{\frac{1}{4}} = \dfrac{12}{23} \)
\( B \) ve \( C \) sayıları arasındaki oranı sadeleştirelim.
\( \dfrac{B}{C} = \dfrac{1}{3} : \dfrac{1}{2} \)
\( = \dfrac{\frac{1}{3}}{\frac{1}{2}} = \dfrac{2}{3} \)
İki orandaki \( B \) katsayılarını eşitlemek için birinci oranı \( 2k \) ile, ikinci oranı \( 23k \) ile genişletelim.
\( \dfrac{A}{B} = \dfrac{12}{23} = \dfrac{24k}{46k} \)
\( \dfrac{B}{C} = \dfrac{2}{3} = \dfrac{46k}{69k} \)
\( A \), \( B \) ve \( C \) sayılarının birbirine oranını aşağıdaki şekilde yazabiliriz.
\( A : B : C = 24k : 46k : 69k \)
Buna göre \( A, B, C \) sayılarına sırasıyla \( 24k, 46k, 69k \) diyebiliriz.
Bu değerleri verilen ifadede yerine koyalım.
\( \dfrac{C - A}{A + B} = \dfrac{69k - 24k}{24k + 46k} \)
\( = \dfrac{45k}{70k} = \dfrac{9}{14} \) bulunur.
\( A : B : C = 3 : 5 : 6 \) olduğuna göre,
\( \dfrac{A}{B} : \dfrac{B}{C} : \dfrac{C}{A} \) oranı kaçtır?
Çözümü Göster\( A : B : C = 3 : 5 : 6 \) olduğuna göre sayılara aşağıdaki değerleri verebiliriz.
\( A = 3k, \quad B = 5k, \quad C = 6k \)
\( \dfrac{A}{B} = \dfrac{3k}{5k} = \dfrac{3}{5} \)
\( \dfrac{B}{C} = \dfrac{5k}{6k} = \dfrac{5}{6} \)
\( \dfrac{C}{A} = \dfrac{6k}{3k} = \dfrac{6}{3} \)
\( \dfrac{A}{B} : \dfrac{B}{C} : \dfrac{C}{A} = \dfrac{3}{5} : \dfrac{5}{6} : \dfrac{6}{3} \)
Sayıları paydaların EKOK'u ile çarpalım.
\( EKOK(5, 6, 3) = 30 \)
\( = \dfrac{3 \cdot 30}{5} : \dfrac{5 \cdot 30}{6} : \dfrac{6 \cdot 30}{3} \)
\( = 18 : 25 : 60 \) bulunur.
\( \dfrac{a}{b} = \dfrac{c}{d} = \dfrac{e}{f} = \dfrac{7}{8} \) olduğuna göre,
\( (\dfrac{4a + 2b}{b})(\dfrac{16c - 7d}{c})(\dfrac{4e - 3f}{f}) \) işleminin sonucu kaçtır?
Çözümü GösterDeğeri istenen ifadeyi düzenleyelim.
\( (\dfrac{4a + 2b}{b})(\dfrac{16c - 7d}{c})(\dfrac{4e - 3f}{f}) \)
\( = (\dfrac{4a}{b} + \dfrac{2b}{b})(\dfrac{16c}{c} - \dfrac{7d}{c})(\dfrac{4e}{f} - \dfrac{3f}{f}) \)
\( = (4 \cdot \dfrac{a}{b} + 2)(16 - 7 \cdot \dfrac{d}{c})(4 \cdot \dfrac{e}{f} - 3) \)
Verilen oranları yerine koyalım.
\( = (4 \cdot \dfrac{7}{8} + 2)(16 - 7 \cdot \dfrac{8}{7})(4 \cdot \dfrac{7}{8} -3) \)
\( = (\dfrac{7}{2} + 2)(16 - 8)(\dfrac{7}{2} - 3) \)
\( = \dfrac{11}{2} \cdot 8 \cdot \dfrac{1}{2} \)
\( = 22 \) bulunur.
172 sayısı \( \frac{1}{2} : \frac{2}{7} : \frac {3}{4} \) sayılarıyla orantılı olacak şekilde üç sayıya ayrılıyor.
Ortadaki sayı kaçtır?
Çözümü GösterOranları paydaların EKOK'u ile genişleterek paydalardan kurtulalım.
\( EKOK(2, 7, 4) = 28 \)
\( \dfrac{1 \cdot 28}{2} : \dfrac{2 \cdot 28}{7} : \dfrac {3 \cdot 28}{4} \)
\( = 14 : 8 : 21 \)
Buna göre sayılara sırasıyla \( 14k \), \( 8k \) ve \( 21k \) diyebiliriz.
Sayıların toplamı 172'dir.
\( 14k + 8k + 21k = 172 \)
\( 43k = 172 \)
\( k = 4 \)
Ortadaki sayı \( 8k = 32 \) olarak bulunur.
Üç arkadaş bir miktar bilyeyi sırasıyla \( \frac{2}{3} : \frac{1}{4} : \frac{5}{6} \) sayılarıyla orantılı olacak şekilde paylaşacaktır.
İkinci kişi 6 bilye aldığına göre toplam kaç bilye vardır?
Çözümü GösterOranları paydaların EKOK'uyla genişleterek paydalardan kurtulalım.
\( EKOK(3, 4, 6) = 12 \)
\( \dfrac{2 \cdot 12}{3} : \dfrac{1 \cdot 12}{4} : \dfrac{5 \cdot 12}{6} \)
\( = 8 : 3 : 10 \)
Buna göre arkadaşların aldıkları bilye sayılarına sırasıyla \( 8k \), \( 3k \) ve \( 10k \) diyebiliriz.
İkinci arkadaş 6 bilye almıştır.
\( 3k = 6 \)
\( k = 2 \)
Toplam \( 8k + 3k + 10k = 21k \) bilye vardır.
Buna göre toplam bilye sayısı \( 21k = 42 \) olarak bulunur.
\( \dfrac{4b + 2c}{a + 4} = -\dfrac{b - c}{c + 6} = \dfrac{3a + 9}{b - 7} \)
olduğuna göre, \( b + 2c \) toplamı kaçtır?
Çözümü GösterBir orantıda oranların paylarının kendi aralarında, paydalarının da kendi aralarında toplamı ya da farkı alınırsa orantı sabiti değişmez.
\( \dfrac{4b + 2c}{a + 4} = \dfrac{-(b - c)}{c + 6} = \dfrac{3a + 9}{b - 7} = k \)
\( \dfrac{4b + 2c + (-b + c) + 3a + 9}{(a + 4) + (c + 6) + (b - 7)} = k \)
\( \dfrac{3a + 3b + 3c + 9}{a + b + c + 3} = k \)
\( \dfrac{3(a + b + c + 3)}{a + b + c + 3} = k \)
\( k = 3 \)
Orantıdaki ikinci oranı bu orantı sabitine eşitleyelim.
\( -\dfrac{b - c}{c + 6} = 3 \)
\( c - b = 3c + 18 \)
\( b + 2c = -18 \) bulunur.
\( x + y + z = 0 \) olduğuna göre,
\( \dfrac{x + y}{z} + \dfrac{y + z}{x} + \dfrac{x + z}{y} \) ifadesinin değeri kaçtır?
Çözümü GösterVerilen eşitliği aşağıdaki üç şekilde düzenleyebiliriz.
\( x + y + z = 0 \)
\( x + y = -z \)
\( y + z = -x \)
\( x + z = -y \)
Bu değerleri verilen ifadede payın yerine koyalım.
\( \dfrac{x + y}{z} + \dfrac{y + z}{x} + \dfrac{x + z}{y} \)
\( = \dfrac{-z}{z} + \dfrac{-x}{x} + \dfrac{-y}{y} \)
\( = (-1) + (-1) + (-1) = -3 \) bulunur.
\( \dfrac{x}{y} = \dfrac{8}{5} \) ve \( \dfrac{y}{z} = \dfrac{15}{8} \) oranları veriliyor.
Buna göre \( x \) sayısı \( z \) sayısının yüzde kaçıdır?
Çözümü Göster\( x : y = 8 : 5 = 24 : 15 \)
\( y : z = 15 : 8 \)
\( y \) katsayıları iki oranda eşit olduğu için üç değişken arasındaki oranı aşağıdaki şekilde yazabiliriz.
\( x : y : z = 24 : 15 : 8 \)
Üç değişkeni bir \( k \) orantı sabiti cinsinden yazalım.
\( x = 24k, \quad y = 15k, \quad z = 8k \)
\( x \) sayısı \( z \) sayısının yüzde \( p \)'si olsun.
\( x = z \cdot \dfrac{p}{100} \)
\( 24k = 8k \cdot \dfrac{p}{100} \)
\( p = \dfrac{2400}{8} = 300 \)
\( x \) sayısı \( z \) sayısının \( \% 300 \)'üdür.
\( x, y, z \in \mathbb{Z^+} \) olmak üzere,
\( \dfrac{xy}{4} = \dfrac{yz}{12} = \dfrac{xz}{15} \)
olduğuna göre, \( x, y, z \) sayılarını küçükten büyüğe doğru sıralayınız.
Çözümü GösterEşitliğin taraflarının paylarını eşitleyelim.
\( \dfrac{xyz}{4z} = \dfrac{xyz}{12x} = \dfrac{xyz}{15y} \)
Paylar eşit olduğu için paydalar da eşit olmalıdır.
\( 4z = 12x = 15y \)
Eşitlikteki katsayıların EKOK'unu bulalım.
\( EKOK(4, 12, 15) = 60 \)
\( k \in \mathbb{Z^+} \) olmak üzere,
\( 4z = 12x = 15y = 60k \)
Değişkenleri \( k \) cinsinden yazalım.
\( x = 5k, \quad y = 4k, \quad z = 15k \)
\( x, y, z \) sayılarının küçükten büyüğe doğru sıralanışı aşağıdaki gibi olur.
\( y \lt x \lt z \)
\( \dfrac{a}{3} = \dfrac{b}{5} = \dfrac{2}{c} \) olduğuna göre,
\( \sqrt{c(a + b)} \) ifadesinin değeri kaçtır?
Çözümü GösterVerilen orantıyı bir orantı sabitine eşitleyelim.
\( \dfrac{a}{3} = \dfrac{b}{5} = \dfrac{2}{c} = k \)
Değişkenleri \( k \) cinsinden yazalım.
\( a = 3k, \quad b = 5k, \quad c = \dfrac{2}{k} \)
Bu değerleri verilen ifadede yerine koyalım.
\( \sqrt{c(a + b)} = \sqrt{\frac{2}{k} \cdot (3k + 5k)} \)
\( = \sqrt{\frac{2}{k} \cdot 8k} \)
\( = \sqrt{16} = 4 \) bulunur.
\( \dfrac{a}{b} = \dfrac{c}{d} = \dfrac{3}{4} \) olduğuna göre,
\( \dfrac{3a + 4c}{3b + 4d} \cdot \dfrac{a - c}{b - d} \) ifadesinin değeri kaçtır?
Çözümü GösterBir orantıda oranların paylarının kendi aralarında, paydalarının da kendi aralarında toplamı ya da farkı alınırsa orantı sabiti değişmez.
Bir orantıdaki oranlar sabit sayılarla genişletildiğinde orantı sabiti değişmez.
\( \dfrac{a}{b} = \dfrac{c}{d} = \dfrac{3}{4} \)
\( \dfrac{a}{b} = \dfrac{-c}{-d} = \dfrac{3}{4} \)
\( \dfrac{a - c}{b - d} = \dfrac{3}{4} \)
\( \dfrac{3a}{3b} = \dfrac{4c}{4d} = \dfrac{3}{4} \)
\( \dfrac{3a + 4c}{3b + 4d} = \dfrac{3}{4} \)
Bu değerleri istenen ifadede yerine koyalım.
\( \dfrac{3a + 4c}{3b + 4d} \cdot \dfrac{a - c}{b - d} = \dfrac{3}{4} \cdot \dfrac{3}{4} \)
\( = \dfrac{9}{16} \) bulunur.
\( \dfrac{4}{xy} = \dfrac{7}{yz} = \dfrac{10}{xz} \) olduğuna göre,
\( \dfrac{14x + 5y}{8z} \) ifadesinin değeri nedir?
Çözümü GösterBirinci ve ikinci oranlar arasındaki eşitliği kullanarak \( x \) ifadesini \( z \) cinsinden yazalım.
\( \dfrac{4}{xy} = \dfrac{7}{yz} \)
\( 4yz = 7xy \)
\( x = \dfrac{4z}{7} \)
Birinci ve üçüncü oranlar arasındaki eşitliği kullanarak \( y \) ifadesini \( z \) cinsinden yazalım.
\( \dfrac{4}{xy} = \dfrac{10}{xz} \)
\( 4xz = 10xy \)
\( y = \dfrac{2z}{5} \)
Bu değerleri verilen ifadede yerine koyalım.
\( \dfrac{14x + 5y}{8z} = \dfrac{14(\frac{4z}{7}) + 5(\frac{2z}{5})}{8z} \)
\( = \dfrac{8z + 2z}{8z} = \dfrac{10z}{8z} \)
\( = \dfrac{5}{4} \) bulunur.
\( \dfrac{ab}{6} = \dfrac{bc}{9} = \dfrac{ac}{8} \)
olduğuna göre, \( a, b, c \) sırasıyla hangi sayılarla orantılıdır?
Çözümü GösterVerilen eşitliğin taraflarını \( abc \) ile bölelim.
\( \dfrac{ab}{6abc} = \dfrac{bc}{9abc} = \dfrac{ac}{8abc} \)
\( \dfrac{1}{6c} = \dfrac{1}{9a} = \dfrac{1}{8b} \)
Eşitliğin taraflarının çarpmaya göre tersini alalım.
\( 9a = 8b = 6c \)
Eşitliğin taraflarını katsayıların EKOK'una bölelim.
\( EKOK(9, 8, 6) = 72 \)
\( \dfrac{9a}{72} = \dfrac{8b}{72} = \dfrac{6c}{72} \)
\( \dfrac{a}{8} = \dfrac{b}{9} = \dfrac{c}{12} \)
Buna göre \( a, b, c \) sırasıyla 8, 9 ve 12 ile orantılıdır.
\( a : b : c = 8 : 9 : 12 \)
İki basamaklı \( (ab), (bc), (cb) \) sayıları sırasıyla 2, 4 ve 7 ile orantılıdır.
\( (bc) + (cb) = 132 \) olduğuna göre, \( a + b + c \) kaçtır?
Çözümü Göster\( (ab), (bc), (cb) \) sayıları arasındaki orantıyı bir orantı sabitine eşitleyelim.
\( \dfrac{(ab)}{2} = \dfrac{(bc)}{4} = \dfrac{(cb)}{7} = k \)
Verilen iki basamaklı sayıları orantı sabiti cinsinden yazalım.
\( (ab) = 2k, \quad (bc) = 4k, \quad (cb) = 7k \)
Bu değerleri verilen eşitlikte yerine yazalım.
\( (bc) + (cb) = 132 \)
\( 4k + 7k = 132 \)
\( 11k = 132 \)
\( k = 12 \)
Orantı sabitini kullanarak iki basamaklı sayıları bulalım.
\( (ab) = 2k = 24 \)
\( (bc) = 4k = 48 \)
\( (cb) = 7k = 84 \)
\( a = 2, \quad b = 4, \quad c = 8 \)
\( a + b + c = 2 + 4 + 8 = 14 \) bulunur.
Bir köyün haritası üzerinde belirlenen iki nokta arasındaki uzaklık 12 cm olarak ölçülüyor. Bu noktalar arasındaki gerçek uzaklık ise 2,7 km'dir.
Bu harita üzerinde seçilen farklı iki nokta arasındaki uzaklık 4,6 cm ise bu noktalar arasındaki gerçek uzaklık kaç km'dir?
Çözümü GösterBulmak istediğimiz uzaklığa \( x \) km diyelim.
Herhangi iki nokta için harita üzerinde ölçülen ve gerçek uzaklıkların oranı sabittir ve haritanın ölçeğine eşittir.
\( \dfrac{12}{2,7} = \dfrac{4,6}{x} \)
İçler - dışlar çarpımı yapalım.
\( 12x = 2,7 \cdot 4,6 \)
\( 12x = \dfrac{27}{10} \cdot \dfrac{46}{10} \)
\( x = \dfrac{207}{200} = 1,035 \) km bulunur.
Bir torbadaki siyah, mavi ve beyaz renkteki bilyelerin sayıları sırayla \( \frac{1}{3} \), \( \frac{2}{5} \) ve \( \frac{1}{2} \) sayılarıyla orantılıdır.
Buna göre, bu torbadaki bilyelerin sayısı en az kaç olabilir?
Çözümü GösterSiyah, mavi ve beyaz renkteki bilyelerin sayılarına sırasıyla \( s \), \( m \) ve \( b \) diyelim.
\( s : m : b = \dfrac{1}{3} : \dfrac{2}{5} : \dfrac{1}{2} \)
Orandaki paydalardan kurtulmak için oranları paydaların EKOK'u ile genişletelim.
\( EKOK(3, 5, 2) = 30 \)
\( s : m : b = \dfrac{1 \cdot 30}{3} : \dfrac{2 \cdot 30}{5} : \dfrac{1 \cdot 30}{2} \)
\( s : m : b = 10 : 12 : 15 \)
Buna göre bilyelerin sayısına sırasıyla \( 10k \), \( 12k \) ve \( 15k \) diyebiliriz.
Bu durumda toplam bilye sayısı \( 10k + 12k + 15k = 37k \) olur.
\( k = 1 \) verirsek bilyelerin sayısı en az 37 olur.
\( \dfrac{a}{b} = \dfrac{c}{d} = \dfrac{e}{f} = \dfrac{5}{3} \)
\( 4a + 8c + 10e = 16 \)
\( 10b + 20d = 5 \)
olduğuna göre, \( f \) kaçtır?
Çözümü Göster\( \dfrac{a}{b} = \dfrac{c}{d} = \dfrac{e}{f} = \dfrac{5}{3} \)
Orantının tüm taraflarını \( \frac{2}{5} \) ile çarpalım.
\( \dfrac{2a}{5b} = \dfrac{2c}{5d} = \dfrac{2e}{5f} = \dfrac{5}{3} \cdot \dfrac{2}{5} \)
Bir orantıdaki oranlar sabit sayılarla genişletildiğinde orantı sabiti değişmez.
Birinci oranı 2 ile, ikinci oranı 4 ile, üçüncü oranı 5 ile genişletelim.
\( \dfrac{4a}{10b} = \dfrac{8c}{20d} = \dfrac{10e}{25f} = \dfrac{2}{3} \)
Bir orantıda oranların paylarının kendi aralarında, paydalarının da kendi aralarında toplamı alınırsa orantı sabiti değişmez.
\( \dfrac{4a + 8c + 10e}{10b + 20d + 25f} = \dfrac{2}{3} \)
Soruda verilen değerleri yerine koyalım.
\( \dfrac{16}{5 + 25f} = \dfrac{2}{3} \)
İçler - dışlar çarpımı yapalım.
\( 16 \cdot 3 = 10 + 50f \)
\( 50f = 38 \)
\( f = \dfrac{19}{25} \) bulunur.
\( \dfrac{x}{y} = \dfrac{a}{b} \)
\( x^2 - y^2 = 9 \)
\( a^2 - b^2 = 144 \)
olduğuna göre, \( \dfrac{y}{b + y} \) ifadesinin alabileceği kaç farklı değer vardır?
Çözümü GösterVerilen orantıyı bir orantı sabitine eşitleyelim.
\( \dfrac{x}{y} = \dfrac{a}{b}= k \)
Değişkenleri orantı sabiti cinsinden yazalım.
\( x = yk, \quad a = bk \)
Verilen ikinci eşitlikte \( x = yk \) yazalım.
\( x^2 - y^2 = 9 \)
\( (yk)^2 - y^2 = 9 \)
\( y^2k^2 - y^2 = 9 \)
\( y^2(k^2 - 1) = 9 \)
\( k^2 - 1 = \dfrac{9}{y^2} \)
Verilen üçüncü eşitlikte \( a = bk \) yazalım.
\( a^2 - b^2 = 144 \)
\( (bk)^2 - b^2 = 144 \)
\( b^2k^2 - b^2 = 144 \)
\( b^2(k^2 - 1) = 144 \)
\( k^2 - 1 = \dfrac{144}{b^2} \)
\( k^2 - 1 \) için bulduğumuz iki ifadeyi birbirine eşitleyebiliriz.
\( \dfrac{9}{y^2} = \dfrac{144}{b^2} \)
\( b^2 = 16y^2 \)
\( b = \pm 4y \)
\( b \)'nin alabileceği iki değer için \( \frac{y}{b + y} \) ifadesinin değerini bulalım.
Durum 1: \( b = 4y \)
\( \dfrac{y}{b + y} = \dfrac{y}{4y + y} = \dfrac{1}{5} \)
Durum 2: \( b = -4y \)
\( \dfrac{y}{b + y} = \dfrac{y}{-4y + y} = -\dfrac{1}{3} \)
İfadenin alabileceği iki farklı değer vardır.
\( \dfrac{x^2 - 2x}{2x - y} = \dfrac{y^2 - 1}{x + 1} = 25 \)
olduğuna göre, \( x + y \) toplamı kaçtır?
Çözümü GösterBir orantıda oranların paylarının kendi aralarında, paydalarının da kendi aralarında toplamı ya da farkı alınırsa orantı sabiti değişmez.
\( \dfrac{x^2 - 2x}{2x - y} = \dfrac{y^2 - 1}{x + 1} = 25 \)
\( \dfrac{x^2 - 2x - (y^2 - 1)}{2x - y - (x + 1)} = 25 \)
\( \dfrac{x^2 - 2x + 1 - y^2}{x - y - 1} = 25 \)
\( \dfrac{(x - 1)^2 - y^2}{x - y - 1} = 25 \)
\( \dfrac{(x - 1 - y)(x - 1 + y)}{x - y - 1} = 25 \)
\( x - 1 + y = 25 \)
\( x + y = 26 \) bulunur.
Bir sınıf başkanlığı seçiminde oy kullananların %22'si Sude'ye, %13'ü Mehmet'e, %16'sı Ahmet'e, %26'sı Ela'ya, %3'ü de Elif'e oy vermiştir. Sınıftaki öğrencilerin geri kalanı ise kararsız oldukları için oy kullanmamıştır.
Kararsız öğrencilerin oyları başkan adayları arasında aldıkları oy oranında dağıtılacaktır. Bu dağıtım işlemi sonrasında Ahmet'in oy oranı yüzde kaç olur?
Çözümü GösterSınıftaki öğrenci sayısına işlem kolaylığı açısından \( 100x \) diyelim.
O halde Sude \( 22x \), Mehmet \( 13x \), Ahmet \( 16x \), Ela \( 26x \) ve Elif \( 3x \) oy almıştır.
\( 22x + 13x + 16x + 26x + 3x = 80x \)
Buna göre \( 100x - 80x = 20x \) öğrenci oy kullanılmamıştır.
Ahmet kullanılan \( 80x \) oydan \( 16x \) oy aldığına göre, \( 20x \) oydan kaç oy alacağını bulmak için bir orantı kuralım.
\( 20x \) oydan Ahmet'e dağılacak oy sayısına \( a \) diyelim.
\( \dfrac{16x}{80x} = \dfrac{a}{20x} \)
\( 16x \cdot 20x = 80x \cdot a \)
\( a = 4x \)
O halde Ahmet'in \( 16x \) olan oy sayısına \( 4x \) oy daha eklenir.
Dağıtım sonrası Ahmet'in oy oranı \( \frac{16x + 4x}{100x} = \% 20 \) olarak bulunur.
Bir miktar cevizin yarısını Ahmet, Mehmet ve Ceren sırasıyla 4, 5 ve 6 ile orantılı olacak şekilde, diğer yarısını Sude, Zeynep ve Ali sırasıyla 7, 8 ve 9 ile orantılı olacak şekilde paylaşıyorlar.
Bu 6 kişiden eşit miktarda ceviz alan iki kişinin toplam ceviz sayısı 480 olduğuna göre, Ceren ve Sude'nin cevizleri toplamı kaçtır?
Çözümü GösterToplam ceviz sayısına \( 2x \) diyelim.
Toplam cevizlerin yarısı olan \( x \) cevizi verilen doğru orantıya göre paylaştıralım.
Ahmet, Mehmet ve Ceren'in ceviz sayısına sırasıyla \( a, b, c \) diyelim.
Ahmet, Mehmet ve Ceren \( x \) cevizi 4, 5 ve 6 ile orantılı olacak şekilde paylaşıyorlar.
Ahmet, Mehmet ve Ceren'in ceviz sayılarının bir \( k \) orantı sabiti cinsinden aşağıdaki şekilde ifade edebiliriz.
\( a = 4k, \quad b = 5k, \quad c = 6k \)
Bu cevizlerin toplamını cevizlerin yarısı olan \( x \) sayısına eşitleyelim.
\( 4k + 5k + 6k = x \)
\( 15k = x \)
Toplam cevizlerin diğer yarısı olan \( x \) cevizi verilen doğru orantıya göre paylaştıralım.
Sude, Zeynep ve Ali'nin ceviz sayısına sırasıyla \( d, e, f \) diyelim.
Sude, Zeynep ve Ali \( x \) cevizi 7, 8 ve 9 ile orantılı olacak şekilde paylaşıyorlar.
Sude, Zeynep ve Ali'in ceviz sayılarının bir \( t \) orantı sabiti cinsinden aşağıdaki şekilde ifade edebiliriz.
\( d = 7t, \quad e = 8t, \quad f = 9t \)
Bu cevizlerin toplamını cevizlerin yarısı olan \( x \) sayısına eşitleyelim.
\( 7t + 8t + 9t = x \)
\( 24t = x \)
Her iki arkadaş grubuna paylaştırılan cevizlerin toplamı eşittir.
\( x = 15k = 24t \)
\( t \) sabitini \( k \) cinsinden yazalım.
\( t = \dfrac{15k}{24} = \dfrac{5k}{8} \)
Sude, Zeynep ve Ali'nin \( t \) cinsinden ceviz sayılarını \( k \) cinsinden yazalım.
\( d = 7t, \quad e = 8t, \quad f = 9t \)
\( d = 7(\frac{5k}{8}), \quad e = 8(\frac{5k}{8}), \quad f = 9(\frac{5k}{8}) \)
\( d = \dfrac{35k}{8}, \quad e = 5k, \quad f = \dfrac{45k}{8} \)
Zeynep'in ve Mehmet'in cevizleri \( 5k \) olacak şekilde birbirlerine eşit ve toplamları 480'dir.
\( 5k + 5k = 480 \)
\( k = 48 \)
Ceren'in cevizlerinin sayısını bulalım.
\( c = 6k \)
\( = 6 \cdot 48 = 288 \)
Sude'nin cevizlerinin sayısını bulalım.
\( d = \dfrac{35k}{8} \)
\( = \dfrac{35 \cdot 48}{8} = 210 \)
Ceren ve Sude'nin toplam ceviz sayısı \( 288 + 210 = 498 \) olarak bulunur.
Ali, Berke ve Can'ın paraları 2, 3 ve 4 sayıları ile orantılıdır.
Ali, Berke'ye, Berke Can'a, Can da Ali'ye başlangıçta sahip oldukları paranın \( \frac{1}{3} \)'ünü veriyor. Buna göre son durumda paralarının oranı kaç olur?
Çözümü GösterAli, Berke ve Can'ın paralarına sırasıyla \( a \), \( b \), \( c \) diyelim.
Üçte bir oranında dağıtım hesaplamasında kolaylık sağlaması açısından orantı sabitine 3'ün bir katı olarak \( 6k \) diyelim.
\( \dfrac{a}{2} = \dfrac{b}{3} = \dfrac{c}{4} = 6k \)
\( a = 12k, \quad b = 18k, \quad c = 24k \)
Herkesin verdiği tutarları hesaplayalım.
Ali Berke'ye \( 12k \cdot \frac{1}{3} = 4k \) verir.
Berke Can'a \( 18k \cdot \frac{1}{3} = 6k \) verir.
Can Ali'ye \( 24k \cdot \frac{1}{3} = 8k \) verir.
Herkesin paraları son durumda aşağıdaki gibi olur.
\( a = 12k - 4k + 8k = 16k \)
\( b = 18k - 6k + 4k = 16k \)
\( c = 24k - 8k + 6k = 22k \)
Son durumdaki paralarının oranını sadeleştirilmiş şekliyle yazabilmek için tutarları EBOB'larına bölelim.
\( EBOB(a, b, c) = (16, 16, 22) = 2 \)
Buna göre son durumdaki paralarının oranı \( 8 : 8 : 11 \) olur.
\( a : b : c = 8 : 8 : 11 \)
3810 cm'lik bir kumaş farklı uzunluklarda üç parçaya ayrılıyor. A parçasının uzunluğunun B parçasının uzunluğuna oranı \( \frac{8}{5} \), B parçasının uzunluğunun C parçasının uzunluğuna oranı \( \frac{13}{17} \)'dir.
Buna göre en uzun parça kaç cm'dir?
Çözümü GösterParçaların uzunluklarına sırasıyla \( a, b, c \) diyelim.
A parçasının uzunluğunun B parçasının uzunluğuna oranı \( \frac{8}{5} \)'tir.
\( a : b = 8 : 5 \)
B parçasının uzunluğunun C parçasının uzunluğuna oranı \( \frac{13}{17} \)'tir.
\( b : c = 13 : 17 \)
İki orandaki \( b \) katsayısını eşitlemek için birinci oranı 13 ile, ikinci oranı 5 ile genişletelim.
\( a : b = 104 : 65 \)
\( b : c = 65 : 85 \)
\( b \) katsayısı iki oranda eşit olduğu için iki oranı tek oranda birleştirebiliriz.
\( a : b : c = 104 : 65 : 85 \)
Buna göre A, B, C parçalarının uzunluklarına sırasıyla \( 104k \), \( 65k \) ve \( 85k \) diyebiliriz.
Üç parçanın uzunlukları toplamı 3810 cm'dir.
\( 104k + 65k + 85k = 3810 \)
\( 254k = 3810 \)
\( k = 15 \)
A parçasının uzunluğunu bulalım.
\( a = 104k = 104 \cdot 15 = 1560 \) cm bulunur.
Bir manavdaki elma, armut ve muzun kilogram fiyatları arasındaki oran 2020 yılında \( 3:7:8 \), 2023 yılında \( 2:6:7 \)'dir.
Bu yıllar arasında muzun kilogram fiyatı %75 arttığına göre, elmanın kilogram fiyatı yüzde kaç artmıştır?
Çözümü Göster2020 yılında elma, armut ve muzun kilogram fiyatlarına sırasıyla \( 3a, 7a, 8a \) diyelim.
2023 yılında elma, armut ve muzun kilogram fiyatlarına sırasıyla \( 2b, 6b, 7b \) diyelim.
Bu yıllar arasında muzun kilogram fiyatı \( \%75 \) artmıştır.
\( 8a + 8a \cdot \dfrac{75}{100} = 7b \)
\( 14a = 7b \)
\( 2a = b \)
2023 yılında elmanın kilogram fiyatını \( a \) cinsinden yazalım.
\( 2b = 2 \cdot 2a = 4a \)
Bu yıllar arasında elmanın kilogram fiyatının yüzde kaç arttığını bulalım.
\( \dfrac{4a - 3a}{3a} = \dfrac{1}{3} = \%33,3 \) artmıştır.
Bir mağazada küçük, orta ve büyük bedenlerde t-shirt ve gömlek satılmaktadır.
Mağazadaki küçük, orta, büyük beden t-shirtlerin sayıları arasındaki oran sırasıyla \( 8:19:5 \)'tir.
Mağazadaki küçük, orta, büyük beden gömleklerin sayıları arasındaki oran sırasıyla \( 4:5:7 \)'dir.
Bu mağazadaki toplam t-shirt sayısı toplam gömlek sayısının 4 katıdır.
Buna göre, orta beden t-shirt sayısının büyük beden gömlek sayısına oranı kaçtır?
Çözümü GösterT-shirt bedenleri arasındaki orana göre her bedendeki t-shirt sayısına sırasıyla \( 8x \), \( 19x \) ve \( 5x \) diyebiliriz.
Gömlek bedenleri arasındaki orana göre her bedendeki gömlek sayısına sırasıyla \( 4y \), \( 5y \) ve \( 7y \) diyebiliriz.
Toplam t-shirt sayısı: \( 8x + 19x + 5x = 32x \)
Toplam gömlek sayısı: \( 4y + 5y + 7y = 16y \)
Toplam t-shirt sayısı toplam gömlek sayısının 4 katıdır.
\( 32x = 4 \cdot 16y \)
\( x = 2y \)
Orta beden t-shirt sayısının büyük beden gömlek sayısına oranını bulalım.
\( \dfrac{19x}{7y} = \dfrac{19 \cdot 2y}{7y} \)
\( = \dfrac{38}{7} \) bulunur.
Bir konserin biletleri 5 gün boyunca satılıyor.
İlk üç günde satılan bilet sayıları arasındaki oran sırasıyla \( 4:11:12 \)'dir.
Son iki günde satılan bilet sayıları arasındaki oran sırasıyla \( 14:13 \)'tür.
1., 3. ve 4. günde satılan bilet sayıları arasındaki oran ise sırasıyla \( 3:9:7 \)'dir.
5 gün boyunca toplam 270 bilet satıldığına göre, en az bilet satılan gün kaç bilet satılmıştır?
Çözümü GösterHer günde sayılan bilet sayılarına sırasıyla \( a, b, c, d, e \) diyelim.
\( a:b:c = 4:11:12 \)
\( d:e = 14:13 \)
\( a:c:d = 3:9:7 \)
Aynı değişkenlerin oranlardaki katsayılarını eşitlemek için \( a:b:c \) oranını 3 ile, \( a:c:d \) oranını 4 ile genişletelim.
\( a:b:c = 12:33:36 \)
\( a:c:d = 12:36:28 \)
\( a \) ve \( c \) katsayıları iki oranda eşitlendiği için \( a:b:c \) ve \( a:c:d \) oranını tek bir oranda birleştirebiliriz.
\( a:b:c:d = 12:33:36:28 \)
\( d:e \) oranını 2 ile genişletelim.
\( d:e = 28:26 \)
\( d \) katsayısı iki oranda eşitlendiği için \( a:b:c:d \) ve \( d:e \) oranlarını tek bir oranda birleştirebiliriz.
\( a:b:c:d:e = 12:33:36:28:26 \)
Bu orana göre her gün satılan bilet sayılarına sırasıyla \( 12k \), \( 33k \), \( 36k \), \( 28k \) ve \( 26k \) diyebiliriz.
\( 12k + 33k + 36k + 28k + 26k = 270 \)
\( 135k = 270 \)
\( k = 2 \)
Buna göre en az bilet satılan 1. günde \( a = 12k = 24 \) bilet satılmıştır.
Bir topluluktaki 21 kişinin yaş ortalaması 28'dir. Bu topluluktan 3 kişi ayrıldığında topluluğun yaş ortalaması 24'e düşüyor.
Topluluktan ayrılan üç kişinin yaşları sırasıyla 9, 10 ve 7 ile orantılı olduğuna göre, bu üç kişiden en büyüğü kaç yaşındadır?
Çözümü GösterTopluluğun yaş ortalaması topluluktaki herkesin yaşları toplamının kişi sayısına bölümüne eşittir.
Topluluktaki kişilerin yaşları toplamına \( p \) diyelim.
\( \dfrac{p}{21} = 28 \)
\( p = 21 \cdot 28 = 588 \)
Topluluktan 3 kişi ayrıldıktan sonra kalan 18 kişinin yaşları toplamına \( t \) diyelim.
\( \dfrac{t}{18} = 24 \)
\( t = 18 \cdot 24 = 432 \)
Bu durumda \( p - t \) farkı topluluktan çıkan 3 kişinin yaşlarının toplamını verir.
\( p - t = 588 - 432 = 156 \)
Bu 3 kişinin yaşlarına sırasıyla \( a \), \( b \) ve \( c \) diyelim.
Bu kişilerin yaşları 9, 10 ve 7 ile orantılıdır.
Buna göre yaşlara sırasıyla aşağıdaki değerleri verebiliriz.
\( a = 9k, \quad b = 10k, \quad c = 7k \)
Bu üç kişinin yaşları toplamı 156'dır.
\( 9k + 10k + 7k = 156 \)
\( 26k = 156 \)
\( k = 6 \)
Topluluktan ayrılan kişiler arasında en büyük olanın yaşı \( b \)'dir.
\( b = 10k = 60 \) olarak bulunur.
Azra, Burak ve Cüneyt'in 90 metreyi koşma süreleri sırasıyla 10, 6 ve 5 ile orantılıdır.
Bu üç kişi aynı anda koşmaya başlayıp aynı anda koşmayı bırakıyorlar. Son durumda Burak ve Cüneyt toplam 561 metre koştuğuna göre, Azra kaç metre koşmuştur?
Çözümü GösterAzra, Burak ve Cüneyt'in 90 metreyi koşma sürelerine sırasıyla \( a \), \( b \) ve \( c \) diyelim.
90 metreyi koşma süreleri arasında orantı kuralım ve orantı sabitine \( k \) diyelim.
\( \dfrac{a}{10} = \dfrac{b}{6} = \dfrac{c}{5} = k \)
Koşma sürelerini orantı sabiti cinsinden yazalım.
\( a = 10k, \quad b = 6k, \quad c = 5k \)
90 metreyi \( 10k \) sürede koşan Azra, birim sürede \( \frac{9}{k} \) metre koşar.
90 metreyi \( 6k \) sürede koşan Burak, birim sürede \( \frac{15}{k} \) metre koşar.
90 metreyi \( 5k \) sürede koşan Cüneyt, birim sürede \( \frac{18}{k} \) metre koşar.
Üç kişinin koşma süresine \( t \) diyelim.
Burak ve Cüneyt birim sürede toplam \( \frac{15}{k} + \frac{18}{k} = \frac{33}{k} \) metre koştuklarına göre, 561 metreyi ne kadar sürede koştuklarını bulalım.
\( t = \dfrac{561}{\frac{33}{k}} = 17k \)
Birim sürede \( \frac{9}{k} \) metre koşan Azra \( 17k \) sürede \( 17k \cdot \frac{9}{k} = 153 \) metre koşar.