Doğru Orantı
İki değişkenin değerleri değişirken oranları sabit kalıyorsa bu iki değişken birbiriyle doğru orantılıdır. Doğru orantılı iki değişkenin bu sabit oranına orantı sabiti denir ve genellikle \( k \) ile gösterilir.
\( k \in \mathbb{R} \) ve \( k \ne 0 \) olmak üzere,
\( \dfrac{y}{x} = k \)
\( y = kx \)
Birbiriyle doğru orantılı \( x \) ve \( y \) değişkenleri arasındaki ilişki \( y \propto x \) şeklinde gösterilir.
Aralarında doğru orantı ilişkisi bulunan iki değişken için \( k \) orantı sabiti, değişkenlerin birbirine karşılık gelen tüm değerleri için sağlanır.
\( \dfrac{y_1}{x_1} = \dfrac{y_2}{x_2} = \dfrac{y_3}{x_3} = \ldots = k \)
İki değişken arasındaki doğru orantı ilişkisini bir örnek üzerinde gösterelim.
Birbiriyle doğru orantılı ve orantı sabiti 3 olan \( x \) ve \( y \) değişkenlerinin farklı değerlerini tablo ve grafik üzerinde gösterelim.
Doğru orantının orantı sabiti 3 ise iki değişkenin değerlerinin oranı her durumda sabit ve 3'e eşittir.
\( \dfrac{y}{x} = 3 \)
Orantı sabiti sağlanacak şekilde değişkenlerin alabilecekleri farklı değerlerden bazılarını bir tabloda gösterelim.
| \( x \) | \( 3 \) | \( 5 \) | \( 7 \) | \( 10 \) | \( 15 \) |
| \( y \) | \( 9 \) | \( 15 \) | \( 21 \) | \( 30 \) | \( 45 \) |
| \( \frac{y}{x} = k \) | \( 3 \) | \( 3 \) | \( 3 \) | \( 3 \) | \( 3 \) |
Değişkenlerin bu değerleri aşağıdaki grafikte işaretlenmiştir. Buna göre doğru orantı analitik düzlemde orijinden geçen ve eğimi \( k \) orantı sabitine eşit olan bir doğruya karşılık gelir.
İkiden fazla \( x, y, z, t \) değişkenleri sırasıyla \( a, b, c, d \) sayıları ile doğru orantılıysa aralarındaki orantı aşağıdaki şekilde ifade edilir.
\( \dfrac{x}{a} = \dfrac{y}{b} = \dfrac{z}{c} = \dfrac{t}{d} = k \)
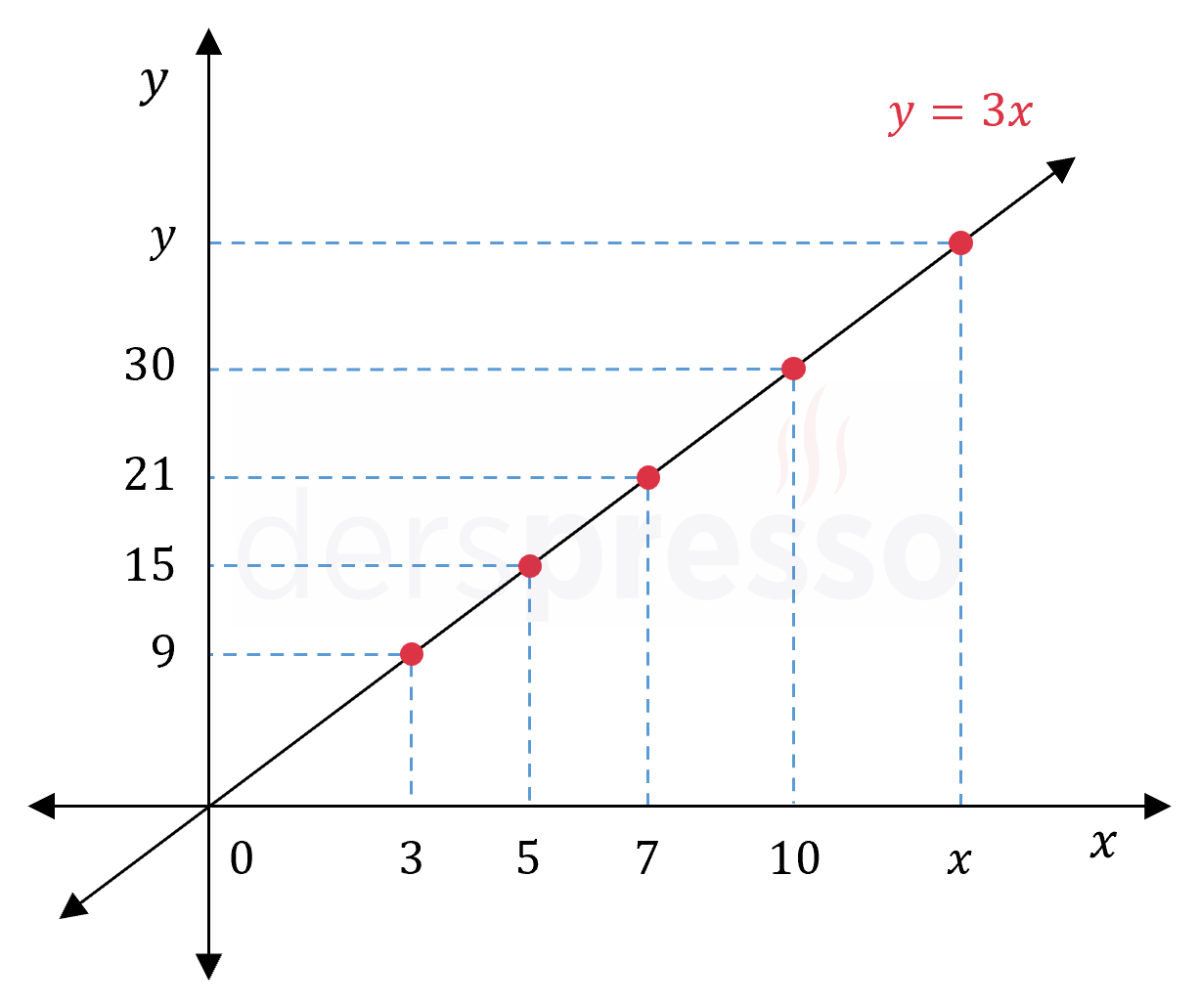
İki değişkenin birbiriyle "orantılı" olduğu belirtildiği durumda doğru orantı anlaşılmalıdır.
Doğru orantıya gerçek hayattan aşağıdaki örnekler verilebilir. Aşağıdaki örneklerin tümünde orantı sabiti ikinci değişkenin birinciye oranı şeklinde düşünülmüştür.
- Sabit hızla hareket eden bir aracın hareket süresi ve aldığı yol: Bu durumda orantı sabiti aracın hızıdır.
- Bir işçinin çalışma süresi ve toplam kazancı: Bu durumda orantı sabiti işçinin saatlik ücretidir.
- Bir çemberin çapı ve çevresi: Bu durumda orantı sabiti pi sayısıdır.
- Alınan benzin miktarı ve ödenen tutar: Bu durumda orantı sabiti benzinin litre fiyatıdır.
- Yapılan pizza sayısı ve kullanılan un miktarı: Bu durumda orantı sabiti bir pizzada kullanılan un miktarıdır.
- Bir miktar dolar ve TL karşılığı: Bu durumda orantı sabiti dolar - TL çevrim kurudur.
- Bir mesafenin kilometre ve mil karşılıkları: Bu durumda orantı sabiti mil - km dönüşüm oranıdır.
- (KDV hariç) ürün bedeli ve hesaplanan KDV tutarı: Bu durumda orantı sabiti KDV oranıdır.
Orantı sabiti çoğu durumda pozitif değer alır, bu da \( x \) ve \( y \) değişkenlerindeki değişimin aynı yönlü olduğu anlamına gelir (\( x \) artarken \( y \) de artar, \( x \) azalırken \( y \) de azalır). Bununla birlikte \( k \) negatif değer de alabilir, bu durumda değişkenlerdeki değişim ters yönlü olur (\( x \) artarken \( y \) azalır, \( x \) azalırken \( y \) artar).
\( \dfrac{y}{x} = -3 \) ise,
\( \dfrac{y}{x} = \dfrac{9}{-3} = \dfrac{-21}{7} = \dfrac{30}{-10} = -3 \)
İki değişken arasındaki doğru orantı ilişkisini ikinci bir örnek üzerinde gösterelim.
100 km'de 5 lt benzin tüketen bir araç 450 km'lik bir yolda kaç lt benzin tüketir?
Aracın km cinsinden katettiği mesafeye \( x \), litre cinsinden tükettiği benzine \( y \) diyelim.
Mesafe arttıkça benzin tüketimi de oranları sabit kalacak şekilde artacağı için, bu iki değişken arasında doğru orantı olduğunu söyleyebiliriz.
\( y \propto x \)
\( \dfrac{y}{x} = k \)
Verilen birinci durumda araç 100 km'de 5 lt benzin tüketiyor.
Verilen ikinci durumda aracın 450 km'de kaç lt benzin tüketeceği soruluyor. Bu miktara \( a \) lt diyelim.
\( a \) değerini bulmak için verilen değerleri doğru orantı formülünde yerine koyalım.
\( \dfrac{y_1}{x_1} = \dfrac{y_2}{x_2} = k \)
\( \dfrac{5}{100} = \dfrac{a}{450} = k \)
\( 100 \cdot a = 5 \cdot 450 \)
\( a = 22,50 \) lt
Buna göre araç 450 km'lik bir yolda 22,50 lt benzin tüketir.
Doğru orantı formülünü kullanarak orantı sabitini bulalım.
\( k = \dfrac{1}{20} \)
Buna göre araç her 1 km yol için \( \frac{1}{20} \) lt benzin tüketir.
Yukarıdaki örnekteki araç 40 lt benzin ile kaç km yol gidebilir?
Bulduğumuz orantı sabitini kullanarak mesafe ya da benzin tüketimi bilinen tüm durumlarda bilinmeyen değişken değerini bulabiliriz.
Aracın 40 lt benzin ile gidebileceği yola \( b \) km diyelim.
\( \dfrac{y}{x} = k \)
\( \dfrac{40}{b} = \dfrac{1}{20} \)
\( b = 800 \) km
Yukarıdaki iki örnekte bulduğumuz değerleri doğru orantının grafiği üzerinde gösterelim.
İki değişken arasındaki doğru orantıyı tanımlayan bu doğru grafiğinin eğimi orantı sabitine eşit ve \( \frac{1}{20} \)'dir.
Bu sorunun bir diğer çözümünde, yukarıdaki grafiği çizdikten sonra üçgen benzerliği kullanabiliriz. Buna göre, doğrunun altında kalan üçgenler benzer oldukları için aşağıdaki orantıyı kurabiliriz.
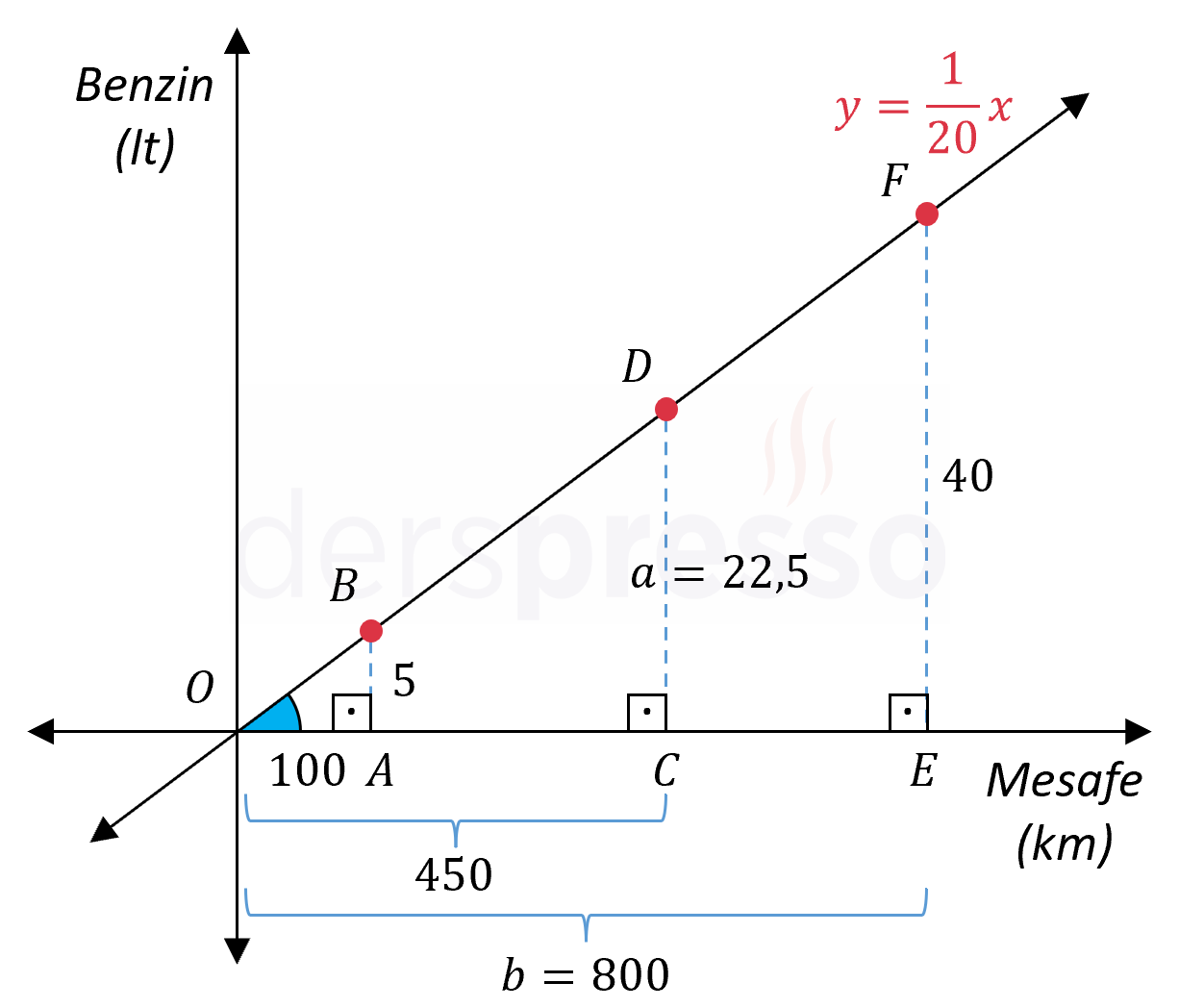
\( \overset{\triangle}{OAB} \sim \overset{\triangle}{OCD} \sim \overset{\triangle}{OEF} \)
\( \dfrac{5}{100} = \dfrac{a}{450} = \dfrac{40}{b} = \dfrac{1}{20} \)
\( a = 22,5 \) lt
\( b = 800 \) km
Bir değişken diğer bir değişkenle doğru orantılı olabileceği gibi, o değişkenin karesi, küpü, karekökü ya da herhangi bir fonksiyonu ile de doğru orantılı olabilir. Bu durumlarda iki değişken arasındaki formül ve grafik ilişkisi aşağıdaki gibi olur.
| Grafik | Doğru Orantı |
|---|---|
|
\( y \propto x^2 \) \( y = kx^2 \) \( y \) değişkeni \( x \)'in karesi ile doğru orantılıdır. |
|
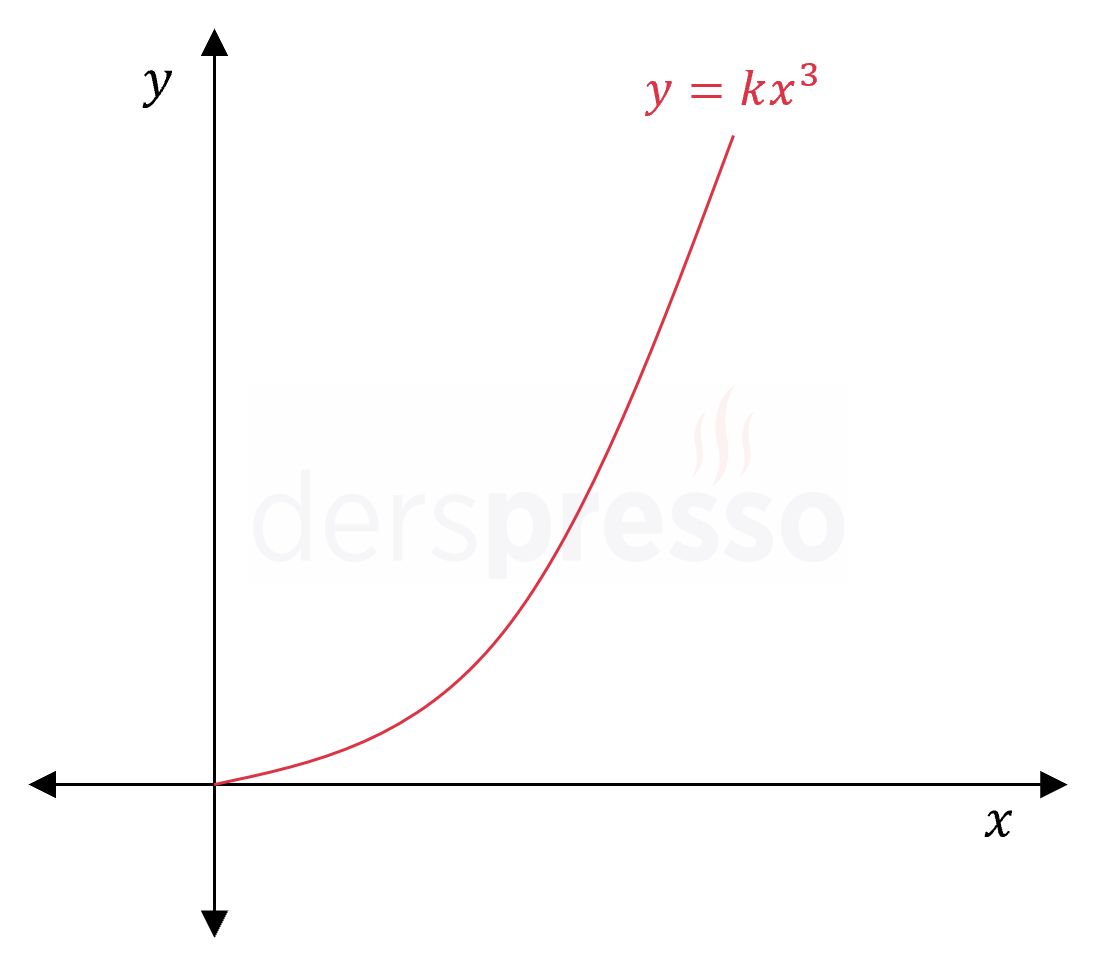
\( y \propto x^3 \) \( y = kx^3 \) \( y \) değişkeni \( x \)'in küpü ile doğru orantılıdır. |
|
\( y \propto \sqrt{x} \) \( y = k\sqrt{x} \) \( y \) değişkeni \( x \)'in karekökü ile doğru orantılıdır. |
Bir buzdolabı 1 saatte 20 Watt elektrik harcıyorsa bir haftada kaç Watt elektrik harcar?
Çözümü Göster172 sayısı \( \frac{1}{2} : \frac{2}{7} : \frac {3}{4} \) sayılarıyla doğru orantılı olacak şekilde üç sayıya ayrılıyor.
Ortadaki sayı kaçtır?
Çözümü GösterÜç doğal sayı \( 2 : 3 : 5 \) sayıları ile doğru orantılıdır.
Bu sayıların karelerinin toplamı 15200 olduğuna göre, sayılardan en küçüğü kaçtır?
Çözümü GösterÜç arkadaş bir miktar bilyeyi sırasıyla \( \frac{2}{3} : \frac{1}{4} : \frac{5}{6} \) sayılarıyla doğru orantılı olacak şekilde paylaşacaktır.
İkinci kişi 6 bilye aldığına göre toplam kaç bilye vardır?
Çözümü GösterBoyunu ölçmek isteyen Elçin, 176 cm boyundaki arkadaşı Ceyhun ile gölgelerinin boyunu ölçüyor.
Elçin'in gölgesinin boyu 21 cm, Ceyhun'un gölgesinin boyu ise 22 cm olduğuna göre, Elçin'in boyu kaç cm'dir?
Çözümü GösterAli, Berke ve Can'ın paraları 2, 3 ve 4 sayıları ile doğru orantılıdır.
Ali, Berke'ye, Berke Can'a, Can da Ali'ye başlangıçta sahip oldukları paranın \( \frac{1}{3} \)'ünü veriyor. Buna göre son durumda paralarının oranı kaç olur?
Çözümü GösterBir torbadaki siyah, mavi ve beyaz renkteki bilyelerin sayıları sırayla \( \frac{1}{3} \), \( \frac{2}{5} \) ve \( \frac{1}{2} \) sayılarıyla doğru orantılıdır.
Buna göre, bu torbadaki bilyelerin sayısı en az kaç olabilir?
Çözümü GösterBir aracın durma mesafesi, frene bastığı andaki hızının karesi ile doğru orantılıdır.
Bu araç saatte 40 km hızla giderken frene bastığında duruş mesafesi 24 m olduğuna göre, saatte 60 km hızla giderken duruş mesafesi kaç metre olur?
Çözümü GösterTarlasına böcek ilacı atacak olan bir çiftçi, kullanacağı ilacın gün cinsinden etki süresinin ilaç miktarının karesiyle doğru orantılı olduğunu öğreniyor.
Bu bilgiye göre 3 ayrı tarlasını ilaçlayan çiftçi tarlalara sırasıyla 5, 6 ve 7 kg ilaç atıyor.
Çiftçi attığı ilaçların tümünü tek bir tarlaya atsaydı ilacın etki süresinin üç tarlaya ayrı ayrı attığı durumdaki etki sürelerinin toplamından 107 gün fazla olacağını hesaplıyor.
Buna göre çiftçinin 5 kg ilaç attığı tarlada ilacın etkisi kaç gün sürer?
Çözümü Göster3810 cm'lik bir kumaş farklı uzunluklarda üç parçaya ayrılıyor. A parçasının uzunluğunun B parçasının uzunluğuna oranı \( \frac{8}{5} \), B parçasının uzunluğunun C parçasının uzunluğuna oranı \( \frac{13}{17} \)'dir.
Buna göre en uzun parça kaç cm'dir?
Çözümü GösterBir manavdaki elma, armut ve muzun kg fiyatları arasındaki orantı 2020 yılında \( 3:7:8 \), 2023 yılında \( 2:6:7 \)'dir.
Bu yıllar arasında muzun kg fiyatı \( \%75 \) arttığına göre, elmanın kg fiyatı yüzde kaç artmıştır?
Çözümü GösterBir mağazada küçük, orta ve büyük bedenlerde t-shirt ve gömlek satılmaktadır.
Mağazadaki küçük, orta, büyük beden t-shirtlerin sayıları arasındaki orantı sırasıyla \( 8:19:5 \)'tir.
Mağazadaki küçük, orta, büyük beden gömleklerin sayıları arasındaki orantı sırasıyla \( 4:5:7 \)'dir.
Bu mağazadaki toplam t-shirt sayısı toplam gömlek sayısının 4 katıdır.
Buna göre, orta beden t-shirt sayısının büyük beden gömlek sayısına oranı kaçtır?
Çözümü GösterBir konserin biletleri 5 gün boyunca satılıyor.
İlk üç günde satılan bilet sayıları arasındaki orantı sırasıyla \( 4:11:12 \)'dir.
Son iki günde satılan bilet sayıları arasındaki orantı sırasıyla \( 14:13 \)'tür.
1., 3. ve 4. günde satılan bilet sayıları arasındaki orantı ise sırasıyla \( 3:9:7 \)'dir.
5 gün boyunca toplam 270 bilet satıldığına göre, en az bilet satılan gün kaç bilet satılmıştır?
Çözümü GösterBir teknoloji mağazasında satılan akıllı saat, kulaklık ve hoparlör arasında fiyatı en yüksek olan akıllı saat, en düşük olan kulaklıktır. Akıllı saat ile hoparlörün satış fiyatlarının farkının toplamına oranı \( \frac{2}{5} \), akıllı saat ile kulaklığın satış fiyatlarının toplamının farkına oranı \( \frac{9}{5} \)'tir.
Bu üç ürünün satışından elde edilen gelir 5040 TL olduğuna göre, hoparlörün fiyatı ne kadardır?
Çözümü GösterSınava hazırlanan bir öğrencinin çözdüğü ilk iki deneme sınavındaki doğru cevap sayılarının oranı sırasıya \( 5 : 7 \), yanlış cevap sayılarının oranı da \( 3 : 2 \)'dir. Öğrenci ilk denemede 30 boş, ikinci denemede 5 boş soru bırakmıştır.
Deneme sınavlarında üç yanlış bir doğruyu götürdüğüne ve her sınav 120 soru olduğuna göre, öğrencinin iki sınavdaki netlerinin oranı nedir?
Çözümü GösterTermometreler içerisinde bulunan sıvının genleşme katsayısına bağlı olarak sıcaklığı gösteren aletlerdir. Ortam sıcaklığı yükselirse termometre içindeki sıvı genleşir ve tüpte yükselir, ortam soğursa büzüşerek tüpte alçalır.
Bir fizik öğretmeni X sıvısını kullanarak bir termometre tasarlıyor. Bu termometre suyun donma noktasını 75°X, kaynama noktasını 225°X olarak ölçüyor.
Yaygın olarak kullanılan Celsius termometresinde ise bu değerler sırasıyla 0°C ve 100°C olarak ölçülüyor.
Buna göre 60°C kaç °X'dir?
Çözümü Göster