Analitik Düzlemde Nokta
Kartezyen koordinat sisteminde bir noktanın konumu, noktanın \( x \) ve \( y \) eksenleri üzerindeki izdüşümlerinin sayısal değerlerinden oluşan \( (a, b) \) sıralı ikilisi ile ifade edilir. Bir noktanın konumunu temsil eden bu ikiliye noktanın koordinatı denir.
\( A(a, b) \)
\( a \): Noktanın \( x \) ekseni üzerindeki izdüşümünün sayısal değeri
\( b \): Noktanın \( y \) ekseni üzerindeki izdüşümünün sayısal değeri
Bazı noktaların koordinatları aşağıdaki şekilde gösterilmiştir.
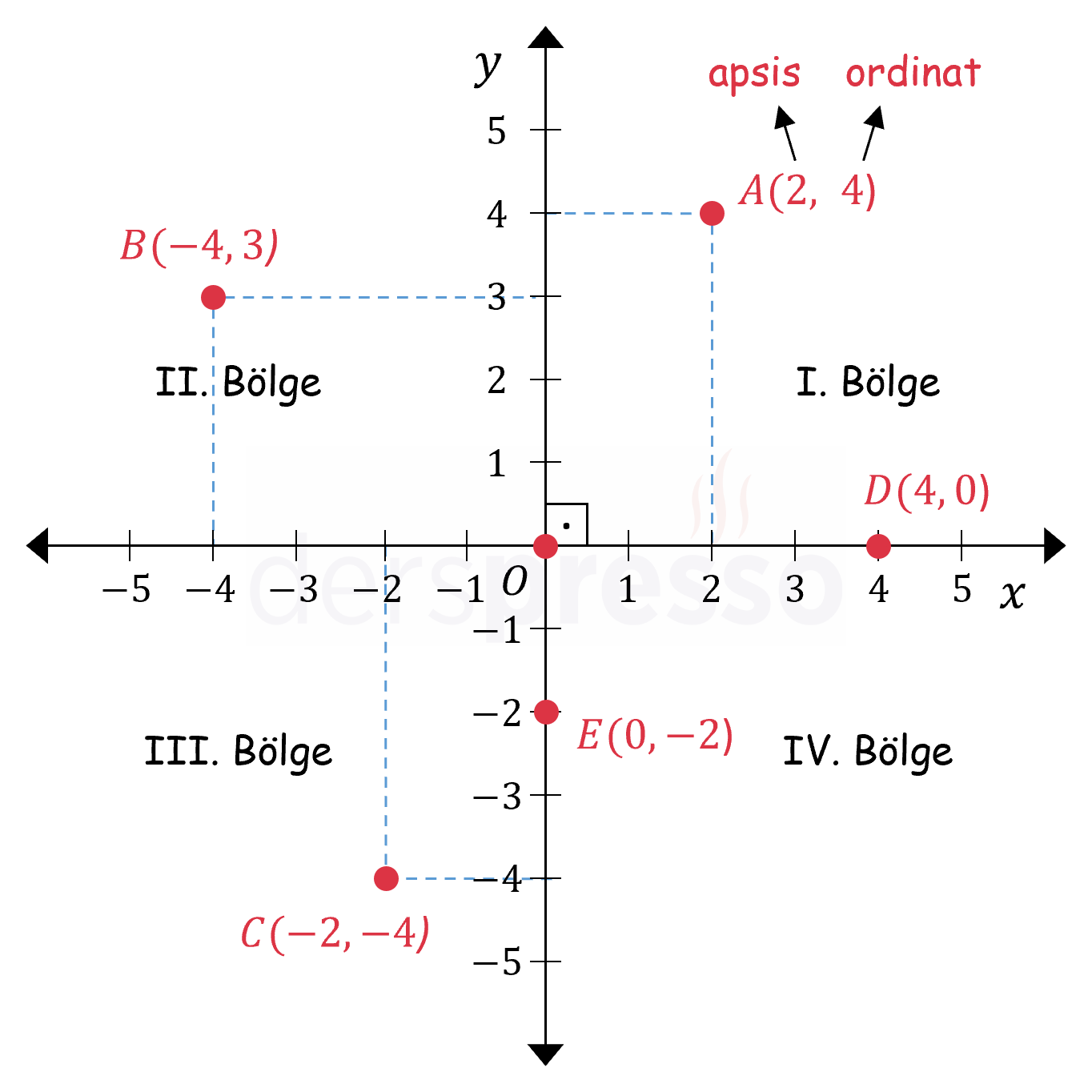
Bir noktanın koordinatının birinci bileşenine o noktanın apsisi denir. Apsis değeri I. ve IV. bölgelerde pozitif, II. ve III. bölgelerde negatiftir.
Bir noktanın koordinatının ikinci bileşenine o noktanın ordinatı denir. Ordinat değeri I. ve II. bölgelerde pozitif, III. ve IV. bölgelerde negatiftir.
\( x \) ekseni üzerindeki noktaların ordinat değeri, \( y \) ekseni üzerindeki noktaların apsis değeri sıfırdır.
İki boyutlu koordinat düzlemindeki tüm noktaların kümesi reel sayılar kümesinin ikili kartezyen çarpımı şeklinde ifade edilebilir.
\( \mathbb{R} \times \mathbb{R} = \mathbb{R}^2 = \{ (x, y) \mid x, y \in \mathbb{R} \} \)
Üçgenin Ağırlık Merkezi
Doğrusal olmayan üç noktanın oluşturduğu üçgenin ağırlık merkezinin koordinatları bu üç noktanın apsis ve ordinat değerlerinin aritmetik ortalaması alınarak bulunur.
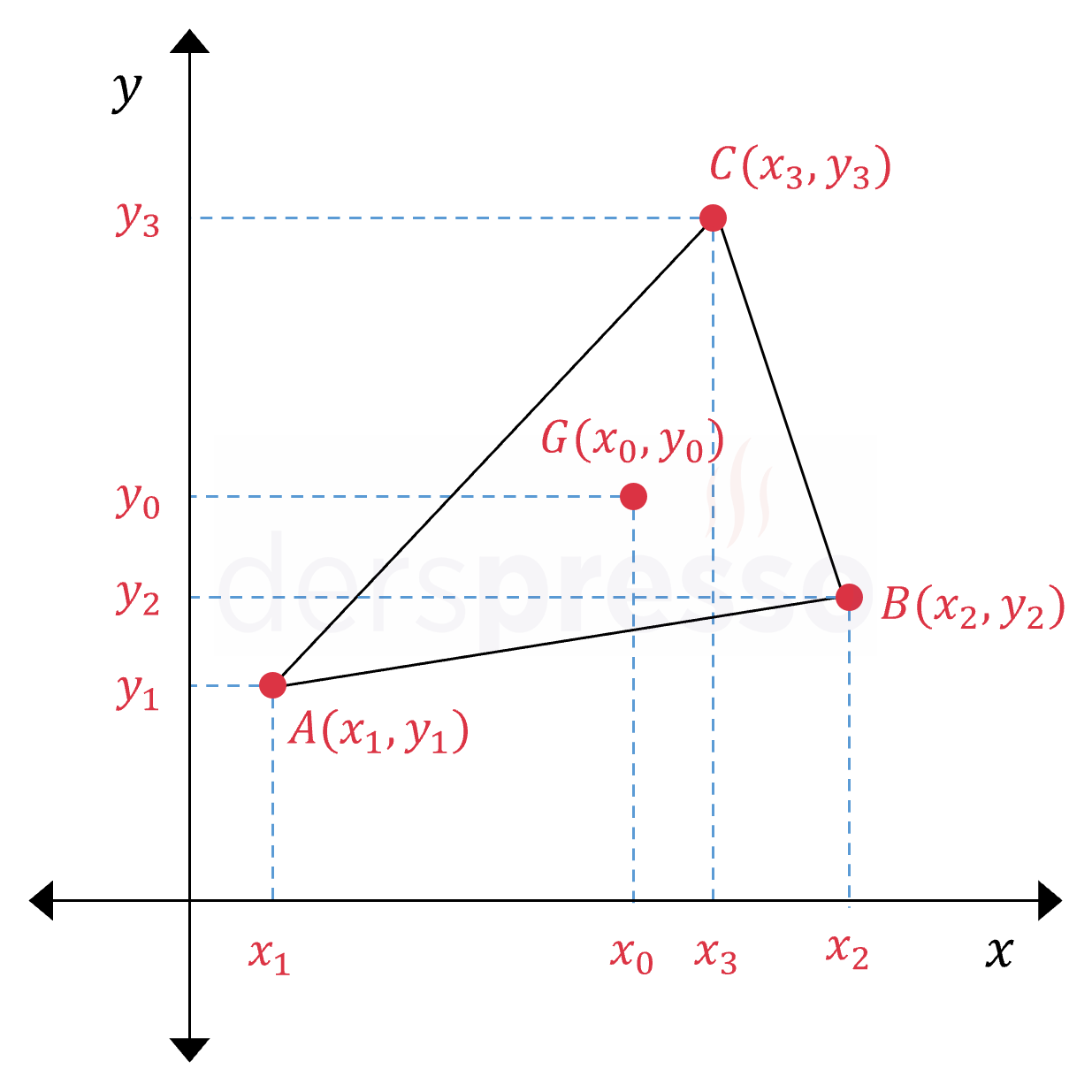
\( A(x_1, y_1), B(x_2, y_2), C(x_3, y_3) \) bir üçgenin köşe noktaları,
\( G(x_0, y_0) \) bu üçgenin ağırlık merkezi olmak üzere,
\( x_0 = \dfrac{x_1 + x_2 + x_3}{3} \)
\( y_0 = \dfrac{y_1 + y_2 + y_3}{3} \)
\( A(2, 3), B(7, -2), C(6, 11) \) noktalarının oluşturduğu üçgenin ağırlık merkezinin koordinatları:
\( x_0 = \dfrac{2 + 7 + 6}{3} = 5 \)
\( y_0 = \dfrac{3 + (-2) + 11}{3} = 4 \)
İSPATI GÖSTER
\( C \) köşesinden \( [AB] \) kenarına \( G \) noktasından geçen bir doğru parçası çizelim.
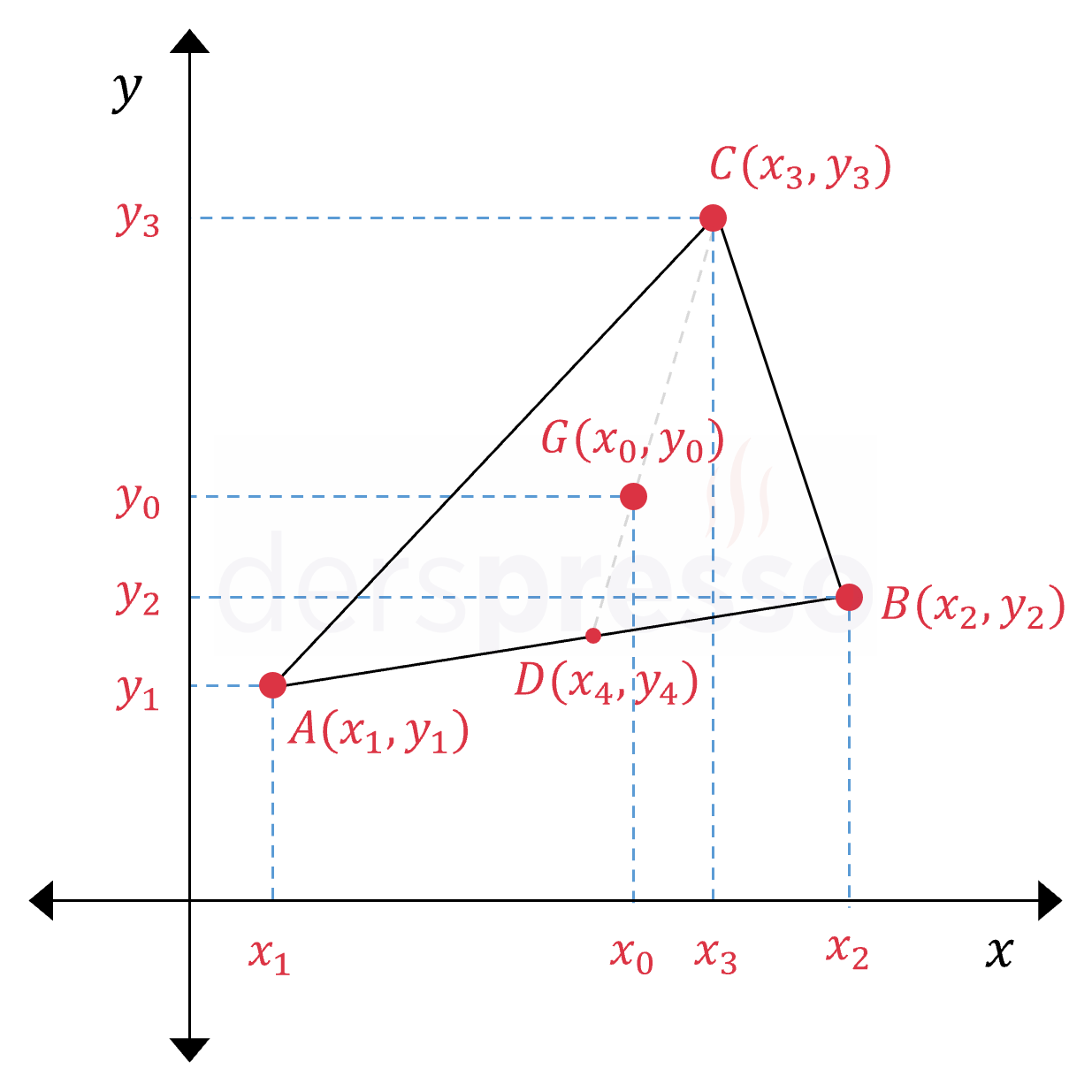
Bir üçgenin ağırlık merkezi aynı zamanda üçgenin kenarortaylarının kesişim noktasıdır, dolayısıyla \( G \) noktasından geçen \( [CD] \) doğru parçası \( [AB] \) kenarının kenarortayıdır ve bu kenarın orta noktasıdır.
Buna göre, \( D \) noktasının koordinatları iki noktanın orta nokta formülünden aşağıdaki gibi olur.
\( x_4 = \dfrac{x_1 + x_2}{2} \)
\( y_4 = \dfrac{y_1 + y_2}{2} \)
\( G \) noktası üçgenin ağırlık merkezi olduğu için, \( [CD] \) kenarortayını \( 2:1 \) oranında keser. Buna göre, \( G \) noktasının koordinatları iki noktayı belirli bir oranda içten bölen nokta formülünden aşağıdaki gibi olur.
\( x_0 = \dfrac{x_3 + 2 \cdot \frac{x_1 + x_2}{2}}{1 + 2} \)
\( = \dfrac{x_1 + x_2 + x_3}{3} \)
\( y_0 = \dfrac{y_3 + 2 \cdot \frac{y_1 + y_2}{2}}{1 + 2} \)
\( = \dfrac{y_1 + y_2 + y_3}{3} \)
Paralelkenarın Köşe Noktaları
Bir paralelkenarın karşılıklı köşelerinin koordinatları toplamı birbirine eşittir. Bu özellik aynı zamanda birer paralelkenar olan dikdörtgen, kare ve eşkenar dörtgen için de geçerlidir.

\( ABCD \) paralelkenarının köşe noktaları \( A(x_1, y_1), B(x_2, y_2), C(x_3, y_3), D(x_4, y_4) \) olmak üzere,
\( x_1 + x_3 = x_2 + x_4 \)
\( y_1 + y_3 = y_2 + y_4 \)
\( A(3, -2), B(6, b), C(8, -3), D(a, -4) \) bir paralelkenarın köşe noktaları ise,
\( 3 + 8 = 6 + a \)
\( a = 5 \)
\( -2 + (-3) = b + (-4) \)
\( b = -1 \)
İSPATI GÖSTER
Paralelkenarlarda köşegenler birbirini ortalar, dolayısıyla köşegenlerin kesişim noktası olan \( K \) noktasının koordinatlarını karşılıklı iki köşenin koordinatları cinsinden aşağıdaki şekilde yazabiliriz.
\( x_0 = \dfrac{x_1 + x_3}{2} = \dfrac{x_2 + x_4}{2} \)
\( y_0 = \dfrac{y_1 + y_3}{2} = \dfrac{y_2 + y_4}{2} \)
Her iki eşitlikte \( K \) noktasının koordinatlarını eşitliğin dışında bırakalım.
\( x_1 + x_3 = x_2 + x_4 \)
\( y_1 + y_3 = y_2 + y_4 \)
Üçgenin Alanı
Doğrusal olmayan üç noktanın oluşturduğu üçgenin alanı aşağıdaki formülle hesaplanır.
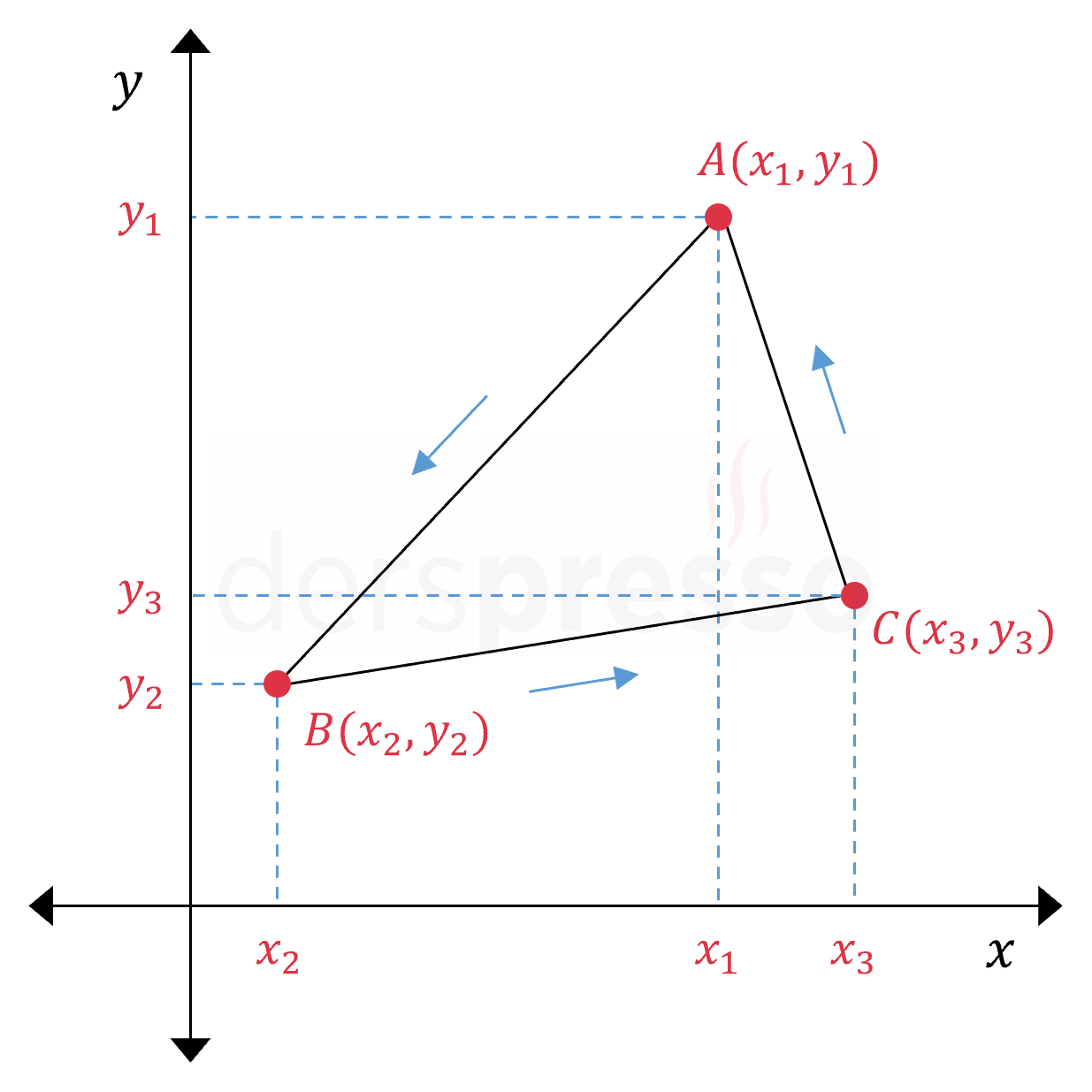
\( A(x_1, y_1), B(x_2, y_2), C(x_3, y_3) \) noktalarının oluşturduğu üçgenin alanı:
\( A(ABC) = \dfrac{1}{2} \left|\begin{matrix} x_1 & y_1 \\ x_2 & y_2 \\ x_3 & y_3 \\ x_1 & y_1 \end{matrix} \right| \)
\( = \dfrac{1}{2} [(x_1y_2 + x_2y_3 + x_3y_1) - (x_2y_1 + x_3y_2 + x_1y_3)] \)
İSPATI GÖSTER
Pozitif alan değeri elde etmek için \( A \), \( B \) ve \( C \) noktalarını üçgenin köşelerine saatin tersi yönünde yerleştirelim.
Üçgeni içine alan aşağıdaki gibi bir \( BDEF \) dikdörtgeni çizelim.
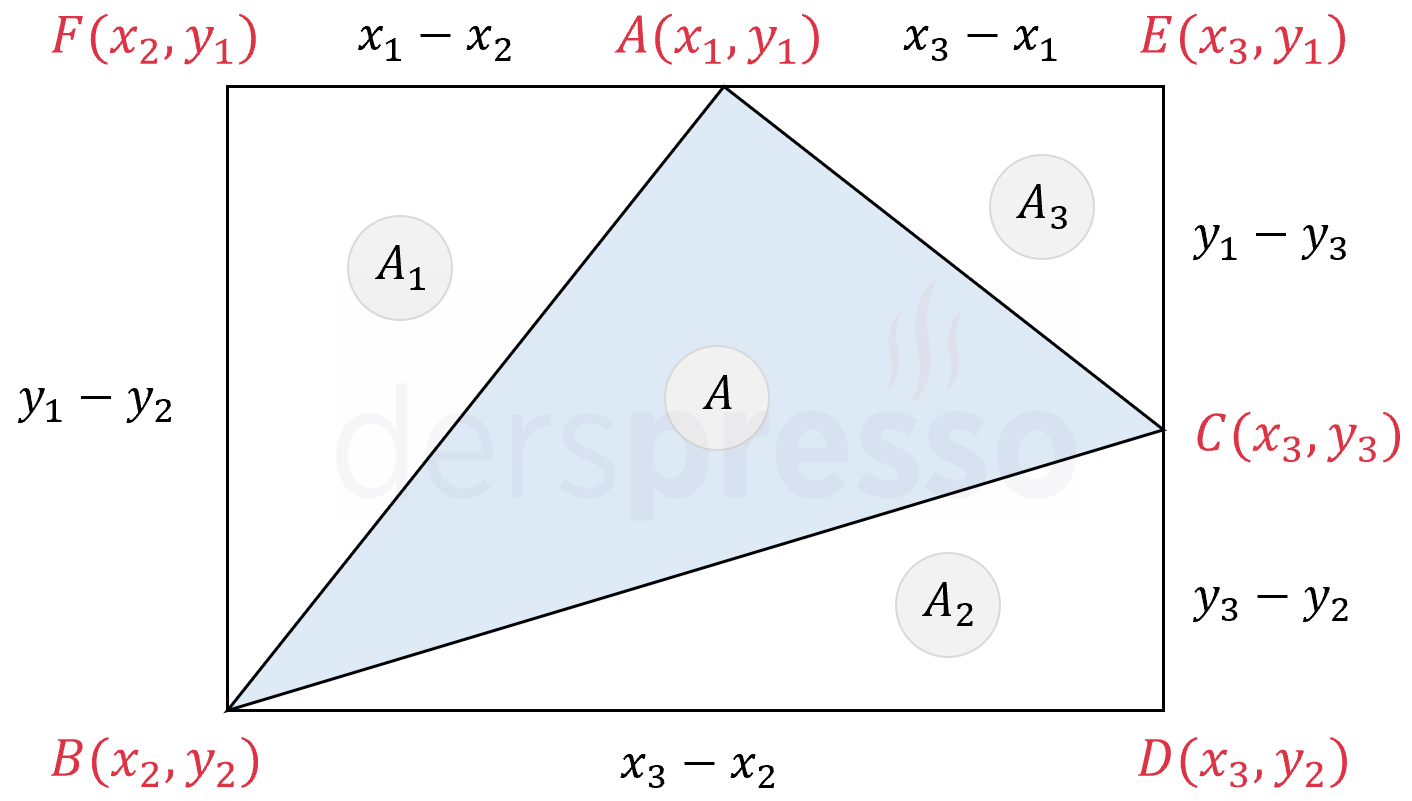
Üçgenin ve dikdörtgenin köşelerinin koordinatları ve köşe noktaları arası uzaklıklar şekilde belirtildiği gibi olur.
Dikdörtgenin içinde oluşan dört üçgenin alanlarına \( A \), \( A_1 \), \( A_2 \) ve \( A_3 \) diyelim.
Alanını bulmak istediğimiz üçgenin alanını dikdörtgenin alanından diğer üç üçgenin alanını çıkarak bulabiliriz.
\( A(ABC) = A(BDEF) - A(AFB) - A(BDC) - A(CEA) \)
\( A = A(BDEF) - A_1 - A_2 - A_3 \)
Dikdörtgenin alanını hesaplayalım.
\( A(BDEF) = (x_3 - x_2)(y_1 - y_2) \)
\( = x_3y_1 - x_3y_2 - x_2y_1 + x_2y_2 \)
Üçgenlerin alanlarını hesaplayalım.
\( A_1 = \dfrac{1}{2}(x_1 - x_2)(y_1 - y_2) \)
\( = \dfrac{1}{2}(x_1y_1 - x_1y_2 - x_2y_1 + x_2y_2) \)
\( A_2 = \dfrac{1}{2}(x_3 - x_2)(y_3 - y_2) \)
\( = \dfrac{1}{2}(x_3y_3 - x_3y_2 - x_2y_3 + x_2y_2) \)
\( A_3 = \dfrac{1}{2}(x_3 - x_1)(y_1 - y_3) \)
\( = \dfrac{1}{2}(x_3y_1 - x_3y_3 - x_1y_1 + x_1y_3) \)
Bu ifadeleri yukarıdaki üçgen alan formülünde yerlerine yazalım.
\( A = A(BDEF) - A_1 - A_2 - A_3 \)
\( = (x_3y_1 - x_3y_2 - x_2y_1 + x_2y_2) - \dfrac{1}{2}(x_1y_1 - x_1y_2 - x_2y_1 + x_2y_2) - \dfrac{1}{2}(x_3y_3 - x_3y_2 - x_2y_3 + x_2y_2) - \dfrac{1}{2}(x_3y_1 - x_3y_3 - x_1y_1 + x_1y_3) \)
Bu işlemdeki sadeleştirmeleri yaptığımızda aşağıdaki formülü elde ederiz.
\( = \dfrac{1}{2} [(x_1y_2 + x_2y_3 + x_3y_1) - (x_2y_1 + x_3y_2 + x_1y_3)] \)
Bu formül üçgenin köşelerinin koordinatları matrise saatin tersi yönünde yerleştirildiğinde pozitif, saat yönünde yerleştirildiğinde negatif sonuç verir, dolayısıyla alan değeri için sonucun mutlak değeri alınmalıdır.
Çokgenin Alanı
Basit (kenarları uç noktalar dışında kesişmeyen) bir çokgenin alanı aşağıdaki formülle hesaplanır. Bu formül hem konveks hem de konkav çokgenler için kullanılabilir.
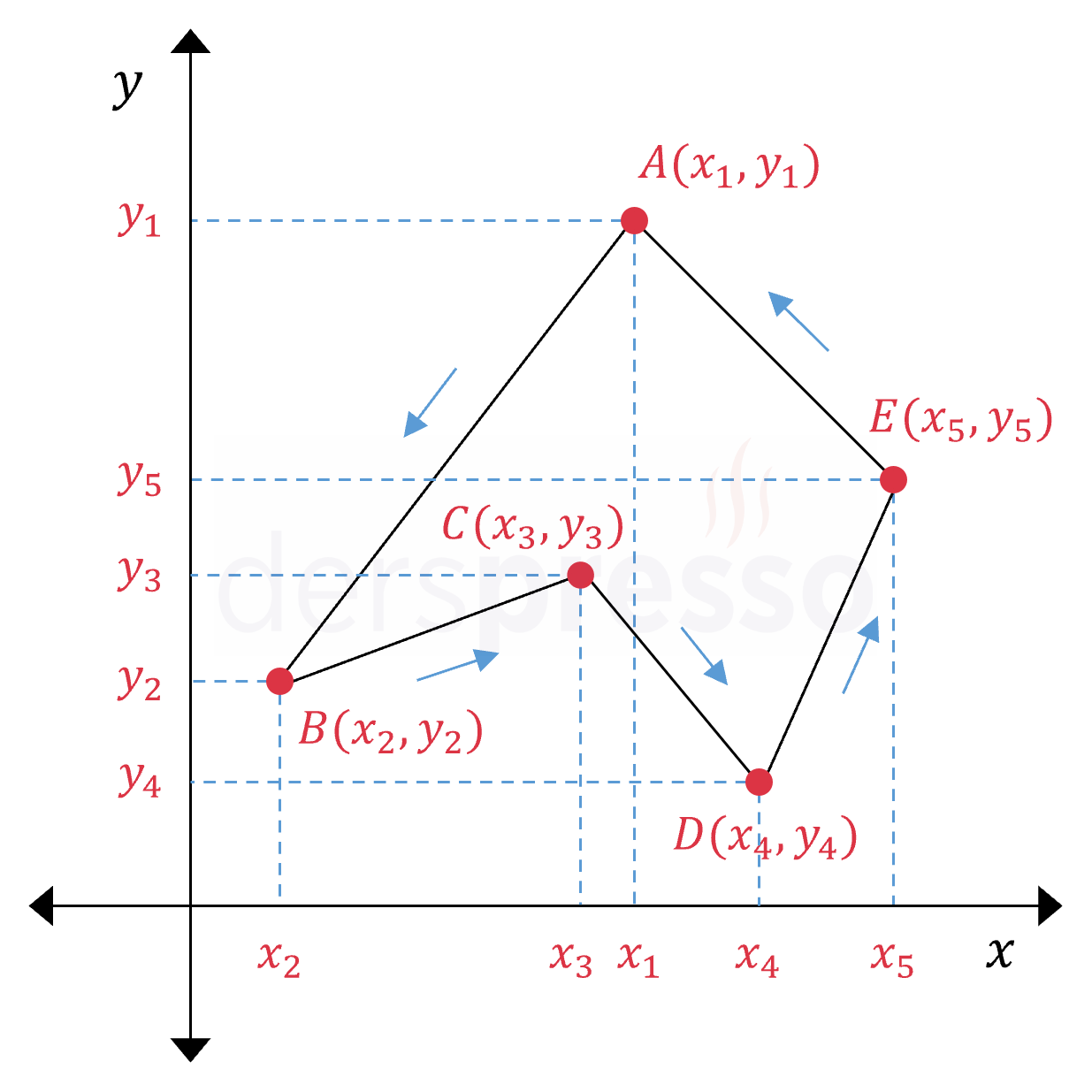
\( ABCDE \) beşgeninin alanı:
\( A(ABCDE) = \dfrac{1}{2} \left|\begin{matrix} x_1 & y_1 \\ x_2 & y_2 \\ x_3 & y_3 \\ x_4 & y_4 \\ x_5 & y_5 \\ x_1 & y_1 \end{matrix} \right| \)
Yukarıdaki formül bir beşgen için verilmiş olsa da herhangi bir çokgen için kullanılabilir.
Bu formül çokgenin köşelerinin koordinatları matrise saatin tersi yönünde yerleştirildiğinde pozitif, saat yönünde yerleştirildiğinde negatif sonuç verir, dolayısıyla alan değeri için sonucun mutlak değeri alınmalıdır.
Analitik düzlemdeki \( A(2 - 7k, k - 5) \) noktasının ordinatı apsisinin dörtte biri olduğuna göre, \( A \) noktası kaçıncı bölgededir?
Çözümü Göster\( A \) noktasının ordinatı apsisinin dörtte biridir.
\( k - 5 = \dfrac{2 - 7k}{4} \)
\( 4(k - 5) = 2 - 7k \)
\( 11k = 22 \)
\( k = 2 \)
\( A \) noktasının koordinatlarında \( k = 2 \) değerini yerine koyalım.
\( A(2 - 7(2), 2 - 5) = A(-12, -3) \)
Buna göre \( A \) noktası III. bölgededir.
\( P(2n - 6, n - 5) \) noktası analitik düzlemde \( y \) ekseni üzerinde olduğuna göre, noktanın orijine olan uzaklığı nedir?
Çözümü Göster\( P \) noktası \( y \) ekseni üzerinde olduğuna göre apsis değeri 0'dır.
\( 2n - 6 = 0 \)
\( n = 3 \)
\( P \) noktasının koordinatlarında \( n = 3 \) değerini yerine koyalım.
\( P(2(3) - 6, 3 - 5) = P(0, -2) \)
Buna göre \( P \) noktasının orijine olan uzaklığı \( \abs{-2} = 2 \) birimdir.
\( A(a + 6, a - 5) \) noktasının \( x \) eksenine olan uzaklığı \( 3 \) birim olduğuna göre, \( a \)'nın alabileceği değerler toplamı kaçtır?
Çözümü Göster\( A \) noktasının \( x \) eksenine olan uzaklığı ordinatının mutlak değerine eşittir.
\( \abs{a - 5} = 3 \)
Bu eşitlik iki durumda sağlanır.
Durum 1:
\( a - 5 = 3 \)
\( a = 8 \)
Durum 2:
\( a - 5 = -3 \)
\( a = 2 \)
Buna göre \( a \)'nın alabileceği değerler toplamı \( 8 + 2 = 10 \) olur.
\( A(3a + 15, a - 1) \) noktası analitik düzlemin IV. bölgesinde olduğuna göre, \( a \)'nın alabileceği kaç tam sayı değeri vardır?
Çözümü GösterIV. bölgedeki bir noktanın apsis ve ordinatının işaretleri \( (+, -) \) olur.
\( A \) noktasının apsisi pozitiftir.
\( 3a + 15 \gt 0 \)
\( a \gt -5 \)
\( A \) noktasının ordinatı negatiftir.
\( a - 1 \lt 0 \)
\( a \lt 1 \)
Buna göre \( a \) değer aralığı aşağıdaki gibidir.
\( -5 \lt a \lt 1 \)
Bu aralıktaki tam sayı değerleri aşağıdaki gibidir.
\( a \in \{-4, -3, -2, -1, 0\} \)
Buna göre \( a \)'nın alabileceği 5 tam sayı değeri vardır.
\( A(-a, b) \) noktası analitik düzlemde IV. bölgede olduğuna göre, \( B(-ab, a) \) noktası kaçıncı bölgededir?
Çözümü Göster\( A(-a, b) \) noktası IV. bölgededir.
IV. bölgedeki noktaların apsis ve ordinatının işaretleri \( (+, -) \) olur.
\( -a \gt 0 \Longrightarrow a \lt 0 \)
\( b \lt 0 \)
Buna göre \( B(-ab, a) \) noktasının apsis ve ordinatının işaretleri \( (-, -) \) olur.
Dolayısıyla \( B \) noktası III. bölgededir.
\( K(2a - 3, -a + 7) \) noktası analitik düzlemde eksenlere eşit uzaklıkta olduğuna göre, \( K \) noktası hangi bölgelerde bulunabilir?
Çözümü Göster\( K \) noktası eksenlere eşit uzaklıkta olduğuna göre, 1. açıortay (\( y = x \)) ya da 2. açıortay (\( y = -x \)) doğrusu üzerindedir ve apsis ve ordinat değerlerinin mutlak değerleri birbirine eşittir.
\( \abs{2a - 3} = \abs{-a + 7} \)
Bu eşitlik iki durumda sağlanır.
Durum 1:
\( 2a - 3 = -a + 7 \)
\( 3a = 10 \)
\( a = \dfrac{10}{3} \)
\( K \) noktasının koordinatlarında bu değeri yerine koyalım.
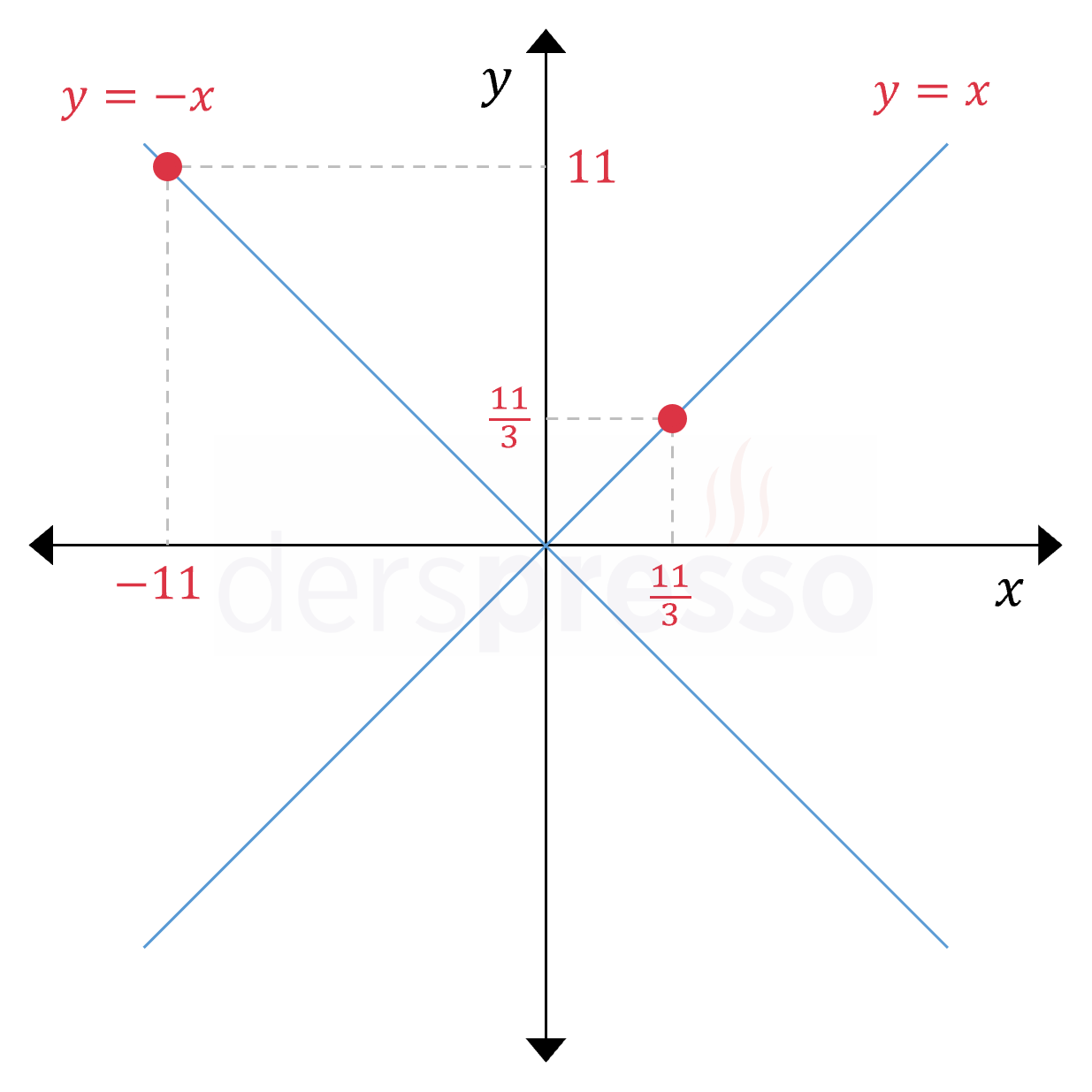
\( K(2(\frac{10}{3}) - 3, -\frac{10}{3} + 7) = K(\frac{11}{3}, \frac{11}{3}) \)
Bu durumda \( K \) noktası I. bölgede bulunur.
Durum 2:
\( 2a - 3 = -(-a + 7) \)
\( 2a - 3 = a - 7 \)
\( a = -4 \)
\( K \) noktasının koordinatlarında bu değeri yerine koyalım.
\( K(2(-4) - 3, -(-4) + 7) = K(-11, 11) \)
Bu durumda \( K \) noktası II. bölgede bulunur.
Buna göre \( K \) noktası I. ya da II. bölgede bulunur ve aşağıdaki şekilde görülebileceği gibi her iki durumda eksenlere eşit uzaklıkta olur.
\( A(3a - 12, 4) \) ve \( B(-17, a + 5) \) noktaları analitik düzlemin aynı bölgesindedir.
Buna göre \( a \)'nın alabileceği kaç farklı tam sayı değeri vardır?
Çözümü Göster\( A \) ve \( B \) noktaları aynı bölgede olduklarına göre, hem apsislerinin hem de ordinatlarının işareti aynıdır.
\( B \) noktasının apsisi negatif olduğuna göre \( A \) noktasının apsisi de negatiftir.
\( 3a - 12 \lt 0 \)
\( a \lt 4 \)
\( A \) noktasının ordinatı pozitif olduğuna göre \( B \) noktasının ordinatı da pozitiftir.
\( a + 5 \gt 0 \)
\( a \gt -5 \)
\( a \) değer aralığı bulduğumuz iki aralığın kesişim kümesidir.
\( -5 \lt a \lt 4 \)
Buna göre \( a \)'nın alabileceği \( 3 - (-4) + 1 = 8 \) farklı tam sayı değeri vardır.
Koordinat düzlemindeki \( A(\frac{m}{n}, m - n) \) noktası II. bölgede olduğuna göre, \( B(m^2 - n, mn) \) noktası kaçıncı bölgededir?
Çözümü GösterII. bölgedeki bir noktanın apsis ve ordinatının işaretleri \( (-, +) \) olur.
\( A \) noktası II. bölgededir.
\( \dfrac{m}{n} \lt 0 \)
Buna göre \( m \) ve \( n \) ters işaretlidir.
\( m - n \gt 0 \)
\( m \gt n \)
Buna göre (\( m \) ve \( n \) ters işaretli oldukları için) \( m \) pozitif, \( n \) negatiftir.
\( B(m^2 - n, mn) \) noktasının apsis ve ordinatının işaretlerini inceleyelim.
\( m^2 \) pozitiftir. Pozitif bir sayıdan negatif bir sayı çıkarıldığında sonuç pozitif olur.
\( m^2 - n \gt 0 \)
\( m \) ve \( n \) ters işaretli oldukları için çarpımları negatiftir.
\( mn \lt 0 \)
Buna göre \( B \) noktasının apsis ve ordinatının işaretleri \( (+, -) \) olur.
Dolayısıyla \( B \) noktası IV. bölgededir.
Analitik düzlemdeki \( A(3, n + 4) \) noktası \( 2m + 1 \) birim sağa, 6 birim aşağı ötelendiğinde \( B(-6, 3n - 8) \) noktası elde ediliyor.
Buna göre \( n - m \) kaçtır?
Çözümü GösterBir nokta \( 2m + 1 \) birim sağa ötelendiğinde apsisi \( 2m + 1 \) birim artar.
\( A(3, n + 4) \longmapsto A'(2m + 4, n + 4) \)
Bir nokta 6 birim aşağı ötelendiğinde ordinatı 6 birim azalır.
\( A'(2m + 4, n + 4) \longmapsto A''(2m + 4, n - 2) \)
Bu dönüşümler sonucunda \( B \) noktası elde ediliyor.
\( A''(2m + 4, n - 2) = B(-6, 3n - 8) \)
İki noktanın eşitliğinde apsis ve ordinat değerleri ayrı ayrı birbirine eşittir.
\( 2m + 4 = -6 \)
\( m = -5 \)
\( n - 2 = 3n - 8 \)
\( n = 3 \)
\( n - m = 3 - (-5) = 8 \) bulunur.
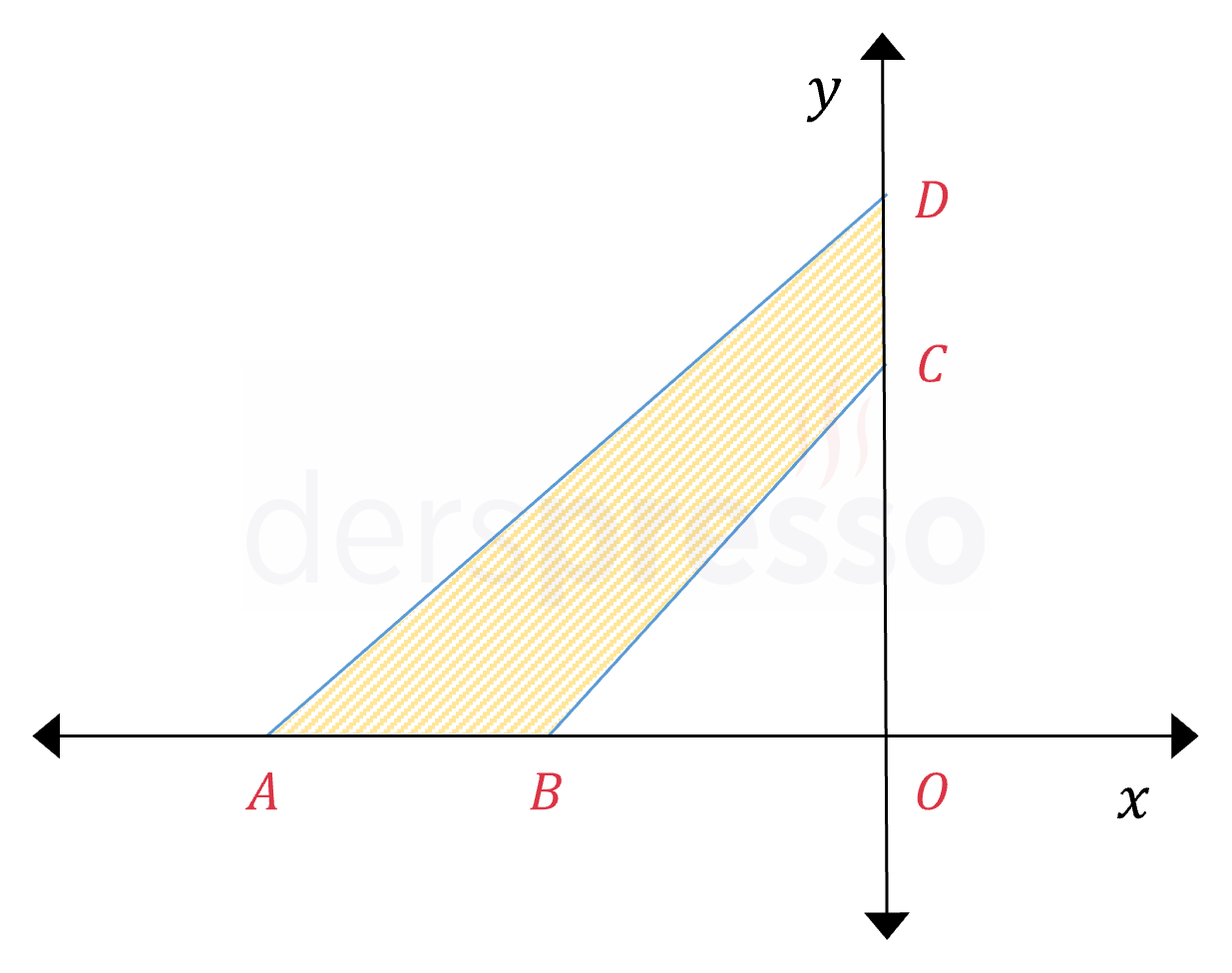
Analitik düzlemde \( AOD \) ve \( BOC \) üçgenleri şekildeki gibi veriliyor.
\( A(-6, 0) \), \( B(-4, 0) \), \( C(0, 5) \), \( D(0, 7) \) olduğuna göre, \( ABCD \) dikdörtgeninin alanı kaç birimkaredir?
Çözümü Göster\( ABCD \) dikdörtgeninin alanını verilen iki üçgenin alanlarının farkı şeklinde yazabiliriz.
\( A(ABDC) = A(AOD) - A(BOC) \)
\( = \dfrac{6 \cdot 7}{2} - \dfrac{4 \cdot 5}{2} \)
\( = 21 - 10 = 11 \) bulunur.
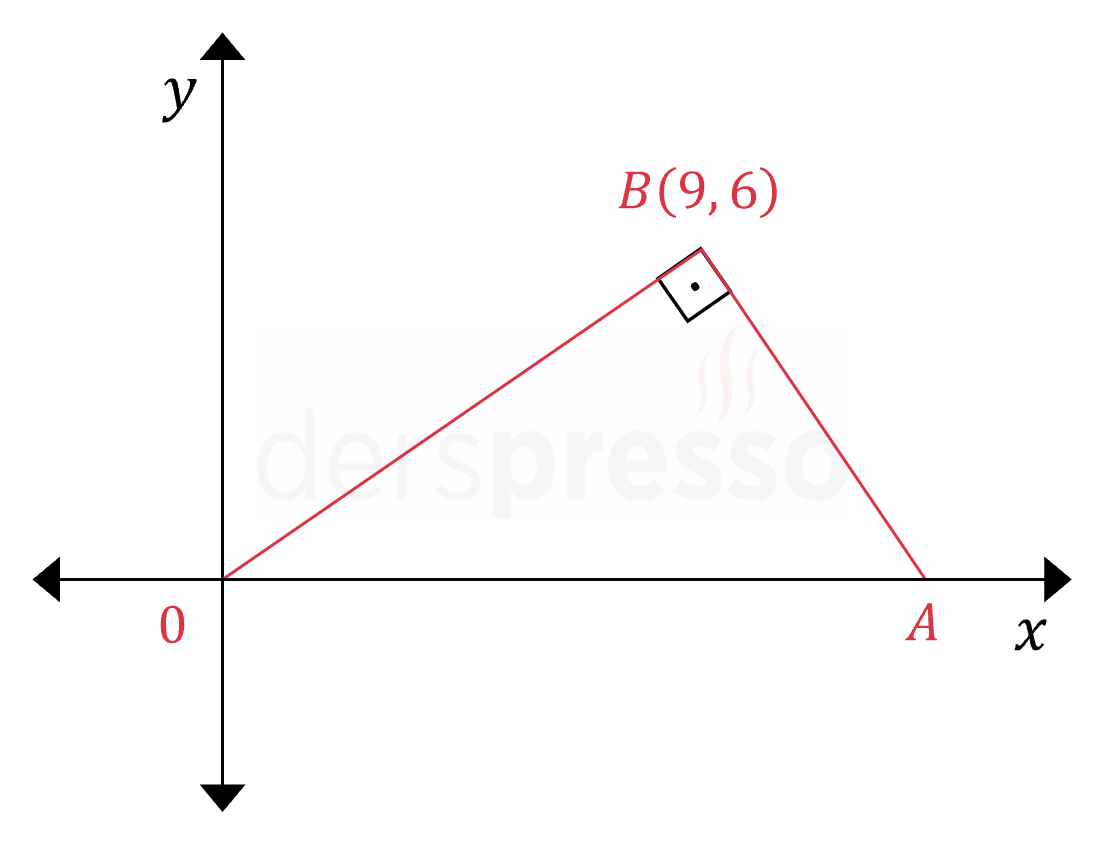
Yukarıdaki şekilde \( \abs{OB} \perp \abs{AB} \) ve \( B(9, 6) \) olduğuna göre, \( A \) noktasının apsisi kaçtır?
Çözümü Göster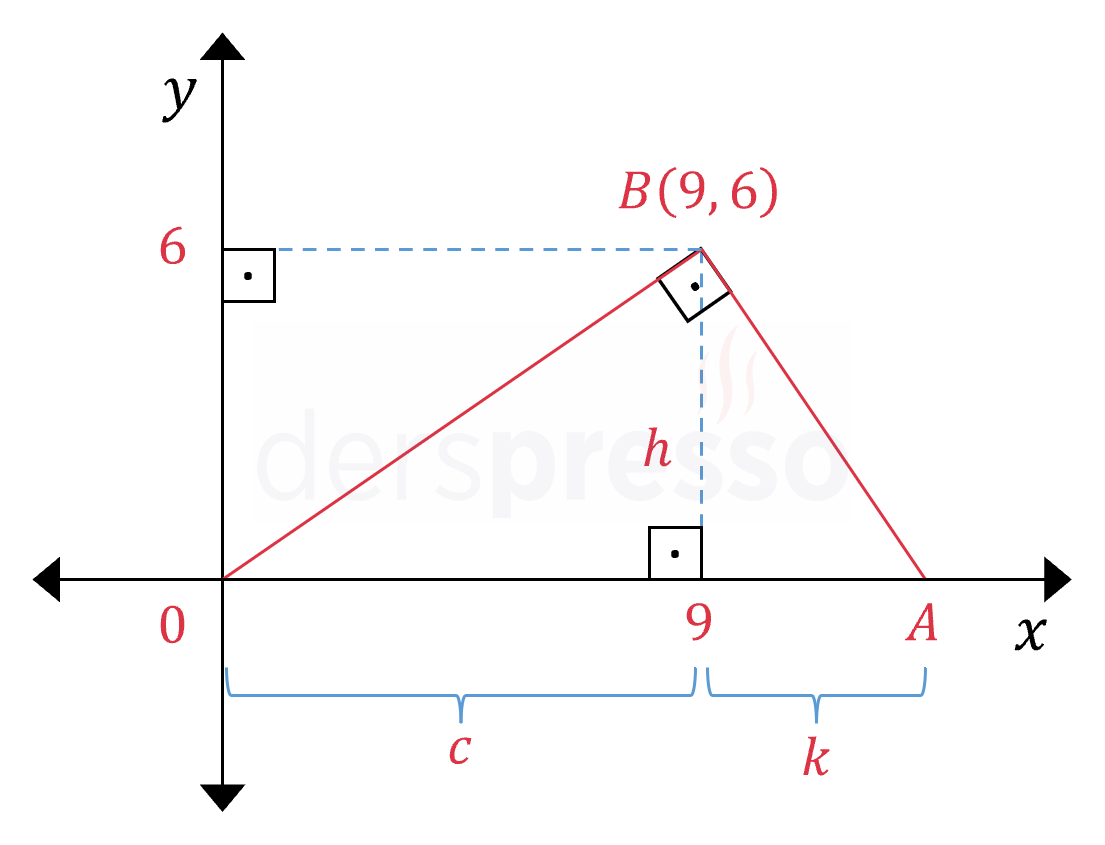
\( B \) noktasından eksenlere birer dikme çizelim.
\( OBA \) bir dik üçgen olduğu için Öklid bağıntısını kullanabiliriz.
\( h^2 = c \cdot k \)
\( 6^2 = 9 \cdot k \)
\( k = 4 \)
Buna göre \( A \) noktasının apsisi \( 9 + k = 13 \) bulunur.

Yukarıdaki şekilde \( [AB] \perp [AC] \) olduğuna göre, \( a \) kaçtır?
Çözümü Göster\( A \) noktasından \( x \) eksenine bir dikme çizelim.
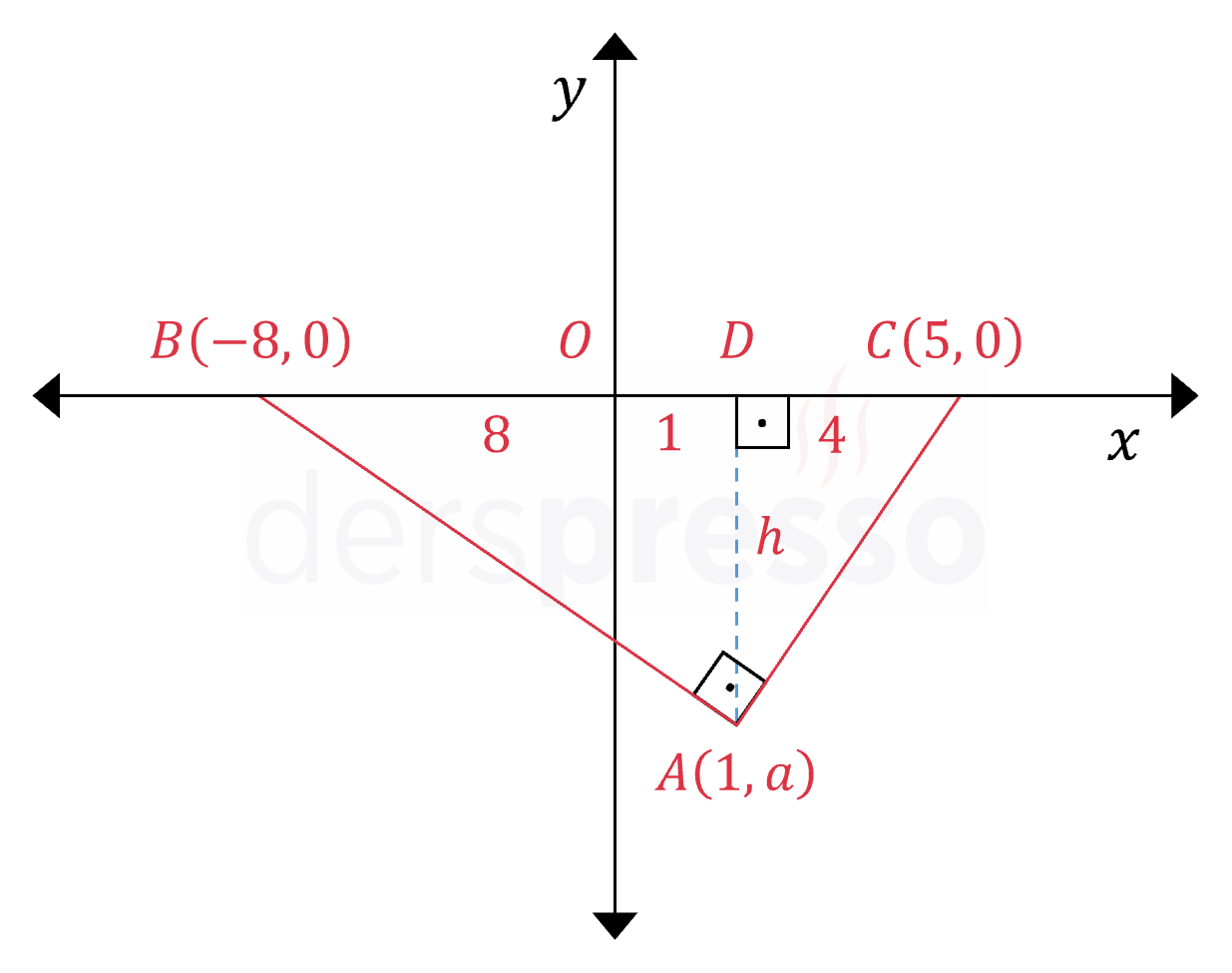
\( D \) noktasının apsis değeri \( A \) noktası ile aynı olur.
\( \abs{OD} = 1 \)
\( \abs{DC} = 5 - 1 = 4 \)
\( BAC \) bir dik üçgen olduğu için Öklid bağıntısını kullanabiliriz.
\( h^2 = \abs{BD} \cdot \abs{DC} \)
\( h^2 = (8 + 1) \cdot 4 = 36 \)
\( h = 6 \)
Buna göre \( x \) eksenine negatif tarafta 6 birim uzaklıkta olan \( A \) noktasının ordinat değeri \( a = -6 \) olur.
Alanı 18 birimkare olan \( ABC \) üçgeninde \( A(2, -1), B(4, 5) \) ve \( C(6, m) \) olduğuna göre, \( m \)'nin alabileceği değerlerin toplamı kaçtır?
Çözümü GösterKöşe noktalarının koordinatları \( A(x_1, y_1) \), \( B(x_2, y_2) \) ve \( C(x_3, y_3) \) olan üçgenin alanı aşağıdaki formülle bulunur.
\( A(ABC) = \dfrac{1}{2} \abs{x_1(y_2 - y_3) + x_2(y_3 - y_1) + x_3(y_1 - y_2)} \)
\( 18 = \dfrac{1}{2} \abs{2(5 - m) + 4(m - (-1)) + 6(-1 - 5)}\)
\( 36 = \abs{10 - 2m + 4m + 4 - 36} \)
\( \abs{2m - 22} = 36 \)
Bu eşitlik iki durumda sağlanır.
Durum 1:
\( 2m - 22 = 36 \)
\( m = 29 \)
Durum 2:
\( 2m - 22 = -36 \)
\( m = -7 \)
\( m \)'nin alabileceği değerlerin toplamı \( -7 + 29 = 22 \) olarak bulunur.
\( A(0, 5) \) noktası ile \( x \) ekseni üzerinde bulunan ve \( A \) noktasına 10 birim uzaklıkta olan \( B \) ve \( C \) noktaları veriliyor. Buna göre, bu üç noktanın oluşturduğu \( ABC \) üçgeninin alanı kaç birimkaredir?
Çözümü GösterVerilen noktaları analitik düzlemde gösterelim.

\( \abs{AO} = 5 \)
\( AOB \) üçgenine Pisagor teoremini uygulayalım.
\( \abs{AB}^2 = \abs{AO}^2 + \abs{BO}^2 \)
\( 10^2 = 5^2 + \abs{BO}^2 \)
\( \abs{BO} = 5\sqrt{3} \)
\( AOC \) üçgenine Pisagor teoremini uyguladığımızda aynı sonucu elde ederiz.
\( \abs{CO} = 5\sqrt{3} \)
\( ABC \) üçgeninin alanını bulalım.
\( A(ABC) = \dfrac{\abs{BC} \cdot \abs{AO}}{2} \)
\( = \dfrac{10\sqrt{3} \cdot 5}{2} \)
\( = 25\sqrt{3} \) bulunur.
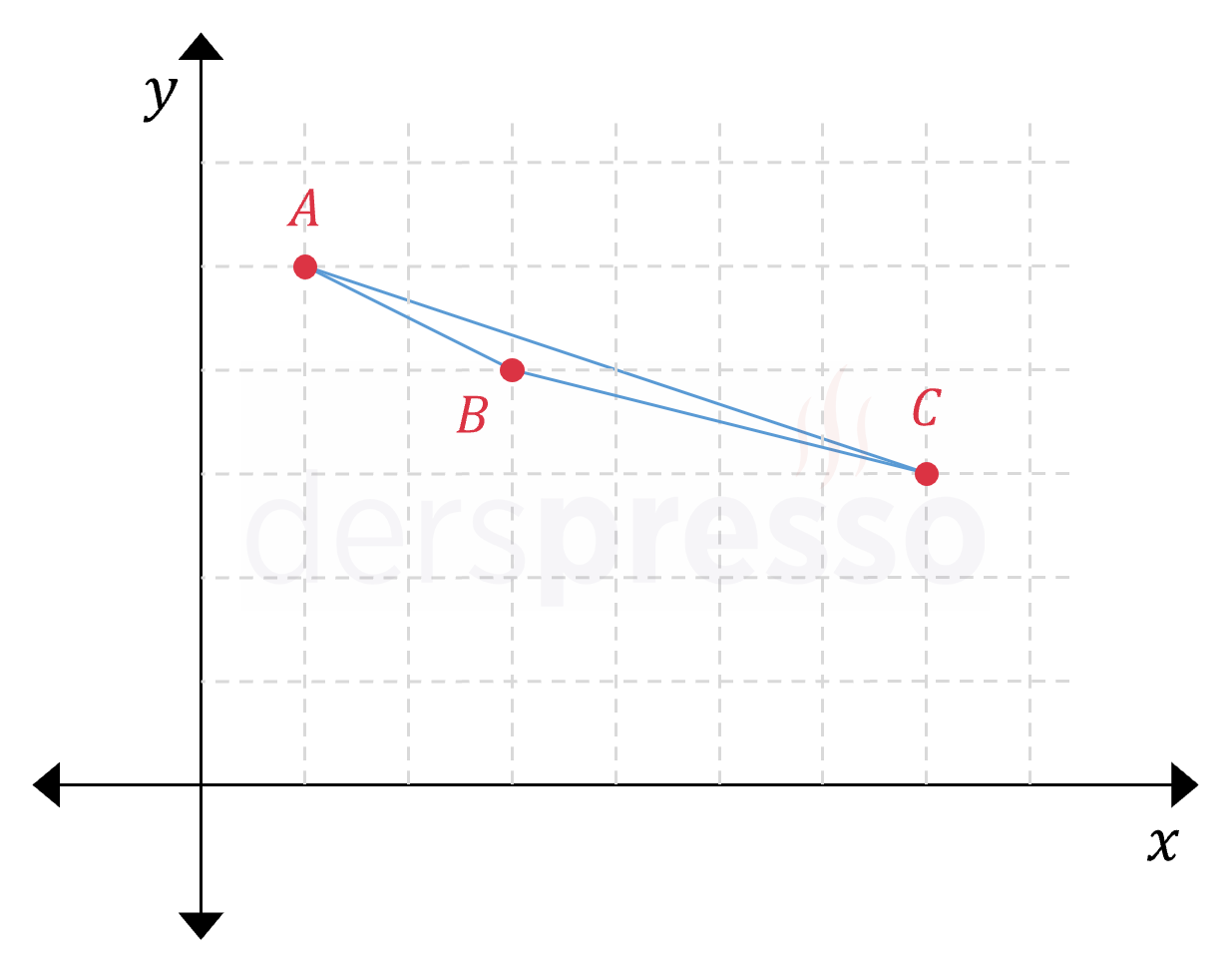
Şekildeki yatay ve dikey kesikli doğrular arasındaki uzaklık 1'er birimdir.
Buna göre \( ABC \) üçgeninin alanı kaç birimkaredir?
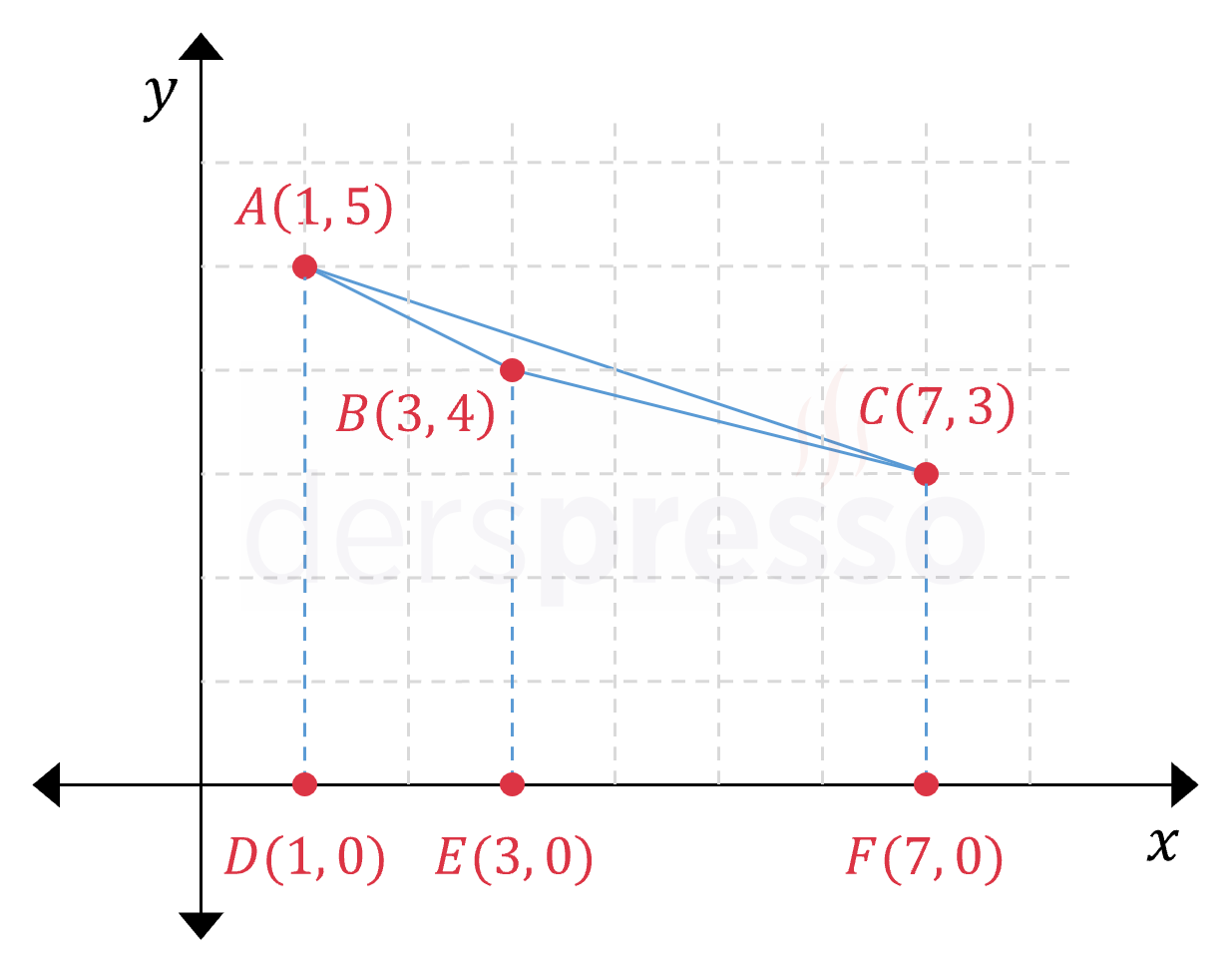
Çözümü GösterÜçgenin köşelerinin koordinatlarını \( A(1, 5) \), \( B(3, 4) \) ve \( C(7, 3) \), bu noktaların \( x \) ekseni üzerindeki izdüşümlerini de \( D(1, 0) \), \( E(3, 0) \) ve \( F(7, 0) \) olarak işaretleyelim.
\( ABC \) üçgeninin alanını iki yöntemle bulabiliriz.
1. yöntem: Analitik
3 noktanın oluşturduğu üçgenin alan formülünü kullanalım.
\( A(1, 5) = A(x_1, y_1) \), \( B(3, 4) = B(x_2, y_2) \) ve \( C(7, 3) = C(x_3, y_3) \) olmak üzere,
\( A(ABC) = \dfrac{1}{2} \abs{(x_1y_2 + x_2y_3 + x_3y_1) - (x_2y_1 + x_3y_2 + x_1y_3)} \)
\( = \dfrac{1}{2} \abs{(1 \cdot 4 + 3 \cdot 3 + 7 \cdot 5) - (3 \cdot 5 + 7 \cdot 4 + 1 \cdot 3)} \)
\( = \dfrac{1}{2} \abs{48 - 46} = 1 \) birimkare
2. yöntem: Geometrik
\( ABC \) üçgeninin alanını \( ADFC \) yamuğunun alanından \( ADEB \) ve \( BEFC \) yamuklarının alanlarını çıkararak bulalım.
\( A(ABC) = A(ADFC) - A(ADEB) - A(BEFC) \)
\( = \dfrac{(5 + 3) \cdot 6}{2} - \dfrac{(5 + 4) \cdot 2}{2} - \dfrac{(4 + 3) \cdot 4}{2} \)
\( = 24 - 9 - 14 = 1 \) birimkare bulunur.
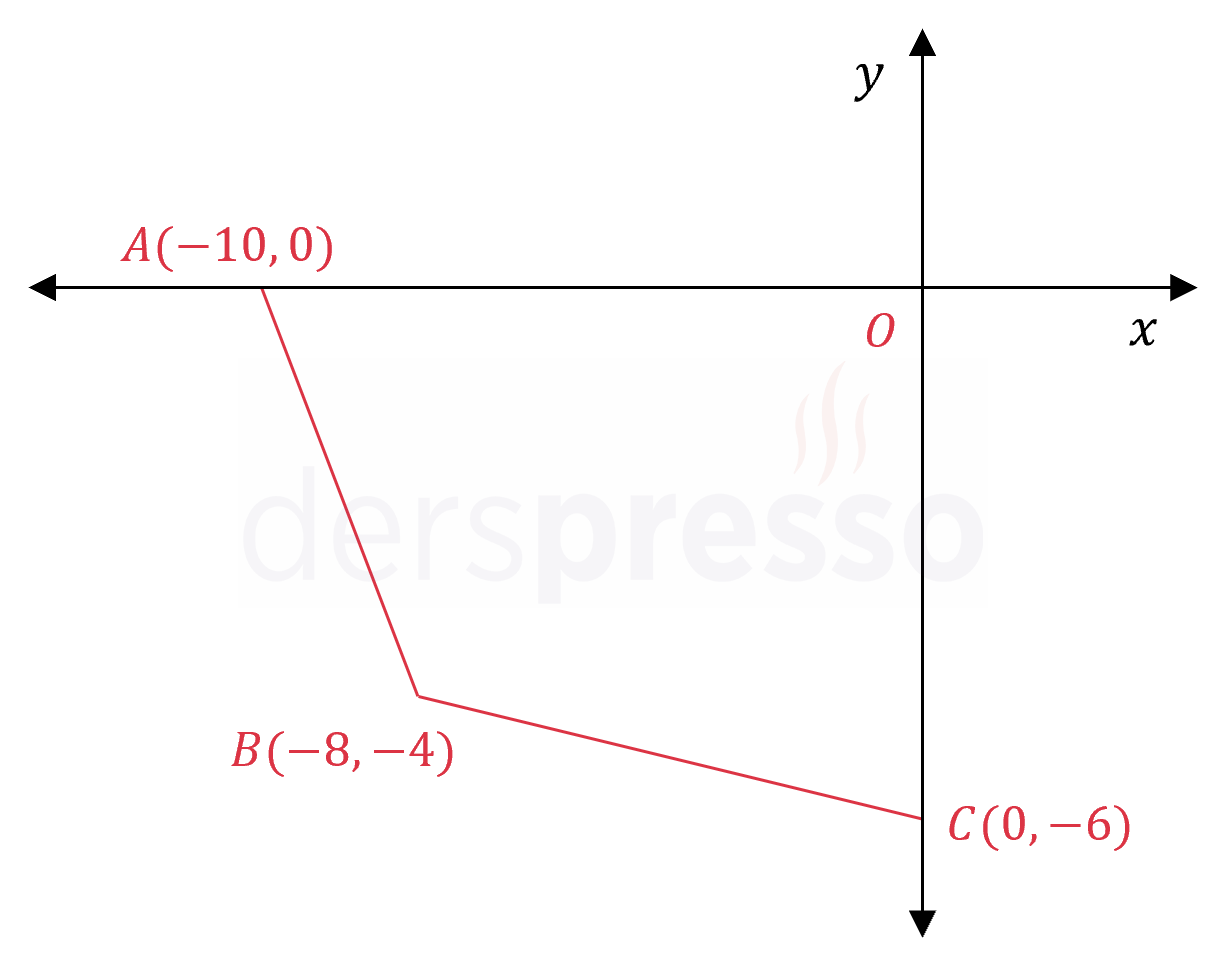
Yukarıdaki şekildeki \( ABCO \) dörtgeninin alanı kaçtır?
Çözümü Göster\( B \) noktasından \( x \) eksenine bir dikme çizelim ve \( x \) eksenini kestiği noktaya \( D \) diyelim.
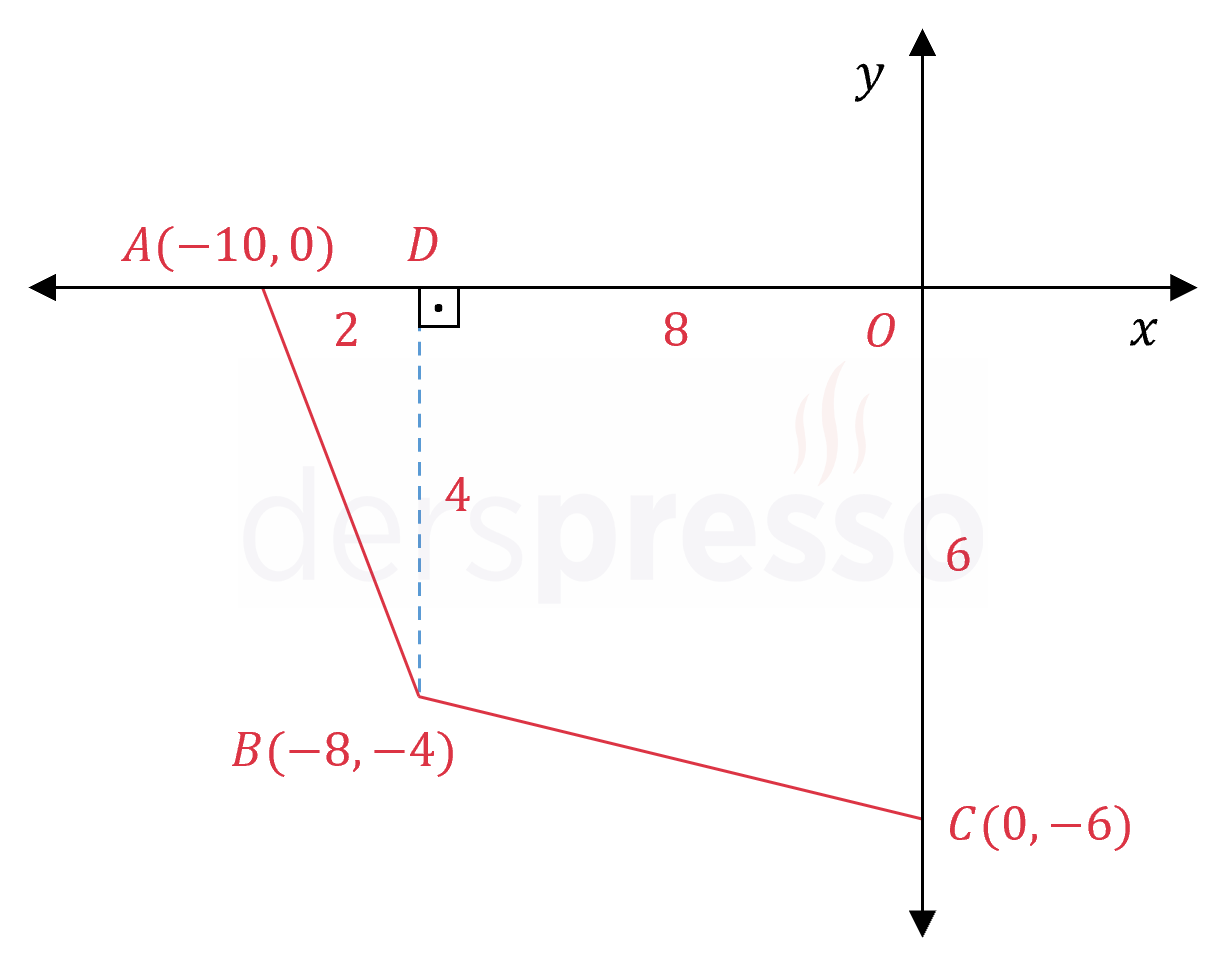
\( [BD] \perp [AO] \)
\( \abs{DO} = 8 \), \( \abs{AD} = 2 \), \( \abs{BD} = 4 \)
\( ABCO \) dörtgeninin alanı, oluşan dik üçgen ve yamuğun alanları toplamına eşittir.
\( A(ABCO) = A(ADB) + A(DBCO) \)
\( ADB \) üçgeninin alanını hesaplayalım.
\( A(ADB) = \dfrac{\abs{AD} \cdot \abs{BD}}{2} \)
\( = \dfrac{2 \cdot 4}{2} = 4 \)
\( DBCO \) yamuğunun alanını hesaplayalım.
\( A(DBCO) = \dfrac{(\abs{BD} + \abs{CO}) \cdot \abs{DO}}{2} \)
\( = \dfrac{(4 + 6) \cdot 8}{2} = 40 \)
\( A(ABCO) = 4 + 40 = 44 \) bulunur.
\( m, n \in \mathbb{R} \) olmak üzere,
Analitik düzlemde \( K(mn, m^3n^4) \) noktası IV. bölgede yer aldığına göre, \( L((m + n)^3, \sqrt[3]{-nm}) \) noktası kaçıncı bölgededir?
Çözümü GösterIV. bölgedeki bir noktanın apsis ve ordinatının işaretleri \( (+, -) \) olur.
\( K \) noktası IV. bölgededir.
\( m^3n^4 \lt 0 \) eşitsizliğini inceleyelim.
\( n^4 \) ifadesi pozitiftir, dolayısıyla \( m^3 \) negatif ve \( m \lt 0 \) olur.
\( mn \gt 0 \) eşitsizliğini inceleyelim.
\( m \lt 0 \) olduğuna göre, \( n \lt 0 \) olur.
\( L \) noktasının bulunduğu bölgeyi bulalım.
İki negatif sayının toplamı negatiftir, dolayısıyla \( m + n \) ve \( (m + n)^3 \) ifadeleri negatif olur.
İki negatif sayının çarpımı pozitiftir, dolayısıyla \( -nm \) negatiftir. Negatif bir sayının küp kökü de negatiftir, dolayısıyla \( \sqrt[3]{-nm} \) ifadesi negatif olur.
\( L \) noktasının hem apsisi hem de ordinatı negatif olduğu için nokta III. bölgededir.
\( a, b \in \mathbb{R} \) olmak üzere,
Analitik düzlemde \( A(a + 4, a - 3) \) noktası IV. bölgede, \( B(b - 2, b - 3) \) noktası III. bölgededir.
Buna göre \( a + b \) toplamının alabileceği en büyük tam sayı değeri kaçtır?
Çözümü Göster\( A \) noktası IV. bölgede olduğuna göre, apsis değeri pozitif, ordinat değeri negatif olur.
\( a + 4 \gt 0 \Longrightarrow a \gt -4 \)
\( a - 3 \lt 0 \Longrightarrow a \lt 3 \)
\( a \) değer aralığı yukarıdaki iki aralığın kesişim kümesidir.
\( -4 \lt a \lt 3 \)
\( B \) noktası III. bölgede olduğuna göre, apsis ve ordinat değerleri negatif olur.
\( b - 2 \lt 0 \Longrightarrow b \lt 2 \)
\( b - 3 \lt 0 \Longrightarrow b \lt 3 \)
\( b \) değer aralığı yukarıdaki iki aralığın kesişim kümesidir.
\( -\infty \lt b \lt 2 \)
\( a + b \) toplamının değer aralığını bulmak için iki eşitsizliği taraf tarafa toplayalım.
\( -\infty \lt a + b \lt 5 \)
Buna göre \( a + b \) toplamının alabileceği en büyük tam sayı değeri 4 olur.
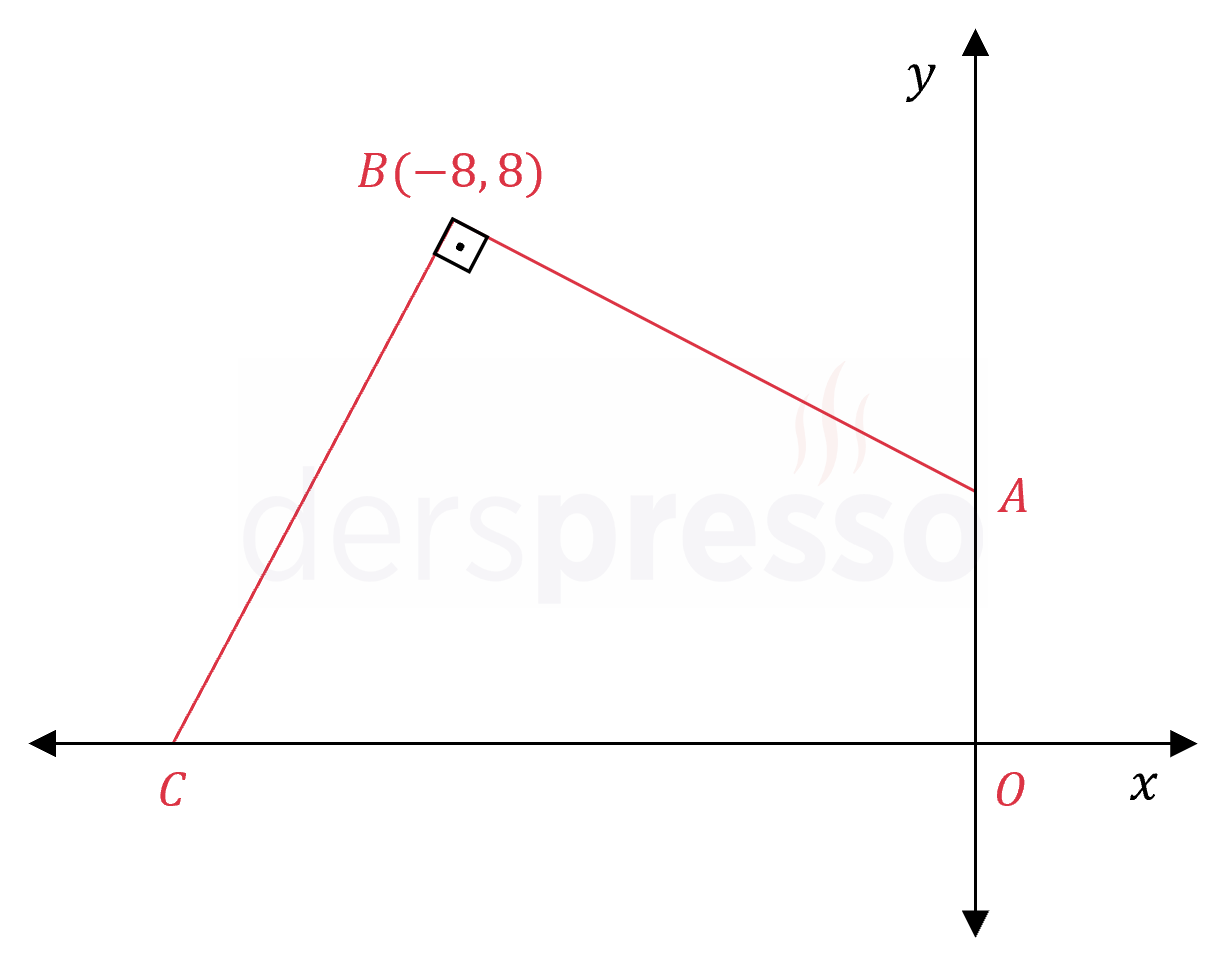
\( ABCO \) bir dörtgendir.
\( [AB] \perp [BC] \) ve \( B(-8, 8) \) olduğuna göre, \( A(ABCO) \) kaçtır?
Çözümü Göster\( B \) noktasından \( x \) ve \( y \) eksenlerine birer dikme çizelim ve eksenleri kestiği noktalara \( E \) ve \( F \) diyelim.
\( B \) noktasının koordinatlarını kullanarak doğru parçalarının uzunluklarını yazalım.
\( \abs{BE} = \abs{BF} = 8 \)
\( m(\widehat{BCE}) = \alpha \) diyelim.
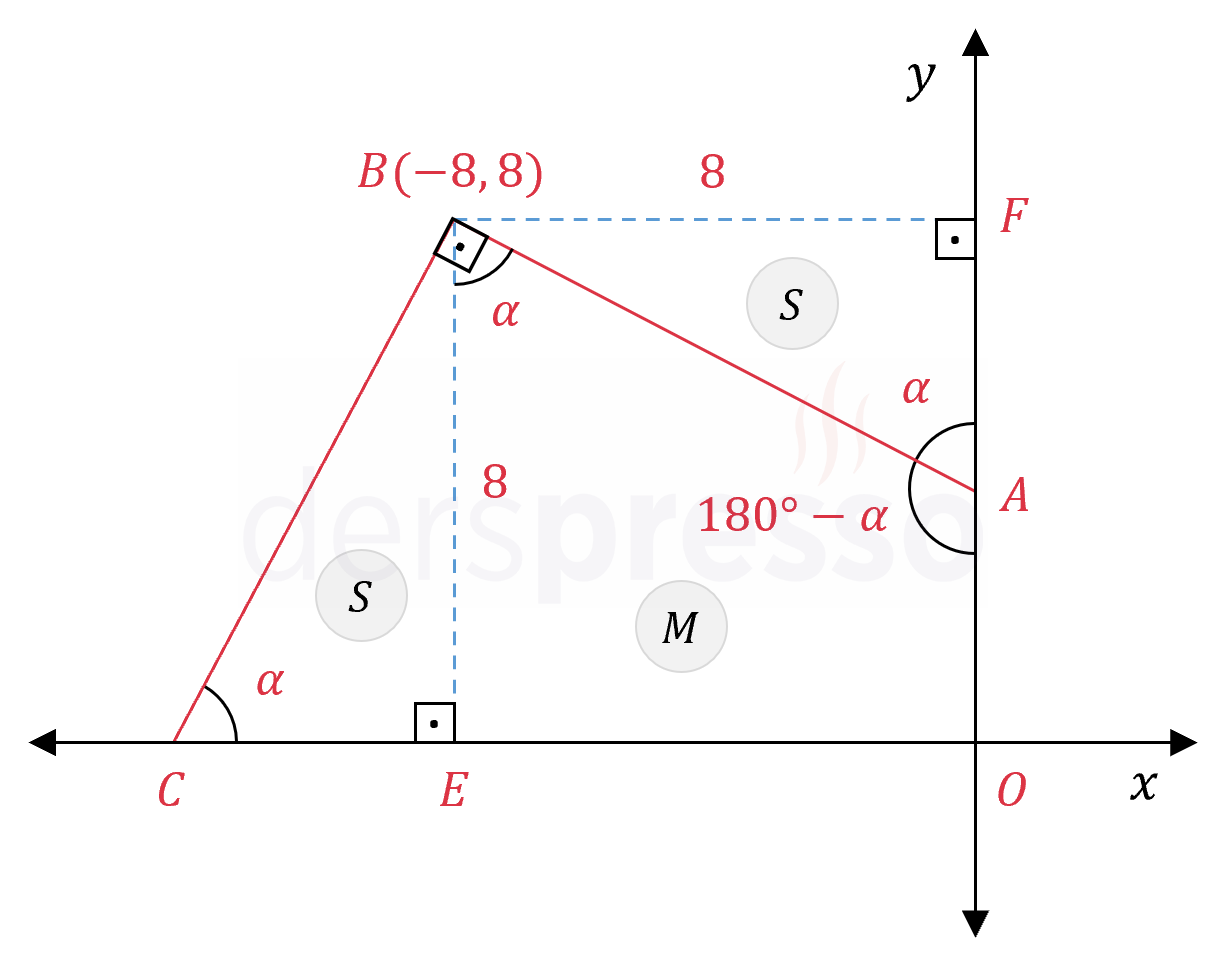
\( m(\widehat{EBA}) = \alpha \)
\( \widehat{EBA} \) ve \( \widehat{BAF} \) iç ters açılardır.
\( m(\widehat{BAF}) = \alpha \)
Açıları ve kenar uzunlukları eşit olan \( BEC \) ve \( BFA \) üçgenleri eş üçgenlerdir.
\( \overset{\triangle}{BEC} \cong \overset{\triangle}{BFA} \)
Oluşan bölgelerin alanlarına değer verelim.
Eş üçgen oldukları için \( A(BEC) = A(BFA) = S \) diyelim.
\( A(BEOA) = M \) diyelim.
Soruda istenen alanı yazalım.
\( A(ABCO) = S + M = A(BEOF) \)
\( A(BEOF) = \abs{BF} \cdot \abs{FO} \)
\( = 8 \cdot 8 = 64 \) bulunur.
\( x \in \mathbb{R^-} \) olmak üzere,
Bir üçgenin köşelerinin koordinatları \( A(-x, 2x), B(2x + 3, 2x), C(-2x - 1, 5 - 3x) \) şeklindedir.
Üçgenin alanı 60 birimkare olduğuna göre, \( x \) kaçtır?
Çözümü GösterÜçgenin köşelerini analitik düzlemde işaretleyelim.

Şekilde görülebileceği gibi, üçgenin \( [AB] \) kenarı \( x \) eksenine paraleldir.
Üçgenin \( [AB] \) kenarını taban, \( [DC] \) doğru parçasını da yükseklik olarak kullanarak üçgenin alanını hesaplayabiliriz.
\( \abs{AB} = 2x + 3 - (-x) = 3x + 3 \)
\( \abs{DC} = 2x - (5 - 3x) = 5x - 5 \)
Üçgenin alanı 60 birimkaredir.
\( A(ABC) = \dfrac{\abs{AB} \cdot \abs{DC}}{2} = 60 \)
\( \dfrac{(3x + 3)(5x - 5)}{2} = 60 \)
\( 3(x + 1) \cdot 5(x - 1) = 120 \)
\( x^2 - 1 = 8 \)
\( x \) negatif olarak veriliyor.
\( x = -3 \) olarak bulunur.
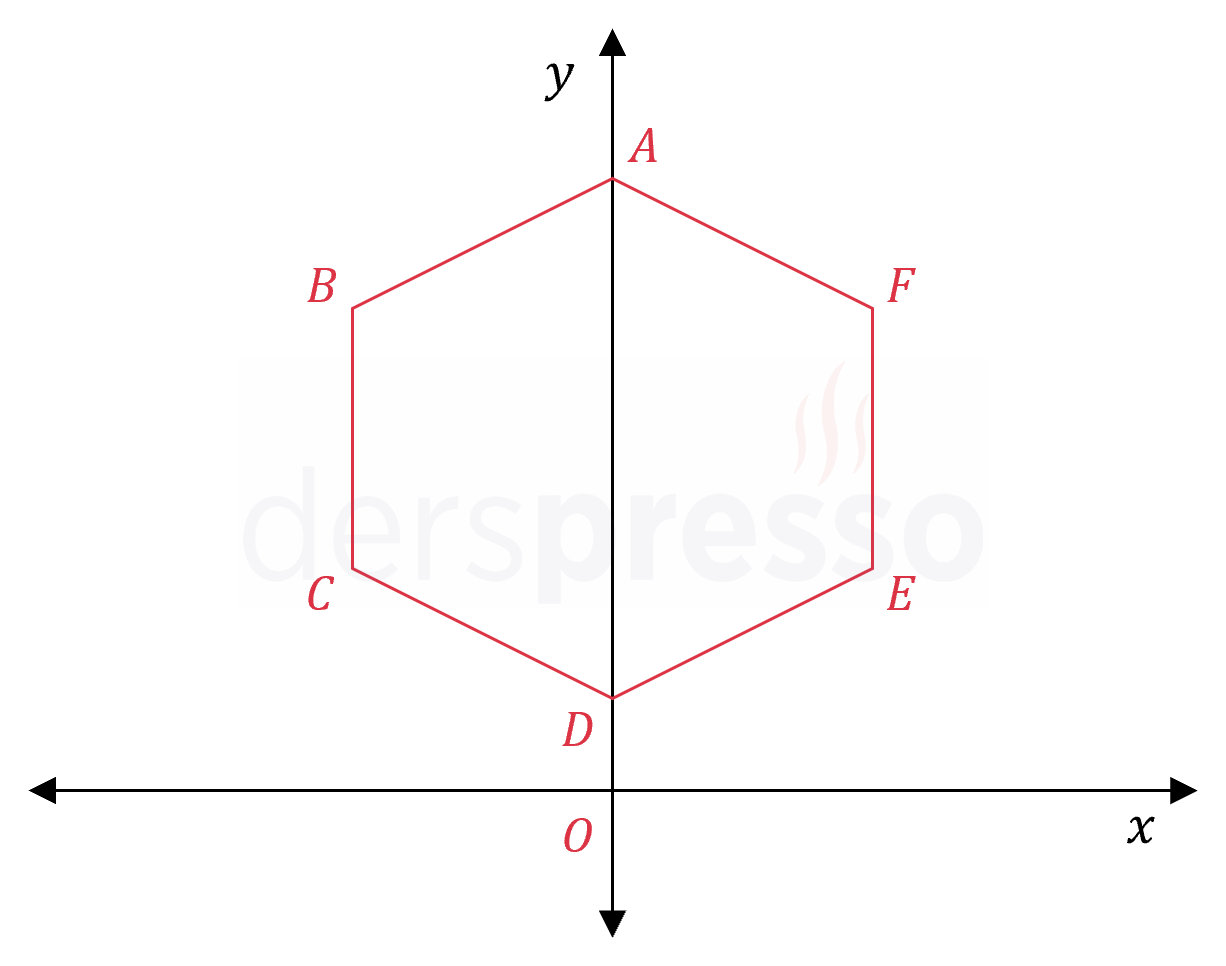
Şekildeki \( ABCDEF \) düzgün altıgeninin ağırlık merkezi \( y \) ekseni üzerindedir.
\( D \) noktasının ordinatı \( \sqrt{3} \), \( B \) noktasının apsisi \( -6 \) olduğuna göre, \( E \) noktasının koordinatları nedir?
Çözümü GösterDüzgün altıgenin ağırlık merkezine \( G \), bir kenar uzunluğuna \( 2a \) diyelim.
\( B \) noktasından \( y \) eksenine bir dikme çizelim ve \( y \) eksenini kestiği noktaya \( H \) diyelim.
\( [BH] \perp [AO] \)
Düzgün altıgende köşelerden merkeze çizilen doğrular 6 eşkanar üçgen oluşturur.
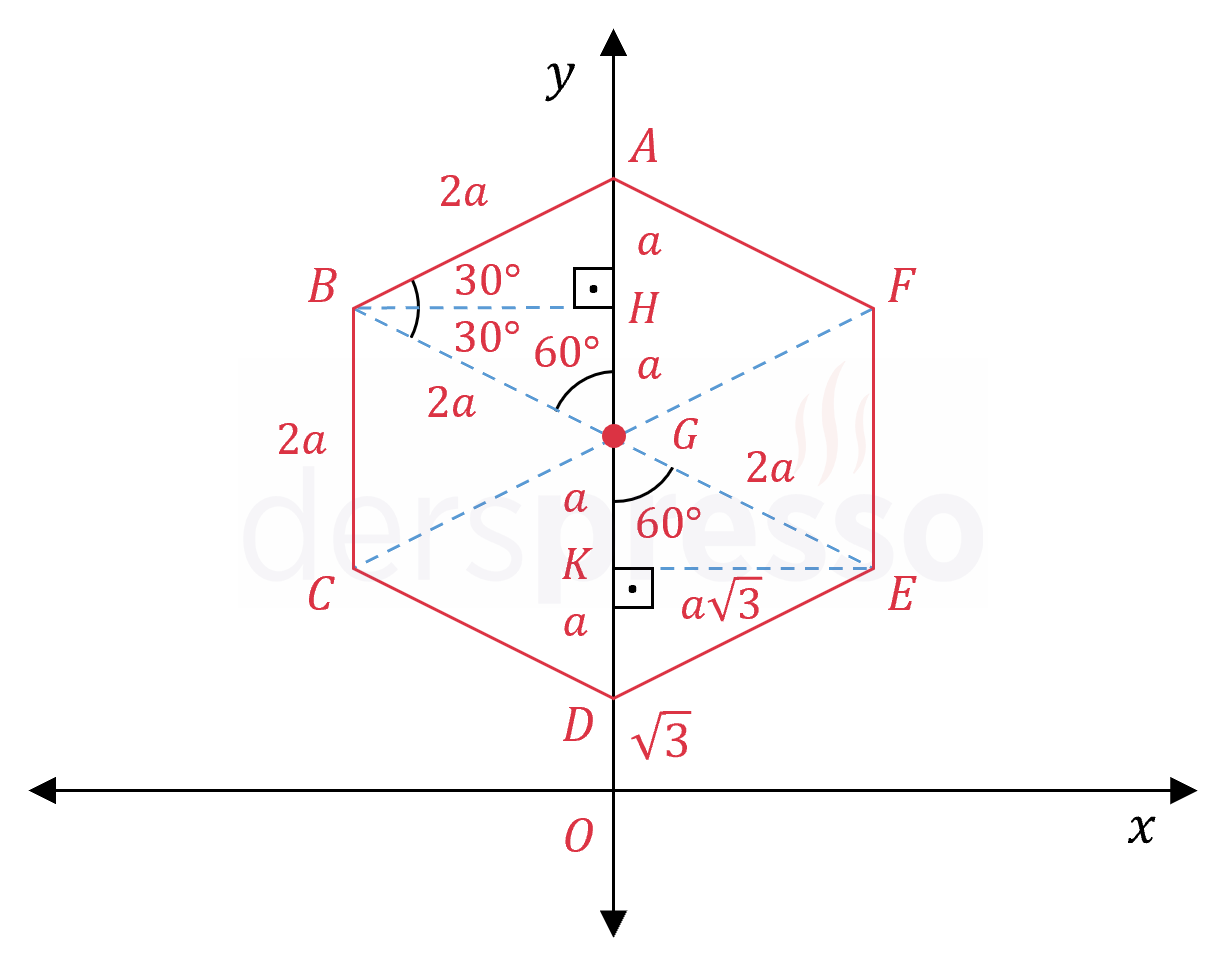
\( [BH] \) doğrusu \( ABG \) üçgeninde kenarortay ve açıortay doğrusudur. Buna göre açıları ve kenar uzunlukları aşağıdaki gibi olur.
\( m(\widehat{ABH}) = m(\widehat{HBG}) = 30° \)
\( m(\widehat{BAG}) = m(\widehat{BGA}) = 60° \)
\( \abs{AH} = \abs{HG} = a \)
\( 30-60-90° \) özel üçgeninde 60°'lik açının gördüğü kenar uzunluğu \( 30° \)'lik açının gördüğü kenar uzunluğunun \( \sqrt{3} \) katıdır.
\( \abs{BH} = a\sqrt{3} \)
\( B \) noktasının \( y \) eksenine olan uzaklığı, noktanın apsisinin mutlak değerine eşittir.
\( B \) noktasının apsisi -6 olarak veriliyor.
\( \abs{BH} = a\sqrt{3} \)
\( 6 = a\sqrt{3} \)
\( a = 2\sqrt{3} \)
\( E \) noktasının koordinatlarını bulalım.
\( E \) noktasından \( y \) eksenine bir dikme çizelim ve \( y \) eksenini kestiği noktaya \( K \) diyelim.
\( [EK] \perp [AO] \)
\( B \) ve \( E \) noktalarının \( y \) eksenine olan uzaklıkları eşittir.
\( \abs{BH} = \abs{EK} = a\sqrt{3} = 6 \)
\( E \) noktasının ordinatı \( \abs{KO} \) değerine eşittir.
\( \abs{KO} = \abs{KD} + \abs{DO} = a + \sqrt{3} \)
\( = 3\sqrt{3} \)
\( E(6, 3\sqrt{3}) \) bulunur.
Analitik düzlemde \( A(-22, 0), B(22, 0) \) ve \( C(0, 22) \) noktalarının oluşturduğu \( ABC \) üçgeninin içinde kalan ve koordinatları tam sayı olan kaç nokta vardır?
Çözümü Göster
Verilen \( ABC \) üçgeni bir ikizkenar üçgendir. Üçgenin I. ve II. bölgeleri birbirine göre simetrik olduğu için I. bölgedeki nokta sayısı II. bölgedeki nokta sayısına eşit olur.
I. bölgede kalan ve koordinatları tam sayı olan noktaların sayısını bulalım.
\( x = 1 \) doğrusu üçgenin kenarını \( (1, 21) \) noktasında keser; bu nedenle \( x = 1 \) doğrusu üzerinde olan, üçgenin kenarları üzerinde olmayan ve koordinatları \( (1, 1) \) ile \( (1, 20) \) arasında olan 20 nokta vardır.
\( x = 2 \) doğrusu üçgenin kenarını \( (2, 20) \) noktasında keser; bu nedenle \( x = 2 \) doğrusu üzerinde olan, üçgenin kenarları üzerinde olmayan ve koordinatları \( (2, 1) \) ile \( (2, 19) \) arasında olan 19 nokta vardır.
\( \vdots \)
\( x = 20 \) doğrusu üçgenin kenarını \( (20, 2) \) noktasında keser; bu nedenle \( x = 20 \) doğrusu üzerinde olan, üçgenin kenarları üzerinde olmayan ve koordinatları \( (20, 1) \) ile \( (20, 1) \) arasında olan 1 nokta vardır.
\( x = 21 \) doğrusu üçgenin kenarını \( (21, 1) \) noktasında keser; bu nedenle \( x = 21 \) doğrusu üzerinde olan, üçgenin kenarları üzerinde olmayan nokta yoktur.
Analitik düzlemin I. bölgesinde bulunan nokta sayısını ardışık sayıların toplam formülü ile bulalım.
\( 20 + 19 + \ldots + 1 = \dfrac{20(20 + 1)}{2} \)
\( = 210 \)
Analitik düzlemin II. bölgesinde de eşit sayıda, yani 210 nokta vardır.
Son olarak \( y = 0 \) doğrusu üzerinde olan ve üçgenin kenarları üzerinde olmayan nokta sayısını bulalım.
\( y = 0 \) doğrusu üzerinde, üçgenin kenarları üzerinde olmayan ve koordinatları \( (0, 1) \) ile \( (0, 21) \) arasında olan 21 nokta vardır.
Buna göre, istenen koşulları sağlayan \( 210 + 210 + 21 = 441 \) nokta vardır.
\( x, y \in \mathbb{Z} \) olmak üzere,
\( \abs{x} + \abs{y} \lt 15 \) eşitsizliğini sağlayan kaç tane \( (x, y) \) ikilisi vardır?
Çözümü GösterSoruyu analitik düzlem üzerinde modelleyerek çözelim.
Eksenler üzerindeki noktaları gözardı ederek koordinat düzleminin birinci bölgesinde eşitsizliği sağlayan noktaları bulalım.
\( x = 1 \) için: \( y \in \underbrace{\{ 1, 2, \ldots, 13 \}}_\text{13 adet} \)
\( x = 2 \) için: \( y \in \underbrace{\{ 1, 2, \ldots, 12 \}}_\text{12 adet} \)
\( \vdots \)
\( x = 13 \) için: \( y \in \underbrace{\{ 1 \}}_\text{1 adet} \)
1. bölgedeki \( (x, y) \) ikililerinin toplam sayısını ardışık sayıların toplam formülü ile bulalım.
\( 1 + 2 + \ldots + 13 = \dfrac{13 \cdot 14}{2} = 91 \)
İfadeler mutlak değer içinde olduğu için bu noktaların diğer bölgelerdeki yansımaları da eşitsizliği sağlar.
\( 4 \cdot 91 = 364 \) nokta
Bu noktalara eksenler üzerinde bulunan noktaları ekleyelim.
\( x \) ekseni üzerinde \( (14, 0) \) ve \( (-14, 0) \) arasında 29 nokta eşitsizliği sağlar.
\( y \) ekseni üzerinde \( (0, 14) \) ve \( (0, -14) \) arasında 29 nokta eşitsizliği sağlar.
\( (x, y) = (0, 0) \) noktası iki eksen üzerinde de bulunduğu için iki eksen üzerindeki noktaların toplamından 1 çıkarmalıyız.
\( 364 + 29 + 29 - 1 = 421 \) ikili bulunur.