Koordinat Düzlemi

Kartezyen koordinat sistemi, bir noktanın konumunun birbirine dik eksenlere olan pozitif/negatif yöndeki uzaklıkları şeklinde ifade edildiği bir sistemdir. Başka koordinat sistemleri de bulunmakla birlikte, kartezyen koordinat sistemi analitik geometride en sık kullanılan koordinat sistemidir.

İki Boyutlu Kartezyen Koordinat Sistemi

İki boyutlu kartezyen koordinat sistemi birbirine dik \( x \) ve \( y \) koordinat eksenlerinden ve bu eksenlerin oluşturduğu koordinat düzleminden (analitik düzlem) oluşur. \( x \) ekseni yatay ekseni, \( y \) ekseni dikey ekseni temsil eder.

Eksenlerin kesişim noktasına başlangıç noktası ya da orijin denir ve genellikle \( O \) ile gösterilir.

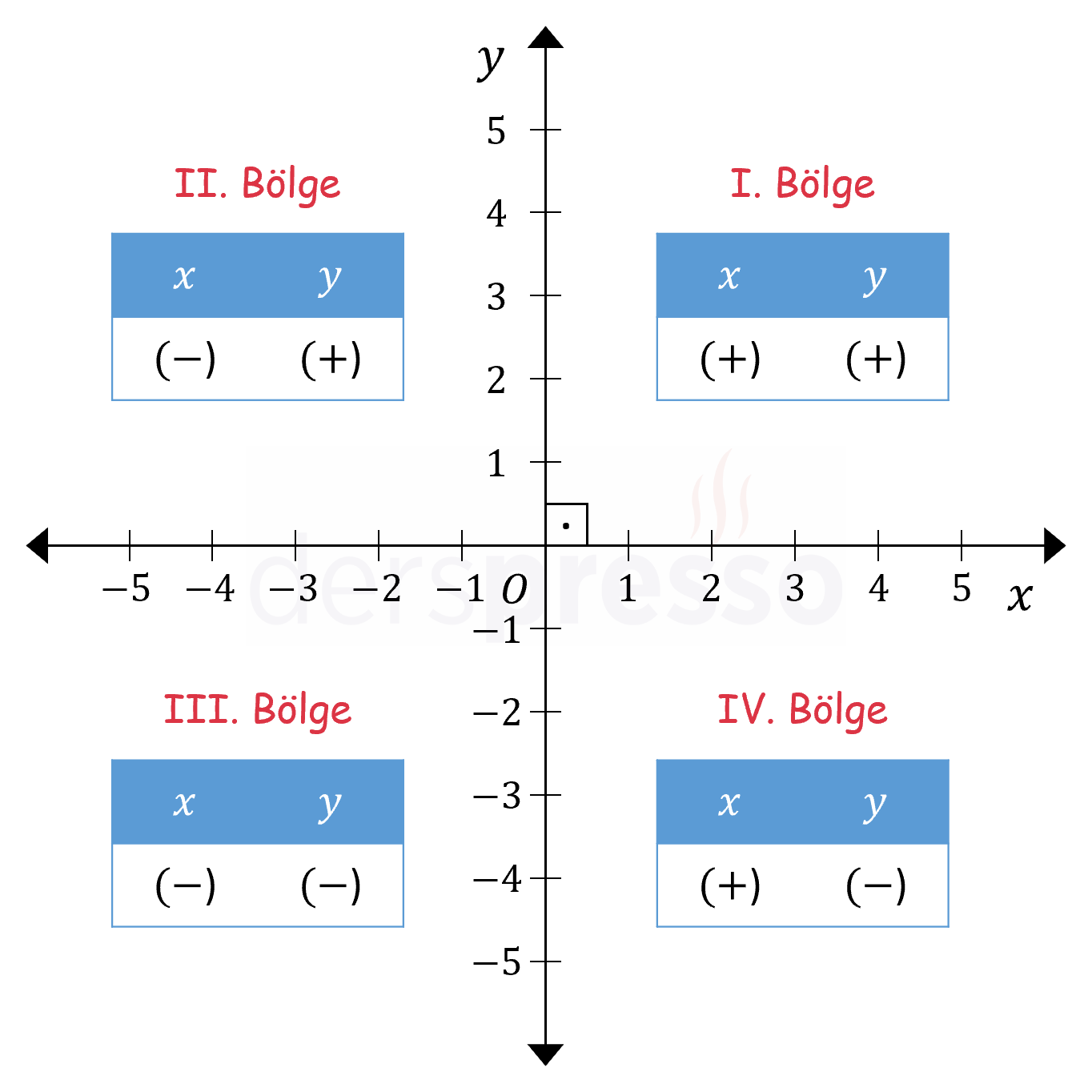
Eksenler analitik düzlemi I., II., III. ve IV. bölge olarak adlandırılan dört bölgeye ayırırlar. Eksenler bu bölgelere dahil değildir.

Sayı doğrusuna benzer şekilde, eksenlerin üzerindeki her nokta birer reel sayıya karşılık gelir. Bu değerler başlangıç noktasında iki eksen için de sıfırdır, \( x \) ekseninde sağa doğru artar, sola doğru azalır, \( y \) ekseninde ise yukarı doğru artar, aşağı doğru azalır.