Çoklu Kümelerde (Tekrarlı) Permütasyon
Permütasyonu bir kümenin elemanlarının her bir farklı dizilişi olarak tanımlamıştık. Küme tanımı gereği bir eleman bir kümede yalnız bir kez bulunabildiği için belirli bir permütasyonda da sadece bir kez yer alabilir.
Kümeler konusunun sonunda kısaca değindiğimiz çoklu kümelerde ise elemanlar birden fazla kez (tekrarlı) bulunabilir, dolayısıyla belirli bir permütasyonda çoklu kümede bulundukları adetlerde yer alabilirler.
Tekrar eden elemanların bulunduğu kümelerin tüm dizilişlerinde birbirinin aynısı dizilişler elde edildiği için çoklu kümeler için farklı bir permütasyon formülü kullanılır.
\( n \) bir çoklu kümenin eleman sayısı,
\( n_1, n_2, \ldots, n_k \) kümedeki \( k \) farklı elemanın çoklu kümede bulunma sayıları olmak üzere,
Permütasyon sayısı \( = \dfrac{n!}{n_1!\ n_2! \ldots n_k!} \)
115777 sayısındaki rakamlarla yazılabilecek 6 basamaklı sayılar:
\( A = \{1, 1, 5, 7, 7, 7\} \)
Permütasyon sayısı \( = \dfrac{6!}{2!\ 3!} \)
4 özdeş matematik, 3 özdeş fizik ve 2 özdeş kimya kitabının bir rafa farklı diziliş sayısı:
\( B = \{\text{M, M, M, M, F, F, F, K, K}\} \)
Permütasyon sayısı\( = \dfrac{9!}{4!\ 3!\ 2!} \)
İSPATI GÖSTER
\( A \) kümesi \( n \) elemanlı bir çoklu küme olsun.
\( A \) kümesindeki \( k \) farklı elemana \( a_1, a_2, \ldots, a_k \) ve bu farklı elemanların çoklu kümede bulunma sayılarına \( n_1, n_2, \ldots, n_k \) diyelim.
Farklı elemanların kümede bulunma sayılarının toplamı \( A \) kümesinin eleman sayısını verir.
\( n_1 + n_2 + \ldots + n_k = n \)
Oluşturulacak farklı dizilişlerdeki her basamağı birer kutu olarak düşünelim. Tekrarlı permütasyon problemini bu noktada bir kombinasyon problemi olarak kurgulayalım.
Birinci adım: \( n_1 \) adet özdeş \( a_1 \) elemanını yerleştirmek için \( n \) kutu arasından \( n_1 \) kutu \( C(n, n_1) \) farklı şekilde seçilebilir.
İkinci adım: \( n_2 \) adet özdeş \( a_2 \) elemanını yerleştirmek için kalan \( n - n_1 \) kutu arasından \( n_2 \) kutu \( C(n - n_1, n_2) \) farklı şekilde seçilebilir.
Üçüncü adım: \( n_3 \) adet özdeş \( a_3 \) elemanını yerleştirmek için kalan \( n - n_1 - n_2 \) kutu arasından \( n_3 \) kutu \( C(n - n_1 - n_2, n_3) \) farklı şekilde seçilebilir.
Son adım: \( n_k \) adet özdeş \( a_k \) elemanını yerleştirmek için kalan \( n - n_1 - \ldots - n_{k - 1} \) kutu arasından \( n_k \) kutu \( C(n - n_1 - \ldots - n_{k - 1}, n_k) \) farklı şekilde seçilebilir.
Tüm bu seçimler birbirinden bağımsız olduğu için, yukarıda bulduğumuz ifadelerin çarpımı \( a_1, a_2, \ldots, a_k \) elemanlarının tümünün \( n \) kutuya farklı yerleştirme sayısını verir.
\( C(n, n_1) \cdot C(n - n_1, n_2) \cdot C(n - n_1 - n_2, n_3) \cdot \ldots \cdot C(n - n_1 - \ldots - n_{k - 1}, n_k) \)
\( \dfrac{n!}{n_1!\ (n - n_1)!} \cdot \) \( \dfrac{(n - n_1)!}{n_2!\ (n - n_1 - n_2)!} \cdot \) \( \dfrac{(n - n_1 - n_2)!}{n_3!\ (n - n_1 - n_2 - n_3)!} \cdot \) \( \ldots \cdot \) \( \dfrac{(n - n_1 - \ldots - n_{k - 1})!}{n_k!\ (n - n_1 - \ldots - n_{k - 1} - n_k)!} \)
Son ifadede paydadaki aşağıdaki ifade \( n_1 + n_2 + \ldots + n_k = n \) olduğu için \( 0! = 1 \)'e eşittir.
\( (n - n_1 - \ldots - n_{k - 1} - n_k)! \) \( = (n - (n_1 + \ldots + n_{k - 1} + n_k))! \) \( = (n - n)! = 0! = 1 \)
İfadede pay ve paydadaki çarpanlar aralarında sadeleştirildiğinde tekrarlı permütasyon formülü elde edilir.
Permütasyon sayısı \( = \dfrac{n!}{n_1!\ n_2! \ldots n_k!} \)
\( 1! = 1 \) olduğu için çoklu kümede sadece 1 kez yer alan elemanlar permütasyon formülünde paydaya dahil edilmeyebilir.
İki örnekle çoklu kümelerin permütasyon formülünün mantığını açıklamaya çalışalım.
4 harfli KİVİ kelimesinin harflerinin standart permütasyon formülüne göre \( 4! = 24 \) dizilişi vardır, ancak "İ" harfi kelimede iki kez bulunduğu için bu dizilişlerin bazıları birbirinin aynısıdır.
"İ" harfleri her dizilişte kendi aralarında \( 2! = 2 \) şekilde yer değiştirebilir ve bu yer değiştirmeler farklı bir diziliş oluşturmaz, dolayısıyla 24 diziliş \( 2! = 2 \)'şerli gruplandığında farklı diziliş sayısı olan \( \frac{4!}{2!} = 12 \) bulunur.
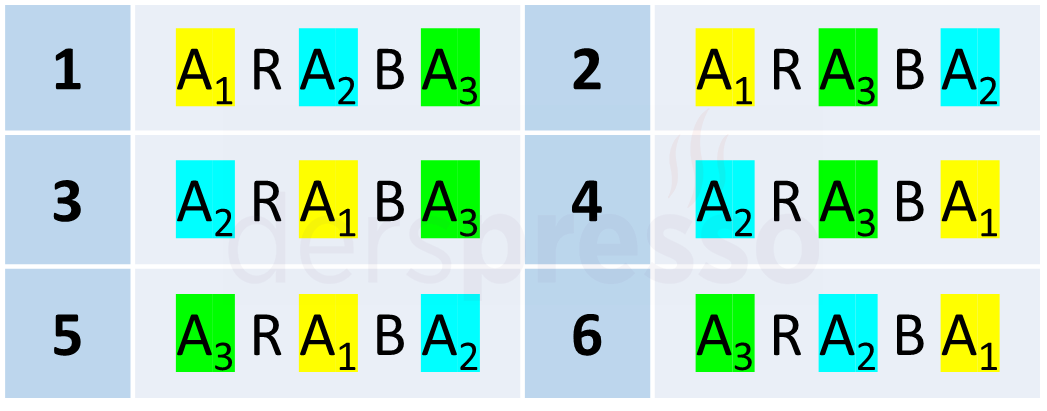
5 harfli ARABA kelimesinin harflerinin standart permütasyon formülüne göre \( 5! = 120 \) dizilişi vardır, ancak "A" harfi kelimede üç kez bulunduğu için bu dizilişlerin bazıları birbirinin aynısıdır.
"A" harfleri her dizilişte kendi aralarında \( 3! = 6 \) şekilde yer değiştirebilir ve bu yer değiştirmeler farklı bir diziliş oluşturmaz, dolayısıyla 120 diziliş \( 3! = 6 \)'şarlı gruplandığında farklı diziliş sayısı olan \( \frac{5!}{3!} = 20 \) bulunur.
DERSPRESSO kelimesinin harfleri ile 10 harfli kaç farklı kelime yazılabilir?
Çözümü Göster1. yöntem:
Tekrarlı permütasyon formülünü kullanalım.
\( A = \{\text{D, E, R, S, P, R, E, S, S, O}\} \)
Çoklu kümede "E" ve "R" harfleri 2'şer kez, "S" harfi 3 kez yer almaktadır.
Yazılabilecek 10 harfli kelimelerin sayısı:
\( \dfrac{10!}{2!\ 2!\ 3!} \)
2. yöntem:
Tekrarlı permütasyon formülünün ispatında kullandığımız yaklaşımı uygulayalım.
DERSPRESSO kelimesinin 10 harfinin her birini birer kutu olarak düşünelim.
Kelimede 2 kez bulunan özdeş "E" harflerini yerleştirmek için bu 10 kutudan 2 kutuyu \( C(10, 2) \) farklı şekilde seçebiliriz.
Kelimede 2 kez bulunan özdeş "R" harflerini yerleştirmek için kalan 8 kutudan 2 kutuyu \( C(8, 2) \) farklı şekilde seçebiliriz.
Kelimede 3 kez bulunan özdeş "S" harflerini yerleştirmek için kalan 6 kutudan 3 kutuyu \( C(6, 3) \) farklı şekilde seçebiliriz.
Kelimede 1'er kez bulunan "D", "P" ve "O" harflerini kalan 3 kutuya \( 3! \) farklı şekilde yerleştirebiliriz.
Çarpma kuralı ile tüm bu farklı seçim ve dizilişlerin çarpımını alalım.
\( C(10, 2) \cdot C(8, 2) \cdot C(6, 3) \cdot 3! \)
\( = \dfrac{10!}{2!\ 8!} \cdot \dfrac{8!}{2!\ 6!} \cdot \dfrac{6!}{3!\ 3!} \cdot 3! \)
Pay ve paydadaki ifadeleri sadeleştirdiğimizde tekrarlı permütasyon formülü ile aynı sonucu elde ederiz.
\( \dfrac{10!}{2!\ 2!\ 3!} \)
Bir madeni para arka arkaya 8 kez atıldığında kaç farklı şekilde 4 yazı ve 4 tura gelebilir?
Çözümü GösterHer yazı-tura atışının sonucunu "Y" ya da "T" olarak kodlayalım. Buna göre örneğin önce 4 yazı sonra 4 tura gelen senaryoyu "YYYYTTTT" şeklinde ifade edebiliriz.
Bu durumda soruyu 4 "Y" ve 4 "T" harfinden oluşan 8 elemanlı bir çoklu kümenin permütasyon sayısı olarak kurgulayabiliriz.
\( A = \{\text{Y, Y, Y, Y, T, T, T, T}\} \)
Permütasyon sayısı:
\( = \dfrac{8!}{4!\ 4!} = 70 \) bulunur.
\( A = \{0, 0, 4, 4, 4, 8, 8\} \) çoklu kümesinin elemanlarını kullanarak 7 basamaklı ve \( 840 \) ile biten kaç farklı doğal sayı yazılabilir?
Çözümü Gösterİstenen koşulu sağlayacak şekilde birer tane 8, 4 ve 0 rakamını sayının son 3 basamağına yerleştirelim.
Kalan \( 0, 4, 4, 8 \) rakamlarını kullanarak 4 basamaklı kaç farklı sayı yazabileceğimizi hesaplayalım.
0 rakamını 1. basamağa yazamayacağımız için bu 4 rakam \( 3 \cdot 3 \cdot 2 \cdot 1 = 18 \) farklı şekilde dizilebilir.
Bu dizilişler içinde 4 rakamı iki kez bulunduğu için bu rakamlar aralarında yer değiştirdiğinde yeni bir sayı oluşmaz, dolayısıyla tekrarlı permütasyon formülü gereği bulduğumuz sayıyı \( 2! \)'e bölmeliyiz.
Yazılabilecek 7 basamaklı ve \( 840 \) ile biten sayı adedi:
\( = \dfrac{18}{2!} = 9 \)
"KARMAKARIŞIK" kelimesinin harfleri ile anlamlı ya da anlamsız yazılabilecek 12 harfli kelimelerin kaç tanesi "K" ile başlayıp "A" ile biter?
Çözümü GösterBirer tane "K" ve "A" harfini kelimenin başında ve sonunda kullanmak üzere ayıralım.
Bu iki harfi ayırdıktan sonra geriye 10 harf kalır. Bu 10 harf içerisinde "A", "R", "K" ve "I" harfleri 2'şer kez bulunur.
Yazılabilecek 10 harfli kelimelerin sayısını bulmak için tekrarlı permütasyon formülünü kullanalım.
Permütasyon sayısı:
\( = \dfrac{10!}{2!\ 2!\ 2!\ 2!} \)
Bu 10 harfli kelimelerin her birinin başına "K" ve sonuna "A" harflerini eklediğimizde istenen koşulu sağlayan kelimeler elde etmiş oluruz.
Ceylin 4 haneli telefon şifresini doğum tarihindeki rakamlar olan 1, 4, 5, 8, 9 rakamlarını kullanarak ve her zaman iki rakam aynı olacak şekilde oluşturuyor.
Şifresini her hafta bu kurala uygun şekilde değiştiren Ceylin, kaç hafta sonunda daha önce kullandığı bir şifreyi tekrar kullanmadan yeni şifre oluşturamaz?
Çözümü GösterŞifrede kullanılmak üzere 5 rakam içinden 3 rakam \( C(5, 3) = 10 \) farklı şekilde seçilebilir.
Seçilen 3 rakam içinden 2 kez kullanılacak olan rakam \( C(3, 1) = 3 \) farklı şekilde seçilebilir.
Bu iki seçim sonucunda 4 haneli ve 2 rakamı aynı olan bir şifre (tekrarlı permütasyon formülü ile) \( \frac{4!}{2!} = 12 \) farklı şekilde oluşturulabilir.
Buna göre Ceylin belirlediği kurala uygun şekilde \( 10 \cdot 3 \cdot 12 = 360 \) farklı şifre oluşturabilir, dolayısıyla 360 hafta sonunda daha önce kullandığı bir şifreyi tekrar kullanmadan yeni şifre oluşturamaz.
Rakamlarından ikisinin çarpımı üçüncü rakamına eşit olan 3 basamaklı kaç sayı vardır?
Çözümü GösterBu koşulu sağlayan sayılar dört şekilde olabilir.
Durum 1: 3 rakam da aynı
Bu duruma uyan tek sayı vardır.
111
Durum 2: 2 rakam aynı, 1 rakam farklı (0 hariç)
Bu duruma uyan rakam kümeleri 10 tanedir.
122, 133, 144, 155, 166, 177, 188, 199, 224, 339
122 sayısının rakamları kullanılarak yazılabilecek 3 basamaklı sayıların sayısı tekrarlı permütasyon formülü ile \( \frac{3!}{2!} = 3 \) olarak bulunur.
10 farklı rakam kümesi için \( 10 \cdot 3 = 30 \) farklı sayı yazılabilir.
Durum 3: x00 formundaki sayılar
Bu duruma uyan 9 sayı vardır.
100, 200, 300, ..., 900
Bu sayılarda rakamların yer değiştirmesi sonucunda oluşan sayılar 3 basamaklı olmayacağı için sayıların permütasyonlarını dikkate alamayız.
Durum 4: 3 rakam da farklı
Bu duruma uyan rakam kümeleri 2 tanedir.
236, 248
236 sayısının rakamları kullanılarak yazılabilecek 3 basamaklı sayıların sayısı \( 3! = 6 \) olarak bulunur.
2 farklı rakam kümesi için \( 2 \cdot 6 = 12 \) farklı sayı yazılabilir.
İstenen koşulu sağlayan toplam \( 1 + 30 + 9 + 12 = 52 \) farklı sayı yazılabilir.
Rakamları çarpımı 1000 olan 7 basamaklı kaç sayı vardır?
Çözümü Göster1000 sayısını asal çarpanlarına ayıralım.
\( 1000 = 5^3 \cdot 2^3 \)
Bu asal çarpanlar ile 7 basamaklı sayı üç farklı şekilde oluşturulabilir.
Durum 1: 5552221 rakamları ile
5552221 rakamlarının farklı dizilişlerini tekrarlı permütasyon formülünü kullanarak bulalım.
\( \dfrac{7!}{3!\ 3!} = 140 \)
Durum 2: 5554211 rakamları ile
5554211 rakamlarının farklı dizilişlerini tekrarlı permütasyon formülünü kullanarak bulalım.
\( \dfrac{7!}{3!\ 2!} = 420 \)
Durum 3: 5558111 rakamları ile
5558111 rakamlarının farklı dizilişlerini tekrarlı permütasyon formülünü kullanarak bulalım.
\( \dfrac{7!}{3!\ 3!} = 140 \)
Rakamları çarpımı 1000 olan 7 basamaklı sayıların toplam adedi bu üç durumda bulduğumuz sayıların toplamına eşittir.
\( 140 + 420 + 140 = 700 \) bulunur.
5 tane 1 rakamı, 4 tane 7 rakamı ve 1 tane 3 rakamı kullanılarak kaç farklı 9 basamaklı sayı oluşturulabilir?
Çözümü GösterElimizde 10 rakam bulunduğu için bir rakam dışarıda kalmak zorundadır.
Dışarda bırakılan rakamın 1, 7 ve 3 olduğu durumları ayrı ayrı inceleyelim.
Durum 1: Dışarıda bırakılan rakam 1
4 tane 1 rakamı, 4 tane 7 rakamı ve 1 tane 3 rakamı ile oluşturulabilecek 9 basamaklı sayıların sayısı:
\( = \dfrac{9!}{4!\ 4!} = 630 \)
Durum 2: Dışarıda bırakılan rakam 7
5 tane 1 rakamı, 3 tane 7 rakamı ve 1 tane 3 rakamı ile oluşturulabilecek 9 basamaklı sayıların sayısı:
\( = \dfrac{9!}{5!\ 3!} = 504 \)
Durum 3: Dışarıda bırakılan rakam 3
5 tane 1 rakamı, 4 tane 7 rakamı ve 0 tane 3 rakamı ile oluşturulabilecek 9 basamaklı sayıların sayısı:
\( = \dfrac{9!}{5!\ 4!} = 126 \)
Bu 3 durum için bulduğumuz sayıların toplamını alalım.
Verilen rakamlarla 9 basamaklı \( 630 + 504 + 126 = 1260 \) farklı sayı oluşturulabilir.
Tersten ve düzden aynı şekilde okunan ifadelere palindrom denir.
İki tane 1, dört tane 2, beş tane 3 rakamı kullanılarak kaç farklı 11 basamaklı palindrom sayı yazılabilir?
Çözümü GösterOluşturulacak sayılar palindrom olacağı için, ilk 5 basamakta kullanılan rakamların aynıları son 5 basamakta kullanılır.
Verilen rakamlardan sadece 3 tek sayıda bulunduğu için 6. basamağa 3 gelmek zorundadır.
Örnek: 13322322331
Oluşturulabilecek palindrom sayısı, bir tane 1, iki tane 2, iki tane 3 rakamı ile oluşturulabilecek 5 basamaklı sayıların sayısına eşittir.
Bu sayıların sayısını tekrarlı permütasyon formülü ile bulalım.
\( \dfrac{5!}{2!\ 2!} = 30 \)
Buna göre, verilen rakamlarla 11 basamaklı 30 palindrom sayı yazılabilir.
4 evli çift bir uçağa binmek için sıraya girecektir. Her kadın sırada eşinin önünde bir yerde olmak koşuluyla, bu 8 kişi kaç farklı şekilde sıraya girebilir?
Çözümü Göster8 kişi hiçbir koşul olmadan \( 8! \) farklı şekilde sıraya girebilir.
Her evli çiftten sadece kadının erkeğin önünde bir yerde olduğu dizilişler geçerli olduğu için, bu diziliş sayısını her çift için \( 2! \)'e bölmeliyiz.
\( \dfrac{8!}{2!\ 2!\ 2!\ 2!} = 2520 \) bulunur.
25242 sayısının rakamları ile oluşturulabilecek tüm 5 basamaklı sayıların aritmetik ortalaması nedir?
Çözümü GösterVerilen sayı içinde "2" rakamı üç kez bulunur.
Bu rakamlar ile 5 basamaklı kaç sayı oluşturulabileceğini tekrarlı permütasyon formülü ile bulalım.
\( \dfrac{5!}{3!} = 5 \cdot 4 = 20 \)
"2", "4" ve "5" rakamlarının sayıları arasında 3:1:1 oranı vardır ve rakamların oluşturulacak sayıların her basamağında kaç kez bulunacağı bu orana göre belirlenir.
Buna göre oluşturulabilecek 20 sayının her basamağında 12 kez "2", 4 kez "4" ve 4 kez "5" kullanılır.
Bu 20 sayının birler basamağındaki rakamların toplamı \( 12 \cdot 2 + 4 \cdot 4 + 4 \cdot 5 = 60 \) olur.
20 sayının onlar basamağında da aynı rakamlar aynı sayıda bulunacağı için bu basamaktaki rakamların basamak değerlerinin toplamı \(60 \cdot 10 = 600 \) olur.
Benzer şekilde, 20 sayının yüzler basamağındaki rakamların basamak değerlerinin toplamı \(60 \cdot 100 = 6000 \) olur.
Benzer şekilde, 20 sayının binler basamağındaki rakamların basamak değerlerinin toplamı \(60 \cdot 1000 = 60000 \) olur.
Benzer şekilde, 20 sayının on binler basamağındaki rakamların basamak değerlerinin toplamı \(60 \cdot 100000 = 6000000 \) olur.
Bu basamak değerlerinin tümünü topladığımızda 20 sayının toplamını elde ederiz.
\( 600000 + 60000 + 6000 + 600 + 60 = 666660 \)
Sayıların ortalamasını bulmak için sayıların toplamını 20'ye bölelim.
\( \dfrac{666660}{20} = 33333 \) bulunur.
Bir anne, okula göndereceği 4 çocuğunun her birine önce çorap, sonra ayakkabı giydirip en son bağcıklarını bağlayacaktır. Çorap, ayakkabı giydirme ve bağcık bağlama sırası her çocuk için aynı olsa da anne bu 12 işlemi herhangi bir sırada yapabilmektedir.
Örnek: 1. çocuk çorap, 2. çocuk çorap, 1. çocuk ayakkabı, 3. çocuk çorap, 1. çocuk bağcık, 2. çocuk ayakkabı, ...
Buna göre anne bu işlemleri kaç farklı sırada yapabilir?
Çözümü Göster1. çocuğa ait çorap, ayakkabı ve bağcığa 1-1-1, diğer çocuklara ait çorap, ayakkabı ve bağcığa da 2-2-2, 3-3-3 ve 4-4-4 diyelim.
Buna göre yapılması gereken 12 işlem aşağıdaki gibi olur.
111222333444
Soruda verilen örnek sıralama için diziliş aşağıdaki gibi olur.
121312......
Bu durumda soru 3'er tane 1, 2, 3 ve 4 sayısının farklı diziliş sayısı problemi şeklinde kurgulanabilir.
Örneğin belirli bir dizilişteki birinci 1 sayısı annenin 1. çocuğa çorap giydirmesine, ikinci 1 sayısı 1. çocuğa ayakkabı giydirmesine, üçüncü 1 sayısı da 1. çocuğun bağcıklarını bağlamasına karşılık gelir.
Tekrarlı permütasyon formülü ile bu sayıların farklı diziliş sayısını bulalım.
\( \dfrac{12!}{3!\ 3!\ 3!\ 3!} = \dfrac{12!}{(3!)^4} \) bulunur.