Dairesel Permütasyon
Dairesel permütasyon problemlerinde bir kümenin elemanlarının doğrusal bir sıra/raf üzerinde değil, yuvarlak bir masa, kolye ya da anahtarlık etrafında farklı dizilişleri hesaplanır.
Saat Yönü Gözetilerek
\( n \) elemanlı bir kümenin elemanlarının dairesel bir düzende ve saat yönünün gözetildiği durumdaki (örneğin yuvarlak masa) farklı dizilişlerini bulmak istiyor olalım. Bu şekildeki bir düzende koltukları konumları itibariyle \( 1, 2, \ldots, n \) şeklinde numaralandırabileceğimiz bir referans noktası yoktur ve belirli bir dizilişte herkes aynı yönde \( 1, 2, \ldots, n \) koltuk kaydığında yeni bir diziliş oluşmaz.
Bunun bir sonucu olarak; saat yönünün gözetildiği dairesel düzendeki farklı diziliş sayısı, doğrusal düzendeki farklı diziliş sayısının koltuk sayısına bölümüne eşittir.
\( n \) koltuk/eleman sayısı olmak üzere,
Dairesel diziliş ve saat yönünün gözetildiği durumda,
Permütasyon sayısı \( = \dfrac{n!}{n} = (n - 1)! \)
6 kişi düz bir masada \( 6! \) farklı şekilde oturabilir.
6 kişi yuvarlak bir masa etrafında \( (6 - 1)! = 5! \) farklı şekilde oturabilir.
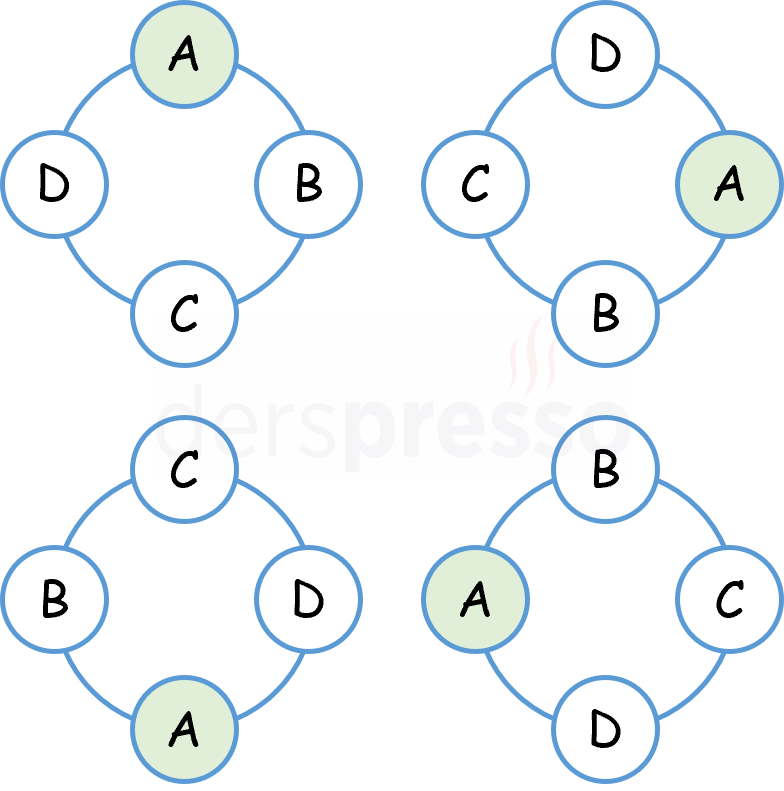
Aşağıdaki şekilde 4 kişilik bir masadaki belirli bir oturma düzeninde herkes saat yönünde \( 1, 2, 3, 4 \) koltuk kaydığında yeni bir oturma düzeni oluşmadığı görülebilir, dolayısıyla koltuk sayısı kadar birbirinin aynısı diziliş oluşur.
4 evli çift ve birer çocukları bir düğünde 12 kişilik yuvarlak bir masada birlikte oturacaklardır.
Kadınlar, erkekler ve çocuklar kendi aralarında yan yana oturmak şartıyla kaç farklı oturma düzeni vardır?
Çözümü GösterÖncelikle 12 kişiyi kadınlar, erkekler ve çocuklar olmak üzere üç grup olarak düşünelim. Bu üç grup yuvarlak masa etrafında \( (3 - 1)! = 2 \) farklı şekilde oturabilir.
Bu 2 oturma düzeninin her birinde 4 kadın, 4 erkek ve 4 çocuk kendi aralarında ayrı ayrı \( 4! \) farklı şekilde yer değiştirebilirler.
Buna göre bu 12 kişi masaya istenen koşulu sağlayacak şekilde \( 2 \cdot 4! \cdot 4! \cdot 4! \) farklı şekilde oturabilir.
Anne, baba ve 3 çocuktan oluşan bir aile yuvarlak bir masa etrafında yemek yiyeceklerdir.
Aile masaya anne ve baba yan yana olmayacak şekilde kaç farklı şekilde oturabilir?
Çözümü GösterHiçbir koşul olmadığı durumdaki farklı diziliş sayısından istenmeyen durumu çıkararak istenen durumu bulalım.
[Anne ve babanın yan yana olmadığı dizilişler] = [Tüm dizilişler] - [Anne ve babanın yan yana olduğu dizilişler]
Hiçbir koşul olmadığı durumda 5 kişilik aile masaya \( (5 - 1)! = 4! = 24 \) farklı şekilde oturabilir.
Anne ve babayı tek bir kişi olarak düşünelim. Bu durumda anne-babadan oluşan grup ve 3 çocuk masaya \( (4 - 1)! = 3! \) farklı şekilde oturabilir. Her oturma düzeninde anne ve baba aralarında \( 2! \) farklı şekilde yer değiştirebileceği için toplam oturma düzeni sayısı \( 3! \cdot 2! = 12 \) olur.
Anne ve babanın yan yana olduğu dizilişleri tüm dizilişlerden çıkararak istenen diziliş sayısını bulalım.
\( 24 - 12 = 12 \) bulunur.
3 doktor, 4 mühendis ve 2 avukat yuvarlak bir masa etrafında, aynı meslekteki kişiler yan yana olacak şekilde kaç farklı şekilde oturabilir?
Çözümü GösterHer meslekteki kişileri birer grup olarak düşünelim. Bu üç grup yuvarlak masaya \( (3 - 1)! = 2 \) farklı şekilde oturabilir.
Her meslek grubundaki kişiler kendi aralarında sırasıyla \( 3! \), \( 4! \) ve \( 2! \) farklı şekilde yer değiştirebilir.
Buna göre bu 9 kişi yuvarlak masa etrafında \( 2 \cdot 3! \cdot 4! \cdot 2! = 576 \) farklı şekilde oturabilir.
Dairesel permütasyon formülü herhangi bir koltuğu diğerlerinden ayıran bir özellik olmadığı varsayımına dayanmaktadır. Masadaki bir koltuğu diğerlerinden ayırt etmemizi sağlayan bir özellik varsa (daha büyük başkan koltuğu, pencerenin yanındaki/kapıya yakın koltuk vb.) koltukları \( 1, 2, \ldots, n \) şeklinde numaralandırabileceğimiz bir referans noktası oluşmuş olur, dolayısıyla belirli bir dizilişte herkes aynı yönde \( 1, 2, \ldots, n \) koltuk kaydığında yeni bir diziliş oluşur ve toplam diziliş sayısı için dairesel değil yine doğrusal permütasyon formülünü kullanmamız gerekir.
\( n \) koltuk/eleman sayısı olmak üzere,
Dairesel diziliş ve saat yönü gözetildiği durumda, bir koltuğu diğerlerinden ayıran bir özellik varsa,
Permütasyon sayısı \( = n! \)

Karşılıklı üçer kişinin oturabildiği pencere kenarındaki dikdörtgen bir yemek masasına anne, baba ve dört çocuktan oluşan bir aile oturacaktır. Aile aşağıdaki her bir düzene göre masaya kaç farklı şekilde oturabilir?
(a) Herkes istediği yere oturacak şekilde
(b) Anne ve baba yan yana olacak şekilde
(c) Anne ve baba karşı karşıya olacak şekilde
(d) Anne ve babanın arasına bir çocuk gelecek şekilde
(e) Anne ve babanın arasına en küçük çocuk gelecek şekilde
(f) Çocuklar yan yana gelmeyecek şekilde
Çözümü Göster(a) seçeneği: Herkes istediği yere oturacak şekilde
Pencere dikdörtgen masanın iki tarafını birbirinden ayırdetmemizi sağlayan bir referans noktası olduğu için bu masayı doğrusal bir oturma düzeni olarak düşünebiliriz.
Buna göre 6 kişi masaya \( 6! \) farklı şekilde oturabilir.
(b) seçeneği: Anne ve baba yan yana olacak şekilde
Anne/baba yan yana olacak şekilde masanın iki tarafında ikişer şekilde olmak üzere 4 farklı şekilde oturabilir ve her oturma düzeninde aralarında \( 2! \) farklı şekilde yer değiştirebilirler.
4 çocuk kalan yerlere \( 4! \) farklı şekilde oturabilir.
Buna göre aile masaya istenen koşulu sağlayacak şekilde \( 4 \cdot 2! \cdot 4! \) farklı şekilde oturabilir.
(c) seçeneği: Anne ve baba karşı karşıya olacak şekilde
Karşılıklı üçer sandalye olduğu için anne/baba bu sandalyelere 3 farklı şekilde oturabilir ve her oturma düzeninde aralarında \( 2! \) farklı şekilde yer değiştirebilirler.
4 çocuk kalan yerlere \( 4! \) farklı şekilde oturabilir.
Buna göre aile masaya istenen koşulu sağlayacak şekilde \( 3 \cdot 2! \cdot 4! \) farklı şekilde oturabilir.
(d) seçeneği: Anne ve babanın arasına bir çocuk gelecek şekilde
Aralarına bir çocuk alacakları için anne/babanın masanın herhangi bir tarafında uçlarda oturması gerekecektir. Buna göre anne/baba masanın 2 tarafından birini seçebilir ve her oturma düzeninde aralarında \( 2! \) farklı şekilde yer değiştirebilirler.
4 çocuk kalan yerlere \( 4! \) farklı şekilde oturabilir.
Buna göre aile masaya istenen koşulu sağlayacak şekilde \( 2 \cdot 2! \cdot 4! \) farklı şekilde oturabilir.
(e) seçeneği: Anne ve babanın arasına en küçük çocuk gelecek şekilde
Aralarına bir çocuk alacakları için anne/babanın masanın herhangi bir tarafında uçlarda oturması gerekecektir. Buna göre anne/baba masanın 2 tarafından birini seçebilir ve her oturma düzeninde aralarında \( 2! \) farklı şekilde yer değiştirebilirler.
En küçük çocuk anne/baba arasına oturacağı için bu çocuk için tek bir oturma düzeni vardır.
Kalan 3 çocuk masanın karşısına \( 3! \) farklı şekilde oturabilir.
Buna göre aile masaya istenen koşulu sağlayacak şekilde \( 2 \cdot 2! \cdot 3! \) farklı şekilde oturabilir.
(e) seçeneği: Çocuklar yan yana gelmeyecek şekilde
Çocukların yan yana gelmemesi için anne/babanın ortadaki sandalyelerde ve karşılıklı oturmaları gerekecektir. Buna göre anne/baba aralarında \( 2! \) farklı şekilde yer değiştirebilirler.
4 çocuk kalan yerlere \( 4! \) farklı şekilde oturabilir.
Buna göre aile masaya istenen koşulu sağlayacak şekilde \( 2! \cdot 4! \) farklı şekilde oturabilir.
Saat Yönü Gözetilmeden
\( n \) elemanlı bir kümenin elemanlarının dairesel bir düzende ve saat yönünün gözetilmediği durumdaki (örneğin kolye, anahtarlık) farklı dizilişlerini bulmak istiyor olalım. Bu şekildeki bir düzende belirli bir diziliş bulunduğu düzlem etrafında ters çevrildiğinde yeni bir diziliş oluşmaz, dolayısıyla dairesel permütasyon ile hesapladığımız farklı diziliş sayısını ikiye bölmemiz gerekir.
Dairesel diziliş ve saat yönü gözetilmediği durumda,
Permütasyon sayısı \( = \dfrac{(n - 1)!}{2} \)
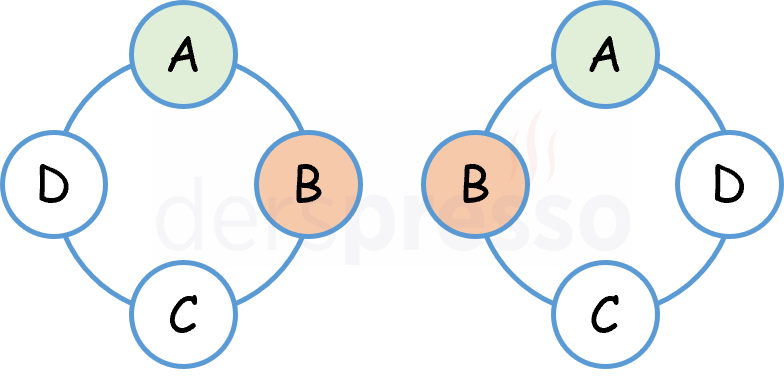
Aşağıdaki şekilde 4 anahtarlı bir anahtarlık belirli bir dizilişte bulunduğu düzlem etrafında ters çevrildiğinde, iki dizilişi birbirinden ayırt edebileceğimiz yeni bir diziliş oluşmadığı görülebilir.
Yukarıdaki formül anahtarlığın üzerinde anahtarlar için bir referans noktası olarak tanımlayabileceğimiz bir nesne olmadığı varsayımına dayanmaktadır. Eğer anahtarlık üzerinde böyle bir nesne varsa (maskot vb.) anahtarları birer kaydırdığımızda da yeni bir diziliş oluşacaktır, dolayısıyla böyle bir durumda doğrusal permütasyon formülü ile bulacağımız farklı diziliş sayısını ikiye bölmemiz gerekir.
Dairesel diziliş ve saat yönü gözetilmediği durumda, referans noktası olabilecek bir nesne varsa,
Permütasyon sayısı \( = \dfrac{n!}{2} \)
8 farklı anahtar maskotsuz bir anahtarlığa kaç farklı şekilde dizilebilir?
Çözümü GösterMaskotsuz anahtarlık (ya da kolyelerde) belirli bir referans noktası olmadığı için yuvarlak masada olduğu gibi anahtarları birer kaydırmamız yeni bir diziliş oluşturmaz. Herhangi bir dizilişte anahtarlığı bulunduğu düzlem etrafında döndürmemiz de yeni bir diziliş oluşturmadığı için toplam diziliş sayısı \( \frac{(n - 1)!}{2} \) olur.
Buna göre \( n = 8 \) için toplam diziliş sayısı \( \frac{7!}{2} = 2520 \) olur.
8 farklı anahtar maskotlu bir anahtarlığa kaç farklı şekilde dizilebilir?
Çözümü GösterMaskotlu anahtarlık (ya da kolyelerde) maskot bir referans noktası olduğu için anahtarları birer kaydırmamız yeni bir diziliş oluşturur, dolayısıyla dairesel permütasyon formülünü kullanamayız. Herhangi bir dizilişte anahtarlığı bulunduğu düzlem etrafında döndürmemiz yeni bir diziliş oluşturmadığı için toplam diziliş sayısı \( \frac{n!}{2} \) olur.
Buna göre \( n = 8 \) için toplam diziliş sayısı \( \frac{8!}{2} = 20160 \) olur.