Matrislerle İşlemler
Sayılar, vektörler, fonksiyonlar ve polinomlar arasında olduğu gibi, matrisler arasında da toplama, çıkarma ve çarpma işlemleri yapılabilir.
Matrislerin Eşitliği
Boyutları ve birbirine karşılık gelen tüm elemanları eşit olan matrislere eşit matrisler denir. \( A \) ve \( B \) matrislerinin eşitliği \( A = B \) şeklinde gösterilir.
\( A \) ve \( B \) boyutları \( m \times n \) olan iki matris olmak üzere,
Her \( i = 1, \ldots, m \) ve \( j = 1, \ldots, n \) için,
\( a_{ij} = b_{ij} \) ise,
\( A \) ve \( B \) eşit matrislerdir.
\( A = \begin{bmatrix} 1 & a \\ 3 & 4 \end{bmatrix} \)
\( B = \begin{bmatrix} 1 & 2 \\ b & 4 \end{bmatrix} \)
\( A = B \) ise,
\( a = 2, \quad b = 3\) olur.
Boyutları farklı iki matris arasında eşitlik söz konusu değildir.
\( \begin{bmatrix} 1 & 1 \\ 1 & 1 \end{bmatrix} \ne \begin{bmatrix} 1 & 1 \\ 1 & 1 \\ 1 & 1 \end{bmatrix} \)
Toplama İşlemi
Boyutu \( m \times n \) olan bir matris sadece aynı boyuttaki bir matrisle toplanabilir ve sonuç yine aynı boyutta bir matris olur.
İki ya da daha fazla matrisi toplarken satır ve sütun numaraları aynı olan elemanlar toplanır ve sonuç toplam matrisinde aynı satır ve sütuna yazılır.
\( A_{m \times n} + B_{m \times n} = C_{m \times n} \) ise,
Her \( i = 1, \ldots, m \) ve \( j = 1, \ldots, n \) için,
\( c_{ij} = a_{ij} + b_{ij} \)
\( \begin{bmatrix} 2 & 5 \\ 3 & 7 \\ -1 & 0 \end{bmatrix} + \begin{bmatrix} 1 & 0 \\ 4 & -1 \\ 9 & 1 \end{bmatrix} = \begin{bmatrix} 3 & 5 \\ 7 & 6 \\ 8 & 1 \end{bmatrix} \)
Toplama İşleminin Özellikleri
Matrislerde toplama işleminin değişme özelliği vardır.
\( A + B = B + A \)
İSPATI GÖSTER
\( A \) ve \( B \) boyutları \( m \times n \) olan matrislerdir.
\( i = 1, \ldots, m \) ve \( j = 1, \ldots, n \) olmak üzere,
\( A + B = [a_{ij}]_{m \times n} + [b_{ij}]_{m \times n} \)
Matrislerin toplamında satır ve sütun numaraları aynı olan elemanlar toplanır ve sonuç toplam matrisinde aynı satır ve sütuna yazılır.
\( = [a_{ij} + b_{ij}]_{m \times n} \)
\( a_{ij} \) ve \( b_{ij} \) skaler büyüklüklerdir ve reel sayılarda toplama işleminin değişme özelliği vardır.
\( = [b_{ij} + a_{ij}]_{m \times n} \)
Bu ifade elemanları sırasıyla \( b_{ij} \) ve \( a_{ij} \) olan iki matris arasındaki toplama işlemidir.
\( = [b_{ij}]_{m \times n} + [a_{ij}]_{m \times n} \)
\( = B + A \)
Matrislerde toplama işleminin birleşme özelliği vardır.
\( (A + B) + C = A + (B + C) \)
İSPATI GÖSTER
\( A \), \( B \) ve \( C \) boyutları \( m \times n \) olan matrislerdir.
\( i = 1, \ldots, m \) ve \( j = 1, \ldots, n \) olmak üzere,
\( (A + B) + C = ([a_{ij}]_{m \times n} + [b_{ij}]_{m \times n}) + [c_{ij}]_{m \times n} \)
Matrislerin toplamında satır ve sütun numaraları aynı olan elemanlar toplanır ve sonuç toplam matrisinde aynı satır ve sütuna yazılır.
\( = [a_{ij} + b_{ij}]_{m \times n} + [c_{ij}]_{m \times n} \)
\( = [(a_{ij} + b_{ij}) + c_{ij}]_{m \times n} \)
\( a_{ij} \), \( b_{ij} \) ve \( c_{ij} \) skaler büyüklüklerdir ve reel sayılarda toplama işleminin birleşme özelliği vardır.
\( = [a_{ij} + (b_{ij} + c_{ij})]_{m \times n} \)
Bu ifade elemanları sırasıyla \( a_{ij} \) ve \( b_{ij} + c_{ij} \) olan iki matris arasındaki toplama işlemidir.
\( = [a_{ij}]_{m \times n} + [b_{ij} + c_{ij}]_{m \times n} \)
İkinci terim elemanları sırasıyla \( b_{ij} \) ve \( c_{ij} \) olan iki matris arasındaki toplama işlemidir.
\( = [a_{ij}]_{m \times n} + ([b_{ij}]_{m \times n} + [c_{ij}]_{m \times n}) \)
\( = A + (B + C) \)
Sıfır matrisi toplama işleminin birim (etkisiz) elemanıdır.
\( A_{m \times n} + O_{m \times n} = A_{m \times n} \)
Çıkarma İşlemi
Boyutu \( m \times n \) olan bir matristen sadece aynı boyuttaki bir matris çıkarılabilir ve sonuç yine aynı boyutta bir matris olur.
Bir matristen diğer bir matrisi çıkarırken satır ve sütun numaraları aynı olan elemanlar birbirinden çıkarılır ve sonuç fark matrisinde aynı satır ve sütuna yazılır.
\( A_{m \times n} - B_{m \times n} = C_{m \times n} \) ise,
Her \( i = 1, \ldots, m \) ve \( j = 1, \ldots, n \) için,
\( c_{ij} = a_{ij} - b_{ij} \)
\( \begin{bmatrix} 2 & 5 \\ 7 & 3 \\ -1 & 1 \end{bmatrix} - \begin{bmatrix} 1 & 0 \\ 4 & -1 \\ 5 & 1 \end{bmatrix} = \begin{bmatrix} 1 & 5 \\ 3 & 4 \\ -6 & 0 \end{bmatrix} \)
Çıkarma İşleminin Özellikleri
Matrislerde çıkarma işleminin değişme özelliği yoktur.
\( A - B \ne B - A \)
Bir matrisin sıfır matrisinden farkı kendisine eşittir.
\( A_{m \times n} - O_{m \times n} = A_{m \times n} \)
Skaler Çarpma İşlemi
Boyutu \( m \times n \) olan bir matris bir reel sayı ile çarpıldığında sonuç yine aynı boyutta bir matris olur.
Bir reel sayı ile bir matrisin çarpımında matrisin tüm elemanları bu reel sayı ile çarpılır ve sonuç çarpım matrisinde aynı satır ve sütuna yazılır.
\( k \in \mathbb{R} \) olmak üzere,
\( kA_{m \times n} = C_{m \times n} \) ise,
Her \( i = 1, \ldots, m \) ve \( j = 1, \ldots, n \) için,
\( c_{ij} = ka_{ij} \)
\( 3\begin{bmatrix} 2 & 5 \\ 7 & 0 \\ -3 & 1 \end{bmatrix} = \begin{bmatrix} 6 & 15 \\ 21 & 0 \\ -9 & 3 \end{bmatrix} \)
Skaler Çarpma İşleminin Özellikleri
Matrislerde skaler çarpma işleminin değişme özelliği vardır.
\( cA = Ac \)
Matrislerde skaler çarpma işleminin birleşme özelliği vardır.
\( c(dA) = (cd)A = d(cA) \)
İSPATI GÖSTER
\( A \) boyutları \( m \times n \) olan bir matristir.
\( i = 1, \ldots, m \) ve \( j = 1, \ldots, n \) olmak üzere,
\( c(dA) = c(d[a_{ij}]_{m \times n}) \)
Bir reel sayı ile bir matrisin çarpımında matrisin tüm elemanları bu reel sayı ile çarpılır ve sonuç çarpım matrisinde aynı satır ve sütuna yazılır.
\( = c([da_{ij}]_{m \times n}) \)
\( = [c(da_{ij})]_{m \times n} \)
\( c \), \( d \) ve \( a_{ij} \) skaler büyüklüklerdir ve reel sayılarda çarpma işleminin birleşme özelliği vardır.
\( = [(cd)a_{ij}]_{m \times n} \)
Bu ifade \( cd \) skaler büyüklüğü ile elemanları \( a_{ij} \) olan matris arasındaki skaler çarpma işlemidir.
\( = (cd)[a_{ij}]_{m \times n} \)
\( = (cd)A \)
Bu ifadenin \( d(cA) \) ifadesine eşit olduğu benzer bir yaklaşımla gösterilebilir.
Matrislerde skaler çarpma işleminin toplama ve çıkarma işlemleri üzerinde soldan ve sağdan dağılma özelliği vardır.
\( c(A + B) = cA + cB \)
\( c(A - B) = cA - cB \)
\( (A + B)c = Ac + Bc \)
\( (A - B)c = Ac - Bc \)
İSPATI GÖSTER
\( A \) ve \( B \) boyutları \( m \times n \) olan matrislerdir.
\( i = 1, \ldots, m \) ve \( j = 1, \ldots, n \) olmak üzere,
\( c(A + B) = c([a_{ij}]_{m \times n} + [b_{ij}]_{m \times n}) \)
Matrislerin toplamında satır ve sütun numaraları aynı olan elemanlar toplanır ve sonuç toplam matrisinde aynı satır ve sütuna yazılır.
\( = c([a_{ij} + b_{ij}]_{m \times n}) \)
Bir reel sayı ile bir matrisin çarpımında matrisin tüm elemanları bu reel sayı ile çarpılır ve sonuç çarpım matrisinde aynı satır ve sütuna yazılır.
\( = [c(a_{ij} + b_{ij})]_{m \times n} \)
\( c \), \( a_{ij} \) ve \( b_{ij} \) skaler büyüklüklerdir ve reel sayılarda çarpma işleminin toplama işlemi üzerinde dağılma özelliği vardır.
\( = [ca_{ij} + cb_{ij}]_{m \times n} \)
Bu ifade elemanları sırasıyla \( ca_{ij} \) ve \( cb_{ij} \) olan iki matris arasındaki toplama işlemidir.
\( = [ca_{ij}]_{m \times n} + [cb_{ij}]_{m \times n} \)
Birinci terim \( c \) skaler büyüklüğü ile elemanları \( a_{ij} \) olan matris arasındaki skaler çarpma işlemidir.
İkinci terim \( c \) skaler büyüklüğü ile elemanları \( b_{ij} \) olan matris arasındaki skaler çarpma işlemidir.
\( = c[a_{ij}]_{m \times n} + c[b_{ij}]_{m \times n} \)
\( = cA + cB \)
Aşağıdaki özdeşliklerin ispatı da benzer bir yaklaşımla yapılabilir.
\( c(A - B) = cA - cB \)
\( (A + B)c = Ac + Bc \)
\( (A - B)c = Ac - Bc \)
Bir matrisin 1 sayısı ile çarpımı kendisine, 0 sayısı ile çarpımı sıfır matrisine eşittir.
\( 1A_{m \times n} = A_{m \times n} \)
\( 0A_{m \times n} = O_{m \times n} \)
Bir matrisin \( -1 \) sayısı ile çarpımı matrisin toplamaya göre tersini verir. Bir matrisin toplamaya göre tersi ile toplamı sıfır matrisini verir.
\( (-1)A = -A \)
\( A_{m \times n} + (-A_{m \times n}) = 0_{m \times n} \)
\( -\begin{bmatrix} 3 & -2 \\ 0 & 5 \end{bmatrix} = \begin{bmatrix} -3 & 2 \\ 0 & -5 \end{bmatrix} \)
Bir skaler çarpma işleminin sonucu sıfır matrisi ise ya skaler sıfırdır ya da çarpılan matris sıfır matrisidir.
\( kA_{m \times n} = 0_{m \times n} \) ise,
\( k = 0 \) veya \( A_{m \times n} = 0_{m \times n} \)
Çarpma İşlemi
İki matris arasındaki çarpma işlemi, toplama ve çıkarma işlemlerinden birkaç açıdan farklıdır.
- İki matris arasında çarpma işlemi yapılabilmesinin koşulu matrislerin boyutlarının aynı olması değil, birinci matrisin sütun sayısının ikinci matrisin satır sayısına eşit olmasıdır.
- Çarpma işlemi matrislerin aynı satır ve sütun numaralı elemanları arasında değil, birinci matrisin her satırı ile ikinci matrisin her sütunu arasında yapılır.
Matrislerde çarpma işleminin mantığını önce biri tek satırlı diğeri tek sütunlu iki matris üzerinde gösterelim. Aşağıdaki gibi \( 1 \times 3 \) satır matrisi ile \( 3 \times 1 \) sütun matrisi arasındaki çarpma işleminin sonucu \( 1 \times 1 \) bir matris olur ve bu matrisin tek elemanı birinci matrisin satırı ile ikinci matrisin sütunundaki elemanların sıralı bir şekilde çarpımlarının toplamına eşittir.
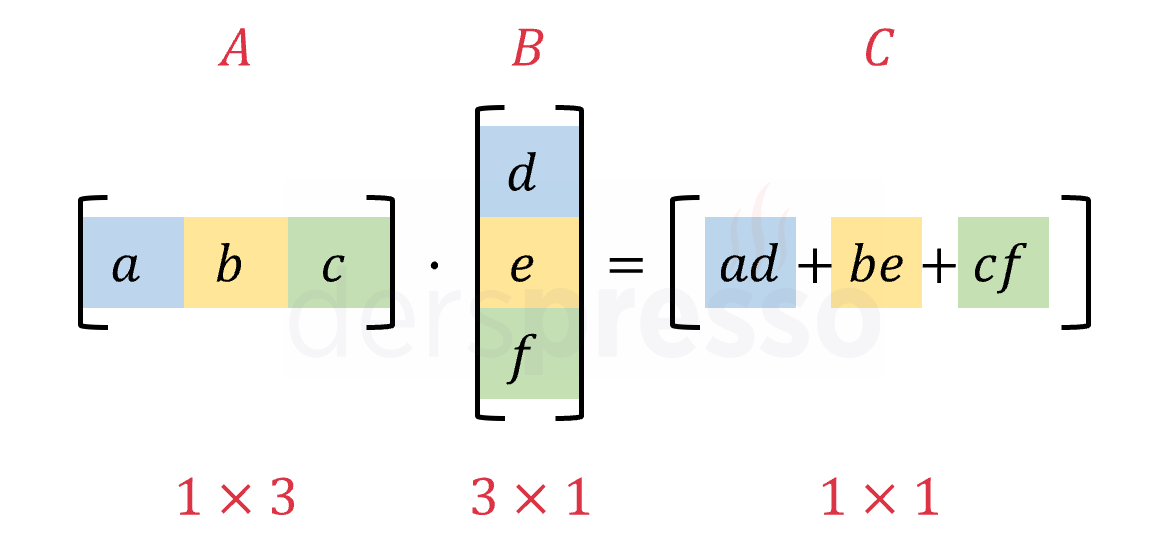
\( A_{1 \times 3}B_{3 \times 1} = C_{1 \times 1} \)
\( c_{11} = ad + be + cf \)
Bu işlemi daha büyük boyutlu matrislere uyarlarsak, boyutu \( m \times n \) olan bir matris sadece satır sayısı kendisinin sütun sayısına eşit olan \( n \times p \) bir matrisle çarpılabilir ve sonuç boyutu \( m \times p \) olan bir matris olur. Bir diğer ifadeyle, sonuç matrisinin satır sayısı birinci matrisin satır sayısı, sütun sayısı ikinci matrisin sütun sayısı olur.
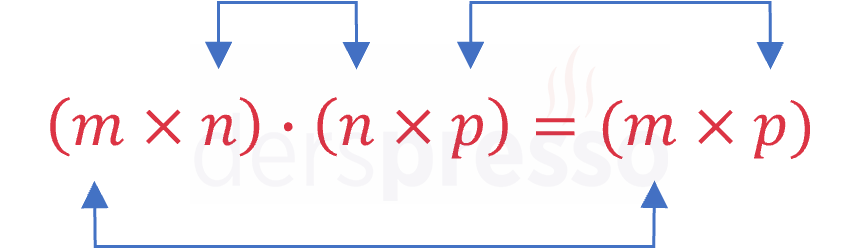
İki matrisin çarpımında birinci matrisin her satırı ile ikinci matrisin her sütunu arasında yukarıda bahsettiğimiz çarpma işlemi yapılır ve birinci matrisin \( i \). satırı ile ikinci matrisin \( j \). sütunu arasındaki çarpma işleminin sonucu sonuç matrisinde \( c_{ij} \) elemanı yerine yazılır.
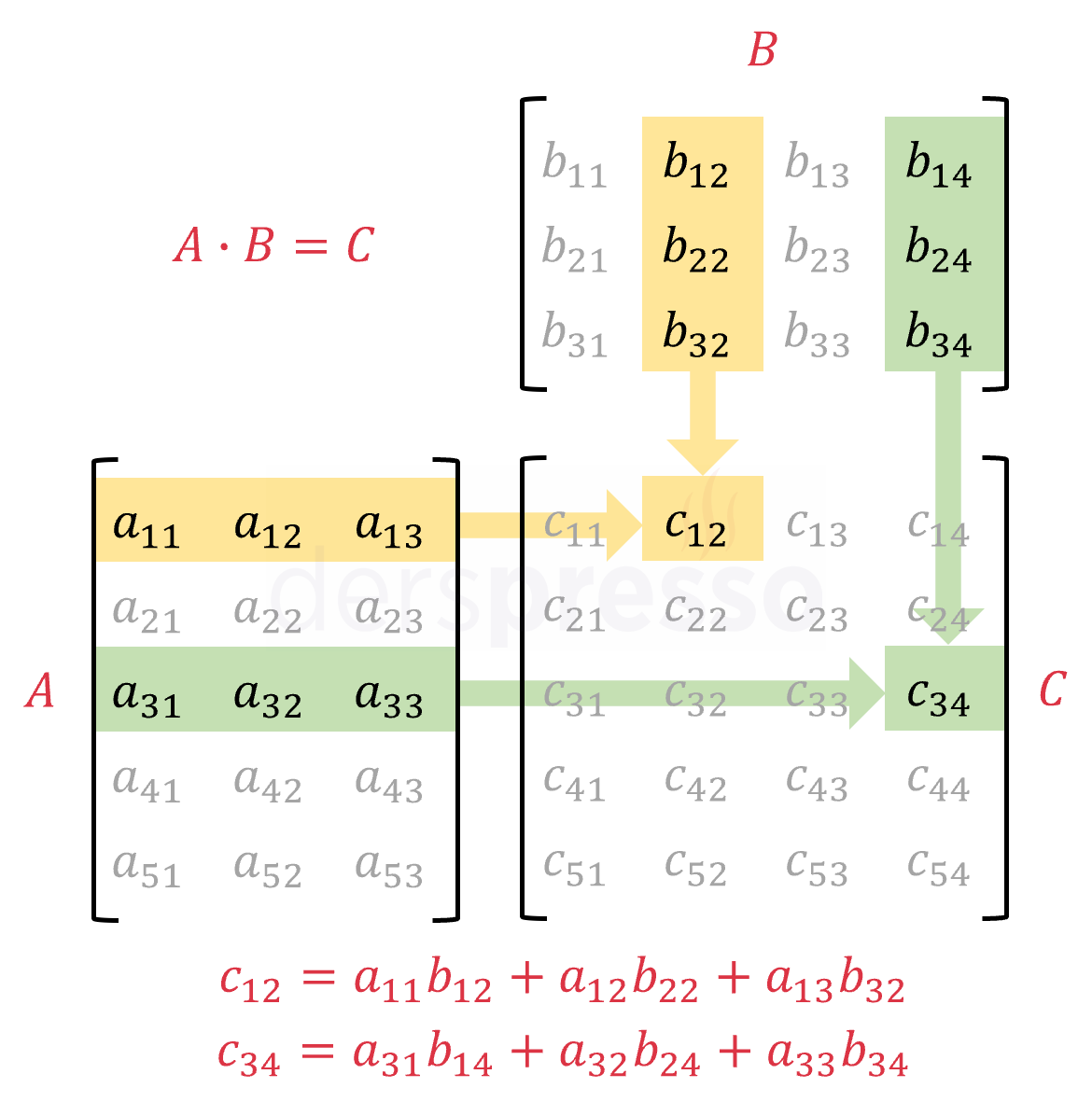
\( A_{m \times n}B_{n \times p} = C_{m \times p} \)
Her \( i = 1, \ldots, m \) ve \( k = 1, \ldots, p \) için,
\( c_{ik} = \displaystyle\sum_{j = 1}^{n} a_{ij}b_{jk} \)
\( = a_{i1}b_{1k} + a_{i2}b_{2k} + \ldots + a_{in}b_{nk} \)
\( \begin{bmatrix} 2 & 5 \\ 7 & 3 \end{bmatrix} \begin{bmatrix} 1 & 0 \\ 4 & -1 \end{bmatrix} \)
\( = \begin{bmatrix} 2 \cdot 1 + 5 \cdot 4 & 2 \cdot 0 + 5 \cdot (-1) \\ 7 \cdot 1 + 3 \cdot 4 & 7 \cdot 0 + 3 \cdot (-1) \end{bmatrix} \)
\( = \begin{bmatrix} 22 & -5 \\ 19 & -3 \end{bmatrix} \)
\( \begin{bmatrix} 2 & 1 & -1 \\ 0 & 3 & 2 \\ 5 & 2 & -3 \\ 4 & 6 & -2 \end{bmatrix} \begin{bmatrix} 3 & 5 \\ -1 & 4 \\ 2 & 0 \end{bmatrix} \)
\( = \begin{bmatrix} 2 \cdot 3 + 1(-1) + (-1) \cdot 2 & 2 \cdot 5 + 1 \cdot 4 + (-1)0 \\ 0 \cdot 3 + 3(-1) + 2 \cdot 2 & 0 \cdot 5 + 3 \cdot 4 + 2 \cdot 0 \\ 5 \cdot 3 + 2(-1) + (-3)2 & 5 \cdot 5 + 2 \cdot 4 + (-3)0 \\ 4 \cdot 3 + 6(-1) + (-2)2 & 4 \cdot 5 + 6 \cdot 4 + (-2)0 \end{bmatrix} \)
\( = \begin{bmatrix} 3 & 14 \\ 1 & 12 \\ 7 & 33 \\ 2 & 44 \end{bmatrix} \)
\( A \) ve \( B \) matrislerinin çarpımı \( AB \) ya da \( A \cdot B \) şeklinde ifade edilebilir.
Çarpma İşleminin Özellikleri
Matrislerde çarpma işleminin genel kural olarak değişme özelliği yoktur, ...
\( AB \ne BA \)
... ancak aşağıdaki gibi bazı özel durumlarda eşitlik sağlanabilir.
Matrixlerden biri sıfır matris ise;
\( AO = OA = O \)
Matrixlerden biri birim matris ise;
\( AI = IA = A \)
Matrixler birbirinin tersi ise;
\( AA^{-1} = A^{-1}A = I \)
Matrixlerin ikisi de köşegen matris ise;
\( AB = BA \)
Matrislerde çarpma işleminin birleşme özelliği vardır.
\( (A_{m \times n}B_{n \times p})C_{p \times q} = A_{m \times n}(B_{n \times p}C_{p \times q}) \)
İSPATI GÖSTER
\( A \), \( B \) ve \( C \) boyutları sırasıyla \( m \times n \), \( n \times p \) ve \( p \times q \) olan matrislerdir.
Önce \( (AB)C \) ifadesinin açılımını yazalım.
\( AB = X \) ve \( XC = Y \) diyelim.
\( (AB)C = XC = Y \)
\( AB = X \) çarpımının sonucunun \( i \). satırının \( j \). sütunundaki eleman aşağıdaki formülle hesaplanır.
\( x_{ij} = \displaystyle\sum_{r = 1}^{n} a_{ir}b_{rj} \)
Bu ifadenin açılımı aşağıdaki gibi olur.
\( = a_{i1}b_{1j} + a_{i2}b_{2j} + \ldots + a_{in}b_{nj} \)
\( XC = Y \) çarpımının sonucunun \( i \). satırının \( j \). sütunundaki eleman aşağıdaki formülle hesaplanır.
\( y_{ij} = \displaystyle\sum_{s = 1}^{p} x_{is}c_{sj} \)
\( x_{is} \) yerine yukarıdaki \( x_{ij} \) formülünü yazalım.
\( = \displaystyle\sum_{s = 1}^{p} (\displaystyle\sum_{r = 1}^{n} a_{ir}b_{rs})c_{sj} \)
İçteki toplam ifadesinin açılımını yazalım.
\( = \displaystyle\sum_{s = 1}^{p} (a_{i1}b_{1s} + a_{i2}b_{2s} + \ldots + a_{in}b_{ns})c_{sj} \)
\( = \displaystyle\sum_{s = 1}^{p} (a_{i1}b_{1s}c_{sj} + a_{i2}b_{2s}c_{sj} + \ldots + a_{in}b_{ns}c_{sj}) \)
\( r = 1, \ldots, n \) ve \( s = 1, \ldots, p \) olmak üzere,
Yukarıdaki ifade sonuç matrisinin \( y_{ij} \) elemanına karşılık gelen her biri \( a_{ir}b_{rs}c_{sj} \) şeklindeki \( np \) adet terimin toplamına eşittir.
Şimdi \( A(BC) \) ifadesinin açılımını yazalım.
\( BC = X \) ve \( AX = Y \) diyelim.
\( A(BC) = AX = Y \)
\( BC = X \) çarpımının sonucunun \( i \). satırının \( j \). sütunundaki eleman aşağıdaki formülle hesaplanır.
\( x_{ij} = \displaystyle\sum_{s = 1}^{p} b_{is}c_{sj} \)
Bu ifadenin açılımı aşağıdaki gibi olur.
\( = b_{i1}c_{1j} + b_{i2}c_{2j} + \ldots + b_{ip}c_{pj} \)
\( AX = Y \) çarpımının sonucunun \( i \). satırının \( j \). sütunundaki eleman aşağıdaki formülle hesaplanır.
\( y_{ij} = \displaystyle\sum_{r = 1}^{n} a_{ir}x_{rj} \)
\( x_{rj} \) yerine yukarıdaki \( x_{ij} \) formülünü yazalım.
\( = \displaystyle\sum_{r = 1}^{n} a_{ir}(\displaystyle\sum_{s = 1}^{p} b_{rs}c_{sj}) \)
İçteki toplam ifadesinin açılımını yazalım.
\( = \displaystyle\sum_{r = 1}^{n} a_{ir}(b_{r1}c_{1j} + b_{r2}c_{2j} + \ldots + b_{rp}c_{pj}) \)
\( = \displaystyle\sum_{r = 1}^{n} (a_{ir}b_{r1}c_{1j} + a_{ir}b_{r2}c_{2j} + \ldots + a_{ir}b_{rp}c_{pj}) \)
\( r = 1, \ldots, n \) ve \( s = 1, \ldots, p \) olmak üzere,
Yukarıdaki ifade sonuç matrisinin \( y_{ij} \) elemanına karşılık gelen her biri \( a_{ir}b_{rs}c_{sj} \) şeklindeki \( np \) adet terimin toplamına eşittir.
İki çarpım işleminin sonucu birbirine eşit olduğuna göre, matrislerde çarpma işleminin birleşme özelliği vardır.
\( (AB)C = A(BC) \)
Matrislerde çarpma işleminin toplama işlemi üzerinde soldan ve sağdan dağılma özelliği vardır.
\( A_{m \times n}(B_{n \times p} + C_{n \times p}) = A_{m \times n}B_{n \times p} + A_{m \times n}C_{n \times p} \)
\( (B_{m \times n} + C_{m \times n})A_{n \times p} = B_{m \times n}A_{n \times p} + C_{m \times n}A_{n \times p} \)
İSPATI GÖSTER
\( A \), \( B \) ve \( C \) boyutları sırasıyla \( m \times n \), \( n \times p \) ve \( n \times p \) olan matrislerdir.
\( B + C = X \) ve \( AX = Y \) diyelim.
\( A(B + C) = AX = Y \)
\( AX \) çarpımının sonucunun \( i \). satırının \( j \). sütunundaki eleman aşağıdaki formülle hesaplanır.
\( y_{ij} = \displaystyle\sum_{r = 1}^{n} a_{ir}x_{rj} \)
Matrislerin toplamında satır ve sütun numaraları aynı olan elemanlar toplanır ve sonuç toplam matrisinde aynı satır ve sütuna yazılır.
\( = \displaystyle\sum_{r = 1}^{n} a_{ir}(b_{rj} + c_{rj}) \)
\( a_{ir} \), \( b_{rj} \) ve \( c_{rj} \) skaler büyüklüklerdir ve reel sayılarda çarpma işleminin toplama işlemi üzerinde dağılma özelliği vardır.
\( = \displaystyle\sum_{r = 1}^{n} (a_{ir}b_{rj} + a_{ir}c_{rj}) \)
Toplam sembolü toplanan ifadedeki terimlere dağıtılabilir.
\( = \displaystyle\sum_{r = 1}^{n} a_{ir}b_{rj} + \displaystyle\sum_{r = 1}^{n} a_{ir}c_{rj} \)
Birinci terim \( AB \) çarpımının sonucunun \( i \). satırının \( j \). sütunundaki elemanın formülüdür.
İkinci terim \( AC \) çarpımının sonucunun \( i \). satırının \( j \). sütunundaki elemanın formülüdür.
Buna göre, \( A(B + C) \) çarpımının sonucunun \( i \). satırının \( j \). sütunundaki eleman, \( AB + AC \) toplamının aynı konumdaki elemanına eşittir.
\( A(B + C) = AB + AC \)
Bir matrisin birim matris ile çarpımının sonucu kendisidir.
\( A_{m \times n}I_n = A_{m \times n} \)
\( I_mA_{m \times n} = A_{m \times n} \)
\( \begin{bmatrix} 5 & 2 \\ 1 & 3 \\ 4 & 7 \end{bmatrix} \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} \)
\( = \begin{bmatrix} 5 \cdot 1 + 2 \cdot 0 & 5 \cdot 0 + 2 \cdot 1 \\ 1 \cdot 1 + 3 \cdot 0 & 1 \cdot 0 + 3 \cdot 1 \\ 4 \cdot 1 + 7 \cdot 0 & 4 \cdot 0 + 7 \cdot 1 \end{bmatrix} \)
\( = \begin{bmatrix} 5 & 2 \\ 1 & 3 \\ 4 & 7 \end{bmatrix} \)
Bir matrisin sıfır matrisi ile çarpımının sonucu sıfır matrisidir.
\( A_{m \times n}O_{n \times p} = O_{m \times p} \)
\( O_{p \times m}A_{m \times n} = O_{p \times n} \)
\( \begin{bmatrix} 8 & 1 \\ 9 & 2 \\ 3 & 6 \end{bmatrix} \begin{bmatrix} 0 & 0 \\ 0 & 0 \end{bmatrix} \)
\( = \begin{bmatrix} 8 \cdot 0 + 1 \cdot 0 & 8 \cdot 0 + 1 \cdot 0 \\ 9 \cdot 0 + 2 \cdot 0 & 9 \cdot 0 + 2 \cdot 0 \\ 3 \cdot 0 + 6 \cdot 0 & 3 \cdot 0 + 6 \cdot 0 \end{bmatrix} \)
\( = \begin{bmatrix} 0 & 0 \\ 0 & 0 \\ 0 & 0 \end{bmatrix} \)
Önümüzdeki bölümde göreceğimiz üzere, bir matrisin tersi ile çarpımının sonucu birim matristir.
\( AA^{-1} = A^{-1}A = I \)
İki reel sayının çarpımı sıfır ise bu sayılardan en az birinin sıfır olduğunu biliyoruz. Bu kural matrisler için her zaman doğru olmayabilir, yani çarpımı sıfır matrisi olan iki matristen en az biri sıfır matrisi olmak zorunda değildir.
\( \begin{bmatrix} 0 & 1 \\ 0 & 2 \end{bmatrix} \begin{bmatrix} 3 & 4 \\ 0 & 0 \end{bmatrix} \)
\( = \begin{bmatrix} 0 \cdot 3 + 1 \cdot 0 & 0 \cdot 4 + 1 \cdot 0 \\ 0 \cdot 3 + 2 \cdot 0 & 0 \cdot 4 + 2 \cdot 0 \end{bmatrix} \)
\( = \begin{bmatrix} 0 & 0 \\ 0 & 0 \end{bmatrix} \)
\( A \) matrisinin tersi varsa aşağıdaki eşitliklerin iki tarafındaki \( A \) matrisleri sadeleşir.
\( A \) tersi alınabilir bir matris ise,
\( AB = AC \Longrightarrow B = C \)
\( BA = CA \Longrightarrow B = C \)
İSPATI GÖSTER
\( A \) matrisi tersi alınabilir bir matris olsun.
\( BA = CA \)
Eşitliğin iki tarafını \( A \) matrisinin tersi ile çarpalım.
\( (BA)A^{-1} = (CA)A^{-1} \)
Matrislerde çarpma işleminin birleşme özelliği vardır.
\( B(AA^{-1}) = C(AA^{-1}) \)
Bir matrisin tersi ile çarpımının sonucu birim matristir.
\( BI = CI \)
Bir matrisin birim matris ile çarpımının sonucu kendisidir.
\( B = C \)
Bir Matrisin Transpozu (Devriği)
Transpoz işleminde bir matrisin satırları sütunlara, sütunları da satırlara taşınır. Buna göre; transpozu alınan matriste \( i \). satır ve \( j \). sütunda bulunan bir \( a_{ij} \) elemanı, transpoz matrisinde \( j \). satır ve \( i \). sütuna taşınır ve matrisin \( a_{ji} \) elemanı olur. Bir \( A \) matrisinin transpozu \( A^T \) ile gösterilir.
\( m \times n \) boyutlarındaki bir matrisin transpozunun boyutları \( n \times m \) olur.
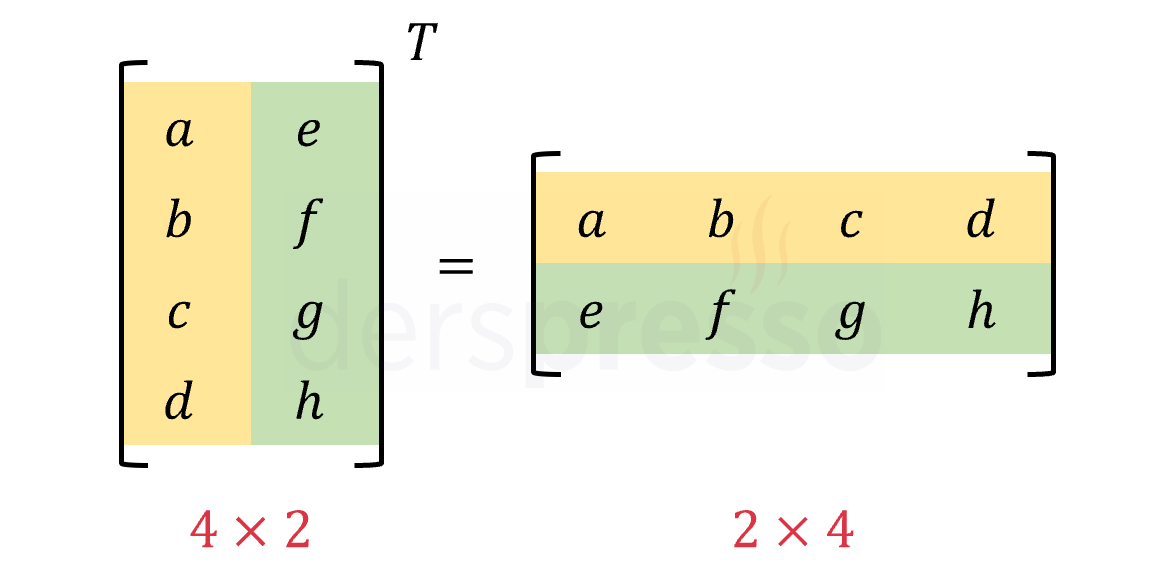
\( A_{m \times n}^T = C_{n \times m} \) ise,
Her \( i = 1, \ldots, m \) ve \( j = 1, \ldots, n \) için,
\( c_{ji} = a_{ij} \)
\( \begin{bmatrix} 2 & 5 \\ 7 & 3 \\ 0 & -4 \\ \end{bmatrix}^T = \begin{bmatrix} 2 & 7 & 0 \\ 5 & 3 & -4 \end{bmatrix} \)
Bir matrisin transpozunun transpozu kendisine eşittir.
\( (A^T)^T = A \)
Simetrik matrislerin transpozu kendisine eşittir. Buna göre, birer simetrik matris olan birim ve sıfır matrislerinin transpozları kendilerine eşittir.
\( A \) simetrik bir matris ise,
\( A^T = A \)
\( I^T = I \)
\( O^T = O \)
Ters simetrik matrislerin transpozu matrisin toplamaya göre tersine eşittir.
\( A \) bir ters simetrik matris ise,
\( A^T = -A \)
\( A = \begin{bmatrix} 0 & -2 & 7 \\ 2 & 0 & 5 \\ -7 & -5 & 0 \end{bmatrix} \)
\( A^T = \begin{bmatrix} 0 & 2 & -7 \\ -2 & 0 & -5 \\ 7 & 5 & 0 \end{bmatrix} \)
Matrisler arasındaki bazı işlemlerin sonucunun transpozu ile ilgili kurallar aşağıdaki gibidir.
\( (A + B)^T = A^T + B^T \)
\( (A - B)^T = A^T - B^T \)
\( (kA)^T = kA^T \)
\( (AB)^T = B^TA^T \)
\( (ABC)^T = C^TB^TA^T \)
\( (A^{-1})^T = (A^T)^{-1} \)