Çemberin Çevresi ve Dairenin Alanı
Çemberin Çevresi
Çemberin çevresi yarıçapının \( 2\pi \) katıdır.
Çemberin çevresi \( = 2\pi r \)
\( x \) derecelik bir merkez açısının gördüğü yayın uzunluğu, açının ölçüsü 360° ile oranlanarak hesaplanabilir.
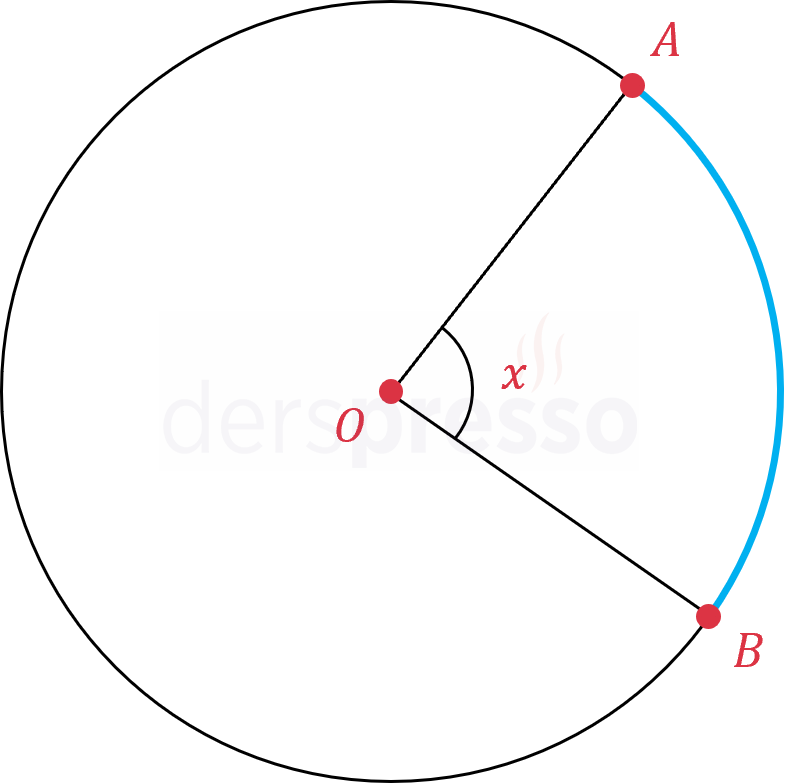
\( \abs{\overset{\LARGE\frown}{AB}} = 2\pi r \cdot \dfrac{x}{360°} \)
Yarıçapı 8 birim olan bir çemberde 45°'lik merkez açının gördüğü yayın uzunluğu:
\( = 2\pi (8) \cdot \dfrac{45°}{360°} = 2\pi \) birim
Dairenin Alanı
Dairenin alanı yarıçapının karesinin \( \pi \) katıdır.
Dairenin alanı \( = \pi r^2 \)
\( x \) derecelik bir merkez açısının oluşturduğu daire diliminin alanı, açının ölçüsü 360° ile oranlanarak hesaplanabilir.
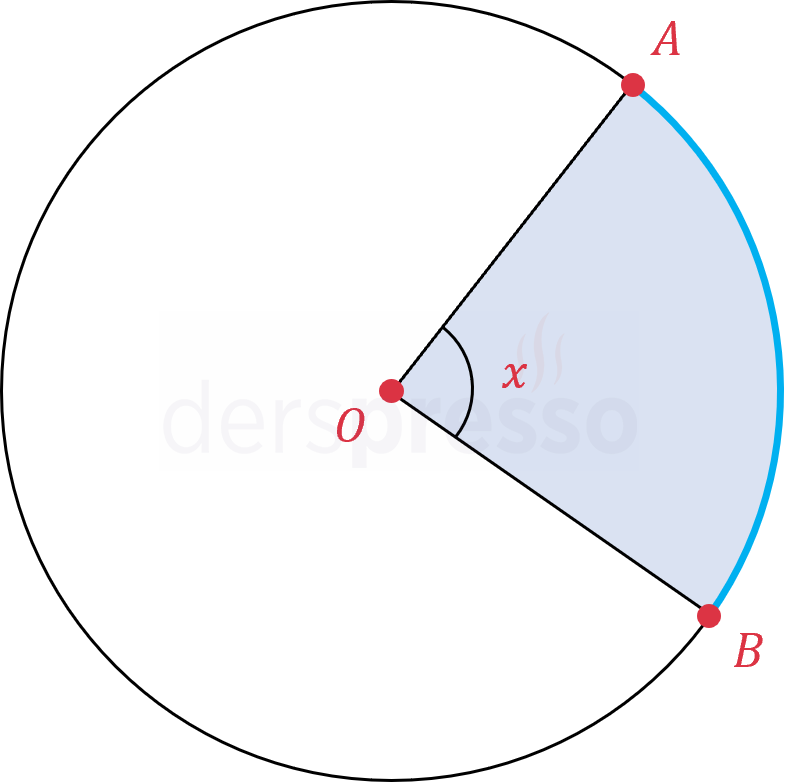
Daire diliminin alanı \( = \pi r^2 \cdot \dfrac{x}{360°} \)
Yarıçapı 8 birim olan bir çemberde 45°'lik merkez açının oluşturduğu daire diliminin alanı:
\( = \pi (8^2) \cdot \dfrac{45°}{360°} = 8\pi \) birimkare
Bu alan formülü yukarıda paylaştığımız yay uzunluğu cinsinden de yazılabilir. Bu durumda daire dilimi alan formülü, üçgen alan formülüne benzer şekilde taban (çember yayı) çarpı yükseklik (yarıçap) bölü 2 biçiminde olmaktadır.
Daire diliminin alanı \( = \dfrac{\abs{\overset{\LARGE\frown}{AB}}r}{2} \)
Yukarıdaki örneklerdeki daire diliminin alanı:
\( = \dfrac{2\pi \cdot 8}{2} = 8\pi \) birimkare
Yarıçapı 5 cm olan daire şeklindeki bir pizza merkezinden 10 eşit dilime bölünüyor.
Pizzanın yan yana olan iki dilimi yendikten sonra kalan pizzanın çevresi kaç cm'dir?
Çözümü Göster2 dilim yendikten sonra kalan pizza aşağıdaki gibi olur.
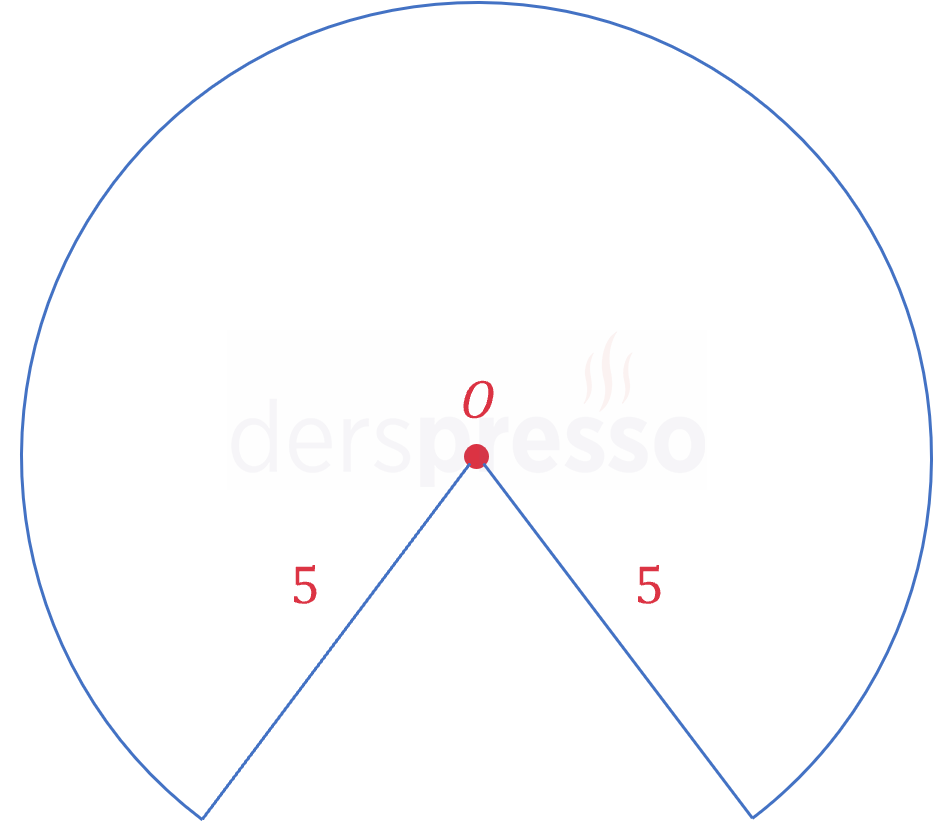
Buna göre, pizzanın çevresi kalan dairenin çevresiyle iki yarıçapın toplamına eşittir.
\( 2\pi r \cdot \dfrac{8}{10} + 2r \)
\( r = 5 \) olarak veriliyor.
\( = 8\pi + 10 \) cm bulunur.
Bir dairenin yarıçapı \( \% 20 \) azaltılırsa alanı % kaç azalır?
Çözümü GösterDairenin yarıçapına \( r = 10 \) diyelim.
Dairenin alanı \( \pi r^2 = 100\pi \) olur.
Yarıçap \( \% 20 \) azaltılırsa yeni yarıçap \( (1 - \frac{20}{100}) \cdot 10 = 8 \) olur.
Bu durumda dairenin alanı \( \pi r^2 = 64\pi \) olur.
Buna göre dairenin yarıçapı \( \% 20 \) azaltılırsa alanı \( \frac{100\pi - 64\pi}{100\pi} = \%36 \) azalmış olur.
Çevreleri eşit olan bir çember ve eşkenar üçgenin alanlarının oranı nedir?
Çözümü GösterÇemberin yarıçapına \( r \), eşkenar üçgenin bir kenar uzunluğuna \( a \) diyelim.
Çember ve eşkenar üçgenin çevreleri eşittir.
\( 2\pi r = 3a \)
\( \dfrac{r}{a} = \dfrac{3}{2\pi} \)
Çember ve eşkenar üçgenin alanlarının oranını bulalım.
\( \dfrac{\pi r^2}{\frac{\sqrt{3}a^2}{4}} = \dfrac{4\pi r^2}{\sqrt{3}a^2} \)
İfadeyi düzenleyelim.
\( = \dfrac{4\pi}{\sqrt{3}} \cdot (\dfrac{r}{a})^2 \)
\( \dfrac{r}{a} = \dfrac{3}{2\pi} \) yazalım.
\( = \dfrac{4\pi}{\sqrt{3}} \cdot (\dfrac{3}{2\pi})^2 \)
\( = \dfrac{4\pi}{\sqrt{3}} \cdot \dfrac{9}{4\pi^2} \)
\( = \dfrac{9}{\sqrt{3}\pi} \)
\( = \dfrac{3\sqrt{3}}{\pi} \) bulunur.

Şekildeki daire diliminin yarıçapı 5 birim, \( \overgroup{AB} \) yayının uzunluğu \( 14 \) birimdir.
Buna göre bu daire diliminin alanı kaçtır?
Çözümü GösterYay ve yarıçap uzunluğu bilinen daire diliminin alanı aşağıdaki formülle hesaplanır.
Daire diliminin alanı \( = \dfrac{\text{Yay uzunluğu} \cdot \text{Yarıçap}}{2} \)
\( = \dfrac{\abs{\overgroup{AB}}r}{2} \)
\( = \dfrac{14 \cdot 5}{2} = 35 \) bulunur.
Çapı 12 cm olan bir dairenin alanının \( 20\pi \) cm\( ^2 \) azalması için çapı kaç cm azaltılmalıdır?
Çözümü GösterDairenin ilk durumdaki yarıçapına \( r_1 \), son durumdaki yarıçapına \( r_2 \) diyelim.
Çapı 12 cm olan dairenin alanını bulalım.
\( 2r_1 = 12 \Longrightarrow r_1 = 6 \)
\( \pi r_1^2 = 36\pi \)
Dairenin alanı \( 20\pi \) azaldığında \( 36\pi - 20\pi = 16\pi \) cm\( ^2 \) olur.
Alanı \( 16\pi \) olan dairenin çapını yarıçapını bulalım.
\( \pi r_2^2 = 16\pi \)
\( r_2 = 4 \)
Buna göre dairenin çapı yeni durumda \( 2r_2 = 8 \) cm olur.
Buna göre, dairenin çapı \( 12 - 8 = 4 \) cm azaltılmıştır.
Bir karenin ve bir dairenin alanları birbirine eşittir. Buna göre bu dairenin çevresinin karenin çevresine oranı nedir?
Çözümü GösterKarenin bir kenar uzunluğuna \( a \) diyelim. Bu durumda karenin alanı \( a^2 \) olur.
Dairenin yarıçapına \( r \) diyelim. Bu durumda dairenin alanı \( \pi r^2 \) olur.
Kare ve dairenin alanlarını birbirine eşitleyelim.
\( a^2 = \pi r^2 \)
Her iki tarafın karekökünü alalım.
\( a = \sqrt{\pi}r \)
Karenin çevresi \( 4a \), dairenin çevresi \( 2\pi r \) olur.
Bu durumda dairenin çevresinin karenin çevresine oranı \( \frac{2\pi r}{4a} \) olur.
\( a \)'nın \( r \) cinsinden karşılığını yazalım.
\( \dfrac{2\pi r}{4a} = \dfrac{2\pi r}{4\sqrt{\pi}r} \)
\( = \dfrac{\pi}{2\sqrt{\pi}} = \dfrac{\sqrt{\pi}}{2} \) bulunur.
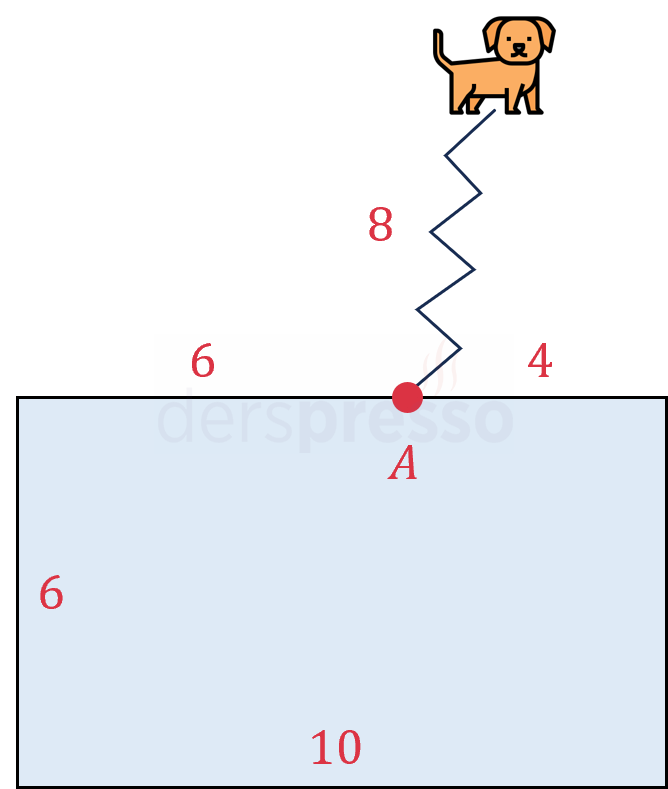
Bir köpek tasmasıyla yukarıdaki şekildeki gibi dikdörtgen bir kulübeye A noktasından bağlanıyor.
Tasmanın uzunluğu 8 metre olduğuna göre, köpek kulübenin etrafında en çok kaç metrekarelik alanı tarayabilir?
Çözümü GösterMerkezi A noktası olarak düşünürsek köpeğin gidebileceği maksimum alan aşağıdaki şekildeki taralı alan olur.
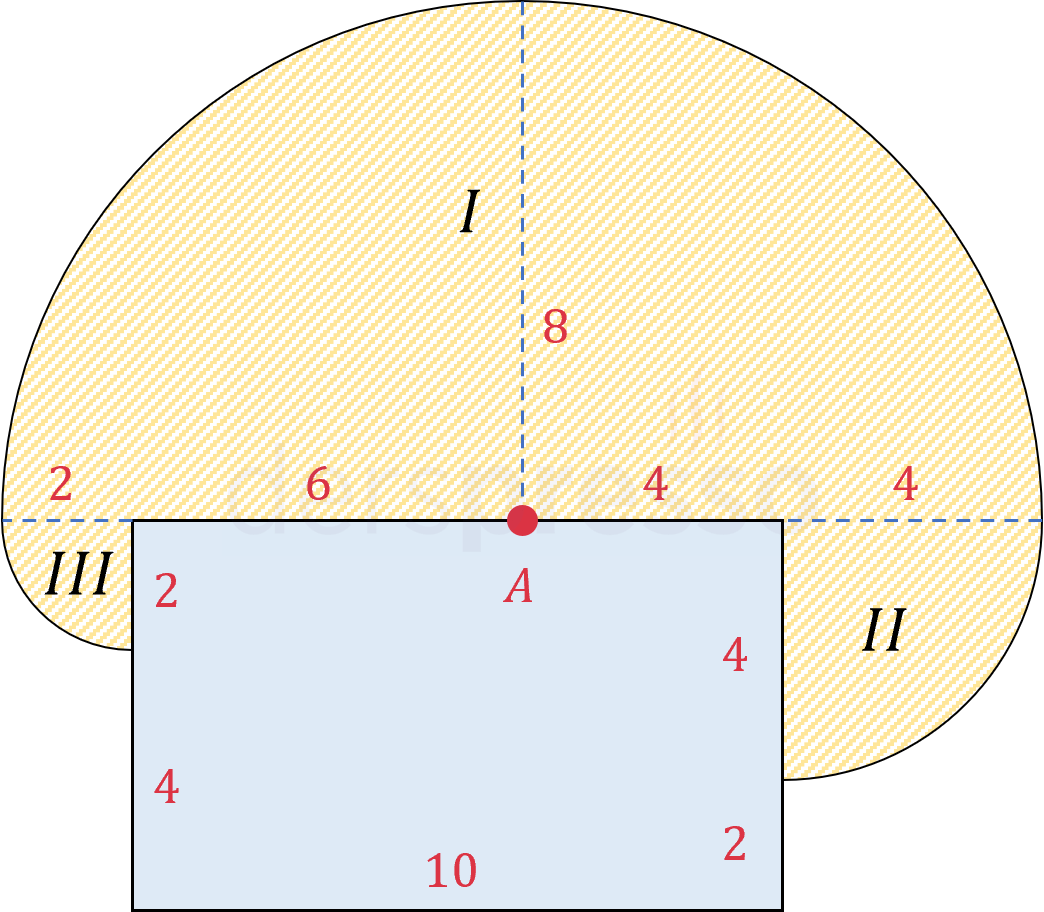
Bu taralı alan I nolu yarım çember ile II ve III nolu çeyrek çemberlerden oluşur.
Bu üç alanın toplamını bulalım.
\( \dfrac{\pi \cdot 8^2}{2} + \dfrac{\pi \cdot 4^2}{4} + \dfrac{\pi \cdot 2^2}{4} \)
\( = 32\pi + 4\pi + \pi \)
\( = 37\pi \) metrekare bulunur.

Yukarıdaki şekilde üç eş merkezli çember ve iki dik çap bulunmaktadır. Verilen üç taralı bölgenin alanları eşittir.
Küçük çemberin yarıçapı 2 olduğuna göre, üç çemberin yarıçapları çarpımı kaçtır?
Çözümü GösterÜç taralı bölgenin alanları eşit olduğuna göre, küçük dairenin ve bu dairenin dışında kalan iki katmanın alanları eşittir.
Küçük dairenin alanı \( = \pi \cdot 2^2 = 4\pi \)
Buna göre ortadaki dairenin alanı \( 8\pi \), dıştaki dairenin alanı \( 12\pi \) olur.
Ortadaki dairenin yarıçapına \( a \), dıştaki dairenin yarıçapına \( b \) diyelim.
Ortadaki dairenin alan formülünü kullanarak yarıçapını bulalım.
\( \pi \cdot a^2 = 8\pi \)
\( a = 2\sqrt{2} \)
Dıştaki dairenin alan formülünü kullanarak yarıçapını bulalım.
\( \pi \cdot b^2 = 12\pi \)
\( b = 2\sqrt{3} \)
Dairelerin yarıçaplarının çarpımını bulalım.
\( 2 \cdot 2\sqrt{2} \cdot 2\sqrt{3} = 8\sqrt{6} \) bulunur.
Osman bir kenarı 100 metre olan kare şeklindeki portakal bahçesinin çevresine tel çit örmeyi planlıyor. Bahçenin sınırları ile çit arasında belirli bir mesafe olmasını istediği için de çitin her noktada bahçeye 20 metre uzaklıkta olmasını istiyor.
Buna göre Osman'ın örmesi gereken çitin uzunluğu toplam kaç metredir? (\( \pi = 3 \) olarak alınız.)
Çözümü GösterOsman'ın örmesi gereken çit karenin kenarları boyunca bahçeye paralel, karenin köşelerinde de çeyrek çember şeklinde olmalıdır.
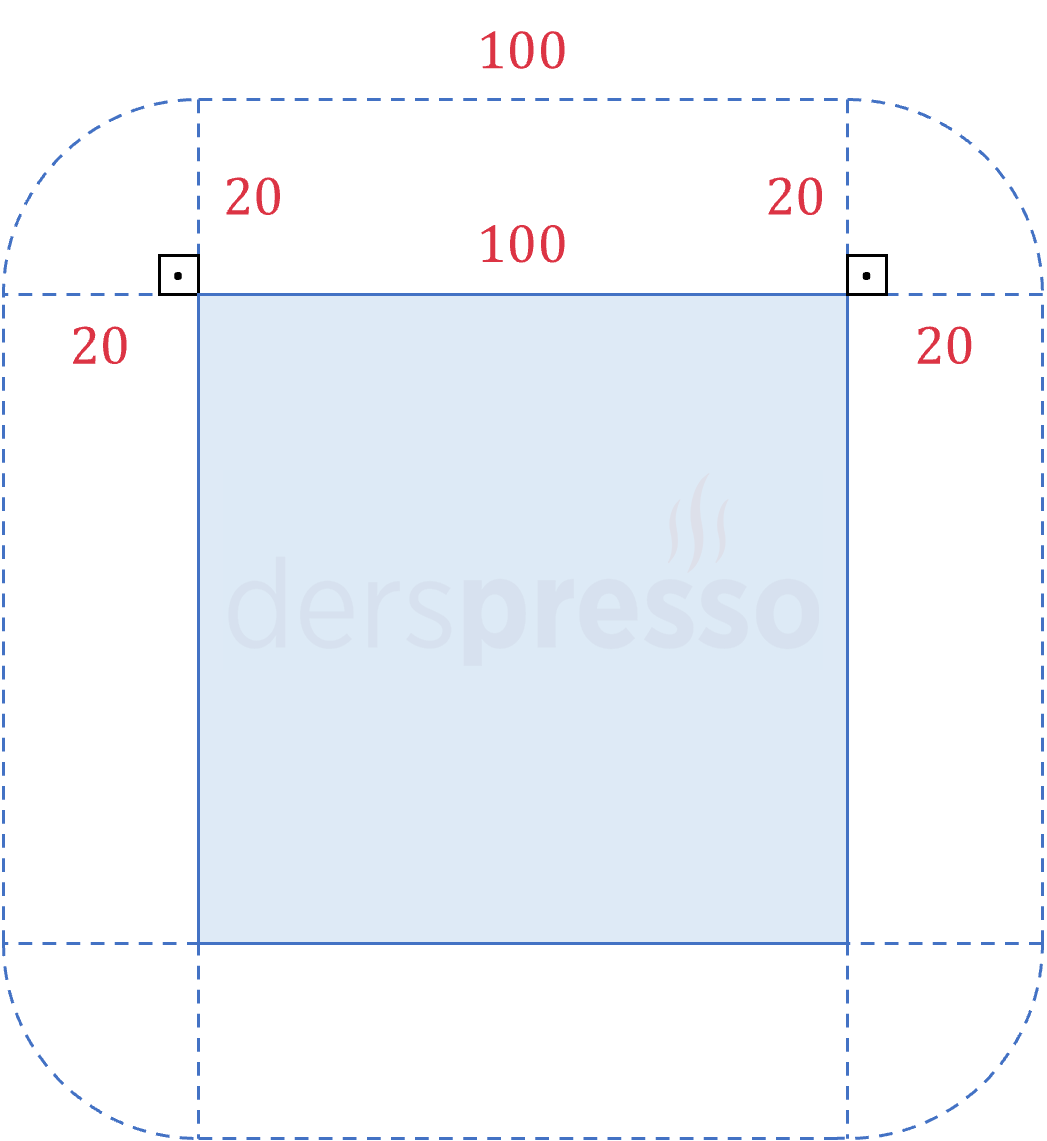
Çitin kenarlara paralel olan düz kısımlarının uzunluğu karenin çevre uzunluğuna eşittir.
\( 100 \cdot 4 = 400 \) metre
Çitin köşe kısımları ise yarıçapı 20 metre olan dört çeyrek çemberin uzunluğuna eşittir.
\( 2\pi r = 2 \cdot 3 \cdot 20 = 120 \) metre
Buna göre ihtiyaç duyulan çit uzunluğu toplam \( 400 + 120 = 520 \) metredir.
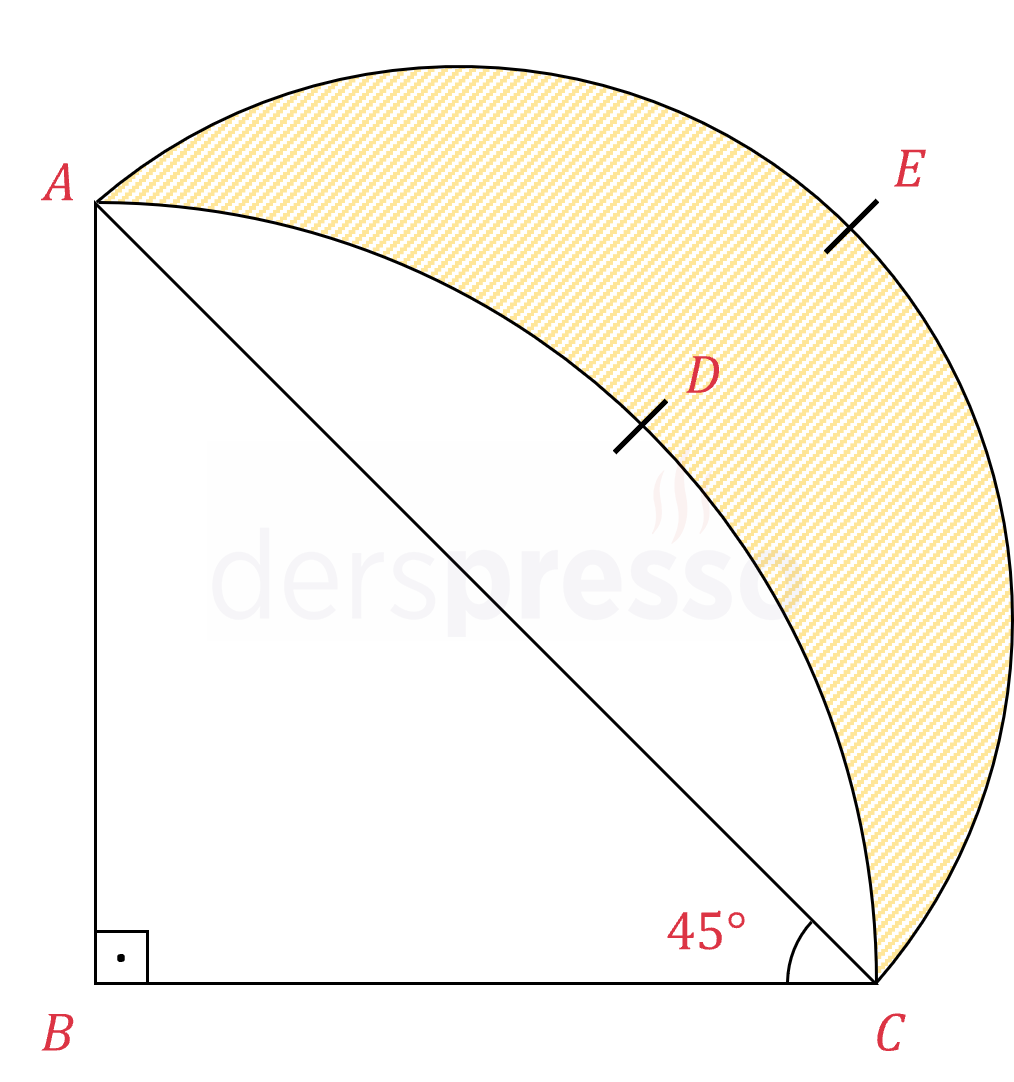
Yukarıdaki şekilde \( ABC \) ikizkenar dik üçgendir.
\( \overgroup{ADC} \), \( B \) merkezli çeyrek çembere ait yaydır.
\( \overgroup{AEC} \), çapı \( [AC] \) olan yarım çembere ait yaydır.
Taralı bölgenin alanı 32 birimkare olduğuna göre, \( \abs{BC} \) uzunluğu kaç birimdir?
Çözümü GösterŞekildeki üç bölgeye \( A_1 \), \( A_2 \) ve \( A_3 \) diyelim.
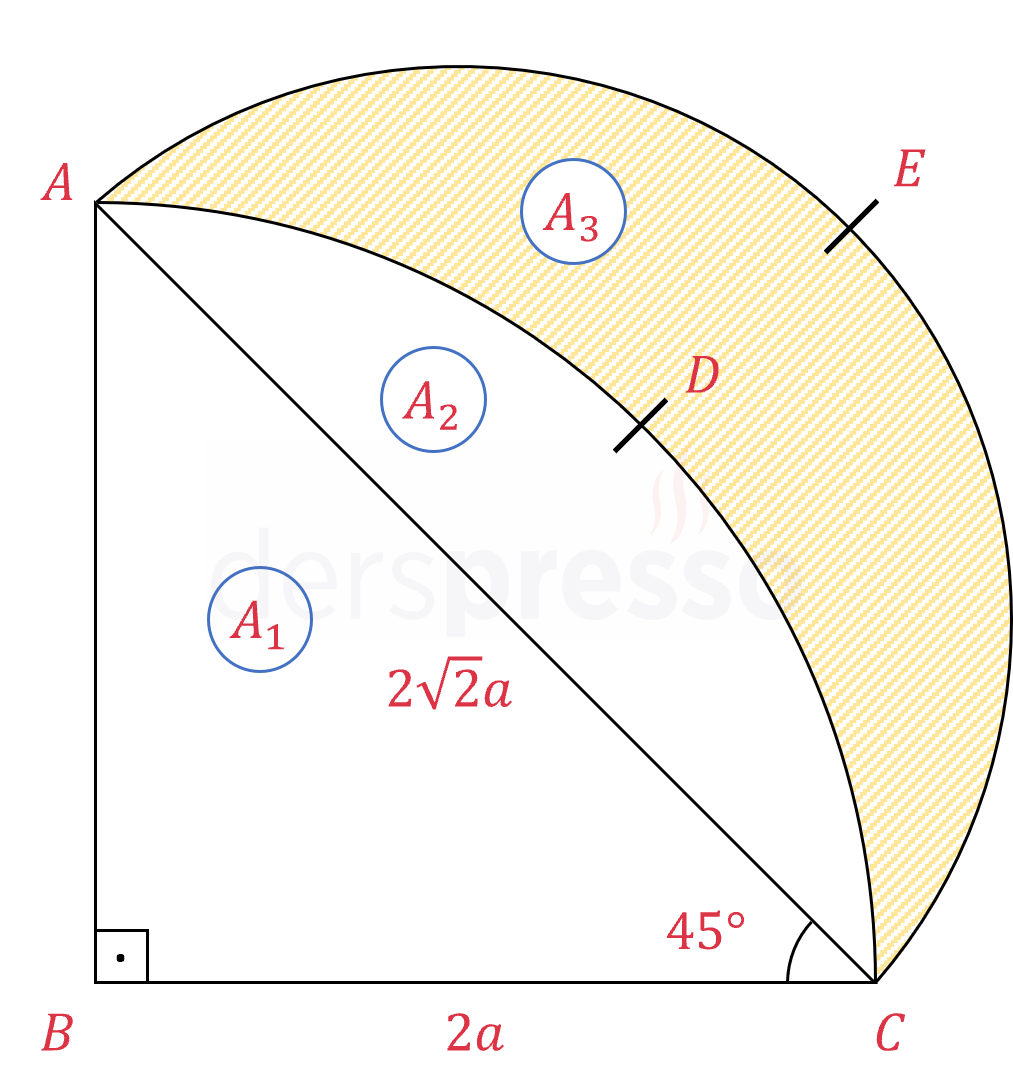
\( ABC \) üçgeninin alanı: \( A_1 \)
\( B \) merkezli çeyrek çemberin alanı: \( A_1 + A_2 \)
Çapı \( [AC] \) olan yarım çemberin alanı: \( A_2 + A_3 \)
\( \abs{BC} \) uzunluğuna \( 2a \) diyelim.
\( ABC \) üçgenine Pisagor teoremini uygulayarak hipotenüs uzunluğunu bulalım.
\( \abs{AC} = \sqrt{(2a)^2 + (2a)^2} = 2\sqrt{2}a \)
\( ABC \) üçgeninin alanını bulalım.
\( A_1 = \dfrac{2a \cdot 2a}{2} = 2a^2 \)
\( B \) merkezli çeyrek çemberin alanını bulalım.
\( A_1 + A_2 = \dfrac{\pi (2a)^2}{4} = \pi a^2 \)
\( A_2 = \pi a^2 - A_1 \)
\( = \pi a^2 - 2a^2 \)
Çapı \( [AC] \) olan yarım çemberin alanını bulalım.
\( A_2 + A_3 = \dfrac{\pi (\sqrt{2}a)^2}{2} = \pi a^2 \)
\( A_3 = \pi a^2 - A_2 \)
\( = \pi a^2 - (\pi a^2 - 2a^2) \)
\( = 2a^2 \)
Bulduğumuz alan 32 birimkaredir.
\( 2a^2 = 32 \)
\( a = 4 \)
\( \abs{BC} = 2a = 8 \) birim bulunur.

Yukarıdaki şekilde \( O \) merkezli ve 4 birim yarıçaplı daire ve köşeleri \( O \) noktası ve daire üzerinde iki nokta olan \( AOC \) üçgeni verilmiştir.
\( \widehat{AOC} \) açısının tümleyeni bütünleyeninin \( \frac{1}{3} \)'üne eşit olduğuna göre, \( \overgroup{AC} \) yayının uzunluğu kaç birimdir?
Çözümü GösterÖlçüleri toplamı 90° olan açılara tümler açılar, 180° olan açılara bütünler açılar denir.
\( \widehat{AOC} \) açısının ölçüsüne \( x \) diyelim.
\( x \) açısının tümleyeni \( 90 - x \), bütünleyeni \( 180 - x \) olur.
\( (180 - x) \cdot \dfrac{1}{3} = 90 - x \)
\( 180 - x = 270 - 3x \)
\( x = 45° \)
Ölçüsü \( a \) derece olan merkez açısının gördüğü yayın uzunluğu aşağıdaki formülle hesaplanır.
Yay uzunluğu \( = 2\pi r \cdot \dfrac{a}{360} \)
\( \overgroup{AC} \) yayının uzunluğunu bulalım.
\( \abs{\overgroup{AC}} = 2\pi r \cdot \dfrac{45}{360} \)
\( = 2\pi \cdot 4 \cdot \dfrac{1}{8} = \pi \) birim bulunur.
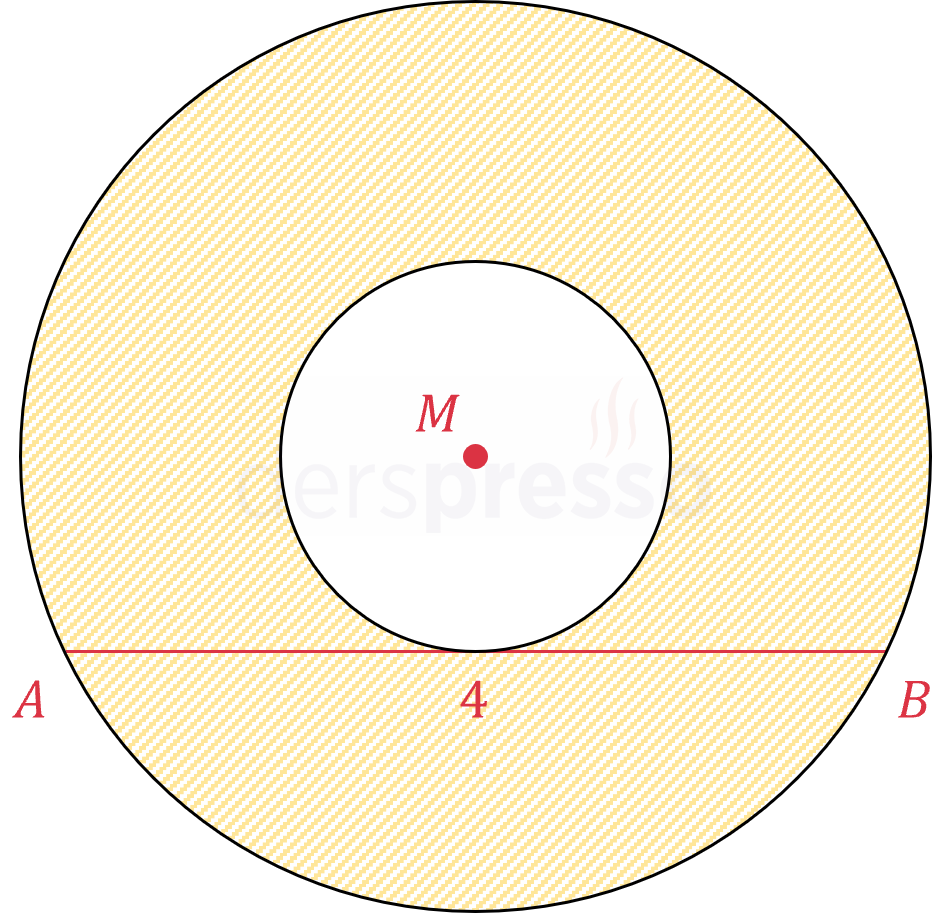
Yukarıda \( M \) merkezli iki çember verilmiştir. \( \abs{AB} = 4 \) olduğuna göre, taralı bölgenin alanı kaç birimkaredir?
Çözümü Gösterİçteki çemberin yarıçapına \( r_1 \), dıştaki çemberin yarıçapına \( r_2 \) diyelim.
\( M \) noktasından \( \abs{AB} \) kirişine bir dikme çizelim.
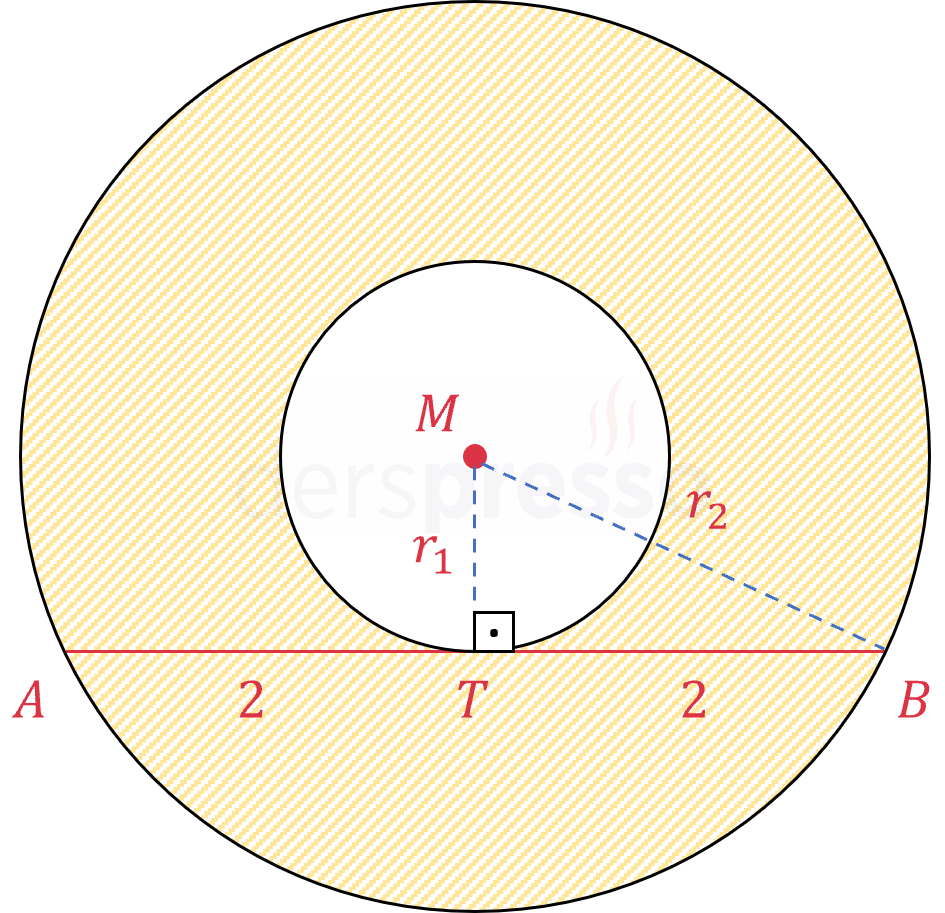
Bir çemberin kirişini dik kesen yarıçap kirişi ortalar.
\( \abs{AT} = \abs{TB} = 2 \)
\( MTB \) üçgeninde Pisagor teoremini uygulayalım.
\( r_1^2 + 2^2 = r_2^2 \)
\( r_2^2 - r_1^2 = 4 \)
Taralı bölgenin alanını bulmak için dıştaki çemberin alanından içteki çemberin alanını çıkaralım.
\( A = \pi r_2^2 - \pi r_1^2 \)
\( = \pi(r_2^2 - r_1^2) \)
Yukarıda bulduğumuz yarıçapların kareleri farkını yerine koyalım.
\( = 4\pi \) bulunur.