Pascal Üçgeni
İsmini Fransız matematikçi Blaise Pascal'dan alan Pascal üçgeninin kümeler, kombinasyon, olasılık, binom açılımı ve diğer pek çok konuda uygulamaları vardır.

Pascal üçgeni aşağıdaki adımlar takip edilerek oluşturulur.
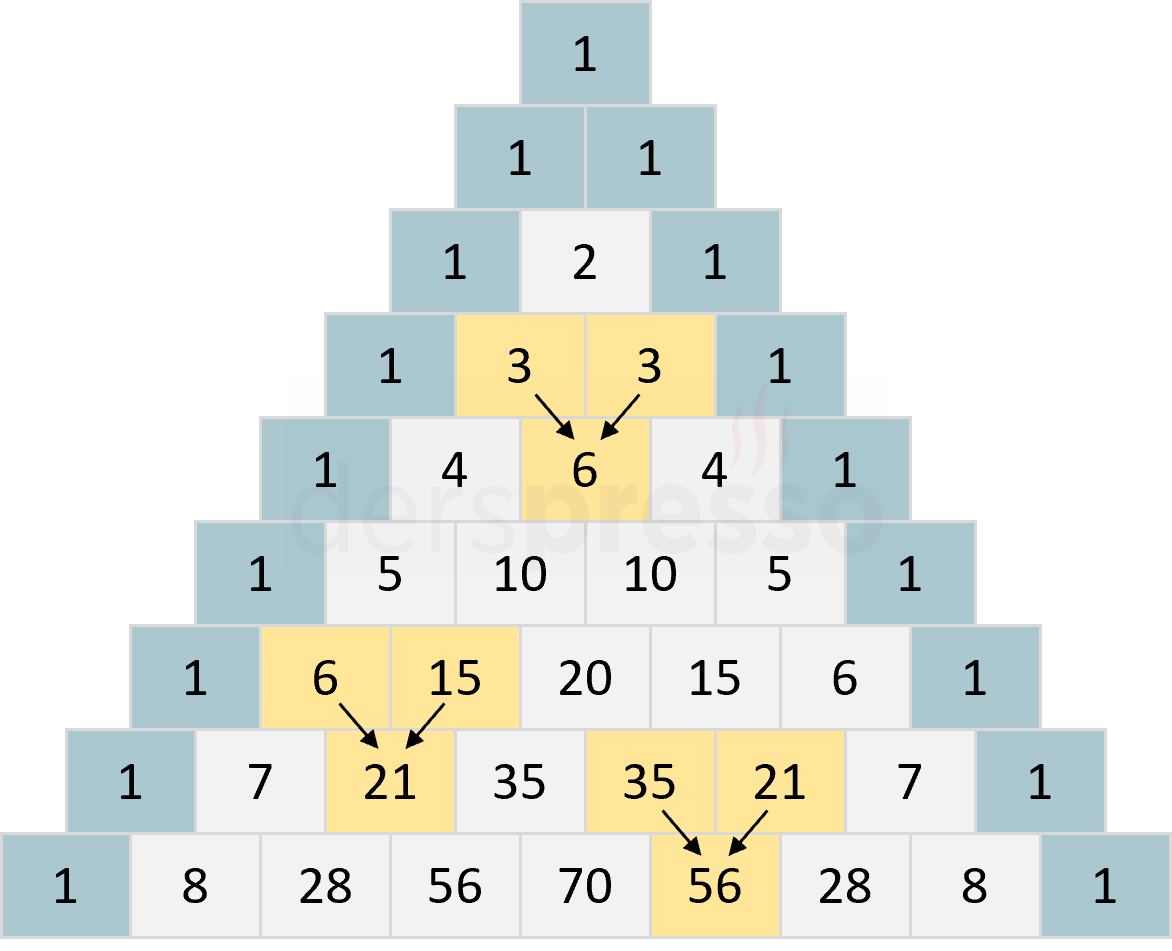
- İlk satırda bir kutu bulunur, sonraki her satırda kutu sayısı birer artarak ilerler.
- İlk satırdaki kutuya 1 yazılır.
- Sonraki her satırda ilk ve son kutulara 1, aralarındaki her kutuya kutunun üst kenarına komşu iki kutudaki sayıların toplamı yazılır.
Pascal Üçgeni ve Kombinasyon
Pascal üçgeninde satırlar ve her satırdaki kutular sıfırdan başlayarak numaralandırılırlar. Buna göre örneğin 6. satırdaki (yeşil satır) kutular 5'in sırasıyla 0'dan 5'e kadarki kombinasyonlarına karşılık gelir.
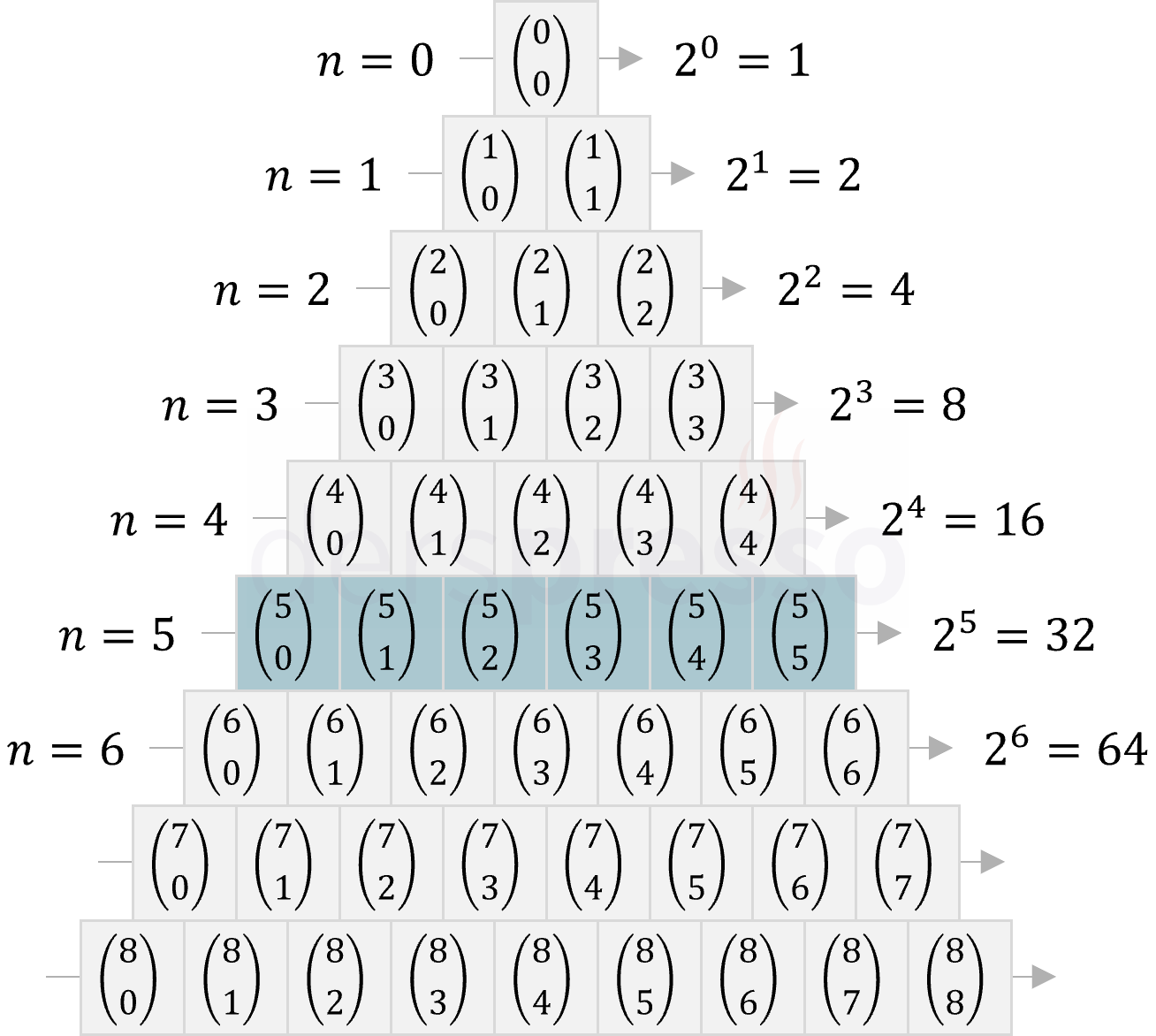
\( n \) no'lu satırdaki \( r \) no'lu kutudaki sayı:
\( \binom{n}{r} = C(n, r) \)
\( n = 10 \) no'lu satırdaki \( r = 3 \) no'lu kutudaki sayı:
\( \binom{10}{3} = C(10, 3) \)
\( = \dfrac{10!}{3!\ 7!} = \dfrac{10 \cdot 9 \cdot 8}{3 \cdot 2} = 120 \)
Kombinasyonun aşağıdaki özelliğinin bir sonucu olarak, Pascal üçgeni ortasından geçen dikey bir doğruya göre simetriktir, yani üçgen bu doğru etrafında katlandığında üst üste gelen kutular aynı sayıları içerir.
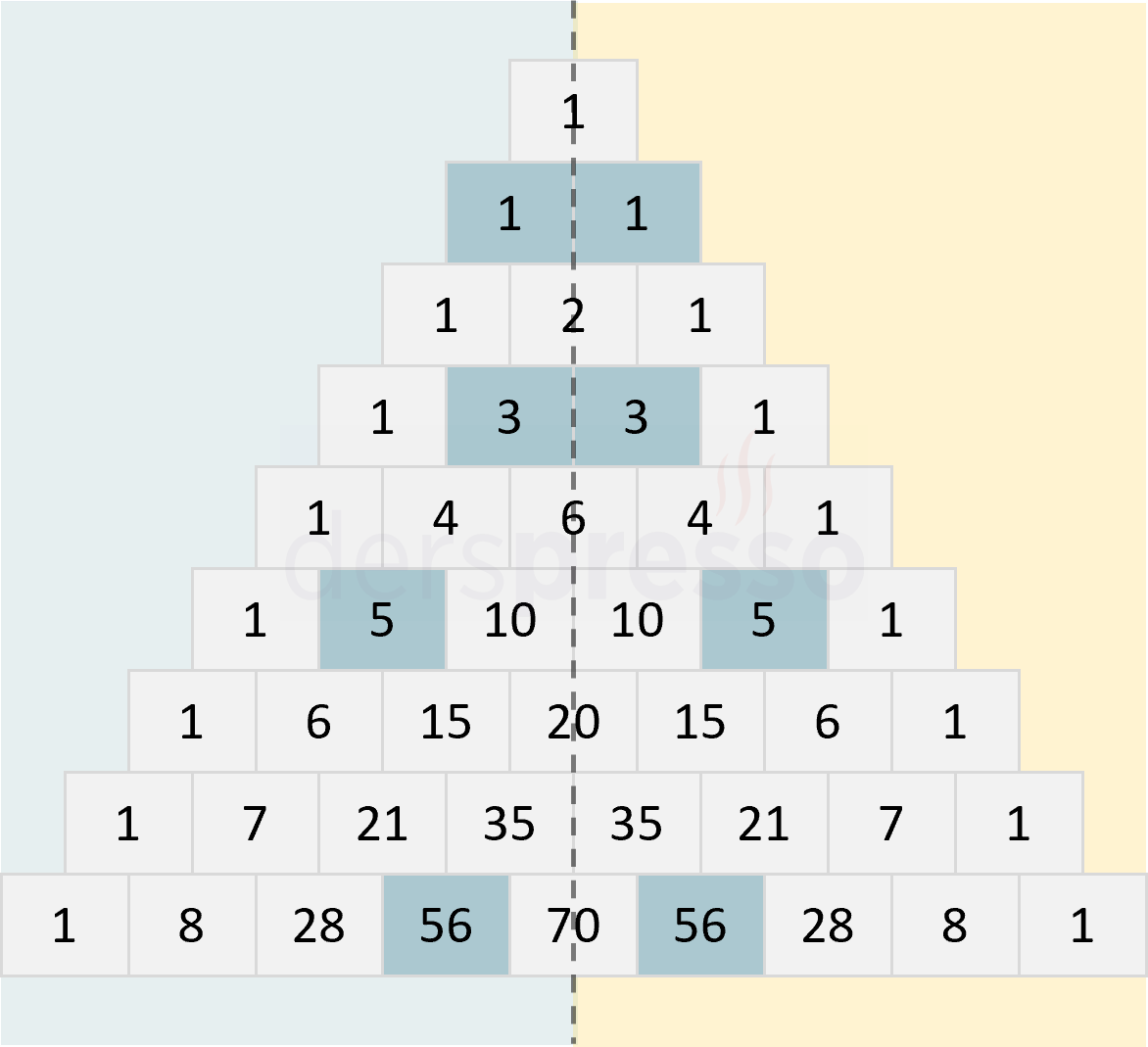
\( \binom{n}{r} = \binom{n}{n - r} \)
\( \binom{5}{1} = \binom{5}{4} = \dfrac{5!}{1!\ 4!} = 5 \)
\( \binom{8}{3} = \binom{8}{5} = \dfrac{8!}{3!\ 5!} = 56 \)
\( \binom{100}{98} = \binom{100}{2} = \dfrac{100!}{98!\ 2!} = 4950 \)
İSPATI GÖSTER
\( n \)'nin \( r \)'li kombinasyonunu yazalım.
\( C(n, r) = \dfrac{n!}{r!\ (n - r)!} \)
Paydadaki iki çarpanın yerini değiştirmemiz sonucu değiştirmez.
\( = \dfrac{n!}{(n - r)!\ r!} \)
Bu ifade \( n \)'nin \( (n - r) \)'li kombinasyonuna eşittir.
\( = C(n, n - r) \)
Bir \( n \) sayısının tüm kombinasyonlarının toplamı \( 2^n \) olduğu için, Pascal üçgeninin \( n \) no'lu satırındaki sayıların toplamı \( 2^n \) olur.
\( \binom{n}{0} + \binom{n}{1} + \ldots + \binom{n}{n - 1} + \binom{n}{n} = 2^n \)
\( \binom{4}{0} + \binom{4}{1} + \binom{4}{2} + \binom{4}{3} + \binom{4}{4} = 2^4 \)
\( 1 + 4 + 6 + 4 + 1 = 16 \)
İSPATI GÖSTER
\( (x + y)^n \) ifadesinin açılımını yazalım.
\( (x + y)^n = \binom{n}{0}x^n + \binom{n}{1}x^{n-1}y + \binom{n}{2}x^{n-2}y^2 + \ldots + \binom{n}{n}y^n \)
\( x = y = 1 \) yazalım.
\( (1 + 1)^n = \binom{n}{0} + \binom{n}{1} + \binom{n}{2} + \ldots + \binom{n}{n} \)
\( 2^n = \binom{n}{0} + \binom{n}{1} + \binom{n}{2} + \ldots + \binom{n}{n} \)
Pascal üçgeninin oluşturulması adımlarında paylaştığımız kural (her sayı üstündeki iki sayının toplamına eşittir) kombinasyon ifadeleri ile yazıldığında Pascal özdeşliği elde edilir.
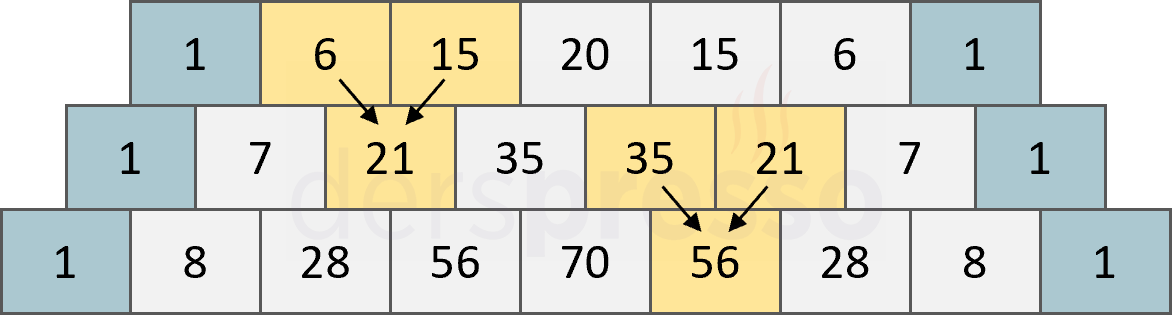
\( \binom{n}{r} + \binom{n}{r + 1} = \binom{n + 1}{r + 1} \)
\( \binom{6}{1} + \binom{6}{2} = \binom{7}{2} \)
\( 6 + 15 = 21 \)
\( \binom{7}{4} + \binom{7}{5} = \binom{8}{5} \)
\( 35 + 21 = 56 \)
İSPATI GÖSTER
İspat 1: Cebirsel
\( C(n, r) + C(n, r + 1) = \dfrac{n!}{r!\ (n - r)!} + \dfrac{n!}{(r + 1)!\ (n - r - 1)!} \)
Paydaları eşitlemek için birinci kesri \( (r + 1) \) ile, ikinci kesri \( (n - r) \) ile genişletelim.
\( = \dfrac{n!\ (r + 1)}{r!\ (r + 1)\ (n - r)!} + \dfrac{n!\ (n - r)}{(r + 1)!\ (n - r - 1)!\ (n - r)} \)
Paydalardaki yeni çarpanları faktöriyellere dahil edelim.
\( = \dfrac{n!\ (r + 1)}{(r + 1)!\ (n - r)!} + \dfrac{n!\ (n - r)}{(r + 1)!\ (n - r )!} \)
Paylardaki çarpanları parantez içlerine dağıtalım.
\( = \dfrac{n!\ r + n! + n!\ n - n!\ r}{(r + 1)!\ (n - r)!} \)
\( = \dfrac{n!\ (n + 1)}{(r + 1)!\ (n - r)!} \)
\( = \dfrac{(n + 1)!}{(r + 1)!\ (n - r)!} \)
Yukarıdaki ifade \( (n + 1) \)'in \( (r + 1) \)'li kombinasyonuna eşittir.
\( = C(n + 1, r + 1) \)
İspat 2: Sayma
\( n \) kişilik bir grup içinden \( r \) kişilik bir ekip seçmek istiyor olalım.
Kombinasyon tanımına göre bu seçim \( C(n, r) \) farklı şekilde yapılabilir.
Alternatif bir yöntemle, gruptaki belirli bir X kişisini ekibe seçtiğimiz ve seçmediğimiz duruma göre problemi iki alt probleme bölelim.
Durum 1:
Gruptaki X kişisi ekibe dahil olacak.
Bu durumda kalan \( n - 1 \) arasından \( r - 1 \) kişi seçmemiz yeterlidir.
Bu seçim \( C(n - 1, r - 1) \) farklı şekilde yapılabilir.
Durum 2:
Gruptaki X kişisi ekibe dahil olmayacak.
Bu durumda kalan \( n - 1 \) arasından \( r \) kişi seçmemiz gerekir.
Bu seçim \( C(n - 1, r) \) farklı şekilde yapılabilir.
Bu iki durum ayrık olaylar oldukları için, her birindeki farklı seçim sayılarının toplamı yukarıda bulduğumuz \( C(n, r) \) değerine eşit olur.
\( C(n - 1, r - 1) + C(n - 1, r) = C(n, r) \)
Elde ettiğimiz özdeşlik tanımdaki özdeşliğe denktir (\( n \to n - 1, r \to r - 1 \)).
\( C(n, r) + C(n, r + 1) = C(n + 1, r + 1) \)
Pascal üçgeninde ilk satır dışındaki satırlarda, çift indisli kutulardaki (yeşil) sayıların toplamı ile tek indisli kutulardaki (gri) sayıların toplamı birbirine ve ayrı ayrı \( 2^{n-1} \) değerine eşittir.
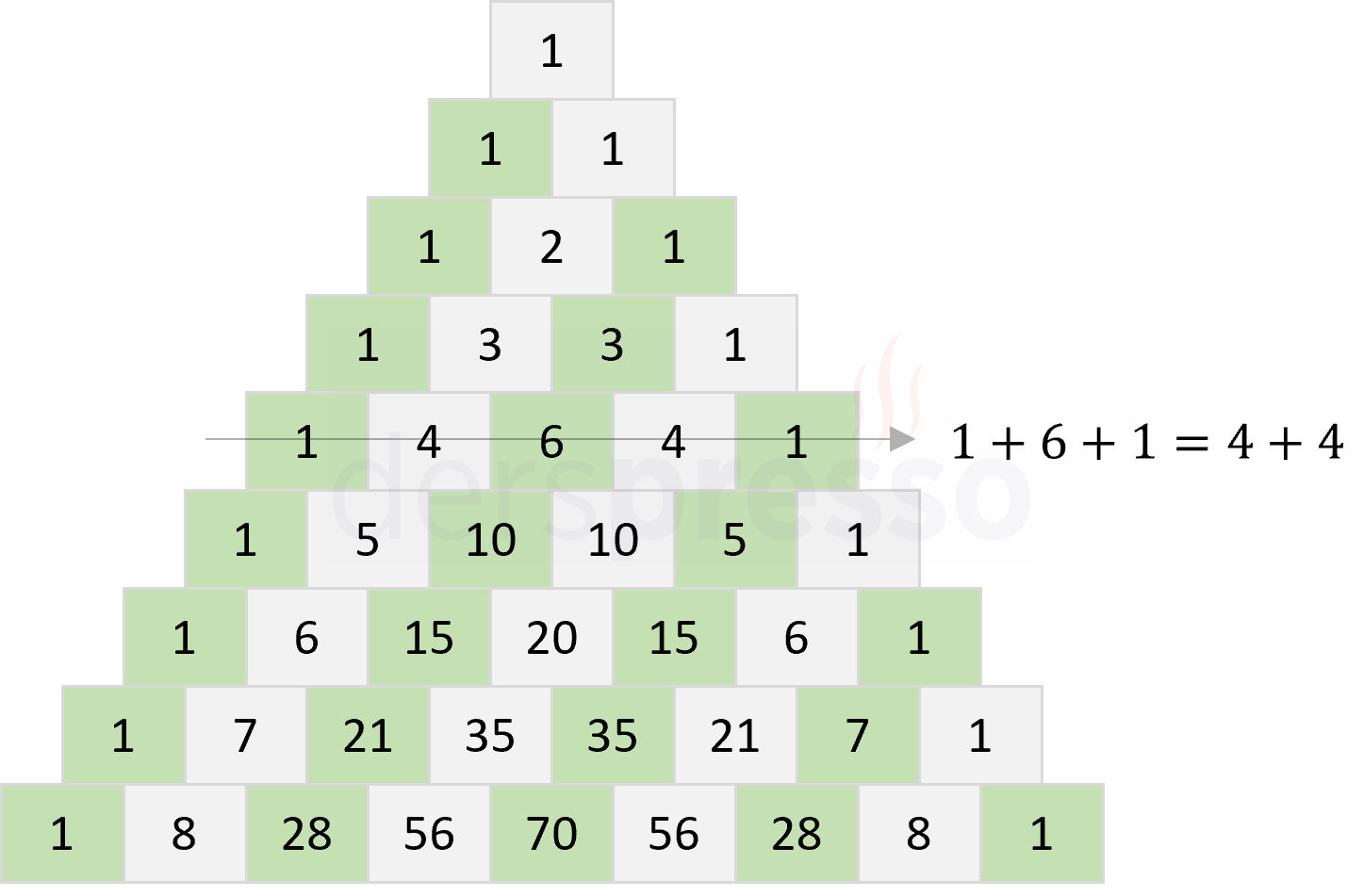
\( \binom{n}{0} + \binom{n}{2} + \binom{n}{4} + \ldots = 2^{n - 1} \)
\( \binom{n}{1} + \binom{n}{3} + \binom{n}{5} + \ldots = 2^{n - 1} \)
\( 1 + 1 = 2 \)
\( 1 + 6 + 1 = 4 + 4 \)
\( 1 + 15 + 15 + 1 = 6 + 20 + 6 \)
İSPATI GÖSTER
\( (1 + x)^n \) ifadesinin açılımını yazalım.
\( (1 + x)^n = \binom{n}{0} + \binom{n}{1}x + \binom{n}{2}x^2 + \binom{n}{3}x^3 + \ldots \)
\( (1 - x)^n \) ifadesinin açılımını yazalım.
\( (1 - x)^n = \binom{n}{0} - \binom{n}{1}x + \binom{n}{2}x^2 - \binom{n}{3}x^3 + \ldots \)
İki eşitliği taraf tarafa topladığımızda her \( \binom{n}{r} \) ifadesinde \( r \)'nin tek sayı olduğu terimler birbirini götürür.
\( (1 + x)^n + (1 - x)^n = 2\left[ \binom{n}{0} + \binom{n}{2}x^2 + \binom{n}{4}x^4 + \ldots \right] \)
\( x = 1 \) yazalım.
\( (1 + 1)^n + (1 - 1)^n = 2\left[ \binom{n}{0} + \binom{n}{2} + \binom{n}{4} + \ldots \right] \)
\( 2^n = 2\left[ \binom{n}{0} + \binom{n}{2} + \binom{n}{4} + \ldots \right] \)
Eşitliğin taraflarını ikiye böldüğümüzde \( r \)'nin çift sayı olduğu terimlerin toplamı aşağıdaki gibi bulunur.
\( \binom{n}{0} + \binom{n}{2} + \binom{n}{4} + \ldots = 2^{n-1} \)
Benzer bir işlemi aynı iki eşitliği birbirinden çıkararak yaptığımızda her \( \binom{n}{r} \) ifadesinde \( r \)'nin çift sayı olduğu terimler birbirini götürür.
\( (1 + x)^n - (1 - x)^n = 2\left[ \binom{n}{1}x + \binom{n}{3}x^3 + \binom{n}{5}x^5 + \ldots \right] \)
\( x = 1 \) yazalım.
\( (1 + 1)^n - (1 - 1)^n = 2\left[ \binom{n}{1} + \binom{n}{3} + \binom{n}{5} + \ldots \right] \)
\( 2^n = 2\left[ \binom{n}{1} + \binom{n}{3} + \binom{n}{5} + \ldots \right] \)
Eşitliğin taraflarını ikiye böldüğümüzde \( r \)'nin tek sayı olduğu terimlerin toplamı aşağıdaki gibi bulunur.
\( \binom{n}{1} + \binom{n}{3} + \binom{n}{5} + \ldots = 2^{n-1} \)
Kombinasyon ile ilişkisi sebebiyle Pascal üçgeninin \( n \) no'lu satırındaki \( r \) no'lu kutudaki \( \binom{n}{r} \) değerinin aşağıdaki anlamları da vardır.
- \( n \) elemanlı bir kümenin \( r \) elemanlı alt kümelerinin sayısı
- \( n \) kişi arasından seçilecek \( r \) kişilik ekiplerin sayısı
- \( (x + y)^n \) şeklindeki bir binom ifadenin açılımındaki \( (r + 1). \) terimin binom katsayısı
Pascal Üçgeninin Özellikleri
Pascal üçgeninin içerdiği bazı sayı dizileri aşağıdaki gibidir.
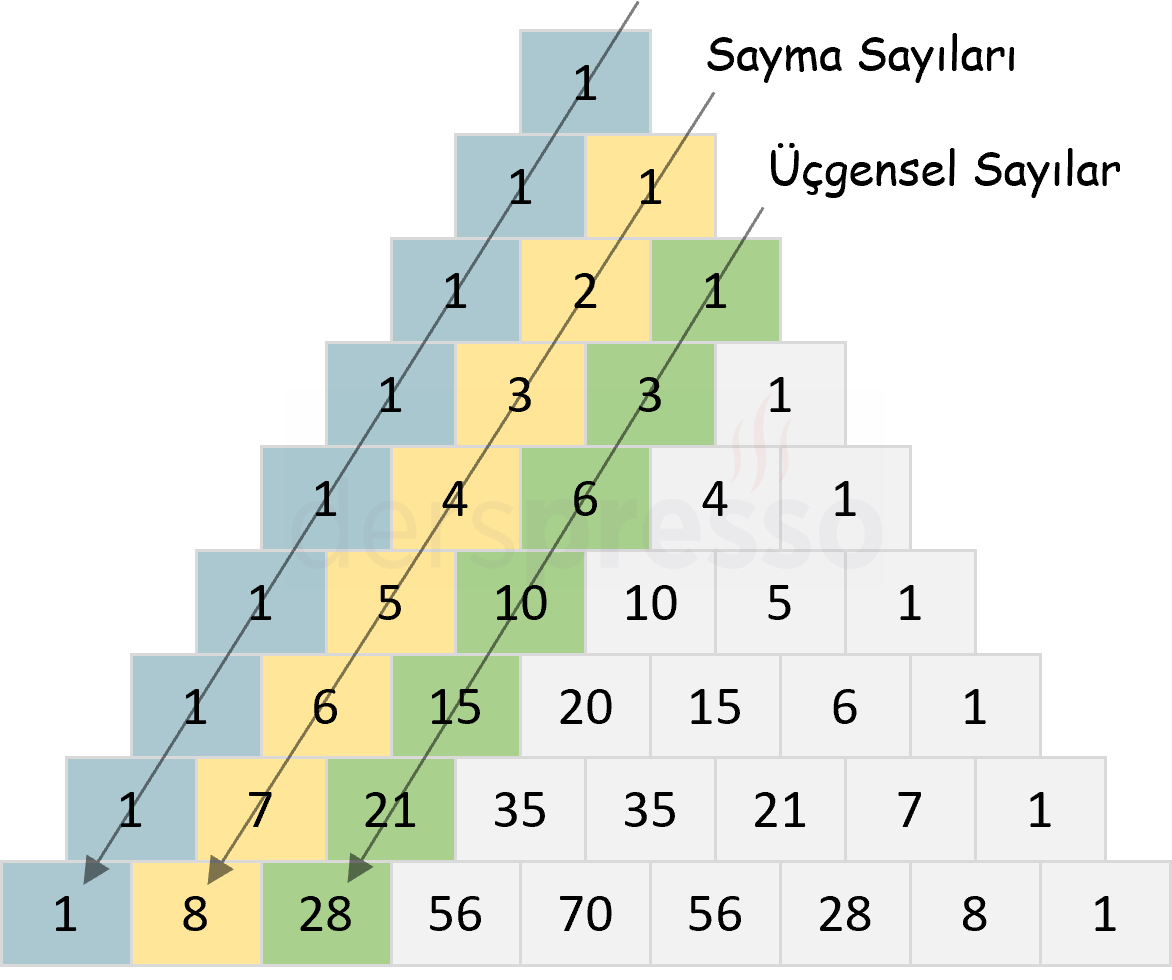
- En dıştaki köşegen sabit 1 sayılarından oluşur.
- Onun bir içindeki köşegen sayma sayılarından oluşur (\( 1, 2, 3, 4, \ldots \)).
- Onun bir içindeki köşegen üçgensel sayılardan oluşur (\( 1, 3, 6, 10, \ldots \)).
Pascal üçgeninin \( n \). satırındaki sayılar soldan sağa tek bir sayı gibi okunduğunda 11'in \( n \). kuvvetini verir. \( n = 5 \)'ten itibaren kutular iki ya da daha çok basamaklı sayılar içerebildiği için, bir kutudaki sayının birler basamağı dışındaki basamaklarındaki sayı soldaki kutudaki sayıya eklenerek ilerlenir.

\( n = 5 \) no'lu satırdaki sayıların 11'in 5. kuvvetini verdiğini gösterelim.
\( n = 5 \) no'lu satırdaki sayıları listeleyelim.
\( 1 - 5 - 10 - \textcolor{red}{10} - 5 - 1 \)
Liste iki basamaklı sayılar içermektedir.
Bu sayılardan en sağdaki olan 10'un onlar basamağındaki sayıyı (1) soldaki kutuya aktaralım.
\( 1 - 5 - \textcolor{red}{11} - 0 - 5 - 1 \)
11'in onlar basamağındaki sayıyı (1) soldaki kutuya aktaralım.
\( 1 - 6 - 1 - 0 - 5 - 1 \)
\( 11^5 = 161,051 \)
Pascal üçgeninde 9 sayının bulunduğu satırdaki en büyük eleman \( a \), bu satırdaki tüm elemanların toplamı \( b \) olduğuna göre, \( b - a \) kaçtır?
Çözümü GösterPascal üçgeninde \( n \) no'lu satırda \( n + 1 \) sayı bulunur.
\( n + 1 = 9 \Longrightarrow n = 8 \)
Bir satırdaki en büyük eleman ortadaki terimdir.
\( a = \binom{8}{4} = \dfrac{8!}{4!\ 4!} = 70 \)
\( n \) no'lu satırdaki sayıların toplamı \( 2^n \) olur.
\( b = 2^8 = 256 \)
\( b - a = 256 - 70 = 186 \) bulunur.
Pascal üçgeninde \( n = 8 \) ve \( n = 9 \) no'lu satırlardaki sayıların 11'in 8. ve 9. kuvvetini verdiğini gösteriniz.
Çözümü Göster\( n = 8 \) no'lu satır:
\( n = 8 \) no'lu satırdaki sayıları listeleyelim.
\( 1 - 8 - 28 - 56 - 70 - 56 - \textcolor{red}{28} - 8 - 1 \)
Liste iki basamaklı sayılar içermektedir.
Bu sayılardan en sağdaki olan 28'in onlar basamağındaki sayıyı (2) soldaki kutuya aktaralım.
\( 1 - 8 - 28 - 56 - 70 - \textcolor{red}{58} - 8 - 8 - 1 \)
Bu sayılardan en sağdaki olan 58'in onlar basamağındaki sayıyı (5) soldaki kutuya aktaralım.
\( 1 - 8 - 28 - 56 - \textcolor{red}{75} - 8 - 8 - 8 - 1 \)
Bu sayılardan en sağdaki olan 75'in onlar basamağındaki sayıyı (7) soldaki kutuya aktaralım.
\( 1 - 8 - 28 - \textcolor{red}{63} - 5 - 8 - 8 - 8 - 1 \)
Bu sayılardan en sağdaki olan 63'ün onlar basamağındaki sayıyı (6) soldaki kutuya aktaralım.
\( 1 - 8 - \textcolor{red}{34} - 3 - 5 - 8 - 8 - 8 - 1 \)
Bu sayılardan en sağdaki olan 34'ün onlar basamağındaki sayıyı (3) soldaki kutuya aktaralım.
\( 1 - \textcolor{red}{11} - 4 - 3 - 5 - 8 - 8 - 8 - 1 \)
11'in onlar basamağındaki sayıyı (1) soldaki kutuya aktaralım.
\( 2 - 1 - 4 - 3 - 5 - 8 - 8 - 8 - 1 \)
\( 11^8 = 214,358,881 \)
\( n = 9 \) no'lu satır:
\( n = 9 \) no'lu satırdaki sayıları listeleyelim.
\( 1 - 9 - 36 - 84 - 126 - 126 - 84 - \textcolor{red}{36} - 9 - 1 \)
Liste iki ve üç basamaklı sayılar içermektedir.
Bu sayılardan en sağdaki olan 36'nın onlar basamağındaki sayıyı (3) soldaki kutuya aktaralım.
\( 1 - 9 - 36 - 84 - 126 - 126 - \textcolor{red}{87} - 6 - 9 - 1 \)
Bu sayılardan en sağdaki olan 87'nin onlar basamağındaki sayıyı (8) soldaki kutuya aktaralım.
\( 1 - 9 - 36 - 84 - 126 - \textcolor{red}{134} - 7 - 6 - 9 - 1 \)
Bu sayılardan en sağdaki olan 134'ün onlar ve yüzler basamağındaki sayıyı (13) soldaki kutuya aktaralım.
\( 1 - 9 - 36 - 84 - \textcolor{red}{139} - 4 - 7 - 6 - 9 - 1 \)
Bu sayılardan en sağdaki olan 139'un onlar ve yüzler basamağındaki sayıyı (13) soldaki kutuya aktaralım.
\( 1 - 9 - 36 - \textcolor{red}{97} - 9 - 4 - 7 - 6 - 9 - 1 \)
Bu sayılardan en sağdaki olan 97'nin onlar basamağındaki sayıyı (9) soldaki kutuya aktaralım.
\( 1 - 9 - \textcolor{red}{45} - 7 - 9 - 4 - 7 - 6 - 9 - 1 \)
45'in onlar basamağındaki sayıyı (4) soldaki kutuya aktaralım.
\( 1 - \textcolor{red}{13} - 5 - 7 - 9 - 4 - 7 - 6 - 9 - 1 \)
13'ün onlar basamağındaki sayıyı (1) soldaki kutuya aktaralım.
\( 2 - 3 - 5 - 7 - 9 - 4 - 7 - 6 - 9 - 1 \)
\( 11^9 = 2,357,947,691 \)