Binom Açılımı
İki terimli (binom) bir ifadenin bir doğal sayı kuvvetinin açılımına binom açılımı denir.
\( (x + y)^n \) şeklindeki bir ifadenin açılımı aşağıdaki gibidir.
\( \binom{n}{k} \) ifadesi \( n \)'nin \( k \)'lı kombinasyonu olmak üzere,
\( (x + y)^n = \binom{n}{0} x^{n - 0}y^0 \) \( + \binom{n}{1} x^{n - 1}y^1 \) \( + \binom{n}{2} x^{n - 2}y^2 \) \( + \ldots + \binom{n}{k} x^{n - k}y^k \) \( + \ldots + \binom{n}{n} x^{n - n}y^n \)
Bu ifadeyi aşağıdaki gibi sadeleştirebiliriz.
\( (x + y)^n = x^n \) \( + \binom{n}{1} x^{n - 1}y \) \( + \binom{n}{2} x^{n - 2}y^2 \) \( + \ldots + \binom{n}{k} x^{n - k}y^k \) \( + \ldots + y^n \)
\( (x + y)^2 = \binom{2}{0} x^2 + \binom{2}{1} x^1y^1 + \binom{2}{2} y^2 \)
\( = x^2 + 2xy + y^2 \)
\( (x + y)^3 = \binom{3}{0} x^3 + \binom{3}{1} x^2y^1 \) \( + \binom{3}{2} x^1y^2 \) \( + \binom{3}{3} y^3 \)
\( = x^3 + 3x^2y + 3xy^2 + y^3 \)
Dikkat edilirse yukarıdaki iki örnekteki binom açılımları daha önce özdeşlikler konusunda gördüğümüz parantez karesi ve kübü açılımları ile aynı sonucu vermektedir.
Binom açılımında vurgulamamız gereken önemli bazı noktalar şunlardır.
- \( n \). dereceden bir binom ifadenin açılımında \( (n + 1) \) terim vardır.
- Binom açılımında terimler binomun ilk teriminin (yukarıdaki açılımda \( x \)) azalan kuvvetlerine göre sıralanır.
- Buna göre birinci teriminin kuvveti açılımda \( n \) ile başlar ve her terimde birer azalarak son terimde 0 olur (\( x^n \to x^{n-1} \to \ldots \to x^1 \to x^0 \)).
- Binomun ikinci teriminin kuvveti açılımda 0 ile başlar ve her terimde birer artarak son terimde \( n \) olur (\( y^0 \to y^1 \to \ldots \to y^{n-1} \to y^n \)).
- Açılımın her teriminde binom terimlerinin kuvvetlerinin toplamı \( n \)'ye eşittir.
\( (x + y)^n \) ifadesinin binom açılımının bir teriminin bileşenleri aşağıdaki gibidir.
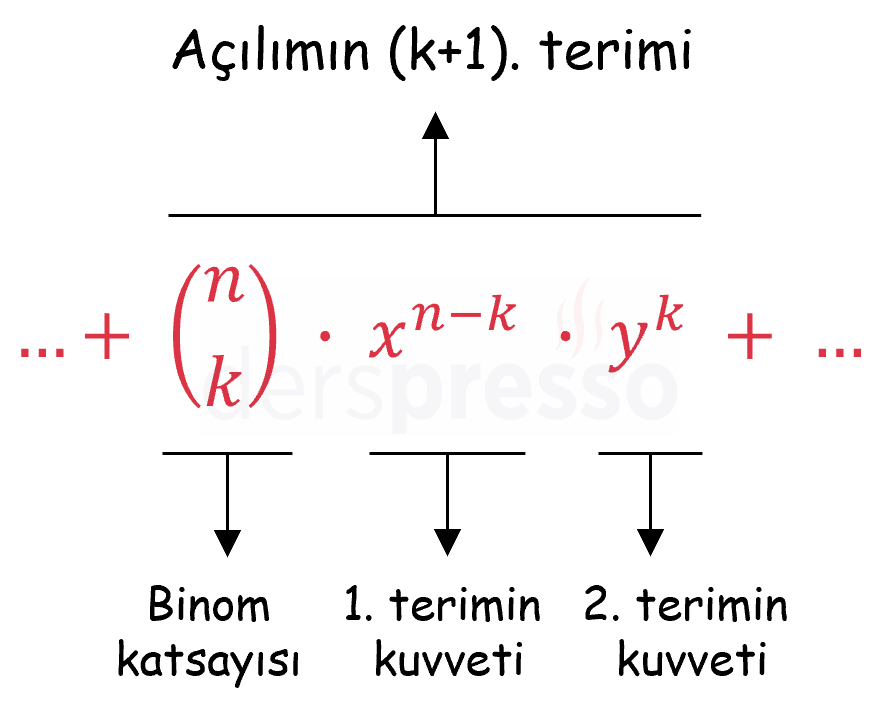
Binom açılımındaki \( \binom{n}{k} \) ifadelerine binom katsayısı adı verilir ve her biri \( n \)'nin \( k \)'lı kombinasyonuna karşılık gelir.
\( \binom{n}{k} = C(n, k) = \dfrac{n!}{k!(n - k)!} \)
Binom açılımını toplama işlemi ile aşağıdaki gibi kısa şekilde yazabiliriz.
\( (x + y)^n = \displaystyle\sum_{k = 0}^{n} \binom{n}{k}x^{n - k}y^k \)
\( (x + y)^6 \) ifadesinin açılımını yazalım.
Çözümü Göster
Farklı Binom Terimleri İçin Binom Açılımı
Yukarıda kullandığımız \( (x + y) \) ifadesinin iki terimi de katsayıları ve kuvvetleri 1 olan değişkenlerdi, ancak binom ifadelerde bu terimler farklı pozitif ya da negatif katsayı ve derecelerde olabilir ya da terimlerden biri sabit bir sayı olabilir.
\( (2x + 3y)^3 \)
\( (5a^2 - 4)^6 \)
\( (x - \dfrac{1}{x})^8 \)
Bu tip ifadelerin açılımı için de yukarıda paylaştığımız genel binom açılım formülünü kullanabiliriz. Yapmamız gereken bu formüldeki \( x \) ve \( y \) değişkenleri yerine ilgili ifadedeki terimleri parantez içinde koymak, daha sonra bu parantezleri açarak terimleri sadeleştirmek olacaktır.
\( (a + 3b)^2 = \binom{2}{0} a^2 + \binom{2}{1} a^1(3b)^1 \) \( + \binom{2}{2} (3b)^2 \)
\( = a^2 + 2a(3b) + (9b^2) \)
\( = a^2 + 6ab + 9b^2 \)
\( (3x - 2y^2)^3 = \binom{3}{0} (3x)^3 \) \( + \binom{3}{1} (3x)^2(-2y^2)^1 \) \( + \binom{3}{2} (3x)^1(-2y^2)^2 \) \( + \binom{3}{3} (-2y^2)^3 \)
\( = (27x^3) + 3(9x^2)(-2y^2) \) \( + 3(3x)(4y^4) \) \( + (-8y^6) \)
\( = 27x^3 - 54x^2y^2 + 36xy^4 - 8y^6 \)
Görebileceğimiz gibi, bu tip ifadelerin açılımındaki terimlerin katsayıları sadece binom katsayısından oluşmamakta ve çarpanlardan gelen katsayıları da içermektedir. Binom katsayısı teriminin sadece \( \binom{n}{k} \) ifadesine karşılık geldiğine dikkat edilmelidir.
Binom ifadenin ikinci teriminin katsayısı negatif ise (\( (x - y) \) gibi) açılımdaki terimlerin katsayıları \( y \)'nin çift kuvvetleri için pozitif, tek kuvvetleri için negatif olur. Dolayısıyla \( (x - y)^n \) ifadesinin açılımında terimlerin katsayıları pozitif ile başlar ve bir pozitif bir negatif şeklinde ilerler (\( + - + - + - \ldots \)).
\( (x^2 - \frac{2}{x})^4 \) ifadesinin açılımını yazalım.
Çözümü Göster
\( (2x^3 - 3y^2)^3 \) ifadesinin açılımını yazalım.
Çözümü Göster
Terim Sayısı
\( (x + y)^n \) şeklindeki bir ifadede \( n \) tane \( (x + y) \) ifadesini çarptığımızda \( 2^n \) terim oluşur. Bu terimler içinde benzer olanları birbiriyle toplayıp çıkardığımızda geriye \( (n + 1) \) terim kalır.
\( (x + y)^3 = (x + y)(x + y)(x + y) \)
\( = (x^2 + xy + xy + y^2)(x + y) \)
\( = x^3 + x^2y + x^2y + xy^2 \) \( + x^2y + xy^2 \) \( + xy^2 + y^3 \)
Görebileceğimiz gibi, tüm terimleri birbiriyle çarpınca \( 2^n = 2^3 = 8 \) terim oluşmaktadır.
\( = x^3 + 3x^2y + 3xy^2 + y^3 \)
Benzer terimleri topladığımızda ise \( n + 1 = 3 + 1 = 4 \) terim kalmaktadır.
\( (4x + 5y)^n \) ifadesinin açılımında 13 terim olduğuna göre, \( n \) doğal sayısı kaçtır?
Çözümü Göster
\( (x + 2)^5 \cdot (x - y)^8 \) ifadesinin tam açılımında kaç terim vardır?
Çözümü Göster
Sabit Terim
Bir binom ifadenin açılımındaki sabit terimi bulmak için ifadedeki tüm değişkenlere 0 değeri verilerek değişkenli terimler yok edilir.
\( (x + y)^8 \) ifadesinin sabit terimi \( = (0 + 0)^8 = 0 \)
\( (2x + 3)^3 \) ifadesinin sabit terimi \( = (2 \cdot 0 + 3)^3 = 27 \)
\( (x^2 - 3)^4 \) ifadesinin açılımındaki sabit terim kaçtır?
Çözümü Göster
Binom ifadelerde sabit terimin oluştuğu bir diğer durum, binom ifadenin terimlerinin pay ve paydada aynı değişkeni içerdiği ve açılımdaki bazı terimlerde bu değişkenlerin birbirini götürdüğü ve terimin değişken kısmının \( x^0 \) olarak kaldığı durumlardır.
Aşağıdaki örnekte ikinci terimde sabit bir terim oluşmuştur.
\( (x + \frac{1}{x})^2 = x^2 + 2x\frac{1}{x} + \frac{1}{x^2} \)
\( = x^2 + 2 + \frac{1}{x^2} \)
Katsayılar Toplamı
Bir binom ifadenin açılımındaki katsayılar toplamını bulmak için ifadedeki tüm değişkenlere 1 değeri verilerek terimlerde sadece katsayılar bırakılır.
\( (x + y)^8 \) ifadesinin katsayılar toplamı \( = (1 + 1)^8 = 2^8 \)
\( (2x + 3)^3 \) ifadesinin katsayılar toplamı \( = (2 \cdot 1 + 3)^3 = 125 \)
\( (a - 3b)^6 \) ifadesinin açılımındaki katsayılar toplamı kaçtır?
Çözümü Göster