Ters Trigonometrik Özdeşlikler
Trigonometrik fonksiyonlar arasındaki özdeşlikleri ters trigonometrik fonksiyonlara uyarlayarak yeni özdeşlikler elde edebiliriz. Bu özdeşlikler ezberlenmesi gereken birer formül değildir, her birinin türetilme mantığının kavranması yeterlidir.
Trigonometrik ve Ters Trigonometrik Fonksiyonların Bileşkesi
Bir Fonksiyonun Kendi Tersiyle Bileşkesi
Bir fonksiyonun tersiyle bileşkesinin birim fonksiyona eşit olduğunu fonksiyonlar konusunda görmüştük.
\( (f \circ f^{-1})(x) = f(f^{-1}(x)) = I = x \)
Benzer şekilde, bir trigonometrik fonksiyonun tersi ile bileşkesi birim fonksiyonu verir.
\( \sin(\arcsin{x}) = x \)
\( \cos(\arccos{x}) = x \)
\( \tan(\arctan{x}) = x \)
\( \cot(\arccot{x}) = x \)
\( \sin(\underbrace{\arcsin{\frac{1}{2}}}_{\frac{\pi}{6}}) = \frac{1}{2} \)
Bir Fonksiyonun Arcsin ile Bileşkesi
Sinüs değeri \( x \) olan bir \( \theta \) açısı için, karşı kenarı \( x \) ve hipotenüsü \( 1 \) olan temsili bir üçgen çizerek diğer trigonometrik fonksiyonların arcsin ile bileşkesini hesaplayabiliriz. Bu üçgende Pisagor teoreminden komşu kenar uzunluğu \( \sqrt{1 - x^2} \) olmaktadır.

\( \sin{\theta} = x \quad \Longleftrightarrow \quad \arcsin{x} = \theta \)
| \( \sin(\arcsin{x}) = x \) | \( \csc(\arcsin{x}) = \dfrac{1}{x} \) |
| \( \cos(\arcsin{x}) = \sqrt{1 - x^2} \) | \( \sec(\arcsin{x}) = \dfrac{1}{\sqrt{1 - x^2}} \) |
| \( \tan(\arcsin{x}) = \dfrac{x}{\sqrt{1 - x^2}} \) | \( \cot(\arcsin{x}) = \dfrac{\sqrt{1 - x^2}}{x} \) |
Bir Fonksiyonun Arccos ile Bileşkesi
Kosinüs değeri \( x \) olan bir \( \theta \) açısı için, komşu kenarı \( x \) ve hipotenüsü \( 1 \) olan temsili bir üçgen çizerek diğer trigonometrik fonksiyonların arccos ile bileşkesini hesaplayabiliriz. Bu üçgende Pisagor teoreminden karşı kenar uzunluğu \( \sqrt{1 - x^2} \) olmaktadır.

\( \cos{\theta} = x \quad \Longleftrightarrow \quad \arccos{x} = \theta \)
| \( \sin(\arccos{x}) = \sqrt{1 - x^2} \) | \( \csc(\arccos{x}) = \dfrac{1}{\sqrt{1 - x^2}} \) |
| \( \cos(\arccos{x}) = x \) | \( \sec(\arccos{x}) = \dfrac{1}{x} \) |
| \( \tan(\arccos{x}) = \dfrac{\sqrt{1 - x^2}}{x} \) | \( \cot(\arccos{x}) = \dfrac{x}{\sqrt{1 - x^2}} \) |
Bir Fonksiyonun Arctan ile Bileşkesi
Tanjant değeri \( x \) olan bir \( \theta \) açısı için, karşı kenarı \( x \) ve komşu kenarı \( 1 \) olan temsili bir üçgen çizerek diğer trigonometrik fonksiyonların arctan ile bileşkesini hesaplayabiliriz. Bu üçgende Pisagor teoreminden hipotenüs uzunluğu \( \sqrt{x^2 + 1} \) olmaktadır.

\( \tan{\theta} = x \quad \Longleftrightarrow \quad \arctan{x} = \theta \)
| \( \sin(\arctan{x}) = \dfrac{x}{\sqrt{x^2 + 1}} \) | \( \csc(\arctan{x}) = \dfrac{\sqrt{x^2 + 1}}{x} \) |
| \( \cos(\arctan{x}) = \dfrac{1}{\sqrt{x^2 + 1}} \) | \( \sec(\arctan{x}) = \sqrt{x^2 + 1} \) |
| \( \tan(\arctan{x}) = x \) | \( \cot(\arctan{x}) = \dfrac{1}{x} \) |
Tümler Açı Formülleri
Birbirini \( 90° \)'ye tamamlayan açıların sinüs-kosinüs, tanjant-kotanjant ve sekant-kosekant değerlerinin eşit olduğunu görmüştük.
\( \sin{x} = \cos(\frac{\pi}{2} - x) \)
\( \tan{x} = \cot(\frac{\pi}{2} - x) \)
\( \sec{x} = \csc(\frac{\pi}{2} - x) \)
Benzer özdeşlikleri ters trigonometrik fonksiyonlar için aşağıdaki şekilde yazabiliriz.
\( \arcsin{x} = \frac{\pi}{2} - \arccos{x} \)
\( \arctan{x} = \frac{\pi}{2} - \arccot{x} \)
\( \arcsec{x} = \frac{\pi}{2} - \arccsc{x} \)
\( \underbrace{\arcsin{\frac{1}{2}}}_{\frac{\pi}{6}} = \frac{\pi}{2} - \underbrace{\arccos{\frac{1}{2}}}_{\frac{\pi}{3}} \)
\( \underbrace{\arctan{1}}_{\frac{\pi}{4}} = \frac{\pi}{2} - \underbrace{\arccot{1}}_{\frac{\pi}{4}} \)
İSPATI GÖSTER
Birinci özdeşlik için aşağıdaki gibi bir dik üçgen çizelim.

\( \alpha = \dfrac{\pi}{2} - \beta \)
\( \sin{\alpha} = x \Longrightarrow \alpha = \arcsin{x} \)
\( \cos{\beta} = x \Longrightarrow \beta = \arccos{x} \)
İlk satırdaki \( \alpha \) ve \( \beta \) yerine bulduğumuz ifadeleri yazalım.
\( \arcsin{x} = \dfrac{\pi}{2} - \arccos{x} \)
Benzer ispatları diğer iki özdeşlik için de verebiliriz.
Diğer Özdeşlikler
Sinüs/kosekant, kosinüs/sekant ve tanjant/kotanjant fonksiyonları (oranların sıfırdan farklı olduğu açılar için) birbirlerinin çarpmaya göre tersi oldukları için, bu fonksiyonların ters fonksiyonları arasında da aşağıdaki özdeşlikleri yazabiliriz.
\( \arcsin{x} = \arccsc{\frac{1}{x}} \)
\( \arccos{x} = \arcsec{\frac{1}{x}} \)
\( \arctan{x} = \arccot{\frac{1}{x}} \)
\( \arcsin{\frac{1}{2}} = \arccsc{2} = \frac{\pi}{6} \)
\( \arctan{\sqrt{3}} = \arccot{\frac{1}{\sqrt{3}}} = \frac{\pi}{3} \)
\( \tan(\arcsin{\dfrac{2}{3}}) \) ifadesinin eşiti kaçtır?
Çözümü Göster\( \arcsin{\dfrac{2}{3}} = x \) diyelim.
\( \sin{x} = \dfrac{2}{3} \)
Bir açının sinüsü \( \frac{2}{3} \) ise karşı kenara 2k, hipotenüse 3k diyebiliriz, bu durumda komşu kenar Pisagor teoreminden \( \sqrt{5}k \) olur.
\( (2k)^2 + (\sqrt{5}k)^2 = (3k)^2 \)
Tanjant değerini karşı kenarın komşu kenara oranı olarak aşağıdaki gibi buluruz.
\( \tan{x} = \dfrac{2k}{\sqrt{5}k} \)
\( = \dfrac{2 \sqrt{5}}{5} \) bulunur.
\( \tan(\arccos{x}) \) ifadesinin eşiti \( x \) cinsinden nedir?
Çözümü Göster\( \arccos{x} = a \) diyelim.
\( \cos{a} = x \)
Bir \( a \) açısının kosinüsü \( x \) ise komşu kenara x, hipotenüse 1 diyebiliriz, bu durumda karşı kenar Pisagor teoreminden \( \sqrt{1 - x^2} \) olur.
\( \tan{a} = \dfrac{\sqrt{1 - x^2}}{x} \)
\( \tan(\arccos{x}) = \tan{a} = \dfrac{\sqrt{1 - x^2}}{x} \) bulunur.
\( 6 \arccot(2x) - \pi = 0 \)
denklemini sağlayan \( x \) değeri nedir?
Çözümü Göster\( 6\arccot(2x) = \pi \)
\( \arccot(2x) = \dfrac{\pi}{6} \)
Ters trigonometrik fonksiyonu normal trigonometrik fonksiyon şeklinde yazalım.
\( \cot{\dfrac{\pi}{6}} = 2x \)
\( \sqrt{3} = 2x \)
\( x = \dfrac{\sqrt{3}}{2} \) bulunur.
\( \arccos{x} + \arctan{\dfrac{\sqrt{3}}{3}} = \dfrac{\pi}{2} \) denklemini sağlayan \( x \) değeri kaçtır?
Çözümü Göster\( \arctan{\dfrac{\sqrt{3}}{3}} = a \) diyelim.
\( \tan{a} = \dfrac{\sqrt{3}}{3} \)
\( a = \dfrac{\pi}{6} \)
Bu değeri verilen denklemde yerine koyalım.
\( \arccos{x} + \dfrac{\pi}{6} = \dfrac{\pi}{2} \)
\( \arccos{x} = \dfrac{\pi}{3} \)
\( \cos{\dfrac{\pi}{3}} = x \)
\( x = \dfrac{1}{2} \) bulunur.
\( \arccot{\dfrac{4}{3}} = x \) ise \( \sin{x} - \cos{x} \) ifadesinin eşiti kaçtır?
Çözümü Göster\( \arccot{\dfrac{4}{3}} = x \) diyelim.
Ters trigonometrik fonksiyonu normal trigonometrik fonksiyon şeklinde yazalım.
\( \cot{x} = \dfrac{4}{3} \)
Komşu kenarın karşı kenara oranı \( \frac{4}{3} \) ise bu bir 3-4-5 üçgenidir.
Buna göre \( \sin{x} = \frac{3}{5} \) ve \( \cos{x} = \frac{4}{5} \) olur.
\( \sin{x} - \cos{x} = \dfrac{3}{5} - \dfrac{4}{5} = -\dfrac{1}{5} \) bulunur.
\( \arcsin{x} = \arccot{\dfrac{2}{3}} \) ise \( x \) kaçtır?
Çözümü Göster\( \arcsin{x} = \arccot{\dfrac{2}{3}} = m \) diyelim.
\( \sin{m} = x \) ve \( \cot{m} = \dfrac{2}{3} \) olur.
\( m \) açısının kotanjantı \( \frac{2}{3} \) ise komşu kenara 2k, karşı kenara 3k diyebiliriz, bu durumda hipotenüs Pisagor teoreminden \( \sqrt{13}k \) olur.
\( (2k)^2 + (3k)^2 = (\sqrt{13}k)^2 \)
Bu kenar oranlarını kullanarak sinüs oranını aşağıdaki gibi buluruz.
\( \sin{m} = \dfrac{3}{\sqrt{13}} = \dfrac{3\sqrt{13}}{13} \)
Buna göre \( x = \sin{m} = \dfrac{3 \sqrt{13}}{13} \) bulunur.
\( \arcsin{\frac{\sqrt{3}}{2}} + \arccos(-\frac{1}{2}) \) ifadesinin en sade halini bulunuz.
Çözümü Göster\( \arcsin{\frac{\sqrt{3}}{2}} = x \) diyelim.
\( \arccos(-\frac{1}{2}) = y \) diyelim.
\( \sin{x} = \dfrac{\sqrt{3}}{2} \)
\( x = \dfrac{\pi}{3} \)
\( \cos{y} = - \dfrac{1}{2} \)
\( y = \dfrac{2\pi}{3} \)
Buna göre \( x + y = \dfrac{\pi}{3} + \dfrac{2\pi}{3} = \pi \) bulunur.
\( 9\arccot(x - \sqrt{3}) - 3\pi = 0 \)
denklemini sağlayan \( x \) değerini bulunuz.
Çözümü Göster\( 9\arccot(x - \sqrt{3}) = 3\pi \)
\( \arccot(x - \sqrt{3}) = \dfrac{\pi}{3} \)
Eşitliğin iki tarafının kotanjantını alalım.
\( \cot(\arccot(x - \sqrt{3})) = \cot{\dfrac{\pi}{3}} \)
Kotanjant ve ters kotanjant birbirinin tersi fonksiyonlardır.
\( x - \sqrt{3} = \dfrac{\sqrt{3}}{3} \)
\( x = \dfrac{4\sqrt{3}}{3} \) bulunur.
\( 3\pi - 9\arccos(x + 1) = 0 \)
denklemini sağlayan \( x \) değeri nedir?
Çözümü Göster\( 9\arccos(x + 1) = 3\pi \)
\( \arccos(x + 1) = \dfrac{\pi}{3} \)
Eşitliğin iki tarafının kosinüsünü alalım.
\( x + 1 = \cos{\dfrac{\pi}{3}} \)
\( x + 1 = \dfrac{1}{2} \)
\( x = -\dfrac{1}{2} \) bulunur.
\( \cos(\dfrac{\pi}{2} + \arccot{3}) \) ifadesinin eşiti kaçtır?
Çözümü Göster\( \arccot{3} = x \) diyelim.
Ters trigonometrik fonksiyonu normal trigonometrik fonksiyon şeklinde yazalım.
\( \cot{x} = 3 \)
\( x \) açısının kotanjantı 3 ise komşu kenara 3k, karşı kenara k diyebiliriz, bu durumda hipotenüs Pisagor teoreminden \( \sqrt{10}k \) olur.
\( k^2 + (3k)^2 = (\sqrt{10}k)^2 \)
\( \cos(\dfrac{\pi}{2} + \arccot{3}) = \cos(\dfrac{\pi}{2} + x) \)
\( = -\sin{x} \)
\( = -\dfrac{1}{\sqrt{10}} = -\dfrac{\sqrt{10}}{10} \) bulunur.
\( \tan(\arcsin{1} + 2\arccos{\dfrac{\sqrt{3}}{2}}) \) ifadesinin eşiti nedir?
Çözümü Göster\( \arcsin{1} = x \) diyelim.
\( \sin{x} = 1 \Longrightarrow x = \dfrac{\pi}{2} \) olur.
\( \arccos{\dfrac{\sqrt{3}}{2}} = y \) diyelim.
\( \cos{y} = \dfrac{\sqrt{3}}{2} \Longrightarrow y = \dfrac{\pi}{6} \) olur.
\( \tan(\arcsin{1} + 2\arccos{\dfrac{\sqrt{3}}{2}}) = \tan(x + 2y) \)
\( = \tan(\dfrac{\pi}{2} + 2 \cdot \dfrac{\pi}{6}) \)
\( = \tan{\dfrac{5\pi}{6}} \)
Tanjant fonksiyonu II. bölgede negatiftir.
\( = -\tan{\dfrac{\pi}{6}} = -\dfrac{\sqrt{3}}{3} \) bulunur.
\( f(x) = 4\arccos{\dfrac{x}{3}} \) ise \( f^{-1}(\pi) \) kaçtır?
Çözümü Göster\( f^{-1}(\pi) = a \) diyelim.
\( f(a) = \pi \) olur.
\( f(x) = 4\arccos{\dfrac{x}{3}} \)
\( f(a) = 4\arccos{\dfrac{a}{3}} = \pi \)
\( \arccos{\dfrac{a}{3}} = \dfrac{\pi}{4} \)
Ters trigonometrik fonksiyonu normal trigonometrik fonksiyon şeklinde yazalım.
\( \cos{\dfrac{\pi}{4}} = \dfrac{a}{3} \)
\( \dfrac{\sqrt{2}}{2} = \dfrac{a}{3} \)
\( a = \dfrac{3 \sqrt{2}}{2} \) olur.
\( \sin(2\arccot{\dfrac{3}{4}}) \) ifadesinin eşiti nedir?
Çözümü Göster\( \arccot{\dfrac{3}{4}} = x \) diyelim.
\( \cot{x} = \dfrac{3}{4} \) olur.
\( x \) açısının kotanjantı \( \frac{3}{4} \) ise komşu kenara 3k, karşı kenara 4k diyebiliriz, bu durumda hipotenüs Pisagor teoreminden \( 5k \) olur.
\( (3k)^2 + (4k)^2 = (5k)^2 \)
\( \sin{x} = \dfrac{4}{5} \)
\( \cos{x} = \dfrac{3}{5} \)
\( \sin{(2\arccot{\dfrac{3}{4}})} = \sin(2x) = 2\sin{x}\cos{x} \)
\( = 2 \cdot \dfrac{4}{5} \cdot \dfrac{3}{5} = \dfrac{24}{25} \) bulunur.
\( \cos{(2\arcsin{\dfrac{2}{3}})} \) ifadesinin eşiti nedir?
Çözümü Göster\( \arcsin{\dfrac{2}{3}} = x \) diyelim.
\( \sin{x} = \dfrac{2}{3} \) olur.
\( \cos{(2\arcsin{\dfrac{2}{3}})} = \cos(2x) \)
Kosinüs yarım açı formülünü kullanalım.
\( = 1 - 2\sin^2{x} \)
\( = 1 - 2(\dfrac{2}{3})^2 = \dfrac{1}{9} \) bulunur.
\( \cos(2\sin^{-1}{x}) \) ifadesinin \( x \) cinsinden en sade hali nedir?
Çözümü Göster\( \sin^{-1}{x} = y \) diyelim.
\( \sin{y} = x \)
\( \cos(2\sin^{-1}{x}) = \cos(2y) \)
Kosinüs yarım açı formülünü kullanalım.
\( = 1 - 2\sin^2{y} \)
\( \sin{y} = x \) olarak bulmuştuk.
\( 1 - 2x^2 \) bulunur.
\( \sin^{-1}[\cos(\sin^{-1}{\dfrac{\sqrt{3}}{2}})] \) işleminin sonucu nedir?
Çözümü Gösterİfadeyi içten dışa doğru giderek çözelim.
\( \sin^{-1}{\dfrac{\sqrt{3}}{2}} = a \) diyelim.
\( \sin{a} = \dfrac{\sqrt{3}}{2} \)
\( a = \dfrac{\pi}{3} \)
\( \sin^{-1}[\cos(\sin^{-1}{\dfrac{\sqrt{3}}{2}})] = \sin^{-1}(\cos{\dfrac{\pi}{3}}) \)
\( = \sin^{-1}{\dfrac{1}{2}} \)
\( \sin^{-1}{\dfrac{1}{2}} = b \) diyelim.
\( \sin{b} = \dfrac{1}{2} \)
\( b = \dfrac{\pi}{6} \)
Cevap \( \frac{\pi}{6} \) olarak bulunur.
\( \sin(\arctan{4} + \arccot{4}) \) ifadesinin değeri nedir?
Çözümü Göster\( \arctan{4} = \alpha \Longrightarrow \tan{\alpha} = 4 \)
\( \arccot{4} = \beta \Longrightarrow \cot{\beta} = 4 \)
\( \tan{\alpha} = \cot{\beta} \) olduğuna göre \( \alpha \) ve \( \beta \) tümler açılardır.
\( \alpha + \beta = \dfrac{\pi}{2} \)
\( \sin(\arctan{4} + \arccot{4}) \)
\( = \sin(\alpha + \beta) \)
\( = \sin{\frac{\pi}{2}} = 1 \) olur.
\( \tan(\frac{3\pi}{2} + \arcsin{\frac{3}{5}}) \) ifadesinin değeri nedir?
Çözümü GösterParantez içindeki açı IV. bölgededir ve bu bölgede tanjant negatiftir.
\( \tan(\frac{3\pi}{2} + \arcsin{\frac{3}{5}}) = -\cot(\arcsin{\frac{3}{5}}) \)
\( \arcsin{\frac{3}{5}} = x \Longrightarrow \arcsin{x} = \dfrac{3}{5} \)
\( x \) açısının sinüsü \( \frac{3}{5} \) ise karşı kenara 3k, hipotenüse 5k diyebiliriz, bu durumda komşu kenar Pisagor teoreminden \( 4k \) olur.
Buna göre \( x \) açısının kotanjantı \( \frac{4}{3} \) olur.
\( = -\cot(\arcsin{\frac{3}{5}}) \)
\( = -\cot(x) = -\dfrac{4}{3} \)
\( \tan(\arctan{5} - \arctan{4}) \) ifadesinin eşiti nedir?
Çözümü GösterTanjant fark formülünü kullanalım.
\( \tan(x - y) = \dfrac{\tan{x} - \tan{y}}{1 + \tan{x}\tan{y}} \)
\( \tan(\arctan{5} - \arctan{4}) = \dfrac{\tan(\arctan{5}) - \tan(\arctan{4})}{1 + \tan(\arctan{5})\tan(\arctan{4})} \)
Tanjant ve ters tanjant birbirinin tersi fonksiyonlardır.
\( = \dfrac{5 - 4}{1 + 5 \cdot 4} = \dfrac{1}{21} \) bulunur.
\( 2\arccos{\dfrac{4}{5}} = \arccos{x} \)
denklemini sağlayan \( x \) değeri nedir?
Çözümü Göster\( \arccos{\dfrac{4}{5}} = \alpha \) diyelim.
\( \cos{\alpha} = \dfrac{4}{5} \) olur.
\( 2\alpha = \arccos{x} \)
\( \cos(2\alpha) = x \)
Kosinüs iki kat açı formülünü kullanalım.
\( 2\cos^2{\alpha} - 1 = x \)
\( 2(\dfrac{4}{5})^2 - 1 = x \)
\( \dfrac{32}{25} - 1 = x \)
\( x = \dfrac{7}{25} \) bulunur.
\( 2\arctan{\dfrac{1}{2}} - \arccos{x} = 0 \)
denklemini sağlayan \( x \) değerini bulunuz.
Çözümü Göster\( \arctan{\dfrac{1}{2}} = y \) diyelim.
\( \tan{y} = \dfrac{1}{2} \) olur.
\( y \) açısı için bir dik üçgen çizelim ve Pisagor teoremi ile üçüncü kenarı bulalım.

\( \cos{y} = \dfrac{2}{\sqrt{5}} \)
Soruda verilen eşitliği düzenleyelim.
\( 2\arctan{\dfrac{1}{2}} = \arccos{x} \)
\( 2y = \arccos{x} \)
Bu eşitlikte iki tarafın kosinüsünü alalım.
\( \cos(2y) = \cos(\arccos{x}) \)
Kosinüs ve ters kosinüs birbirinin tersi fonksiyonlardır.
\( \cos(2y) = x \)
Kosinüs iki kat açı formülünü kullanalım.
\( 2\cos^2{y} - 1 = x \)
\( 2(\dfrac{2}{\sqrt{5}})^2 - 1 = x \)
\( x = \dfrac{3}{5} \) bulunur.
\( \arctan{\dfrac{2}{3}} + \arctan{\dfrac{4}{5}} = \arctan{a} \)
denklemini sağlayan \( a \) değeri kaçtır?
Çözümü Göster\( \arctan{\dfrac{2}{3}} = x \) diyelim.
\( \tan{x} = \dfrac{2}{3} \) olur.
\( \arctan{\dfrac{4}{5}} = y \) diyelim.
\( \tan{y} = \dfrac{4}{5} \) olur.
\( x + y = \arctan{a} \)
Eşitliğin iki tarafının tanjantını alalım.
\( \tan(x + y) = \tan(\arctan{a}) \)
Tanjant ve ters tanjant birbirinin tersi fonksiyonlardır.
\( \tan(x + y) = a \)
Tanjant toplam formülünü kullanalım.
\( \tan(x + y) = \dfrac{\tan{x} + \tan{y}}{1 - \tan{x}\tan{y}} \)
\( a = \dfrac{\frac{2}{3} + \frac{4}{5}}{1 - \frac{2}{3} \cdot \frac{4}{5}} \)
\( = \dfrac{\frac{22}{15}}{\frac{7}{15}} = \dfrac{22}{7} \) bulunur.
\( \arcsin{x} = \arccos(2x) \)
denklemini sağlayan \( x \) değerlerini bulunuz.
Çözümü GösterEşitliğin değerine \( \alpha \) diyelim.
\( \arcsin{x} = \arccos(2x) = \alpha \)
\( \sin{\alpha} = x \) olur.
\( \cos{\alpha} = 2x \) olur.
İkinci eşitlikte \( x = \sin{\alpha} \) yazalım.
\( \cos{\alpha} = 2\sin{\alpha} \)
\( \tan{\alpha} = \dfrac{1}{2} \)
\( \alpha \) açısı için bir dik üçgen çizelim.

Üçgeni kullanarak \( \sin{\alpha} \) değerini bulalım.
\( \sin{\alpha} = \dfrac{1}{\sqrt{5}} \)
\( \sin{\alpha} \) \( x \)'e eşittir.
Çözüm kümesi: \( x = \dfrac{1}{\sqrt{5}} \)
\( 2\arctan{\dfrac{3}{x}} = \arctan{\dfrac{2x}{9}} \)
denklemini sağlayan \( x \) değerlerini bulunuz.
Çözümü Göster\( \arctan{\dfrac{3}{x}} = \alpha \) diyelim.
\( \tan{\alpha} = \dfrac{3}{x} \) olur.
\( \arctan{\dfrac{2x}{9}} = 2\alpha \)
\( \tan(2\alpha) = \dfrac{2x}{9} \) olur.
Tanjant iki kat açı formülünü kullanalım.
\( \tan(2\alpha) = \dfrac{2\tan{\alpha}}{1 - \tan^2{\alpha}} \)
\( \dfrac{2x}{9} = \dfrac{2 \cdot \frac{3}{x}}{1 - (\frac{3}{x})^2} \)
\( \dfrac{2x}{9} = \dfrac{\frac{6}{x}}{\frac{x^2 - 9}{x^2}} \)
\( \dfrac{2x}{9} = \dfrac{6x}{x^2 - 9} \)
İçler - dışlar çarpımı yapalım.
\( 2x^3 - 18x = 54x \)
\( 2x^3 - 72x = 0 \)
\( 2x(x - 6)(x + 6) = 0 \)
\( x = 0 \) değeri \( \frac{3}{x} \) ifadesini tanımsız yaptığı için geçerli bir çözüm değildir.
Çözüm kümesi: \( x \in \{-6, 6\} \)
\( x \gt -1 \) olmak üzere,
\( \arctan{x} + \arctan{\dfrac{1 - x}{1 + x}} \) ifadesinin eşiti nedir?
Çözümü Göster\( \arctan{x} = \alpha \) diyelim.
\( \tan{\alpha} = x \) olur.
\( \arctan{\dfrac{1 - x}{1 + x}} = \beta \) diyelim.
\( \tan{\beta} = \dfrac{1 - x}{1 + x} \) olur.
İşlemin sonucuna \( a \) diyelim.
\( \arctan{x} + \arctan{\dfrac{1 - x}{1 + x}} = a \)
\( \alpha + \beta = a \)
Eşitliğin iki tarafının tanjantını alalım.
\( \tan(\alpha + \beta) = \tan{a} \)
\( \tan{a} = \dfrac{\tan{\alpha} + \tan{\beta}}{1 - \tan{\alpha}\tan{\beta}} \)
Bulduğumuz değerleri yerlerine koyalım.
\( = \dfrac{x + \frac{1 - x}{1 + x}}{1 - x \cdot \frac{1 - x}{1 + x}} \)
\( = \dfrac{\frac{x + x^2 + 1 - x}{1 + x}}{\frac{1 + x - x + x^2}{1 + x}} \)
\( = \dfrac{x^2 + 1}{x^2 + 1} = 1 \)
Tanjant değeri 1 olan açı ölçüsü \( \frac{\pi}{4} \)'tür.
\( a = \dfrac{\pi}{4} \) bulunur.
\( 2\arctan{\dfrac{1 - x}{1 + x}} = \arctan{x} \)
eşitliğini sağlayan \( x \) değeri nedir?
Çözümü Göster\( \arctan{\dfrac{1 - x}{1 + x}} = \alpha \) diyelim.
\( \tan{\alpha} = \dfrac{1 - x}{1 + x} \) olur.
\( 2\alpha = \arctan{x} \)
\( x = \tan(2\alpha) \)
Tanjant iki kat açı formülünü kullanalım.
\( \tan(2\alpha) = \dfrac{2\tan{\alpha}}{1 - \tan^2{\alpha}} \)
\( x = \dfrac{2\frac{1 - x}{1 + x}}{1 - (\frac{1 - x}{1 + x})^2} \)
\( x = \dfrac{\frac{2 - 2x}{1 + x}}{1 - \frac{1 - 2x + x^2}{1 + 2x + x^2}} \)
\( x = \dfrac{\frac{2 - 2x}{1 + x}}{\frac{1 + 2x + x^2 - 1 + 2x - x^2}{1 + 2x + x^2}} \)
\( x = \dfrac{\frac{2 - 2x}{1 + x}}{\frac{4x}{(1 + x)^2}} \)
\( x = \dfrac{1 - x^2}{2x} \)
İçler - dışlar çarpımı yapalım.
\( 2x^2 = 1 - x^2 \)
\( 3x^2 = 1 \)
\( x = \pm \dfrac{1}{\sqrt{3}} = \pm \dfrac{\sqrt{3}}{3} \)
\( x \)'in negatif değeri için eşitliğin sol tarafı pozitif sağ tarafı negatif olduğu için \( x = -\frac{\sqrt{3}}{3} \) geçerli bir çözüm değildir.
Çözüm kümesi: \( x = \dfrac{\sqrt{3}}{3} \)
\( \sin(2\arctan{x}) \) ifadesinin \( x \) cinsinden eşiti nedir?
Çözümü Göster\( \arctan{x} = \alpha \) diyelim.
\( x = \tan{\alpha} \) olur.
\( \sin(2\arctan{x}) = \sin(2\alpha) \)
Sinüs iki açı formülünü kullanalım.
\( = 2\sin{\alpha}\cos{\alpha} \)
\( \alpha \) açısı için bir dik üçgen çizelim.

\( \cos{\alpha} = \dfrac{1}{\sqrt{x^2 + 1}} \)
\( \sin{\alpha} = \dfrac{x}{\sqrt{x^2 + 1}} \)
Bulduğumuz değerleri yerine yazalım.
\( = 2\dfrac{x}{\sqrt{x^2 + 1}} \cdot \dfrac{1}{\sqrt{x^2 + 1}} \)
\( = \dfrac{2x}{x^2 + 1} \) bulunur.
\( x \in \mathbb{R} \) olmak üzere,
\( \arctan{\dfrac{x - 4}{x - 3}} + \arctan{\dfrac{x - 5}{x - 1}} = \dfrac{\pi}{4} \)
denkleminin çözüm kümesi nedir?
Çözümü Göster\( \arctan{\dfrac{x - 4}{x - 3}} = \alpha \) diyelim.
\( \tan{\alpha} = \dfrac{x - 4}{x - 3} \) olur.
\( \arctan{\dfrac{x - 5}{x - 1}} = \beta \) diyelim.
\( \tan{\beta} = \dfrac{x - 5}{x - 1} \) olur.
Soruda verilen eşitlikte yerine yazalım.
\( \alpha + \beta = \dfrac{\pi}{4} \)
Eşitliğin iki tarafının tanjantını alalım.
\( \tan(\alpha + \beta) = \tan{\dfrac{\pi}{4}} = 1 \)
Tanjant toplam formülünü kullanalım.
\( \dfrac{\tan{\alpha} + \tan{\beta}}{1 - \tan{\alpha}\tan{\beta}} = 1 \)
Bulduğumuz değerleri yerine yazalım.
\( \dfrac{\frac{x - 4}{x - 3} + \frac{x - 5}{x - 1}}{1 - \frac{x - 4}{x - 3} \cdot \frac{x - 5}{x - 1}} = 1 \)
İçler - dışlar çarpımı yapalım.
\( \dfrac{x - 4}{x - 3} + \dfrac{x - 5}{x - 1} = 1 - \dfrac{(x - 4)(x - 5)}{(x - 3)(x - 1)} \)
\( \dfrac{x^2 - 5x + 4 + x^2 - 8x + 15}{(x - 3)(x - 1)} = \dfrac{x^2 - 4x + 3 - (x^2 - 9x + 20)}{(x - 3)(x - 1)} \)
\( \dfrac{2x^2 - 13x + 19}{(x - 3)(x - 1)} = \dfrac{5x - 17}{(x - 3)(x - 1)} \)
Çözüm kümesinin \( x = 1 \) ya da \( x = 3 \) içeremeyeceğini not ederek paydaları sadeleştirelim.
\( 2x^2 - 13x + 19 = 5x - 17 \)
\( 2x^2 - 18x + 36 = 0 \)
\( x^2 - 9x + 18 = 0 \)
\( (x - 3)(x - 6) = 0 \)
\( x = 3 \) sorudaki kesirli ifadeyi tanımsız yaptığı için geçerli bir çözüm değildir.
Çözüm kümesi: \( x = 6 \)
\( 8\arctan(2x^2 - 5x + 1) + 2\pi = 0 \)
denklemini sağlayan \( x \) değerlerini bulunuz.
Çözümü GösterTrigonometrik ifadeyi yalnız bırakalım.
\( 8\arctan(2x^2 - 5x + 1) = -2\pi \)
\( \arctan(2x^2 - 5x + 1) = -\dfrac{\pi}{4} \)
\( \tan(-\dfrac{\pi}{4}) = 2x^2 - 5x + 1 \)
\( 2x^2 - 5x + 1 = -1 \)
\( 2x^2 - 5x + 2 = 0 \)
\( (2x - 1)(x - 2) = 0 \)
Denklemin çözümü bu çarpanları sıfır yapan değerlerdir.
Çözüm kümesi: \( x \in \{\frac{1}{2}, 2\} \)
\( \arccot(12x) = \arctan(3x) \)
olduğuna göre, \( x \)'in pozitif değeri nedir?
Çözümü Göster\( \arccot(12x) = \arctan(3x) = \alpha \) diyelim.
\( \cot{\alpha} = 12x \) olur.
\( \tan{\alpha} = 3x \) olur.
Bir açının tanjant ve kotanjant değerlerinin çarpımı 1'dir.
\( \tan{\alpha} \cdot \cot{\alpha} = 36x^2 = 1 \)
\( x^2 = \dfrac{1}{36} \)
\( x = \pm \dfrac{1}{6} \)
\( x \)'in pozitif değeri \( \frac{1}{6} \) olarak bulunur.
\( \tan(\arcsin(-\frac{5}{13})) + \cos(\arcsin{\frac{24}{25}}) \)
ifadesinin sonucu kaçtır?
Çözümü Göster\( \arcsin(-\frac{5}{13}) = x \) diyelim.
\( \sin{x} = -\dfrac{5}{13} \) olur.
Arc sinüs fonksiyonu I. ve IV. bölgelerde tanımlı olduğu için sinüs değeri negatif olan \( x \) açısı IV. bölgededir.
\( \arcsin{\frac{24}{25}} = y \) diyelim.
\( \sin{y} = \dfrac{24}{25} \) olur.
Arc sinüs fonksiyonu I. ve IV. bölgelerde tanımlı olduğu için sinüs değeri pozitif olan \( y \) açısı I. bölgededir.
\( x \) ve \( y \) açıları için birer dik üçgen çizelim ve Pisagor teoremi ile üçüncü kenarları bulalım.

Üçgenleri kullanarak ihtiyacımız olan trigonometrik oranları bulalım.
\( \tan{x} = -\dfrac{5}{12} \)
\( \cos{y} = \dfrac{7}{25} \)
\( \tan(\arcsin(-\frac{5}{13})) + \cos(\arcsin{\frac{24}{25}}) = \sin{x} + \cos{y} \)
\( = -\dfrac{5}{12} + \dfrac{7}{25} = -\dfrac{41}{300} \) bulunur.
\( \sin(\arcsin{x^2}) - \arcsin(\sin(2x)) = -\dfrac{3}{4} \)
Buna göre \( \arcsin{x} \) ifadesinin değeri kaçtır?
Çözümü GösterBir trigonometrik fonksiyonun tersi ile bileşkesi birim fonksiyonu verir.
\( \sin(\arcsin{x^2}) = x^2 \)
\( \arcsin(\sin(2x)) = 2x \)
\( x^2 - 2x = -\dfrac{3}{4} \)
İçler - dışlar çarpımı yapalım.
\( 4x^2 - 8x = -3 \)
\( 4x^2 - 8x + 3 = 0 \)
\( (2x - 1)(2x - 3) = 0 \)
\( x = \frac{1}{2} \) ya da \( x = \frac{3}{2} \)
Ters sinüs fonksiyonunun tanım kümesi \( [-1, 1] \) aralığıdır, buna göre \( x = \frac{3}{2} \) değeri geçerli bir çözüm değildir.
\( \arcsin{\frac{1}{2}} = \dfrac{\pi}{6} \) bulunur.
\( 0 \lt x \lt \frac{\pi}{2} \) olmak üzere,
\( \tan(\arcsin(\cos{x})) \) ifadesinin en sade hali nedir?
Çözümü Göster\( \arcsin(\cos{x}) = \alpha \) diyelim.
\( \sin{\alpha} = \cos{x} \) olur.
\( \alpha \) açısı için bir dik üçgen çizelim ve Pisagor teoremi ile üçüncü kenarı bulalım.
\( \abs{AB} = \sqrt{1 - \cos^2{x}} = \sin{x} \)

Üçgeni kullanarak ihtiyacımız olan trigonometrik oranı bulalım.
\( \tan(\arcsin(\cos{x})) = \tan{\alpha} \)
\( = \dfrac{\cos{x}}{\sin{x}} \)
\( = \cot{x} \) bulunur.
\( \cos(\pi - \dfrac{1}{2}\arccsc{\dfrac{13}{5}}) \) ifadesinin eşiti nedir?
Çözümü Göster\( \arccsc{\dfrac{13}{5}} = x \) diyelim.
\( \csc{x} = \dfrac{13}{5} \) olur.
\( \sin{x} = \dfrac{5}{13} \)
\( x \) açısı için bir dik üçgen çizelim.

Üçgeni kullanarak \( \cos{x} \) değerini bulalım.
\( \cos{x} = \dfrac{12}{13} \)
\( \cos(\pi - \dfrac{x}{2}) = -\cos{\frac{x}{2}} \)
Kosinüs iki kat açı formülünü kullanalım.
\( \cos{x} = 2\cos^2{\dfrac{x}{2}} - 1 \)
\( 2\cos^2{\dfrac{x}{2}} - 1 = \dfrac{12}{13} \)
\( \cos^2{\dfrac{x}{2}} = \dfrac{25}{26} \)
\( \cos{\dfrac{x}{2}} = \dfrac{5}{\sqrt{26}} = \dfrac{5\sqrt{26}}{26} \)
\( \cos(\pi - \dfrac{x}{2}) = -\cos^2{\dfrac{x}{2}} = -\dfrac{5\sqrt{26}}{26} \) bulunur.
\( \tan(\cos^{-1}(\sin(\sec^{-1}{\dfrac{13}{5}}))) \) ifadesinin sonucu nedir?
Çözümü Göster\( \tan(\cos^{-1}(\sin(\sec^{-1}{\dfrac{13}{5}}))) \)
\( \sec^{-1}{\dfrac{13}{5}} = \alpha \) diyelim.
\( = \tan(\cos^{-1}(\sin{\alpha})) \)
\( \alpha \) açısı için bir dik üçgen çizelim.

\( \sin{\alpha} = \dfrac{12}{13} \)
\( = \tan(\cos^{-1}{\dfrac{12}{13}}) \)
\( \cos^{-1}{\dfrac{12}{13}} = \beta \) diyelim.
\( = \tan{\beta} \)
\( \beta \) açısı için bir dik üçgen çizelim.

\( \tan{\beta} = \dfrac{5}{12} \) bulunur.
\( \arctan{\dfrac{1}{3}} + \arccot{2} \) ifadesinin eşiti nedir?
Çözümü Göster\( \arctan{\dfrac{1}{3}} = x \) diyelim.
\( \tan{x} = \dfrac{1}{3} \) olur.
\( \arccot{2} = y \) diyelim.
\( \cot{y} = 2 \Longrightarrow \tan{y} = \dfrac{1}{2} \) olur.
\( \arctan{\dfrac{1}{3}} + \arccot{2} = a \) diyelim.
Eşit açıların trigonometrik değerleri de eşit olur.
\( \tan(\arctan{\dfrac{1}{3}} + \arccot{2}) = \tan{a} \)
\( \tan(x + y) = \tan{a} \)
Tanjant toplam formülünü kullanalım.
\( = \dfrac{\tan{x} + \tan{y}}{1 - \tan{x}\tan{y}} = \dfrac{\frac{1}{3} + \frac{1}{2}}{1 - \frac{1}{3} \cdot \frac{1}{2}} \)
\( = \dfrac{\frac{5}{6}}{\frac{5}{6}} = 1 = \tan{a} \)
Buna göre \( a = \dfrac{\pi}{4} \) olur.
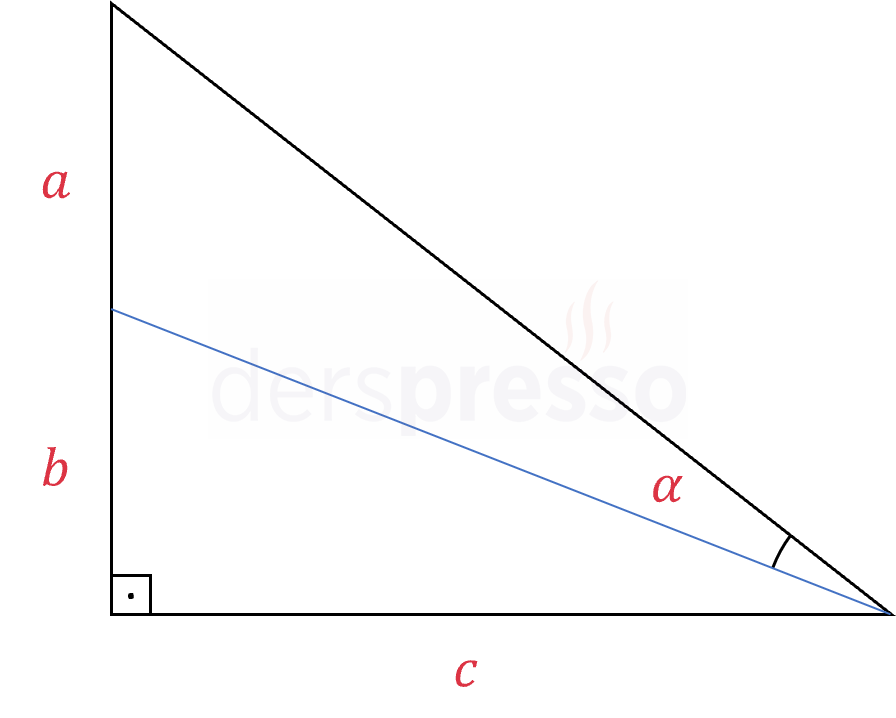
Yukarıdaki şekildeki \( \alpha \) açısı \( a, b, c \) uzunlukları cinsinden nedir?
Çözümü Göster\( \alpha \) açısının altındaki açıya \( \beta \) diyelim.
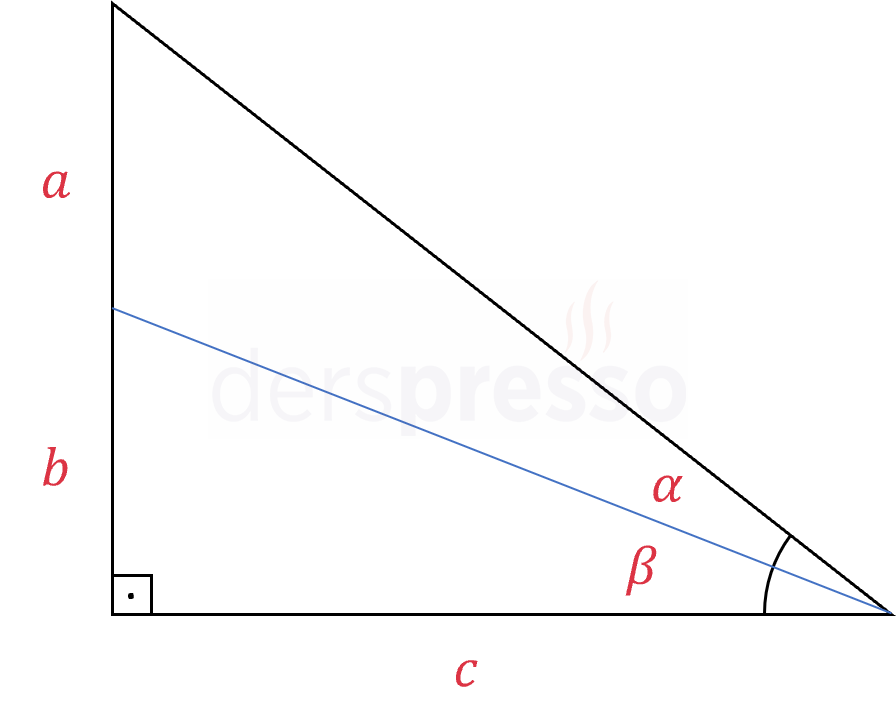
\( \alpha \) açısını aşağıdaki şekilde yazabiliriz.
\( \alpha = (\alpha + \beta) - \beta \)
\( \alpha + \beta \) değerini bulalım.
\( \tan(\alpha + \beta) = \dfrac{a + b}{c} \)
\( \alpha + \beta = \arctan{\dfrac{a + b}{c}} \)
\( \beta \) değerini bulalım.
\( \tan{\beta} = \dfrac{b}{c} \)
\( \beta = \arctan{\dfrac{b}{c}} \)
Bu iki değeri yukarıdaki formülde yerine koyalım.
\( \alpha = (\alpha + \beta) - \beta \)
\( = \arctan{\dfrac{a + b}{c}} - \arctan{\dfrac{b}{c}} \)
\( \arccot(x - 1) - \arctan(x + 2) = 0 \) denkleminin çözüm kümesi nedir?
Çözümü Göster\( \arccot(x - 1) = \arctan(x + 2) \)
Bu eşitliğin değerine \( \beta \) diyelim.
\( \arccot(x - 1) = \arctan(x + 2) = \beta \)
\( \arccot(x - 1) = \beta \Longrightarrow \cot{\beta} = x - 1 \)
\( \arctan(x + 2) = \beta \Longrightarrow \tan{\beta} = x + 2 \)
Bir açının tanjantı ile kotanjantının çarpımı 1'dir.
\( \tan{\beta} \cdot \cot{\beta} = 1 \)
\( (x - 1)(x + 2) = 1 \)
\( x^2 + x - 3 = 0 \)
2. derece denklem kök formülü ile kökler aşağıdaki gibi bulunur.
\( x_1 = \dfrac{-1 + \sqrt{13}}{2} \)
\( x_2 = \dfrac{-1 - \sqrt{13}}{2} \)
Çözüm kümesi: \( x = \{ -\frac{\sqrt{13} + 1}{2}, \frac{\sqrt{13} - 1}{2} \} \)
\( x \gt 0 \) olmak üzere,
\( \arctan{x} + \arctan{\dfrac{1}{x}} \) ifadesinin eşiti nedir?
Çözümü Göster\( \arctan{x} = \alpha \) diyelim.
\( x = \tan{\alpha} \) olur.
\( \arctan{\dfrac{1}{x}} = \beta \) diyelim.
\( \dfrac{1}{x} = \tan{\beta} \) olur.
\( \alpha \) açısı için bir dik üçgen çizelim.

Bu üçgende \( \alpha \) açısının tümler açısı olan açı için \( \frac{1}{x} \) tanjant oranı sağladığı için bu tümler açı \( \beta \) olur.
\( \alpha + \beta = \dfrac{\pi}{2} \) olarak bulunur.
\( \arccos{\dfrac{1}{\sqrt{5}}} + \arccos{\dfrac{1}{\sqrt{10}}} \) ifadesinin sonucu kaçtır?
Çözümü Göster\( \arccos{\dfrac{1}{\sqrt{5}}} = x \) diyelim.
\( \cos{x} = \dfrac{1}{\sqrt{5}} \) olur.
\( \arccos{\dfrac{1}{\sqrt{10}}} = y \) diyelim.
\( \cos{y} = \dfrac{1}{\sqrt{10}} \) olur.
\( \arccos{\dfrac{1}{\sqrt{5}}} + \arccos{\dfrac{1}{\sqrt{10}}} = \alpha \) diyelim.
\( x + y = \alpha \)
Eşitliğin iki tarafının kosinüsünü alalım.
\( \cos(x + y) = \cos{\alpha} \)
Kosinüs toplam formülünü kullanalım.
\( \cos(x + y) = \cos{x}\cos{y} - \sin{x}\sin{y} \)
\( x \) ve \( y \) açıları için birer dik üçgen çizelim ve Pisagor teoremi ile üçüncü kenarları bulalım.

Üçgenleri kullanarak ihtiyacımız olan trigonometrik oranları bulalım.
\( \sin{x} = \dfrac{2}{\sqrt{5}} \)
\( \sin{y} = \dfrac{3}{\sqrt{10}} \)
\( \cos(x + y) = \dfrac{1}{\sqrt{5}} \cdot \dfrac{1}{\sqrt{10}} - \dfrac{2}{\sqrt{5}} \cdot \dfrac{3}{\sqrt{10}} \)
\( = \dfrac{1}{\sqrt{50}} - \dfrac{6}{\sqrt{50}} = -\dfrac{5}{\sqrt{50}} \)
\( = -\dfrac{5}{5\sqrt{2}} = -\dfrac{\sqrt{2}}{2} \)
\( \cos{\alpha} = -\dfrac{\sqrt{2}}{2} \)
Ters kosinüsü alınan \( \frac{1}{\sqrt{5}} \) ve \( \frac{1}{\sqrt{10}} \) değerleri pozitif olduğu için \( x \) ve \( y \) dar açılardır.
\( \dfrac{\pi}{2} \lt x + y \lt \pi \)
\( \dfrac{\pi}{2} \lt \alpha \lt \pi \)
\( \alpha = \dfrac{3\pi}{4} \) bulunur.
\( 0 \le x \le 2\pi \) olmak üzere,
\( 2\arctan(\sin{x}) = \arctan(2\sec{x}) \)
denkleminin çözüm kümesini bulunuz.
Çözümü Göster\( \arctan(\sin{x}) = \alpha \) diyelim.
\( \tan{\alpha} = \sin{x} \) olur.
\( \arctan(2\sec{x}) = 2\alpha \)
\( \tan(2\alpha) = 2\sec{x} \) olur.
Tanjant iki kat açı formülünü kullanalım.
\( \tan(2\alpha) = \dfrac{2\tan{\alpha}}{1 - \tan^2{\alpha}} \)
\( 2\sec{x} = \dfrac{2\sin{x}}{1 - \sin^2{x}} \)
\( \dfrac{1}{\cos{x}} = \dfrac{\sin{x}}{1 - \sin^2{x}} \)
Pisagor özdeşliğini kullanalım.
\( \dfrac{1}{\cos{x}} = \dfrac{\sin{x}}{\cos^2{x}} \)
\( \cos^2{x} = \sin{x}\cos{x} \)
\( \cos^2{x} - \sin{x}\cos{x} = 0 \)
\( \cos{x}(\cos{x} - \sin{x}) = 0 \)
Denklemin çözümü bu çarpanları sıfır yapan değerlerdir.
Çarpan 1: \( \cos{x} = 0 \)
Kosinüs fonksiyonu \( [0, 2\pi] \) aralığında 0 değerini aşağıdaki açı değerlerinde alır.
\( x \in \{\frac{\pi}{2}, \frac{3\pi}{2}\} \)
Çarpan 2: \( \cos{x} - \sin{x} = 0 \)
\( \cos{x} = \sin{x} \)
\( \dfrac{\sin{x}}{\cos{x}} = 1 \)
\( \tan{x} = 1 \)
Tanjant fonksiyonu \( [0, 2\pi] \) aralığında 1 değerini aşağıdaki açı değerlerinde alır.
\( x \in \{\frac{\pi}{4}, \frac{5\pi}{4}\} \)
Denklemin çözüm kümesi iki çarpanın çözüm kümelerinin birleşim kümesidir.
Çözüm kümesi: \( x \in \{\frac{\pi}{4}, \frac{\pi}{2}, \frac{5\pi}{4}, \frac{3\pi}{2}\} \)
\( \sin(\arcsin{\dfrac{3}{5}} + \arccos{x}) = 1 \)
eşitliğini sağlayan \( x \) değeri nedir?
Çözümü GösterSinüsü alınan ifade için genel çözümü yazalım.
\( k \in \mathbb{Z} \) olmak üzere,
\( \arcsin{\dfrac{3}{5}} + \arccos{x} = \dfrac{\pi}{2} + 2\pi k \)
Ters sinüs fonksiyonunun görüntü kümesi \( [-\frac{\pi}{2}, \frac{\pi}{2}] \) aralığı, ters kosinüs fonksiyonunun görüntü kümesi \( [0, \pi] \) aralığıdır.
Buna göre iki fonksiyonun toplamının en geniş görüntü kümesi \( [-\frac{\pi}{2}, \frac{3\pi}{2}] \) olabilir, dolayısıyla \( k \) sadece 1 olabilir.
\( \arcsin{\dfrac{3}{5}} + \arccos{x} = \dfrac{\pi}{2} \)
\( \arccos{x} = \dfrac{\pi}{2} - \arcsin{\dfrac{3}{5}} \)
Eşitliğin iki tarafının kosinüsünü alalım.
\( x = \cos(\dfrac{\pi}{2} - \arcsin{\dfrac{3}{5}}) \)
Tümler açıların sinüs - kosinüs değerleri birbirine eşittir.
\( = \sin(\arcsin{\dfrac{3}{5}}) \)
Sinüs ve ters sinüs birbirinin tersi fonksiyonlardır.
\( = \dfrac{3}{5} \) bulunur.
\( x \gt 0 \) olmak üzere,
\( \tan(\arctan(3x) - \arctan{2}) + \tan(\arctan{3} - \arctan(2x)) = \dfrac{3}{8} \)
eşitliğini sağlayan \( x \) değeri kaçtır?
Çözümü Göster\( \arctan(3x) = \alpha \) diyelim.
\( \tan{\alpha} = 3x \) olur.
\( \arctan{2} = \beta \) diyelim.
\( \tan{\beta} = 2 \) olur.
\( \tan(\arctan(3x) - \arctan{2}) = \tan(\alpha - \beta) \)
Tanjant fark formülünü kullanalım.
\( \tan(\alpha - \beta) = \dfrac{\tan{\alpha} - \tan{\beta}}{1 + \tan{\alpha}\tan{\beta}} \)
\( = \dfrac{3x - 2}{1 + 6x} \)
\( \arctan{3} = \alpha \) diyelim.
\( \tan{\alpha} = 3 \) olur.
\( \arctan(2x) = \beta \) diyelim.
\( \tan{\beta} = 2x \) olur.
\( \tan(\arctan{3} - \arctan(2x)) = \tan(\alpha - \beta) \)
Tanjant fark formülünü kullanalım.
\( \tan(\alpha - \beta) = \dfrac{\tan{\alpha} - \tan{\beta}}{1 + \tan{\alpha}\tan{\beta}} \)
\( = \dfrac{3 - 2x}{1 + 6x} \)
Soruda verilen eşitlikte yerlerine yazalım.
\( \dfrac{3x - 2}{1 + 6x} + \dfrac{3 - 2x}{1 + 6x} = \dfrac{3}{8} \)
\( \dfrac{x + 1}{1 + 6x} = \dfrac{3}{8} \)
İçler - dışlar çarpımı yapalım.
\( 8x + 8 = 3 + 18x \)
\( 10x = 5 \)
\( x = \dfrac{1}{2} \) bulunur.
\( \arcsin{x} + \arccos{\dfrac{4}{5}} = 2\arctan{\dfrac{4}{3}} \)
eşitliğini sağlayan \( x \) değeri nedir?
Çözümü Göster\( \arccos{\dfrac{4}{5}} = \alpha \) diyelim.
\( \cos{\alpha} = \dfrac{4}{5} \) olur.
\( \arctan{\dfrac{4}{3}} = \beta \) diyelim.
\( \tan{\beta} = \dfrac{4}{3} \) olur.
\( \arcsin{x} + \alpha = 2\beta \)
\( \arcsin{x} = 2\beta - \alpha \)
Eşitliğin iki tarafının sinüsünü alalım.
\( x = \sin(2\beta - \alpha) \)
Sinüs fark formülünü kullanalım.
\( = \sin(2\beta)\cos{\alpha} - \cos(2\beta)\sin{\alpha} \)
Sinüs ve kosinüs iki kat açı formüllerini kullanalım.
\( = 2\sin{\beta}\cos{\beta}\cos{\alpha} - (2\cos^2{\beta} - 1)\sin{\alpha} \)
\( \alpha \) ve \( \beta \) açıları için birer dik üçgen çizelim.

\( \sin{\alpha} = \dfrac{3}{5} \)
\( \sin{\beta} = \dfrac{4}{5} \)
\( \cos{\beta} = \dfrac{3}{5} \)
Bulduğumuz değerleri yerine yazalım.
\( = 2\dfrac{4}{5} \cdot \dfrac{3}{5} \cdot \dfrac{4}{5} - (2 \cdot \dfrac{9}{25} - 1) \cdot \dfrac{3}{5} \)
\( = \dfrac{96}{125} - (\dfrac{18 - 25}{25}) \cdot \dfrac{3}{5} \)
\( = \dfrac{96}{125} + \dfrac{21}{125} \)
\( = \dfrac{117}{125} \) bulunur.
\( 0 \lt x \lt \dfrac{3\pi}{2} \) olmak üzere,
\( 2\arctan{\dfrac{3}{2}} + \arctan{\dfrac{12}{5}} \)
ifadesinin eşiti nedir?
Çözümü Göster\( \arctan{\dfrac{3}{2}} = \alpha \) diyelim.
\( \tan{\alpha} = \dfrac{3}{2} \) olur.
\( \arctan{\dfrac{12}{5}} = \beta \) diyelim.
\( \tan{\beta} = \dfrac{12}{5} \) olur.
İşlemin sonucuna \( x \) diyelim.
\( x = 2\arctan{\dfrac{3}{2}} + \arctan{\dfrac{12}{5}} \)
\( = 2\alpha + \beta \)
Eşitliğin iki tarafının kosinüsünü alalım.
\( \cos{x} = \cos(2\alpha + \beta) \)
Kosinüs toplam formülünü kullanalım.
\( \cos{x} = \cos(2\alpha)\cos{\beta} - \sin(2\alpha)\sin{\beta} \)
Sinüs ve kosinüs iki kat açı formüllerini kullanalım.
\( \cos{x} = (2\cos^2{\alpha} - 1)\cos{\beta} - 2\sin{\alpha}\cos{\alpha}\sin{\beta} \)
\( \alpha \) ve \( \beta \) açıları için birer dik üçgen çizelim.

\( \sin{\alpha} = \dfrac{3}{\sqrt{13}} \)
\( \cos{\alpha} = \dfrac{2}{\sqrt{13}} \)
\( \sin{\beta} = \dfrac{12}{13} \)
\( \cos{\beta} = \dfrac{5}{13} \)
Bulduğumuz değerleri yerine yazalım.
\( \cos{x} = (2\dfrac{4}{13} - 1) \cdot \dfrac{5}{13} - 2 \cdot \dfrac{3}{\sqrt{13}} \cdot \dfrac{2}{\sqrt{13}} \cdot \dfrac{12}{13} \)
\( = -\dfrac{25}{169} - \dfrac{144}{169} \)
\( \cos{x} = -1 \)
\( \arctan{x} \) fonksiyonu \( x \)'in pozitif değerlerinde pozitif, negatif değerlerinde negatif değer alır.
Soruda ters tanjantı alınan iki değer de pozitif olduğu için karşılık geldikleri açılar pozitiftir.
Buna göre \( x = \pi \) bulunur.
\( \arctan(\sqrt{5} - 2) + \arctan(\sqrt{5} + 2) \)
ifadesinin değerini bulunuz.
Çözümü Göster\( \arctan(\sqrt{5} - 2) = x \) diyelim.
\( \tan{x} = \sqrt{5} - 2 \) olur.
\( \arctan(\sqrt{5} + 2) = y \) diyelim.
\( \tan{y} = \sqrt{5} + 2 \) olur.
İki ifadenin çarpımını alalım.
\( \tan{x} \cdot \tan{y} = (\sqrt{5} - 2)(\sqrt{5} + 2) \)
\( = (\sqrt{5})^2 - 2^2 = 1 \)
\( \tan{x} \cdot \cot{x} = 1 \) olduğuna göre \( \tan{y} = \cot{x} \) olmalıdır.
\( \tan{y} = \cot(\frac{\pi}{2} - y) = \cot{x} \)
Buna göre \( x \) ve \( y \) tümler açılardır.
\( \arctan(\sqrt{5} - 2) + \arctan(\sqrt{5} + 2) = x + y \)
\( = \dfrac{\pi}{2} \) bulunur.