Ters Trigonometrik Fonksiyonların Grafikleri

Aşağıda altı ters trigonometrik fonksiyonun grafiği her fonksiyonun ana fonksiyonu ile birlikte verilmiştir. Her grafikte \( x \) ekseni ters trigonometrik fonksiyon için trigonometrik orana ve \( y \) ekseni radyan cinsinden açı ölçüsüne karşılık gelirken, ana fonksiyon için tam tersi durum söz konusudur.

Tüm ters fonksiyonlarda olduğu gibi, trigonometrik fonksiyonlarda da ana fonksiyon ve ters fonksiyonların grafikleri \( y = x \) doğrusuna göre simetriktir.

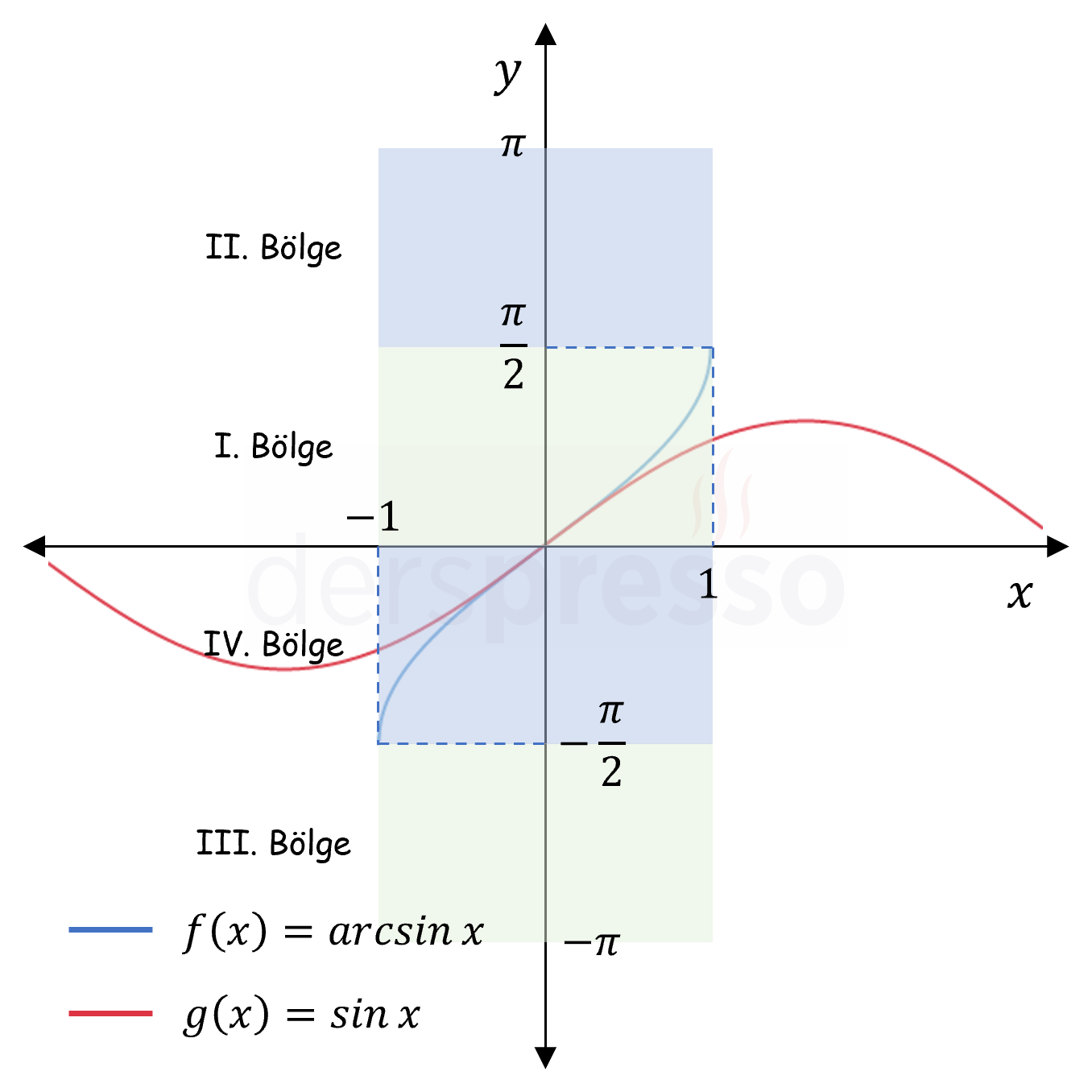
Arc Sinüs Fonksiyon Grafiği

Ters sinüs fonksiyonunun tanım ve görüntü kümesi ve grafiği aşağıdaki gibidir.

Fonksiyon	Tanım Kümesi	Görüntü Kümesi
\( \sin{x} \)	\( \mathbb{R} \)	\( [-1, 1] \)
\( \arcsin{x} \)	\( [-1, 1] \)	\( \left[ -\dfrac{\pi}{2}, \dfrac{\pi}{2} \right] \)

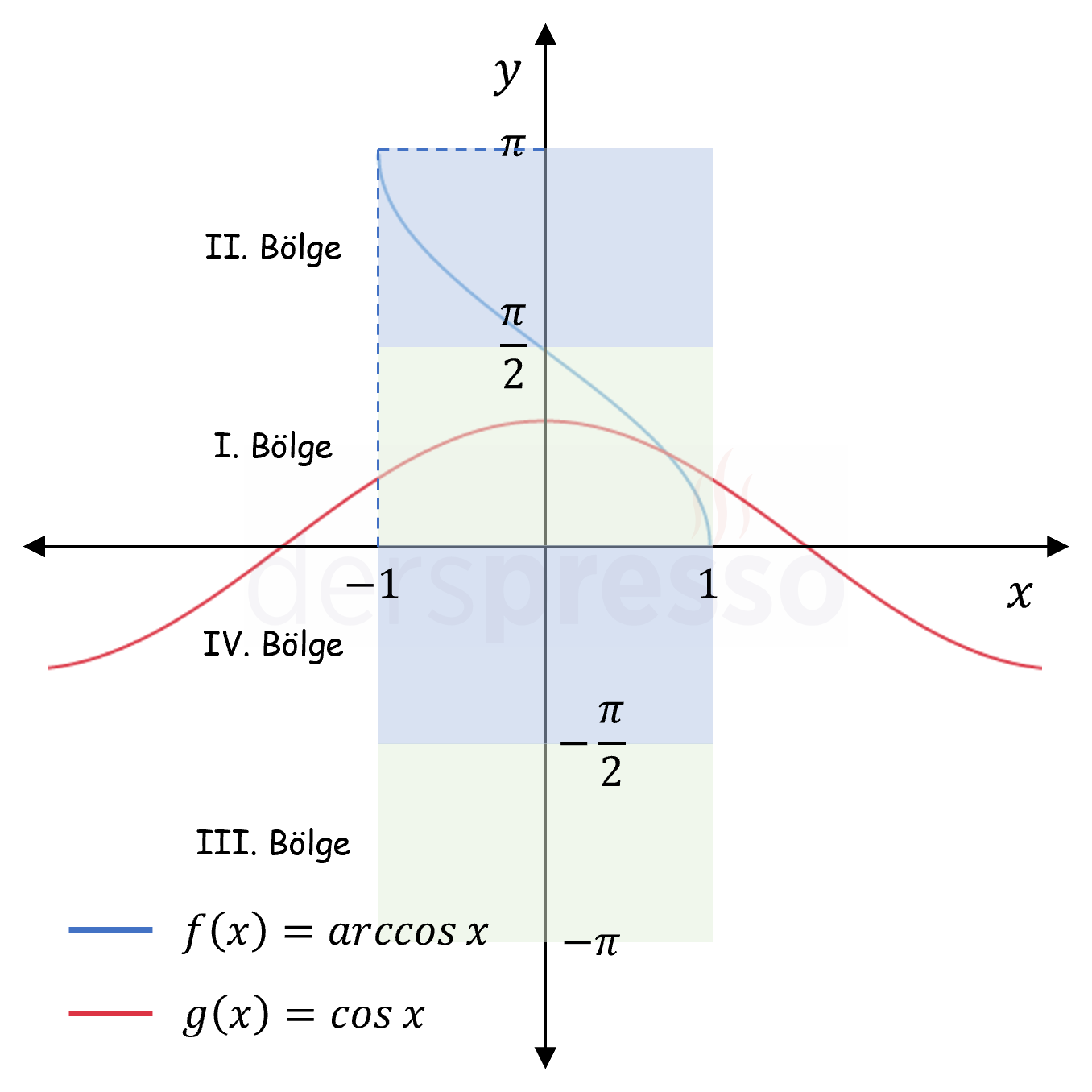
Arc Kosinüs Fonksiyon Grafiği

Ters kosinüs fonksiyonunun tanım ve görüntü kümesi ve grafiği aşağıdaki gibidir.

Fonksiyon	Tanım Kümesi	Görüntü Kümesi
\( \cos{x} \)	\( \mathbb{R} \)	\( [-1, 1] \)
\( \arccos{x} \)	\( [-1, 1] \)	\( [0, \pi] \)

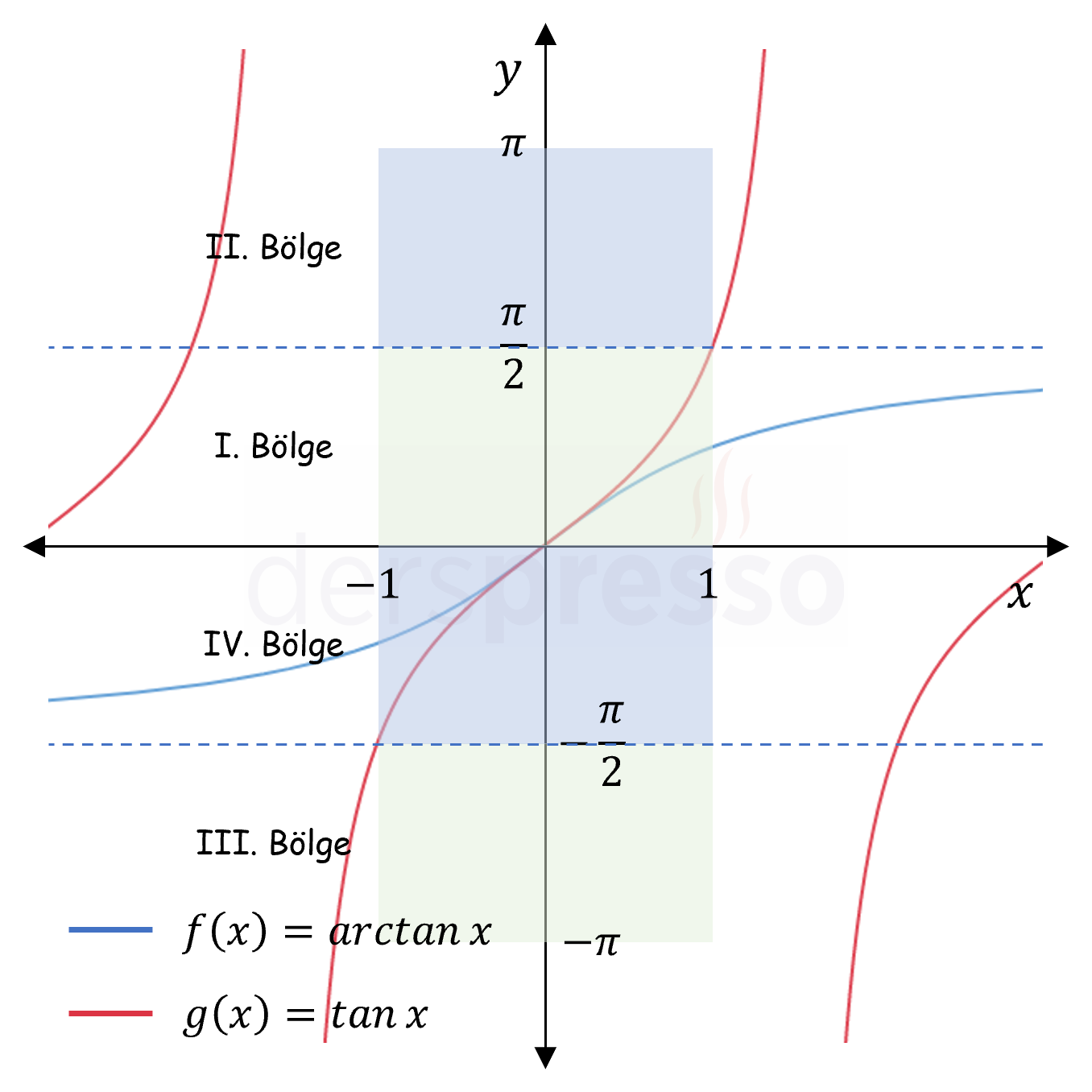
Arc Tanjant Fonksiyon Grafiği

Ters tanjant fonksiyonunun tanım ve görüntü kümesi ve grafiği aşağıdaki gibidir.

Fonksiyon	Tanım Kümesi	Görüntü Kümesi
\( \tan{x} \)	\( \mathbb{R} - \{ \frac{\pi}{2} + k\pi, k \in \mathbb{Z} \} \)	\( \mathbb{R} \)
\( \arctan{x} \)	\( \mathbb{R} \)	\( \left( -\dfrac{\pi}{2}, \dfrac{\pi}{2} \right) \)

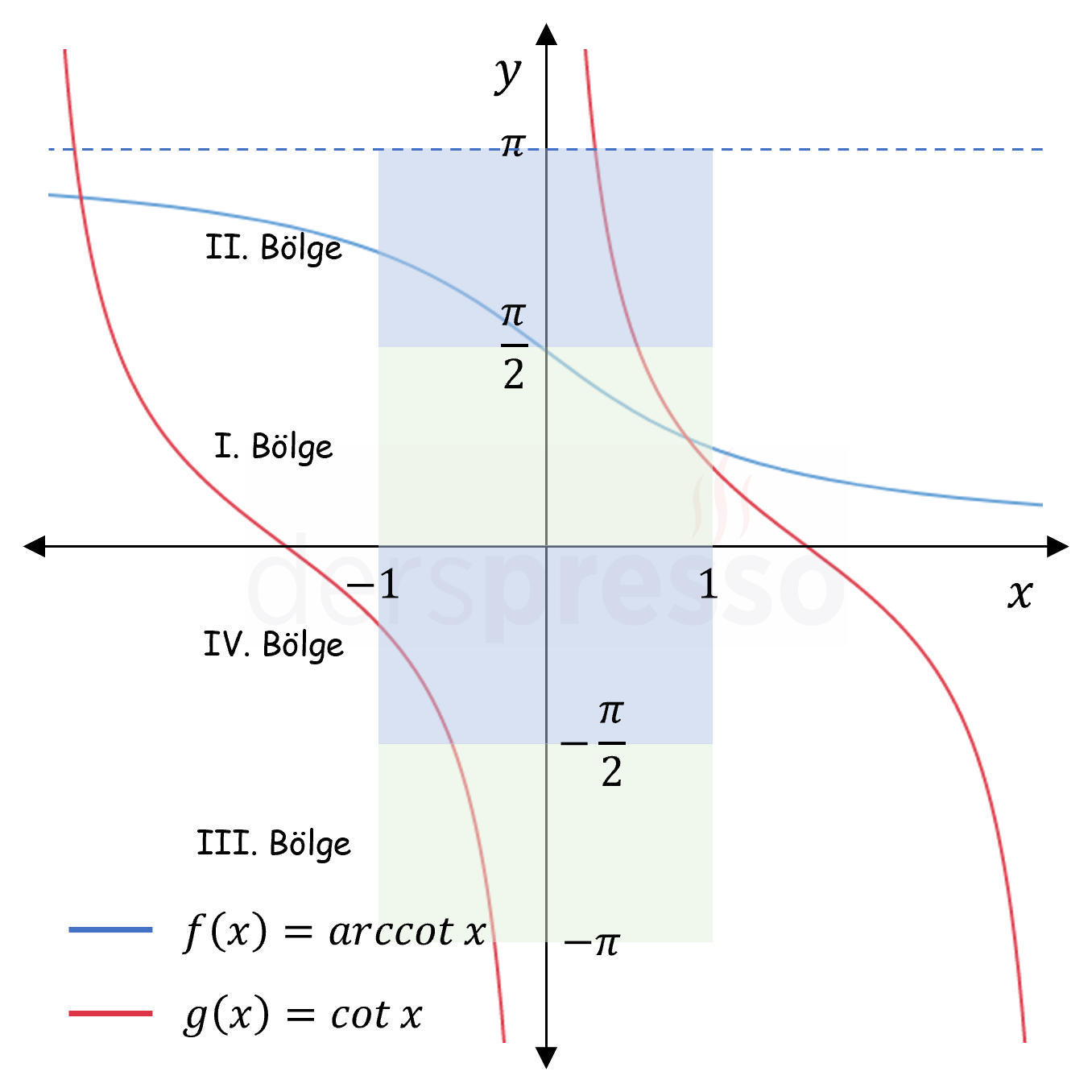
Arc Kotanjant Fonksiyon Grafiği

Ters kotanjant fonksiyonunun tanım ve görüntü kümesi ve grafiği aşağıdaki gibidir.

Fonksiyon	Tanım Kümesi	Görüntü Kümesi
\( \cot{x} \)	\( \mathbb{R} - \{ k\pi, k \in \mathbb{Z} \} \)	\( \mathbb{R} \)
\( \arccot{x} \)	\( \mathbb{R} \)	\( (0, \pi) \)

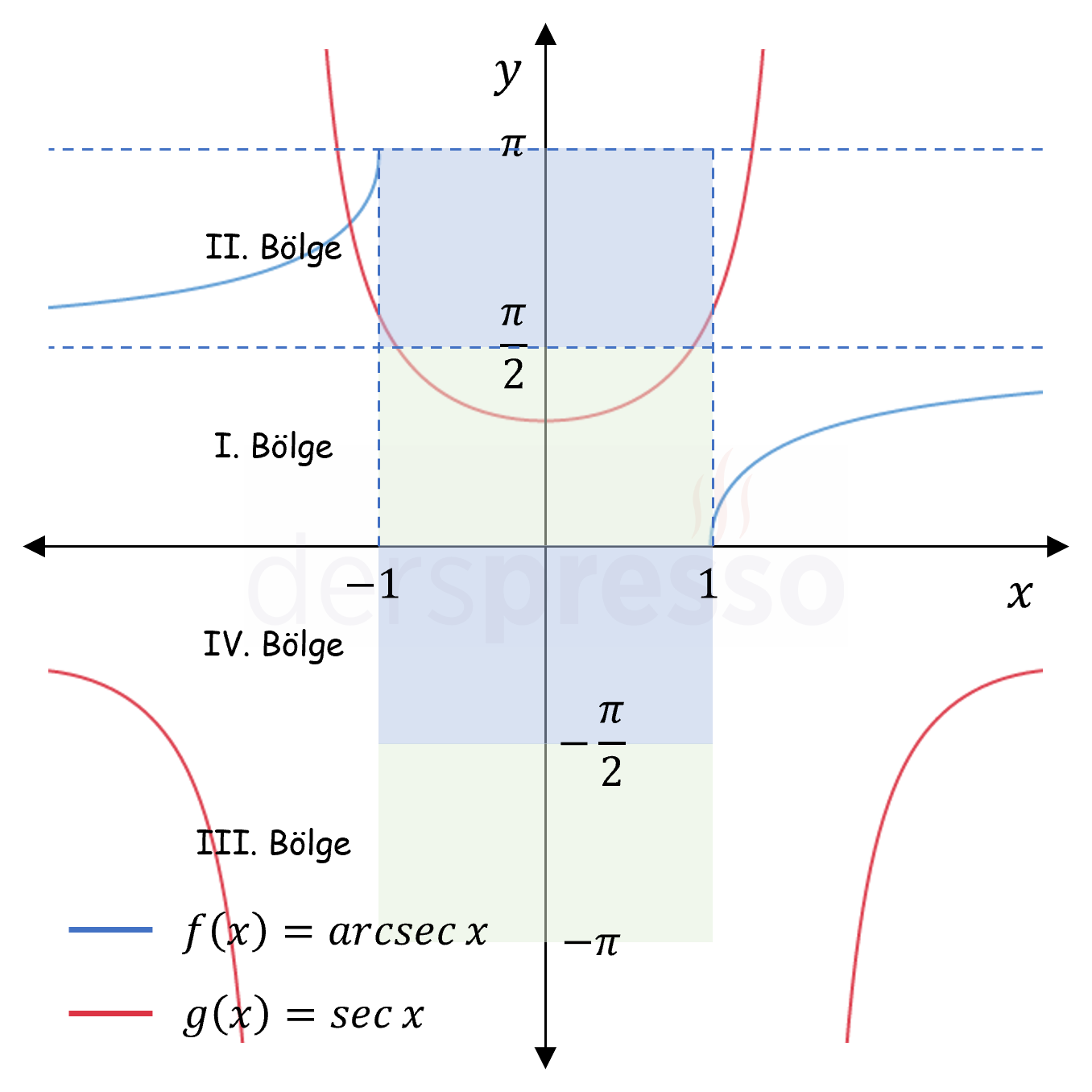
Arc Sekant Fonksiyon Grafiği

Ters sekant fonksiyonunun tanım ve görüntü kümesi ve grafiği aşağıdaki gibidir.

Fonksiyon	Tanım Kümesi	Görüntü Kümesi
\( \sec{x} \)	\( \mathbb{R} - \{ \frac{\pi}{2} + k\pi, k \in \mathbb{Z} \} \)	\( \mathbb{R} - (-1, 1) \)
\( \arcsec{x} \)	\( \mathbb{R} - (-1, 1) \)	\( [0, \pi] - \left\{ \dfrac{\pi}{2} \right\} \)

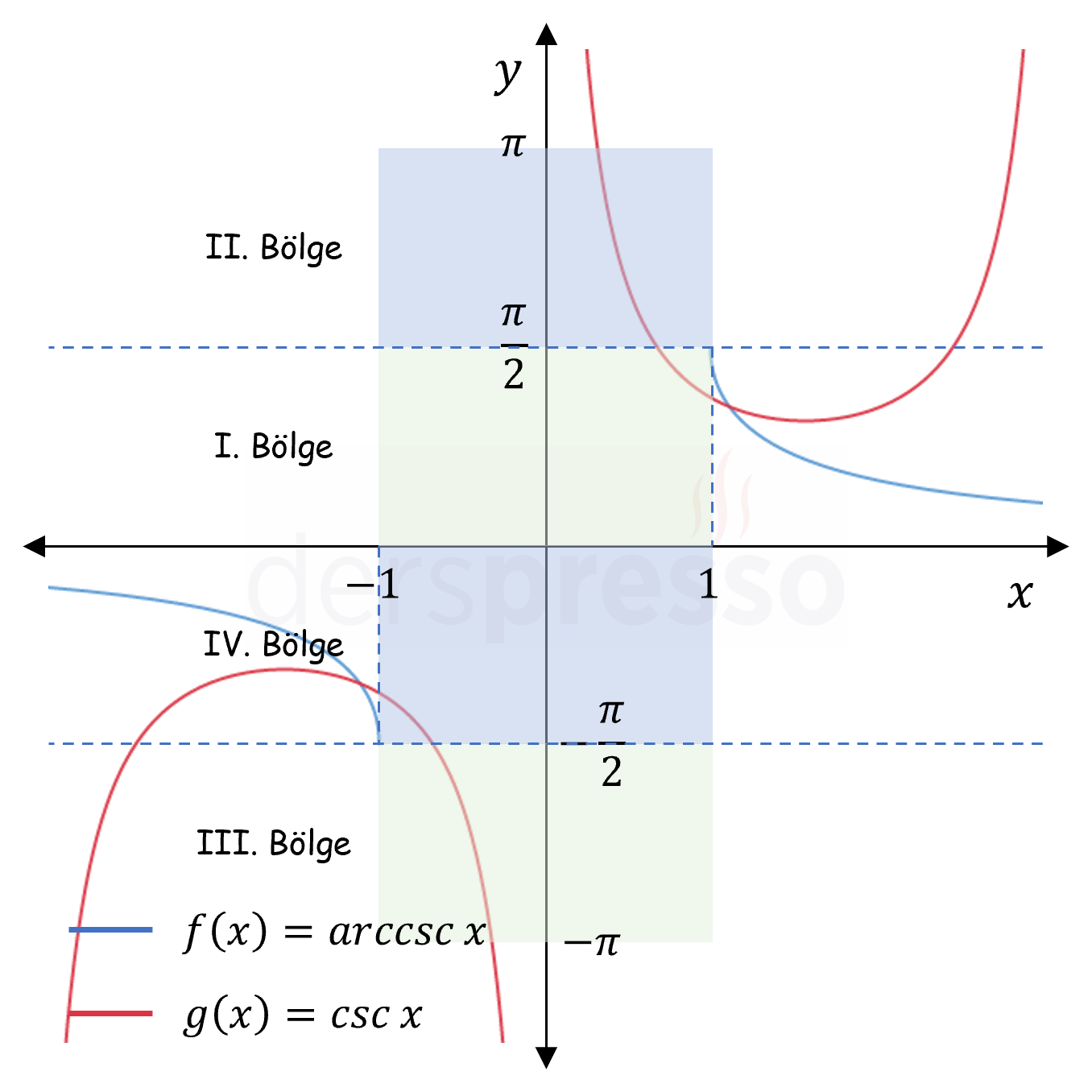
Arc Kosekant Fonksiyon Grafiği

Ters kosekant fonksiyonunun tanım ve görüntü kümesi ve grafiği aşağıdaki gibidir.

Fonksiyon	Tanım Kümesi	Görüntü Kümesi
\( \csc{x} \)	\( \mathbb{R} - \{ k\pi, k \in \mathbb{Z} \} \)	\( \mathbb{R} - (-1, 1) \)
\( \arccsc{x} \)	\( \mathbb{R} - (-1, 1) \)	\( \left[ -\dfrac{\pi}{2}, \dfrac{\pi}{2} \right] - \{ 0 \} \)