Özdeş Nesnelerin Özdeş Kutulara Dağıtımı
Bu problem tipinde amaç özdeş \( n \) nesnenin özdeş \( k \) kutuya dağıtım sayısını hesaplamaktır. Nesneler ve kutular özdeş olduğu için iki özdeş kutudaki iki nesnenin aralarında yer değiştirmesi yeni bir dağıtım oluşturmaz.
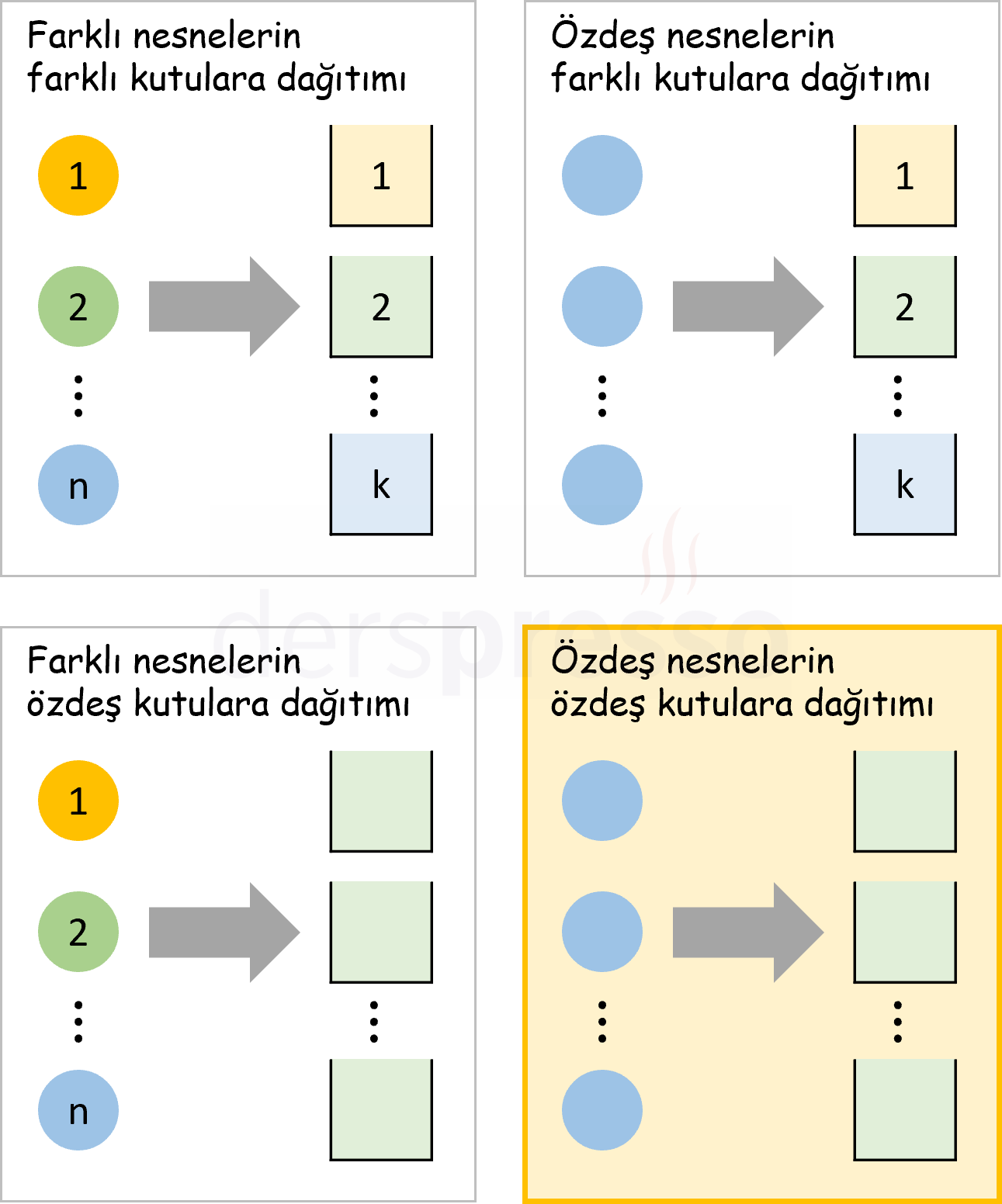
Bu problem tipini her kutuya dağıtılabilecek nesne sayısına göre dört başlık altında inceleyebiliriz.
Her Kutuda Herhangi Bir Sayıda Nesne
Bu problem tipinde nesneler kutulara herhangi bir koşul olmaksızın dağıtılır (bazı kutular boş kalabilir ya da bir kutuya birden fazla nesne konabilir).
\( n \) özdeş nesnenin \( k \) özdeş kutuya herhangi bir koşul olmaksızın farklı dağıtım sayısı \( = \displaystyle\sum_{i = 1}^{k} p_i(n) \)
Özdeş nesnelerin \( k \) özdeş kutuya dağıtımını bir tam sayının \( k \) parçaya parçalanış problemi olarak düşünebiliriz. Bu problem tipinde bazı kutular boş kalabildiği için farklı dağıtım sayısı sadece \( k \) parçaya parçalanışları değil, \( 1, 2, \ldots, k - 1 \) parçaya parçalanışları da içerir.
Önceki bölümlerde gördüğümüz üzere, \( n \) tam sayısının boş olmayan \( k \) parçaya parçalanışı tam sayı parçalanışı ile hesaplanır ve \( p_k(n) \) ile gösterilir. Buna göre bir tam sayının \( 1, 2, \ldots, k \) parçaya parçalanış sayılarının toplamı aşağıdaki gibi olur.
\( p_1(n) + p_2(n) + \ldots + p_k(n) \) \( = \displaystyle\sum_{i = 1}^{k} p_i(n) \)
Her Kutuda En Fazla Bir Nesne
Bu problem tipinde nesneler kutulara her kutuda en fazla bir nesne olacak şekilde dağıtılır. Her kutuda en fazla bir nesne olabileceği için, bu problemlerde \( n \le k \) koşulunun sağlanması gerekir (nesne sayısı kutu sayısından fazla olamaz), aksi takdirde farklı dağıtım sayısı 0 olur.
\( n \le k \) olmak üzere,
\( n \) özdeş nesnenin \( k \) özdeş kutuya her kutuda en fazla bir nesne olacak şekilde farklı dağıtım sayısı \( = 1 \)
Bu problem tipinde iki özdeş kutudaki birer özdeş nesne kutular arasında yer değiştirirse ya da bir kutudaki nesne boş özdeş bir kutuya aktarılırsa yeni bir dağıtım oluşmaz. Bu yüzden nesneler kutulara tek bir şekilde dağıtılabilir.
Her Kutuda En Az Bir Nesne
Bu problem tipinde nesneler kutulara her kutuda en az bir nesne olacak şekilde dağıtılır. Her kutuda en az bir nesne olabileceği için, bu problemlerde \( n \ge k \) koşulunun sağlanması gerekir (nesne sayısı kutu sayısından az olamaz), aksi takdirde farklı dağıtım sayısı 0 olur.
\( n \ge k \) olmak üzere,
\( n \) özdeş nesnenin \( k \) özdeş kutuya her kutuda en az bir nesne olacak şekilde dağıtım sayısı \( = p_k(n) \)
Özdeş nesnelerin \( k \) özdeş kutuya dağıtımını bir tam sayının \( k \) parçaya parçalanış problemi olarak düşünebiliriz. Önceki bölümlerde gördüğümüz üzere, \( n \) tam sayısının boş olmayan \( k \) parçaya parçalanışı tam sayı parçalanışı ile hesaplanır ve \( p_k(n) \) ile gösterilir.
9 özdeş kayısı 3 saklama poşetine her poşette en az bir kayısı olmak koşuluyla kaç farklı şekilde konabilir?
Çözümü GösterHer Kutuda Tek Bir Nesne
Bu problem tipinde nesneler kutulara her kutuda sadece bir nesne olacak şekilde dağıtılır. Her kutuda sadece bir nesne olabileceği için, bu problemlerde \( n = k \) koşulunun sağlanması gerekir (nesne sayısı kutu sayısına eşit olmalıdır), aksi takdirde farklı dağıtım sayısı 0 olur.
\( n = k \) olmak üzere,
\( n \) özdeş nesnenin \( k \) özdeş kutuya her kutuda tek bir nesne olacak şekilde dağıtım sayısı \( = 1 \)
Bu problem tipinde iki özdeş kutudaki birer özdeş nesne kutular arasında yer değiştirirse yeni bir dağıtım oluşmaz. Bu yüzden nesneler kutulara tek bir şekilde dağıtılabilir.