Permütasyon Tanımı
Bir \( A \) kümesinin elemanlarının bir sıra gözetilerek farklı dizilişlerinin her birine \( A \) kümesinin bir permütasyonu denir. Permütasyonda elemanların diziliş sırası önemlidir, yani aynı elemanların her farklı dizilişi yeni bir permütasyon oluşturur.
\( n \) elemanlı \( A \) kümesinin permütasyonlarının sayısı \( n! \) formülü ile hesaplanır.
\( A = \{ a_1, a_2, \ldots, a_n \} \) olmak üzere,
Permütasyon sayısı \( = n! \)
\( A = \{a, b, c\} \) olmak üzere,
Permütasyon sayısı \( = 3! = 6 \)
\( A \) kümesinin permütasyonları:
abc, acb, bac, bca, cab, cba
İSPATI GÖSTER
Permütasyon sayısı çarpma yoluyla sayma yöntemi ile türetilebilir.
\( A \) kümesinin permütasyonlarını (farklı dizilişlerini) kümenin \( n \) elemanını \( n \) kutuya dağıtarak oluşturalım.
- \( n \) elemandan herhangi biri 1. kutuya yerleştirilir.
- Kalan \( n - 1 \) elemandan herhangi biri 2. kutuya yerleştirilir.
- Kalan \( n - 2 \) elemandan herhangi biri 3. kutuya yerleştirilir.
- Bu şekilde sağa doğru ilerledikçe kalan \( n - k + 1 \) elemandan herhangi biri \( k \). kutuya yerleştirilir.
- En son kalan \( 2 \) eleman \( (n - 1) \). kutuya yerleştirilir.
- En son kalan \( 1 \) eleman \( n \). kutuya yerleştirilir.

Her kutuya mutlaka bir eleman yerleştirildiği için, her kutudaki seçenek sayılarının çarpımı toplam farklı diziliş sayısını verir.
\( n \cdot (n - 1) \cdot (n - 2) \ldots 2 \cdot 1 = n! \)
Küme tanımı gereği bir eleman bir kümede yalnız bir kez bulunabildiği için belirli bir permütasyonda da sadece bir kez yer alabilir, dolayısıyla aşağıdaki dizilişler \( A \) kümesinin birer permütasyonu değildir.
\( A = \{a, b, c\} \) olmak üzere,
\( A \) kümesinin permütasyonu olmayan dizilişler:
aab, bbb, cac
Bununla birlikte, önümüzdeki bölümlerde inceleyeceğimiz çoklu kümelerde (tekrarlı) permütasyonda kümeler belirli elemanları birden fazla kez içerebilirler ve bu kümelerin permütasyonlarında bu elemanlar çoklu kümede bulundukları sayıda bir dizilişte yer alabilirler.
\( A = \{a, a, b\} \) bir çoklu küme olmak üzere,
\( A \) çoklu kümesinin (tekrarlı) permütasyonları:
aab, aba, baa
r'li Permütasyon
\( n \) elemanlı bir \( A \) kümesinin \( r \) sayıda elemanının bir sıra gözetilerek farklı dizilişlerinin her birine \( A \) kümesinin \( r \)'li permütasyonu denir.
\( n \) elemanlı bir \( A \) kümesinin \( r \)'li permütasyonu \( P(n, r) \) ile gösterilir ve aşağıdaki formülle hesaplanır.
\( n, r \in \mathbb{N}, \quad r \le n \) olmak üzere,
\( P(n, r) = \dfrac{n!}{(n - r)!} \)
\( A = \{ a, b, c, d \} \) olmak üzere,
\( A \) kümesinin 1'li permütasyonları:
\( P(4, 1) = \dfrac{4!}{(4 - 1)!} = 4 \)
a, b, c, d
\( A \) kümesinin 2'li permütasyonları:
\( P(4, 2) = \dfrac{4!}{(4 - 2)!} = 12 \)
ab, ac, ad, ba, bc, bd, ca, cb, cd, da, db, dc
\( A \) kümesinin 3'lü permütasyonları:
\( P(4, 3) = \dfrac{4!}{(4 - 3)!} = 24 \)
abc, acb, bac, bca, cab, cba, abd, adb, bad, bda, dab, dba, acd, adc, cad, cda, dac, dca, bcd, bdc, cbd, cdb, dbc, dcb
İSPATI GÖSTER
\( r \)'li permütasyon sayısı çarpma yoluyla sayma yöntemi ile türetilebilir.
\( A \) kümesinin \( r \)'li permütasyonlarını (farklı dizilişlerini) kümenin \( n \) elemanını \( r \) kutuya dağıtarak oluşturalım.
- \( n \) elemandan herhangi biri 1. kutuya yerleştirilir.
- Kalan \( n - 1 \) elemandan herhangi biri 2. kutuya yerleştirilir.
- Kalan \( n - 2 \) elemandan herhangi biri 3. kutuya yerleştirilir.
- Bu şekilde sağa doğru ilerledikçe kalan \( n - k + 1 \) elemandan herhangi biri \( k \). kutuya yerleştirilir.
- En son kalan \( n - r + 2 \) eleman \( (r - 1) \). kutuya yerleştirilir.
- En son kalan \( n - r + 1 \) eleman \( r \). kutuya yerleştirilir.

Her kutuya mutlaka bir eleman yerleştirildiği için, her kutudaki seçenek sayılarının çarpımı toplam farklı diziliş sayısını verir.
\( n \cdot (n - 1) \cdot (n - 2) \ldots (n - r + 2) \cdot (n - r + 1) = \dfrac{n!}{(n - r)!} \)
Pratik bir yöntem olarak, \( P(n, r) \) ifadesini hesaplamak için \( n \)'den başlayarak ve birer geriye giderek \( r \) sayının çarpımı alınır.
\( P(n, r) = \underbrace{n(n - 1)(n - 2) \ldots(n - r + 1)}_\text{r adet} \)
\( P(5, 1) = 5 \)
\( P(5, 2) = 5 \cdot 4 \)
\( P(5, 3) = 5 \cdot 4 \cdot 3 \)
\( P(5, 4) = 5 \cdot 4 \cdot 3 \cdot 2 \)
\( P(5, 5) = 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1 = 5! \)
\( n \) elemanlı bir kümenin \( n \)'li ve \( r \)'li permütasyonları arasındaki matematiksel ilişkiyi aşağıdaki şekilde ifade edebiliriz.
\( P(n, n) = P(n, r) \cdot (n - r)! \)
\( n! = \dfrac{n!}{(n - r)!} \cdot (n - r)! \)
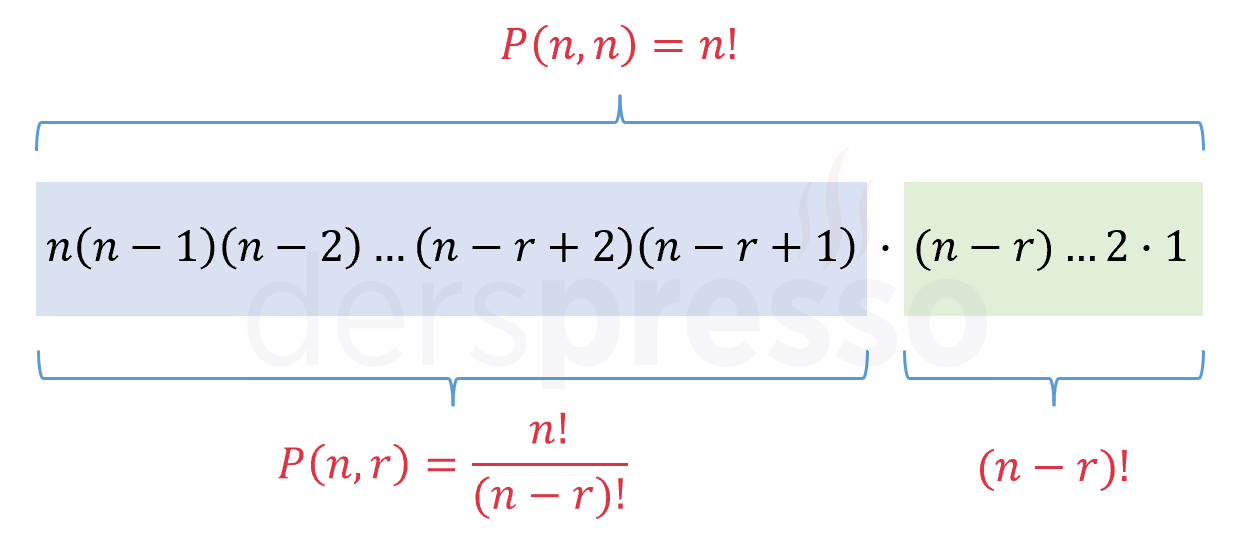
Permütasyon İşlem Kuralları
Hatırlatma olarak, 0 ve 1'in faktöriyel değerleri 1'dir.
\( 0! = 1! = 1 \)
\( r \)'li permütasyon formülünde \( r = n \) konduğunda permütasyon formülü elde edilir.
\( P(n, n) = \dfrac{n!}{(n - n)!} = n! \)
\( n \) elemanlı bir kümenin \( (n - 1) \)'li ve \( n \)'li permütasyon sayıları birbirine eşittir. Mantıksal bir açıklama olarak, bir kümenin her \( n - 1 \)'li permütasyonunun sonuna permütasyonda bulunmayan 1 eleman tek bir şekilde eklenebileceği için, \( n - 1 \)'li permütasyon ve \( n \)'li permütasyon sayıları birbirine eşit olur.
\( P(n, n - 1) = P(n, n) \)
\( P(5, 5) = 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1 = 5! \)
\( P(5, 4) = 5 \cdot 4 \cdot 3 \cdot 2 = 5! \)
İSPATI GÖSTER
\( P(n, n - 1) = \dfrac{n!}{(n - (n - 1))!} \)
\( = \dfrac{n!}{1!} = n! \)
\( = P(n, n) \)
\( n \) elemanlı bir kümenin 1'li permütasyonlarının sayısı \( n \)'dir ve bu permütasyonların her biri kümenin bir elemanından oluşur.
\( P(n, 1) = n \)
\( A = \{ 1, 2, 3, 4 \} \) olmak üzere,
\( P(4, 1) = \dfrac{4!}{(4 - 1)!} = 4 \)
\( A \) kümesinin 1'li permütasyonları:
1, 2, 3, 4
İSPATI GÖSTER
\( n \) elemanlı bir kümenin 0'lı permütasyonlarının sayısı 1'dir ve bu permütasyon boş kümedir.
\( P(n, 0) = 1 \)
\( A = \{ 1, 2, 3, 4 \} \) olmak üzere,
\( P(4, 0) = \dfrac{4!}{(4 - 0)!} = 1 \)
\( A \) kümesinin 0'lı permütasyonu: \( \emptyset \)
İSPATI GÖSTER
\( \dfrac{P(4, 3) \cdot P(7, 1)}{P(3, 2) + P(8, 0)} \) işleminin sonucu kaçtır?
Çözümü Göster\( P(n, r) = \dfrac{n!}{(n - r)!} \)
Pratik bir yöntem olarak, \( P(n, r) \) ifadesini hesaplamak için \( n \)'den başlayarak ve birer geriye giderek \( r \) sayının çarpımı alınır.
İfadedeki permütasyon işlemlerini yapalım.
\( P(4, 3) = 4 \cdot 3 \cdot 2 = 24 \)
\( P(7, 1) = 7 \)
\( P(3, 2) = 3 \cdot 2 = 6 \)
\( P(8, 0) = \dfrac{8!}{(8 - 0)!} = 1 \)
\( \dfrac{P(4, 3) \cdot P(7, 1)}{P(3, 2) + P(8, 0)} = \dfrac{24 \cdot 7}{6 + 1} \)
\( = 24 \) bulunur.
\( n \in \mathbb{N} \) olmak üzere,
\( P(7, n - 4) \) işleminin sonucunu en büyük yapan \( n \) değerlerinin toplamı kaçtır?
Çözümü GösterPermütasyon ifadesinin açılımını yazalım.
\( P(7, n - 4) = \dfrac{7!}{(7 - (n - 4))!} = \dfrac{7!}{(11 - n)!} \)
Bu kesirli ifadenin en büyük değerini alması için paydadaki \( (11 - n)! \) ifadesi en küçük değerini almalıdır.
Faktöriyel ifadesi en küçük değerini iki şekilde alır.
\( 0! = 1! = 1 \)
Her iki durum için \( n \) değerini bulalım.
\( (11 - n)! = 0! \Longrightarrow n = 11 \)
\( (11 - n)! = 1! \Longrightarrow n = 10 \)
Bu değerlerin toplamı \( 11 + 10 = 21 \) olarak bulunur.
\( P(n + 1, 4) = 9P(n,3) \) olduğuna göre, \( n \) kaçtır?
Çözümü Göster\( P(n, r) = \dfrac{n!}{(n - r)!} \)
Pratik bir yöntem olarak, \( P(n, r) \) ifadesini hesaplamak için \( n \)'den başlayarak ve birer geriye giderek \( r \) sayının çarpımı alınır.
Bu yöntem ile eşitlikteki permütasyon ifadelerinin açılımını yazalım.
\( (n + 1)n(n - 1)(n - 2) = 9n(n - 1)(n - 2) \)
Eşitliğin iki tarafındaki ortak çarpanları sadeleştirelim.
\( n + 1 = 9 \)
\( n = 8 \) bulunur.
\( P(n + 2, 3) = 4P(n, 2) + 18P(n, 1) \) ise \( n \) kaçtır?
Çözümü Göster\( P(n, r) = \dfrac{n!}{(n - r)!} \)
Pratik bir yöntem olarak, \( P(n, r) \) ifadesini hesaplamak için \( n \)'den başlayarak ve birer geriye giderek \( r \) sayının çarpımı alınır.
Bu yöntem ile eşitlikteki permütasyon ifadelerinin açılımını yazalım.
\( (n + 2)(n + 1)n = 4n(n - 1) + 18n \)
\( (n + 2)(n + 1)n = n(4n + 14) \)
\( (n + 2)(n + 1) = 4n + 14 \)
\( n^2 + 3n + 2 = 4n + 14 \)
\( n^2 - n - 12 = 0 \)
\( (n + 3)(n - 4) = 0 \)
\( n = -3 \) veya \( n = 4 \)
Permütasyon içindeki sayı negatif olamayacağı için \( n = 4 \) olur.
\( a \gt b \) olmak üzere, \( a \) ve \( b \) pozitif ardışık tek sayılardır.
\( P(a, b) = 36b! \) olduğuna göre, \( a + b \) toplamı kaçtır?
Çözümü Göster\( P(a, b) = \dfrac{a!}{(a - b)!} \)
\( \dfrac{a!}{(a - b)!} = 36b! \)
\( a \) ve \( b \) ardışık tek sayılar ve \( a \gt b \) olduğuna göre, \( a = b + 2 \) yazabiliriz.
\( \dfrac{(b + 2)!}{(b + 2 - b)!} = 36b! \)
\( \dfrac{(b + 2)!}{2!} = 36b! \)
\( (b + 2)! = 72b! \)
\( (b + 2)(b + 1)b! = 72b! \)
\( (b + 2)(b + 1) = 72 \)
Çarpımları 72 olan pozitif ardışık tam sayılar 8 ve 9'dur.
\( b + 2 = 9, \quad b = 7 \)
\( a = 7 + 2 = 9 \)
\( a + b = 9 + 7 = 16 \) bulunur.
\( n \gt 3 \) olmak üzere,
\( P(n + 3, n - 3) = 56 \) olduğuna göre, \( n \) kaçtır?
Çözümü Göster\( P(n, r) = \dfrac{n!}{(n - r)!} \)
\( P(n + 3, n - 3) = \dfrac{(n + 3)!}{(n + 3 - (n - 3))!} \)
\( = \dfrac{(n + 3)!}{6!} \)
Soruda verilen eşitliğin sağ tarafındaki 56 sayısını ardışık iki sayının çarpımı şeklinde yazalım.
\( 8 \cdot 7 = 56 \)
\( \dfrac{(n + 3)!}{6!} = 8 \cdot 7\)
\( (n + 3)! = 8 \cdot 7 \cdot 6! \)
\( (n + 3)! = 8! \)
\( n + 3 = 8 \)
\( n = 5 \) bulunur.
\( A \) kümesinin 5'li permütasyonlarının sayısı 2'li permütasyonlarının sayısının 60 katına eşit olduğuna göre, \( A \) kümesinin eleman sayısı kaçtır?
Çözümü Göster\( A \) kümesinin eleman sayısına \( n \) diyelim.
\( A \) kümesinin 5'li permütasyonları \( P(n, 5) \), 2'li permütasyonları \( P(n, 2) \) ile gösterilir.
Soruda verilen bilgiyi denklem şeklinde yazalım.
\( P(n, 5) = 60P(n, 2) \)
Permütasyon ifadelerinin açılımını yazalım.
\( \dfrac{n!}{(n - 5)!} = 60 \cdot \dfrac{n!}{(n - 2)!} \)
\( \dfrac{(n - 2)!}{(n - 5)!} = 60 \)
\( \dfrac{(n - 2)(n - 3)(n - 4)(n - 5)!}{(n - 5)!} = 60 \)
\( (n - 2)(n - 3)(n - 4) = 60 \)
Çarpımları 60 olan ardışık tam sayılar 3, 4 ve 5'tir.
Eşitliğin sol tarafındaki çarpanlardan en büyüğü \( n - 2 \) olur.
\( n - 2 = 5 \)
\( n = 7 \) bulunur.
\( P(17, m) = 16^3 - 16 \) olduğuna göre, \( m \) kaçtır?
Çözümü Göster\( P(n, r) = \dfrac{n!}{(n - r)!} \)
Pratik bir yöntem olarak, \( P(n, r) \) ifadesini hesaplamak için \( n \)'den başlayarak ve birer geriye giderek \( r \) sayının çarpımı alınır.
Bu yöntem ile eşitlikteki permütasyon ifadelerinin açılımını yazalım.
\( \underbrace{17 \cdot 16 \cdot \ldots \cdot (17 - m + 1)}_{m} = 16(16 - 1)(16 + 1) \)
\( 17 \cdot 16 \cdot \ldots \cdot (17 - m + 1) = 17 \cdot 16 \cdot 15 \)
\( 17 - m + 1 = 15 \)
\( m = 3 \) bulunur.
\( P(n + 4, 2) + P(n + 2, n) = n^2 + 7n + 72 \)
olduğuna göre, \( n \) kaçtır?
Çözümü GösterEşitlikteki permütasyon ifadelerinin açılımını yazalım.
\( \dfrac{(n + 4)!}{(n + 4 - 2)!} + \dfrac{(n + 2)!}{(n + 2 - n)!} = n^2 + 7n + 72 \)
\( \dfrac{(n + 4)!}{(n + 2)!} + \dfrac{(n + 2)!}{2!} = n^2 + 7n + 72 \)
\( (n + 4)(n + 3) + \dfrac{(n + 2)!}{2} = n^2 + 7n + 72 \)
\( n^2 + 7n + 12 + \dfrac{(n + 2)!}{2} = n^2 + 7n + 72 \)
\( \dfrac{(n + 2)!}{2} = 60 \)
\( (n + 2)! = 120 \)
\( (n + 2)! = 5! \)
\( n = 3 \) bulunur.